Polymer microlenses for quantifying cell sheet mechanics

Abstract

Mechanical interactions between individual cells and their substrate have been studied extensively over the past decade; however, understanding how these interactions change as cells interact with neighboring cells in the development of a cell sheet, or early stage tissue, is less developed. We use a recently developed experimental technique for quantifying the mechanics of confluent cell sheets. Living cells are cultured on a thin film of polystyrene [PS], which is attached to a patterned substrate of crosslinked poly(dimethyl siloxane) [PDMS] microwells. As cells attach to the substrate and begin to form a sheet, they apply sufficient contractile force to buckle the PS film over individual microwells to form a microlens array. The curvature for each microlens is measured by confocal microscopy and can be related to the strain and stress applied by the cell sheet using simple mechanical analysis for the buckling of thin films. We demonstrate that this technique can provide insight into the important materials properties and length scales that govern cell sheet responses, especially the role of stiffness of the substrate. We show that intercellular forces can lead to significantly different behaviors than the ones observed for individual cells, where focal adhesion is the relevant parameter.

Introduction

As a cell adheres to a surface, its contractile nature^1,2 causes it to exert traction forces at its points of adhesion on a substrate.^2–5 These forces are generated by the binding of integrins to ligands in the extracellular matrix and the actomyosin cytoskeleton, generating traction forces at the sites of adhesion.⁶ At the single cell level, these forces have been studied extensively over the last several years by primarily using substrates with tractable mechanical properties, due to patterning and/or chemical modifications (e.g. crosslinking ratio).^7–9 With these methods, it has been shown that individual cells can induce traction forces on a surface on the order of 10 nN,^8–10 depending on the cell type but also to a certain extent on the properties of the substrate itself, especially its modulus and/or stiffness (which has also been shown to have an effect on growth,¹¹ adhesion¹¹ and migration of cells¹²).

Although extensive studies have been conducted on single cell mechanics, the mechanics of cell sheets, which is highly relevant in the tissue engineering field, have been relatively unexplored. For cell sheets, the mechanics are not only dictated by the focal adhesion traction forces but also by the forces transmitted by intercellular junctions to neighboring cells. Although the relative contributions from these two sources of cell forces have not been quantified systematically, recent results by Janmey et al.¹¹ and Trepat et al.¹³ suggest significant differences between the mechanics of single cells and those of cell sheets. Specifically, Janmey et al. showed that individual cells and cell sheets respond differently to the substrate modulus, suggesting that focal adhesion and intercellular junctions are independent and in some way antagonist mechanisms, with probably different length scale and different range of forces. Their qualitative observations indicate that cell sheet morphology is independent of substrate modulus, suggesting that intercellular junction strength dominates the forces transmitted through focal adhesion sites. In other words, a cell within a cell sheet is more sensitive to its neighbors than to the substrate in which it is attached.

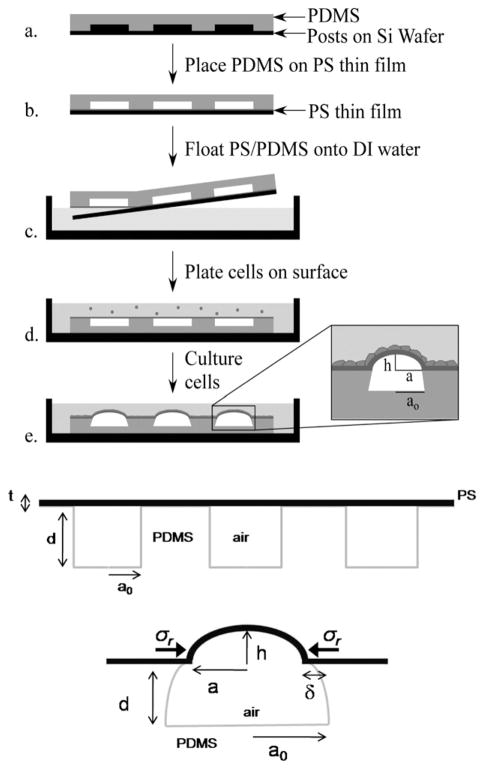
To quantitatively study the relative strength of intercellular junctions and focal adhesions, patterned substrates made with microsized posts, which have been used successfully for studying single cell mechanics, provide limited information as the measured response is local on the length scale of a post (1–2 μm).⁹ To overcome this limitation, Zimberlin et al. recently introduced an alternative strategy, which relies upon novel substrates that consist of a thin polystyrene (PS) film attached to a microwell patterned substrate of crosslinked polydimethylsiloxane (PDMS). This approach eliminates topographic effects in the early stages of cell growth and allows multiple length scales to be probed. In brief, upon cell culturing and attachment to the PS surface, the cell sheet exerts traction forces on the substrate. In the same way these forces lead to inward bending of PDMS microposts, they here bend inward the walls of the compliant PDMS wells (see Fig. 1). Because the thin PS film resists stretching, it accommodates the imposed deformation by bending, or buckling to form well-defined microlens arrays.¹⁴

Fig. 1.

Scheme of the fabrication of the microlenses substrates (top). Scheme of the substrate and definition of the parameters of the system (bottom).

From the height of the buckled microlenses, the strain exerted by the cell sheet can be determined:

$$\frac{h}{a_0}\approx \sqrt{2\epsilon }$$ (1)

in the small strain regime (as determined in previous work,¹⁴ ε is below 10⁻², in consequence the ε² term in the square root can be neglected), with h the height of the microlens, a₀ the initial radius of the microwell and ε the radial strain applied by the cells: $\epsilon =\frac{a_0-a}{a_0}=\frac{\delta }{a_0}$.

Using this approach, Zimberlin et al.¹⁴ showed that epithelial (LLC-Pk1) cell sheets apply nearly twice as much strain to the substrate compared to fibroblasts (NIH/3T3) cell sheets, in stark contrast to the relative strengths of these cell types at the single cell level. ^8,9 This behavior was directly attributed to the role of the intercellular junctions, which are present in greater density for the epithelial cell sheets.

Building upon the initial observations and conclusions of Zimberlin¹⁴ et al. and Jamney et al.,¹¹ in the present paper we investigate the role of substrate stiffness on the mechanical response of a cell sheet. Furthermore, we extend the quantitative analysis of microlens-based cell sheet measurements to quantify the stresses exerted by the cell sheet, thus providing the ability to quantitatively compare previous measurements of single cell forces to the forces exerted on the level of cell sheets. The knowledge gained by these and subsequent studies on cell sheets are critical for understanding early tissue formation from a mechanical point of view.

Material and methods

Fabrication of molds: Photolithography

SU-8 2100 negative thick photoresist (Microchem) was spun coat onto a silicon wafer at 500 rpm (acceleration 100 rpm/s) for 10 s, then at 1000 rpm (300 rpm/s) for 45s. The resist was then prebaked for 5 min at 65 °C and soft baked at 90 °C for 30 min. Subsequently it was exposed for 70 s (OAI 500W DUV, intensity = 20 mJ cm⁻²) with a mask of circles of varying radii from 40–400 μm. The resist was then postbaked for 15 min at 65 °C and 15 min at 90 °C and developed during 30 min in SU-8 developer (Microchem) to reveal arrays of posts. The feature height for these posts was close to 200 μm.

Fabrication of surfaces

Crosslinked poly(dimethyl siloxane) [PDMS] was prepared by mixing Dow Corning Sylgard 184 with catalyst (1: 20 ratio) and degassing for 15 min. The PDMS mixture was then poured onto the substrates prepared via photolithography and subsequently cured at 70 °C for three hours to produce a surface of holes upon separation. The PDMS modulus was measured by contact mechanics and is approximately 0.75 MPa. The depth of the wells was measured by optical microscopy and using an image analysis software (ImageJ).

Thin films of PS were prepared by spincoating a PS/toluene solution at 4000 rpm for 30 s on glass slides that had been UV-Ozone treated (Jelight UVO cleaner, 342) for 5 min. 2.5 mg mL⁻¹ of rubrene (Aldrich) was added to the PS/toluene solution to make the surface fluorescently active. The thickness of the dried polystyrene films was varied between 180 and 1600 nm by changing the concentration of the PS/toluene solution and measured with an interferometer (Filmetrics). The modulus, E, of the PS film was measured using SIEBIMM technique.¹⁵ A slightly low value, E ~ 2 GPa, compared to the bulk modulus, 3 GPa, was measured for each thickness and will be used in the following analysis.

The PDMS substrates were then placed hole-side down onto the PS films. The PS/PDMS pair was floated off in DI-water and placed onto glass bottom culture dishes (MatTek), PS face up. The substrates were then oxygen plasma treated (Harrick Plasma Cleaner, PDC-001) for 8 min to increase the hydrophilicity of the surface.

Cell culture and immunofluorescence

NIH/3T3 mouse fibroblasts were cultured in Dulbecco’s modified Eagle’s medium (DMEM) containing 10% calf serum and 1% P/S solution. LLC-Pk1 epithelial cells expressing GFP-actin were cultured as described previously.¹⁶ Microlens measurements were made once confluence was reached on the whole substrate, roughly 5 days after the cells were plated.

To localize cadherin, epithelial cells on the appropriate substrate were fixed in 3.7% formaldehyde for 10 min and treated with lysis buffer consisting of 0.5% Triton X-100, 80 mM piperazine-N,N′-bis(2-ethanesulfonic acid) pH 6.9, 1 mM MgSO₄, and 5 mM EGTA for 1 min and rinsed in calcium and magnesium free PBS (PBS−/−) containing 0.1% Tween and 0.02% sodium azide (PBS/Tw/Az). To localize α-actinin, cells were fixed in 0.25% glutaraldehyde, rinsed in PBS/Tw/Az and incubated in lysis buffer for 1 min. Cells were incubated in Rabbit anti-cadherin antibodies or Mouse α-actinin antibodies (Sigma-Aldrich, St. Louis, MO), prepared in PBS/Tw/Az containing 1% BSA, at a 1: 200 (cadherin) or 1: 500 (α-actinin) for 2 h at 37 °C or overnight at room temperature. Cells were rinsed extensively in PBS/Tw/Az and incubated in Cy3 labeled fluorescent secondary antibodies (Jackson ImmunoResearch Laboratories, West Grove, PA) at the dilution recommended by the manufacturer.

Measurement of microlens properties

The height of the microlenses was measured with confocal microscopy (Zeiss LSM 510 Meta Confocal System) by imaging the fluorescence of the doped PS fim (Fig. 2.c) and the GFP-actin in the case of the LLC-Pk1 cells. Excess media had been removed and a glass cover slip was placed over the system to facilitate imaging while inverted. Space between the coverslip and the top of the microlenses was fixed to ensure that the two surfaces were not touching. Culture medium filled the gap. Measurements were made using a 10x objective (4 μm resolution in z-space) and when the buckling height was lower than 10 μm, with a 25x objective (1 μm resolution in z-space).

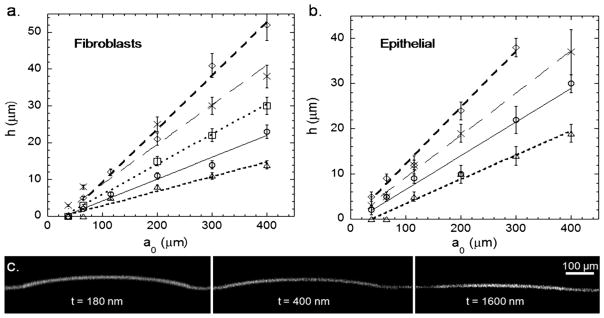
Fig. 2.

a. h versus a₀ for several thicknesses for fibroblasts (◇: 180 nm, x: 400 nm, □: 750 nm, ○: 1050 nm, △: 1600 nm) with the corresponding linear fits b. epithelial cells (data point for 750 nm are almost identical to those obtained with 400 nm films and were not included for clarity purpose), same symbols. c. Confocal images of rubrene-doped PS microlenses with same radii and different thicknesses for epithelial cells.

Results

We measured the height of the microlenses h for six a₀ (40, 70, 110, 200, 300 and 400 μm) at five different PS thicknesses (180 nm, 400 nm, 750 nm, 1050 nm and 1600 nm). For each thickness t of the PS film and for both fibroblasts and epithelial cells, h increased linearly with a₀. The slope of the curve dh/da₀ decreased with increasing thickness (Fig. 2.a. for fibroblasts, 2.b. for epithelial cells) and for the smaller radii. No buckling is observed for the thickest films and for the smallest values of a₀. The observation of no buckling indicates that the critical stress for buckling, which is strongly dependent on the thickness of the PS film (see below for details), is not achieved in these cases, or that the buckled deflections are smaller than the resolution of the confocal microscope ~ 1 micron.

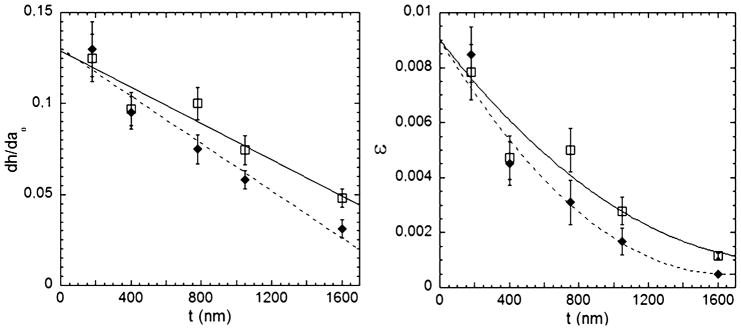
Plotting the slope of h vs. a₀ as a function of the thickness of the PS film for both cell types (Fig. 3a), a linear dependence is observed. The extrapolated value for zero thickness gives a value independent of cell type near 0.13 (0.129 for epithelial cells, 0.13 for fibroblasts); whereas, the slope value depends on the cell type (−0.5 nm⁻¹ for epithelial, −0.65 nm⁻¹ for fibroblasts).

Fig. 3.

a. dh/da₀ as a function of t for epithelial cells (□) and fibroblasts (◆). b. Strain exerted by the cells as a function of t (same symbols).

Using eqn (1), we plot the strain exerted by the cells for every thickness (Fig. 3b). For both cell types, the cell sheet strain increases with decreasing thickness of the PS film. Also, the strain applied by epithelial cells for PS thicknesses greater than 500 nm is larger than strains applied by fibroblasts.¹⁴

Using the linear dependence observed in Fig. 3a, and according to eqn (1), we fit the strain to a second-order polynomial to describe the dependence on thickness. These fitted trendlines help to clarify that the strains for both cell types converge at small thickness (Fig. 3b). It is important to note that by changing the well radius a₀, we are actually changing the “probe” with which we investigate the cell sheet. In other words, by studying the buckling of the circular plate defined by a₀ we mainly restrict our property measurements to cells that reside on the wells or in the immediate vicinity. As a rough estimate, for a₀ = 400 μm, the microlens is probing the behavior of ~1000 cells within the cell sheet, whereas this number drops to ~10 cells for a₀ ~ 40 μm. Interestingly, within the precision of our measurements, as long as buckling occurs, no significant changes are observed in the h vs. a₀ slopes. This suggests strongly that a small number of cells within the cell sheet still reflect the collective behavior of the cell sheet rather than the behavior of a single cell.¹¹

Discussion

In these experiments, the main result is that for both cell types the strain induced by a cell sheet attachment on the substrate decreases with increasing thickness of the PS film substrate. Although the y-intercept, or zero thickness limit of this trend, is approximately equal for both cell types, the slope differs and leads to different cell sheet strains as substrate thickness increases. These observations imply that the stresses exerted by cell sheets are changing as a function of the PS thickness, which is related to substrate stiffness. This data suggests that the intercellular junctions are playing an increasingly important role for thicker, stiffer substrates.¹⁴ To understand these observations further, we build upon classical models to quantify the cell sheet stresses as a function of the measured cell sheet strains.

The radial stress exerted by the cell sheet on the PS film can be quantified by applying a version of the Stoney’s equation,¹⁷ developed recently by Klein.¹⁸ Stoney’s equation predicts the residual stress in a thin film coated on a thick substrate as a function of the curvature of the bilayer, assuming the film thickness is much less than the substrate thickness. Applying this to our system, the cell sheet is the “film” and the PS is the substrate; therefore, the thickness assumption does not hold. To account for the thickness of the coated film, Klein modified Stoney’s equation such that:

$${\sigma }_{\mathit{film}}=\frac{{\text{E}}_s{t}_{s}C}{6(1-{\nu }_s)}\left(t_s/t_f\right)\left(\frac{1+\gamma {(t_s/t_f)}^3}{1+(t_s/t_f)}\right)\text{with}\gamma =\frac{{\text{E}}_{\text{f}}(1-{\nu }_s)}{{\text{E}}_{\text{s}}(1-{\nu }_f)}$$ (3)

where C is the curvature, E_i, v_i, and t_i respectively the Young’s modulus, the Poisson’s ratio and the thickness of the substrate (i = s) or the film (i = f).

Using AFM measurements, Janmey et al. have determined that the elastic moduli of NIH/3T3 cells are on the order of 10⁴ Pa. ¹⁹ This range was also observed using microrheology techniques on human airway smooth muscle (HASM) cells.²⁰ Thus, for the range of PS thickness used for our experiments, assuming that this range of moduli also apply for epithelial cells, we have in both cases γ (t_s/t_f) ≪ 1.

For this limit, eqn (3) can be estimated as:

$${\sigma }_{\mathit{cells}}\approx \frac{E_{PS}}{3(1-{\nu }_{PS})}\left(\frac{t^2}{{t_{\mathit{cells}}}^2+t_{\mathit{cells}}t}\right)\left(\frac{h}{a_0}\right)\left(\frac{t}{a_0}\right)$$ (4)

where C and the subscripts have been substituted to reflect our system.

In this equation, an unknown parameter is the thickness of the cell sheet t_cells. A cell sheet does not have a homogeneous thickness. Confocal images on single cells give thicknesses of about 5 microns near the nucleus of the cell, decreasing to values smaller than 1 micron at the edge of the cell, with values that can differ slightly from one cell type to the other.²¹ Accordingly, we approximate the “active” cell sheet thickness as 1 μm for determining the cell sheet stress, which is consistent with recent measurements of Féréol et al. who showed that the paxillin, one of the proteins responsible for cell’s attachment, aggregated in the 1 micron thick region at the edge of the cell.²²

Furthermore, this approximation can be confirmed by using the fact that the stress applied by the cell sheet must exceed the critical radial stress σ_c required to buckle a simply supported circular PS film^22,23:

$${\sigma }_{\mathit{cells}}\ge {\sigma }_c=\frac{{2.16}^2{\text{E}}_{\text{PS}}}{12(1-{\upsilon }_{{\text{PS}}^2})}{\left(\frac{t}{a_0}\right)}^2$$ (5)

Therefore, combining eqn (4) and (5), we determine that the largest effective thickness that satisfies all observation is t_cells ≈ 1 μm, consistent with measurements discussed above.

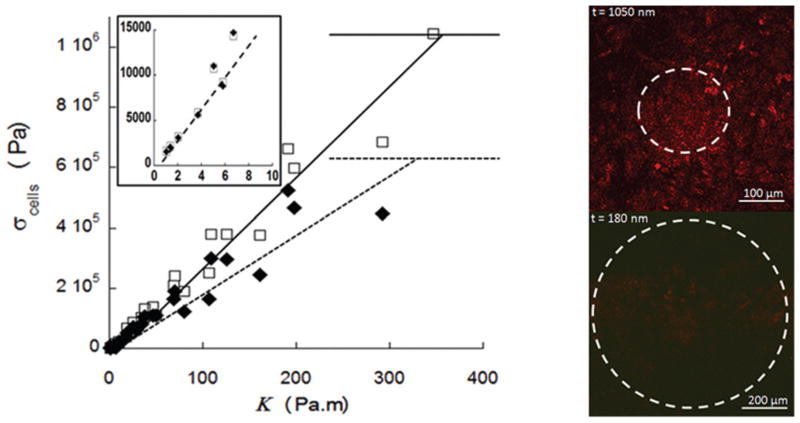
From eqn (4), we plot (Fig. 4) the stress of the cell sheet for both cell types as a function of the bending stiffness of the PS plate, estimated as:^23,24

Fig. 4.

a. Stresses applied by fibroblasts (◆) and epithelial cells (□) as a function of the bending stiffness of the PS plate and linear fits. Inset: Stresses applied by the monolayers as the function of stiffness in the low stiffness regime (same units and symbols). b. Immunostaining of cadherin for epithelial cells on substrates with stiffness of 150 Pa m (top) and 1 Pa m (bottom).

$$\kappa =2\pi {\text{E}}_{\text{PS}}\frac{t^2}{a_0}$$ (6)

Several lessons can be learned from this plot. First, it can be seen that for both cell types, the cell sheet exerts greater stresses as the stiffness of the substrate is increased, with a linear dependence. The magnitude of the stress ranges from 1 kPa to 1 MPa for stiffnesses ranging from 1 Pa m to 350 Pa m. Furthermore, three regimes can be distinguished. First, for low stiffnesses (1 < κ < 10 Pa m) epithelial cells and fibroblasts exert similar stresses (see Fig. 4 inset). It is important to note here that this regime corresponds to the smaller PS thicknesses studied where the measured values of dh/da₀ at a given t were almost identical for both cell types (see Fig. 3a). Using eqn (4) and comparing the two cell types at in this regime, this leads to extremely close (but not identical) values for stresses.

In the second regime (10 < κ < 350 Pa m), the cell sheet stress for both cell types increases strongly with the stiffness of the substrate, reaching values on the (100 kPa)−(1 MPa) range, with higher stresses for the epithelial cell sheet.

The third regime is at high stiffnesses (>350 Pa m) where no buckling is observed. Here, σ_cells ≤ σ_c, which leads to plateau values for the cell sheet stress near 1 MPa for epithelial cells and 0.6 MPa for fibroblasts.

To determine if cell sheets cultured on substrates of different stiffness show differences in cell-to-cell adhesions or cell to substrate adhesions, we stained cells for cadherin, a component of cell-to-cell adhesions or α-actinin, which localizes to cell-to-substrate adhesions (focal adhesions). Cadherin was present on cells grown on stiff substrates (Fig. 4b., top) but was greatly reduced when cells were cultured on softer substrates, e.g. below 10 Pa m (Fig. 4b., bottom). No difference in the pattern of α-actinin staining was detected. These observations suggest that substrate stiffness regulates the development of cellular adhesions and in consequence the stresses exerted by the cell sheet.

Based upon results on the influence of the substrate modulus,^9,11 the role of stiffness (rather than simply modulus) on the stress level exerted by the cells has to the best of our knowledge only been studied extensively by Ladoux and coworkers.²⁵ They have looked at several mechanical aspects of cells by looking at the deflection of functionalized PDMS micro-pillars on which cells are grown. Using micro-pillars with different radii and heights, i.e. varying the stiffness of the substrate from 0.001 to 0.2 Pa m, Ladoux and coworkers showed that the average force exerted by cells (3T3 fibroblasts and Madin–Darby Canine Kidney (MDCK) epithelial cells) per pillar increased with stiffness in the low stiffness regime. However, when the stiffness became higher than 0.1 Pa m, independent of the cell type, the average force reached a plateau. The average force plateau achieved by islands of epithelial cells is ~20 nN compared to ~10 nN for single cells (both epithelial and fibroblasts), though the maximal values reached were as high as 80 nN.

To compare the average force per pillar to stresses measured with our microlens approach, we account for the typical area for a focal adhesion site in Ladoux’s substrates by the area of a pillar and their hexagonal arrangements. The estimated average stress is on the order of 5 kPa for both single epithelial and fibroblasts. This result is consistent with the stresses ranging from 3 to 5.5 kPa reported by other researchers on various cell types, who have measured forces on substrates of a single stiffness.^26,7 Therefore, taking into account the discrepancy between different cell types or lines, it can be assumed that the typical stress due to focal adhesions for a single cell is within the range 1–10 kPa. For our measurements (Fig. 4), the range of stresses for cell sheets of NIH/3T3 fibroblasts and LLCPk1 epithelial cells is between 1 to 10³ kPa.

Comparing these results with our experiments, it is important to note the different range of stiffnesses probed by micro-pillars and microlens techniques. For micro-pillar experiments of Ladoux, κ ranged from 0.001 to 0.2 Pa m. For our microlens measurements, κ ranged from 1 to 350 Pa m. Thus, for the largest κ values from micro-pillar measurements and the smallest κ values for microlens measurements (first regime), we observe that both techniques yield similar stress values for both fibroblasts and epithelial cells. In this first regime, both cell types exert similar stresses, suggesting that the mechanical forces are dominated by focal adhesion junctions and not intercellular junctions, whose density varies significantly with the cell type.¹⁴ In consequence, the forces measured in the first regime compare with forces measured for single cells using the micro-pillar method.

Our microlens measurements further allow us to see that these force values increase for increasing stiffness and that the cell types exert significantly different levels of stress (second and third regime). To explain these observations, it is helpful to express the stress for a cell sheet as follows:

$${\sigma }_{\mathit{cells}}\approx \left(\frac{F_{\text{focal}}+F_{\text{intercellular}}}{f}\right)\rho$$ (7a)

where F_focal is the contribution due to the focal adhesions in a cell sheet, F_{intercellular} is the contribution due to the intercellular junctions, f the number of adhesion sites and ρ the areal density of adhesion sites. This simple expression makes the assumption that the forces can be decoupled.

Using the linear dependence of the stress with stiffness (Fig. 4), eqn (7a) can be rewritten as:

$$\frac{F_{\text{intercellualr}}}{f}\sim \frac{1}{m}\kappa \frac{\rho }{f}-\frac{F_{\text{focal}}}{f}$$ (7b)

where m is a constant, with the unit of a length, depending on the cell type (m_fibro ≈ 500 μm, m_eptih ≈ 350 μm, see Fig. 4).

This equation shows that the intercellular forces overcome the focal adhesion forces when a “critical” stiffness is reached. It also shows that these forces can be tuned by either changing the number (or density) of adhesion sites, or by changing κ, the substrate stiffness. This suggests that being able to control both the adhesion sites and the stiffness of substrates could be a powerful tool to gain more knowledge in the mechanics of cell sheets and especially to decouple the focal adhesion effects from the strength of the intercellular junctions.

Conclusions

In this paper, we have shown that microlens substrates are useful for quantifying not only the strain¹⁴ applied by a cell sheet as it attaches and grows but also the stress exerted by these cells. This technique provides a great tool to decouple the role of the intercellular junctions versus focal adhesions in cell sheet mechanics.

We have quantified the behavior of cell sheets of two cell types, fibroblast and epithelial, in terms of stresses exerted as they attach to a substrate. We have demonstrated that the collective behavior of a cell sheet differs strongly from previous measurements on single cells: in particular, cell sheets apply larger stresses than single cells on substrate of greater stiffness. This difference demonstrates the importance of the forces exerted by the intercellular junctions compared to ones by the focal adhesions in the early development in tissues. In summary, this technique will be useful for continuing to understand the complex coupling between forces transmitted via focal adhesion sites and those transmitted through intercellular junctions in cell sheets.