Abstract
The dynamic model for the growth of a bacterial population described by Baranyi and Roberts (J. Baranyi and T. A. Roberts, Int. J. Food Microbiol. 23:277-294, 1994) was applied to model the lag period and exponential growth of Listeria monocytogenes under conditions of fluctuating temperature and water activity (aw) values. To model the duration of the lag phase, the dependence of the parameter h0, which quantifies the amount of work done during the lag period, on the previous and current environmental conditions was determined experimentally. This parameter depended not only on the magnitude of the change between the previous and current environmental conditions but also on the current growth conditions. In an exponentially growing population, any change in the environment requiring a certain amount of work to adapt to the new conditions initiated a lag period that lasted until that work was finished. Observations for several scenarios in which exponential growth was halted by a sudden change in the temperature and/or aw were in good agreement with predictions. When a population already in a lag period was subjected to environmental fluctuations, the system was reset with a new lag phase. The work to be done during the new lag phase was estimated to be the workload due to the environmental change plus the unfinished workload from the uncompleted previous lag phase.
The bacterial life cycle includes symmetrical division at regular time intervals. The resulting exponential increase in the number of individuals may lead to food spoilage or infectious disease. The lag phase is a delay before exponential growth commences. Cells in lag phase do not divide. Previous work has shown that exponential growth can be predicted with a high degree of accuracy as a straightforward response to the current growth environment (2, 21, 25, 26, 29). Conversely, predictions of the duration of the lag phase as a function of the current growth conditions are usually highly inaccurate. Numerous studies have shown that such predictions are not accurate because the lag phase is influenced not only by the current growth environment but also by the history of the cells, including previous growth conditions, stresses, cell physiological states, etc. (1, 8, 9, 13, 17, 19, 22, 31).
Mechanistic modeling of the lag phase was first performed by Baranyi et al. (3, 4) and Hills et al. (15, 16). In the model of Baranyi et al., the lag period comprises the time required to overcome an initial hurdle (h0), which requires adaptation work. In the model of Hills et al. a lag time occurs because cell division is delayed until the cell biomass (or some essential cell component proportional to the biomass) increases and reaches the maximum value for a particular environment. Therefore, these models describe the duration of the lag period as the time required to carry out the work necessary for cells to get ready to divide. It has been shown that h0 is equal to the product of the exponential growth rate and the lag time when the rate at which the work is carried out is equal to the maximum specific growth rate (μmax) (3). Robinson et al. (28) studied the relationship between the duration of the lag phase and the growth rate. They found that there were not simple relationships for all environmental conditions, and they studied in detail the effects of several environmental factors on the relationship between the lag and growth rate. With the same purpose, Mellefont and Ross (20) defined the relative lag time (RLT) to quantify the effect of the environment on the work to be done and the rate at which that work is done during the lag phase. The RLT is the ratio of the lag time to the doubling time, and it is therefore proportional to h0; in fact, RLT = h0/ln(2). Numerous authors have described the dependence of h0 on the history of the inoculum (12, 23, 30).
Therefore, h0 is a well-understood and applied parameter in food microbiology that is used to measure a theoretical quantity of work that must be done before exponential growth occurs. Our goal was to study the dependence of this parameter on the previous and current environmental conditions in order to predict the duration of the lag period and the transitions from exponential phase to lag phase and vice versa under fluctuating environmental conditions.
MATERIALS AND METHODS
Strain and inoculum preparation.
Listeria monocytogenes F6861, isolated from cheese, was maintained at −80°C. Immediately before experiments, it was revitalized by growth in two consecutive subcultures in tryptone soya broth (TSB) (Oxoid/Unipath catalog no. CM129) at 37°C for 24 h.
Application of sudden temperature and aw downshifts to exponentially growing populations.
The effects of the previous and current temperature and water activity (aw) values on bacterial growth were measured by using viable plate counts (VPC) and optical density (OD) (Table 1). The aw was modified by adding NaCl to the medium. aw was calculated from the percentage of NaCl using the data of Resnik and Chirife (27), and the relationship is as follows:
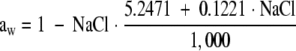 |
(1) |
Below we refer to aw and NaCl indistinctively.
TABLE 1.
Conditions under which growth was measured
| Previous temp (°C) | Previous NaCl concn (%) | Current temp (°C) | Current NaCl concn (%) | Current temp − previous temp (°C) | Current NaCl concn − previous NaCl concn (%) | Method(s)a |
|---|---|---|---|---|---|---|
| Decrease in temp at several temp and NaCl concn | ||||||
| 10 | 0.5 | 6 | 0.5 | −4 | 0 | VPC |
| 15 | 0.5 | 6 | 0.5 | −9 | 0 | VPC |
| 25 | 0.5 | 6 | 0.5 | −9 | 0 | VPC |
| 37 | 0.5 | 6 | 0.5 | −31 | 0 | VPC |
| 10 | 3 | 6 | 3 | −4 | 0 | VPC |
| 15 | 3 | 6 | 3 | −9 | 0 | VPC |
| 25 | 3 | 6 | 3 | −19 | 0 | VPC |
| 37 | 3 | 6 | 3 | −31 | 0 | VPC |
| 10 | 6 | 6 | 6 | −4 | 0 | VPC |
| 15 | 6 | 6 | 6 | −9 | 0 | VPC |
| 25 | 6 | 6 | 6 | −19 | 0 | VPC |
| 37 | 6 | 6 | 6 | −31 | 0 | VPC |
| 10 | 10 | 6 | 10 | −4 | 0 | VPC |
| 15 | 10 | 6 | 10 | −9 | 0 | VPC |
| 25 | 10 | 6 | 10 | −19 | 0 | VPC |
| 37 | 10 | 6 | 10 | −31 | 0 | VPC |
| 15 | 0.5 | 10 | 0.5 | −5 | 0 | VPC |
| 25 | 0.5 | 10 | 0.5 | −15 | 0 | VPC |
| 37 | 0.5 | 10 | 0.5 | −27 | 0 | VPC |
| 15 | 3 | 10 | 3 | −5 | 0 | VPC |
| 25 | 3 | 10 | 3 | −15 | 0 | VPC |
| 37 | 3 | 10 | 3 | −27 | 0 | VPC |
| 15 | 6 | 10 | 6 | −5 | 0 | VPC |
| 25 | 6 | 10 | 6 | −15 | 0 | VPC |
| 37 | 6 | 10 | 6 | −27 | 0 | VPC |
| 15 | 10 | 10 | 10 | −5 | 0 | VPC |
| 25 | 10 | 10 | 10 | −15 | 0 | VPC |
| 37 | 10 | 10 | 10 | −27 | 0 | VPC |
| 25 | 0.5 | 15 | 0.5 | −10 | 0 | OD |
| 37 | 0.5 | 15 | 0.5 | −22 | 0 | OD |
| 25 | 3 | 15 | 3 | −10 | 0 | OD |
| 37 | 3 | 15 | 3 | −22 | 0 | OD |
| 25 | 6 | 15 | 6 | −10 | 0 | OD |
| 37 | 6 | 15 | 6 | −22 | 0 | OD |
| 25 | 10 | 15 | 10 | −10 | 0 | OD |
| 37 | 10 | 15 | 10 | −22 | 0 | OD |
| 37 | 0.5 | 25 | 0.5 | −12 | 0 | OD |
| 37 | 3 | 25 | 3 | −12 | 0 | OD |
| 37 | 6 | 25 | 6 | −12 | 0 | OD |
| 37 | 10 | 25 | 10 | −12 | 0 | OD |
| Increase in NaCl concn at several temp and NaCl concn | ||||||
| 6 | 0.5 | 6 | 10 | 0 | 9.5 | OD |
| 6 | 3 | 6 | 10 | 0 | 7 | OD |
| 6 | 6 | 6 | 10 | 0 | 4 | OD |
| 10 | 0.5 | 10 | 10 | 0 | 9.5 | OD |
| 10 | 3 | 10 | 10 | 0 | 7 | OD |
| 10 | 6 | 10 | 10 | 0 | 4 | OD |
| 15 | 0.5 | 15 | 10 | 0 | 9.5 | OD, VPC |
| 15 | 3 | 15 | 10 | 0 | 7 | OD, VPC |
| 15 | 6 | 15 | 10 | 0 | 4 | OD, VPC |
| 25 | 0.5 | 25 | 10 | 0 | 9.5 | OD |
| 25 | 3 | 25 | 10 | 0 | 7 | OD |
| 25 | 6 | 25 | 10 | 0 | 4 | OD |
| 37 | 0.5 | 37 | 10 | 0 | 9.5 | OD |
| 37 | 3 | 37 | 10 | 0 | 7 | OD |
| 37 | 6 | 37 | 10 | 0 | 4 | OD, VPC |
| 6 | 0.5 | 6 | 6 | 0 | 5.5 | OD |
| 6 | 3 | 6 | 6 | 0 | 3 | OD |
| 10 | 0.5 | 10 | 6 | 0 | 5.5 | OD |
| 10 | 3 | 10 | 6 | 0 | 3 | OD |
| 15 | 0.5 | 15 | 6 | 0 | 5.5 | OD, VPC |
| 15 | 3 | 15 | 6 | 0 | 3 | OD, VPC |
| 25 | 0.5 | 25 | 6 | 0 | 5.5 | OD |
| 25 | 3 | 25 | 6 | 0 | 3 | OD |
| 37 | 0.5 | 37 | 6 | 0 | 5.5 | OD |
| 37 | 3 | 37 | 6 | 0 | 3 | OD |
| 6 | 0.5 | 6 | 3 | 0 | 2.5 | OD |
| 10 | 0.5 | 10 | 3 | 0 | 2.5 | OD |
| 15 | 0.5 | 15 | 3 | 0 | 2.5 | OD, VPC |
| 25 | 0.5 | 25 | 3 | 0 | 2.5 | OD |
| 37 | 0.5 | 37 | 3 | 0 | 2.5 | OD |
| No change in the environment | ||||||
| 25 | 0.5 | 25 | 0.5 | 0 | 0 | OD |
| 25 | 3 | 25 | 3 | 0 | 0 | OD |
| 25 | 6 | 25 | 6 | 0 | 0 | OD |
| 25 | 10 | 25 | 10 | 0 | 0 | OD |
| 37 | 0.5 | 37 | 0.5 | 0 | 0 | OD |
| 37 | 3 | 37 | 3 | 0 | 0 | OD |
| 37 | 6 | 37 | 6 | 0 | 0 | OD |
| 37 | 10 | 37 | 10 | 0 | 0 | OD |
OD, optical density; VPC, viable plate counting.
A calibration curve to relate OD and bacterial concentration was constructed. From a culture growing exponentially at 37°C or 15°C with 0.5% NaCl, 10 different inocula were prepared by 2-fold serial dilution in fresh medium with 0.5%, 3%, or 10% added NaCl at 37°C or 15°C. The concentrations ranged from ca. 5 × 102 CFU/ml to ca. 5 × 106 CFU/ml. Three hundred microliters of each inoculum was dispensed into 10 wells of a sterile 100-well multiwell plate. Multiwell plates were incubated at 37°C or 15°C. At appropriate time intervals, the OD was measured by using a Bioscreen C automatic plate reader (Labsystems, Helsinki, Finland). Simultaneously, samples were plated on tryptone soya agar (TSA) (Oxoid/Unipath catalog no. CM131). The plates were incubated at 37°C for 24 to 48 h. The relationship between the bacterial concentration and the OD was found not to be affected by the temperature or aw shifts. Similarly, Francois et al. (14) found that the relationship between optical density and plate counts for L. monocytogenes was not affected by aw between 0.945 (ca. 9% NaCl) and 0.995 (ca. 0.5% NaCl) and temperatures above 4°C. The relationship between the bacterial concentration and OD was found to be linear in this range and is described as follows:
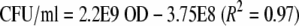 |
(2) |
To measure the effect of the previous environment on the amount of work to be done when a culture is adjusting to new conditions, cultures were grown under several conditions and transferred to new environments, as indicated in Table 1. To do this, 10 ml TSB (with added NaCl if required) was inoculated with ca. 103 CFU/ml and incubated at the target temperature until the OD was 0.2. The exponentially growing cultures were immediately transferred to new growth conditions, as indicated in Table 1. Growth in the new environment was measured by using OD or VPC.
In the new environments, growth parameters were determined from OD measurements by using the 2-fold dilution method as previously described (10). Ten inocula were prepared from an exponentially growing culture by 2-fold serial dilution in fresh medium (with added NaCl if required) already at the target temperature. The concentrations ranged from ca. 5 × 102 CFU/ml to ca. 5 × 106 CFU/ml. Three hundred microliters of each inoculum was dispensed into 10 wells of a sterile 100-well multiwell plate. Every plate contained 10 replicate wells containing each of the 10 inocula. The plates were incubated at the target temperature, and the OD was measured at appropriate time intervals by using the Bioscreen plate reader.
When growth under the new conditions was estimated by using VPC, 100 ml of TSB (with added NaCl if required) already at the target temperature was inoculated with ca. 103 CFU/ml of an exponentially growing culture. Cultures were incubated at the target temperatures. At appropriate time intervals, samples were plated on tryptone soya agar (TSA) (Oxoid/Unipath catalog no. CM131). The plates were incubated at 37°C for 24 to 48 h. Growth curves were determined in duplicate.
To compare the measurement methods, growth was monitored by using both OD and VPC under six of the experimental conditions at 15°C and under one of the experimental conditions at 37°C (Table 1).
Estimation of parameters for populations subjected to sudden temperature and aw downshifts.
For OD measurements, the detection time was estimated to be the time required to reach an OD of 0.2 in each well of the multiwell plate. The relationship between the detection time (Dt) and the natural logarithm of the initial concentration in the well (X0) was estimated by linear regression with two parameters, a and b, as follows:
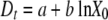 |
(3) |
where a and b are the regression coefficients. From equation 3, the maximum specific growth rate (μmax) could be calculated as follows:
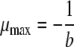 |
(4) |
In addition, the amount of work to be done during the lag phase (h0) was estimated as follows:
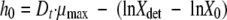 |
(5) |
where Xdet is the bacterial concentration at the detection time, which was 7.07 × 107 CFU/ml, as determined by using equation 2.
In the case of VPC measurements, μmax and h0 were estimated by fitting the model of Baranyi and Roberts (3) to the growth measurements.
Growth parameters at 15°C with several aw shifts estimated by the 2-fold dilution method and VPC were compared. As previously reported (7), the measurement method did not have any effect on estimation of the parameters.
Modeling the dependence of h0 and μmax on the growth conditions.
The dependence of h0 on the decrease in temperature was modeled as follows:
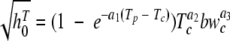 |
(6) |
where T is the temperature, the subscripts p and c indicate previous and current conditions, respectively, 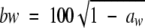 , and a1, a2, and a3 are model parameters estimated by nonlinear regression.
, and a1, a2, and a3 are model parameters estimated by nonlinear regression.
The model was fitted to the 48 observations obtained with cultures grown at temperatures equal to or higher than the current growth temperature (Table 1). After we checked that the effect of the difference between the previous and current temperatures on h0 was significant, parameter forward selection F tests were used to decide whether the effects of the current temperature and aw were significant. Both the a2 and a3 parameters were significantly different from zero and therefore included in the model.
Similarly, the dependence of h0 on the decrease in the aw or the increase in NaCl or bw was modeled as follows:
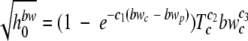 |
(7) |
where c1, c2, and c3 are model parameters estimated by nonlinear regression.
This model was fitted to the 38 data points obtained with cultures grown at aw values equal to or higher than that of the current growth medium (Table 1). After the significance of the effect of the difference between the previous and current aw values on h0 was assessed, parameter forward selection F tests were used to decide whether the effects of the current temperature and aw were significant. Both the c2 and c3 parameters were significantly different from zero and therefore included in the model.
The dependence of μmax on the current growth conditions was modeled by using a square-root-type function (26) with an added term,  , to model the effect of the aw.
, to model the effect of the aw.
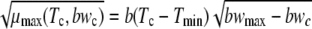 |
(8) |
The model parameters, b, Tmin, and bwmax were estimated by nonlinear regression. The model was fitted to the rates measured under all conditions shown in Table 1. Parameter stepwise selection was run for the model. No parameters could be removed from the model.
Dynamic modeling.
The differential form of the model of Baranyi and Roberts (3) was used to predict the bacterial concentration (x) under environmental conditions that fluctuated with time (t):
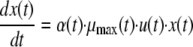 |
(9) |
where u(t) and α(t) are parameters that have been described previously (3) and μmax(t) is calculated using equation 8.
α(t) takes values between 0 and 1 and quantifies the theoretical readiness of the population to divide; it is 0 when bacteria are not able to divide and 1 when cells are in exponential growth.
As explained by Baranyi and Roberts (3), the lag period is caused by a critical substance (q) which is quantified in their model by using q(t) and
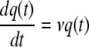 |
(10) |
where ν is the specific rate at which the substance is produced during the lag phase. Like Baranyi and Roberts (3), we also assumed that ν(t) = μmax(t).
The relationship between the amount of a critical substance (q) and the theoretical readiness to grow (α) with the amount of work to be done during the lag phase (h) is:
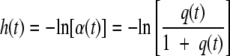 |
(11) |
h(t) quantifies the amount of work remaining to be done at time t during the lag, where h(0) = h0 is the initial value for any arbitrarily chosen time zero.
To solve equation 9, estimates of the initial values for x(ti) = xi and q(ti) = qi or, equivalently, for h(ti) = hi, are needed for any time that the environment fluctuates (ti). Thus, ti (where i = 0, 1, 2…) is the time for the ith environmental fluctuation, including the time at which the culture is initiated (t = 0).
We assumed that the bacterial concentration was not affected by the environmental fluctuation and therefore that the value for xi is the bacterial concentration at the time of the fluctuation. However, when the environment fluctuates, the amount of work to be done during the lag (hi) may change, initiating a new lag period. The method used for estimation of hi according to the environmental fluctuation and the stage of the population is described below. Using equation 12, the initial value (qi) can be derived from hi as follows:
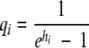 |
(12) |
Estimation of hi at the time of environmental fluctuation.
At time zero, when a culture is initiated, h0 is the initial amount of work to be done to adapt to the new growth conditions. If there is some work to be done, this work is carried out progressively at a certain rate, and when the work is completed, the population enters exponential growth phase. At any time fluctuations in the environment can modify the rate at which the work is done, but they may also increase the workload. Therefore, the system has to be reset with a new value to start a new lag period.
When a population subjected to an environmental change was already in lag phase, the new value for the workload quantifies the work to be done due to the environmental change plus the unfinished work that should have been done during the incomplete lag phase. Since the unfinished workload is zero for a population in exponential phase, the new workload comprises only the work to be done due to the environmental change.
Therefore, the value for hi at the time of the ith fluctuation of the temperature and/or aw (ti) was estimated as follows:
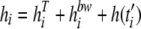 |
(13) |
where hiT and hibw are the workloads due to fluctuation of the temperature and aw, as estimated from equations 6 and 8, respectively. If the population subjected to the environmental change was already in lag phase, h(ti′) was the amount of work remaining to be done at the time ti′, which was the instant immediately before the fluctuation.
Simulations were carried out by using second-order Runge-Kutta methods and an in-house program written in Visual Basic.
Validation of the experimental model using fluctuating environments.
To evaluate the performance of the model, a population under fluctuating temperature and aw conditions was monitored by using VPC. Inocula were prepared as described above. One hundred milliliters of TSB (with added NaCl if required) already at the target temperature was inoculated with ca. 103 CFU/ml of a population growing exponentially under the same conditions to avoid an initial lag. During the incubation period, the conditions were suddenly and successively changed when populations were in exponential phase, as well as in lag phase. To change the temperature, bottles were transferred to a water bath set at the required temperature. The change in temperature with time was measured by applying a thermocouple to a replicate bottle containing uninoculated medium. To decrease the aw of the medium, quantities of sterile NaCl were added aseptically to the medium, which was stirred for a few minutes to dissolve the NaCl.
At appropriate time intervals, samples were plated on TSA. The plates were incubated at 37°C for 24 to 48 h. Growth curves were determined in duplicate.
RESULTS
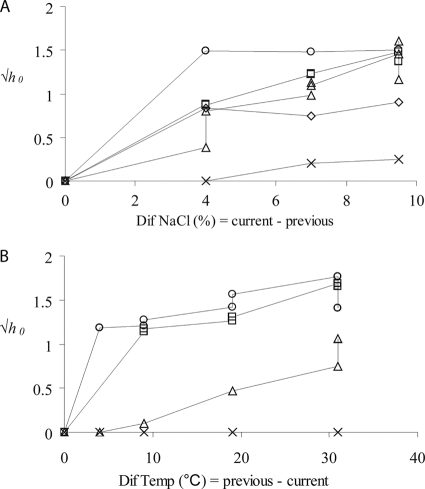
To measure the dependence of the amount of work to be done during the lag period on the previous and current growth conditions, exponentially growing populations were subjected to sudden downshifts of temperature and aw. In many cases, growth was halted and cells started to divide again only after a lag period. Figure 1 shows that the amount of work to be done during the lag increased as the aw decreased compared to the aw in the previous environment and as the final growth temperature (Fig. 1A) and aw values (data not shown) were closer to the limits at which growth occurred. Similarly, the amount of work to be done increased as the temperature decreased compared to the temperature in the previous environment and as the final growth conditions were more stringent (Fig. 1B). Therefore, the amount of work to be done during the lag period depended on the magnitude of the change between the previous and current environments, as well as on the current growth conditions.
FIG. 1.
Effect of the previous and current environments on the amount of work to be done during the lag phase. h0 depended on the magnitude of the sudden change in the aw or temperature and also on the final temperature and aw values. (A) Effect of an increase in the level of NaCl on h0 at 6°C (○), 10°C (□), 15°C (▵), 28(⋄), and 37°C (×). The final level of NaCl was 10%. (B) Effect of a decrease in temperature on h0 with 10% (○), 6% (□), 3% (▵), and 0.5% (×) NaCl. The final temperature was 6°C.
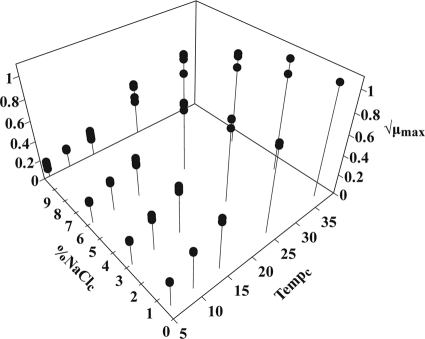
The maximum specific growth rate depended only on the current growth conditions and was not affected by the previous environment (Fig. 2). It increased as the temperature or the aw of the medium increased.
FIG. 2.
Square roots of the maximum specific growth rates (h−1) (μmax) at several temperatures and at several values for the aw adjusted with NaCl.
Table 2 shows the parameters of the equations used to model the dependence of the amount of work on the difference between the previous and current growth temperatures and on the current temperature and to model the dependence of the amount of work on the difference between the previous and current aw and on the current aw. The estimated parameters of the model of the maximum specific growth rate are also shown in this table. These models were fitted to observations for constant environments and used to predict the growth rate and hi at different times in fluctuating environments.
TABLE 2.
Estimation of the model parameters
| Model | Parameter | Estimated value | SE | R2 |
|---|---|---|---|---|
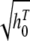 |
a1 | −0.5625 | 0.3168 | 0.78 |
| a2 | −0.9049 | 0.1347 | ||
| a3 | 0.6368 | 0.0912 | ||
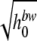 |
c1 | −0.2409 | 0.0732 | 0.89 |
| c2 | −0.6846 | 0.0991 | ||
| c3 | 0.5571 | 0.0723 | ||
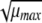 (h−1) (h−1) |
b | 0.005920 | 0.0001640 | 0.99 |
| Tmin | −3.178 | 0.3962 | ||
| bwmax | 31.09 | 0.4262 |
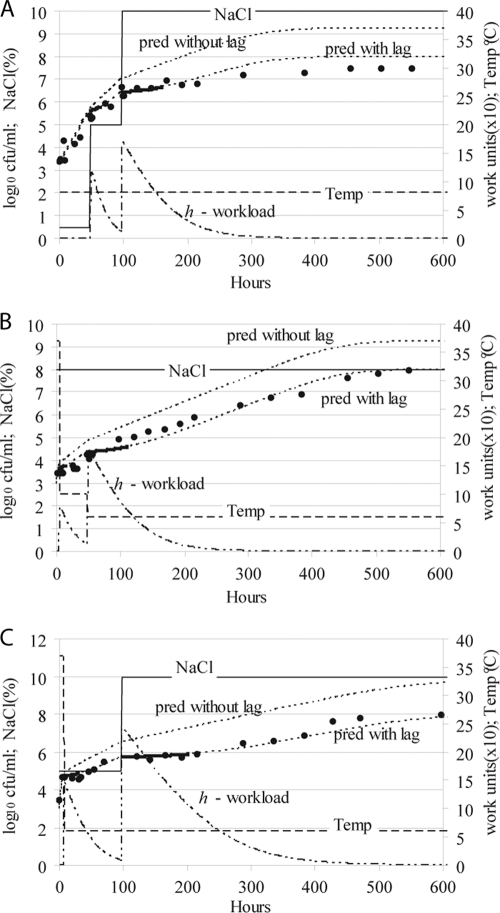
Figure 3 shows the predicted and observed transitions from exponential phase to lag phase and vice versa. In the experiment whose results are shown in Fig. 3A, the level of NaCl in the medium was suddenly increased from 0.5 to 5%. The exponentially growing population entered a lag period, the duration of which was accurately predicted. When this population began to grow again, the level of NaCl in the medium was increased from 5 to 10%. The observed duration of the new lag period was accurately predicted.
FIG. 3.
Transition from exponential phase to lag phase and vice versa. Predicted (dotted lines) and observed (filled circles) bacterial concentrations at fluctuating temperatures (solid line) and aw values (expressed as levels of NaCl by a dashed line). One of the lines for predicted values does not consider any lag phase (pred without lag). The lag phase is indicated by a thick line over the dotted line for the predicted values, and its duration was determined by the time needed to carry out work to adapt to the environmental changes (the kinetics of this work is indicated by a dashed and dotted line). The environmental changes applied to exponentially growing populations comprised (A) two successive and sudden increases in the NaCl level, (B) two successive and sudden decreases in temperature, and (C) a decrease in temperature followed by an increase in the NaCl level.
A similar experiment was carried out for temperature (Fig. 3B). An exponentially growing population was subjected to two sudden decreases in temperature, while the aw of the medium was constant. The temperature was decreased first from 37 to 10°C and later, when the population was growing exponentially again, from 10 to 6°C. Both changes caused a lag period, which was in good agreement with the predictions.
The results of an experiment combining sudden changes in both environmental factors are shown in Fig. 3C. A decrease in the temperature from 37 to 6°C was followed by an increase in the level of NaCl in the medium from 5 to 10%. An exponentially growing population was subjected to both changes, and it responded by halting growth and entering a lag phase. The predictions were also similar to the observations.
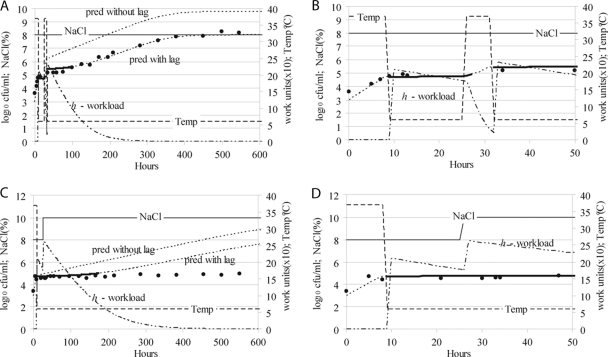
Figure 4 shows the predicted and observed bacterial concentrations when a population already in lag phase was subjected to environmental fluctuations. Moreover, in the experiment whose results are shown in Fig. 4A, the effect of an increase in temperature on a population already in lag phase was evaluated. Initially, the temperature was decreased from 37 to 6°C, which resulted in entry of the population into a lag phase. Before this lag period was finished, the temperature was increased to 37°C. This scenario was an extrapolation of our model since we did not measure the effect of temperature upshifts on the work to be done. Based on results of other workers (20), we assumed that the workload did not change as a result of the increase in temperature. However, the rate at which work was carried out increased immediately, so that after 4 h of incubation at 37°C practically all work was done (Fig. 4B). Therefore, when after 6 h of incubation at 37°C the temperature was decreased to 6°C, the population was in exponential phase, and a new lag period started (Fig. 4A).
FIG. 4.
Environmental fluctuations affecting populations already in lag phase. Predicted (dotted lines) and observed (filled circles) bacterial concentrations at fluctuating temperatures (dashed line) and aw values (expressed as levels of NaCl by a solid line). In panels A and C, one of the predicted lines does not consider any lag phase (pred without lag). The lag phase is indicated by a thick line over the dotted line for the predicted values, and its duration was determined by the time needed to carry out work to adapt to the environmental changes (the kinetics of this work is indicated by a dashed and dotted line). When an increase in temperature was applied to a population in lag phase, the workload was carried out at a higher rate according to the new temperature, shortening the lag phase (panel A, full period; panel B, first 50 h). When an increase in the NaCl level was applied to a population already in lag phase, initially, due to a decrease in temperature, the work to be done increased, starting a new, longer lag period. The bacterial cells were assumed to carry out both workloads due to temperature and to aw simultaneously (panel C, full period; panel D, first 50 h).
In the experiment whose results are shown in Fig. 4C, the temperature was decreased from 37 to 6°C, which initiated a lag period. Before this lag period was finished, the level of NaCl in the medium was increased from 8 to 10%. This decrease in the aw resulted in an increase in the work to be done and therefore a new, longer lag period. Figure 4D shows the kinetics of the work to be done in this scenario. The initial work caused by the initial decrease in temperature was carried out at the specific rate characteristic of the environment until the aw suddenly decreased. When this happened, both the work to be done and the rate at which the work was carried out changed. The workload increased because of the additional work to be done due to the sudden decrease in the aw. The rate at which the work was carried out decreased because of the decrease in the aw. It was assumed that the bacterial cells carried out both workloads (the workload due to the temperature and the workload due to the aw) simultaneously (Fig. 4D). A relatively long lag phase (ca. 200 h) followed by exponential growth was predicted, while the population did not start to grow during the observation period (ca. 600 h) (Fig. 4C).
DISCUSSION
We found that the work to be done depended not only on the magnitude of the difference between the previous and current environments but also on the current growth conditions, so that the amount of work required to adapt to a given decrease in temperature or aw was greater at low aw values and at low temperatures. Skandamis and Le Marc (P. N. Skandamis and Y. Le Marc, Agricultural University of Athens, personal communication) also found that the work to be done depended on the magnitude of the acid and osmotic shift between the previous and current conditions and on the stringency of the new environmental conditions. Several authors have reported that significant lag periods due to sudden temperature downshifts were observed only at low temperatures (6, 18). Baranyi et al. (5) observed that a lag phase was not induced by temperature downshifts from between 17 and 25°C to 5°C in Brochrothrix thermosphacta, but a significant lag was observed when the final temperature was 3°C. The similarity of the final values for the temperature indicated that the work to be done for a given temperature downshift increased when the final temperature decreased. Dependence of the work to be done on the final aw value has been reported for several food-borne bacteria, including L. monocytogenes (19). Mellefont et al. found that the ratio of the lag to the generation time increased abruptly as the final aw value was closer to the limit for growth of L. monocytogenes. Similarly, the dependence of this ratio on the final pH value has been pointed out for several bacteria (11). These findings indicate that the adaptation work to be done during the lag period depends both on the magnitude of the environmental change and on the final growth conditions.
In the model of Baranyi and Roberts (3) the duration of the lag phase is under control of the function α(t), as described in equations 9 and 11. This function quantifies the theoretical readiness of the population to divide. As the population progressively synthesizes the critical substance causing the lag phase or carries out the work to be done, the value of α(t) increases. Once the maximum value, which is 1, is reached, the population starts to grow exponentially at μmax. At any time (ti) when the environment fluctuates, the rate at which the work is done changes instantaneously, and the amount of work to be done is has a new value, hi. The parameter h0 is a particular case of hi that quantifies the initial amount of work to be done at the initiation of the culture or any other arbitrarily chosen time zero. We have shown that the amount of work to be done depends on the previous and current environments and that when this amount changes, the model predicts a new lag period depending on the new value for the work to be done (Fig. 3 and 4). When the population was already in lag phase, this new value was estimated to be the workload due to the environmental change plus the unfinished workload from the uncompleted previous lag period, while for a population in exponential phase the work to be done depended only on the environmental change. Application of this model to fluctuating environments has been described previously (5). Baranyi et al. found that the amount of work to be done by a population in early stationary phase grown at 25°C and transferred to temperatures between 5 and 25°C was constant and that once the population was growing exponentially, a lag was not induced by any change in temperature in this range. With our experimental data, we modeled a situation in which the amount of work to be done depended on the previous and current environments. Therefore, an increase in the duration of the lag could be predicted if the population subjected to the environmental change was already in lag phase or a transition to lag phase was predicted for populations growing exponentially.
For Fig. 4A, we assumed that the increase in temperature during the lag phase did not affect the amount of work but the duration of the lag was markedly shorter because the rate was higher at a high temperature. Some authors have reported that a sudden increase in temperature increases the work to be done in Escherichia coli (30) and L. monocytogenes (12), while Mellefont and Ross (20) found that the workload was not affected by sudden upshifts of temperature in Klebsiella oxytoca and E. coli.
Figure 4C shows predictions and observations when both aw and temperature decreased and affected a population in lag phase. Under these conditions, the population did not start to grow during the observation period. We did not measure experimentally the amount of work to be done when both aw and temperature decrease simultaneously. It was assumed that the effects of these two factors on the amount of work to be done were additive. However, according to the results shown in Fig. 4, when fluctuations of both factors simultaneously affected a population already in lag phase, their effect was greater than expected from addition of their individual effects, resulting in no growth during the observation period. Thus, further experimental work is needed to investigate the interaction between these factors when they are applied simultaneously to a population in lag phase.
In order to evaluate the advantages of incorporating the lag phase in the modeling approach, predictions for when the population stops growing and enters lag phase were compared with predictions for when the population keeps growing at a relatively low rate characteristic of the environment (Fig. 3 and 4A and C). For a population entering a lag phase for the first time, the accuracies of the predictions obtained by using both approaches were similar during the lag period itself. However, in all cases, the differences between predictions became evident later during exponential growth phase. The predictions of the model with lag phase were considerably more accurate than those of the model without log phase when compared with observations through the entire growth curve.
Our model for the work to be done was developed for exponentially growing populations subjected to sudden decreases in aw or temperature. Predictions may not be accurate for extrapolation to populations in stationary phase. Delignette-Muller et al. (12) reported that the work necessary to adapt to an environmental change is greater for populations in stationary phase than for populations in exponential phase. Several authors (1, 22) have shown that as the time spent in stationary phase increases, the work to be done increases. Furthermore, the metabolic and intracellular activities during the lag period vary noticeably depending on the time spent in stationary phase (24).
An increase in the complexity of the modeling approaches so that they include the lag period when the impact of food environments on bacterial population dynamics is predicted seems to be justified. This requires greater complexity in the experimental design to determine the effect of previous environments on the bacterial response to the current conditions. Additionally, in order to apply these models and obtain qualitatively better predictions, the input information needs to include not only details concerning the current growth environment but also details concerning the history of the bacterial population.
Acknowledgments
We gratefully acknowledge support by BBSRC core strategic grants 42230A and 42266A. M.M.-C. received a fellowship from “Fundación CAJAMURCIA.”
Footnotes
Published ahead of print on 5 March 2010.
REFERENCES
- 1.Augustin, J. C., L. Rosso, and V. Carlier. 2000. A model describing the effect of temperature history on lag time for Listeria monocytogenes. Int. J. Food Microbiol. 57:169-181. [DOI] [PubMed] [Google Scholar]
- 2.Baranyi, J., and C. Pin. 2001. Modelling microbial safety, p. 383-400. In L. M. M. Tijskens, M. L. A. T. M. Hertog, and B. M. Nicolai (ed.), Food process modelling. Woodhead Publishing Limited, Cambridge, England.
- 3.Baranyi, J., and T. A. Roberts. 1994. A dynamic approach to predicting bacterial growth in food. Int. J. Food Microbiol. 23:277-294. [DOI] [PubMed] [Google Scholar]
- 4.Baranyi, J., T. A. Roberts, and P. J. McClure. 1993. A non-autonomous differential equation to model bacterial growth. Food Microbiol. 10:43-59. [Google Scholar]
- 5.Baranyi, J., T. P. Robinson, A. Kaloti, and B. M. Mackey. 1995. Predicting growth of Brochothrix thermosphacta at changing temperature. Int. J. Food Microbiol. 27:61-75. [DOI] [PubMed] [Google Scholar]
- 6.Berry, E. D., and P. M. Foegeding. 1997. Cold temperature adaptation and growth of microorganisms. J. Food Prot. 60:1583-1594. [DOI] [PubMed] [Google Scholar]
- 7.Biesta-Peters, E. G., M. W. Reij, H. Joosten, L. G. Gorris, and M. H. Zwietering. 2010. Comparison of two optical-density-based methods and a plate count method for estimation of growth parameters of Bacillus cereus. Appl. Environ. Microbiol. 76:1399-1405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Breand, S., G. Fardel, J. P. Flandrois, L. Rosso, and R. Tomassone. 1999. A model describing the relationship between regrowth lag time and mild temperature increase for Listeria monocytogenes. Int. J. Food Microbiol. 46:251-261. [DOI] [PubMed] [Google Scholar]
- 9.Buchanan, R. L., and L. A. Klawitter. 1991. Effect of temperature history on the growth of Listeria monocytogenes Scott A at refrigeration temperatures. Int. J. Food Microbiol. 12:235-245. [DOI] [PubMed] [Google Scholar]
- 10.Cuppers, H. G. A. M., and J. P. Smelt. 1993. Time to turbidity measurement as a tool for modeling spoilage by Lactobacillus. J. Ind. Microbiol. Biotechnol. 12:168-171. [Google Scholar]
- 11.Delignette-Muller, M. L. 1998. Relation between the generation time and the lag time of bacterial growth kinetics. Int. J. Food Microbiol. 43:97-104. [DOI] [PubMed] [Google Scholar]
- 12.Delignette-Muller, M. L., F. Baty, M. Cornu, and H. Bergis. 2005. Modelling the effect of a temperature shift on the lag phase duration of Listeria monocytogenes. Int. J. Food Microbiol. 100:77-84. [DOI] [PubMed] [Google Scholar]
- 13.Dufrenne, J., E. Delfgou, W. Ritmeester, and S. Notermans. 1997. The effect of previous growth conditions on the lag phase time of some foodborne pathogenic micro-organisms. Int. J. Food Microbiol. 34:89-94. [DOI] [PubMed] [Google Scholar]
- 14.Francois, K., F. Devlieghere, A. R. Standaert, A. H. Geeraerd, I. Cools, J. F. Van Impe, and J. Debevere. 2005. Environmental factors influencing the relationship between optical density and cell count for Listeria monocytogenes. J. Appl. Microbiol. 99:1503-1515. [DOI] [PubMed] [Google Scholar]
- 15.Hills, B. P., and B. M. Mackey. 1995. Multi-compartment kinetic models for injury, resuscitation, induced lag and growth in bacterial cell populations. Food Microbiol. 12:333-346. [Google Scholar]
- 16.Hills, B. P., and K. M. Wright. 1994. A new model for bacterial growth in heterogeneous systems. J. Theor. Biol. 168:31-41. [DOI] [PubMed] [Google Scholar]
- 17.Hudson, J. A. 1993. Effect of pre-incubation temperature on the lag time of Aeromonas hydrophila. Lett. Appl. Microbiol. 16:274-276. [Google Scholar]
- 18.Li, K.-Y., and J. A. Torres. 1993. Microbial growth estimation in liquid media exposed to temperature fluctuations. J. Food Sci. 58:644-648. [Google Scholar]
- 19.Mellefont, L. A., T. A. McMeekin, and T. Ross. 2003. The effect of abrupt osmotic shifts on the lag phase duration of foodborne bacteria. Int. J. Food Microbiol. 83:281-293. [DOI] [PubMed] [Google Scholar]
- 20.Mellefont, L. A., and T. Ross. 2003. The effect of abrupt shifts in temperature on the lag phase duration of Escherichia coli and Klebsiella oxytoca. Int. J. Food Microbiol. 83:295-305. [DOI] [PubMed] [Google Scholar]
- 21.Pin, C., and J. Baranyi. 1998. Predictive models as means to quantify the interactions of spoilage organisms. Int. J. Food Microbiol. 41:59-72. [DOI] [PubMed] [Google Scholar]
- 22.Pin, C., and J. Baranyi. 2008. Single-cell and population lag times as a function of cell age. Appl. Environ. Microbiol. 74:2534-2536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Pin, C., F. G. Garcia de, J. A. Ordonez, and J. Baranyi. 2002. Analysing the lag-growth rate relationship of Yersinia enterocolitica. Int. J. Food Microbiol. 73:197-201. [DOI] [PubMed] [Google Scholar]
- 24.Pin, C., M. D. Rolfe, M. Muñoz-Cuevas, J. C. D. Hinton, M. W. Peck, N. J. Walton, and J. Baranyi. 2009. Network analysis of the transcriptional pattern of young and old cells of Escherichia coli during lag phase. BMC Syst. Biol. 3:108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Presser, K. A., D. A. Ratkowsky, and T. Ross. 1997. Modelling the growth rate of Escherichia coli as a function of pH and lactic acid concentration. Appl. Environ. Microbiol. 63:2355-2360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ratkowsky, D. A., R. K. Lowry, T. A. McMeekin, A. N. Stokes, and R. E. Chandler. 1983. Model for bacterial culture growth rate throughout the entire biokinetic temperature range. J. Bacteriol. 154:1222-1226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Resnik, S. L., and J. Chirife. 1988. Proposed theoretical aw values at various temperatures for selected solutions to be used as reference sources in the range of microbial growth. J. Food Prot. 51:419-423. [DOI] [PubMed] [Google Scholar]
- 28.Robinson, T. P., M. J. Ocio, A. Kaloti, and B. M. Mackey. 1998. The effect of the growth environment on the lag phase of Listeria monocytogenes. Int. J. Food Microbiol. 44:83-92. [DOI] [PubMed] [Google Scholar]
- 29.Rosso, L., J. R. Lobry, S. Bajard, and J. P. Flandrois. 1995. Convenient model to describe the combined effects of temperature and pH on microbial growth. Appl. Environ. Microbiol. 61:610-616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Swinnen, I. A., K. Bernaerts, and J. F. Van Impe. 2006. Modelling the work to be done by Escherichia coli to adapt to sudden temperature upshifts. Lett. Appl. Microbiol. 42:507-513. [DOI] [PubMed] [Google Scholar]
- 31.Whiting, R. C., and L. K. Bagi. 2002. Modeling the lag phase of Listeria monocytogenes. Int. J. Food Microbiol. 73:291-295. [DOI] [PubMed] [Google Scholar]