A Comprehensive System for Intraoperative 3D Brain Deformation Recovery

Abstract

During neurosurgery, brain deformation renders preoperative images unreliable for localizing pathologic structures. In order to visualize the current brain anatomy, it is necessary to nonrigidly warp these preoperative images to reflect the intraoperative brain. This can be accomplished using a biomechanical model driven by sparse intraoperative information. In this paper, a linear elastic model of the brain is developed which can infer volumetric brain deformation given the cortical surface displacement. This model was tested on both a realistic brain phantom and in vivo, proving its ability to account for large brain deformations. Also, an efficient semiautomatic strategy for preoperative cortical feature detection is outlined, since accurate segmentation of cortical features can aid intraoperative cortical surface tracking.

1 Introduction

Successful neurosurgical interventions require precise localization of pathologic tissue. Localization inaccuracies, most often due to intraoperative brain deformation [17], can lead to unsuccessful resections, impairment of physical or mental abilities or death. Despite these consequences, compensating for the effects of brain shift remains an open problem.

Biomechanicalmodels guided by sparse intraoperative data can provide 3D deformation recovery based on the brain’s material properties. These brain models vary greatly in complexity and computational expense. Some authors propose nonlinear [17] or anisotropic [6] models. These detailed models require more computation, brain parameter estimation or information that is infrequently obtained from neurosurgical patients, such as white matter structure obtained from Diffusion Tensor Imaging (DTI). While this additional information, when available, may improve deformation calculations in some areas of the brain, the comparison to homogeneous linear models has been limited and generally based on small deformations. At the same time, accurate results have been achieved with linear elastic models (LEMs). In experiments done by Paulsen et al. [12], Navier’s equation was shown to predict the displacement of brain tissue when subject to a body force. In interesting extensions of this work [4,8], the poroelastic model achieved accurate results when guided by surface data or fiducial marker displacement and solved inversely. In [15], it was shown that volumetric results could be obtained by relying solely on direct measurements of the cortical surface as displacement boundary conditions for an LEM. Based on these promising results, an LEM was chosen in this work. The model depends on two parameters of brain tissue, Young’s Modulus and Poisson’s ratio, both of which can be easily obtained from the literature [7].

The boundary conditions of the biomechanical model are based on the fixed skull and the intraoperative displacement of cortical surface. In previous related work, we have calculated intraoperative cortical surface displacement using a deformable model guided by stereo camera images [2,3]. In our work, as well as in similar research performed by other groups [1,9,16], the importance of using cortical features to aid the surface deformation estimation has been established. Therefore, in this paper, we have developed a novel semiautomatic 3D sulci extraction technique, developed specifically for this application, which affords easier and more reliable segmentation of preoperative features.

2 Method

The method for brain shift compensation can be divided into three main steps. (1) Preoperative processing. In this step, the cortical surface and the sulci on that surface are extracted. The semiautomatic process for performing this extraction is developed below. (2) Intraoperative Deformation Estimation. The displacement of the exposed cortical surface is determined at this stage. Though this step is very important for the overall result, it is not the focus of this paper. The cortical surface displacement field can be obtained from any deformation tracking algorithm [1,2,3,9,16]. However, this surface deformation must then be propagated through the brain volume. (3) Volumetric Determination. This is the method of estimating brain volumetric changes, in this case, using a linear elastic model. The contributions of this paper are the development of steps (1) and (3).

2.1 Preoperative Processing

In order to extract the preoperative cortical surface and feature positions, the preoperative MRI is first skull stripped and segmented into brain and nonbrain regions. This is performed automatically using the freely available BioImage Suite software [10]. The resulting image, I, is a mapping from spatial position to a greylevel intensity, I : R³ → R. A level set surface from this image is the set of points x₁, …, x_n ∈ R³ : I(x₁, …, x_n) = c where c is a constant value. Since a large gradient exists between the brain and nonbrain regions, an appropriate value of c (normally around one-third of the maximum intensity) will yield a level set corresponding to the brain surface.

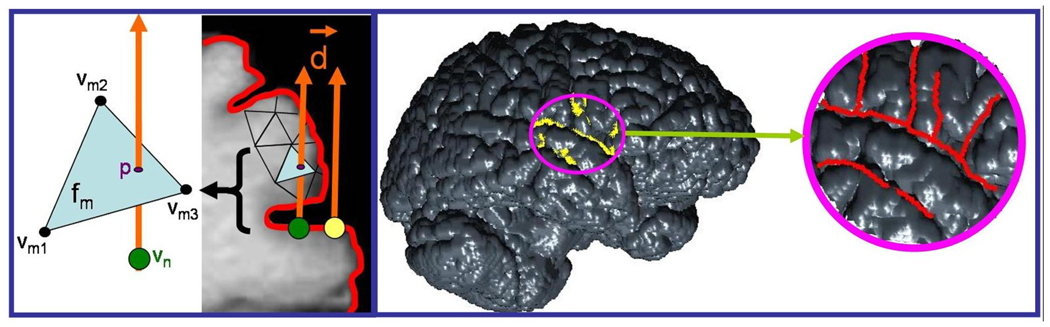
Unlike the gyri, which are fully exposed, the sulci can run deep under the surface. Therefore, determining the points at which the triangulated surface vertices transition from being exposed to being occluded should guide the sulci extraction. To determine if the n^th vertex, υ_n, is occluded by the m^th face of the surface, f_m, first the plane of f_m is determined through simple geometry:

$$({\upsilon }_{m2}-{\upsilon }_{m1})\times ({\upsilon }_{m3}-{\upsilon }_{m1})=\overrightarrow{n_m},\overrightarrow{n_m}•(x-{\upsilon }_{m1})=0$$ (1)

where $\overrightarrow{n_m}$ is the normal to face f_m, (υ_m1, υ_m2, υ_m3) define the vertices of face f_m, and x is a point on the plane. (See the left side of Figure 1).

Fig. 1.

The left side shows the transition between an exposed vertex (yellow) and a vertex occluded by face f_m (green) on one slice of a brain MRI. Explanation of the variables is in the text. On the right, the entire brain surface is shown. The area of the craniotomy is outlined in magenta. The yellow points are automatically detected by the algorithm as transition points between exposed and occluded mesh vertices. Using these as a guide allows easier and more accurate sulci detection.

To be occluded by face f_m, a line originating at point υ_n and traveling in the direction of the viewer (υ_n + d⃗ • t, where t is the parameterization constant and d⃗ is the viewer direction) must intersect the plane defined in equation (1) inside face f_m. In this case, the viewer direction is defined as being normal to the current face which contains υ_n. The intersection point, p, can be found by solving the simultaneous equations:

$$p={\upsilon }_n+\overrightarrow{d}•t_p,\text{where}\overrightarrow{n_m}•(p-{\upsilon }_{m1})=0$$ (2)

where t_p is the value of the parameter that yields the intersection. Once the intersection to the plane is calculated, one only needs to determine if p lies inside face f_m. Point p is within the face f_m if, for each pair of two vertices defining one edge of f_m, $\overrightarrow{{\upsilon }_{m1}{\upsilon }_{m2}},\overrightarrow{{\upsilon }_{m2}{\upsilon }_{m3}},\overrightarrow{{\upsilon }_{m1}{\upsilon }_{m3}}$, p is on the same side of that edge as the remaining vertex, υ_m3, υ_m1, υ_m2, respectively. To determine, for example, if p is on the same side of $\overrightarrow{{\upsilon }_{m1}{\upsilon }_{m2}}$ as υ_m3 one needs to ensure that ((υ_m2 − υ_m1) × (p − υ_m1)) • ((υ_m2 − υ_m1) × (υ_m3 − υ_m1)) >= 0.

If the above inequality holds true for all three edges, then the point lies within that triangular face [5]. In this case, it also means that the point is occluded by that face. By performing this test on all the vertices in the craniotomy region, the vertices that are on the border between exposed and occluded can be automatically highlighted. These vertices signal the edge of a sulcus and can be used as a guide in sulci extraction. (See the right side of Figure 1.) At this point, the user can choose to connect the highlighted vertices in whichever order or orientation needed.

The main drawback of this method is that it is dependent on view angle. We are currently working on extending this method by repeating the above process for varying view angles and combining the results to surround the sulci from both sides. This would make the method more robust and may require less user input in the final stages. The single viewpoint method did, however, provide promising initial results. It is difficult to compare the accuracy of the semiautomatically detected sulci versus the manually outlined sulci, since there is no ground truth. However, since the goal of the sulcal extraction is to aid in cortical surface detection, the results can be evaluated based on which method enables better cortical surface tracking. Using an in vivo test case, results of a surface tracking algorithm (details of the algorithmare provided in [2]) were compared using either manually segmented (as they were in [3]) or semiautomatically segmented sulci as algorithm inputs. As Table 1 shows, the semiautomatically detected sulci provided a more accurate initialization of the algorithm and therefore better results.

Table 1.

Errors (in mm) were calculated as the distance between the predicted surface and twelve intraoperatively tracked points used for validation. Details about the deformation algorithm, which requires the preoperative locations of the sulci, can be found in [2].

	mean	max	std
Total Deformation	4.49	7.24	2.03
Deformation Algorithm Error (Manually Segmented Sulci)	1.05	3.08	0.86
Deformation Algorithm Error (Semiautomatically Segmented Sulci)	0.58	1.01	0.22

2.2 Intraoperative Deformation Estimation

Once the cortical surface and sulci have been extracted, the next step is to calculate the intraoperative deformation. Methods for intraoperative deformation estimation often rely on cortical surface features, such as sulci or blood vessels, either warping the features from the preoperative images to their intraoperative positions using robust point matching [1], an iterative closest point technique [16], or a deformable model [2,3]. Whether blood vessels or sulci are used, accurate sulcal segmentation may aid the process since vessels often parallel the sulcal and gyral patterns [9]. Therefore, the guided sulcal extraction can aid most deformation estimation algorithms.

The details of the deformation estimation algorithms are beyond the scope of this paper. Regardless of the method used, however, the result can be formulated as a dense displacement field over each node of the exposed cortical surface.

2.3 Volumetric Determination

The dense displacement field found in the previous step can be applied to the brain volume using finite element analysis, in which the brain is modeled as a linear elastic material. Given the displacements of points on the intraoperative cortical surface, p_i, calculated from the surface detection algorithm, the deformation throughout the brain volume, V, can be calculated using an energy minimization framework [11].

$$\widehat{\upsilon }=\text{arg}\underset{\upsilon }{\text{min}}\left({\displaystyle {\int }_{V}W(\alpha ,\upsilon ,m)+{\displaystyle \sum _{i=1}^{N}c(p_i)|u(p_i)-\upsilon (p_i){|}^2}}\right)$$ (3)

where N is the total number of cortical surface points used to guide the model, u(p_i) is the known 3D displacement at each point p_i, υ(p_i) is the 3D LEM displacement at p_i. The confidence in each measurement is set by c(p_i), in which the surface displacements are imposed as boundary conditions. W(α, υ, m) is a positive semi-definite functional defining the approximation strategy which, in this case, is internal energy. It is defined as W = ϵ^T Cϵ, a function of α, the parameter vector, the displacement field, υ, and m, the spatial position.

The energy minimization was performed using the finite element analysis software package ABAQUS (ABAQUS, Inc., Providence RI). The model inputs were the tetrahedral brain volume mesh, a surface representing the surrounding skull, Young’s modulus (66.7 kPa) and Poisson’s ratio (0.48) of brain [7]. Surface displacements were applied as boundary conditions and the cortex and skull surfaces were defined as contact surfaces, enforcing that the brain will not deform past the rigid confines of the skull. This constraint keeps the deformation physically meaningful because it allows the entire surface to sink inward or along the skull surface; however, only in the region of the craniotomy can it bulge outward.

The output of the finite element analysis is the displacement at every node in the brain mesh. Since the goal is to produce a displacement field at every point of the original MRI image from which the mesh was obtained, it was necessary to resample the resulting displacements in image space. This was performed using trilinear interpolation.

3 Results

The above method has been applied to both phantom and in vivo cases. Although the ultimate test of the algorithm lies in its application to in vivo cases, the brain phantom provides an opportunity to test the volume finite element analysis completely before it is applied to patient data.

3.1 Volume Phantom Validation

The brain phantom, described in detail in [3], consists of a skull mold modeled from a neurosurgical patient’s MRI. This mold has a removable section corresponding to the site of that patient’s craniotomy. The brain tissue is simulated using Sylgard 527 Silicone Dielectric Gel (Dow Corning, Midland, MI) which has been proven to have the same mechanical properties of brain [13]. Deformation was created by inflating or deflating a balloon in the center of the silicone gel. To account for this balloon in the model, an additional boundary condition was set such that the deformation would cause the balloon to collapse. This was necessary due to the volume of the balloon, which is large relative to the phantom brain volume, and does not collapse physiologically in the direction of gravity, but rather inward, toward the balloon center. The total volumetric deformation can be tracked using MRI to view the MR opaque plastic markers uniformly placed throughout the phantom volume.

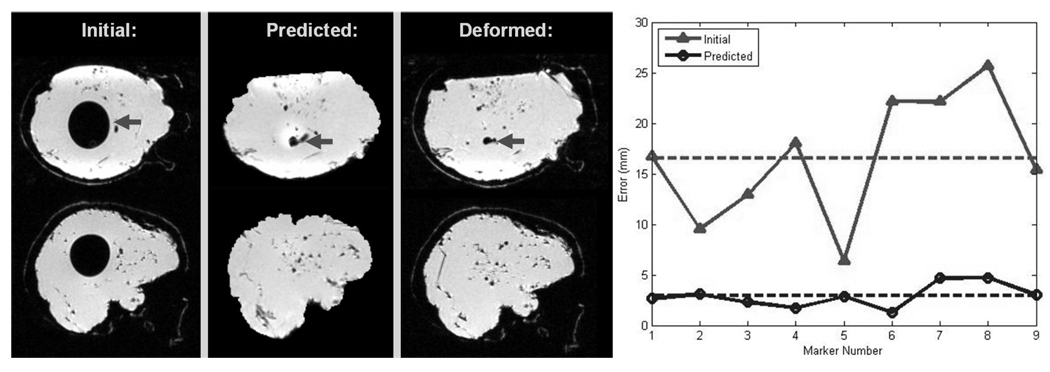
Figure 2 shows the accuracy of the volumetric deformation result. Although the mean deformation of the markers was quite high (16.56 ± 6.27 mm), the model was able to track most of the movement. The mean error was reduced to under 3 mm, accounting for 82.5% of the total deformation.

Fig. 2.

The left side shows the same slice of an Initial, Predicted, and Deformed (for validation) Phantom MR Image. The inner balloon (dark arrow) collapses in the Deformed Image and this is captured by the Predicted Image. Qualitatively, the Predicted Image appears similar in shape and deformation pattern as the image taken for validation. For quantitative comparison, the locations of nine landmarks were obtained from each of the MR images with the locations of the Deformed Image considered as the ground truth. The mean errors (16.56 mm for Initial and 2.93 mm for Predicted) are shown with dashed lines in the graph on the right.

3.2 In Vivo Data

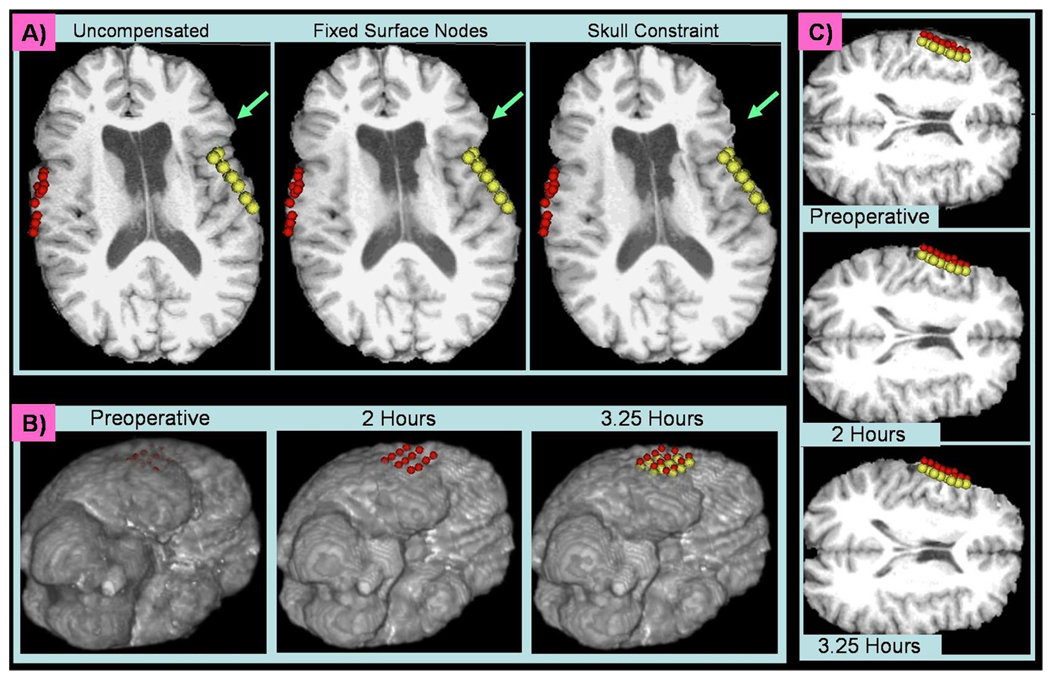
Encouraged by the results of the phantom experiments, volume deformation recovery was then applied to in vivo cases. As explained in Section 2.3, the position of the skull was used to constrain the deformation of the surface nodes that do not lie within the craniotomy region. This allows for a more physiological deformation than fixing the surface nodes that are not exposed. Figure 3A illustrates this effect on a case in which a bilateral craniotomy was performed. With fixed surface nodes, the regions near the craniotomy cannot move, even when the deformation becomes large. This effect is most obvious in the region indicated by the aqua arrow, which is located in the same relative position on all three images. The deformation decreases sharply to zero outside the craniotomy region if the surface nodes are fixed. However, when constrained by the skull, the region indicated by the aqua arrow is allowed to deform inward as well, resulting in a more natural deformation.

Fig. 3.

A) A slice of the preoperative MRI (left) which has either been deformed using fixed surface nodes (middle) or a skull constraint (right). The red and yellow spheres indicate the surface points acquired during surgery. The aqua arrows are located in the same location on each image. B) One slice of the preoperative (right) and predicted intraoperative initial (middle) and final (left) MR image. As the surface sinks toward the midline over time, the deformation is propagated through the hemisphere and the ventricle begins to collapse. The red spheres were acquired by the neurosurgeon two hours into surgery and the yellow spheres were acquired 75 minutes later. C) Volume Renderings of the Preoperative (left) and Predicted (middle and right) MR Images. The same red and yellow spheres from (B) are plotted here relative to the volume renderings of the deforming brain.

To check for deformation consistency, volumetric model deformation calculations also were performed at two time points of a single surgery. Figure 3B shows the surface deformation over time relative to a set of intraoperative points acquired 2 hours into surgery (red) and 3.25 hours into surgery (yellow). Though a rigid midline was not added as a constraint, the relatively small amount of deformation confines the movement mostly to a single hemisphere. However, the deformation is significant enough to cause a noticeable change in the size of the ipsilateral ventricle. Figure 3C shows the same deformation in a 3D view.

4 Discussion

A simple, efficient method of semiautomatic sulci segmentation was outlined in this paper. Using these semiautomatically extracted sulci resulted in better cortical surface tracking. Although accurate sulcal segmentation of the whole brain has been proposed before, through the use of deformable atlases or other techniques such as neural networks [14], these algorithms are more computationally expensive and time-consuming than the simple sulcal extraction proposed here. Though some types of research may require the use of these other methods, this work has shown that for the purposes of brain deformation recovery, the method proposed in this paper produces reliable results.

The proposed LEM also produced promising results. In phantom experiments, the LEM was able to compensate for large deformations, as are often seen intraoperatively. However, the need for an additional term to account for the internal balloon’s collapse may indicate that a more detailed model, such as one which takes into account cerebrospinal fluid drainage or the collapse of fluid-filled ventricles, is necessary in cases of large in vivo deformations. Future work with this model will therefore involve quantitative analysis of the in vivo data and assessment using volumetric intraoperative imaging. However, qualitatively, the proposed biomechanical model produced consistent and visually accurate results in vivo.