Summary
Background
Around 80% of all cardiovascular deaths occur in developing countries. Assessment of those patients at high risk is an important strategy for prevention. Since developing countries have limited resources for prevention strategies that require laboratory testing, we assessed if a risk prediction method that did not require any laboratory tests could be as accurate as one requiring laboratory information.
Methods
The National Health and Nutrition Examination Survey (NHANES) was a prospective cohort study of 14 407 US participants aged between 25–74 years at the time they were first examined (between 1971 and 1975). Our follow-up study population included participants with complete information on these surveys who did not report a history of cardiovascular disease (myocardial infarction, heart failure, stroke, angina) or cancer, yielding an analysis dataset N=6186. We compared how well either method could predict first-time fatal and non-fatal cardiovascular disease events in this cohort. For the laboratory-based model, which required blood testing, we used standard risk factors to assess risk of cardiovascular disease: age, systolic blood pressure, smoking status, total cholesterol, reported diabetes status, and current treatment for hypertension. For the non-laboratory-based model, we substituted body-mass index for cholesterol.
Findings
In the cohort of 6186, there were 1529 first-time cardiovascular events and 578 (38%) deaths due to cardiovascular disease over 21 years. In women, the laboratory-based model was useful for predicting events, with a c statistic of 0·829. The c statistic of the non-laboratory-based model was 0·831. In men, the results were similar (0·784 for the laboratory-based model and 0·783 for the non-laboratory-based model). Results were similar between the laboratory-based and non-laboratory-based models in both men and women when restricted to fatal events only.
Interpretation
A method that uses non-laboratory-based risk factors predicted cardiovascular events as accurately as one that relied on laboratory-based values. This approach could simplify risk assessment in situations where laboratory testing is inconvenient or unavailable.
Introduction
Cardiovascular disease is one of the leading causes of death worldwide,1 with 80% of cases occurring in low-income and middle-income countries.2,3 Some developing countries spend less than US$27 per head on health care each year, compared with $3727 in high-income countries.4 Because of the limited resources available in low-income settings, finding low-cost strategies for prevention of cardiovascular disease is a priority. A well-established primary prevention strategy is to use prediction rules or risk scores to identify those at higher risk in order to target specific behavioural or drug interventions. Most risk scores have included age, sex, hypertension, smoking status, diabetes mellitus, lipid values, or family history.5–8
Unfortunately, less attention has been directed at developing risk scores that would be easier to use in clinical practice without loss of predictive discrimination. In developed countries, a prediction rule that requires a laboratory test is an inconvenience; but in low-income countries, with limited testing facilities, such analysis can be too expensive to use at all. Cardiovascular disease prediction charts with and without the need for cholesterol testing for the different world regions have been released by WHO, but have not been compared with any of the standard prediction rules or validated in any cohort.9–11 In an attempt to simplify risk prediction, we assessed in a real cohort whether a prediction rule that does not need laboratory testing could predict cardiovascular disease events as effectively as one that uses laboratory-based values. Both models were assessed in the National Health and Nutrition Examination Survey (NHANES) Follow-up Study cohort.
Methods
We compared two risk prediction models: the laboratory-based model, which required blood testing, and the non-laboratory-based model, which required only history and physical examination measures. We compared how well either model could predict first-time fatal and non-fatal cardiovascular events in the NHANES I Epidemiologic Follow-up Study (NHEFS) cohort. In the laboratory-based model we used similar risk factors to those used in the Framingham risk score—sex, age (years), systolic blood pressure (mm Hg), smoking status (past or current vs never), total cholesterol, reported diabetes status (yes/no), and current treatment for raised blood pressure (yes/no). High-density lipoprotein (HDL) was not measured in NHEFS, and thus is not included in the prediction model. In our non-laboratory-based model we used the same risk factors but replaced total cholesterol with body-mass index.
Study population
NHANES I used multistage, stratified, probability sampling to select a representative sample of US individuals, a non-institutionalised population aged 1–74 years.12 NHEFS was a prospective cohort study of all NHANES I participants aged between 25–74 years (N=14 407) at the time they were first examined (between 1971 and 1975). The study was designed to assess the relation between various factors measured at baseline and the development of events over time. Some of the surveys had additional information gathered beyond the baseline medical examination and laboratory measurements, including questionnaires about previous conditions and information on smoking status at baseline. Our study population included participants with complete information in these surveys who did not report a history of cardiovascular disease (myocardial infarction, heart failure, stroke, angina) or cancer, yielding an analysis dataset N=6186.
Procedures
Baseline information included a medical history, medical examination, anthropometric measurements, and laboratory testing between 1971 and 1975. The baseline questionnaires included information about previous medical conditions, smoking status, and medication use in the past 6 months. Frozen blood samples were sent to the Centers for Disease Control and Prevention for measurement of total serum cholesterol using standard techniques.
Members of the original cohort then provided additional information in designated follow-up studies in 1982–84, 1987, and 1992.13–16 NHEFS obtained information on mortality, overnight stays at health care facilities and nursing homes, medical history, and current health status. Medical records, pathology reports, and electrocardiographs were collected and reviewed by investigators from the National Institutes of Health and the National Center for Health Statistics. All cardiovascular disease events that were classified by International Classification of Diseases, ninth revision (ICD-9) on discharge documentation and that occurred between the baseline survey and subsequent follow-up were included. Nearly all deaths (98%) were verified with death certificates and cause of deaths coded with the ICD-9. The validity of using outcome data from these sources has been reported elsewhere.17
Statistical analysis
We used Cox proportional hazards regression to assess the laboratory-based model and compared it with the non-laboratory-based model. Our outcome was a collection of endpoints for cardiovascular disease: death, myocardial infarction, stroke, congestive heart failure, and coronary revascularisation including coronary artery bypass grafting and percutaneous transluminal coronary angioplasty. We also assessed the models with the more restricted outcomes of cardiovascular disease and deaths. Outcomes were modelled through the last follow-up period in 1992. All continuous variables (age, systolic blood pressure, total cholesterol, and body-mass index) were transformed using natural logs as done in the Framingham study.18 All statistical analyses were done with SAS (version 9), and all testing was done at the 5% significance level.
The predictive discrimination of the two models was assessed over a series of characteristics: sensitivity, specificity, positive and negative predictive values, and the percentage correctly classified. These test char acteristics were assessed at four different levels of 5-year risk, using leave-one-out cross-validation, which provided a less optimistically biased assessment of the predictive accuracy. In leave-one-out cross-validation, for a given observation, the model was fit excluding that observation from the dataset and the observation classified on the basis of the resulting fitted model. This process was repeated for every observation in the dataset and the results were combined. By excluding a given observation it cannot potentially affect the fitted model used to classify itself, which ensured an unbiased estimate of predictive discrimination.
In addition to the predictive test characteristics, we used receiver operator characteristic (ROC) curves based on the Cox regression models. The ROC curve measures the discrimination of a prediction model and is the graph of the true-positive rate (sensitivity) against the false-positive rate (1-specificity). The c statistic (or area under the curve) is a useful single-number summary and represents an estimate of the probability that the model assigns a higher risk to those who have cardiovascular disease events than to those who do not.19,20 An ROC curve was constructed for each model and the c statistic for each model was calculated. The Hosmer and Lemeshow goodness of fit statistic was also calculated for calibration of the models. Cox regression models were also run using SUDAAN statistical analysis software to assess the effect of the complex sampling design of NHEFS. Analyses included participants who were lost to follow-up; results were roughly the same with and without the inclusion of these individuals.
Role of the funding source
The funding source had no role in study design, data collection, data analysis, data interpretation, or writing of the report. The corresponding author had full access to all the data in the study and had final responsibility for the decision to submit for publication.
Results
The baseline characteristics of the population are listed in table 1. By design, the NHANES cohort was representative of the adult population in the USA. With the exception of higher rates of smoking in men and a higher proportion of women receiving treatment for hypertension, the risk factor distributions were similar between the sexes. During the 21 year follow-up, there were 44 509 person-years of follow up. Overall, there were 3400 events related to cardiovascular disease among 1529 individuals. The 578 deaths due to cardiovascular disease represented 38% of all deaths in the cohort.
Table 1.
Risk factor profile in the NHEFS population
| Women (n=3349) |
Men (n=2837) | |
|---|---|---|
| Age, years | 47·4 (14·1) | 48·3 (14·0) |
| Systolic blood pressure (mm Hg) | 131·0 (23·3) | 133·8 (19·8) |
| Total cholesterol (mg/dL) | 222·5 (48·1) | 218·9 (44·6) |
| Current smoking (%) | 36·19 | 48·64 |
| Past smoking (%) | 10·27 | 24·92 |
| Diabetes (%) | 4·09 | 3·56 |
| Body-mass index | 25·5 (5·7) | 25·8 (4·13) |
| Current treatment for hypertension (%) | 11·41 | 7·65 |
Data are mean (SD).
Table 2 shows the β coefficients, standard errors, and p values for the two Cox regression models predicting cardiovascular disease events. Both predictive models adequately discriminated risk. In women, the laboratory-based model was useful for predicting events, with a c statistic (95% CI) of 0·829 (0·813–0·845). The c statistic of the non-laboratory-based model was 0·831 (0·816–0·847). The test for significant difference between the two c statistics was a χ2 result of 2·476 (p=0·116). In men, the c statistic for the laboratory-based model was 0·784 (0·766–0·801) and for the non-laboratory-based model was 0·783 (0·765–0·800). The test for significant difference between the two c statistics was a χ2 result of 0·555 (p=0·457).
Table 2.
Laboratory-based and non laboratory-based models for predicting cardiovascular disease outcomes
| Women (n=3349) | Men (n=2837) | |||||||
|---|---|---|---|---|---|---|---|---|
| β | SE | HR | p value | β | SE | HR | p value | |
| Laboratory-based* | ||||||||
| Age† | 3·702 | 0·226 | 40·527 | <0·0001 | 3·444 | 0·180 | 31·27 | <0·0001 |
| Systolic blood pressure† | 1·842 | 0·260 | 6·310 | <0·0001 | 1·706 | 0·247 | 5·507 | <0·0001 |
| Current smoker | 0·551 | 0·083 | 1·735 | <0·0001 | 0·547 | 0·072 | 1·728 | <0·0001 |
| History of diabetes | 0·711 | 0·131 | 2·037 | <0·0001 | 0·688 | 0·145 | 1·990 | <0·0001 |
| History of blood pressure treatment |
0·382 | 0·093 | 1·466 | <0·0001 | 0·246 | 0·105 | 1·99 | <0·0001 |
| Total cholesterol† | 0·577 | 0·205 | 1·780 | 0·005 | 0·767 | 0·183 | 2·154 | 0·0191 |
| Non-laboratory-based‡ | ||||||||
| Age† | 3·904 | 0·218 | 49·608 | <0·0001 | 3·560 | 0·182 | 35·196 | <0·0001 |
| Systolic blood pressure† | 1·545 | 0·267 | 4·689 | <0·0001 | 1·627 | 0·251 | 5·091 | <0·0001 |
| Current smoker | 0·571 | 0·083 | 1·770 | <0·0001 | 0·568 | 0·073 | 1·766 | <0·0001 |
| History of diabetes | 0·649 | 0·130 | 1·914 | <0·0001 | 0·641 | 0·145 | 1·898 | <0·0001 |
| History of blood pressure treatment |
0·367 | 0·092 | 1·443 | <0·0001 | 0·220 | 0·105 | 1·246 | 0·037 |
| Body-mass index† | 0·847 | 0·198 | 2·332 | <0·0001 | 0·727 | 0·242 | 2·069 | 0·0026 |
HR=hazard ratio. β=beta coefficient.
C statistic (95% CI): 0·829 (0·813–0·845) for women; 0·784 (0·766–0·801) for men.
Natural logarithm of the continuous variable.
C statistic (95% CI): 0·831 (0·816–0·847) for women; 0·783 (0·765–0·800) for men.
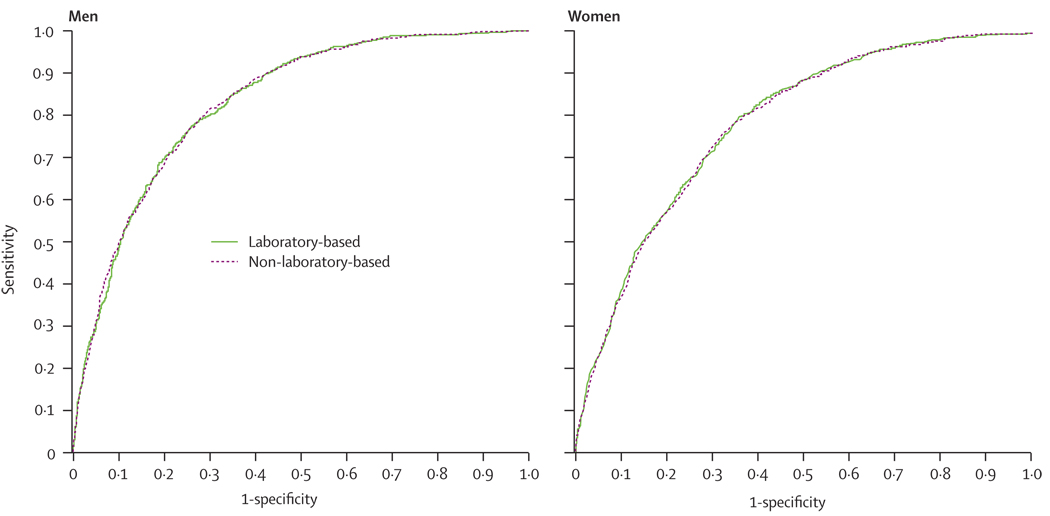
The ROC curves in figure 1 show the large amount of overlap in the predictive discrimination of the two models for both women and men. Adding body-mass index to the laboratory-based model did not improve the predictive discrimination in either sex (c statistic 0·785 for men and 0·833 for women).
Figure 1.
ROC curves for laboratory-based and non-laboratory-based methods for prediction of cardiovascular disease
A broad definition of cardiovascular disease, including revascularisation, was used, but the difference between the two models remained small with narrower endpoints. The analysis with cardiovascular deaths only resulted in c statistics of 0·820 for the laboratory model and 0·821 for the non-laboratory model in the men, with similar results for women (0·858 for laboratory-based and 0·860 non-laboratory-based). An analysis using total death as the endpoint, where the possibility of misclassification is kept to a minimum, yielded c statistics of 0·85 for women and 0·86 for men in the non-laboratory-based models; the c statistics were no different in the laboratory-based models.
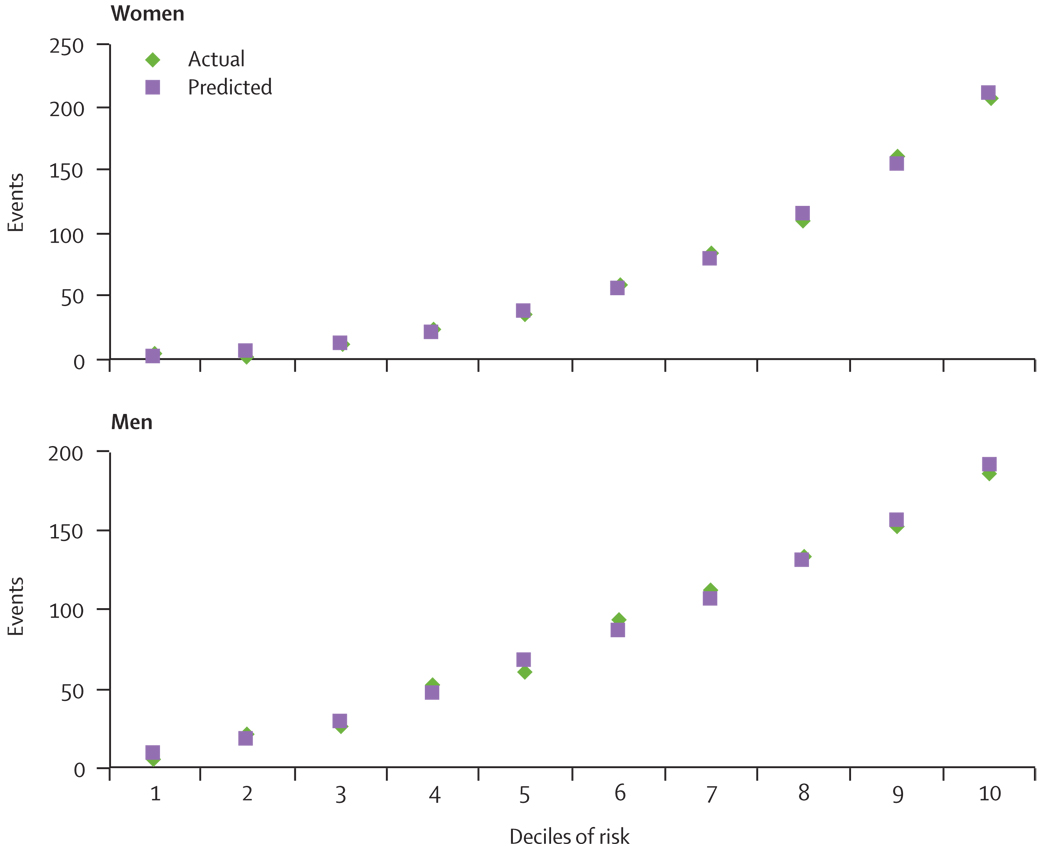
The Hosmer and Lemeshow goodness of fit results for the laboratory-based models suggest good calibration across the various levels of absolute risk. χ2 was 6·70 (p=0·570) for men and 6·62 (p=0·579) for women. For the non-laboratory-based model, χ2 values of 6·61 (p=0·579) for men and 3·45 (p=0·903) for women also suggest that the estimates of both models fit the data. The calibration of the non-laboratory-based model is shown in figure 2, indicating the predicted and actual events across the 10 deciles of risk for men and women.
Figure 2.
Actual and predicted cardiovascular disease events by deciles of risk for the non-laboratory-based model
The predictive discrimination of both models against the various screening test characteristics is shown in table 3. There was no significant difference in any of the characteristics between the two models at each of the risk thresholds tested for women or men. The sensitivity and specificity of both tests were also similar for each model at each risk threshold. As expected, the sensitivity declined and specificity increased for both models as the risk threshold definition increased. Sensitivity was 85% (men) and 77% (women) at the lowest threshold (5%, 5-year risk) and less than 10% at the highest threshold (30%, 5-year risk). The positive predictive value for both models was roughly 75% for both sexes when the threshold was a 5-year risk of cardiovascular disease greater than 30%. The negative predictive value for both models was greater than 80% (women) and 70% (men) at all levels of risk.
Table 3.
Predictive discrimination of models at different 5-year cardiovascular risk thresholds
| 5% | 10% | 20% | 30% | |
|---|---|---|---|---|
| Women | ||||
| Sensitivity (95% CI) | ||||
| Laboratory-based model | 76·8 (73·6–79·9) | 51·7 (48·0–55·4) | 18·3 (15·6–21·3) | 5·0 (3·5–6·9) |
| Non-laboratory-based model | 76·4 (73·2–79·5) | 53·5 (49·8–57·2) | 17·6 (15·0–20·8) | 5·1 (3·6–7·0) |
| Specificity (95% CI) | ||||
| Laboratory-based model | 73·4 (71·7–75·1) | 88·3 (87·0–89·5) | 97·5 (96·8–98·0) | 99·5 (99·2–99·8) |
| Non-laboratory-based model | 73·5 (71·8–75·2) | 88·4 (87·1–89·6) | 97·7 (97·1–98·3) | 99·5 (99·2–99·7) |
| Positive predictive value (95% CI) | ||||
| Laboratory-based model | 44·2 (41·4–47·0) | 54·8 (51·0–58·6) | 66·3 (59·3–72·9) | 75·0 (60·4–86·4) |
| Non-laboratory-based model | 44·2 (41·4–47·0) | 55·9 (52·2–59·6) | 68·1 (60·9–74·7) | 74·0 (59·7–85·4) |
| Negative predictive value (95% CI) | ||||
| Laboratory-based model | 92·0 (90·8–93·2) | 87·0 (85·6–88·2) | 81·3 (80·0–82·7) | 80·4 (79·0–81·7) |
| Non-laboratory-based model | 91·9 (90·7–93·0) | 87·4 (86·1–88·6) | 81·2 (79·8–82·6) | 80·4 (79·0–81·7) |
| Men | ||||
| Sensitivity (95% CI) | ||||
| Laboratory-based model | 85·0 (82·4–87·3) | 60·4 (57·1–63·7) | 26·0 (23·0–29·1) | 8·9 (7·1–11·0) |
| Non-laboratory-based model | 84·8 (82·4–87·1) | 60·2 (56·9–63·5) | 24·8 (21·9–27·8) | 8·8 (7·0–10·9) |
| Specificity (95% CI) | ||||
| Laboratory-based model | 57·8 (55·4–59·9) | 78·5 (76·6–80·3) | 93·7 (92·6–94·8) | 98·6 (98·0–99·1) |
| Non-laboratory-based model | 56·7 (54·5–59·0) | 78·3 (76·4–80·1) | 93·7 (92·5–94·7) | 98·6 (98·0–99·1) |
| Positive predictive value (95% CI) | ||||
| Laboratory-based model | 47·1 (44·6–49·6) | 55·5 (52·2–58·9) | 64·9 (59·6–69·9) | 73·6 (64·1–81·7) |
| Non-laboratory-based model | 46·5 (44·0–49·0) | 55·2 (52·0–58·4) | 63·5 (58·2–68·7) | 74·4 (64·5–82·1) |
| Negative predictive value (95% CI) | ||||
| Laboratory-based model | 89·6 (87·8–91·3) | 81·7 (79·9–83·4) | 74·1 (72·3–75·8) | 71·2 (69·5–72·9) |
| Non-laboratory-based model | 89·3 (87·5–91·0) | 81·6 (79·8–83·3) | 73·7 (72·0–75·5) | 70·9 (69·2–72·6) |
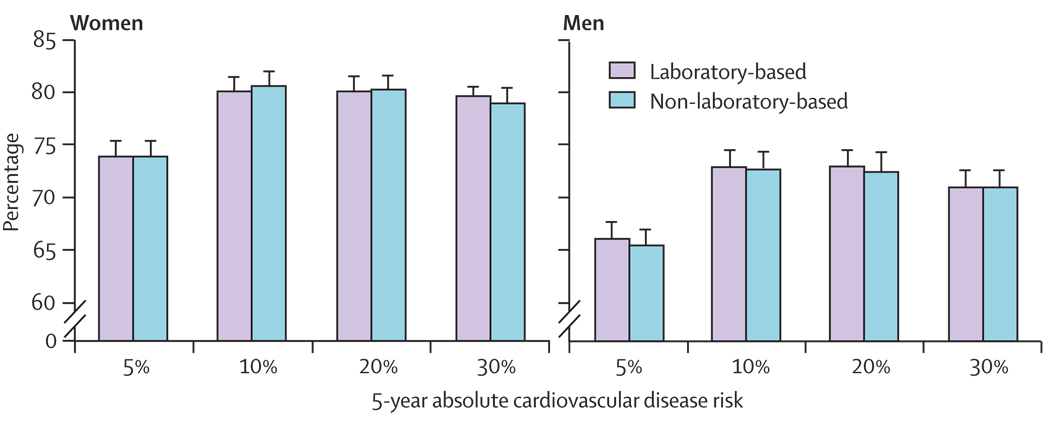
The c statistic is a good summary value of the overall predictive discrimination of the two models. However, since most clinical decisions regarding treatment are often based on a specific absolute level of risk, we sought to establish if the risk models differentially classified patients correctly at four different levels of 5-year risks for cardiovascular disease commonly used in guidelines. The percentage correctly classified is determined by adding up the number of true negatives (those below the risk threshold who did not go on to have a cardiovascular disease event) and the true positives (those who were above the risk threshold and eventually did have an event) divided by the total number of individuals in the sample (figure 3). The two different models correctly classified the patients at the same rates across the four commonly used risk levels in clinical guidelines. Both models correctly classified over 80% of women and 70% of men when the threshold for risk of an outcome during follow-up (over 5 years) was set at 10% or greater. This percentage correctly classified dropped as the risk threshold dropped, with both models correctly classifying 75% of women and 65% of men when the 5% threshold was used. Results using SUDAAN were similar to results using the cohort unadjusted for the sampling. For example, the non-laboratory model of the whole cohort for both the adjusted was 0·8050 and unadjusted was 0·8054. Similar results were also seen for the laboratory-based model (0·806 adjusted and 0·805 unadjusted). Analyses included participants who were lost to follow-up; results were much the same with and without the inclusion of these individuals.
Figure 3.
Patients correctly classified as high or low risk at various cutoff levels of 5-year risk
Discussion
Our study shows that a non-laboratory-based risk method that uses information easily obtained in one outpatient visit can predict cardiovascular disease outcomes as accurately as one that requires laboratory testing. Our values of predictive discrimination of 0·83 (women) and 0·78 (men) for the non-laboratory-based model are no different than the corresponding values in the laboratory-based model. Further, this study showed that the prediction method in the NHEFS cohort using these easily obtainable risk factors (age, systolic blood pressure, smoking status, blood pressure treatment status, history of diabetes mellitus, and body-mass index) was as useful as other methods recommended for screening for cardiovascular disease6,8,21–23 with c statistics between 0·64 and 0·86.
WHO has released guidelines for the prevention of cardiovascular disease24 that included two sets of risk assessment charts. The first WHO charts used the same risk factors we used in our laboratory-based model. The second set of charts removed cholesterol and retained the remaining risk factors. This step was a positive move towards a simplified screening process in resource-poor settings; however, given that the WHO charts were not based on a cohort with prospective outcomes of cardiovascular disease, the investigators were not able to assess the predictive discrimination of either of their charts or make any comparisons between them. Further, until now, this approach has not been validated in any of the WHO regions or countries where it is intended to be used. The present study provides strong support for the WHO approach.
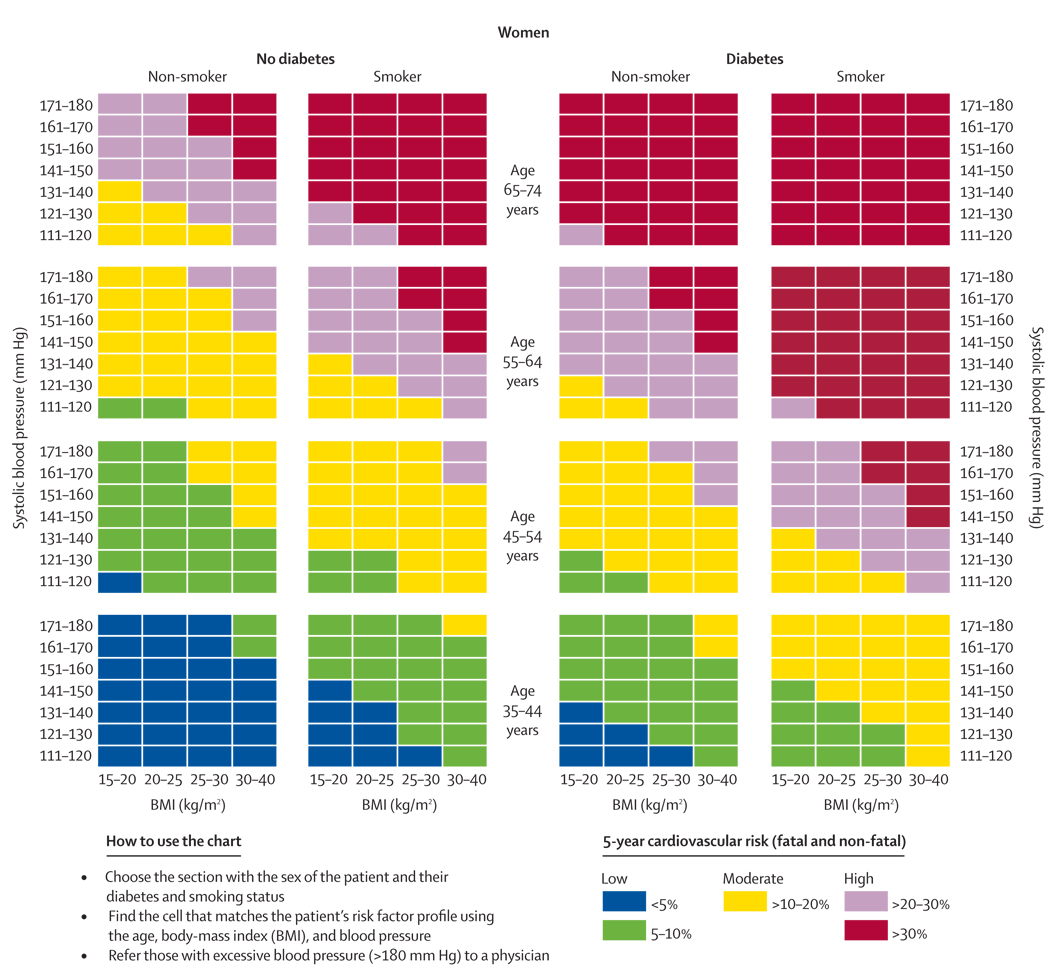
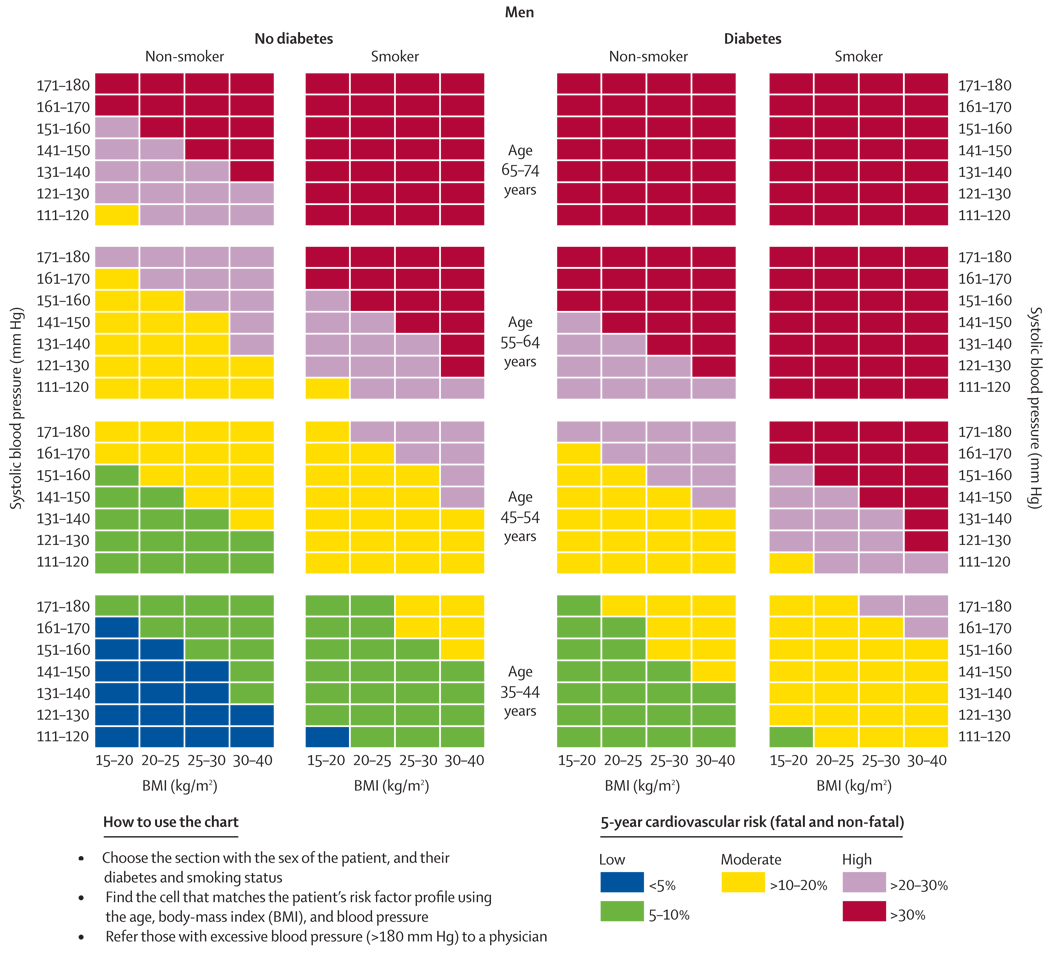
The next step in the process of moving towards wider use of simplified scoring mechanism is further validation and calibration in individual countries, which can be done in one of two ways. Countries could develop their own charts using their own cohort data. This was the process used to design the SCORE system7 for high-risk and low-risk regions of Europe. We would recommend that any country with prospective cohort data create their own non-laboratory-based charts and assess their discrimination compared with a laboratory-based method. Alternatively, countries or regions without cohort data could calibrate the risk-factors using national or regional data for cardiovascular morbidity and mortality rates. This process has been done in New Zealand25 and China26 using the Framingham risk equations. Until these country or region-specific scores are available, health providers could consider using the WHO non-laboratory-based charts or the chart shown in figures 4 and 5.
Figure 4.
Risk prediction chart for cardiovascular disease using non-laboratory-based measures (women)
Figure 5.
Risk prediction chart for cardiovascular disease using non-laboratory-based measures (men)
Our chart differs from the WHO chart in that it includes body-mass index and is the only chart that is based on a model compared formally with a laboratory-based model using a prospectively followed cohort. Nonetheless, countries should recognise that the WHO charts, or our charts, might overestimate or underestimate absolute risk. The potential error in estimation would need to be weighed against the health losses associated with no screening at all. There is a similar challenge whenever data from one country are generalised to another, whether it is for risk prediction or intervention trials. The results of the INTERHEART27 study suggest, however, that the relative risks are similar across most countries, so the ranking of individuals according to relative risk is preserved even if absolute risk is overestimated or underestimated. Resources can still be efficiently allocated to those at highest risk by adjusting treatment thresholds according to an individual country’s priorities.
In addition to the overall predictive discrimination, there are other reasons for focusing on a non-laboratory screening method in developing countries. The first includes its ability to correctly classify patients at the thresholds that most prevention guidelines choose for initiating treatment. Other considerations include practicality, cost, and feasibility. The non-laboratory-based model correctly classified most men and women at the 10% and 20% 5-year risk thresholds and was not inferior to the laboratory-based model. At most, the rates of correct classification differed by less than 1% and none of the differences were significant (figure 3).
In practical terms, if a patient has difficulty returning for a fasting blood test (if even available) on a different day, then the opportunity to assist in prevention is lost. The advantage of a non-laboratory-based method of risk prediction is that it can be applied in one clinic visit with minimum equipment needed—tape measure, scale, and sphygmamometer or automated blood pressure machine. A risk prediction value can be ascertained and a treatment decision can be made within the same 5–10 min visit without the cost or the time needed to wait for laboratory results. Others have suggested that waist-to-hip ratio is also easily measured and could add greater predictive discrimination over body-mass index. However, whether the measurement of waist-to-hip ratio in routine practice is as easy to accurately measure as body-mass index is not clear. If it is better in practice, this method would even strengthen the non-laboratory-based model. Unfortunately, waist-to-hip ratio measurements were not available in the NHEFS baseline dataset to confirm this suggestion.
In developed countries, the added cost of cholesterol testing is about $10 for the test and an additional $20–$80 if an additional visit is needed. The rates for developing countries are $1–$3 for the test and $3–$7 for an additional visit.28 In India, which spends around $31 per person on health care each year,4 guidelines recommending cholesterol screening to risk stratify patients would need more than 10% of the entire Indian health-care budget to be devoted to this one laboratory test with little or no added benefit beyond what is already available without laboratory testing. Therefore, the added costs of cholesterol testing would make screening with laboratory-based guidelines prohibitive. Further, in many developing countries, the personal cost of being seen at a health facility can be quite high. A patient often must take a day off work to see the nurse or doctor. There are additional costs of the health-care workers’ time. Finally, most countries do not have the facilities or health-care workforce to implement such laboratory-based screening.
We could imagine a two-tiered approach to the management of those at risk for cardiovascular disease. Those who are at low risk could be given advice about a healthy lifestyle and be reassessed in 5–10 years. Our negative predictive value of around 90% for men and women at low risk suggests that this strategy is reasonable. Those who are at high risk could be provided with counselling about possible risk-factor management and possibly medical treatments such as a multidrug regimen like the polypill where resources are available. Lim and colleagues11 in the Lancet Chronic Diseases Series recommended the use of a chart with the same non-laboratory-based risk factors to identify those eligible for a multidrug intervention. Like the WHO charts, this method has not been validated in a cohort, although the positive predictive value of 75% for those at high risk also suggests this strategy is reasonable. For people at the boundary of low risk and high risk, laboratory testing might be useful for further risk stratifying for certain individuals when available.
Several attempts to enhance the predictive discrimination of the Framingham Heart Study score by adding biomarkers have had mixed results. The analyses in the Atherosclerosis Risk in Communities (ARIC) Study29 and the Framingham Off spring Study30,31 suggested that little additional information was gained when other blood-based novel risk factors were added to the traditional risk factors. However, the Reynolds32 score for women, which added hsCRP and haemoglobin A1c, had a marginally higher c statistic (0·808) than the Framingham covariates (0·791), but led to a reclassification of many women to higher or lower risk groups.
One limitation of our study is that it represents a population from the USA. We do not know whether the proposed risk score would be as useful in developing countries. Unfortunately, few low-income countries have cohort data to make these estimates. As a result, most countries have been using the Framingham risk equation or similar with blood-based parameters to support their guidelines. Our results suggest that this simpler method is probably no worse yet substantially cheaper and simpler to implement. Also, this cohort from the 1970s has a risk distribution and treatment levels that are similar to many developing countries that are currently going through the same stage of epidemiological transition that the USA cohort was at the time. The high prevalence of smoking, especially in men, is typical of low-income and middle-income countries (around 49% for men).33 Also, the prevalence (36%) of hypertension in the NHANES I cohort34 is similar to the rates seen in eastern Europe and Latin America.35 Rates of treatment for hypertension were only about 10% and there was no use of statins throughout most of the time of the cohort follow-up.
Another limitation is that we used total cholesterol, but did not include HDL cholesterol as is done in the updated Framingham5 and Procam6 scoring mechanism, since this information was not collected in NHANES I. Total cholesterol is a reasonable independent risk factor for cardiovascular disease34–38 However, the fact that a risk factor is a good independent predictor is only a necessary condition but not a sufficient condition for its inclusion in a model of multiple risk factors.39 Its added value to a list of other readily available information seems limited. The predictive discrimination of the laboratory-based model might improve if HDL was included. However, even if the model was marginally improved, whether it would be worth the added cost and inconvenience in developing countries is unclear. Certainly, cost-effectiveness analyses will need to be done to assess the additional value of HDL cholesterol to a non-laboratory-based model in other datasets.
In summary, we found that a non-laboratory-based method using blood pressure levels and treatment status, age, smoking status, body-mass index, and a history of diabetes yielded results similar to one that uses laboratory testing when predicting cardiovascular disease events. Further, this risk factor information can be obtained non-invasively in about 5–10 min. Although this method requires further validation and calibration, use of a simple non-laboratory approach, as suggested by the WHO, could have profound effects on the affordability and availability of an adequate screening programme in developing countries. Initial screening without blood testing could lead to the quick initiation of treatment without the added cost or inconvenience of laboratory testing, and would also keep any potential loss to follow-up due to the extra step in testing to a minimum.
Acknowledgments
TAG is funded through the Fogarty International Center grant from the National Institutes of Health: 1K01TW007141-01.
Footnotes
Contributors
TAG and JMG conceived the idea and design for the study. TAG drafted the paper. TAG, CRY, and SA developed and analysed the dataset and prepared the tables and figures. GF oversaw the statistical testing. TAG and JMG interpreted the results. All authors participated in the revision of the manuscript before submission. TAG will serve as guarantor of the paper. All authors have seen and given final approval to the final text.
Conflict of interest statement
We declare that we have no conflict of interest.
References
- 1.Lopez A, Mathers C, Ezzati M, Jamison, Murray C. Global burden of disease and risk factors. Washington DC: Oxford University Press and World Bank; 2006. [PubMed] [Google Scholar]
- 2.Murray CJ, Lopez AD. Mortality by cause for eight regions of the world: Global Burden of Disease Study. Lancet. 1997;349:1269–1276. doi: 10.1016/S0140-6736(96)07493-4. [DOI] [PubMed] [Google Scholar]
- 3.Gaziano T, Reddy KS, Paccaud F, Horton S. Cardiovascular disease. In: Jamison D, et al., editors. Disease control priorities in developing countries. 2nd edn. New York: Oxford University Press and World Bank; 2006. pp. 645–662. [Google Scholar]
- 4.World Bank. Washington DC: World Bank; World development indicators. 2007
- 5.Wilson PW, D’Agostino RB, Levy D, Belanger AM, Silbershatz H, Kannel WB. Prediction of coronary heart disease using risk factor categories. Circulation. 1998;97:1837–1847. doi: 10.1161/01.cir.97.18.1837. [DOI] [PubMed] [Google Scholar]
- 6.Assmann G, Cullen P, Schulte H. Simple scoring scheme for calculating the risk of acute coronary events based on the 10-year follow-up of the prospective cardiovascular Munster (PROCAM) study.[erratum appears in Circulation 2002; 105: 900] Circulation. 2002;105:310–315. doi: 10.1161/hc0302.102575. [DOI] [PubMed] [Google Scholar]
- 7.Conroy RM, Pyorala K, Fitzgerald AP, et al. Estimation of ten-year risk of fatal cardiovascular disease in Europe: the SCORE project. Eur Heart J. 2003;24:987–1003. doi: 10.1016/s0195-668x(03)00114-3. [DOI] [PubMed] [Google Scholar]
- 8.Ferrario M, Chiodini P, Chambless LE, et al. Prediction of coronary events in a low incidence population. Assessing accuracy of the CUORE Cohort Study prediction equation. Int J Epidemiol. 2005;34:413–421. doi: 10.1093/ije/dyh405. [DOI] [PubMed] [Google Scholar]
- 9.Lindholm LH, Mendis S. Prevention of cardiovascular disease in developing countries. Lancet. 2007;370:720–722. doi: 10.1016/S0140-6736(07)61356-7. [DOI] [PubMed] [Google Scholar]
- 10.Mendis S, Lindholm LH, Mancia G, et al. World Health Organization (WHO) and International Society of Hypertension (ISH) risk prediction charts: assessment of cardiovascular risk for prevention and control of cardiovascular disease in low and middle-income countries. J Hypertens. 2007;25:1578–1582. doi: 10.1097/HJH.0b013e3282861fd3. [DOI] [PubMed] [Google Scholar]
- 11.Lim SS, Gaziano TA, Gakidou E, et al. Prevention of cardiovascular disease in high-risk individuals in low-income and middle-income countries: health effects and costs. Lancet. 2007;370:2054–2062. doi: 10.1016/S0140-6736(07)61699-7. [DOI] [PubMed] [Google Scholar]
- 12.US Department of Health and Human Services (DHHS) Hyattsville, MD: Centers for Disease Control and Prevention; National Center for Health Statistics. First National Health and Nutrition Examination Survey (NHANES I) 1971–1975
- 13.Cohen BB, Barbano HE, Cox CS, et al. Plan and operation of the NHANES I Epidemiologic Follow-up Study, 1982–1984: National Center for Health Statistics. Vital and Health Statistics report. 1987 [PubMed] [Google Scholar]
- 14.Finucane FF, Freid VM, Madans JH, et al. Plan and operation of the NHANES I Epidemiologic Follow-up Study, 1986: National Center for Health Statistics. Vital and Health Statistics report. 1990 [PubMed] [Google Scholar]
- 15.Cox CS, Rothwell ST, Madans JH, et al. Plan and operation of the NHANES I Epidemiologic Follow-up Study, 1987: National Center for Health Statistics. Vital and Health Statistics report. 1992 [PubMed] [Google Scholar]
- 16.Cox CS, Mussolino M, Rothwell ST, et al. Plan and operation of the NHANES I Epidemiologic Follow-up Study, 1992: National Center for Health Statistics. Vital and Health Statistics report. 1997 [PubMed] [Google Scholar]
- 17.Madans JH, Reuben CA, Rothwell ST, Eberhardt MS. Differences in morbidity measures and risk factor identification using multiple data sources: the case of coronary heart disease. Stat Med. 1995;14:643–653. doi: 10.1002/sim.4780140521. [DOI] [PubMed] [Google Scholar]
- 18.Anderson KM, Odell PM, Wilson PW, Kannel WB. Cardiovascular disease risk profiles. Am Heart J. 1991;121:293–298. doi: 10.1016/0002-8703(91)90861-b. [DOI] [PubMed] [Google Scholar]
- 19.Harrell FE, Jr, Califf RM, Pryor DB, Lee KL, Rosati RA. Evaluating the yield of medical tests. JAMA. 1982;247:2543–2546. [PubMed] [Google Scholar]
- 20.Pencina MJ, D’Agostino RB. Overall C as a measure of discrimination in survival analysis: model specific population value and confidence interval estimation. Stat Med. 2004;23:2109–2123. doi: 10.1002/sim.1802. [DOI] [PubMed] [Google Scholar]
- 21.Conroy RM, Pyorala K, Fitzgerald AP, et al. Estimation of ten-year risk of fatal cardiovascular disease in Europe: the SCORE project. Eur Heart J. 2003;24:987–1003. doi: 10.1016/s0195-668x(03)00114-3. [DOI] [PubMed] [Google Scholar]
- 22.D’Agostino RB, Sr, Grundy S, Sullivan LM, Wilson P CHD Risk Prediction Group. Validation of the Framingham coronary heart disease prediction scores: results of a multiple ethnic groups investigation. JAMA. 2001;286:180–187. doi: 10.1001/jama.286.2.180. [DOI] [PubMed] [Google Scholar]
- 23.Collinson P. Of bombers, radiologists, and cardiologists: time to ROC. Heart. 1998;80:215–217. doi: 10.1136/hrt.80.3.215. [DOI] [PubMed] [Google Scholar]
- 24.WHO. Prevention of cardiovascular disease. Geneva: World Health Organization; Guidelines for the assessment and management of total cardiovascular risk. 2007
- 25.National Health Committee. Wellington, New Zealand: Core Services Committee, Ministry of Health; Guidelines for the management of mildly raised blood pressure in New Zealand. 1995
- 26.Liu J, Hong Y, D’Agostino RB, Sr, et al. Predictive value for the Chinese population of the Framingham CHD risk assessment tool compared with the Chinese Multi-Provincial Cohort Study. JAMA. 2004;291:2591–2599. doi: 10.1001/jama.291.21.2591. [DOI] [PubMed] [Google Scholar]
- 27.Yusuf S, Hawken S, Ounpuu S, et al. Effect of potentially modifiable risk factors associated with myocardial infarction in 52 countries (the INTERHEART study): case-control study. Lancet. 2004;364:937–952. doi: 10.1016/S0140-6736(04)17018-9. [DOI] [PubMed] [Google Scholar]
- 28.Rodgers A, Lawes C, Gaziano T, Vos T. The growing burden of risk from high blood pressure, cholesterol, and bodyweight. In: Jamison D, editor. Disease control priorities in developing countries. New York: Oxford University Press and the World Bank; 2006. [PubMed] [Google Scholar]
- 29.Folsom AR, Chambless LE, Ballantyne CM, et al. An assessment of incremental coronary risk prediction using C-reactive protein and other novel risk markers: the Atherosclerosis Risk in Communities Study. Arch Intern Med. 2006;166:1368–1373. doi: 10.1001/archinte.166.13.1368. [DOI] [PubMed] [Google Scholar]
- 30.Wang TJ, Gona P, Larson MG, et al. Multiple biomarkers for the prediction of first major cardiovascular events and death. N Engl J Med. 2006;355:2631–2639. doi: 10.1056/NEJMoa055373. [DOI] [PubMed] [Google Scholar]
- 31.Ware JH. The limitations of risk factors as prognostic tools. N Engl J Med. 2006;355:2615–2617. doi: 10.1056/NEJMp068249. [DOI] [PubMed] [Google Scholar]
- 32.Ridker PM, Buring JE, Rifai N, Cook NR. Development and validation of improved algorithms for the assessment of global cardiovascular risk in women: the Reynolds Risk Score. JAMA. 2007;297:611–619. doi: 10.1001/jama.297.6.611. [DOI] [PubMed] [Google Scholar]
- 33.Jha P, Chaloupka FJ, Moore J, et al. Tobacco addiction. In: Jamison D, et al., editors. Disease control priorities in developing countries. 2nd edn. New York: Oxford University Press and the World Bank; 2006. pp. 869–885. [Google Scholar]
- 34.Burt VL, Cutler JA, Higgins M, et al. Trends in the prevalence, awareness, treatment, and control of hypertension in the adult US population. Data from the health examination surveys, 1960 to 1991. Hypertension. 1995;26:60–69. doi: 10.1161/01.hyp.26.1.60. [DOI] [PubMed] [Google Scholar]
- 35.Kearney PM, Whelton M, Reynolds K, Muntner P, Whelton PK, He J. Global burden of hypertension: analysis of worldwide data. Lancet. 2005;365:217–223. doi: 10.1016/S0140-6736(05)17741-1. [DOI] [PubMed] [Google Scholar]
- 36.Law MR, Wald NJ, Thompson SG. By how much and how quickly does reduction in serum cholesterol concentration lower risk of ischaemic heart disease? BMJ. 1994;308:367–372. doi: 10.1136/bmj.308.6925.367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Law MR, Wald NJ, Wu T, Hackshaw A, Bailey A. Systematic underestimation of association between serum cholesterol concentration and ischaemic heart disease in observational studies: data from the BUPA study. BMJ. 1994;308:363–366. doi: 10.1136/bmj.308.6925.363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gofman JW, Lindgren F. The role of lipids and lipoproteins in atherosclerosis. Science. 1950;111:166–171. doi: 10.1126/science.111.2877.166. [DOI] [PubMed] [Google Scholar]
- 39.Greenland P, O’Malley P. When is a new prediction marker useful? A consideration of lipoprotein-associated phospholipase A2 and C-reactive protein for stroke risk. Arch Intern Med. 2005;165:2454–2456. doi: 10.1001/archinte.165.21.2454. [DOI] [PubMed] [Google Scholar]