Analysis of ¹³C^α and ¹³C^β chemical shifts of cysteine and cystine residues in proteins: a quantum chemical approach

Abstract

Cysteines possess a unique property among the 20 naturally occurring amino acids: it can be present in proteins in either the reduced or oxidized form, and can regulate the activity of some proteins. Consequently, to augment our previous treatment of the other types of residues, the ¹³C^α and ¹³C^β chemical shifts of 837 cysteines in disulfide-bonded cystine from a set of seven non-redundant proteins, determined by X-ray crystallography and NMR spectroscopy, were computed at the DFT level of theory. Our results indicate that the errors between observed and computed ¹³C^α chemical shifts of such oxidized cysteines can be attributed to several effects such as: (a) the quality of the NMR-determined models, as evaluated by the conformational-average (ca) rmsd value; (b) the existence of high B-factor or crystal-packing effects for the X-ray-determined structures; (c) the dynamics of the disulfide bonds in solution; and (d) the differences in the experimental conditions under which the observed ¹³C^α chemical shifts and the protein models were determined by either X-ray crystallography or NMR-spectroscopy. These quantum-chemical-based calculations indicate the existence of two, almost non-overlapped, basins for the oxidized and reduced –SH ¹³C^β, but not for the ¹³C^α, chemical shifts, in good agreement with the observation of 375 ¹³C^α and 337 ¹³C^β resonances from 132 proteins by Sharma and Rajarathnam (2000). Overall, our results indicate that explicit consideration of the disulfide bonds is a necessary condition for an accurate prediction of ¹³C^α and ¹³C^β chemical shifts of cysteines in cystines.

Introduction

Cystine (with disulfide bonds formed) and cysteine residues are important for protein structure and function. In their reduced form, cysteines participate in the active site of different enzymes and, together with histidine, are the two most common residues involved in the coordination of zinc ions in Zn-finger motifs (which are the most commonly observed structural motifs in transcription factors; Kornhaber et al. (2006). In the last few years, it has been recognized that disulfide bonds are not only inert structural elements. But, on the contrary, pairs of cysteines play an active role in the catalytic cycle of enzymes such as thioredoxin, switching between the reduced and oxidized forms. The activity of some proteins is regulated by the redox state of the cysteines or by their glutathionylation and nitrosylation (Wouters et al. 2007 and references therein).

In a seminal work, de Dios et al. (1993) showed that chemical shifts of proteins can be computed accurately by quantum chemical approaches. The motivation to compute ¹³C^α chemical shifts arises from the fact that they are exquisitely sensitive to, and depend mainly on, the backbone torsional angles (ϕ, ψ; Spera and Bax 1991), although the influence of the side-chain torsional angles, χ’s, cannot be disregarded (Havlin et al. 1997; Pearson et al. 1997; Xu and Case 2001; Sun et al. 2002; Villegas et al. 2007; Vila et al. 2009). This property enables us to treat each residue X of a protein as a terminally-blocked tripeptide with the sequence Ac-GXG-NMe, with X in the conformation of the experimental protein structure and, hence, permitting the parallelization of the quantum-mechanical calculations. Following this procedure, ¹³C^α chemical-shift computations are feasible for proteins of any size and topology, e.g., by using the recently-introduced CheShift server (Vila et al. 2009).

However, the above protocol to compute ¹³C^α chemical shifts for any naturally occurring amino acid in proteins breaks down for cystines because: (a) cystines cannot be treated as single tripeptides; (b) the cysteines involved in disulfide bonds usually are separated by at least four consecutive residues in the sequence, making quantum-chemical calculations impossible with existing computational resources, if all the intervening residues between the two bonded cysteines are taken into account; and (c) there is no evidence that the ¹³C^α chemical shifts for the cysteines of disulfide bonds can be obtained straightforwardly from those for reduced cysteine. For these reasons, previous calculations of ¹³C^α chemical shifts for cysteines, e.g., by using the CheShift server, were always carried out by assuming that the cysteine residues were in their reduced form.

In order to compute the ¹³C^α chemical shifts of cysteines in disulfide bonds, in this work we present an extension of an existing protocol (Vila and Scheraga 2009) that will enable us to compute the ¹³C^α chemical shifts for cysteines in disulfide bonds accurately. In order to test this new methodology, seven protein models, rich in disulfide bonds, obtained by both NMR spectroscopy and X-ray crystallography, are considered. Each of these seven proteins was subjected to a ¹³C^α-based chemical-shift validation analysis, i.e., by using the ca-rmsd (Vila et al. 2007; Vila and Scheraga 2009) as a scoring function. This analysis enables us to shed light on the origin of errors between observed and computed ¹³C^α chemical-shift values for cysteines in disulfide bonds as well as to detect the existence of local flaws in the amino acid sequence. Finally, a brief analysis of the dependence of ¹³C^α and ¹³C^β chemical shifts on the redox state of the cysteines was also carried out. This analysis enables us to determine how well the DFT-based computations of the ¹³C^α and ¹³C^β chemical shifts agree with existing statistical-based analyses of observed ¹³C^α and ¹³C^β chemical-shift distributions as functions of the oxidation state of cysteines in proteins (Sharma and Rajarathnam 2000).

Materials and methods

Experimental set of structures

A set of seven proteins was considered in this work (see Table 1). Additional information regarding the set of structures used and how they were selected can be found in the Supplementary Material.

Table 1.

Set of proteins for which the ¹³C^α chemical shift was computed

PDB codea	Experimental conditionsb	Number of residuesc	BMRB accession coded	ca-rmsde (ppm)	ca-rmsdf (ppm)
1Z2F (20)g	NMR (N/A; 290 K; 5.7)	121 (9)	[6111]	3.5	4.25 (3.56)
1M8N (1)g	X-ray (2.45 Å; 100 K; 5.2)	120 (9)		3.2	4.38 (3.68)
2I83 (20)h	NMR (N/A; 310 K; 6.7)	158 (6)	[5903]	2.45	2.21 (1.64)
1UUH (1)h	X-ray (2.2 Å; 100 K; 5.5)	150 (6)		2.47	3.1 (2.35)
1HJD (20)	NMR (N/A; 300 K; 7.0)	101(2)	[4731]	6.08	4.13 (3.65)
1I1J (1)	X-ray (1.39 Å; 100 K; 8.2)	101 (2)		5.16	3.81 (3.39)
1IK0 (30)	NMR (N/A; 298 K; 6.0)	113 (4)	[5004]	4.92	2.37 (2.01)
3BPO (1)	X-ray (3.00 Å; 100 K; 6.0)	98 (4)		5.21	2.9 (2.62)
1D2B (29)i	NMR (N/A; 293 K; 6.0)	119 (4)	[4327]	2.61	2.74 (2.27)
2J0T (1)i	X-ray (2.54 Å; 100 K; 7.5)	119 (4)		2.56	3.43 (2.84)
1BPI (1)	X-ray (1.09 Å; 125 K; N/A)	58 (6)	[5359]	1.67 [0.86]	1.65 (2.03)
1D0D (1)	X-ray (1.62 Å; 298 K; 6.5)	58 (6)		1.33 [1.09]	1.94 (2.39)
1G6X (1)	X-ray (0.86 Å; 100 K; 7.5)	58 (6)		2.39 [1.05]	1.78 (2.20)
1K6U (1)	X-ray (1.00 Å; 100 K; 7.5)	58 (6)		2.39 [0.97]	2.02 (2.49)
5PTI (1)	X-ray (1.09 Å; N/A; N/A)	57 (6)		1.66 [1.08]	1.69 (2.11)
6PTI (1)j	X-ray (1.7 Å; N/A; N/A)	56 (6)		2.37 [0.64]	1.81 (2.29)
1HA8 (20)	NMR (N/A; 290 K; 4.6)	51 (10)	[4979]	4.42	3.16 (4.57)

^aFour-symbol code for the deposited structure in the Protein Data Bank (Berman et al. 2000). In parentheses, the number of determined conformations for each protein

^bExperimental conditions under which the proteins listed in column one were determined. The resolution (Å), temperature (K) and pH, are in parentheses. For all the NMR structures, DSS was used as the reference for the observed ¹³C^α chemical shifts

^cTotal number of residues for each protein listed in column one. The number of cysteine residues in cystine for each protein is indicated between parentheses. For the same protein, and for three out of five cases, the total number of residues of each structure solved by NMR spectroscopy and X-ray crystallography are not the same; the reasons for the observed experimental difference in the total number of residues, can be found in the original papers cited in “Materials and methods” section

^dBMRB (Ulrich et al. 2007) accession number under which the observed ¹³C^α chemical shifts can be found

^eca-rmsd computed from only the cysteine residues in cystines. The ca-rmsd values without cysteine in position 14, only for the six BPTI models, are shown in brackets

^fca-rmsd computed for non-cysteine residues; in parenthesis, the normalized size-independent ca-rmsd₇₆

^gThe all heavy-atom rmsd value between the (1Z2F) NMR- and the X-ray-determined (1M8N) structure is ~0.65 Å. Differences between the 1Z2F and 1M8N models are located mainly in two loop regions (Li et al. 2005), namely for residues 90–93 and 106–110, near the C-terminal region. The X-ray-determined structure (1M8N) was solved as a dimer, but such oligomerization is not observed in solution and, hence, the NMR-determined structure (1Z2F) was solved as a monomer (Li et al. 2005). There is an odd number (nine) of cysteines listed in parentheses in column three because the observed ¹³C^α chemical-shift value for one of the cysteines is missing

^hThe X-ray determined model (1UUH) was solved without ligand bound, while the NMR-determined structure (2I83) was solved with bound ligand. Several regions of the Hyaluronan-binding domain of the CD 44 protein undergo conformational changes upon ligand binding, as reflected by a high (~7.7 Å) all-heavy-atom rmsd between the 1UUH and 2I83 protein models. Most of the conformational changes occur at the C-terminal portion, i.e., for the last ~39 residues of the protein. Excluding the C-terminal portion from the rmsd analysis, a value of ~1.8 Å is obtained, indicating that there are still significant conformational differences between the 1UUH and 2I83 protein models

ⁱThe rmsd between the X-ray model (2J0T) and the average NMR-determined conformation (1D2B) is 1.49 Å (Iyer et al. 2007). Conceivably, most of the conformational differences between these models arise from the fact that the NMR-derived structure (1D2B) was solved as a monomer while the X-ray-determined protein (2J0T) was solved as a dimer

^jProtein refined by neutron diffraction data

Method to compute ¹³C^α chemical shifts

The computations of the ¹³C^α chemical shifts involve a series of approximations: (a) for each cysteine residue C not involved in a disulfide bond, the computation of the ¹³C^α shielding was carried out on a terminally-blocked tripeptide with the sequence Ac-GCG-NMe, with C in the conformation of the regularized experimental protein structure, and the sulfhydryl group was protonated. Then, the ¹³C^α and ¹³C^β chemical shift for each amino acid residue C was computed at the OB98/6-311+G(2d,p) level of theory (Vila and Scheraga 2009), while the remaining residues in the tripeptide were treated at the OB98/3-21G level of theory, i.e., by using the locally-dense approach (Chesnut and Moore 1989; all the computed ¹³C^α and ¹³C^β shielding values $({\sigma }_{\text{subst},\text{th}}^n,\text{with }n=\alpha \text{ or }\beta )$ were calculated by using the gauge-invariant atomic orbital (GIAO) method at the DFT level of theory as implemented in the GAUSSIAN 03 suite of programs (Frisch et al. 2004); (b) each of the cysteine residues C_i and C_j (with i and j denoting the position in the sequence) forming a disulfide bond were, first, treated as a terminally-blocked tripeptide, namely, Ac-GC_iG-NMe and Ac-GC_jG-NMe, respectively, with C_i and C_j and their disulfide group in the conformation of the regularized experimental protein structure, and protonated; secondly, the cysteines in cystine were treated as if in a hexapeptide in the computation, as shown in Fig. 1.

Fig. 1.

Ribbon diagram of the hexapeptide model used to compute the ¹³C^α and ¹³C^β chemical shifts for cysteines in disulfide bonds. The hexapeptide is formed by two tripeptides Ac-GC_iG-NMe and Ac-GC_jG-NMe, with C_i and C_j and the disulfide bond in the conformation of the regularized experimental protein structure, and the Gly, Ac and NMe residues in their energy-minimized structure. The Cys residues with their disulfide bond are colored in orange, the Gly residues are colored white and the blocking end-groups are red and blue for Ac and NMe, respectively

Further information regarding the regularized geometry adopted for the calculations and details of the method can be found in the Supplementary Material.

Computation of the conformationally-averaged rmsd (ca-rmsd)

in several previous papers (Vila et al. 2007, 2008, 2009; Vila and Scheraga 2008, 2009) and, hence, we reproduce here, for the reader’s convenience only, the main definitions. For further details, see Supplementary Material.

Under the assumptions of fast conformational averaging, the computation of the ca-rmsd for a protein containing N amino acids residues, is given by (Vila et al. 2007): $\mathit{\text{ca}}-{\text{rmsd}}^n={{[(1/N){\displaystyle {\sum }_{\mu =1}^N({}^{13}{C}_{\text{observed},\mu }^n-<{}^{13}{C}_{\text{computed},\mu }^n>})}^2]}^{1/2}\text{ with }n=\alpha \text{ or }\beta ,\text{ and }<{}^{13}{\mathrm{C}}_{\text{computed}}^n{>}_{\mu }=(1/\mathrm{\Omega }){\displaystyle {\sum }_{i=1}^{\mathrm{\Omega }}{}^{13}{\mathrm{C}}_{\mu ,i}^n}$, for a given amino acid residue μ and with Ω the total number of protein conformations. Evidently, if Ω = 1; ca-rmsdⁿ ≡ rmsdⁿ; as for any single structure. In addition, for each amino acid μ, we define an error function ${\mathrm{\Delta }}_{\mu }^n=({}^{13}{\mathrm{C}}_{\text{observed},\mu }^n-{}^{13}{\mathrm{C}}_{\text{computed},\mu }^n)$, with n = α or β.

A normalized rmsd for comparing different protein structures

In the absence of a gold-standard, it is common practice in the field of protein structure determination to compare NMR-derived conformations against a single X-ray derived structure. However, the corresponding X-ray structure does not always exist and, more important, even if it exists, a single X-ray structure may, or may not, be a better representation of the observed ¹³C^α chemical shifts in solution than an NMR- or X-ray-determined ensemble of conformations (Vila and Scheraga 2009; Arnautova et al. 2009). Nevertheless, attempts to adopt the rmsd, between observed and predicted ¹³C^α chemical shifts for a protein structure solved at high accuracy, as a quality-model against which to compare other NMR-derived structures have a drawback. Among others, it is well known that the rmsd parameter is a reliable indicator of the global property of protein structures containing the same, or similar, number of residues (Maiorov and Crippen 1995; Betancourt and Skolnick 2001; Carugo and Pongor 2001). In other words, the rsmd is affected by the conformation similarity and the overall sizes of the proteins being compared (Maiorov and Crippen 1995). In the Supplementary Material section, we provide a discussion of this problem by analyzing the rmsd’s of a set of 24 proteins, solved by NMR spectroscopy, with a broad number of residues (N) ranging from 48 to 370. A solution to this important problem lies beyond the goal of this manuscript and, hence, we adopted the expression proposed by Carugo and Pongor (2001), as a normalized size-independent rmsd, viz.,

$${\text{rmsd}}_L=\frac{\text{rmsd}}{1+\text{ln}\sqrt{N/L}}$$ (1)

where N is the number of residues in the sequence of any given protein, L is the number of residues in the protein chosen as a reference, and rmsd_L is the normalized, size-independent rmsd value that would be measured if the given structure under consideration contains L residues. It is worth noting that Eq. 1 breaks down for N lower than ~14 residues for L ~100, because the rmsd becomes negative. This is not a problem because we are dealing with proteins, not oligopeptides.

For the purpose of this work, we chose L = 76, as the reference residue number, i.e., with L representing the size of the ubiquitin protein, a highly-accurately-solved NMR protein structure, e.g., 1D3Z (Cornilescu et al. 1998), with a ca-rmsd of 2.20 ppm (Vila and Scheraga 2009). Use of Eq. 1 to compare the quality of NMR-derived ensembles of structures with different sizes, in terms of ¹³C^α chemical shifts, can be carried out by substituting ca-rmsd for rmsd and ca-rmsd_L for rmsd_L. For this purpose, it is useful to define a ca-rmsd₇₆ cutoff value beyond which a need for further refinement of any given protein is necessary. Consequently, a ca-rmsd₇₆ = 2.6 ppm as a cutoff value was adopted (see Supplementary Material for details leading to this selection).

Results and discussion

Analysis of the NMR and X-ray conformations

A comparative analysis, in terms of the ca-rmsd, among each of the NMR-determined models and the corresponding X-ray structure for all these proteins was performed. From these analyses we can conclude the following: There are three proteins (see Table 1), Interleukin 13, the hyaluronan-binding domain of CD44 and the N-terminal domain of human tissue inhibitor of metalloproteinases-1, for which the ca-rmsd from the NMR-derived ensembles (1IK0, 2I83 and 1D2B) is similar or slightly better than the X-ray determined structures (3BPO, 1UUH and 2J0T); there are two other proteins, MIA protein and antifreeze protein CfAFP-501, for which the opposite is true, i.e., the rmsd of the X-ray structure (1I1J and 1M8N) is better than the ca-rmsd derived from the NMR ensemble of conformations (1HJD and 1Z2F). However, there is always at least one NMR-determined protein model for which the agreement between computed and observed ¹³C^α chemical shifts for cysteines in cystines is better than for the X-ray structure model (see for example Fig. S1 in Supplementary Material).

The analysis presented above must be complemented with a detailed analysis of the errors between observed and computed ¹³C^α chemical shifts, their origin and, if possible, a search for local flaws in the sequence, i.e., those that might reveal the need for further global or local refinement. Such analysis will be discussed in the next sub-sections.

Analysis of the errors

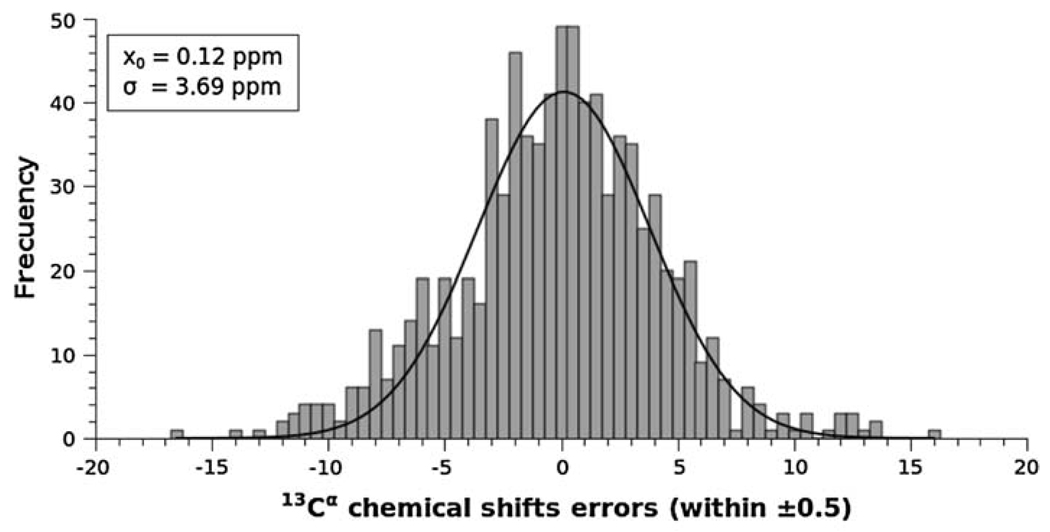
The frequencies of the error per-residue, ${\mathrm{\Delta }}_{\mu }^{\alpha }$, for all the cysteines in cystines, i.e., for 801 cysteine residues of cystines of all proteins, except BPTI, listed in Table 1, can be fit to a Gaussian distribution, with a mean value x₀ = 0.12 ppm, and standard deviation σ = 3.69 ppm (see Fig. 2). The resulting mean value (x_o = 0.12 ppm) is very close to the ideal one (x_o = 0.0 ppm) indicating that there is no need for further reference corrections, although the standard deviation (σ = 3.69 ppm) is significantly higher than the standard deviation (σ = 1.64 ppm) observed by Wang and Jardetzky (2002) for all cysteine residues of cystines. The observed standard deviation of σ = 1.64 ppm for the ¹³C^α chemical shifts pertains to cystines in only the β-strand conformation [the values from residues in statistical-coil and α-helix conformations were not included because the Wang and Jardetzky (2002) database does not contain enough statistics for oxidized cysteine residues]. Despite this, the computed high standard deviation (σ = 3.69 ppm) from 801 cystine residues of cysteine signals the following two possible problems: either the method is not accurate enough or most of the six protein structures used for the test (that does not include the BPTI models) need global or local refinement.

Fig. 2.

Frequency of the error, ${\mathrm{\Delta }}_{\mu }^{\alpha }$, between computed and observed ¹³C^α chemical shifts, for each of the 801 cysteine residues in cystines computed in this work, i.e., from all proteins listed in Table 1, except BPTI. The data were binned using an interval of 0.5 ppm, and then fit to a Gaussian function with a mean value x₀ = 0.12 ppm, and standard deviation σ = 3.69 ppm

In order to determine whether the method is the origin of this problem, the following test was carried out. Six X-ray-determined BPTI structures, solved at 1.7 Å, or better, resolution (see Table 1), with low B-factors, namely for PDB id 1BPI, 1D0D, 1G6X, 1K6U, 5PTI and 6PTI, were used to compute the ¹³C^α chemical shift of each of the six cystines in each structure. The results indicate that the per-residue errors, except for all cysteines at position 14 and one cysteine (from 5PTI) at position 55 have values of ${\mathrm{\Delta }}_{\mu }^{\alpha }\le 1.64$ (data not shown). A brief analysis of the cysteines at position 14 for all the BPTI models will be presented below in a separate sub-section. In general, the average error over all cysteine residues, after excluding the six cysteines at position 14, is only 0.73 ppm, with a standard deviation of σ = 0.47 ppm. This standard deviation is ~8 times lower than the one obtained from the analysis of the 801 cystine residues (σ = 3.69 ppm) and within the observed standard deviation (σ = 1.64 ppm) obtained by Wang and Jardetzky (2002). This result enables us to rule out the method as the main source of the errors. These results also indicate that further refinement of the set of seven proteins, solved by both NMR spectroscopy and X-ray crystallography, might be necessary. In order to investigate this assumption, in the following section, we validate, first, the NMR- and, second, the X-ray-determined proteins, in terms of the ca-rmsd as the scoring function. Special attention to the factors that could contribute to the computed high standard deviation (σ = 3.69 ppm) will be explored.

Validation of the NMR-derived proteins

If the global quality of all the NMR-derived proteins listed in Table 1 were the main source of the high computed-standard deviation, then these proteins, as a whole, i.e., considering all non-cysteine residues, should have a higher ca-rmsd₇₆ value, computed by using Eq. 1, than a given cutoff, namely 2.6 ppm (see “Materials and methods” section). In column six of Table 1, we listed both the ca-rmsd and the ca-rmsd₇₆ value (in parentheses) for all non-cysteine residues. A comparative analysis against the chosen cutoff value indicates that three of the NMR-determined proteins show ca-rmsd₇₆ values greater than 2.6 ppm, namely proteins 1Z2F, 1HJD, and 1HA8, respectively, and the remaining three, namely proteins 2I83, 1IKO, and 1D2B, respectively, show a lower ca-rmsd₇₆ value. This result, by itself, does not enable us to reach any conclusive evidence indicating whether the global quality of the NMR-determined structures is the main origin of the high computed value for the standard deviations.

Does the above result imply that a local refinement, i.e., for only the cysteine residues of cystine, of the NMR-determined structures might be necessary? In order to answer this question, the ca-rmsd per-cysteine residue (shown in parentheses in column five, Table 1) for non-BPTI models was compared with the average ca-rmsd per-cysteine residue computed from the six BPTI models, after excluding Cys14 of the BPTI models (for the reasons explained below). The average ca-rmsd per-cysteine from the six BPTI models (0.95 ppm) is between ~3 and ~6 times lower than the ca-rmsd per-cysteine from any NMR-determine structure listed in Table 1 and, hence, indicates that the cysteine residues of cystine, in fact, must be locally refined.

Validation of the X-ray-derived proteins

In order to provide some insight into the most significant differences between observed and computed ¹³C^α chemical shifts computed for the X-ray determined structures, in the next sub-section we present a detailed analysis for the Cys14 of BPTI.

As possible sources of errors, the influence of the B-factors and the experimental conditions under which the X-ray and NMR experiments were carried out are discussed for two proteins, namely for Interleukin 13 and Melanoma inhibitory activity protein, in the Supplementary Material.

Residue Cys14 of the X-ray-solved models of BPTI

A detailed analysis of all the cysteines of cystine at position 14 in the sequence of the six BPTI X-ray-derived models (listed in Table 1) reveals an average error, ${\mathrm{\Delta }}_{\mu }^{\alpha }=4.73$, and a standard deviation of σ = 1.56 ppm (data not shown). These values should be compared with the average value and standard deviation obtained for all cysteine residues of cystine after excluding the six cysteines at position 14, namely 0.73 and 0.47 ppm, respectively (data not shown).

Because disulfide bonds are observed to have several degrees of freedom (Van Wart and Scheraga 1976, 1977), disulfide-bond dynamics undergo significant conformational changes in solution (Otting et al. 1993; Sharma and Rajarathnam 2000). In this connection Otting et al. (1993) carried out a detailed NMR analysis of disulfide-bond isomerization in BPTI and in BPTI (G36S), a mutant protein with Gly replaced by Ser at position 36. Among other important findings, the authors found a slow dynamic equilibrium between two conformers with different chirality of the disulfide bond formed by Cys14 and Cys38, indicating that internal mobility prevails in this part of the molecule. Overall, flipped disulfide bonds may occur frequently in proteins in solution (as in BPTI) despite the conformational restraints imposed by the three dimensional structure (Otting et al. 1993) and, conceivably, this could be the origin of the significant difference between the observed (in solution) and computed (in a crystal) ¹³C^α chemical shifts of Cys14.

Analysis of the ¹³C^α and ¹³C^β chemical shifts as function of the redox state

As is well known (Sharma and Rajarathnam 2000), the redox state of cysteine residues can be straightforwardly inferred from ¹³C^β, but not from ¹³C^α, chemical shifts. This conclusion was obtained by Sharma and Rajarathnam (2000) after statistical analysis of data from 375 ¹³C^α and 337 ¹³C^β resonances from 132 proteins.

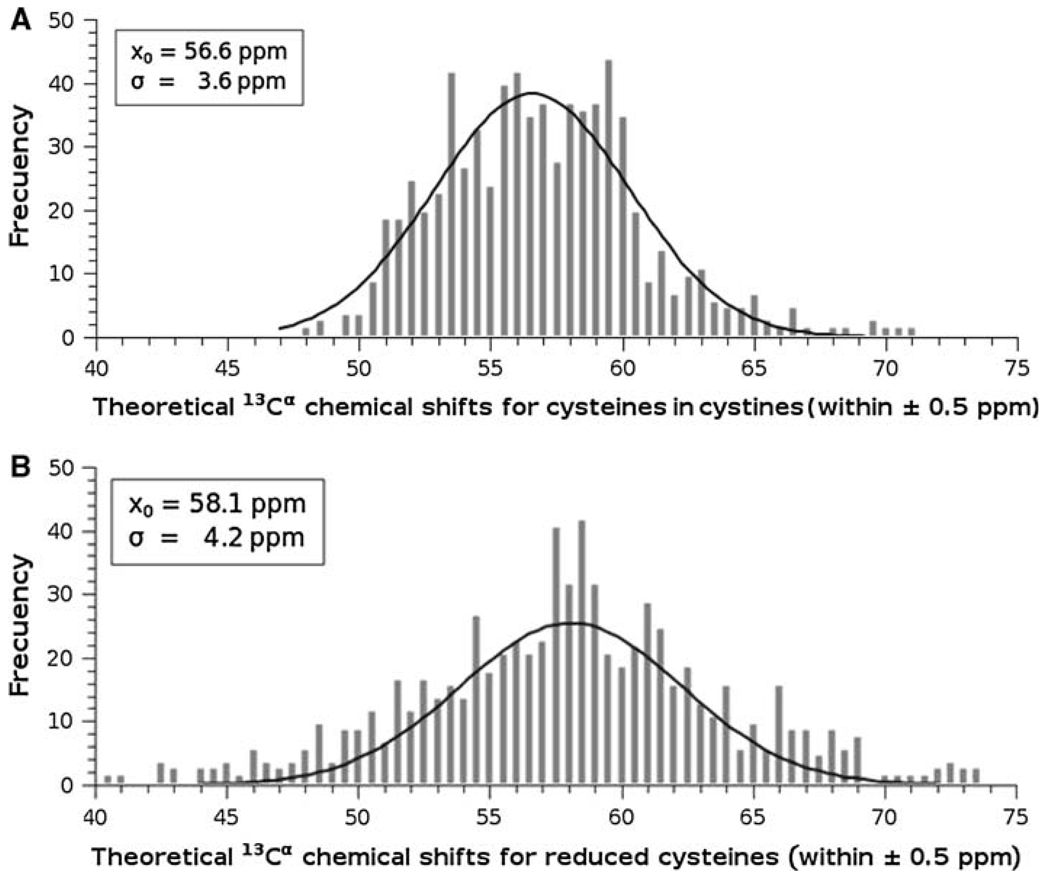
In the same computations of the ¹³C^α shielding of a given residue by the DFT methodology, we also obtain the shielding value of all nuclei in the residue, not only for the ¹³C^α nucleus; among them, also for the ¹³C^β atom. Thus, we can investigate whether our theoretical calculations can reproduce the observed redox-induced behavior (Sharma and Rajarathnam 2000) of both the ¹³C^α and ¹³C^β chemical shifts. Hence, the ¹³C^α and ¹³C^β chemical shifts for the cysteines in cystine in both oxidation states for all proteins listed in Table 1 were obtained for each cysteine in both tripeptides and hexapeptides in the conformation of the regularized experimental protein structure. The distributions of the computed ¹³C^α and ¹³C^β chemical shifts for the cysteine residues in cystine and for reduced cysteines for all proteins listed in Table 1 are shown in Fig. 3 and Fig. 4, respectively. As shown in Fig. 3 and Fig. 4, these distributions can be modeled by a Gaussian function with a mean, x₀, value and standard deviation, σ. These Figures also show the existence of two, almost non-overlapped, basins for the ¹³C^β (see Fig. 4), but not for the ¹³C^α (see Fig. 3), chemical shifts. These results are in good agreement with the observed ¹³C^α and ¹³C^β chemical-shift values for cysteine residues in cystine and cysteine residues (Sharma and Rajarathnam 2000). As to whether such good agreement is quantitative or only qualitative follows.

Fig. 3.

Frequency of the computed ¹³C^α chemical shifts for all 837 cysteines in cystine: A for cysteines in cystine. The data were binned using an interval of 0.5 ppm, and then fitted to a Gaussian function with a mean value x₀ = 56.6 ppm, and standard deviation of σ = 3.6 ppm; B same as A for reduced cysteines; with x₀ = 58.1 ppm, and standard deviation of σ = 4.2 ppm

Fig. 4.

Frequency of the computed ¹³C^β chemical shifts for all 837 cysteines in cystine: A for cysteines in cystine. The data were binned using an interval of 0.5 ppm, and then fitted to a Gaussian function with a mean value x₀ = 42.1 ppm, and standard deviation σ = 5.8 ppm; B same as A for reduced cysteines; with x₀ = 27.3 ppm, and standard deviation σ = 2.4 ppm

Using the values that characterize the Gaussian distribution, shown in Fig. 3 and Fig.4, enables us to make a straightforward comparison with the observed (Sharma and Rajarathnam 2000) redox-induced shift effects. The values obtained for the computed ¹³C^α chemical shifts of cysteines in cystines, x₀ = 56.6 ppm, and σ = 3.6 ppm (see Fig. 3A), and reduced cysteines, x₀ = 58.1 ppm, and σ = 4.2 ppm (see Fig. 3B), are in good agreement with the observed (Sharma and Rajarathnam 2000) ¹³C^α chemical shifts values, x_o = 55.5 ppm, and σ = 2.5 ppm, and x_o = 59.3 ppm and σ = 3.2 ppm, respectively. A similar conclusion pertains to the computed ¹³C^β chemical shifts of cysteines in cystines, x₀ = 42.1 ppm, and σ = 5.8 ppm (see Fig. 4A), and reduced cysteines, x₀ = 27.3 ppm, and σ = 2.4 ppm (see Fig. 4B), which also show good agreement with the observed values, x_o = 40.7 ppm, and σ = 3.8 ppm, and x_o = 28.3 ppm and σ = 2.2 ppm, respectively (Sharma and Rajarathnam 2000). Overall, our theoretical calculations are in good quantitative agreement with the observed ¹³C^α and ¹³C^β chemical-shift values for reduced and oxidized cysteine residues (Sharma and Rajarathnam 2000).

These results on oxidized and reduced cysteines raise the question as to whether the computed ¹³C^α chemical shifts from reduced cysteines can be inferred from the values obtained from the cysteines in cystine, and vice versa. A visual inspection of Fig. 3 seems to indicate that the Gaussian distribution of the cysteines in cystine (Fig. 3A) is shifted by ~3 ppm with respect to the Gaussian distribution of the reduced cysteines (Fig. 3B). Does this observation imply that the computed ¹³C^α shielding for a given reduced cysteine can be obtained by applying a constant shift to the computed value from the oxidized state? The answer is no, for the following reason. The computed downfield shielding for reduced cysteine, with respect to the cysteines in cystine, is not equal for all cysteine residues nor do all cysteines show such a downfield shielding. In fact, ~33% of all 837 cysteines in cystine show upfield, rather than downfield, shielding (data not shown). This result indicates that explicit consideration of the disulfide bonds is a necessary condition for an accurate prediction of ¹³C^α chemical shifts of cysteines in cystines. In other words, the computed ¹³C^α chemical shifts from oxidized cysteines cannot be inferred straightforwardly from the values computed for the reduced state.

The above results are linked to the predictions of the recently introduced (Vila et al. 2009) ¹³C^α chemical shift (CheShift) server because the predictions of the ¹³C^α chemical shift of CheShift are valid only for reduced cysteine, and not for cysteine residues in cystine. Given that numerous proteins contain a large number of cysteine residues in cystine, a solution to this important problem is under investigation in our research group, and the results will be published elsewhere.

Conclusions

In this work, we present a method to compute, accurately, the ¹³C^α chemical shifts for cysteines in cystine. This new method has been applied to a selected, non-redundant, set of protein models, rich in disulfide bonds, determined by both NMR spectroscopy and X-ray crystallography. In particular, the analysis of a set of high-quality, X-ray-determined, protein models of BPTI enables us to both show the accuracy of the method to compute ¹³C^α chemical shifts for the cysteines in cystine and to rule out the proposed DFT-computational methodology as the main source of the computed errors in the chosen set of proteins. Thus, the errors between computed and observed ¹³C^α chemical shifts for the cysteines of cystine originated in several factors that include, but are not limited to, the need for further refinement of NMR-determined conformations, the presence of high B-factors, as for X-ray-determined conformations, or poor representation of the disulfide-bond dynamics in solution by a single conformation, etc.

By using quantum-chemical-based calculations we have been able to illustrate that ¹³C^β, but not ¹³C^α, chemical shifts (see Fig. 3, Fig. 4) show two, almost non-overlapped, basins, in good agreement with the observation of Sharma and Rajarathnam (2000) and, hence, providing a validation of the methodology used here to compute ¹³C^α and ¹³C^β chemical shifts of cysteines as a function of the redox state. Moreover, we have been able to demonstrate that the disulfide bond significantly affects the computed values of the ¹³C^α and ¹³C^β chemical shifts and, hence, explicit consideration of the presence of a disulfide bond is necessary for an accurate prediction of ¹³C^α and ¹³C^β chemical shifts of cysteines in cystines.