Abstract
We develop mathematical techniques for analyzing detailed Hodgkin-Huxley like models for excitatory-inhibitory neuronal networks. Our strategy for studying a given network is to first reduce it to a discrete-time dynamical system. The discrete model is considerably easier to analyze, both mathematically and computationally, and parameters in the discrete model correspond directly to parameters in the original system of differential equations. While these networks arise in many important applications, a primary focus of this paper is to better understand mechanisms that underlie temporally dynamic responses in early processing of olfactory sensory information. The models presented here exhibit several properties that have been described for olfactory codes in an insect's Antennal Lobe. These include transient patterns of synchronization and decorrelation of sensory inputs. By reducing the model to a discrete system, we are able to systematically study how properties of the dynamics, including the complex structure of the transients and attractors, depend on factors related to connectivity and the intrinsic and synaptic properties of cells within the network.
Keywords: Neuronal networks, discrete dynamics, olfactory system, transient synchrony
1. Introduction
Oscillations and other patterns of neuronal activity arise throughout the central nervous system [1-6]. These oscillations have been implicated in the generation of sleep rhythms, epilepsy, Parkinsonian tremor, sensory processing, and learning [7-12]. Oscillatory behavior also arises in such physiological processes as respiration, movement, and secretion [13-15]. Models for the relevant neuronal networks often exhibit a rich structure of dynamic behavior. The behavior of even a single cell can be quite complicated [16-18]. An individual cell may, for example, fire repetitive action potentials or bursts of action potentials that are separated by silent phases of near quiescent behavior [19-21]. Examples of population rhythms include synchronized oscillations, in which many cells in the network fire at the same time, and clustering, in which the entire population of cells breaks up into subpopulations or clusters; every cell within a single cluster fires synchronously and different blocks are desynchronized from each other [22-24]. Of course, much more complicated population rhythms are possible. The activity may, for example, propagate through the network in a wave-like manner, or exhibit chaotic dynamics [23-28].
There has been tremendous effort in trying to understand the cellular mechanisms responsible for these rhythms. This has led to numerous mathematical models, often based on the Hodgkin-Huxley formalism [29]. Most work done on these models has consisted of computational studies with little mathematical analysis. This is because realistic models typically consist of very large systems of nonlinear differential equations. As pointed out above, even a single cell's dynamics can be very complicated. In addition, the coupling between cells within a network can be either excitatory or inhibitory and may include multiple time scales [24]. Since a neuronal system may involve combinations of different types of cells and different types of coupling, it is easy to understand why mathematical analysis of these networks is extremely challenging.
Numerous researchers have considered idealized networks, which capture important features of the more realistic system; see, for example, [24,30]. Examples of such networks include integrate-and-fire models, firing rate models, coupled relaxation oscillators and phase oscillators. These studies have certainly been very useful; however, it is often not clear what the precise relationship is between details of the biophysical network and those of the idealized model. The biophysical systems involve large numbers of parameters that characterize the intrinsic and synaptic currents. Moreover, the underlying network architecture may be quite complicated. These details are usually absent in the reduced models, making it difficult to understand the precise role of a particular current, or the network architecture, in producing the resulting population rhythm. Furthermore, a network's behavior is not apt to be controlled by a single component, but rather by combinations of processes within and between cells.
A primary goal of this paper is to develop mathematical techniques for analyzing detailed biophysical models for excitatory-inhibitory neuronal networks. While these networks arise in numerous applications, including models for thalamocortical sleep rhythms [11] and Parkinson's tremor [12], the focus of this paper will be to apply our mathematical methods to better understand mechanisms that underlie temporally dynamic responses in early processing of olfactory sensory information [31-37]. In the insect and mammalian olfactory systems, any odor will activate a subset of receptor cells, which then project this sensory information to a neural network in the Antennal Lobe (AL) (insects [38]) or Olfactory Bulb (OB) (mammals [39]) of the brain. Processing in this network transforms the sensory input to give rise to dynamic spatiotemporal patterns that can be measured in the projection neurons (PN) that provide output to other brain centers [35,36]. These output patterns typically consist of subgroups of PNs firing synchronously, and the pattern of synchronous PNs evolves at rates of 20-30 Hz. Any given PN might synchronize with different PNs at different stages, or episodes, in this rhythm. This sequential activation of different groups of PNs gives rise to a transient series of output patterns that through time converges to a stable steady state [36,37].
However, the mechanisms that give rise to these dynamic patterns [31,40-42], as well as their roles in odor perception [33,43] remain controversial. Behavioral data indicate that animals need only a few hundred milliseconds to effectively discriminate most pairs of odorants [44,45], and more difficult discriminations require slightly more time [46,47]. If animals use information in either the transient or attractor phase of any proposed dynamic process, the behavioral data can set important time constraints for that process to produce discriminable patterns. This, in turn, can set constraints on network properties including the underlying network architecture. Neural activity patterns that represent odorants in the AL are statistically most separable at some point during the transient phase, well before they reach a final state [37]. The time frame for reaching this point of maximal difference is consistent with behavioral studies [44]. This means that dynamic processing in the AL may serve to decorrelate sensory representations through early transients rather than by reaching a fixed point or a stable attractor.
In this paper, we consider a minimal biophysical model that reproduces several known features of the olfactory neural networks in the OB and AL. These features include decorrelation of sensory inputs and dynamic reorganization of synchronous firing patterns. Our strategy for studying these complex networks is to first reduce the model to a discrete-time dynamical system. If we know which subset of cells fire during one episode, then the discrete model determines which subset of cells fire during the next episode. This defines a map from the set of subsets of cells to itself. The discrete model is considerably easier to analyze, both mathematically and computationally, than the original model and, using the discrete model, we determine how the structure of transients and attractors depend on parameters.
We will consider two different Hodgkin-Huxley type network models. Model I is perhaps the simplest model that exhibits dynamic reorganization of synchronous firing patterns. Considering such a simple network allows us to more easily describe the reduction to a discrete-time dynamical system. In Model II, we consider a more detailed Hodgkin-Huxley type model that incorporates additional currents and exhibits more realistic firing patterns. This model is closely related to the network model proposed by Bazhenov et al [40,41] and the mechanisms underlying transient patterns of synchronization in both models are similar. However, it remains unclear how properties of the dynamics, including the complex structure of the transients and attractors, depend on factors related to connectivity and the intrinsic and synaptic properties of cells within the network. The mathematical techniques developed in this paper allow us to systematically study how the model's emergent firing patterns depend on model parameters, including the network architecture.
2. Methods
2A. The two models
We consider two neuronal network models. Model I consists of a single layer of cells coupled through mutual inhibition. Activity spreads through the network via post-inhibitory rebound; however, this can also be interpreted as delayed excitation that is not dependent on post-inhibitory rebound per se. This is the simplest network that exhibits dynamic reorganization of synchronous firing patterns and decorrelation of sensory inputs. By considering this simple network, we can give explicit examples that more easily explain the mechanism underlying dynamic reorganization of synchronous firing patterns. As we shall see, even this simple network may exhibit a rich structure of multiple transients and attractors. It will be useful to understand how this rich dynamics arises in a simple network before moving onto a more complicated model.
In Model I, the equations for each cell can be written in the form:
| (1) |
where IL = gL(v-vL), INa = gNamτ3(v)(1-n)(v-vNa) and IK = gKn4(v-vK) represent leak, sodium and potassium currents, respectively, and I0 is an external current. All of the nonlinear functions and parameters used in the simulations that follow are given in the Appendix.
The term Isyn represents the synaptic current. For cell i, Isyn = gsyn(vi – vsyn) ∑jsj where the sum is over those cells that send synaptic input to cell i. The variables sj satisfy a first-order differential equation of the form:
| (2) |
where Hβ(x) = 1/(1+exp(−x/σs)) is a smooth approximation of the Heaviside step function. Note that if cell j fires an action potential, so that vj > σv, then the synaptic variable sj activates at a rate determined by the parameters σ and σ. On the other hand, if cell j is silent, so that vj < σv, then the synapse turns off at the rate σ.
The synapses we have considered so far are direct since they activate as soon as a membrane crosses the threshold. It will sometimes be necessary to consider more complicated connections. These will be referred to as indirect synapses. To model indirect synapses, we introduce a new independent variable xi for each cell, and replace (2) with the following equations for each (xj,sj):
The effect of an indirect synapse is to introduce a delay from the time one cell jumps up until the time the other cell feels the synaptic input. For example, if cell 1 fires, a secondary process is turned on when v1 crosses the threshold βv. The synaptic variable s1 does not turn on until x1 crosses some threshold βx.
Model II consists of two layers of excitatory (E-) and inhibitory (I-) cells. Each E-cell excites some subset of I-cells, which provide inhibitory input to some subset of E-cells, as well as other I-cells. The cells may also receive an external current, corresponding, for example, to input from sensory cells in the periphery. We note that excitatory-inhibitory networks similar to Model II have been proposed as models for the subthalamopallidal network within the basal ganglia underlying Parkinsonian tremor [12] and the inhibitory reticular nucleus cells and the excitatory thalamocortical cells network within the thalamus underlying certain sleep rhythms [11]. Since the intrinsic properties of neurons within the insect AL are unknown, we will use this model to develop the mathematical techniques and then explore how properties of the network depend on parameters, including the underlying architecture.
In Model II, each cell is modeled as before, except the I-cells also have a calcium-dependent potassium current, IAHP, and a high-threshold calcium current, ICa, while the E-cells have a low-threshold calcium current, IT. Hence, each E-cell satisfies equations of the form:
| (3) |
where and IE is an external current. Each I-cell satisfies equations of the form:
| (4) |
where , IAHP = gAHP [Ca/(30+Ca)](v–vK) and II is an external current.
The synaptic input from structure A to a cell i in structure B is given by IBA = gBA(vi – vA)∑sj where the sum is over all cells in A that send synaptic input to cell i. The indices A and B can take values E for excitatory or I for inhibitory. The synaptic variables sj satisfy an equation of the form (2).
2B. Presentation of an odor
To model the presentation of an odor, we assume that an odor activates a certain subset of receptors [48] and this, in turn, increases the external input to some of the E-cells. For Model II, we assume that there are two constants, IE0 and IE1, such that if a given E-cell does receive input from receptors during the presentation of an odor, then IE = IE1; if the E-cell does not receive input from the receptors then IE = IE0. The constants IE1 and IE0 are chosen so that E-cells that receive input from receptors are able to participate in network synchronous activity, while E-cells that do not receive input from receptors are not. Since Model I is used primarily to motivate the discrete-time dynamical system, we simply assume that all the cells in Model I receive input from receptors.
2C. Distance between solutions
In what follows, we will compute how the distance between two solutions of Model II evolve with time. By this we mean the following: As we shall see, each solution consists of distinct episodes in which some subset of E-cells fire. If there are NE E-cells, then for the kth episode, we can define an NE-dimensional vector {a1, a2, ... , aNE} where ai = 1 if the E-cell i fires during this episode and ai = 0 if it does not. Then the distance between two solutions during the kth episode is the Hamming distance between the two corresponding vectors.
3. Numerical simulations
3A. Solutions of Model I
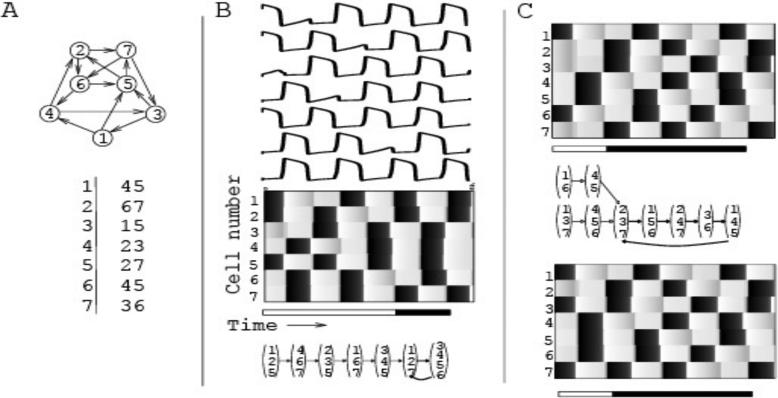
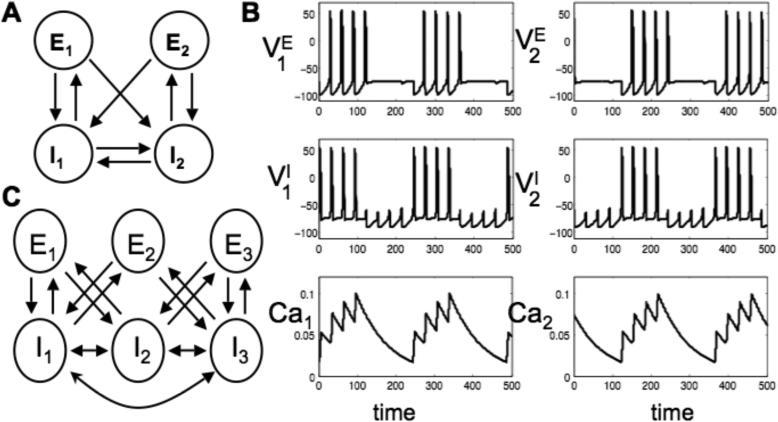
Three emergent properties of the models – synchrony, dynamic reorganization, and transient/attractor dynamics – are represented in Fig. 1B where we show solutions of the Model I with seven cells (architecture shown in Fig. 1A) and indirect synapses. These properties have all been described for olfactory codes in the AL [37,42]. After the initial input, each succeeding response consists of episodes in which some subset of the cells fire in synchrony. These subsets change from one episode to the next. Moreover, two different cells may belong to the same subset for one episode but belong to different subsets during other episodes. For example, cell 1 and cell 2 fire together during the first episode, but during the fourth episode, cell 1 fires and cell 2 does not. This is dynamic reorganization. After a transient period (consisting of 5 episodes in Fig. 1B), which is characterized by a sequence of activation patterns, the response becomes periodic. For example, in Fig. 1B the cells that fire during the sixth episode are cells 1, 2 and 7. These are precisely the same cells that fire during the eighth (last shown) episode. This subset of cells continues to fire together every second episode thereafter. Different initial conditions produce different transients that may either approach different attractors (Figs. 1B and 1C (top)), or they may approach the same attractor (Fig. 1C).
Figure 1.
An example of Model I. (A) The network consists of 7 cells with connections indicated by arrows. The connectivity is summarized in a table (bottom), in which the left column shows the indices of all cells, and the remaining columns show the indices of all cells that receive connections from the cell on the left. B) An example of network activity. The top panel shows the time courses of voltage in all 7 cells over 8 epochs of activity. Grey scale in the checkerboard panels corresponds to the magnitude of voltage, with black areas indicating spikes. After a transient (white part of the time bar under the checkerboard) the response converges to a repeating pattern (black part of the time bar). The bottom panel shows the orbit of the discrete dynamical system corresponding to this example. (C) Solutions of the same network, but with different initial conditions. These solutions have different transients (white parts of the time bars), but they converge to the same attractor (which, in turn, is different from the one in B).
3B. Solutions of Model II
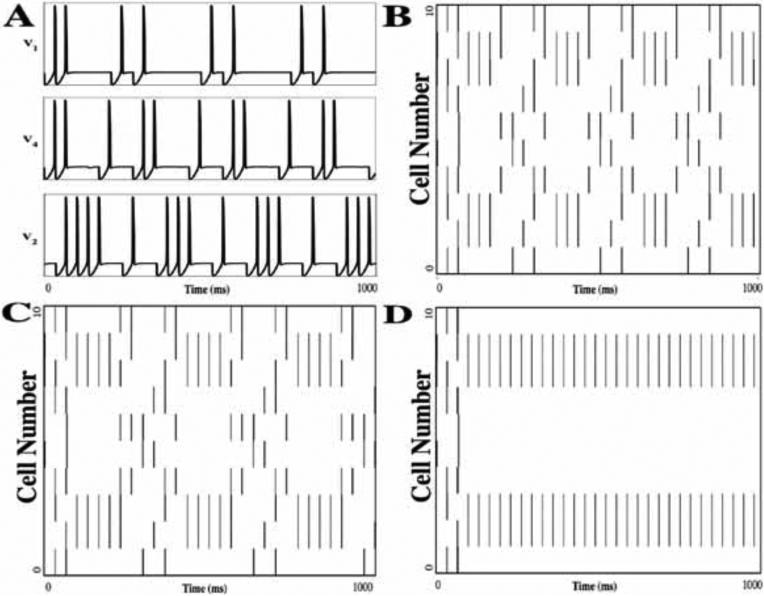
Solutions of Model II are shown in Fig. 2. Here there are 10 E-cells and 6 I-cells. Each E-cell receives input from 3 I-cells, chosen at random, and each I-cell receives input from 2 E-cells, again chosen at random, and from all other I-cells. Note that the solution exhibits the emergent properties described above: there are distinct episodes in which some subpopulation of E-cells synchronize with each other and membership of this subpopulation changes from episode to episode. After a transient period of several episodes, the response becomes periodic. As is the case for Model I, different initial conditions may produce different transients that may or may not approach the same attractor (not shown). Figs. 2B, C and D illustrate how the solution changes as we increase the parameter kCa, corresponding to the decay rate of calcium in the I-cells. For the solutions shown in Figs. 2B (kCa=2) and 2C (kCa=3.8), certain E-cells may fire for several consecutive episodes, while others are silent, and then other E-cells eventually ‘take over’ and fire for several episodes. For the solution shown in Fig. 2D (kCa=7) some of the E-cells fire every episode, while the other E-cells remain silent.
Figure 2.
An example of Model II dynamics. The network consists of 10 E-cells and 6 I-cells. Each E-cell receives input from 3 I-cells, chosen at random, and each I-cell receives input from 2 E-cells chosen at random, as well as all other I-cells. (A) The time course of voltage for three of the E-cells. A cell may fire for several subsequent episodes and then remain silent for several episodes. Two E-cells may fire synchronously during some episodes but not during others. (B) The entire E-cell network activity over 1000 ms. Each row corresponds to the activity of one of the E-cells; a vertical line indicates a spike. (C,D) Solutions of the same network as in panels A, B with different values of kCa (the rate of decay of calcium in the I-cells). In B, C and D, kCa = 2, 3.8 and 7, respectively. Values of other parameters are listed in Tables 1 and 2 except gIE =.025, gII =1.
Note that changing kCa in the I-cells has a significant impact on the network's firing properties. In brief, kCa is related to the rate of uptake of calcium in the I-cells. When an I-cell fires an action potential, calcium enters the cell and this strengthens the outward current IAHP. If the calcium level is sufficiently high – that is, IAHP is sufficiently strong – then the cell will be unable to fire in response to excitatory input from an E-cell. Since kCa helps control the rate at which calcium builds up in the cell, it also helps to determine the number of consecutive episodes that I-cell fires before other I-cells take over. This, in turn, is related to the number of consecutive episodes that an E-cell may fire. We note that if kCa is too large (as in Fig. 2D), then calcium will be unable to build up in the cell. Hence, some cells may continue to fire indefinitely, and the resulting inhibition prevents other I-cell from firing.
3C. Discrimination of odors
Studies have suggested that dynamic processing may serve to enhance discriminability of sensory patterns. For example, experiments have demonstrated that neural activity patterns that represent odorants in the AL are statistically most separable at some point during the transient phase, well before they reach a final state [37]. Recently, Fernandez et al [45] studied the time-dependent response of PNs in the honeybee AL to binary mixtures of pure odors. They demonstrated that there is a smooth transition in the time-dependent neural representation of the PNs in response to a smooth transition in the ratios of components in the binary mixtures.
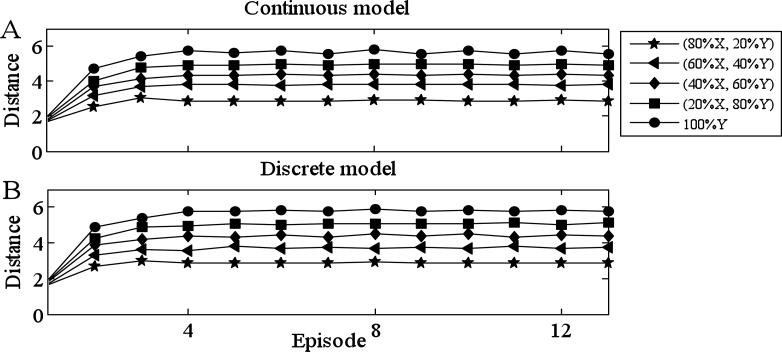
Fig. 3 demonstrates that Model II can reproduce several features of these experiments. We presented the network with mixtures of two distinct odors (odor X and odor Y) and evaluated how the Hamming distance between the firing patterns corresponding to the mixture and one of the pure odors evolve with time. For the simulations shown in Fig. 3A, the entire network consisted of 10 E-cells and 6 I-cells. Each E-cell receives input from 3 I-cells, chosen at random, and each I-cell receives input from 3 E-cells, again chosen at random, and from all other I-cells. We found that the network more robustly discriminates between mixtures if there are reciprocal connections. Here, we assume that if there is an E → I connection, then we add an I → E connection. Each pure odor corresponded to the activation of 5 E-cells and we assumed that the two odors activated non-overlapping sets of E-cells. As in [45], we considered mixtures in which the ratio of the two odors was varied 100:0 (base), 80:20, 60:40, 40:60, 20:80 and 0:100. For each ratio, we numerically generated a mixed odor as follows. Consider, for example, the ratio 80:20. Then each E-cell in odor X had a .8 probability of being activated — that is, IE = IE1 in this E-cell — and each E-cell in odor Y had a .2 probability of being activated. After generating the mixture, we computed the Hamming distance, as defined earlier, between the averaged firing pattern corresponding to the mixture and one of the pure odors. We chose initial conditions so that precisely one E-cell, chosen at random, in the mixture fired during the initial episode. We did this for 200 randomly chosen mixtures and then averaged the distances at each episode.
Figure 3.
Discrimination of odors. A network of 10 E- and 6 I-cells is presented with mixtures of two pure odors, X and Y. The pure odors activate disjoint subsets of 5 E-cells. For each fixed ratio of the two pure odors, 200 mixtures are randomly generated, as described in the text. The figure displays the distance (defined in the text) between the averaged firing pattern corresponding to the mixture and one of the pure odors (odor X) during each successive episode. The baseline is 100% odor X, different curves correspond to different ratios of X to Y: 80:20, 60:40, 40:60, 20:80 and 0:100. Values of other parameters are listed in Tables 1 and 2. (A) Full continuous model; (B) discrete counterpart (see section 5B).
This figure demonstrates that there is a smooth transition in the time-dependent firing patterns as the mixture varies from pure odor X to pure odor Y. Fig. 3B shows the results of simulations of the discrete model (described below) corresponding to this network.
4. Analysis of Model I
4A. The discrete-time dynamical system for Model I
Fig. 1 demonstrates that even small networks of simple cells are capable of producing dynamic reorganization. Moreover, each response is characterized by a transient followed by an attractor. We wish to determine how firing properties of larger networks, such as the number and lengths of different transients and attractors, depend on parameters in the models, including the underlying network architecture. Our strategy for studying more complicated networks is to first reduce the model to a discrete-time dynamical system: if we know which subset of cells fire during one episode, then the discrete model determines which subset of cells fire during the next episode. This defines a map from the set of subsets of cells to itself. As we shall see, the map also depends on the ‘state’ of each cell. For example, whether a cell responds to input may depend on whether that cell had fired during the preceding episode; it may also depend on the number of inputs that the cell receives.
We begin by reviewing results in [49] where the discrete dynamical system for Model I, and more general excitatory-inhibitory networks, is formally defined. We then present new simulations of the discrete model in which we consider how the lengths of transients and attractors depend on the connection probability.
We illustrate the discrete dynamical system for the Model I using the example shown in Fig. 1. We assume, for now, that a given cell fires during a given episode if and only if the following two conditions are satisfied: (i) the given cell receives input from at least one other cell that fired during the preceding episode; and (ii) the given cell did not fire during the preceding episode. Note that a cell fires via post-inhibitory rebound and (ii) implies that cells cannot fire during two consecutive episodes. Solutions of the Model II do not necessarily satisfy this property – that is, cells may fire during consecutive episodes – and, therefore, better account for firing patterns observed in many neuronal systems including olfaction.
If we know which cells fire during one episode, then, using this assumption and the network architecture, it is a simple matter to determine which cells fire during the next episode. Consider, for example, the solution shown in Fig. 1C (top). We choose initial conditions so that cells 1 and 6 fire during the first episode. These cells send input to cells 4 and 5, and these are the cells that fire during the second episode. These cells, in turn, send input to cells 2, 3 and 7, which fire during the third episode. These cells then send input to cells 1, 3, 5, 6 and 7. However, because cells 3 and 7 fire during the third episode, and cells cannot fire on two subsequent episodes, it follows that the cells that fire during the fourth episode are 1, 5 and 6. Continuing in this way, we can determine which cells fire during each subsequent episode.
The discrete model simply keeps track of which subset of cells fire during each episode. Since there are seven cells, there are 27 possible states of the discrete model and the discrete dynamics defines an orbit on this set of states. Each nontrivial orbit consists of two components: there is an initial transient until the orbit returns to a subset that it has already visited. The orbit must then repeat itself. Every orbit must eventually become periodic or is a trivial orbit in which all cells become activated or quiescent. This is because the number of states is finite. The entire discrete dynamics for this example is shown in [49]. We do not show the trivial orbits.
We generalize the definition of the discrete dynamical system in two ways. We assume that each cell, say i, is assigned two positive integers: pi, corresponding to the length of the cell's refractory period, in units of episodes or activity cycles, and Θi, corresponding to the cell's firing threshold, in units of number of inputs necessary to fire. Now suppose that some subset of cells, say σ, fire during an episode. Cell i will then fire during the next episode if it receives input from at least σi cells in σ and if it has not fired in the preceding pi episodes. Hence, if we know which subset of cells fire during one episode, along with each cell's refractory period, then the network architecture determines which cells fire during the next episode, along with the corresponding refractory periods. This then defines the discrete dynamical system. A more formal definition of the discrete model is given in [50].
4B. Numerical simulations of the discrete model
We now use the discrete dynamical system to examine how the numbers and lengths of transients and attractors depend on network parameters. We used networks with 150 cells and a random selection of 1000 initial conditions. In different simulations, cells were connected randomly with a fixed probability of connection from cell i to cell j. In each simulation, a proportion of cells (η) had refractory period pi = 2 and the remaining cells had refractory period 1. Similarly, a proportion of cells (θ) had a threshold θI = 2 and the remaining cells had threshold 1.
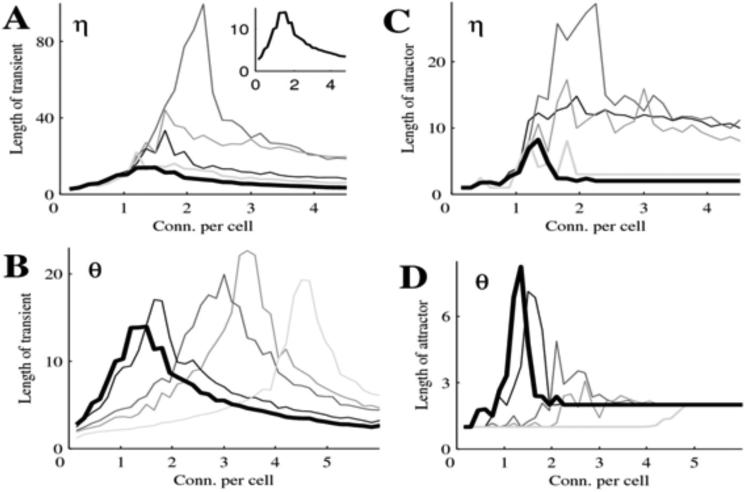
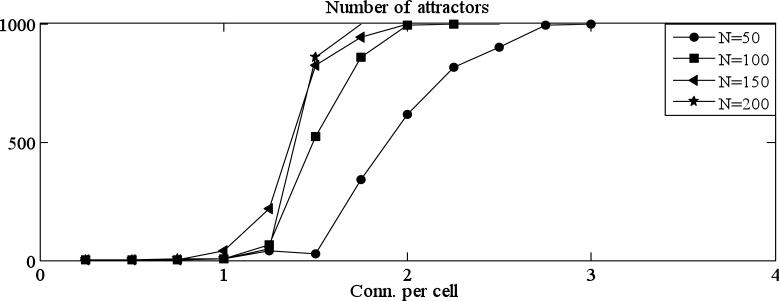
Consider first the case for η = 0 and θ = 0, in which all cells have refractory period and threshold of 1 (thick black curve in Fig. 4 A-D). The average length of both transients (Fig. 4 A, B) and attractors (Fig. 4 C, D) first increases with connectivity and peaks between 1 and 2 connections per cell. At higher connection probabilities, all lengths decline. Therefore, increasing connectivity produces a sharp transition at which lengths of transients and attractors are maximal. Increasing θ (Fig. 4 A, C) changed the shapes of these curves. In particular, the connectivity that produces the sharp transition increases with θ and peaks when θ = 0.5, which corresponds to half of the cells in the network having refractory period of 2. The lengths of transients and attractors are also highest at that value of θ. Likewise, increasing θ changed the shapes of the curves such that the sharp transitions tended to occur at higher connectivities. The lengths of transients at the sharp transition were maximal for intermediate levels of θ. There is also a sharp transition in the number of attractors at approximately that same connectivity (Fig. 5). We note that there are a huge number of attractors for connection probabilities greater than the sharp transition. An example is shown in Fig. 5. Here we considered networks with 50, 100, 150 and 200 cells, and computed the number of distinct attractors reached by solutions starting with a sample of 1000 random initial activation patterns. Note that for higher values of connectivity, each trajectory has its own attractor (the graphs reach 1000).
Figure 4.
Properties of transients and attractors in a 150-cells Model I network. Each point is averaged over 8 matrices of connectivity, and 1000 initial conditions for each matrix. (A,B) Properties of transients. (C,D) properties of attractors. Thick black curve (inset in A drawn to different scale) is the basic case when the threshold θ =0 and the refractory period η = 0. In the top row (A,C) different shades correspond to changes in the fraction of the cells with refractory period 2 (η). In the second row (B,D) different shades correspond to changing the fraction of the cells with threshold 2 (η). For each row changing of shade of thin lines from black to light grey corresponds, respectively, to η or η equaling 0.2, 0.5, 0.7, 1.
Figure 5.
There are a huge number of attractors for sufficiently high connection probability. We computed the number of distinct attractors reached by solutions starting with a sample of 1000 random initial activation patterns. Note that for higher values of connectivity, each trajectory has its own attractor (the graphs reach 1000).
4C. Mathematically rigorous results
It is not clear at this point what the precise relationship is between the differential equations model and the discrete dynamical system. One would like to demonstrate that every orbit of the discrete model is, in some sense, realized by a solution of the continuous differential equations model. We have addressed this issue in [49] where we considered both purely inhibitory and excitatory-inhibitory networks in which every cell satisfies equations of the form (1). We rigorously proved that, for excitatory-inhibitory networks, it is possible to choose the intrinsic and synaptic parameters in the continuous model so that for any connectivity between the E-cells and the I-cells, there is a one-toone correspondence between solutions of the continuous and discrete systems. In particular, properties of the transients and attractors in the two systems are equivalent. For this result, we assumed that the inhibitory synapses are indirect. The choice of parameters depends only on the size of the network and the refractory period pi; in [49], we considered only the case ΘI = 1. A detailed analysis of the discrete dynamical system model is given in [50]. In that paper, we investigated how the connectivity of the network influences the prevalence of so-called minimal attractors – that is, attractors in which every cell fires as soon as it reaches the end of its refractory period. We demonstrate that in the case of randomly connected networks, there is a phase transition: if the connectivity is above the phase transition, then almost all states of the system belong to a fully active minimal attractor; if the connectivity is below the phase transition, then almost none of the states belong to a minimal attractor. This result allows us to estimate the number of attractors if the connectivity is above the phase transition; in particular there are a large number of stable oscillatory patterns. We also demonstrate that there is a second phase transition. If the probability of connection is above this second phase transition, but below the first, then most but not all cells will fire as soon as they reach the end of their refractory period.
5. Analysis of Model II
We now turn to Model II. The discrete model is more difficult to define for several reasons. There are now two cell layers and both the E- and the I-cells contain additional currents that may impact on the firing patterns. In order to explain mechanisms underlying the network's firing properties and to motivate the discrete dynamical system, we first consider two small networks.
5A.Two simple networks
First consider the network of two E–cells and two I-cells shown in Fig. 6A. Each E-cell excites both I-cells, each I-cell inhibits one of the E-cells and the two I-cells inhibit each other. A solution is shown in Fig. 6B. Note that E-I pairs take turns firing a series of 4 action potentials.
Figure 6.
Two examples of Model II. (A) A model with two E- and two I-cells. (B) Activity of the model from A: voltage of the E-cells (top), voltage of the I-cells (middle) and calcium in the I-cells (bottom). E-I pairs take turns firing four action potentials. Activity in a pair stops when the calcium level in the I-cell becomes too large. (C) A network example with three E- and three I-cells. Properties of this network are discussed in the text.
The mechanism underlying this activity pattern is the following: Suppose that one of the I-cells, say I1, spikes. The resulting inhibition allows E1 to spike during the next episode; however, the response to inhibition is not simply post-inhibitory rebound as it was in for Model I. Now inhibitory input to E1 deinactivates the inward current IT and, once the inhibitory input wears off sufficiently, E1 responds with an action potential. Once E1 fires, it sends excitatory input to both I-cells; however, only one of the I-cells responds with an action potential. This is because when one of the I-cells fires, it inhibits the other I-cell, preventing it from firing. Note in Fig. 6B that I1, fires several action potentials before I2 ‘takes over’. Each time I1 fires, it inhibits I2, delaying I2's response to excitatory input. This allows I1 to respond first for several episodes. However, each time that I1 fires, its calcium level increases and this strengthens the outward current IAHP, thereby delaying I1's response to excitatory input. Once IAHP becomes sufficiently strong – that is, the calcium level in I1 becomes sufficiently high – I2 responds first to excitatory input.
Other mechanisms come into play when we consider larger networks. In larger networks, we must consider the number of excitatory or inhibitory inputs that a cell receives during each episode. I-cells that receive more excitatory input than other I-cells tend to fire first and, thereby, inhibit other I-cells. On the other hand, E-cells that receive more inhibitory input than other E-cells tend to respond later than the other E-cells. As we explain shortly, these late-firing E-cells may not be important for the subsequent dynamics.
Consider the network shown in Fig. 6C. There are now 3 E-cells and 3 I-cells and each I-cell sends inhibitory input to the other two I-cells. Suppose that E1 and E3 fire together during some episode. This results in excitatory input to all three I-cells; however, I2 receives input from both E1 and E3, while I1 and I3 receive input from only one of these E-cells. Hence, I2 will tend to fire earlier than the other two I-cells and, if it does, prevent the other two I-cells from firing. We note, however, that whether I2 fires first depends on the relative calcium levels of the three I-cells. Once the calcium level in I2 builds up sufficiently, either I1 or I3 (or both) ‘takes over’ and responds to excitation from E1 and E3.
Now suppose that I1 and I3 fire synchronously during some episode (and not I2). Then all three E-cells receive inhibitory input. However, E2 receives input from both I-cells, while E1 and E3 receive input from only one I-cell. Hence, the total inhibitory input to E2 takes longer to wear off and E1 and E3 fire together before E2 does so. We note that even if E2 does fire (after E1 and E3), then this is not important for the subsequent dynamics. If, for example, E1 and E3 induce I2 to fire (as described above) then I2 will send inhibition to both I1 and I3. When E2 does fire, it will excite I1 and I3; however, these cells will be unable to fire because of the inhibitory input from I2.
Similar mechanisms underlie firing patterns in larger networks. In brief, suppose that some subset of I-cells fire. The E-cells that fire during the next episode are those that receive input from the smallest positive number of I-cells. Next suppose that some subset of E-cells fire. Whether or not an I-cell, say Ii, responds to the resulting excitation depends on three factors: (i) the number of E-cells that Ii receives excitation from; (ii) the number of I-cells that Ii received inhibition from during the previous episode; and (iii) the calcium level of Ii. If an I-cell does fire, then it will tend to inhibit other I-cells, preventing them from firing. However, there may be a small delay from when one I-cell fires until its synaptic variable activates and inhibits other I-cells. Hence, even if there is all-to-all coupling among the I-cells, once one I-cell fires, there is a ‘window of opportunity’ for other I-cells to respond. This will all be made more precise in the following section where we more formally define the discrete dynamical system.
5B. The discrete-time dynamical system
In order to formally define the discrete-time dynamical system, it will be convenient to introduce some notation. We consider the discrete time τ ∊ {0, 1, ...}. Each discrete time unit corresponds to a separate episode. We denote the state of each I-cell, Ii, at the discrete time τ as Si(τ) = (Fi(τ), CaDi(τ)). Here, Fi(τ) = 1 if Ii fires at discrete time τ and Fi(τ) = 0 if it does not; CaDi(τ) represents the calcium level – if the discrete time τ corresponds to the continuous time t, then CaDi(τ) = Cai(t).
Assume that there are N I-cells. The state of the discrete model at time τ is then ∑(∑) = {S1(∑), S2(∑), ... , SN(∑)}. We will define a map π: π(π) → π(π + 1). That is, if we know which I-cells fire and what the calcium levels of all the I-cells are at one episode, then the map determines this information at the next episode. This map then generates the discrete-time dynamical system.
We note that the state of the model involves the I-cells, not the E-cells. As the first example above demonstrates, it is critically important to keep track of the calcium levels of all the I-cells. As we shall see, if we know which I-cells fire during a given episode, then we can determine which E-cells fire during the next episode from the network architecture.
It will be convenient to consider both the discrete time π and the continuous time t. We assume that π=0 corresponds to t=0 and refer to this time as the 0th episode. The derivation of π is given in several steps. We assume that we are given an initial state π(0); this specifies which I-cells fire initially and the initial calcium levels of all of the I-cells. The first step is to determine which E-cells fire during the next, or 1st, episode. We then compute the calcium levels of all the I-cells during the 1st episode. The final step is to determine which I-cells fire during the 1st episode.
Step 1: Which E-cells fire during the 1st episode? Let JI denote the subset of I-cells that fire during the 0th episode; that is, JI = {i: Fi(0) = 1}. We assume that the E-cells that fire during the 1st episode are those that receive the minimal positive number of inputs from I-cells in JI. Denote this subset of E-cells as JE.
We note that for the continuous model, other E-cells may also fire. However, these E-cells either receive input from a larger number of I-cells than those in JE or they do not receive any input; hence, they must fire after the E-cells in JE. Our numerical simulations demonstrate that these late firing E-cells do not impact on the subsequent dynamics unless there is very sparse coupling among the I-cells. The reason for this was given in the second example in the preceding section.
We assume that the E-cells in JE fire when t=T. Note that T should depend on the number of I-cells that cells in JE receive input from. Here we simply assume that T is some fixed constant. Later, we describe how T is chosen and discuss the validity of this assumption.
Step 2: What are the calcium levels of the I-cells? We assume that every time an I-cell spikes, its calcium level increases by a fixed amount ACa, which is chosen later. Moreover, between spikes, calcium levels decrease at the exponential rate φCakCa (see eq. (4)). Hence, the calcium level of the I-cell Ii at the 1st episode is given by
| (5) |
Step 3: Which I-cells fire during the 1st episode? It remains to determine which I-cells fire during the 1st episode. Note that if an I-cell does fire, then it may inhibit other I-cells, preventing them from firing. We must, therefore, determine the I-cell that fires first and then determine which other I-cells are ‘stepped on’ by this I-cell. Other I-cells may fire if they do not receive inhibitory input from an I-cell that has already fired. There may also be a delay from when one I-cell fires until its synaptic variable activates and inhibits other I-cells. It is, therefore, possible for other I-cells to fire if they are able to do so within some prescribed ‘window of opportunity’.
We consider the continuous model and estimate the membrane potential of each I-cell. From this, we will compute the time (if it exists) at which the membrane potential would cross a prescribed threshold vθ and fire if no other I-cells fire during this episode. This then determines the order in which the I-cells would fire if they are not ‘stepped on’ by other I-cells. We can then determine which I-cells actually do fire during the 1st episode as follows. We assume that an I-cell fires if its membrane potential reaches threshold before it receives inhibitory input from another I-cell that has already fired. We further assume that there is a delay, δ, from when one I-cell fires until its synaptic variable activates and inhibits other I-cells. An I-cell will not fire if it receives inhibitory input before its membrane potential reaches threshold.
We now estimate the membrane potential, vi(t), of a given I-cell. The analysis is split into two parts. First we estimate vi when t=T, the time when E-cells in JE fire. We next consider the time interval from when E-cells fire until the I-cell would cross threshold if no other I-cells fire during this episode. In what follows we will make several assumptions on the dynamics; these assumptions are justified in the next section when we compare solutions of the continuous and discrete models.
For 0 < t < T, each I-cell lies in its silent phase. We assume that during this time the membrane potential is in pseudo steady-state; that is,
We further assume that the excitatory input and the sodium, calcium and potassium currents are negligible. It follows that, while silent, vi satisfies
| (6) |
where z(Cai) = Cai/(30+Cai) and SII = ∑sj is the total synaptic input from other I-cells. This is a linear equation for vi. We have already determined Cai(T) in Step 2. Hence, in order to obtain an explicit expression for vi(T), we need to estimate SII(T).
We assume that when an I-cell, Ij, fires, its synaptic variable, sj, is set to 1; in between spikes, sj decays exponentially at the rate β given in (2). We further assume that if Ij does not fire during an episode, then sj is negligible during the next episode. Hence, if Ii receives input from KI active I-cells during the 0th episode, then SII(T) = KI exp{–βT}. Together with (6), this then gives an explicit approximation for vi(T): vi = A/B where
and
Now consider the time from t=T until vi crosses the threshold vθ. Denote this time as ti. Assuming that the sodium, potassium and calcium currents are still negligible, we find that vi(t) satisfies the linear differential equation:
| (7) |
together with the initial condition v(T)=vi(T). Here SIE is the total synaptic input from the E-cells. Since |T-ti| is small, we assume that for T < t < ti, Cai(t) = Cai(T) and SII(t) = SII(T) are constant. We further assume that while an E-cell is active, its synaptic variable is equal to 1. It follows that SIE = KE where KE is the number of active E-cells that vi receives input from. We can now solve (7) explicitly and compute the time at which vi(ti) = vθ. This gives
| (8) |
where,
and
We note that ti may not be defined, in which case we say it is ∞. This may be the case if the I-cell does not receive any excitatory input; that is, KE = 0.
To determine which I-cells fire during the 1st episode, we let TI = min{ti}. The first I-cell that fires during the 1st episode is the one with tj = TI. This I-cell may then inhibit some other I-cells preventing them from firing. We assume that there is a delay, δ, from when one I-cell fires until its synaptic variable activates and inhibits other I-cells. Hence, an I-cell, Ik, will fire during the 1st episode if tk < TI + δ. Other I-cells may also fire if they do not receive inhibitory input. These I-cells may then inhibit other I-cells, after the delay, and so on. We note that if there is too much discrepancy in the firing times of the I-cells, then this may disrupt the near synchronous firing patterns, leading to instabilities.
Now that we have determined which I-cells fire during the 1st episode, and, from (5), the calcium levels of all the I-cells, we can define the map π: ∑(0) → ∑(1). This then defines the discrete dynamical system.
Choosing parameters
The discrete model depends on four parameters, which are not given explicitly in the continuous model. These are: (i) T, the time between episodes; (ii) ACa, the step increase in calcium after an I-cell spikes; (iii) vθ, the firing threshold; and (iv) δ, the delay from when one I-cell fires until it can suppress the firing of another I-cell. To choose these parameters, we simply solve the continuous model for a moderately sized network. It is then a simple matter to estimate these parameters for this one example. We then plug these parameters into the discrete model and test how well the discrete model predicts the behavior of the continuous model over a wide range of initial conditions, model parameters and network architectures.
Summary of the discrete-time dynamical system
Here we summarize how one derives the discrete-time dynamical system corresponding to a given E-I network. First we choose the parameters T, vδ, ACa and δ as described above.
In order to define the discrete-time dynamical system, we must define a map from the set of states to itself. Assume that we are given a state ∑(0) = {S1(0), ... , SN(0)} where each Si(0)=(Fi(0),CaDi(0)). Let JI = {i: Fi(0) = 1}. These are the I-cells that fire during the 0th episode. Then let JE be those E-cells that receive the minimal positive number of inputs from I-cells in JI. These are the E-cells that fire during the 1st episode.
The next step is to determine the calcium levels of the I-cells during the 1st episode. These are CaDi(1) = Cai(T) = (CaDi(0) + Fi(0) ACa) exp{–φCakCa T}.
Finally, we need to determine which I-cells fire during the 1st episode. For each I-cell, Ii, let, KI be the number of inputs that Ii receives from cells in JI, KE equal the number of inputs that Ii receives from cells in JE.,vi(T) = A/B where A and B were defined above, and let ti be as defined in (8). Then an I-cell, Ik, will fire during the 1st episode if tk < min{tj} + φ. We therefore let Fi(1)=1 if ti < min{tj} + φ and Fi(1)=0, otherwise.
Since we now know the calcium levels of all the I-cells at the 1st episode and which I-cells fire during the 1st episode, we can define the map π: π(0) →(1).
5C. Justification of the discrete model
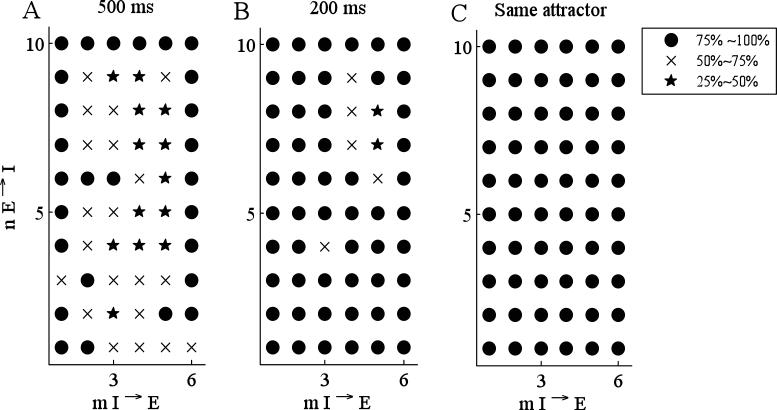
The network we used to choose parameters for the discrete model and to test its validity contained 10 E-cells and 6 I-cells. We found that T=32.5, π=.12, ACa =.1785, and vπ =−60. After choosing these parameters, we tested whether the discrete model accurately predicts which cells fire. The results are summarized in Fig. 7; this can be viewed as a 10 × 6 matrix of symbols. For the symbol at position (m,n), we randomly chose 20 networks in which every I-cell receives connections from n E-cells, and every E-cell receives connections from m I-cells. For each network, we randomly chose 5 different initial conditions. Hence, at each symbol, we compared the discrete and continuous models for 100 simulations. Each symbol represents the percentage of all simulations in which the discrete model matched the firing pattern of the continuous model over A) 500 ms and B) 200 ms. Even if solutions of the continuous and discrete models do not agree over some transient, they may still approach the same attractor. Fig. 7C shows the percentage of all simulations in which the continuous and discrete models do have the same attractor. In Fig. 7, a black circle represents between 75% and 100% match, an ‘x’ represents between 50% and 75% match, and a pentagram represents between 25% and 50% match. We do not expect the discrete model to perfectly match the continuous model over a wide range of connectivities and parameter values. In the derivation of the discrete model, we made a number of simplifying assumptions. For example, we assumed that the time between episodes is always fixed, while this should depend on the number of inputs the active E-cells receive. Moreover, we assumed that calcium increases by a fixed amount when an I-cell fires; however, the precise nature of the I-cell action potential depends on how many E-cells it receives input from and this influences how much calcium enters the cell.
Figure 7.
Comparison between the continuous and the discrete models in a network of 10 E- and 6 I-cells. For each grid point at position (m,n), 20 networks are randomly chosen in which every I-cell receives connections from n E-cells and every E-cell receives connections from m I-cells. For each such network, 5 different initial conditions are chosen at random. The marker type corresponds to the percentage of simulations in which the continuous and the discrete models had the same firing patterns for A) 500 ms and B) 200 ms. In C), the marker type corresponds to the percentage of simulations in which the continuous and the discrete model reach the same attractor, regardless of the transient. Values of parameters are listed in Tables 1 and 2.
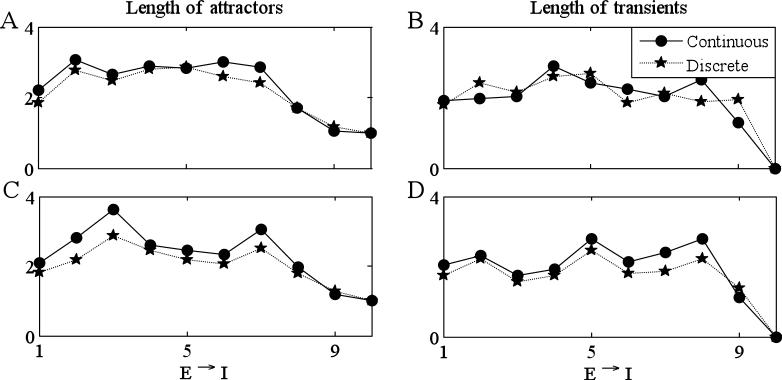
To further justify the discrete model, we tested how well it predicts the length of transients and attractors, even when the precise firing patterns may not match. Sample results are shown in Fig. 8, which represents column 4 in Fig. 7A. (Here, we averaged the length of transients and attractors over 100 stimuli.) We note that this is the column for which the match in Fig. 7 between the continuous and discrete models is worst. Note that the discrete model does an excellent job in predicting the behavior of the continuous model. In Fig. 8B, we change the parameters gAHP =15 and kCa =35 (from gAHP =25 and kCa =20 in Fig. 8A) to test whether the match between the discrete and continuous models is robust under changes in parameters. Finally, Fig. 3B demonstrates that the discrete model reproduces the results concerning binary mixture shown in Fig. 3A.
Figure 8.
The discrete model predicts the lengths of attractors and transients. For each simulation used for Figure 7, we computed the lengths of attractors and transients and then averaged over all simulations corresponding to a fixed number of connections. (A) Attractors and transients for the same simulations as in column 4 in Figure 7. In (B), gAHP is changed from 25 to 15 and kCa is changed from 20 to 35. Values of other parameters are listed in Tables 1 and 2.
5D. Numerical simulations of the discrete model
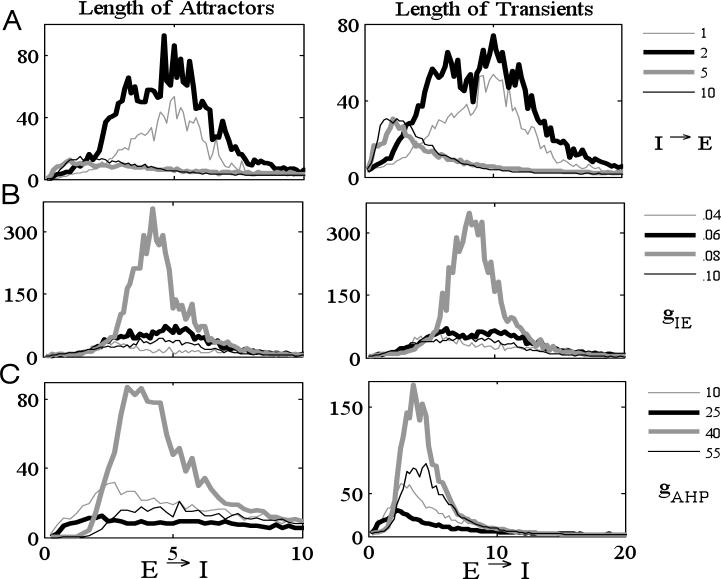
Fig. 9A shows how the lengths of attractors (left) and transients (right) depend on connection probability. Each curve represents a fixed I → E probability and is plotted against changes in the E → I probability. For example, for the thick black curves we generated networks in which each E-cell received input from 2 I-cells, chosen at random. We rescaled the maximal synaptic conductances gEI, gIE, and gII by the connection probabilities. For example, if gIE is the default value of the maximal synaptic conductance for an E → I connection, then along each black curve we divided gEI by 2. Unless stated otherwise, all the other parameters are the same (and given in Table 2) for each simulation. We considered networks with 100 E-cells and 40 I-cells. At each connection probability, we generated 100 different random networks with 20 different initial conditions. Hence, at each connection probability, we used 2000 simulations. We then took the mean of the lengths of attractors and transients. Note that along each of these curves, the maximum lengths of both transients and attractors reaches a maximum value at some intermediate E → I probability connection. Similarly, if we fix the E → I connection probability, then maximum lengths of transients and attractors are achieved at intermediate values of I → E connection probabilities. These results are similar to those obtained for Model I.
Figure 9.
Numerical simulations of the discrete model (100 E-cells and 40 I-cells). At each number of incoming connections, we considered 100 different random networks with 20 different initial conditions and then took the average length of attractor and transient. Each curve is plotted against the average number of E → I connections per cell. (A) Dependence of the lengths of attractors (left) and transients (right) on number of connections. Each curve represents a fixed number of I → E connections. (B,C) Dependence of lengths of attractors and transients on parameters gIE (B) and gAHP (C). Here we fixed the number of I → E connections (2 I → E in (B) and 5 I → E in (C)). Same parameter values as in Tables 1 and 2.
Table 2.
Parameter values for I-cells
| parameter | value | parameter | value | parameter | value | parameter | value |
|---|---|---|---|---|---|---|---|
| gNa | 60 | vNa | 55 | φ m | −37 | φ m | 10 |
| gK | 5 | vK | −80 | vCa | 120 | gCa | .1 |
| φmCa | −35 | φmCa | 2 | gL | .18 | vL | −55 |
| φ n | −50 | φ n | .1 | φ n0 | 1.5 | φ n1 | 1.35 |
| φ 0n | −12 | φ 0n | −40 | φ v | −40 | φ s | 2 |
| φ Ca | .007 | gAHP | 25 | kCa | 20 | φ | 12 |
| φ | .25 | gIE | .06 | gII | 2 | vI | −90 |
| vE | 90 | II | −2.5 |
Figs. 9 B, C illustrate how these results depend the parameters gIE, corresponding the E → I synaptic strength, and gAHP, corresponding the maximal conductance of the IAHP current in the I-cells. For each figure, we fixed the I → E probability (2 I → E for Fig. 9 B and 5 I → E for Fig. 9 C); each curve corresponds to a fixed value of the parameter. Note that the maximal lengths of transients and attractors are achieved for intermediate values of the parameters, as well as intermediate E →I connection probabilities. These results are similar to those shown in Fig. 4 for Model I in which we varied the firing threshold Θ. Note that both gAHP and gIE impact on the ability of an I-cell to respond to excitatory input. Clearly, increasing gIE makes it easier for an I-cell to respond. Since IAHP is an outward potassium current, increasing gAHP makes it more difficult for the I-cell to respond.
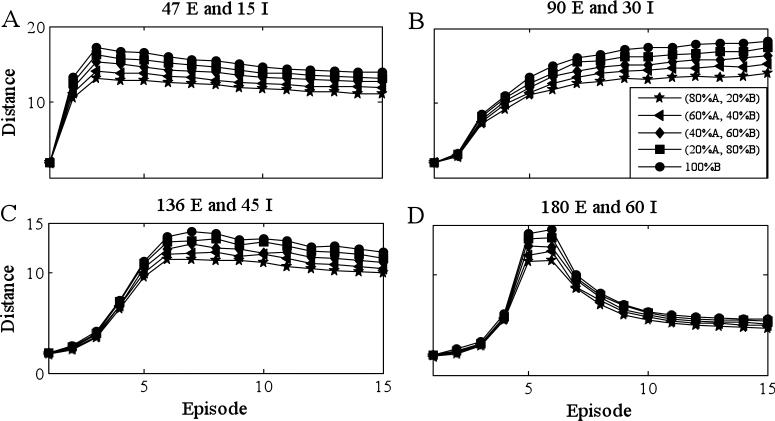
For Fig. 10, we presented the network with mixtures of two distinct odors (odor X and odor Y) and evaluated how the Hamming distance between the firing patterns corresponding to the mixture and one of the pure odors evolve with time. We considered networks with 300 E-cells and 100 I-cells. Different panels correspond to different connection probabilities. For example, 47 E and 15 I (Panel A) means each I-cell gets input from 47 randomly chosen E-cells and each E-cell gets input from 15 I-cells, chosen at random except, as in Fig. 3, we assumed that if there is an E → I connection, then there is also an I → E connection. Each pure odor corresponded to the activation of 30 E-cells and we assumed that the two odors activated non-overlapping sets of E-cells. As before, we considered mixtures in which the ratio of the two odors was varied 100:0 (base), 80:20, 60:40, 40:60, 20:80 and 0:100. All other procedures are the same as Fig. 3. We did this for 1000 different randomly chosen networks and initial conditions and then took the average distance. Note that maximal discrimination of mixtures occurs for intermediate connection probabilities (Panel B). Moreover, in Panels C, D, the distances reach a maximum value after approximately 5-10 cycles. In order to estimate the time our model takes to reach maximal separation, we assume that one step in our model equals one oscillation in the field potential measured in projection fields of AL PNs. That is a reasonable assumption, because each cycle of oscillation in the field potential corresponds to one set of synchronized PNs. Those sets are updated approximately every 30-50 ms (20-30 Hz). Using the longer estimate, 5-10 cycles corresponds to 250-500 ms, which is consistent with behavioral and electrophysiological data [37,44].
Figure 10.
Discrimination of odors for the discrete model, larger network (300 E-cells, 100 I-cells). Each pure odor corresponds to the activation of 30 E-cells and the two odors activated non-overlapping sets of E-cells. Different panels correspond to different number of connections in the network. The figure displays the distance (defined in the text) between the averaged firing pattern corresponding to the mixture and one of the pure odors (odor X). For each connection probability, we used 1000 different networks and initial conditions and then took the average distance. The baseline is 100% odor X, different curves correspond to ratios of odors X to Y: 80:20, 60:40, 40:60, 20:80 and 0:100. Values of other parameters are listed in Tables 1 and 2 except kCa =15 and gAHP =55.
6. Discussion
The primary goal of this paper is to develop mathematical techniques for analyzing a general class of excitatory-inhibitory neuronal networks. While this type of network arises in many important applications, including models for thalamic sleep rhythms and models for activity patterns within the basal ganglia, there has been very little mathematical analysis of them. Previous analytic studies have considered idealized cells with special structure of network connectivity, such as all-to-all, nearest neighbor, sparse or Mexican hat coupling. This paper represents the first attempt to analyze arbitrarily large excitatory-inhibitory networks with Hodgkin-Huxley like neurons and arbitrary network architecture. While the cells within our network include specific ionic currents that contribute to the emergent population rhythm, we feel that the mathematical techniques developed in this paper should help in the study of other neuronal networks as well.
We have shown that it is possible to reduce the full model to a discrete-time dynamical system. The discrete-time dynamical system is defined explicitly in terms of the model parameters; these include the maximal ionic conductances and reversal potentials, the strength and decay rates of synaptic connections, and the network architecture. Since the discrete system is considerably easier to solve numerically, this allows us to systematically study how emergent firing patterns depend on specific network parameters.
We have considered two model networks. Mechanisms underlying the firing patterns of Model I are considerably easier to analyze than those for Model II and we have, in fact, developed a detailed mathematical theory for when Model I can be rigorously reduced to the discrete dynamical system and how the nature of the transients and attractors depend on network properties [49,50]. It is interesting that a model as simple as Model I, which consists of a single layer of cells and only includes the most basic ionic currents, can exhibit firing patterns with properties similar to those seen in the AL. These properties include synchrony, dynamic reorganization and transient/attractor dynamics.
Model II is more complicated since it includes additional ionic currents and more complex interactions among the cells. We note that Model II is similar to the model proposed by Bazhenov et al [40,41], who also described mechanisms underlying these firing patterns. In particular, Bazhenov et al considered the role of the IAHP current in allowing for competition among the inhibitory cells. The analysis in this paper demonstrates that other mechanisms, not explicitly discussed in [40,41], come into play. For example, a critically important component that determines whether a cell will fire is the number of inputs it receives from the other cells in the network. By comparing solutions of the full model to the discrete dynamical system, we can be confident that all of the key components are accounted for. Moreover, Bazhenov et al do not describe the long transients now reported for locusts [37] and honey bees [36,45]. The transients may be important for the output of the AL, because the best (maximal) separation of different odors, which is important for behavioral discrimination, may occur during the transient compared to a ‘fixed point’ at which the pattern no longer evolves [37].
We considered as inputs for the model a (binary) mixture of two different odors. Fernandez et al [45] recently showed that gradations from one extreme mixture (100:0) through the other extreme (0:100) produce smooth changes in the perception of the odorants. That is, a 70:30 mixture elicits a level of response similar to 90:10, and the response changes smoothly as the mixture grades farther away from 90:10. This is correlated to smooth changes in the trajectories of the transients measured through calcium imaging in the AL. Our model is capable of reproducing smooth, almost linear, changes in the trajectories through PN-space. This is not a trivial finding, because it is not clear that computational networks like these would exhibit this behavior with small alterations of stimulus input.
A more important finding is that the behavior of the network changes dramatically with alterations of parameters such as connectivity and refractory period. These transitions take the form of changes in the lengths of transients or size of attractors. Furthermore, it was mostly sparse connectivity that maximized these outputs. For example, at a very low average connectivity, transients increase rapidly in length with increases in connectivity, then decreased with higher connectivities. The implication is that the network can be fine tuned to produce long transients for separation and discriminability of similar odors, such as when odor mixtures are similar in ratio [45]. Such low connectivity has neither been confirmed nor ruled out in the AL. Thus this prediction of the model remains to be experimentally tested.
Plasticity in the AL and OB has now been well documented (reviewed in [51]). Association of odors with one or another kind of reinforcement produces stable alterations in the response of cells in the network and in the PN output [52-57]. Several different modulators are involved in AL and OB networks and likely mediate the presence of reinforcement. For example, in the honey bee the biogenic amine octopamine is released into the AL as a result of reinforcement of an odor with sucrose feeding [58.59]. This reinforcement signal may change processing in the AL such that the transients are pushed farther apart and odors become, presumably, more discriminable [45]. Our model can now be used to make specific predictions of how these reinforcement signals may be altering the network to accomplish the changes observed in empirical studies.
Table 1.
Parameter values for E-cell
| parameter | value | parameter | value | parameter | value | parameter | value |
|---|---|---|---|---|---|---|---|
| gNa | 60 | vNa | 55 | βm | −37 | βm | 10 |
| gK | 5 | vK | −80 | β L | .18 | vL | −60 |
| gT | 8 | vCa | 120 | βmT | −63 | β mT | 7.8 |
| β n | −50 | β n | .1 | β n0 | 1.5 | β n1 | 1.35 |
| β 0n | −40 | β 0n | −12 | φ r | .75 | φ r | −85 |
| φ r | −.1 | φ r0 | .01 | φ r1 | 4.99 | φ 0r | −68 |
| φ 0r | −2.2 | φ v | −10 | φ s | .2 | IE1 / IE0 | −2.8/−5.6 |
| φ | 15 | φ | .8 | gEI | 12 | vI | −100 |
7. Acknowledgment
This work was partially funded by the NSF under agreement 0112050 and the NIH grant 1 RO1 DC007997-01 and from NIH-NCRR (NCRR RR014166).
Appendix: Nonlinear functions and parameter values
If X = m, n, r, mT or mCa, then we can write X∞(v) as X∞(v) = 1/(1+exp(-(v-θX) / σX)). Moreover, if X = n or r, then τX = τX0 + τX1 / (1+exp(-(v-τ0X) / τ0X)).
For Model I, Cm=1, gL=2.25, vL=−60.0, gNa=37.5, vNa=55, gK=45, vK=−80, gsyn=.2, vsyn=−100, α=2, β=.09, βx=.009, βx=.009, βm=−30, βm=15, βn=−45, βn=−3, βv=−56, βx=.2, βs=.1, βx=.01, βn0=1, βn1=10, β0n=−20, β0n=.1, I0=15.
Unless stated elsewhere, we used the following parameters for Model II: Cm=1 for both. In Figs. 3, 7, 8, 9 and 10, we rescaled the maximal synaptic conductances by the number of connections: gIE =0.06 / # of connected E-cells, gEI = 12 / # of connected I-cells, gII =2 / # of connected I-cells.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Llinas RR. The intrinsic electrophysiological properties of mammalian neurons: Insights into central nervous system function. Science. 1988;242:1654–1664. doi: 10.1126/science.3059497. [DOI] [PubMed] [Google Scholar]
- 2.Jacklet JW. Neuronal and Cellular Oscillators. Marcel Dekker Inc; New York: 1989. [Google Scholar]
- 3.Steriade M, Jones EG, Llinas RR. Thalamic Oscillations and Signaling. Wiley; New York: 1990. [Google Scholar]
- 4.Steriade M, Jones E, McCormick D, editors. Thalamus. II. Elsevier; Amsterdam: 1997. [Google Scholar]
- 5.Traub RD, Miles R. Neuronal Networks of the Hippocampus. Cambridge University Press; New York: 1991. [Google Scholar]
- 6.Buzsaki G, Llinas R, Singer W, Berthoz A, Christen . Temporal Coding in the Brain. Springer-Verlag; New York, Berlin and Heidelberg: 1994. [Google Scholar]
- 7.Gray CM. Synchronous oscillations in neuronal systems: Mechanisms and functions. J. Comput. Neuroscience. 1994;1:11–38. doi: 10.1007/BF00962716. [DOI] [PubMed] [Google Scholar]
- 8.Jeffreys JGR, Traub RD, Whittington MA. Neuronal networks for induced ‘40 Hz’ rhythms. Trends in Neuroscience. 1996;19:202–207. doi: 10.1016/s0166-2236(96)10023-0. [DOI] [PubMed] [Google Scholar]
- 9.Steriade M, Contreras D, Amzica F. Synchronized sleep oscillations and their paroxysmal developments. Trends in Neuroscience. 1994;17:199–208. doi: 10.1016/0166-2236(94)90105-8. [DOI] [PubMed] [Google Scholar]
- 10.Kandel ER, Schwartz JH, Jessell TM. Principles of Neural Science. Norwalk, Conn.; Appleton & Lange: 1991. [Google Scholar]
- 11.Wang X-J, Golomb D, Rinzel J. Emergent spindle oscillations and intermittent burst firing in a thalamic model: specific neuronal mechanisms. Proc. Natl. Acad. Sci. USA. 1995;92:5577–5581. doi: 10.1073/pnas.92.12.5577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bevan MD, Magill PJ, Terman D, Bolam JP, Wilson CJ. Move to the rhythm: oscillations in the subthalamic nucleus-external globus pallidus network. Trends in Neuroscience. 2002;25:523–531. doi: 10.1016/s0166-2236(02)02235-x. [DOI] [PubMed] [Google Scholar]
- 13.Cohen AH, Rossignol S, Grillner S, editors. Neural Control of Rhythmic Movements in Vertebrates. John Wiley and Sons, Inc.; New York: 1988. [Google Scholar]
- 14.Chay TR, Keizer J. Minimal model for membrane oscillations in the pancreatic beta-cell. Biophys. J. 1983;42:181–190. doi: 10.1016/S0006-3495(83)84384-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Butera RJ, Rinzel J, Smith JC. Models of respiratory rhythm generation in the pre-Botzinger complex: I. Bursting pacemaker model. J. Neurophysiology. 1999;82:382–397. doi: 10.1152/jn.1999.82.1.382. [DOI] [PubMed] [Google Scholar]
- 16.Chay TR, Rinzel J. Bursting, beating, and chaos in an excitable membrane model. Biophys. J. 1985;47:357–366. doi: 10.1016/S0006-3495(85)83926-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Terman D. Chaotic spikes arising from a model for bursting in excitable membranes. SIAM J. Appl. Math. 1991;51:1418–1450. [Google Scholar]
- 18.Terman D. The transition from bursting to continuous spiking in an excitable membrane model. J. Nonlinear Sci. 1992;2:133–182. [Google Scholar]
- 19.Rinzel J. Bursting oscillations in an excitable membrane model. In: Sleeman BD, Jarvis RJ, editors. Ordinary and Partial Differential Equations. Springer-Verlag; New York: 1985. [Google Scholar]
- 20.Rinzel J. A formal classification of bursting mechanisms in excitable systems. In: Gleason AM, editor. Proceedings of the International Congress of Mathematicians. American Mathematical Society; Providence, RI: 1987. pp. 15778–1594. [Google Scholar]
- 21.Izhikevich EM. Neural excitability, spiking, and bursting. International Journal of Bifurcation and Chaos. 2000:10. [Google Scholar]
- 22.Golomb D, Rinzel J. Clustering in globally coupled inhibitory neurons. Physica D. 1994;72:259–282. [Google Scholar]
- 23.Kopell N, LeMasson G. Rhythm genesis, amplitude modulation and multiplexing in a cortical architecture. Proc. Natl. Acad. Sci. USA. 1994;91:10586–10590. doi: 10.1073/pnas.91.22.10586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Rubin J, Terman D. Geometric singular perturbation analysis of neuronal dynamics. In: Fiedler B, Ions G, Kopell N, editors. Handbook of Dynamical Systems, vol. 3: Towards Applications. Elsevier; Amsterdam: 2002. [Google Scholar]
- 25.Destrehan A, Bal T, McCormick D, Sejnowski T. Ionic mechanisms underlying synchronized oscillations and propagating waves in a model of ferret thalamic slices. J. Neurophysiology. 1996;76:2049–2070. doi: 10.1152/jn.1996.76.3.2049. [DOI] [PubMed] [Google Scholar]
- 26.Rinzel J, Terman D, Wang X-J, Ermentrout B. Propagating activity patterns in large-scale inhibitory neuronal networks. Science. 1998;279:1351–1355. doi: 10.1126/science.279.5355.1351. [DOI] [PubMed] [Google Scholar]
- 27.Golomb D, Ermentrout GB. Continuous and lurching traveling pulses in neuronal networks with delay and spatially-decaying connectivity. Proc. Natl. Acad. Sci., USA. 1999;96:13480–13485. doi: 10.1073/pnas.96.23.13480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bressloff PC, Coombes S. Traveling waves in a chain of pulse-coupled integrate-and-fire oscillators with distributed delays. Physica D. 1999;130:232–254. [Google Scholar]
- 29.Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in a nerve. J. Physiology. 1952;117:165–181. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kopell N, Ermentrout B. Mechanisms of phase-locking and frequency control in pairs of coupled neural oscillators. In: Fiedler B, Iooss G, Kopell N, editors. Handbook of Dynamical Systems, vol. 3: Towards Applications. Elsevier; Amsterdam: 2002. [Google Scholar]
- 31.Laurent G, Stopfer M, Friedrich RW, Rabinovich MI, Volkovskii A, Abarbanel HD. Odor encoding as an active, dynamical process: experiments, computation, and theory. Annu. Rev. Neurosci. 2001;24:263–297. doi: 10.1146/annurev.neuro.24.1.263. [DOI] [PubMed] [Google Scholar]
- 32.Kay LM, Stopfer M. Information processing in the olfactory systems of insects and vertebrates. Semin. Cell Dev. Biol. 2006;17:433–442. doi: 10.1016/j.semcdb.2006.04.012. [DOI] [PubMed] [Google Scholar]
- 33.Mainen ZF. Behavioral analysis of olfactory coding and computation in rodents. Curr. Opin Neurobiol. 2006;16:429–434. doi: 10.1016/j.conb.2006.06.003. [DOI] [PubMed] [Google Scholar]
- 34.Wilson RI, Mainen ZF. Early events in olfactory processing. Annu. Rev Neuroscience. 2006;29:163–201. doi: 10.1146/annurev.neuro.29.051605.112950. [DOI] [PubMed] [Google Scholar]
- 35.Sachse S, Galizia CG. The coding of odour-intensity in the honeybee antennal lobe: local computation optimizes odour representation. Eur. J. Neurosci. 2003;18:2119–2132. doi: 10.1046/j.1460-9568.2003.02931.x. [DOI] [PubMed] [Google Scholar]
- 36.Galan RF, Sachse S, Galizia, C.G. CG, Herz AV. Odor-driven attractor dynamics in the antennal lobe allow for simple and rapid olfactory pattern classification. Neural Comput. 2004;16:999–1012. doi: 10.1162/089976604773135078. [DOI] [PubMed] [Google Scholar]
- 37.Mazor O, Laurent G. Transient dynamics versus fixed points in odor representations by locust antennal lobe projection neurons. Neuron. 2005;48:661–673. doi: 10.1016/j.neuron.2005.09.032. [DOI] [PubMed] [Google Scholar]
- 38.Vosshall LB, Wong AM, Axel R. An olfactory sensory map in the fly brain. Cell. 2000;102:147–159. doi: 10.1016/s0092-8674(00)00021-0. [DOI] [PubMed] [Google Scholar]
- 39.Mombaerts P. Molecular biology of odorant receptors in vertebrates. Annu. Rev. Neurosci. 1999;22:487–509. doi: 10.1146/annurev.neuro.22.1.487. [DOI] [PubMed] [Google Scholar]
- 40.Bazhenov M, Stopfer M, Rabinovich M, Abarbanel HD, Sejnowski TJ, Laurent G. Model of cellular and network mechanisms for odor-evoked temporal patterning in the locust antennal lobe. Neuron. 2001;30:569–581. doi: 10.1016/s0896-6273(01)00286-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Bazhenov M, Stopfer M, Rabinovich M, Huerta R, Abarbanel HD, Sejnowski TJ, Laurent G. Model of transient oscillatory synchronization in the locust antennal lobe. Neuron. 2001;30:553–567. doi: 10.1016/s0896-6273(01)00284-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Gelperin A. Olfactory computations and network oscillation. J. Neurosci. 2006;26:1663–1668. doi: 10.1523/JNEUROSCI.3737-05b.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Rinberg D, Koulakov A, Gelperin A. Speed-accuracy tradeoff in olfaction. Neuron. 2006;51:351–358. doi: 10.1016/j.neuron.2006.07.013. [DOI] [PubMed] [Google Scholar]
- 44.Uchida N, Mainen ZF. Speed and accuracy of olfactory discrimination in the rat. Nat. Neurosci. 2003;6:1224–1229. doi: 10.1038/nn1142. [DOI] [PubMed] [Google Scholar]
- 45.Fernandez PC, Locatelli FL, Rennell N, Deleo G, Smith BH. Associative conditioning tunes transient dynamics of early olfactory processing. J. Neuroscience. 2009;29:10191–10202. doi: 10.1523/JNEUROSCI.1874-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Abraham NM, Spors H, Carleton A, Margrie TW, Kuner T, Schaefer AT. Maintaining accuracy at the expense of speed: stimulus similarity defines odor discrimination time in mice. Neuron. 2004;44:744–747. doi: 10.1016/j.neuron.2004.11.017. [DOI] [PubMed] [Google Scholar]
- 47.Friedrich RW, Laurent G. Dynamic optimization of odor representations by slow temporal patterning of mitral cell activity. Science. 2001;291:889–894. doi: 10.1126/science.291.5505.889. [DOI] [PubMed] [Google Scholar]
- 48.Kreher SA, Mathew D, Kim J, Carlson JR. Translation of sensory input into behavioral output via an olfactory system. Neuron. 2008;59:110–24. doi: 10.1016/j.neuron.2008.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Terman D, Ahn S, Wang X, Just W. Reducing neuronal networks to discrete dynamics. Physica D. 2008;237:324–338. doi: 10.1016/j.physd.2007.09.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Just W, Ahn S, Terman D. Minimal attractors in digraph system models of neuronal networks. Physica D. 2008;237:3186–3196. [Google Scholar]
- 51.Davis RL. Olfactory learning. Neuron. 2004;44(1):31–48. doi: 10.1016/j.neuron.2004.09.008. [DOI] [PubMed] [Google Scholar]
- 52.Brennan PA, Keverne, E.B. EB. Neural mechanisms of mammalian olfactory learning. Prog. Neurobiol. 1997;51(4):457–81. doi: 10.1016/s0301-0082(96)00069-x. [DOI] [PubMed] [Google Scholar]
- 53.Faber T, Joerges J, Menzel R. Associative learning modifies neural representations of odors in the insect brain. Nat. Neurosci. 1999;2(1):74–8. doi: 10.1038/4576. [DOI] [PubMed] [Google Scholar]
- 54.Kay LM, Laurent G. Odor- and context-dependent modulation of mitral cell activity in behaving rats. Nat. Neurosci. 1999;2(11):1003–9. doi: 10.1038/14801. [DOI] [PubMed] [Google Scholar]
- 55.Stopfer M, Laurent G. Short-term memory in olfactory network dynamics. Nature. 1999;402(6762):664–8. doi: 10.1038/45244. [DOI] [PubMed] [Google Scholar]
- 56.Daly KC, Christensen TA, Lei H, Smith, B.H. BH, Hildebrand JG. Learning modulates the ensemble representations for odors in primary olfactory networks. Proc. Natl. Acad. Sci. U.S.A. 2004;101(28):10476–81. doi: 10.1073/pnas.0401902101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Yu D, Ponomarev A, Davis RL. Altered representation of the spatial code for odors after olfactory classical conditioning; memory trace formation by synaptic recruitment. Neuron. 2004;42(3):437–49. doi: 10.1016/s0896-6273(04)00217-x. [DOI] [PubMed] [Google Scholar]
- 58.Hammer M, Menzel R. Multiple sites of associative odor learning as revealed by local brain microinjections of octopamine in honeybees. Learn Mem. 1998;5(1-2):146–56. [PMC free article] [PubMed] [Google Scholar]
- 59.Farooqui T, Robinson K, Vaessin H, Smith BH. Modulation of early olfactory processing by an identified octopaminergic reinforcement pathway in the honeybee. J. Neuroscience. 2003;23:5370–80. doi: 10.1523/JNEUROSCI.23-12-05370.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]