Turbidity corrected Raman spectroscopy for blood analyte detection

Abstract

A major challenge in quantitative biological Raman spectroscopy, particularly as applied to transcutaneous Raman spectroscopy measurements, is overcoming the deleterious effects of scattering and absorption (turbidity). The Raman spectral information is distorted by multiple scattering and absorption events in the surrounding medium, thereby diminishing the prediction capability of the calibration model. To account for these distortions, we present a novel analytical method, that we call turbidity corrected Raman spectroscopy (TCRS), which is based on the photon migration approach and employs alternate acquisition of diffuse reflectance and Raman spectra. We demonstrate that on application of TCRS, the widely varying Raman spectra observed from a set of tissue phantoms having the same concentration of Raman scatterers but different turbidities tend to collapse onto a single spectral profile. Furthermore, in a prospective study employing physical tissue models with varying turbidities and randomized concentrations of Raman scatterers and interferents, a 20% reduction in prediction error is obtained by applying the turbidity correction procedure to the observed Raman spectra.

1. Introduction

Blood analytes provide valuable information for the diagnosis of many diseases and related health conditions. Development of painless, non-invasive methods for measuring such analytes has been extensively investigated, especially for blood glucose detection (excellent reviews can be found in the literature ^{1, 2}). This area has received considerable attention, as diagnosis and therapeutic monitoring of diabetes necessitates direct measurement of blood glucose ^{3, 4}. A non-invasive method for measuring blood glucose levels would be an important advance, given the large number of diabetics, some of whom must undergo glucose testing several times each day. Near infrared (NIR) Raman spectroscopy, which combines the substantial penetration depth of NIR light with the excellent chemical specificity of Raman spectroscopy, offers a promising solution for non-invasive detection of blood glucose and other analytes.

Several research groups, including our own, have reported Raman spectroscopy based glucose predictions at physiologically relevant concentrations in serum ⁵, whole blood ⁶ and other in vitro samples, such as human eye aqueous humor ^{7, 8}. Promising studies in transcutaneous Raman spectroscopy in human volunteers have also been conducted ^{9, 10}. However, prospective application has proven to be challenging, particularly when the calibration model developed on one subject is applied to a different subject. We attribute much of the difficulty in implementing successful prospective prediction methods to variations in tissue optical properties characteristic of a human subject population. Variations in turbidity, defined as the combined effects of scattering and absorption, alter the tissue sampling volume, diminishing the concentration prediction accuracy on prospective samples. Turbidity also gives rise to intensity and shape distortions in the Raman spectra and introduces non-analyte specific variance into the calibration model that deteriorates the prediction capability. Overcoming the effects of optical property variations is one of the central challenges in quantitative biological Raman spectroscopy. In other words, in order to accurately predict blood analyte concentrations in a group of human subjects, a methodology for extracting intrinsic (true) line shape and intensity information from the observed Raman spectra is needed.

One approach developed to reduce the aforementioned effects of the variations in optical properties on the prediction capability of the regression model was presented by Chaiken et. al. ¹¹. They conducted an in vivo study employing tissue modulation on the fingertip. Although reasonable glucose measurement accuracy was reported, the results showed that differences among individuals added significant error to the actual concentration estimates.

The necessity for correcting for variations in turbidity is widely acknowledged in the non-invasive glucose detection literature, especially NIR absorption spectroscopy ^{1, 2, 12, 13}. Over the past decade, researchers in the field of fluorescence spectroscopy have also extensively studied the effects of turbid media on the observed fluorescence spectra ^{14, 15}. Correction schemes using a variety of experimental and analytical approaches have been developed to remove distortions induced in the fluorescence spectra due to multiple scattering and absorption ^16-24. For example, our laboratory has developed intrinsic fluorescence extraction methodologies using diffuse reflectance spectroscopy, based on the principle that fluorescent and diffusely reflected photons undergo similar scattering and absorption events in the turbid medium ^{16, 17}.

While methods for extracting intrinsic fluorescence have been widely employed, only a little work has been done in developing an analogous methodology for Raman spectroscopy. In one such scheme, employed to study powder samples, the Raman signal was related to the measured diffuse reflectance as a function of the Kubelka-Munk absorption or scattering coefficients ²⁵. However, the Kubelka-Munk formulation, which assumes that elastic scattering is isotropic, cannot be readily extended to biological tissues, where scattering is highly anisotropic ^{26, 27}. Aarnoutse et. al. ²⁸ have also reported a method using simultaneous absorption measurements to correct for the absorbance of Raman scattered light by the media in catalysis reactions. In this method, only the effect of variations in sample absorption was considered, whereas in biological tissues variations in scattering are substantially more important ^{29, 30}. Matousek et al. have proposed a novel method for retrieval of Raman spectra from subsurface layers in diffusely scattering media, which is based on the idea of collecting of Raman scattered light from surface regions laterally offset away from the excitation laser spot ³¹. This method, however, is useful for extracting depth-resolved spectral information and is not suitable for application in samples where Raman scatterers are distributed throughout the turbid medium of interest.

Recently, our laboratory has developed a method to reduce the deleterious effects of turbidity variations in concentration predictions using Raman spectroscopy. As in the aforementioned case of fluorescence correction, this method is based on the use of diffuse reflectance at the same tissue region to correct for turbidity variations. Two of our laboratory's recent publications have presented a method (Intrinsic Raman Spectroscopy (IRS)) that corrects for the turbidity-induced sampling volume variations and relates the observed (sampled) concentration to the true concentration of the analyte of interest by means of a universal calibration curve ^{32, 33}. However, using a Monte Carlo technique (as proposed in IRS³²) to determine a universal calibration curve has the limitation that the Raman scattering coefficients must be known accurately for the given constituents, which is a non-trivial task. In addition, for the experimental IRS technique³³ used for derivation of the calibration curve, one needs to create tissue phantoms with the same composition of constituents as found in each tissue type. Since glucose forms a minute part of the total tissue Raman spectrum (as small as 0.3%), there remains substantial uncertainty as to the prospective applicability of this calibration curve in vivo. Furthermore, it also requires the explicit determination of the optical properties of the tissue site, specifically the reduced scattering coefficient (μ_s′(λ)). Prediction of blood analyte concentrations from human subjects under clinical conditions necessitates the introduction of a new method which is independent of tissue composition and geometry invariant.

Here we present a different approach, which we call turbidity corrected Raman spectroscopy (TCRS), that overcomes these difficulties by correcting for intensity and shape distortions in the observed Raman spectra. This approach also employs alternate acquisition of diffuse reflectance spectra and is based on the photon migration picture. In the following, we derive an analytical relation connecting the observed Raman spectrum, the diffuse reflectance spectrum and the turbidity corrected Raman spectrum. We then study a set of tissue phantoms having the same concentration of Raman scatterers, but different background turbidities, and demonstrate that on application of TCRS, the turbidity-induced distortions in intensity and line shapes are removed, and the spectra tend to collapse onto a single spectral profile. The results show that TCRS can recover intrinsic line shape and intensity information from the acquired Raman spectrum in a turbid medium for the range of optical properties found in biological tissues. Furthermore, in a set of prospective studies which employ phantoms of varying turbidities and randomized concentrations of Raman scatterers and interferents, we obtain a 20% reduction in prediction error by applying the turbidity correction procedure to the observed Raman spectra. To the best of our knowledge, this is the first demonstration of enhanced prospective prediction accuracy employing turbidity corrected Raman spectra, and it opens the pathway to improved prospective prediction accuracy in transcutaneous Raman spectroscopy.

2. Theoretical Approach

Turbidity corrected Raman spectroscopy provides an analytical model that expresses the turbidity corrected Raman spectrum in terms of the observed Raman and diffuse reflectance spectra. The following mathematical formulation builds on the probabilistic framework of the photon migration approach. The photon migration approach, first introduced by Weiss and co-workers ^{34, 35}, has been extensively used to quantify the diffuse reflectance and fluorescence spectra acquired from biological tissues by Wu et al ¹⁶ and Zhang et al ¹⁷ of our laboratory. In this approach, light propagation in turbid medium is modeled as the ensemble average of the probabilistic photon migration paths distributed within the turbid medium and the realization probability of the full path of each individual photon, governed by the albedo a = μ_s/(μ_s+μ_a), with μ_s and μ_a the scattering and absorption coefficients, respectively. Mathematically, the diffuse reflectance spectrum, R, can then be expressed as:

$$R=\sum _{n=1}^{\infty }{\rho }_n{a}^n,$$ (1)

where ρ is the probability of a photon escaping the input face of the medium after n tissue interaction events and is related to the photon migration path through the medium. The escape probability function is characterized by the scattering phase function and the excitation-collection geometry of the system:

$${\rho }_n=S(1-g)exp\left[-S(1-g)n\right],$$ (2)

where g is the anisotropy coefficient and S is an instrument-specific constant that depends on the excitation-collection geometry ¹⁷. The instrument parameter S must be calibrated for the system under consideration before further spectral analysis can be carried out. As is evident from the above expression, S is smaller for more diffusely scattered light and vice-versa.

Using the correspondence between Raman scattered and diffusely reflected photons, the observed Raman spectrum can be defined as the ensemble average of the photon migration paths and the realization probability of the individual paths, which is now mediated not only by the absorption and elastic scattering coefficients but also by the Raman scattering coefficient:

$${\left({\mathit{Raman}}_{\mathit{OBS}}\right)}_{xm}=\sum _{n=1}^{\infty }\left[\frac{I_x}{h{v}_x}\sum _{i=0}^{n-1}\left(h{v}_m\right){\rho }_{ni}\left[{\mathit{\text{a}}}_x^i\left(\frac{{\mu }_{Rx}}{{\mu }_{ax}+{\mu }_{sx}}\right)a_m^{n-i-1}\right]\right],$$ (3)

where the subscripts x and m represent the Raman excitation (ν_x) and emission (ν_m) frequencies, respectively; Raman_OBS is the observed Raman spectrum; h is Planck's constant; i is the position of the node at which Raman scattering occurs; I_x is the excitation intensity; and μ_R is the Raman scattering coefficient.

From Eq. (3), it can be observed that an incident photon at frequency ν_x undergoes i scattering and absorption events prior to undergoing an inelastic Raman scattering event, with probability μ_Rx/(μ_ax + μ_sx), and then undergoes (n-i-1) further scattering and absorption events at frequency ν_m before escaping from the medium. It should be noted that the escape probability function, ρ_ni, is also influenced by the position of the node at which Raman scattering occurs because the scattering coefficient, before and after Raman scattering, has different values at the excitation and emission frequencies ¹⁷. Importantly, the role of photon path in the Raman scattering process can be clearly described from Eq. (3), and the similarity between diffuse reflectance and Raman photon paths should be noted.

The turbidity-corrected Raman spectrum, which we define as the spectrum that would be obtained if Raman scattering was the only photon interaction event in the medium, is given by:

$${\left({\mathit{Raman}}_{\mathit{TC}}\right)}_{xm}=\frac{I_x}{h{v}_x}({\mu }_{Rx}l)h{v}_m,$$ (4)

where Raman_TC is the turbidity-corrected Raman spectrum; and l is the effective photon path length in the medium. Specifically, the effective photon path length in turbid tissue is a function of the absorption and scattering properties of the sample.

Relating Eq. (4) to Eq. (3) using the diffuse reflectance defined in Eq. (1), we obtain:

$${\left({\mathit{Raman}}_{\mathit{TC}}\right)}_{xm}=\frac{{\left({\mathit{Raman}}_{\mathit{OBS}}\right)}_{xm}}{\frac{{\left(R_{0m}{R}_{0x}\right)}^{\stackrel{1}{}/\underset{2}{}}}{S{\mu }_{sx}^{\prime }l}\frac{R_x}{R_{0x}}\left(\frac{R_m}{R_{0m}}+S(1-g)\right)},$$ (5)

where R₀ is the diffuse reflectance spectrum that would be obtained from a sample with the same scattering coefficient but zero absorption coefficient, and μ_s′ is the reduced scattering coefficient (μ_s′=μ_s(1-g)).

When the absorption in the tissue is weak (i.e., μ_s′≫μ_a), Eq. (5) can be simplified to obtain:

$${\left({\mathit{Raman}}_{\mathit{TC}}\right)}_{xm}=\left[S\right]\left[{\mu }_{sx}^{\prime }l\right]\left[\frac{{\left({\mathit{Raman}}_{\mathit{OBS}}\right)}_{xm}}{\sqrt{R_x{R}_m}}\right],$$ (6)

This approximation is valid for biological samples of interest in the NIR (700-1000 nm), where 5<μ_s′<20 cm^-1 and 0.08<μ_a<1.3 cm^{-1 36,37}.

Equation (6) is key to implementing TCRS and is comprised of three factors: (a) the instrument-specific constant, S; (b) the sample-dependent factor (μ_sx′l) (as the optical path length through the tissue is a function of the scattering and absorption properties of the tissue themselves); and (c) the diffuse reflectance-based turbidity correction factor ((Raman_OBS)_xm/√(R_xR_m)). As can be seen, this factor depends on the diffuse reflectance measured at both Raman excitation and emission frequencies. This accounts for the feature of Raman scattering in which a frequency shift from ν_x to ν_m is induced in the outgoing (Raman scattered) photons.

Before applying Eq. (6), we need to determine the instrument-specific constant (first factor in Eq. (6)) and the dependence of the average path length on the optical properties of the tissue (second factor in Eq. (6)). The optical properties can, in turn, be estimated by fitting the observed diffuse reflectance spectra to the model of Zonios et. al. ³⁸. It is important to note that when applying a standard partial least squares (PLS) protocol ³⁹ using the turbidity corrected Raman spectra, there is no need to determine the instrument-specific constant, as it cancels out during the calibration/prediction procedure. Nevertheless this constant is required for performing explicit multivariate calibration studies such as ordinary least squares (OLS) ³⁹. In the calibration study of Sec. 4, we determine this constant, as well as the functional dependence of the average photon path length on the sample optical properties.

Additionally, it is necessary to estimate the diffusely reflected light at the Raman excitation frequency (R_x), as all frequencies close to the laser line are cut off by the notch filter that is used to suppress the elastically scattered light. Due to the absence of any significant absorbers in biological tissue in the NIR range and the slowly varying nature of the scattering coefficient, the diffusely reflected light at the Raman emission frequency can be readily estimated by extrapolating a low-order polynomial which provides the best fit to the observed diffuse reflectance spectrum at the excitation frequency.

3. Experimental methods

Instrumentation

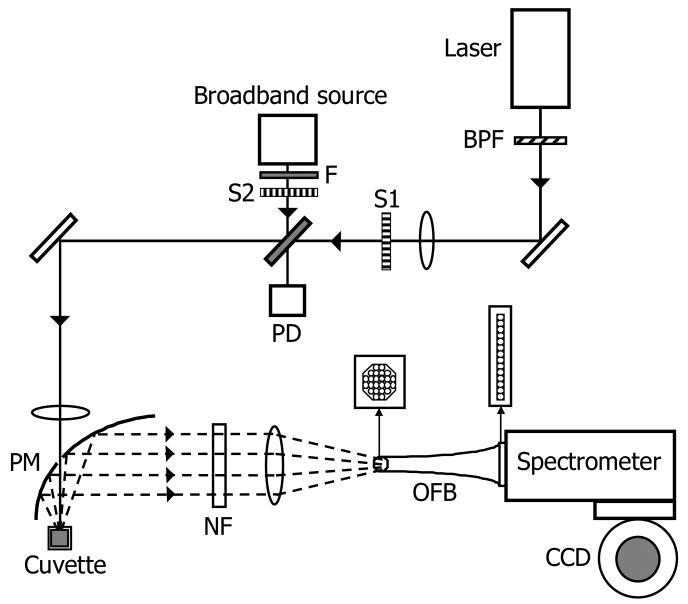
The experimental setup used for the excitation and collection of Raman and diffuse reflectance spectra is similar to the ones described in our laboratory's earlier publications ^{6, 33}. A schematic of the experimental arrangement is shown in Fig. 1. Briefly, an 830-nm external cavity diode laser (Process Instruments) was used as the Raman excitation source for acquisition of Raman spectra. The laser beam was focused onto the sample with an average power of ∼100 mW and a spot diameter of ∼1 mm. We employed a half-paraboloidal mirror (Perkin-Elmer, Inc.) as the primary collection element, the specifications of which are detailed in Enejder et al ⁶. Additionally, a tungsten-halogen lamp (Avantes AvaLight-HAL-S) was used as a broadband source to obtain diffuse reflectance spectra from the sample. The beam diameter and average power of the broadband source at the sample were measured to be approximately 1 mm and 100 μW, respectively. The tissue phantoms were held in a standard fused silica cuvette. The sample interface was aligned so as to enable the specular reflection, which does not contain any analyte information, to escape through the hole in the paraboloidal mirror.

Fig.1.

Schematic of the experimental setup. BPF: bandpass filter; S1-S2: shutters; F: Absorption filter; PD: photodiode; PM: paraboloidal mirror; NF: notch filter; OFB: optical fiber bundle.

The back-scattered light was collected and directed by the paraboloidal mirror towards a notch filter to suppress the excitation (Rayleigh) peak. The light was then focused using an optical fiber bundle onto the slit of a modified f/1.4 spectrograph (Kaiser Optical Systems, Inc.). A liquid nitrogen cooled deep depletion CCD detector (1″×1″) (Princeton Instruments) having high quantum efficiency in the NIR range was used to acquire the spectra. The spectral resolution of the system was 8 cm^-1.

The Raman and diffuse reflectance spectra were acquired alternately with an acquisition time per sample of 20 seconds each. Owing to the large area of the CCD the final images obtained were curved, and a curvature correction algorithm was applied before vertical binning ⁴⁰. The resultant spectra were subject to cosmic ray removal, background correction and Savitzky-Golay smoothing algorithm ⁴¹. The diffuse reflectance spectra were calibrated using a reference standard of 20% intralipid solution. Spectra of samples were acquired randomly with respect to the constituents' concentrations. Spectra were collected three times over a one week period. The acquired spectra at different times for each phantom were identical within the shot noise variability. We can therefore conclude that there is no chemical activity in the created tissue phantoms.

Physical Tissue Models

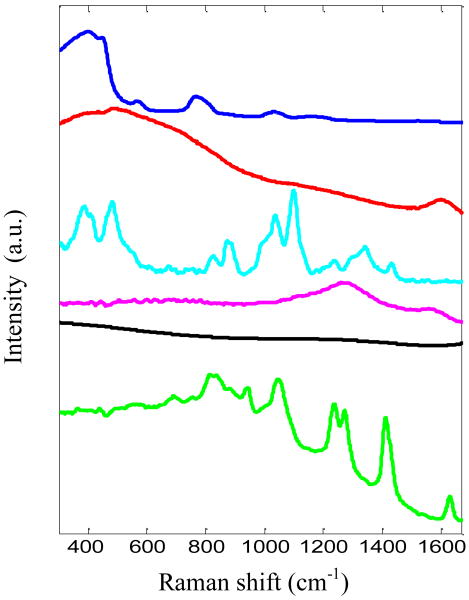
Tissue phantom studies were performed to (1) calibrate the instrument; (2) validate the TCRS formalism; and (3) analyze its performance in prospective prediction, respectively. The objective of the calibration study (1) was to determine the functional dependence of the second factor of Eq. (6) (μ_sx′l) on the optical properties of the samples, and to estimate the instrument-specific constant S (first factor of Eq. (6)). The validation study (2) was designed to characterize the effectiveness of the TCRS methodology in correcting turbidity induced variations in the observed Raman spectra. For both of these studies, ordinary least squares (OLS) regression was employed to find the concentration of the components, especially that of the analyte of interest, as OLS provides the most accurate results when the spectra of all the analytes can be individually measured, as in this case. The spectra of the tissue model constituents, which were used in the OLS analysis, are shown in Fig. 2. Employing OLS for the calibration and validation studies ensures that the first and second factors of Eq. (6) are determined accurately and that the effectiveness of TCRS is analyzed in the absence of any spurious correlations that might be generated in an implicit calibration strategy.

Fig. 2.

Spectra of OLS model components: cuvette, water, glucose, India ink, fluorescence background and intralipid (shown in order from top to bottom and offset for clarity)

Finally, the prospective prediction study (3) was performed to quantitatively test the prospective prediction capability of TCRS. This study simulated the clinical conditions in which the Raman and diffuse reflectance spectra are being acquired from a human subject. Under such circumstances, in which the spectra (or concentrations) of all constituents are unknown a priori, an implicit calibration framework must be employed. Thus, to replicate the protocol followed in a clinical study, the results of the prospective prediction study were analyzed using partial least squares (PLS) analysis.

The tissue phantoms were prepared by pipetting glucose (Sigma Aldrich), creatinine (Sigma Aldrich), intralipid (Baxter Healthcare), India ink (Super Black India Ink, Speedball Art Products Co.) and distilled water into clean glass vials. Aliquots of these tissue models were taken in a fused silica cuvette for spectroscopic measurements performed at room temperature. Between each measurement, the cuvette was washed three times with distilled water and dried. The phantoms were stored in the refrigerator at 4°C to avoid contamination.

India ink and intralipid were used as the primary absorber and scatterer to simulate tissue absorption and scattering in the NIR range. Specifically, the scattering and absorption coefficients were varied from 24 to 130 cm^-1 (at 830 nm) and 0.08 to 1.3 cm^-1 (at 830 nm), respectively, similar to the ranges observed in human biological tissue ^{36, 37}. The values of the anisotropy parameter (g) used in the tissue models, 0.8-0.9 ⁴², were chosen to be comparable to the typical values of g observed in biological tissue ³⁶. Glucose and creatinine, both of which have characteristic Raman spectral profiles, functioned as the analyte of interest and spectral interferent, respectively. All three tissue phantom studies – (1) calibration, (2) validation and (3) prospective prediction – were performed multiple times on different days to examine the reproducibility of the TCRS approach.

In the calibration and validation studies, 20 and 36 tissue phantoms were constructed, respectively. In these studies, the Raman scatterer (glucose) concentration was kept constant at 500mM. The elastic scattering and absorption coefficients were varied randomly in the ranges mentioned above. In both calibration and validation studies, creatinine was not employed, as the aim was to characterize the effectiveness of TCRS in extracting intrinsic line shape and intensity information of glucose Raman spectrum acquired from a turbid medium.

In the prospective prediction study, 48 tissue phantoms of randomly varying turbidities were prepared with randomized concentrations of glucose and creatinine in the range 4-30mM. This range of glucose concentrations spans hypoglycemic to hyperglycemic levels, in excess of that typically observed in human subjects. The scattering and absorption coefficients were randomly varied over the same ranges used in the calibration and validation studies.

4. Results and Discussion

(1) Calibration Study

The observed Raman spectra from the 20 samples, used to calibrate the instrument and to characterize the dependence of the average photon path length on the sample optical properties, showed a significant spread in the spectral profiles over the entire NIR wavelength region. Note that the concentration of glucose in all the samples was kept constant; therefore the Raman spectra that would be obtained in the absence of multiple scattering and absorption would be expected to be the same for all the samples. The resulting difference between the observed spectra and the spectra that would be expected in a clear medium can be primarily attributed to variations in turbidity over the tissue phantoms.

To quantify the spread of the observed spectra, we define a “spread index”, which is evaluated as the ratio of the difference in maximum and minimum intensity to the maximum intensity at the same specific wavelength for all spectra. The mean spread index calculated over all wavelengths for the observed spectra from 20 tissue phantoms was found to be 7.2%. On application of the diffuse reflectance-based turbidity correction factor ((Raman_OBS)_xm/√(R_xR_m), third factor in Eq. (6)), the mean spread index was reduced to 1.62%. In other words, this reduced spread index was obtained by application of Eq. (6), where the first and second factors were held constant. The observed Raman spectra tend to collapse onto a single spectral profile on application of the diffuse reflectance-based turbidity correction factor alone.

It is expected that there would be a negligible dependence of the second factor of Eq. (6), μ_sx′l, on the tissue optical properties, as the average photon pathlength is inversely proportional to the reduced scattering coefficient in weakly absorbing medium ⁴³. Nevertheless, an optimization procedure was used to estimate the representative function for the average pathlength (for the second factor in Eq. (6)) that minimizes the magnitude of the mean spread index for the 20 tissue phantoms. This minimization is an indicator of better spectral collapse than that obtained by using the diffuse reflectance-based turbidity correction factor alone, thereby enhancing the ability of TCRS in extracting more precise intrinsic line shape and intensity information from the acquired spectra.

A power law function of absorption (μ_a) and reduced scattering coefficients (μ_s′) was chosen to represent the dependence of average photon pathlength on the optical properties of the turbid media. It is to be noted that during this optimization procedure, the instrument dependent constant S (first factor of Eq. (6)) was set equal to 1 and the power law function was multiplied with a unit dimensional constant to match the length units of the optical path length, l. Varying the power law exponents, we observed that the minimum spread index was obtained when the average pathlength was set equal to (μ_s′) ^-0.97(μ_a)^0.1. This value of the minimum spread index was 1.58%, as compared to the 1.62% we obtained using only the diffuse reflectance-based turbidity correction factor in Eq. (6). The obtained weak dependence ((μ_s′) ^0.03(μ_a)^0.1) of this factor (μ_s′l) on the tissue optical properties is expected, as mentioned before. Due to this weak functional form and the subsequent negligible reduction shown in the mean spread index function, we conclude that this factor is very weakly dependent on tissue optical parameters. We ignore the dependence of μ_a and μ_s′ on this factor in further analysis.

To determine the instrument-specific constant, S, we used the turbidity corrected spectra (obtained after application of the third factor of Eq. (6)) in conjunction with the Raman spectra of the tissue phantom constituents in a standard OLS protocol. The instrument-specific constant that yielded the smallest prediction error was S=0.9. Once S was determined, it was held fixed for all subsequent studies.

(2) Validation study

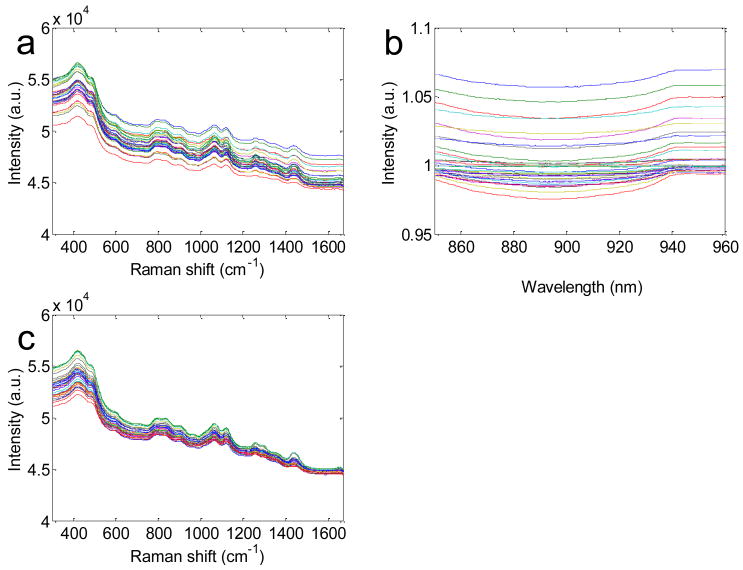
The effectiveness of the TCRS formulation in prospectively extracting turbidity free Raman information was tested on a separate set of 36 physical tissue models in which the concentration of the primary Raman scatterer was held constant. Similar to the calibration study, we found that the observed Raman spectra displayed appreciably different profiles (as shown in Fig. 3(a)), although in a clear medium, the uniform concentration of the Raman scatterer in each tissue phantom should give rise to the same Raman spectral profile. The mean spread index over all wavelengths for the observed Raman spectra was found to be 8.5%. On application of TCRS, the observed Raman spectra of the 36 phantoms tended to collapse onto one spectral profile as observed by the reduction of the mean spread index to 3.1% (Fig. 3(c)). Thus, TCRS provides an average reduction of 64% over all wavelengths and up to 93% in the glucose fingerprint region (800-1400 cm^-1). It is notable that this substantial reduction is made in part possible by the fact that TCRS is also able to correct for the turbidity-induced variations in the fluorescence in the tissue phantom, due to the fluorescent and diffusely reflected photons undergoing similar absorption and scattering events ^{16, 17}.

Fig. 3.

(a) Observed Raman spectra and (b) normalized diffuse reflectance spectra of 20 representative tissue phantoms demonstrating typical spread. (c) Turbidity corrected Raman spectra showing that on the removal of turbidity-induced variations, Raman spectra of (a) tend to collapse onto each other.

Despite the significant improvement shown by the application of the TCRS methodology, the effect of absorption and scattering on Raman line shape and intensity is not completely removed. There are two primary reasons behind the deviation from perfect coalescence observed in the spectral set here: (a) the presence of shot noise due to a large fluorescence background and (b) effects of photobleaching. We have observed that the former is of greater significance than the photobleaching effect given the short duration of the experiments. We are currently investigating frequency-domain fluorescence removal techniques, such as shifted excitation Raman difference spectroscopy (SERDS)⁴⁴, to remove the fluorescence background.

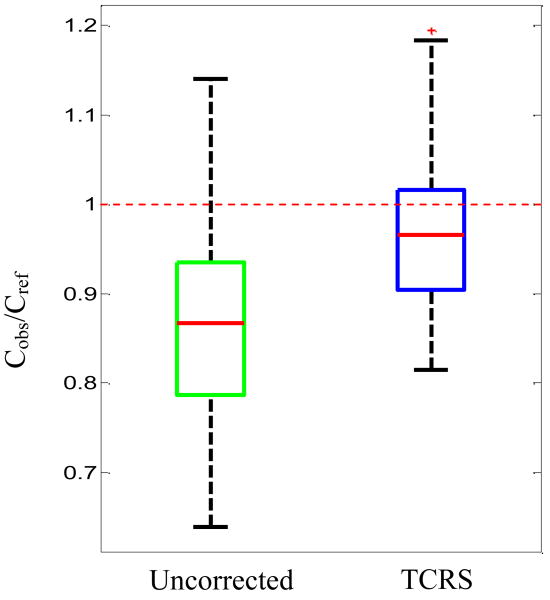
Additionally, OLS regression was used on the 36 phantom spectra to study the ability of TCRS to provide improved quantitative prediction capability. When the calibration model was used in conjunction with the uncorrected Raman spectra, the observed prediction error was 17.1%. In contrast, when the turbidity corrected Raman spectra were used, the prediction error dropped to 9.5%, a reduction of approximately 44%. To visualize this improvement, we show the boxplot of the ratio of predicted glucose concentrations (C_obs), obtained using uncorrected and turbidity corrected Raman spectra respectively, to the reference glucose concentrations (C_ref) in Fig. 4. The mean value of C_obs/C_ref is observed to be 0.87 and 0.98 for the uncorrected and turbidity corrected data respectively, thereby showing that the calibration model using turbidity corrected spectra is able to predict with a higher degree of accuracy. The standard deviation of the C_obs/C_ref values is found to be 0.12 and 0.09 for the uncorrected and turbidity corrected data, respectively, implying that the precision, i.e. the degree of reproducibility, of the concentration predictions is 25% higher for the turbidity corrected calibration model.

Fig. 4.

Boxplot of ratio of predicted glucose concentrations (C_obs), to the reference glucose concentrations (C_ref) for uncorrected and turbidity corrected data. The dotted red line at 1 indicates the position where the observed glucose concentrations (extracted from OLS analysis) are equal to the reference glucose concentrations in the samples.

(3) Prospective Prediction study

The third study was used to compare and contrast the prospective prediction capability of the calibration models developed using uncorrected and turbidity corrected Raman spectra. In contrast to the calibration and intrinsic Raman studies described above, here the concentrations of glucose and creatinine were varied in a random manner over the 48 tissue phantoms. Creatinine was used as a spectral interferent to simulate an in vivo environment in which spectral interferents are present besides the analyte of interest (glucose). In order to simulate the conditions of a clinical study, where the spectra (or concentrations) of tissue constituents are not known a priori, an implicit calibration strategy was used to analyze the results of this study. The uncorrected and turbidity corrected Raman spectra were randomly divided into calibration and prediction sets, containing 36 and 12 tissue phantom spectra, respectively. A standard PLS calibration procedure, into which the spectra and the corresponding glucose concentrations were input, was iterated 500 times to evaluate an average value of prediction error that is expected to be obtained in a general scenario. For both the calibration models, developed using uncorrected and turbidity corrected Raman spectra, respectively, 5 loading vectors were used in the PLS procedure. This was in accordance with the number of loading vectors that minimized the error in leave-one-out cross validation performed on the calibration set.

Figure 5 shows the boxplot of root-mean-square error of prediction (RMSEP) values obtained for glucose concentrations using both uncorrected and TCRS-corrected data. The mean prediction errors were 5.8 mM and 4.7 mM for the uncorrected and TCRS-corrected data, respectively, thereby demonstrating an approximately 20% reduction in prediction error on application of TCRS. In addition, the standard deviation of the 500 RMSEP values was reduced from 1.4 mM to 1.1 mM for the uncorrected and TCRS-corrected data, respectively. As discussed in the following section, this reduction brings the standard deviation close to the theoretical limit when measurement noise is the only source of uncertainty. This prospective prediction study thus illustrates that TCRS substantially removes concentration errors associated with turbidity. This is an important step towards practical implementation of transcutaneous Raman scattering in human subjects.

Fig. 5.

Boxplot of RMSEP obtained for glucose concentrations from 500 iterations using uncorrected and TCRS-corrected data.

(4) Effect of turbidity correction on minimum uncertainty measurement

As mentioned above, in transcutaneous Raman scattering measurements, when contributions to measurement uncertainty due to turbidity (and any other spurious factors) are eliminated, measurement noise becomes the factor limiting measurement precision. We denote the limiting uncertainty in concentration estimation as Δc. Based on the error analysis framework introduced by Lorber and Kowlaski^{45, 46}, we have derived an expression which, for the k^th analyte, relates Δc_k to the measurement noise (σ), the signal strength (norm) of the specific analyte (s_k), and its overlap with the other interfering constituents in the model (olf_k):^{45, 46}

$$\mathrm{\Delta }{c}_k=\frac{\sigma }{s_k}{\mathit{olf}}_k.$$ (7)

The overlap factor can range from 1 (no overlap with interferents) to infinity (complete overlap). The estimated uncertainty cannot be reduced beyond this physical limit, regardless of the calibration algorithm used for prediction. For our study, σ=61.03 (photon counts), s_k=83.74 (photon counts/mM) and olf_k=1.43, giving Δc_k=1.04 mM. (It is to be noted that σ is calculated from the residual between the observed spectra and the best fit over the whole spectrum). This result provides a measure of the effectiveness of TCRS, which reduces the concentration estimation uncertainty from 1.4 to 1.1 mM (Fig. 5), bringing us reasonably close to the theoretical limit of 1.04 mM.

This demonstrates that TCRS is able to substantially remove the uncertainty arising from the turbidity-induced distortions in the measured Raman spectra.

5. Conclusion

A central challenge in quantitative biological Raman spectroscopy, particularly applied to transcutaneous measurements, is overcoming the effects of subject-to-subject turbidity induced non-analyte specific variations. To account for these variations, we have developed a novel method, turbidity corrected Raman spectroscopy (TCRS), which is based on the photon migration approach and employs alternate acquisition of Raman and diffuse reflectance spectra. The new methodology developed here can be directly used in clinical studies, as it does not require the determination of tissue optical properties and the creation of tissue mimicking phantoms for calibration purposes. Our results clearly demonstrate that the TCRS methodology can extract intrinsic line shapes and intensity information from Raman spectra acquired in a turbid medium and provides a significant tool for prospective prediction studies. It is expected that TCRS will play a vital role in advancing Raman spectroscopy as a potential tool for transcutaneous concentration measurements of blood analytes. The methodology presented here could be potentially extended to recalcitrant industrial process monitoring problems and analysis of contaminated fluid samples for environmental monitoring, where chemical quantification in turbid media is crucial.