Abstract
Purpose: The nonlocal influence from distant magnetization will affect the magnetic field at a voxel in question. Existing reports on BOLD simulation only consider vasculature inside a single voxel, thus omitting the contribution from the surrounding regions. In this article, the authors study the effect of the surrounding vasculature on the magnetic field and the BOLD signal at a cortical voxel by numerical simulation.
Methods: A cortical voxel is generated as a cubic bin filled with randomly networked capillary vessels. First, the authors generate a cortical voxel with a random vessel network and embed it in a greater voxel by filling its surrounding region with vasculatures by different strategies. Next, they calculate the blood-susceptibility-induced magnetic field (BOLD field) at the voxel of interest (VOI) by a Fourier transform technique for different surrounding scenarios and varying surrounding extent. The BOLD field inhomogeneity is described by a radial distribution with a collection of cubic shell masks. The surrounding extent is defined by a collection of concentric cubes, which encase the VOI. Given a BOLD field in the presence of surrounding vasculature, they calculate BOLD signals by intravoxel dephasing.
Results: The influence from the surroundings on the BOLD field at a voxel in question mainly happens at the boundary. The most influence to the BOLD signal is from the inner surroundings. For a 160×160×160 μm3 voxel embedded in a 480×480×480 μm3 greater region, the surroundings could disturb the magnetic field by an amount in the range of [−0.002, 0.010] ppmT and could change the BOLD signal ratio in the range of [2.5%, 10%]. (These results were generated from the setting of ΔχbB0=3 ppmT, capillary={2.5,6,9} μm, and relaxation time=60 ms).
Conclusions: The surrounding vasculature will impose a magnetic field disturbance at the voxel in question due to the nonlocal influence of magnetization. Simulation results show that the surrounding vasculature significantly alters the magnetic field (up to 0.01 ppmT) and BOLD signal (typically no more than 10%) at the central voxel and thus should be considered in accurate BOLD modeling.
Keywords: computational fMRI, BOLD simulation, cortical voxel, vessel network, intravoxel dephasing, surroundings
INTRODUCTION
The underlying blood oxygen level dependent (BOLD) mechanism assumes that brain activity causes blood oxygenation level variation, which changes the blood magnetic property in terms of magnetic susceptibility [Δχ∼1 ppm: Parts per million (1×10−6)]. Venous blood exhibits paramagnetic behavior due to deoxyhemoglobin (Δχ<0), while arterial blood with oxyhemoglobin is diamagnetic (Δχ>0). The difference in magnetic susceptibility results in magnetic field variation during functional MRI (fMRI) experiment.1, 2 The susceptibility-induced magnetic field inhomogeneity is responsible for the observed fMRI signal. There have been a number of studies on fMRI BOLD modeling3, 4, 5, 6, 7 and on numerical simulations.6, 8, 9, 10 Although the change in susceptibility is local, the effect of magnetic field is not local because of 1∕r3 decay in the case of magnetic dipoles and spheres and 1∕r2 decay for the case of infinite cylinders.2 Thus, a susceptibility change in neighboring voxels can affect the BOLD signal in the voxel of interest (VOI). We address this problem through numerical simulation.
Recently, a Fourier model has been proposed to calculate the susceptibility-induced magnetic field.11, 12, 13 This technique can accommodate any susceptibility distribution associated with arbitrary vessel geometry,14, 15 and it also has been used to calculate the susceptibility-induced magnetic field across an array of voxels for a fMRI study.7
Due to the nonlocal influence of magnetic field, the susceptibility variations in the surrounding regions, albeit very small (Δχ∼1 ppm), will change magnetic field in neighboring voxels. This effect has not been carefully studied in previous studies. In this paper, we investigate the effect of surrounding vasculature on BOLD signal by generating different random vessel geometries with a known blood volume fraction and vessel radius, and simulating the intravoxel BOLD signal by considering static dephasing. Highlighting the effect of the surrounding vasculature, we do not include diffusion effect in this work. The method is based on simulating the BOLD signal in the region of interest by systematically enclosing it in larger regions of interest of different sizes. Martindale et al.6 calculated the magnetic field in a voxel by embedding it in a region four times its size. However, they were primarily concerned with truncation effects of Fourier transformation. In this paper, we study the effect of the surrounding vasculature by configuring different surrounding scenarios with a varying surrounding extent for the VOI.
METHODOLOGY
BOLD-induced magnetic field calculation
For BOLD simulation, the essential step is to calculate the magnetic field change (ΔBz) in the direction of the main magnetic field B0 caused by a change in blood susceptibility Δχb. In the rotating frame the change in the phase of a stationary precessing spin is given by Δϕ(r,t)=γΔBz(r)t, where γ is the gyromagnetic ratio. If we assume that the proton density is the same for the tissue and the vasculature, the BOLD signal at relaxation time t is given by
| (1) |
where α is a proportionality constant and V is the region of interest.
The susceptibility difference between the blood-carrying vasculature and the tissue Δχb is modeled by1, 9
| (2) |
where Y stands for oxygen saturation level, Hct for blood hematocrit, and Δχdo for the susceptibility difference between oxygenated and deoxygenated blood. Equation 2 represents a relationship between our numerical simulation and the BOLD physiology.
The vessel geometry in a voxel is modeled by
| (3) |
Then the spatial distribution of the susceptibility difference is given by
| (4) |
The magnetic field resulting from Δχ can be calculated by a Fourier model, as given by11, 12
| (5) |
where (kz,kz,kz) denotes the coordinates in Fourier domain and FT stands for Fourier transform. If we assume that blood is confined in vessels, as described by Eq. 4, then we can obtain the BOLD-induced magnetic field distribution, called BOLD field and denoted by ΔBz(r), by
| (6) |
where IFT stands for inverse Fourier transform and ⊗ is for convolution. The three-dimensional (3D) convolution kernel, , accounts for the nonlocal influence of the BOLD field. Since ΔχbB0 always appears as a composite parameter, we can carry out Eq. 6 with the unit setting of ΔχbB0=1 ppmT and then update the results by simply scaling with specific values for the blood-induced magnetic susceptibility Δχb and the main static magnetic field B0 afterward.6 Moreover, the linear product parameter ΔχbB0 reveals an equivalence between Δχb and B0 by a reciprocal relationship: An increase in Δχb is equivalent to an increase in B0 for ΔχbB0=const. In particular, we can make use of this reciprocity to detect small change in blood susceptibility by using a strong magnet. However, the BOLD signal is nonlinearly related to Δχb and B0 (see below).
Vessel networks
The vessel network is simulated as a collection of infinite cylinders randomly oriented and homogeneously distributed in a 160×160×160 μm3 cubic voxel.6 The voxel is discretized into an N×N×N array (N=128) for numeric simulation. The effect of the surrounding vasculature on the BOLD field of the voxel is studied by embedding the voxel in a larger 3N×3N×3N volume. This greater voxel (GV) consists of 27 N×N×N voxels: The central voxel is the VOI, and the 26 voxels adjacent to the VOI are the surroundings which will be filled with or without vasculatures by different strategies (see below). For numerical simulation, the vascular geometry is digitally represented in the same support array that is used for GV discretization. Since the vasculature assumes a binary pattern in a voxel as described in Eq. 3, we can statistically characterize this random pattern by blood volume fraction, denoted by bfrac henceforth. For the vasculature in a voxel with a N×N×N support array, bfrac can be calculated by
| (7) |
Similarly, we can calculate bfrac for a GV by summing over 27N3 entries in the 3N×3N×3N array. For cortical voxel simulation, we generate the vasculature by controlling the capillary occupancy portion by bfrac=2%, in accordance with other reports.6 Since cortex consists of only microvessels or capillaries (radius=[2,10] μm as provided by vaculature anatomy1), we use three typical capillaries: Radius={2.5,6,9} μm.
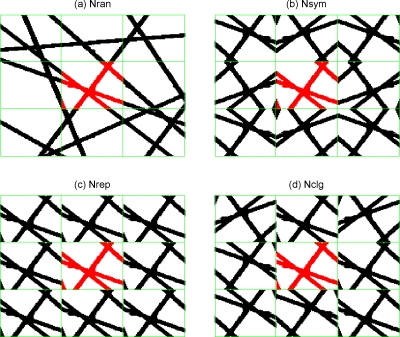
We illustrate our strategies of filling the surrounding voxels by 2D illustration in Fig. 1. Specifically, Fig. 1a shows a vessel network in a GV which encloses the VOI at the central voxel (vessels in the VOI are highlighted in red). The vasculature in Fig. 1a is a characteristic of randomness and smooth connections in GV, so we call it a random network and denote it by Nran. Based on the VOI, we can create other surroundings by using its copies and its renditions by flipping or permuting (i.e., 90° rotation) for avoiding digital interpolations associated with arbitrary rotations). Figure 1b shows a symmetrical network (denoted by Nsym), in which the 26 voxels are of spatial symmetry with respect to the central VOI. Figure 1c is a simple tessellation with the replicas of the VOI, so it is called replica network and is denoted by Nrep. Figure 1d is a tessellation using random renditions of the VOI (by flipping or permuting), so it is called a collage network and is denoted by Nclg. Finally, we include a zero-padded network (denoted by Nzp) where the surroundings have been completely omitted. It is noted that any rendition of the VOI by {“flipping,” “permutation,” “rotation”} maintains the bfrac value [Eq. 7].
Figure 1.
2D illustration of vessel networks surrounding a VOI (situated in the central panel). (a) Random network (Nran), (b) symmetric network (Nsym), (c) replica network (Nrep), and (d) collage network (Nclg).
Effect of surroundings on BOLD field in VOI
Collectively, there are five options that can be used for augmenting a VOI, which are notated byX={“Nran,” “Nrep,” “Nsym,” “Nclg,” “Nzp”}. Except for the same VOI at the central voxel, the 26 voxels surrounding the VOI assume different vasculature. A realistic simulation on the surrounding vasculature requires similar bfrac values (called bfrac uniformity henceforth) over the 27 voxels in GV. This uniformity condition can be exactly satisfied by {Nrep, Nsym, Nclg} and is well approximated by Nran. After configuring the surroundings for a VOI in GV, the BOLD magnetic field can be calculated by the Fourier method in Eq. 6. Since Nsym possesses both bfrac uniformity and vessel continuity, we select it as the reference when examining the BOLD field differences due to different surroundings, that is, BX−Nsym(x,y,z)=BX(x,y,z)−BNsym(x,y,z) for X={“Nran,” “Nrep,” “Nclg,”“Nzp”}.
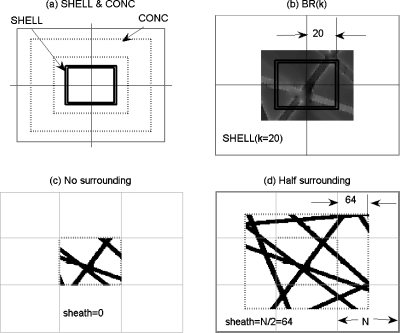
Fourier transform is sensitive to sharp transitions and boundary truncations, and the boundary extension can reduce the Gibbs effects.16 It is expected that regions around the boundary of the VOI is more vulnerable to the surroundings than the inner region. In order to characterize this center-to-peripheral distribution, we calculate the radial behavior of BX−Nsym(x,y,z) over VOI. To avoid digital interpolation, we delineate the N×N×N array into a collection of N∕2 concentric cubic shells, as illustrated in Fig. 2a. Each cubic shell assumes a 1 unit thickness, which can be expressed by
with
| (8) |
where CUBE is defined for a digital cube with even-numbered dimension (N=even, centered at N∕2+1) and k stands for the shell radius (in measure of city-block distance). Considering the shell as a spatial mask, the radial distribution of BX−Nsym(x,y,z), denoted by one variable function BR(k), can be calculated by
| (9) |
where the (2k)3 represents the cubic volume for a cube of 2k length and the division is for shell average. Figure 2b illustrates a cubic shell that is used to calculate the radial distribution of the magnetic field. The cancellation associated with the summation in Eq. 9 may conceal the positive and negative disturbances happening in a shell. Therefore, we render the summation over absolute difference and thereby characterizing the BOLD field disturbance difference by BR|X−Nsym|(k) alternatively.
Figure 2.
2D illustration of 3D masks. (a) Concentric shell and concentric cube, (b) a shell mask applied to BR(k) calculation, (c) case of no surrounding (VOI in Nzp), and (d) case of half-maximum surrounding [Nran is masked by CONC(sheath=N∕2)] for the VOI.
BOLD field perturbation versus surrounding extent
We calculate the magnetic field resulting from varying surrounding extent by using a collection of concentric cubes encasing VOI. The contributions only from the surroundings can be calculated by assigning zeros to VOI. We implement this strategy by using a collection of concentric cubic masks, as expressed by
| (10) |
with
where the parameter sheath denotes the thickness of surrounding extent and CONC represents a VOI-excluded volume. Figure 2c illustrates sheath=0 for no surrounding, and Fig. 2d a case of sheath=N∕2. The maximum surrounding thickness for our study with a GV (in size of 3N×3N×3N) corresponds to sheath=N.
Since a CONC in Eq. 10 masks out the VOI at the central voxel, the confinement geometry VX(x,y,z)CONC(x,y,z;sheath) only produces the contribution of the surrounding vasculature to the magnetic field at VOI, denoted by δBX(x,y,z;sheath). Let BX(x,y,z;sheath) denote the magnetic field, due to VOI plus its surroundings, it can be calculated from the geometry VX(x,y,z)CUBE(x,y,z;sheath+N∕2). In order to readily compare the influences from different surrounding thicknesses, we reduce δBX(x,y,z;sheath) to by performing average over VOI. In particular, we are interested to know the difference between no surrounding (sheath=0) and maximum surrounding (sheath=N) scenarios, that is, for X={“Nran,” “Nsym,” “Nrep,” “Nclg”}. Note that Nzp is excluded here because δBX(x,y,z;sheath)=0 for any sheath value.
BOLD signal simulation in the presence of surroundings
The BOLD signal due to intravoxel dephasing is calculated from a discrete version of Eqs. 1, 6, that is,
| (11) |
where the surrounding scenario (X) and the surrounding extent (sheath) are explicitly parametrized. The nonzero-contrast BOLD signal is attributed to the BOLD field inhomogeneity (BX(x,y,z;sheath)≠const), which, in turn, is caused by a BOLD activity in terms of Δχ [cf. Eqs. 2, 3, 4, 5, 6]. Furthermore, a bipolar distribution (assuming both positive and negative values) of BX(x,y,z;sheath) in general incurs more dephasing than a unipolar (positive-only or negative-only) distribution. This phenomenon will be observed in our simulation. Upon obtaining the BOLD signals due to different surroundings (in terms of X and sheath), we compare them with reference to SNzp(t) by a percentage,
| (12) |
where SNzp(t) is chosen as the baseline signal because zero padding is usually used for volume augmentation if there is no knowledge about the exterior.
NUMERICAL SIMULATIONS
Parameter setting and simulation flowchart
The parameters and their settings in our simulation are listed in Table 1, in which some of the parameter values are adopted from Ref. 6. Our simulation program is designed as the flowchart in Fig. 3. It starts with generating a cortical voxel in a 3N×3N×3N support array (N=128) with random capillaries and under the condition of bfrac=0.02. The central part with a size of N×N×N array is then cut out and used as a VOI. Three typical capillaries (with radius={2.5,6,9} μm) are used to generate different random vasculatures. With the discrete interval of 1.25 μm, the capillaries assume infinite cylinders with diameter of {4,10,14} in units of grid interval. For each VOI, its surrounding vasculatures are filled with the strategies (X) as described previously. With the input of parameter setting in Table 1 and the configured vascular geometry in GV, the BOLD field, and signal calculations can be automatically carried out in our simulation program.
Table 1.
Parameters for the numerical simulation.
| Nomenclature | Notations and values | Remark |
|---|---|---|
| BOLD susceptibility | Δχb=0.27 ppm×4π | In MKS metrics (Ref. 6) |
| Main static field | B0=3 T | Main static magnetic field |
| Voxel size | 160×160×160 μm3 | physical size of VOI (Ref. 6) |
| Voxel array | N×N×N (N=128) | Support array of VOI |
| Greater voxel array | 3N×3N×3N (N=128) | Support array of GV |
| Grid resolution | 1.25 μm (=160 μm∕N) | Discrete interval of support array |
| Capillaries | {2.5,6,9} μm | Typical capillary radiuses |
| Scenarios of extravoxel vessel network in GV | X={Nran, Nsym, Nrep, Nclg, Nzp} | Nran is realistic random network, others are renditions of VOI. |
| Blood volume fraction | bfrac=2% | Vasculature occupancy [Eq. 7] |
| Cubic shell mask | SHELL(k), k=0,1,2,…,N∕2−1 | k is shell radius [Eq. 8] |
| Radial distribution of BX−Nsym(x,y,z) in VOI | BRX−Nsym(k) | Average over cubic shells in VOI [Eq. 9] |
| Concentric cubic mask | CONC(x,y,z;sheath) | Encasing VOI with thickness=sheath [Eq. 10] |
| Surrounding thickness | Sheath=0,1,2,…,N | Sheath=0 for no surrounding, sheath=N for max surrounding in GV |
| BOLD signal baseline | SNzp(t) | BOLD signal of zero-padded VOI |
| BOLD change percentage | PercentX(t,sheath) | Def. in Eq. 12 |
Figure 3.
Flowchart of our simulation program (N=128, the colon symbol “:” is a MATLAB notation for running index).
Results
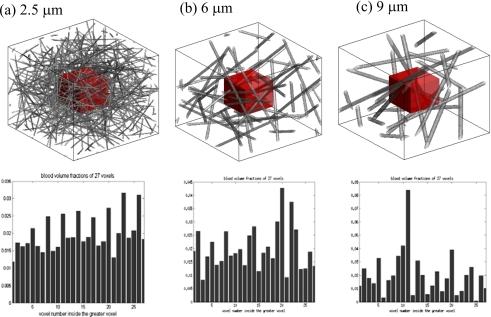
The vessel geometry in Nran is distributed in a GV with a 3N×3N×3N support array. Partitioning the GV into 27 N×N×N voxels, the central region is reserved for the VOI. Figure 4 shows three random networks (Nran) for three capillaries, with the VOI being delineated in a box therein. The bfrac values for 27 voxels in Nran are calculated using Eq. 7 and showed at the bottom row in Fig. 4 and in Table 2. Although the bfrac over a GV is controlled to be close to 0.02 during random vessel network generation, the bfrac values of the 27 voxels vary. Especially, as the capillary size increases, it is difficult to generate a vessel geometry under the condition of bfrac=0.02.
Figure 4.
Top row: Nran geometries (in size of 384×384×384 array) for three capillary radiuses: (a) 2.5 μm, (b) 6 μm, and (c) 9 μm. The central voxels are VOI (highlighted in boxes). Bottom row: bfrac values of 27 voxels (in size 128×128×128 array) in the corresponding Nran above.
Table 2.
Statistics of bfrac values of Nran for capillaries {2.5,6,9} μm.
| Term | 2.5 μm | 6 μm | 9 μm | Remark |
|---|---|---|---|---|
| bfrac of VOI | 0.026 30 | 0.028 30 | 0.020 12 | Average over VOI |
| bfrac of GV | 0.0198±0.0052 | 0.0200±0.0083 | 0.020±0.0169 | Statistics of 27 voxels in GV |
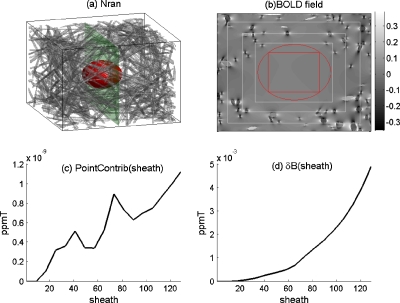
Nran is a realistic vessel network because the vessels extend continuously outside VOI and across voxels in GV. In order to understand the effect of surrounding vasculature, we generate a birdnestlike Nran, which has a void VOI at the center and is filled with cluttered vasculature around the VOI. Figure 5a shows a birdnest Nran, in which all vessel cylinders do not penetrate the central VOI. The birdnest Nran was generated with cylindrical vessels connecting two points randomly populated on the surface of GV-circumscribed sphere with the distances lower than a threshold, so it bears a void VOI-circumscribed egg region therein. Since there are no vessels passing through the VOI, this hollow Nran allows us to demonstrate the magnetic field contribution from the surrounding vasculature in the absence of vessel truncations at the voxel boundaries in GV. Figure 5b shows the magnetic field pattern at a slice indicated in Fig. 5a, which was calculated by Eq. 6 with the setting of ΔχbB0=1 ppmT for the full surrounding sheath=N. By using the sheathing model as described above, we can examine the distance-dependent surrounding contribution in terms of point contribution,
| (13) |
for the radial distances at sheath=[1,N]. It is noted that the denominator in Eq. 13 denotes the number of grid points on a cubic shell (thickness=1) at a radial distance sheath, hence the point contribution. The point contrib(sheath) for the particular case in Fig. 5a was calculated by Eq. 13 and presented in Fig. 5c, which shows a general decay with respect to the surrounding distance sheath, with an exception for a dent in the nearest surroundings (at small sheaths) that can be explained by the void egg region around the cubic VOI, as indicted by a circle in Fig. 5b. The fluctuation for farther surrounding is due to the random vessel geometry. Although the point contrib(sheath) in Eq. 13 is very small [∼10−9 ppmT in Fig. 5c], the accumulative contribution is noticeable (∼10−3 ppmT) as seen in Fig. 5d. For the surrounding extent in the range of sheath=[0,N], Fig. 5d shows that the accumulative contribution increases. However, no saturation is observed around sheath=N; this may be explained by the fact that the blood volume increases cubically with distance (∝4πr3∕3) and outpaces the nonlocal magnetization decay in the range of sheath=[0,N]. Although Nran is a realistic vessel network, it is very difficult to generate an Nran that has the same bfrac value over the GV and its 27 constituent voxels (see Fig. 4). In order that the effects of the surrounding vasculature are not confounded by fluctuation in bfrac, we adopt the surrounding-configuring strategies, X={“ran,” “sym,” “rep,” “clg”}, as described previously. The bfrac uniformity is achieved for {sym, rep, clg} at the sacrifice of vessel smoothness across voxel boundaries. However, the realistic Nran is always included as one case of the surrounding configurations all through the following study.
Figure 5.
Demonstration of the effect of the surrounding vasculature in the absence of vessel discontinuity with a birdnestlike Nran. (a) Nran geometry with a void VOI-circumscribed egg region (marked by a ball). (b) The magnetic field pattern (grayscale bar unit: ppmT) at a slice as marked in a vertical plane in (a), in which the central box corresponds to the VOI and the circle to the egg in (a). (c) The point contribution from different surrounding distances [calculated by Eq. 13]. (d) The accumulative contribution with respect to expanding surroundings.
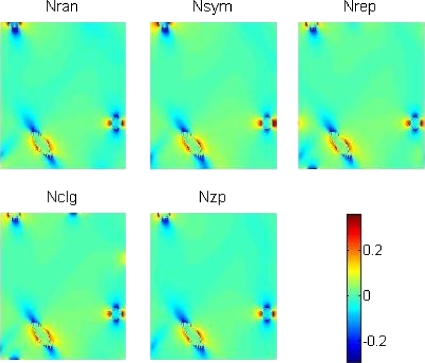
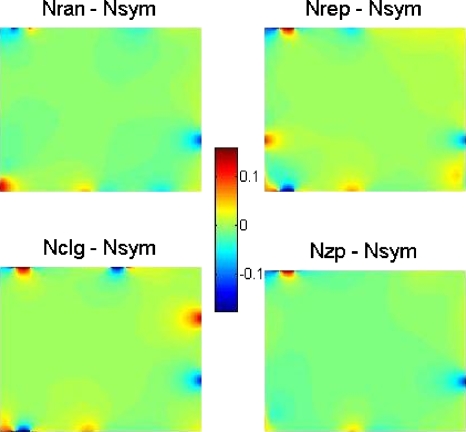
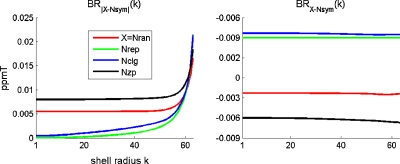
For each GV that is filled with vessel networks, we calculate the magnetic field distribution by Eq. 6 with the unit setting of ΔχbB0=1 ppmT. Figure 6 shows the cross-sectional distributions of the BOLD fields for five vessel networks, Fig. 7 the corresponding BOLD field difference with reference to Nsym, that is, BX−Nsym(x,y,z), and Fig. 8 the radial behavior of BX−Nsym(x,y,z) in Fig. 7 by BR|X−Nsym|(k) and BRX−Nsym(k). It is seen that the major BOLD field difference occurs around the voxel boundary (where shell radius k approaches N∕2). The remarkable difference between BR|X−Nsym|(k) and BRX−Nsym(k) reveals a fact that BX−Nsym(x,y,z) is of bipolar distribution. If the bipolar disturbances are balanced (positive variation=negative variation), they will cancel each other during the spatial integration in Eq. 11.
Figure 6.
BOLD field distribution over a cross section at y=0 of the VOI. The BOLD fields were calculated in the presence of five different surrounding vessel networks {Nran, Nsym, Nrep, Nclg, Nzp}. The unit of the grayscale bar is ppmT.
Figure 7.
BOLD field difference of BX−Nsym(x,y,0;N). The unit of the grayscale bar is ppmT.
Figure 8.
Radial shell distribution of inhomogeneous BOLD field within VOI due to different surroundings. Cancellation of bipolar magnetic field disturbance explains the difference between BR|X−Nsym|(k) and BRX−Nsym(k).
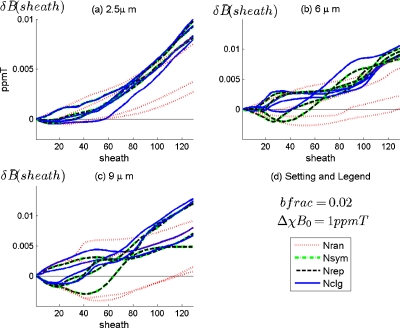
The effect of the surrounding extent on the BOLD field at VOI is demonstrated in Fig. 9 for different surrounding scenarios and for {2.5,6,9} μm capillary networks. In general, increases as more surroundings are included (sheath increases). The near small surroundings (sheath is small) produce bipolar field disturbance, which tends to become positive-only as the surrounding thickness increases. For large vessels, there is a wide range for the surrounding thickness to cause bipolar BOLD field disturbance. Moreover, large vessels disturb stronger than small capillaries.
Figure 9.
Effect of the surrounding vasculature in terms of different surrounding scenarios [indicated by legend in (d)] and varying surrounding thickness (sheath) on the average BOLD field over the VOI. Graphs with the same line style indicate realizations with the same parameter setting (different in random vessel network geometry).
The bounds for BOLD field disturbance due to different surroundings (calculated with a data set of eight realizations) are collected in Table 3. The results show that the surrounding vasculature can contribute to the BOLD field at VOI by an amount in the range of [−0.003, 0.010] ppmT, where the upper bound 0.010 ppmT corresponds to the maximum surrounding cases (sheath=N), while the lower bound −0.003 ppmT corresponds to a small surrounding (0<sheath<N) due to negative disturbance (see the downward curves in Fig. 9).
Table 3.
Bounds for BOLD field variations at VOI due to different surroundings (X). Low=min{δBX(x,y,z;sheath)}, high=max{δBX(x,y,z;sheath)}. The statistics was based on eight realizations for each parameter setting with bfrac=0.02. Data format: (x±δx)10−3 ppmT.
| X | 2.5 μm | 6 μm | 9 μm | |||
|---|---|---|---|---|---|---|
| Low | High | Low | High | Low | High | |
| Nran | −0.29±0.2 | 5.5±2.7 | −1.0±1.2 | 4.5±3.9 | −1.9±2.2 | 4.9±4.3 |
| Nsym | −0.19±0.2 | 8.9±0.8 | −1.0±1.1 | 9.3±0.8 | −1.6±1.2 | 9.0±3.6 |
| Nrep | −0.19±0.2 | 8.9±0.8 | −1.0±1.1 | 9.3±0.8 | −1.6±1.2 | 9.0±3.6 |
| Nclg | −0.23±0.2 | 9.1±0.8 | −0.3±0.1 | 9.3±0.8 | −0.9±0.6 | 10.1±2.3 |
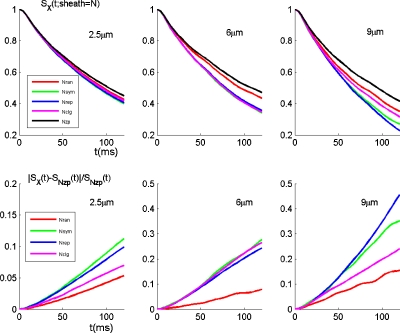
For BOLD signal calculation, we consider a 3 T scanner by setting ΔχbB0=3 ppmT, which roughly corresponds to a parametrical setting (according to Ref. 6): Hct=0.4,Y=0.75, Δχb=0.27 ppm×4π, and B0=3 T. The BOLD signals are generated by intraVOI dephasing by Eq. 11, which are parametrized by the surrounding scenario (X), capillary size, and relaxation time (t). The results are shown at the top row in Fig. 10. The BOLD signal change ratios are calculated by Eq. 12 and their behavior versus relaxation time is shown at the bottom row in Fig. 10. It is seen that the realistic random network (Nran, generated by program at the initial stage in Fig. 3) gives rise to the lowest signal change. For 60 ms relaxation, the percentX(t=60) values are calculated and collected in Table 4. The results show that the BOLD signal change ratio due to the surroundings takes on a value in the range of [2.5%, 10%].
Figure 10.
Effect of the surrounding vasculature on BOLD signal decay (top row) and on BOLD signal contrast (bottom row). The results were calculated for four surrounding scenarios: X={Nran, Nsym, Nrep, Nclg} and three capillaries: {2.5,6,9} μm with the reference to Nzp (baseline). The legends for the plots are provided at the left-hand panels.
Table 4.
BOLD signal change percentages (percentX) due to different surroundings (X). The results were calculated by Eq. 12 at t=60 ms and sheath=N.
| 2.5 μm | 6 μm | 9 μm | |
|---|---|---|---|
| PercentNran (%) | 3.9 | 9.3 | 2.5 |
| PercentNsym (%) | 6.3 | 10.7 | 8.5 |
| PercentNrep (%) | 5.0 | 9.7 | 9.8 |
| PercentNclg (%) | 4.4 | 8.5 | 4.0 |
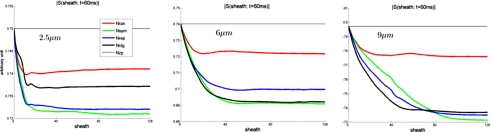
The effect of the surrounding thickness on BOLD signal is demonstrated in Fig. 11. As sheath increases, the extraVOI vasculature influence on the BOLD signal decreases. The significant influences from the surroundings occur at the inner surrounding with a small thickness, which are capillary dependent. Specifically, the most influential surrounding extent for 2.5 μm capillary is in the range of sheath=[0,N∕3] (corresponding to [0,53] μm), and those for {6,9} μm capillaries are roughly sheath=[0,N∕2] or [0,80] μm.
Figure 11.
Effect of the surrounding thickness on BOLD signal decay for three capillaries {2.5,6,9} μm (sheath=0 for no surrounding, sheath=128 for maximum surrounding).
DISCUSSION
Vessel network geometry generation is the most computation intensive part in our simulation. For Nran generation with small capillaries (radius<3 μm), it is relatively easy to control bfrac=0.02 over a GV (in size of 3N×3N×3N array) as well as its 27 constituent voxels (in size of N×N×N array). However, as capillary size increases, the program control of the condition bfrac=0.02 becomes ever difficult; specifically, the loop for |bfrac−0.02|<0.001, for example, tends to be endless. We demonstrated the bfrac distributions for three vessels networks generated with {2.5,6,9} μm capillaries (see Fig. 4). This observation is understandable from the fact that, for larger vessels, fewer number of cylinders are needed to fill a region for a vessel occupancy (bfrac=2% for our simulation); as the region is subdivided, some parts may contain more vessels than others, thus resulting uneven bfrac distribution.
In order to provide surrounding vasculature to a specific VOI under the condition of bfrac uniformity and vessel continuity, we propose five surrounding scenarios: {Nsym, Nrep, Nclg, Nran, Nzp}, of which the first three maintain identical bfrac values (bfrac=0.02 for all 27 voxels in GV) and {Nran, Nsym} maintain vessel continuity as well. We do not suggest configuring the extraVOI vasculatures by repeating the vessel generation program because of randomness or irreproducibility. For comparing BOLD field disturbance among different surroundings, we select Nsym as the reference network because it is a characteristic of bfrac uniformity, vessel continuity, and reproducibility.
Given a surrounding scenario from {Nran, Nsym, Nrep, Nclg, Nzp}, we study the effect of varying surrounding extent (with the parameter sheath). Due to computational workload, we only extend a N×N×N voxel (N=128) to a 3N×3N×3N greater voxel, which limits the surrounding extent by sheath=[0,N]. It is expected that by increasing the surrounding extent, to a 10N×10N×10N array or bigger, we may observe the influence from the voxels in a volume of activation. Other limitations in our simulation include the removal from consideration of spin diffusion and of the intravascular-extravascular separation. These topics deserve further investigations.
Our simulation shows the bipolar magnetic field disturbance from surrounding vasculature (see Fig. 9). For a cortical voxel consisting of tiny capillaries, only a small surrounding extent (small sheath) imposes a bipolar disturbance; moreover, the positive disturbance is much stronger than the negative disturbance. As sheath increases, there is no negative disturbance. In other words, the vasculature in a large surrounding extent tends to impose positive disturbance on the BOLD field of VOI. The results in Fig. 9 also show that larger capillaries lead to a stronger bipolar disturbance for a larger extent. The BOLD field disturbances in Fig. 9 are responsible for the BOLD signal behaviors in Fig. 11. On the one hand, at small sheath, the bipolar disturbance increases the intravoxel dephasing, thereby accelerates the BOLD signal decay. In this way, we explain the fast drop in Fig. 11. On the other hand, at large sheath, the negative BOLD field disturbance disappears, so the positive-only BOLD field disturbance imposes an offset (b0>0) to the BOLD signal by a factor of exp(−iγb0t), which is equivalent to an slight increase in the main static magnetic field, which increases the precession speed and slows down the signal decay; thereby, we explain the flat behavior at large sheath. Further investigation on bipolar BOLD distribution and intravoxel dephasing due to surrounding vasculature is worthwhile. We should mention that we do not observe the saturation behavior with the surrounding thickness range, sheath=[0,N] (corresponding to [0,160] μm). Probably, this may be due to insufficient sheath.
Our simulation program demands a massive amount of memory (∼30 Gbytes) and a disk storage (∼5 Tbytes). The 3D FFT on the greater voxel consumes most of this memory. It remains a challenge to render 3D FFT on a large array, say 1024×1024×1204 or larger. Vessel geometry generation under the condition of bfrac uniformity is rather time consuming, especially for large capillaries. Other computation loads include BOLD field analysis and BOLD signal calculation. In this work, we used three capillaries (radius={2.5,6,9} μm) for realistic cortical voxel simulation. For each capillary, we repeated our simulation program eight times to generate eight realizations for each cortical voxel setting. Based on the repetitions, we observed the surrounding effect with a rough statistical characterization.
SUMMARY AND CONCLUSION
We generate a cortical voxel in a region of 480×480×480 μm3 by filling it with random capillaries (three capillaries with radius={2.5,6,9} μm are used). The central region (in size of 160×160×160 μm3) is considered as a VOI. In addition, we create other surroundings for the VOI by four strategies: “Symmetry,” “replica,” “collage,” and “zero padding.” For each of these surrounding scenarios, we calculate the BOLD field with the setting of ΔχbB0=1 ppmT and analyze the field differences due to different surroundings with reference to the symmetrical network. Further, we study the effect of varying surrounding extent (in a range of [0,160] μm) for each surrounding scenario. Given a BOLD field disturbance distribution over the VOI (from different surrounding scenarios with varying surrounding thickness), we simulate the BOLD signals by intravoxel dephasing and thereby compare the results with the baseline signal of zero-padding scenario (no surrounding). Because of the randomness associated with the vessel network generation procedure, the simulation results are never reproducible, especially for large vessels. Notwithstanding the irreproducibility, we observe the surrounding effect by performing eight realizations for each parameter setting. The main findings and conclusions are as follows: (1) The nonlocal influence of blood magnetization on BOLD field and signal can be characterized by a 3D convolution kernel associated with the Fourier model; (2) large vessels assert more influence on BOLD signal than small vessels; (3) the surrounding vasculature imposes a bipolar disturbance on BOLD field at small surrounding extent, and this bipolar disturbance evolves into positive-only as the surrounding extent increases; (4) the surrounding vasculatures with similar statistical properties (in terms of randomness, blood volume fraction, and capillary diameter) reveal similar effects on the central VOI; and (5) the most influence on BOLD signals is from the vasculature within the inner surrounding layer.
Specifically, for a 160×160×160 μm3 voxel embedded in a 480×480×480 μm3 volume, the surroundings could disturb the magnetic field by an amount in the range of [−0.002, 0.010] ppmT and could change the BOLD signal ratio in the range of [2.5%, 10%]. (These results were generated from the setting of ΔχbB0=3 ppmT, capillary={2.5,6,9} μm, and relaxation time=60 ms).
ACKNOWLEDGMENTS
This research was supported by the NIH (Grant Nos. 1R01EB006841 and 1R01EB005846) and NSF (Grant No. 0612076).
References
- Buxton R. B., Introduction to Functional Magnetic Resonance Imaging: Principle and Techniques (Cambridge University Press, Cambridge, 2002). [Google Scholar]
- Reitz J. R., Milford F. J., and Christy R. W., Foundations of Electromagnetic Theory (Addison-Wesley, New York, 1993). [Google Scholar]
- Boxerman J. L., Hamberg L. M., Rosen B. R., and Weisskoff R. M., “MR contrast due to intravascular magnetic susceptibility perturbations,” Magn. Reson. Med. 34, 555–566 (1995). 10.1002/mrm.1910340412 [DOI] [PubMed] [Google Scholar]
- Yablonskiy D. A. and Haacke E. M., “Theory of NMR signal behavior in magnetically inhomogeneous tissues: The static dephasing regime,” Magn. Reson. Med. 32, 749–763 (1994). 10.1002/mrm.1910320610 [DOI] [PubMed] [Google Scholar]
- Zhao F., Jin T., Wang P., Hu X., and Kim S. G., “Sources of phase changes in BOLD and CBV-weighted fMRI,” Magn. Reson. Med. 57, 520–527 (2007). 10.1002/mrm.21159 [DOI] [PubMed] [Google Scholar]
- Martindale J., Kennerley A. J., Johnston D., Zheng Y., and Mayhew J. E., “Theory and generalization of Monte Carlo models of the BOLD signal source,” Magn. Reson. Med. 59, 607–618 (2008). 10.1002/mrm.21512 [DOI] [PubMed] [Google Scholar]
- Feng Z., Caprihan A., Blagoev K. B., and Calhoun V. D., “Biophysical modeling of phase changes in BOLD fMRI,” Neuroimage 47(2), 540–548 (2009). 10.1016/j.neuroimage.2009.04.076 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boxerman J. L., Bandettini P. A., Kwong K. K., Baker J. R., Davis T. L., Rosen B. R., and Weisskoff R. M., “The intravascular contribution to fMRI signal change: Monte Carlo modeling and diffusion-weighted studies in vivo,” Magn. Reson. Med. 34, 4–10 (1995). 10.1002/mrm.1910340103 [DOI] [PubMed] [Google Scholar]
- Hoogenraad F. G., Pouwels P. J., Hofman M. B., Reichenbach J. R., Sprenger M., and Haacke E. M., “Quantitative differentiation between BOLD models in fMRI,” Magn. Reson. Med. 45, 233–246 (2001). [DOI] [PubMed] [Google Scholar]
- Menon R. S., “Simulation of BOLD phase and magnitude changes in a voxel,” Proceedings of International Society for Magnetic Resonance in Medicine, 2003, Vol. 11, p. 1719 (unpublished).
- Marques J. P. and Bowtell R., “Application of a Fourier-based method for rapid calculation of field inhomogeneity due to spatial variation of magnetic susceptibility,“ Concepts Magn. Reson., Part B 25, 65–78 (2005). 10.1002/cmr.b.20034 [DOI] [Google Scholar]
- Koch K. M., Papademetris X., Rothman D. L., and de Graaf R. A., “Rapid calculations of susceptibility-induced magnetostatic field perturbations for in vivo magnetic resonance,” Phys. Med. Biol. 51, 6381–6402 (2006). 10.1088/0031-9155/51/24/007 [DOI] [PubMed] [Google Scholar]
- Salomir R., de Senneville B. D., and Moonen C. T. W., “A fast calculation method for magnetic field inhomogeneity due to an arbitrary distribution of bulk susceptibility,” Concepts Magn. Reson., Part B 19, 26–34 (2003). 10.1002/cmr.b.10083 [DOI] [Google Scholar]
- Pathak A. P., Ward B. D., and Schmainda K. M., “A novel technique for modeling susceptibility-based contrast mechanisms for arbitrary microvascular geometries: The finite perturber method,” Neuroimage 40, 1130–1143 (2008). 10.1016/j.neuroimage.2008.01.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marques J. P. and Bowtell R. W., “Using forward calculations of the magnetic field perturbation due to a realistic vascular model to explore the BOLD effect,” NMR Biomed. 21, 553–565 (2008). 10.1002/nbm.1224 [DOI] [PubMed] [Google Scholar]
- Chen Z., “Local volume reconstruction from width-truncated cone-beam projections by convolution backprojection,” Opt. Eng. (Bellingham) 47, 017001 (2008). 10.1117/1.2835454 [DOI] [Google Scholar]