Assessing operating characteristics of CAD algorithms in the absence of a gold standard

Abstract

Purpose: The authors examine potential bias when using a reference reader panel as “gold standard” for estimating operating characteristics of CAD algorithms for detecting lesions. As an alternative, the authors propose latent class analysis (LCA), which does not require an external gold standard to evaluate diagnostic accuracy.

Methods: A binomial model for multiple reader detections using different diagnostic protocols was constructed, assuming conditional independence of readings given true lesion status. Operating characteristics of all protocols were estimated by maximum likelihood LCA. Reader panel and LCA based estimates were compared using data simulated from the binomial model for a range of operating characteristics. LCA was applied to 36 thin section thoracic computed tomography data sets from the Lung Image Database Consortium (LIDC): Free search markings of four radiologists were compared to markings from four different CAD assisted radiologists. For real data, bootstrap-based resampling methods, which accommodate dependence in reader detections, are proposed to test of hypotheses of differences between detection protocols.

Results: In simulation studies, reader panel based sensitivity estimates had an average relative bias (ARB) of −23% to −27%, significantly higher (p-value <0.0001) than LCA (ARB −2% to −6%). Specificity was well estimated by both reader panel (ARB −0.6% to −0.5%) and LCA (ARB 1.4%–0.5%). Among 1145 lesion candidates LIDC considered, LCA estimated sensitivity of reference readers (55%) was significantly lower (p-value 0.006) than CAD assisted readers’ (68%). Average false positives per patient for reference readers (0.95) was not significantly lower (p-value 0.28) than CAD assisted readers’ (1.27).

Conclusions: Whereas a gold standard based on a consensus of readers may substantially bias sensitivity estimates, LCA may be a significantly more accurate and consistent means for evaluating diagnostic accuracy.

INTRODUCTION

Computer aided detection (CAD) algorithms aim to assist radiologists to detect lesions in breast, colon, and lung cancer.^{1, 2, 3} The current goal of CAD algorithms is to act as a second reader, pointing out missed potential lesions.⁴ For instance, a number of recent studies have found that the addition of CAD readings improve upon solely radiologist based readings in terms of sensitivity of lung nodule detection.^{5, 6, 1, 7, 8}

In the absence of a tissue-based reference standard, expert human reader opinions are used as “gold standard” for evaluating the efficacy of CAD assisted reading.⁹ The presence of considerable variability in expert lesion readings¹⁰ suggests the possibility that they may be imperfect. Imperfect gold standards can result in biased sensitivity estimates: Consider an almost perfect reference test (R) with 100% sensitivity and 95% specificity. Now consider a new perfect diagnostic test Y with 100% sensitivity and specificity. Assuming (i) independence of Y and R results conditional on true disease status and (ii) disease prevalence of 20%, the apparent sensitivity of Y using R as gold standard is only 83% (Appendix A). The apparent loss in sensitivity arises because the perfect test “fails” to detect “lesions” falsely detected by the gold standard. Even a few “false positives” can have a substantial impact on apparent sensitivity when prevalence is low [Eq. A5]. Consensus readings from a multiple expert reader panel have been suggested to reduce the reference reader error impact.¹¹ Even with consensus panels, we show in this paper that the problem of bias persists.

To overcome such bias, we have developed a method using latent class analysis (LCA) for estimation and comparison of free-response operating characteristics (FROC) of lung lesion diagnostic protocols from multiple observer readings.¹² LCA has previously been used for assessment of other diagnostic tests with imperfect gold standards, e.g., nucleic acid amplification tests,¹³ stool guaiac tests for detecting colon cancer,¹⁴ presence∕absence of pleural thickening from chest x rays, etc.¹⁴ In LCA, each lesion candidate is assumed to have an underlying true status (lesion or nonlesion), known as its “latent class.” These are estimated from a combination of reference panel and CAD assisted readings using a maximum likelihood procedure detailed in Appendix B. The latent class is used as gold standard for calculation of FROC. Because it uses both sets of readings, LCA should intuitively yield a better gold standard, particularly when CAD assisted readings are more accurate than reference panel readings. In Sec. 2, we develop a bibinomial model for counts of the number of detections per lesion candidate by a reader panel, with or without CAD assistance. This model assumes conditional independence of detections as well as uniform operating characteristics (OCs) across readers and lesion candidates. The simplified model allows us make simulation based comparisons between reader panel based OC estimates against LCA based ones, which are unaffected by potential confounding factors such as dependence on nodule and reader characteristics. Although LCA based estimates are shown to depend on reader performance (i.e., their operating characteristics), our results (Sec. 3) show that LCA estimates are significantly less affected than reader panel based estimates in our simulation studies across a range of OC settings. It is to be noted that some assumptions made in LCA modeling, such as constant OC across lesion candidates as well as conditional independence in ratings across readers, are typically not valid for many real settings. These limitations are elaborated in Sec. 4. To overcome these limitations for application to real data, we develop resampling-based methodology for comparison of diagnostic methods that takes into account variation in detection probabilities and correlations in reader ratings within and across lesions. We apply LCA to readings (both CAD assisted and free search) on a collection of marked images from the Lung Image Database Consortium (LIDC) database.¹¹ In Sec. 4, we indicate how some of the additional sources of variability may be incorporated into the model. We also develop methodology for comparison of diagnostic methods that takes into account variation in detection probabilities and correlations in reader ratings within and across lesions.

MATERIALS AND METHODS

Latent class model

For each candidate lesion i, the data are counts of readers who rate it as a lesion in the reference group Y_Ri and CAD assisted (CAD) group Y_Ci. The latent class of candidate i is denoted by L_i=1 if it is a lesion and 0 if not. For an actually positive lesion, its probability of detection (sensitivity) is denoted T_R and T_C in the reference and CAD groups, respectively. For an actually negative lesion, the corresponding probabilities of nondetection (specificity) are 1−F_R and 1−F_C. In certain studies, ratings may be available on an ordinal confidence scale (e.g., 0–5). There, T_R and F_R would correspond to a point on the ROC curve of the detection procedure at a certain confidence threshold.

For initial model building, we assume that (i) OCs are constant across lesions nodule candidates and readers within a group (i.e., reference or CAD assisted); (ii) ratings across lesion candidates are independent; and (iii) conditional on the latent class, readers’ ratings on candidate i are mutually independent. Then the distribution of counts can be characterized by four separate conditional binomial distributions

$$Y_{Ri}|L_i=1\sim \text{Bin}\left(K_R,T_R\right),Y_{Ri}|L_i=0\sim \text{Bin}\left(K_R,F_R\right),$$ (2.1)

$$Y_{Ci}|L_i=1\sim \text{Bin}\left(K_C,T_C\right),Y_{Ci}|L_i=0\sim \text{Bin}\left(K_C,F_C\right),$$

where K_R and K_C are the number of readers in the reference and CAD groups, respectively. Further, we model the distribution of latent class variables as Bernoulli, i.e., L_i∼Bin(1,ρ), where ρ is the fraction of positive lesions among candidate lesions. When L_i are known, maximum likelihood estimates of OCs, i.e., T_R, T_C, F_R, and F_C, are given by respective proportions of detections within lesion and nonlesion classes. Because latent classes are unknown, we propose joint estimation of OCs and latent classes. Starting from an initial guess for latent classes, we obtain iteratively refined estimates. In each iteration, estimated OCs are used to update latent class estimates and vice versa. This process is continued till convergence. Appendix B gives technical details. The algorithm converges to the same set of estimates irrespective of initial guess (except all zeros).

Simulation experiment

A comparison of a reader panel and LCA was conducted with data generated using model 2.1, with K_R=K_C=4 readers and ρ=0.1. The OCs of individual reference readers T_R and 1−F_R are chosen from all possible pairs of values in 0.6, 0.7, 0.8, 0.9, and 0.95. Two examples of CAD OC settings were chosen: (i) T_R=0.70 and 1−F_R=0.95 and (ii) T_R=0.85 and 1−F_R=0.80. One represents a conservative reader (lower sensitivity, higher specificity), the other an aggressive reader (higher sensitivity, lower specificity). Reader panel based estimates of T_C and F_C are computed using the proportion of “consensus detections,” i.e., a lesion candidate is identified as actually positive when a predetermined threshold of K_R(=3) or more reference readers agree it is positive, i.e., when Y_R≥K_R. Other choices of K_R were either too aggressive (2∕4 in agreement) or too conservative (4∕4 in agreement), i.e., they would overestimate or underestimate, respectively, the proportion of actually positive nodules. For each combination of reader panel and CAD OC parameters, the experiment was replicated 500 times. Average relative bias $\left(\text{ARB}\right)=0.04{\theta }^{-1}{\sum }_{m=1}^5{\sum }_{j=1}^5\left({\widehat{\theta }}_{mj}-\theta \right)$, where θ is the true parameter value and ${\widehat{\theta }}_{mj}$ is the average estimate (across 500 replications) at the mth T_R and jth F_R values, m,j=1,…,5. LCA and reader panel based sensitivity and specificity estimates are compared using a paired t-test of absolute bias values: $\left|{\widehat{\theta }}_{mj}-\theta \right|$. Under the null hypothesis of no difference between the two methods, the test statistic will follow a Student’s t distribution with 24 degrees of freedom, assuming a normal distribution of the absolute bias values.¹⁵ Naïve standard errors (SEs) of a proportion p, such as T_R, F_R, T_c, and F_C, are computed using the formula for binomial proportions¹⁶

$$\text{SE}=\sqrt{p\left(1-p\right)∕n}.$$ (2.2)

Application of LCA to LIDC data set

Free search by K_R=4 readers (trained radiologists) on 36 thoracic CT scans with section thickness <2.0 mm obtained from the LIDC repository yielded 250 unique nodule markings (reference), which were encoded in an XML file accompanying the DICOM data from the CT scans.¹⁷ Because patient deidentification occurred outside of our institutions and we were never privy to protected health information, our IRB classified this project as nonhuman subjects research. Each marking was assigned a count (1–4) based on the number of readers that indicated it as a lesion (confidence ratings were unavailable). Note that these readers had access to each other’s readings before making a final decision. A CAD algorithm (SNO-CAD) (Ref. ¹⁸) was subsequently applied to all CT scans. A distinct set of 895 candidates with SNO-CAD scores (independent of reader detections) higher than 1.25 was identified.⁷ The combined 1145 lesion candidates were independently reviewed by a separate set of K_C=4 radiologists who were blinded to each other’s detections. Separate readers were used in the two groups because (i) we did not have access to the original LIDC readers to perform CAD assisted readings, (ii) it avoids a learning curve bias, and (iii) it is consistent with the conditional independence assumption inherent in LCA.¹⁹ The design of the study also reflects the role of CAD as a second reader, i.e., to supplement the readings of the first reader. LCA was applied to the combined detections set. Because the number of true negatives is unknown, we report the average number of false positives per patient (FPP) instead of specificity.

Robust standard errors

Naïve standard errors calculated using Eq. 2.2 assume conditional independence between readers and also independence across lesion candidates. These assumptions may not be realistic. For more “robust” standard errors, we repeatedly resampled entire cases from the list of lesion candidates to generate many “bootstrap” samples.²⁰ For each of 1000 such bootstrap samples, LCA was applied to obtain parameter estimates ${\widehat{T}}_R^b,\widehat{\text{F}}{\text{PP}}_R^b,{\widehat{T}}_C^b,\widehat{\text{F}}{\text{PP}}_C^b,{\widehat{\rho }}^b$. Robust standard error estimates were computed empirically, e.g., $\text{SE}\left({\widehat{T}}_R\right)=\sqrt{{999}^{-1}{\sum }_{b=1}^{1000}{\left({\widehat{T}}_R^b-{\overline{T}}_R\right)}^2}$, where ${\overline{T}}_R$ is the average across bootstrap samples. Confidence intervals (95%) of parameter estimates were constructed from 2.5% and 97.5% quantiles of their bootstrapped distribution.²⁰

Hypothesis testing by randomization

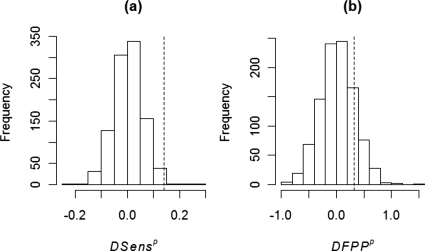
To test the hypotheses H₀:T_R=T_C versus H₁:T_C>T_R, the test statistic $\Delta \text{Sens}={\widehat{T}}_C-{\widehat{T}}_R$ is computed. The null distribution of ΔSens was numerically approximated from repeatedly generated “randomized” samples of reader counts obtained by randomly permuting the original data between reference and CAD groups within each case.²¹ For each of 1000 randomized samples p, LCA based parameter estimates ${\widehat{T}}_R^p,{\widehat{T}}_C^p$ and $\Delta {\text{Sens}}^p={\widehat{T}}_R^p-{\widehat{T}}_C^p$ were computed. The empirical distribution of ΔSens^p across randomized samples approximates the desired null distribution [Fig. 1a]. Randomization takes into account pairwise correlations between reader ratings in a manner similar to the paired t-test.²¹ A similar procedure is applied for testing differences in FPP between protocols [Fig. 1b].

Figure 1.

Distribution of test statistics for (a) differences of sensitivity (ΔSens^p) and (b) differences of average false positives per patient (ΔFPP^p) between reader panel and CAD readings for LIDC data set. Distributions were calculated under null hypothesis of no difference between reading methods using a randomization test (with 1000 replications). The value of the observed test statistic is indicated by a dotted vertical line.

RESULTS

Simulation experiments

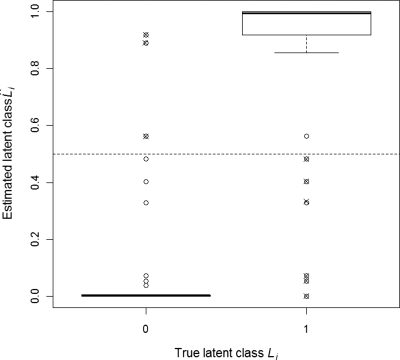
The estimated latent class ${\widehat{L}}_i$ is any number between 0 and 1, rather than exactly 0 or 1 (Appendix B), but were close to their true values in our studies (Fig. 2). Each detection can be marked positive or negative by mapping ${\widehat{L}}_i$ to either 0 or 1, whichever is nearest. Using this rule, only 9∕1000 cases would be misclassified in Fig. 2. For all 500×25×2=25 000 data sets (Sec. 2B), LCA converged within 50 iterations. In all 50 cases, LCA estimated sensitivity was more accurate than reader panel estimates, particularly at low reference reader specificities (1−F_R<0.8) (Table 1). In setting (i) T_R=0.70 and 1−F_R=0.95, ARB of sensitivity estimation by LCA and the reader panel were −2% and −27%, respectively (mean absolute difference of −18%, p-value <0.001 from paired t-test). In setting (ii) T_R=0.85 and 1−F_R=0.80, ARB of sensitivity estimation by LCA and the reader panel were −6% and −23%, respectively (mean absolute difference of −14%, p-value <0.001 from paired t-test). ARB of specificity estimation by LCA and the reader panel were 0.4% and −0.6%, respectively (mean absolute difference of 0.2%, p-value=0.03 from paired t-test). Specificity was uniformly well estimated (average relative bias less than 1.5% for both reader panel and LCA estimates in both settings), with LCA indicating slight overestimation and reader panel slight underestimation at lower reader specificities (Table 2).

Figure 2.

Latent class estimates plotted against true lesion status for one replication of simulation experiment (n=1000 lesion candidates, 10% true lesions, four readers each in reference and CAD assisted groups). True sensitivity and specificity for individual readers is T_R=0.60 and 1−F_R=0.95 in reference group, and T_C=0.70 and 1−F_C=0.95 in CAD group. Estimated sensitivity and specificity for individual readers is T_R=0.60 and 1−F_R=0.95 in reference group, and T_C=0.70 and 1−F_C=0.95 in CAD group. Note that estimated latent class values are probabilities, which can take any value between 0 (not a lesion) and 1 (lesion). Using a decision rule of assigning lesion status if the estimated status value is more than 0.5 (depicted by dotted line), the misclassification error rate is 0.009. Misclassified points are shown as crossed circles.

Table 1.

Results of low sensitivity, high specificity simulation experiment. Comparison of a) sensitivity and b) specificity estimates of a CAD assisted group from simulation experiment with four readers per group, 1000 lesion candidates. The fraction of nodule candidates that are actually positive is ρ=0.10. Operating characteristics of individual readers in the reference panel are given in rows as sensitivity (Se) and in columns as specificity (Sp). The operating characteristics of the CAD assisted group are set as: sensitivity=0.70, specificity=0.95. White columns (RP, reader panel) are estimated apparent sensitivities using lesions identified by three or more reference readers as gold standard. Gray shaded columns (LCA) are estimated sensitivities using LCA in the same datasets. Each reported value is the average of 500 replicates. For sensitivity, average standard deviations of the reader panel and LCA based estimates are 0.02 and 0.03, respectively. For specificity, average standard deviations of the reader panel and LCA based estimates are 0.005 and 0.007, respectively.

Sp	0.6		0.7		0.8		0.9		0.95
Se	RP	LCA	RP	LCA	RP	LCA	RP	LCA	RP	LCA
a
0.6	0.20	0.67	0.30	0.65	0.48	0.66	0.66	0.70	0.69	0.70
0.7	0.24	0.65	0.35	0.65	0.52	0.69	0.67	0.70	0.70	0.70
0.8	0.27	0.65	0.39	0.68	0.55	0.70	0.67	0.70	0.70	0.70
0.9	0.29	0.69	0.41	0.70	0.57	0.70	0.68	0.70	0.70	0.70
0.95	0.30	0.70	0.42	0.70	0.57	0.70	0.68	0.70	0.70	0.70
b
0.6	0.92	0.97	0.93	0.97	0.93	0.96	0.94	0.95	0.94	0.95
0.7	0.94	0.97	0.94	0.96	0.94	0.95	0.94	0.95	0.94	0.95
0.8	0.95	0.96	0.95	0.95	0.95	0.95	0.95	0.95	0.95	0.95
0.9	0.95	0.95	0.95	0.95	0.95	0.95	0.95	0.95	0.95	0.95
0.95	0.95	0.95	0.95	0.95	0.95	0.95	0.95	0.95	0.95	0.95

Table 2.

Results of high sensitivity, low specificity simulation experiment. Comparison of a) sensitivity and b) specificity estimates of CAD assisted group from simulation experiment with four readers per group, 1000 lesion candidates. Fraction of nodule candidates that are actually positive is ρ=0.10. Operating characteristics of individual readers in the reference panel are given in rows as sensitivity (Se) and in columns as specificity (Sp). The operating characteristics of the CAD assisted group are set as: sensitivity=0.85, specificity=0.80. White columns (RP, reader panel) are estimated apparent sensitivities using lesions identified by three or more reference readers as gold standard. Grey shaded columns (LCA) are estimated sensitivities using LCA in the same datasets. Each reported value is the average of 500 replicates. For sensitivity, average standard deviations of the reader panel and LCA based estimates are both 0.01. For specificity, average standard deviations reader panel and LCA based estimates are 0.008 and 0.017, respectively.

Sp	0.6		0.7		0.8		0.9		0.95
Se	RP	LCA	RP	LCA	RP	LCA	RP	LCA	RP	LCA
a
0.6	0.35	0.72	0.45	0.71	0.63	0.72	0.81	0.82	0.84	0.84
0.7	0.39	0.71	0.50	0.71	0.67	0.77	0.82	0.84	0.85	0.85
0.8	0.42	0.71	0.54	0.76	0.70	0.83	0.82	0.85	0.85	0.85
0.9	0.44	0.74	0.56	0.82	0.72	0.85	0.83	0.85	0.85	0.85
0.95	0.45	0.79	0.57	0.84	0.72	0.85	0.83	0.85	0.85	0.85
b
0.6	0.77	0.85	0.78	0.84	0.78	0.82	0.79	0.80	0.79	0.80
0.7	0.79	0.84	0.79	0.83	0.79	0.81	0.79	0.80	0.79	0.80
0.8	0.80	0.83	0.80	0.81	0.80	0.80	0.80	0.80	0.80	0.80
0.9	0.80	0.82	0.80	0.80	0.80	0.80	0.80	0.80	0.80	0.80
0.95	0.80	0.81	0.80	0.80	0.80	0.80	0.80	0.80	0.80	0.80

LIDC data set

Of n=1145 lesion candidates, 250 were marked as lesions by at least one reference reader and 313 candidates were marked as lesions by at least one CAD reader. The reader panel based sensitivity estimate for CAD assisted readers was 0.83. LCA converged in 30 steps. Estimates of latent class indicators suggest most lesion candidates were well characterized because they are concentrated around 0 or 1 (Fig. 3). Robust standard errors are considerably larger than naïve estimates (Table 3).

Figure 3.

Distribution of estimated lesion status values estimated using latent class methodology for LIDC data set with n=1145 lesion candidates, K=4 readers in both reference and CAD groups (0 is definitely not a nodule, 1 is definitely a nodule). Estimated parameters are given in Table 3.

Table 3.

Estimates based upon LCA for the LIDC dataset, with n=1145 nodule candidates, K=4 readers in both free read and CAD assisted groups. T_R, T_C: Sensitivity of reference (free read) and CAD groups, respectively. FPP_R, FPP_C: Average false positives per patient of reference and CAD assisted groups, respectively. ρ: Fraction of TP nodules in data. Naïve estimates of standard error are calculated using a formula for binomial proportions, which assumes conditional independence of diagnoses across readers and nodule candidates (third column). Naïve estimates of standard errors can’t be computed for FPP because the number of true negative nodules is unknown. Robust estimates of standard error, which do not assume independence, are obtained from bootstrap resampling of data (fourth column).

Parameter	Estimate	SE (Naïve)	SE (Bootstrap)
TR	0.55	0.01	0.04
TC	0.69	0.01	0.10
FPPR	0.95	N∕A	0.77
FPPC	1.27	N∕A	0.22
ρ	0.22	0.01	0.03

Based on LCA estimates, the observed difference of $\Delta \text{Sens}={\widehat{T}}_C-{\widehat{T}}_R=0.69-0.55=0.14$ yields a p-value of 0.006 for the test H₀:T_R=T_C versus H₁:T_C>T_R using the permutation based randomization procedure (Sec. 2E). A 95% confidence interval for ΔSens computed from bootstrap samples is (0.03, 0.41) (Sec. 2E). A hypothesis test conducted using these bootstrap samples yielded a p-value of 0.004. The observed difference of ΔFPP=FPP_C−FPP_R=1.27−0.95=0.32 yields an empirical two sided p-value of 0.28 for the test H₀:FPP_R=FPP_C versus H₁:FPP_C≠FPP_R. A 95% confidence interval for ΔFPP computed from bootstrap samples is (−1.25, 1.54).

DISCUSSION

Our simulation study shows that the use of consensus reference panel readings as a gold standard can lead to substantial bias in estimation of sensitivity of a new diagnostic protocol, and that this bias can be particularly large when reference reader specificity is below 0.8. Additionally, the degree of bias appears to vary with the operating characteristics of both the reader panel and the CAD algorithm. Hence, relative rankings of CAD algorithms produced from reader panel based reference standards may be erroneous. By contrast, LCA based estimation of sensitivity can deliver substantial reductions in bias over the reader panel estimate even at low reader specificities. In addition, LCA produces estimates of the OCs of reference readers. These can in turn be used to better assess the accuracy of the estimate. Finally, LCA is particularly suited to comparisons of two diagnostic protocols (e.g., free search versus CAD assisted) because unlike a reader panel, it does not require a third panel of readers as reference standard.

We used a simple model for detections in our simulation studies to highlight the problem with reader panel estimates and the relative success of LCA. We now discuss some possible limitations of the proposed model and how they might be addressed in future work. The model presented for reader detections assumes (i) constant OC across readers lesion candidates, (ii) independent reader ratings across lesion candidates, and (iii) conditionally independent ratings across readers. In practice, these assumptions may not hold. For instance, operating characteristics may depend on factors such as size, shape, location, etc. They may also depend on the aggressiveness and∕or level of training of the reader. It may be possible to model the dependence of detection probabilities on the aforementioned factors using a variance components model.²² Additionally, the conditional independence assumption may not be tenable. For instance, readers might agree more readily on large lesions than on small ones, leading to correlated ratings across readers. In particular, we note that for the free read detections on the LIDC data set, the conditional independence assumption is violated because readers had access to each others’ detections before making a final judgment. It is likely that this induced a positive correlation between their detections. In turn, this can lead to a positive bias on estimates of sensitivity and specificity.¹⁹ Thus, caution should be exercised in interpreting the estimated sensitivity and false positive per patient values for the LIDC data set. However, we note that estimates of the difference of sensitivities (or specificities) between free read and CAD assisted methods are likely to be relatively less affected by this bias. Since a common term causes the bias for both methods,¹⁹ taking the difference is likely to eliminate a substantial part of this bias. Development of a validated model for inter-reader dependence is critical to overcome such bias because incorrect specification of the dependence structure can also lead to bias in LCA estimates.⁹ It is likely, for instance, that the nature of dependence would be different in the free read and CAD assisted group.²³

Despite the aforementioned limitations in our current model, inferences based on it should remain valid when the robust resampling-based procedures described in Secs. 2D, 2E are used. The resampling procedure mimics the potential dependence in reader ratings described above, thus generating appropriate standard errors for estimates. For the LIDC data set, the confidence interval for the difference in sensitivities between methods is quite wide. This suggests that incorporating important sources of variability in sensitivity into the model, such as lesion size or location and differences in decision threshold between readers, may yield narrower confidence intervals than those generated by the resampling method.¹⁰

APPENDIX A: CALCULATION OF APPARENT SENSITIVITY WITH IMPERFECT GOLD STANDARD

Let the sensitivity or true positive fraction and false positive fraction (FPF) of the binary (1="disease present", 0="disease absent") reference test R be T_R and F_R, respectively, and similarly T_Y and F_Y for the new diagnostic test Y. True disease status is denoted by D (1=disease present, 0=disease absent) with prevalence probability ρ. Then the apparent sensitivity of Y with respect to R can be calculated as

$$P\left[Y=1|R=1\right]=P\left[\left(Y=1\right)\cap \left(R=1\right)\right]∕P\left[R=1\right].$$ (A1)

Now

$$P\left[R=1\right]=P\left[R=1|D=1\right]P\left[D=1\right]+P\left[R=1|D=0\right]P\left[D=0\right]=\rho T_R+\left(1-\rho \right)F_R$$ (A2)

and

$$P\left[\left(Y=1\right)\cap \left(R=1\right)\right]=P\left[\left(Y=1\right)\cap \left(R=1\right)|D=1\right]P\left[D=1\right]+P\left[\left(Y=1\right)\cap \left(R=1\right)|D=0\right]P\left[D=0\right].$$ (A3)

Under the assumption of conditional independence between the tests Y and R given true lesion status, we have

$$P\left[\left(Y=1\right)\cap \left(R=1\right)\right]=P\left[Y=1|D=1\right]P\left[R=1|D=1\right]P\left[D=1\right]+P\left[Y=1|D=0\right]P\left[R=1|D=0\right]P\left[D=0\right]=T_Y{T}_R\rho +F_Y{F}_R\left(1-\rho \right).$$ (A4)

Substituting Eqs. A2, A4 in Eq. A1, we get

$$P\left[Y=1|R=1\right]=\left\{T_Y{T}_R\rho +F_Y{F}_R\left(1-\rho \right)\right\}∕\left\{\rho T_R+\left(1-\rho \right)F_R\right\}.$$ (A5)

Note that in the special case that F_R=0, Eq. A5 gives P[Y=1|R=1]=T_Y, which implies that the apparent sensitivity is unbiased. In general, however, it is biased when F_R≠0. The result in the introduction follows by setting T_R=1, F_R=0.05, T_Y=1, F_Y=0, and ρ=0.2 in Eq. A5.

APPENDIX B: MAXIMUM LIKELIHOOD ESTIMATION FOR LCA

The following is an operationally correct derivation of the expectation-maximization (EM) algorithm for LCA as applied to multiple reader ratings. A more mathematically rigorous derivation for the general LCA case can be found in Ref. 19. Under a latent class model, the unconditional likelihood of the reader counts Y_Ri and Y_Ci in the reference and CAD assisted groups, respectively, is given by

$$\text{Lik}\left(Y_{Ri},Y_{Ci}\right)=P\left(Y_{Ri},Y_{Ci}|L_i=1\right)P\left(L_i=1\right)+P\left(Y_{Ri},Y_{Ci}|L_i=0\right)P\left(L_i=0\right).$$ (B1)

Now model B1 postulates that conditional on the latent class L_i of the ith lesion candidate, i=1,…,n, obtained from N patients, the reader counts Y_Ri and Y_Ci follow independent binomial distributions, whose likelihood is of the form given in Eqs. B3, B4, B5, B6, B7 (Lik₁ and Lik₃ for L_i=1, Lik₂ and Lik₄ for L_i=0). Under the conditional independence assumption, their joint likelihood is the product of their individual likelihoods. Finally, the distribution of the latent class (0 or 1) is Bernoulli, with a likelihood of the form B7. Conditional on the latent class L_i being observed, it follows from Eq. B1 that we can write the likelihood of the reader counts Y_Ri and Y_Ci as

$$\text{Lik}\left(Y_{Ri},Y_{Ci}\right)={\text{Lik}}_{5i}\times {\left({\text{Lik}}_{1i}\times {\text{Lik}}_{3i}\right)}^{L_i}{\left({\text{Lik}}_{2i}\times {\text{Lik}}_{4i}\right)}^{1-L_i},$$ (B2)

where

$${\text{Lik}}_{1i}=\left(\begin{array}{c}{K}_R\\ Y_{Ri}\end{array}\right)T_R{}^{Y_{Ri}}{\left(1-T_R\right)}^{K_R-Y_{Ri}},$$ (B3)

$${\text{Lik}}_{2i}=\left(\begin{array}{c}{K}_R\\ Y_{Ri}\end{array}\right)F_R{}^{Y_{Ri}}{\left(1-F_R\right)}^{K_R-Y_{Ri}},$$ (B4)

$${\text{Lik}}_{3i}=\left(\begin{array}{c}{K}_C\\ Y_{Ci}\end{array}\right)T_C{}^{Y_{Ci}}{\left(1-T_C\right)}^{K_F-Y_{Ci}},$$ (B5)

$${\text{Lik}}_{4i}=\left(\begin{array}{c}{K}_C\\ Y_{Ci}\end{array}\right)F_C{}^{Y_{Ci}}{\left(1-F_C\right)}^{K_C-Y_{Ci}},$$ (B6)

$${\text{Lik}}_{5i}={\rho }^{L_i}{\left(1-\rho \right)}^{1-L_i}.$$ (B7)

Thus, the combined log likelihood over all lesion candidates, i=1,…n, can be written as

$$\text{log}\text{\hspace{0.17em}Lik}\left(T_R,F_R,T_C,F_C,\rho \right)=\sum _{i=1}^n\text{log}{\text{Lik}}_{5i}+\sum _{i:L_i=1}\left(\text{log}{\text{Lik}}_{1i}+\text{log}{\text{Lik}}_{3i}\right)+\sum _{i:L_i=0}\left(\text{log}{\text{Lik}}_{2i}+\text{log}{\text{Lik}}_{4i}\right).$$ (B8)

Note that the likelihood is now represented as a function of parameters rather than data, to facilitate maximization with respect to them. To maximize log Lik with respect to T_R, we differentiate it and set to 0. Note that T_R only appears in the term log Lik_1i, hence,

$$\frac{\partial }{\partial T_R}\text{log}\text{\hspace{0.17em}Lik}\left(T_R,F_R,T_C,F_C,\rho \right)=\sum _{i:L_i=1}\left(\frac{Y_{Ri}}{T_R}-\frac{K_R-Y_{Ri}}{1-T_R}\right)=\sum _{i=1}^n{L}_i\left(\frac{Y_{Ri}}{T_R}-\frac{K_R-Y_{Ri}}{1-T_R}\right)=0.$$ (B9)

Solving Eq. B9 gives ${\widehat{T}}_R=\sum L_i{Y}_{Ri}∕K_R\sum L_i$. Estimates for other parameters, obtained by analogous steps, are given as follows:

$$\text{M}\text{step}:{\widehat{T}}_R=\frac{\sum L_i{Y}_{Ri}}{K_R\sum L_i},{\widehat{F}}_R=\frac{\sum \left(1-L_i\right)Y_{Ri}}{K_R\sum \left(1-L_i\right)},$$ (B10)

$${\widehat{T}}_C=\frac{\sum L_i{Y}_{Ci}}{K_C\sum L_i},{\widehat{F}}_C=\frac{\sum \left(1-L_i\right)Y_{Ci}}{K_C\sum \left(1-L_i\right)},$$

$$\widehat{\rho }=\frac{\sum L_i}{N}.$$

Differentiating the likelihood a second time gives

$$\frac{{\partial }^2}{\partial T_R^2}\text{log}\text{\hspace{0.17em}Lik}\left(T_R,F_R,T_C,F_C,\rho \right)=-\sum _{i=1}^n{L}_i\left(\frac{Y_{Ri}}{T_R^2}+\frac{K_R-Y_{Ri}}{{\left(1-T_R\right)}^2}\right)<0\forall T_R∊\left(0,1\right).$$ (B11)

We note that second derivatives of the log likelihood with respect to other parameters are similarly negative. Further, because of the separable (product) nature of the likelihood, the mixed derivatives, e.g., ∂²∕∂T_R∂F_R log Lik(T_R,F_R,T_C,F_C,ρ), are all 0. Together with Eq. B11, this implies that the matrix of second derivatives of the likelihood is negative definite. Hence the estimators of T_R,F_R,T_C,F_C,ρ given in Eq. B10 are indeed maximum likelihood estimates.¹⁶

In practice, the latent classes are unknown, so we estimate them by their conditional expectation given the known data. Since L_i is a binary variable, we observe that E[L_i|Y_Ri,Y_Ci]=P[L_i=1|Y_Ri,Y_Ci]. By Bayes’s theorem²⁴

$$P\left[L_i=1|Y_{Ri},Y_{Ci}\right]=\frac{P\left[Y_{Ri},Y_{Ci}|L_i=1\right]P\left[L_i=1\right]}{P\left[Y_{Ri},Y_{Ci}|L_i=1\right]P\left[L_i=1\right]+P\left[Y_{Ri},Y_{Ci}|L_i=0\right]P\left[L_i=0\right]}=\frac{\rho {\text{Lik}}_{1i}{\text{Lik}}_{3i}}{\left\{\rho {\text{Lik}}_{1i}{\text{Lik}}_{3i}+\left(1-\rho \right){\text{Lik}}_{2i}{\text{Lik}}_{4i}\right\}}$$

as required. Here Lik_1i,Lik_2i,Lik_3i,Lik_4i are defined in Eqs. B3, B4, B5, B6, B7.

$$\text{E}\text{step}:{\widehat{L}}_i=E\left[L_i|Y_{Ri},Y_{Ci}\right]=\frac{\rho {\text{Lik}}_{1i}{\text{Lik}}_{3i}}{\left\{\rho {\text{Lik}}_{1i}{\text{Lik}}_{3i}+\left(1-\rho \right){\text{Lik}}_{2i}{\text{Lik}}_{4i}\right\}}.$$ (B12)

Estimators in Eqs. B10, B12 are interdependent, in that computation of one set of estimators requires knowledge of the other set of estimators. To overcome this problem, the E and M steps are successively iterated. Each pair of steps causes some increase in the likelihood.²³ The process is continued till convergence, i.e., an additional iteration does not produce any appreciable increase in the likelihood. The algorithm can be summarized as follows.

EM algorithm for LCA

• (1)Intialize the ${\widehat{L}}_i$; compute Lik(0)=log Lik using Eq. B8; set Lik(1)=Lik(0)+100;
• (2)
  While (Lik(1)>Lik(0)+10⁻⁵){

  • a.
    Compute ${\widehat{T}}_F,{\widehat{F}}_F,{\widehat{T}}_C,{\widehat{F}}_C,\widehat{\rho }$ using the data and ${\widehat{L}}_i$ by Eq. B10.
  • b.
    Update ${\widehat{L}}_i$ using ${\widehat{T}}_F,{\widehat{F}}_F,{\widehat{T}}_C,{\widehat{F}}_C,\widehat{\rho }$ and the data by Eq. B12.
  • c.
    Reset Lik(0)=Lik(1); recompute Lik(1) using Eq. B8.}
• (3)Finally, compute ${\text{FPP}}_F=n{\widehat{F}}_F∕N,{\text{FPP}}_C=n{\widehat{F}}_C∕N$

  where FPP stands for false positives per patient.

This procedure is one of a class of maximum likelihood estimation procedures known as the EM algorithm.²⁵ The algorithm converges to the same set of estimates irrespective of the choice of initial ${\widehat{L}}_i$ (except when they are chosen to be all 0). The EM algorithm yields the same maximum likelihood estimators one would have obtained had one constructed the likelihood without using the unknown data (in this case the latent classes).²⁵ This alternative process leads to a more complex mixture model. However, in the problem of lesion detection, estimates of the latent classes are of intrinsic interest, hence the EM algorithm may be preferable. Finally, we note that the method of conversion from FPF to FPP is similar to the approach of Ref. 23.