Computer aided automatic detection of malignant lesions in diffuse optical mammography

Abstract

Purpose: Computer aided detection (CAD) data analysis procedures are introduced and applied to derive composite diffuse optical tomography (DOT) signatures of malignancy in human breast tissue. In contrast to previous optical mammography analysis schemes, the new statistical approach utilizes optical property distributions across multiple subjects and across the many voxels of each subject. The methodology is tested in a population of 35 biopsy-confirmed malignant lesions.

Methods: DOT CAD employs multiparameter, multivoxel, multisubject measurements to derive a simple function that transforms DOT images of tissue chromophores and scattering into a probability of malignancy tomogram. The formalism incorporates both intrasubject spatial heterogeneity and intersubject distributions of physiological properties derived from a population of cancer-containing breasts (the training set). A weighted combination of physiological parameters from the training set define a malignancy parameter (M), with the weighting factors optimized by logistic regression to separate training-set cancer voxels from training-set healthy voxels. The utility of M is examined, employing 3D DOT images from an additional subjects (the test set).

Results: Initial results confirm that the automated technique can produce tomograms that distinguish healthy from malignant tissue. When compared to a gold standard tissue segmentation, this protocol produced an average true positive rate (sensitivity) of 89% and a true negative rate (specificity) of 94% using an empirically chosen probability threshold.

Conclusions: This study suggests that the automated multisubject, multivoxel, multiparameter statistical analysis of diffuse optical data is potentially quite useful, producing tomograms that distinguish healthy from malignant tissue. This type of data analysis may also prove useful for suppression of image artifacts.

INTRODUCTION

Diffuse optics and automated cancer diagnosis

Diffuse optical spectroscopy (DOS) utilizes light in the low absorption window¹ between 650 and 950 nm to measure chromophore concentrations and scattering in deep tissues. Information about concentrations of water, lipid, oxy (HbO₂), deoxy (Hb), and total hemoglobin (Hb_t), as well as blood oxygen saturation (StO₂), and tissue scattering (i.e., the reduced scattering coefficient, ${\mu }_s^{\prime }$) are readily derived with the optical techniques.

Diffuse optical tomography (DOT) utilizes many point measurements on the surface of tissue to reconstruct concentrations of chromophores and scattering parameters in the interior of the tissue. Images are obtained by inverting the heterogeneous diffusion equation. A recent review by Arridge and Schotland² describes various techniques needed to perform this inversion. The results are three-dimensional (3D) maps of optical properties and chromophore concentrations. The reconstructed parameters have been correlated with the physiological signatures of tumors. For example, optically measured Hb_t has been correlated with microvessel density measured by histopathology,³ and ${\mu }_s^{\prime }$ has been correlated with cellular volume fraction and mean size.⁴ Leff et al.⁵ recently reviewed DOT breast tumor contrasts in Hb_t and StO₂. Some disagreements remain in the diffuse optics community about which optically measured parameters are the most important indicators of malignancy; recent work, for example, on water⁶ and collagen⁷ has opened up additional possibilities.

While current incarnations of multiwavelength DOT provide 3D images of several physiological parameters associated with cancer metabolism and growth, unambiguous 3D maps of healthy and malignant tissue are sometimes elusive. DOT images require simultaneous interpretation of multiparameter data at each spatial point, and images sometimes exhibit significant inter- and intrasubject variation in the absolute and relative values of these parameters. Together, these factors limit DOT image analysis to skilled practitioners of the art. In this contribution, we address this issue. In particular, we introduce a novel algorithm for automated identification of malignant and healthy tissue based on a statistical analysis of diffuse optical data from a population of known cancers.

The requirement for skilled readers is not unique to optics; most clinical imaging technologies have similar constraints and various techniques for automated breast cancer detection and diagnosis have been explored to ameliorate this situation. Notably, computer-aided detection (CAD) in x-ray mammography screening relies upon high-spatial-resolution 2D intensity projections to automatically identify tumors in images based on structural features such as spiculation and microcalcification.^{8, 9, 10}

The formalism presented herein for DOT CAD employs multiparameter, multivoxel, multisubject measurements to derive a simple function that transforms DOT images of tissue chromophores and scattering into a “probability of malignancy” tomogram. The formalism incorporates both intrasubject spatial heterogeneity and intersubject distributions of physiological properties derived from a population of cancer-containing breasts (the “training set”). We extract a weighted combination of physiological parameters from the training set to define a “malignancy parameter” (M), with the weighting factors optimized to separate training-set voxels from healthy and cancerous tissue. We then examine the utility of M, employing 3D DOT images from an additional subject (the “test set”).

Limitations of current diffuse optics analysis

To better appreciate the need for DOT CAD, consider the typical analysis scheme currently employed in the field. First, the lesions in each subject are identified, then tissue is divided into “healthy” and “lesion” regions, and average optical properties are computed for each region. Finally, these regionally averaged optical properties and differences thereof are assessed across the population. With this approach, the spatial information from DOT images is reduced to a few numbers. Such an analysis implicitly ignores the spatial heterogeneity of cancers^{11, 12, 13} and healthy tissues.¹⁴

Grand averages of DOT data across multiple studies suggest that malignant lesions can be differentiated from healthy tissue by Hb_t.⁵ In recent work¹⁵ using the same data set as in the analysis to be presented herein, we performed such regional averaging from DOT images; we then demonstrated that benign and malignant lesions could be separated with a univariate analysis of the ratio of the mean lesion and healthy tissue values of Hb_t, ${\mu }_s^{\prime }$, and an empirically derived optical index combining Hb_t, ${\mu }_s^{\prime }$, and StO₂. For example, this work found that the benign and malignant lesions had a statistically significant different ratio of the Hb_t region means (e.g., ⟨Hb_t⟩_Lesion∕⟨Hb_t⟩_Healthy).

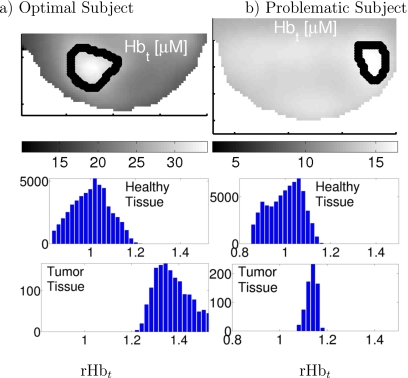
Volume element histograms of rHb_t (Hb_t∕⟨Hb_t⟩_Healthy) reveal more information than distribution means. Histograms of two subjects are shown in Fig. 1. Figure 1a shows an optimal subject wherein the lesion is clearly distinguishable from healthy tissue. Figure 1b shows a problematic subject; here, variations in the healthy region (which include possible image reconstruction artifacts) extend the distribution of healthy tissue rHb_t into the range of cancer tissue rHb_t. The first lesion [Fig. 1a] can be readily identified with the simple normalization procedures described above and a cutoff of rHb_t=1.2. The same procedure and cutoff for case two [Fig. 1b], however, would miss the cancer completely; furthermore, adjustment of the cutoff to include the tumor causes incorrect assignment of some healthy regions. These observations suggest a more sophisticated analysis using all available spatial information is desirable. Additionally, simple thresholding in a single optical parameter ignores the potential utility of multiparameter data and ignores possible spatially heterogeneous signatures of cancers and healthy tissues.

Figure 1.

(Top row) Slices from 3D tomograms from subjects with breast cancer. Lesions are denoted by the thick black line. Histogram of rHb_t for healthy (middle row) and cancer (bottom row) voxels, segmented as shown in the top row. Data are normalized as rHb_t=Hb_t∕⟨Hb_t⟩_H for each subject. The left column (a) shows a lesion with clearly separated means and distinct distributions; and the right column (b) shows a subject wherein the healthy Hb_t distribution overlaps that of the cancer region. This normalization approach is standard in the “typical” DOT analysis, and the example is taken from our previous work (Ref. ¹⁵). Note that the “typical DOT” scheme shown in the figure utilizes a normalization that is different from Eq. 1.

Thus far, a few groups applied statistical analysis techniques to multiparameter optical measurements, including applications to arthritic joints,¹⁶ high-risk¹⁷ or high mammographic density^{18, 19} breast tissue, and to various “endoscopic” measurements or excised tissues.²⁰ The data sets employed thus far, however, have limited spatial information and orders of magnitude fewer measurements per subject than, for example, the breast tomograms utilized in the analysis to be presented herein. A few researchers implemented automated image methods with DOT to identify lesions in a particular subject.^{21, 22, 23} This per-subject analysis, however, neglects information about the common signatures of cancer across a population. Still other researchers pursued hypothesis-driven multiparameter optical metrics with DOS^{24, 25} and DOT.^{15, 26} Such metrics are dependent on the underlying hypotheses, however, and are often empirically chosen combinations of equally weighted parameters. Chance et al.²⁷ explored two-parameter signatures of breast cancer, graphically identifying malignant lesions, but the separation lines were manually selected for the specific data set.

Thus, previous studies fall into two groups. Some considered spatial variation in cancers, but neglected common signatures across a population. Others considered population signatures, but used only regionally averaged measurements. Furthermore, few, if any, applied statistical optimization techniques to multiparameter optical signatures of cancer across a population. By contrast, the methods we present herein utilize data from many voxels in many subjects to statistically optimize a multiparameter probability of malignancy.

METHODS

Data set used in this analysis

Our data set consists of 3D tomograms of total hemoglobin concentration (Hb_t), blood oxygen saturation (StO₂), and reduced scattering coefficient $\left({\mu }_s^{\prime }\right)$ in 35 biopsy-confirmed cancer-bearing breasts. DOT images from these subjects were collected with a parallel plate optical imaging system described in previous works.^{15, 36} Table 1 contains the demographics of the population used, separated by clinical diagnosis.

Table 1.

Demographic breakdown of cancers in this study. IDC: Invasive ductal carcinoma; DCIS: Ductal carcinoma in situ; ILC: Invasive lobular carcinoma; LCIS: Lobular carcinoma in situ; and BMI: Body mass index. Numeric data are given as mean±standard deviation. 16 subjects were premenopausal and 19 were postmenopausal.

No.	Diagnosis	Age (yr)	BMI (kg∕m2)	Tumor size (cm3)
8	IDC	44±11	27±6.2	2.9±1.2
2	DCIS	60±4.9	29±6.6	0.7±0.28
2	ILC	62±3.5	22±2	1.4±0.35
22	IDC & DCIS	49±10	28±7	1.8±0.97
1	DCIS & LCIS	39±0	19±0	5±0
35	All	49±11	27±6.5	2.1±1.2

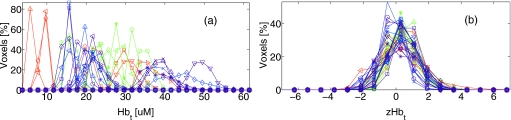
The cancers in this analysis had an average volume of 6.7±5.2 cm³, corresponding to 841±656 image voxels. The average size of the entire breast was 374±231 cm³, corresponding to 4.7×10⁴±2.9×10⁴ image voxels.³⁷ Note, for each parameter, traditional regional averaging analysis of these data, as described above, reduces these ∼5×10⁴ data points per subject to two numbers (cancer and healthy region averages). Figure 1 shows sample intrasubject spatial heterogeneity of these regions, and Fig. 2a plots the distribution of Hb_t for the healthy regions of all subjects.

Figure 2.

Intrasubject data normalization brings intersubject data distribution close to a normal distribution. The left figure (a) shows absolute values of Hb_t; and the right figure (b) shows the population distribution of zHb_t after intrasubject normalization [see Eq. 1 and note that each subject is normalized individually]. Each trace represents the healthy region of one subject. For clarity of presentation, the vertical axis is normalized to the total number of voxels in each subject.

We demonstrate the new statistical analysis method with a leave-one-out cross-validation (e.g., as described by Hastie et al.²⁸), in which 34 out of our 35 subjects serve as the training set and the remaining subject provides the test data. Permuting these sets, such that each subject serves as the test set once, provides 35 training∕test data combinations and enables estimation of classification accuracy. Note that gold standard segmentation of the DOT images into tumor and healthy regions is required for the training set to train the classifier (i.e., for the logistic regression model) and is required for the test set classification validation (i.e., to assess how well the classifier performed compared to the gold standard in a new data set).

Both training set normalization (described below) and testing of our method require “gold standard” spatial localization of the cancers; a full description of the procedure utilized to identify cancer regions is given in Ref. 15. Briefly, a traditional clinical imaging method, typically MRI, was used to approximately locate each tumor. We then selected nearby regions of high optical contrast as the starting point for a region-growing algorithm to identify the spatial extent of the tumor. A 2 cm border region about the tumor and voxels within 1 cm of the source and detector plane was excluded from the training data; the remainder of the breast is defined as healthy tissue. We exclude these boundary regions to reduce the effect of physiological changes near the tumor, errors in tumor positioning, and optode artifacts. In the training set, we assume perfect segmentation into malignant and healthy tissue. In the test set, gold standard segmentation is used only to determine the accuracy of our malignancy prediction.

Algorithm to calculate probability of malignancy

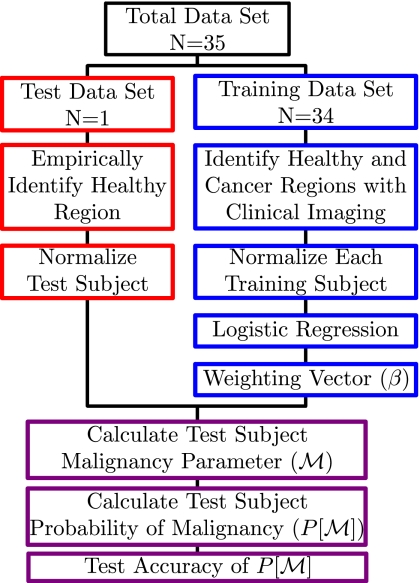
The image analysis has two parts: First, we determine the probability of malignancy function based on the population of known cancers. Then, we test the resulting function on another data set. We iterate this process, exchanging members of the training and test sets to improve the generalizability of our results.

We chose Hb_t, StO₂, and ${\mu }_s^{\prime }$ as our fundamental physiological variables. We also tested the combination of Hb, HbO₂, and ${\mu }_s^{\prime }$, but little difference was found (results not shown). A schematic of the normalization, analysis, and testing protocol is given in Fig. 3.

Figure 3.

Data processing flow chart for each iteration of the leave-one-out protocol. See text for details.

Intrasubject normalization

The first step of this analysis is to normalize the tomographic data across the training sample, as distributions of optical properties vary significantly between subjects. We carry out this procedure for each physiological parameter in both healthy and cancer tissues. To illustrate, consider the total hemoglobin concentration, Hb_t. Figure 2a shows the reconstructed Hb_t for all healthy tissue voxels in all subjects. We see that the spread of Hb_t values is quite large, complicating the use of these data across the sample. Therefore, for each subject, we compute X=ln[Hb_t], the healthy tissue mean ⟨X⟩_H, and the healthy tissue standard deviation σX_H. Note that ⟨X⟩_H and σX_H are calculated individually over the healthy regions in each subject, thereby capturing both inter- and intrasubject tissue heterogeneity. A similar set of data (i.e., X=ln[Hb_t]) is obtained for malignant tissue in each subject in the training set. Together, these quantities permit calculation of the “Z-score” for each variable in each voxel of each subject, e.g.,

$$z{\text{Hb}}_{t_d}^{\left(s,k\right)}=\frac{X_d^{\left(s,k\right)}-{⟨X^s⟩}_H}{\sigma X_H^s}=\frac{\text{ln}\left[{\text{Hb}}_{t_d}^{\left(s,k\right)}\right]-{⟨\text{ln}\left[{\text{Hb}}_t^s\right]⟩}_H}{\sigma {\left[\text{ln}\left[{\text{Hb}}_t^s\right]\right]}_H}.$$ (1)

Here, the subscript index d=H,M specifies healthy (H) and malignant (M) regions; the superscript index s=1:N_s, specifies a subject in the training set, and the superscript index $k=1\text{:}{N}_v^{\left(s,d\right)}$ specifies voxel number within the healthy or malignant region in each subject. Note that the Z-score for both the healthy and malignant regions depends on the mean and standard deviation of the healthy region.

After the Z-score procedure, the distributions of physiological parameters in each voxel across subjects in the sample are much more similar. Figure 2b shows this for Hb_t in the healthy regions across 35 subjects. Note that this intrasubject normalization brings the intersubject voxel chromophore distribution close to a zero-centered Gaussian distribution, permitting us to more sensibly combine data across multiple subjects.

A particularly attractive feature of this data normalization is the explicit inclusion in the normalized variable of the subject-dependent characteristic spatial fluctuations in each parameter via the distribution width (σX_H). Previous work in the field (e.g., as reviewed by Leff et al.⁵) used only the ratio of cancer to healthy values for each parameter; the previous approach accounts for the wide variation in mean parameter values between subjects, but ignores the differences in optical parameter distribution widths found in each subject’s healthy tissue. With the normalization scheme described here, lesion contrast is scaled to the variation in healthy tissue. Similarly, we compute the Z-score for StO₂ and ${\mu }_s^{\prime }$.

For the remainder of this paper, we will be computing and manipulating the normalized physiological variables: $z{\text{Hb}}_{t_d}^{\left(s,k\right)}$, $z{\text{StO}}_{2_d}^{\left(s,k\right)}$, and $z{\mu }_{sd}^{\prime \left(s,k\right)}$. Since we use identically sized voxels for all subjects, we expect that each tissue type (H,M) in each subject to have a different number of voxels; i.e., $N_v^{\left(s,d\right)}$, is not constant. In order to avoid weighting the data unduly toward healthy or malignant tissue, we set $N_v^{\left(s,d\right)}=N_v=40$. Therefore, the same number of voxels randomly selected from each region and each subject is used for the next level of our analysis. We chose N_v=40 because the smallest tumors in our data set had ∼140 voxels and our analysis scheme depends on independent measurements from each voxel. With this choice for N_v, the median voxel separation in the 35 tumor regions was 1.2 cm. We therefore do not expect spatial correlation due to DOT resolution to strongly affect results by reducing the independence between measurements.

Drawing N_v=40 voxels from the tumor and healthy regions in each of 35 subjects provides a set of 1400 tumor and 1400 healthy voxels defined by our gold standard segmentation. We utilize this set of voxels in our leave-one-out protocol, removing all voxels of the test subject from the total data set so that the remaining 1360 voxels from each region serve as the training set for classification. The trained classification rule is then applied to the test set to predict malignancy. The entire procedure is then repeated for the other test subjects. Choosing an equal number of voxels from each region improves our estimate of the accuracy of our classification technique under the leave-one-out cross-validation protocol, which will be discussed in Sec. 3.

Training set analysis procedure

The tomographic data of all subjects in the training set, i.e., data from all chromophores in N_v voxels of the healthy and malignant regions of each of N_s subjects, are combined into a single matrix. Using a logistic regression model with the known malignancy status of each voxel as the outcome and the normalized tomographic data as predictors, we fit a weight vector $\vec{\beta }=\left[{\beta }_{z{\text{Hb}}_t},{\beta }_{z{\text{StO}}_2},{\beta }_{z{\mu }_s^{\prime }},{\beta }_0\right]$ and compute the vector ${\mathcal{M}}_d^{\left(s,k\right)}$, whose elements define a scalar malignancy parameter for each voxel in each region of each subject. For the logistic regression model, M is the log odds of malignancy,

$${\mathcal{M}}_d^{\left(s,k\right)}=\left[\begin{array}{c}{\mathcal{M}}_H^{1,1}\\ ⋮\\ {\mathcal{M}}_H^{1,N_v}\\ ⋮\\ \approx \\ ⋮\\ {\mathcal{M}}_H^{N_s,1}\\ ⋮\\ {\mathcal{M}}_H^{N_s,N_v}\\ {\mathcal{M}}_M^{1,1}\\ ⋮\\ {\mathcal{M}}_M^{1,N_v}\\ ⋮\\ \approx \\ ⋮\\ {\mathcal{M}}_M^{N_s,1}\\ ⋮\\ {\mathcal{M}}_M^{N_s,N_v}\end{array}\right]=\left[\begin{array}{cccc}z{\text{Hb}}_{t_H}^{1,1}& z{\text{StO}}_{2_H}^{1,1}& z{\mu }_{sH}^{\prime 1,1}& 1\\ ⋮& ⋮& ⋮& ⋮\\ z{\text{Hb}}_{t_H}^{1,N_v}& z{\text{StO}}_{2_H}^{1,N_v}& z{\mu }_{sH}^{\prime 1,N_v}& 1\\ ⋮& ⋮& ⋮& ⋮\\ \approx & \approx & \approx & \approx \\ ⋮& ⋮& ⋮& ⋮\\ z{\text{Hb}}_{t_H}^{N_s,1}& z{\text{StO}}_{2_H}^{N_s,1}& z{\mu }_{sH}^{\prime N_s,1}& 1\\ ⋮& ⋮& ⋮& ⋮\\ z{\text{Hb}}_{t_H}^{N_s,N_v}& z{\text{StO}}_{2_H}^{N_s,N_v}& z{\mu }_{sH}^{\prime N_s,N_v}& 1\\ z{\text{Hb}}_{t_M}^{1,1}& z{\text{StO}}_{2_M}^{1,1}& z{\mu }_{sM}^{\prime 1,1}& 1\\ ⋮& ⋮& ⋮& ⋮\\ z{\text{Hb}}_{t_M}^{1,N_v}& z{\text{StO}}_{2_M}^{1,N_v}& z{\mu }_{sM}^{\prime 1,N_v}& 1\\ ⋮& ⋮& ⋮& ⋮\\ \approx & \approx & \approx & \approx \\ ⋮& ⋮& ⋮& ⋮\\ z{\text{Hb}}_{t_M}^{N_s,1}& z{\text{StO}}_{2_M}^{N_s,1}& z{\mu }_{sM}^{\prime N_s,1}& 1\\ ⋮& ⋮& ⋮& ⋮\\ z{\text{Hb}}_{t_M}^{N_s,N_v}& z{\text{StO}}_{2_M}^{N_s,N_v}& z{\mu }_{sM}^{\prime N_s,N_v}& 1\end{array}\right]\left[\begin{array}{c}{\beta }_{z{\text{Hb}}_t}\\ {\beta }_{z{\text{StO}}_2}\\ {\beta }_{z{\mu }_s^{\prime }}\\ {\beta }_0\end{array}\right].$$ (2)

In forming ${\mathcal{M}}_d^{\left(s,k\right)}$, we thus account for measurements taken across multiple subjects and measurements taken across multiple spatial locations in each subject. The right most column of 1’s in the Z-matrix relates to β₀ and introduces an offset that could, in principle, include effects from additional parameters (e.g., variations in tissue fat content, age, etc.) not considered in the present analysis (see Refs. ^{29, 30} for more details on this latter point).

From M, we compute a probability of malignancy using the function

$$P\left[{\mathcal{M}}_d^{\left(s,k\right)}\right]=\frac{1}{1+e^{-{\mathcal{M}}_d^{\left(s,k\right)}}}.$$ (3)

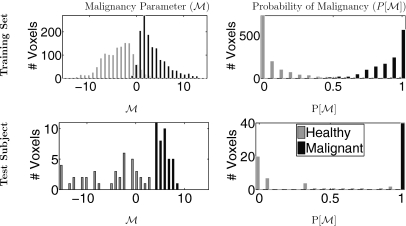
Our goal is to identify a weighting vector $\vec{\beta }$ that maximizes the difference in probability between voxels in healthy $\left(P\left[{\mathcal{M}}_H^{\left(s,k\right)}\right]\right)$ and malignant $\left(P\left[{\mathcal{M}}_M^{\left(s,k\right)}\right]\right)$ regions in our training set. In performing this logistic regression, we assume that each element of M is independent. $\vec{\beta }$ is optimized by minimizing the difference between P[M] and the gold standard diagnosis, plotted against M (see Ref. 31 for a more detailed description of logistic regression).³⁸ This results in a $\vec{\beta }$ such that $P\left[{\mathcal{M}}_H^{\left(s,k\right)}\right]\simeq 0$ and $P\left[{\mathcal{M}}_M^{\left(s,k\right)}\right]\simeq 1$. Optimized M and P[M] are shown in Fig. 4 for typical training and test sets.

Figure 4.

Example of training (34 subjects, top row) and test (1 subject, bottom row) set M and P[M]. N_v=40 voxels were randomly selected from each region in each subject, as described in Sec. 2B1 (i.e., 1360 voxels from each of the training healthy and tumor regions and 40 voxels from the healthy and tumor regions of the test subject). Left column: Malignancy parameter (M) for each subject (s), voxel in training set (k), and diagnosis ${\mathcal{M}}_d^{\left(s,k\right)}$. Right column: Optimized probability of malignancy $P\left[{\mathcal{M}}_d^{\left(s,k\right)}\right]$. The test subject is also shown in Fig. 1a; note the improved separation between the malignant and healthy regions.

Test subject normalization

The output from the logistic regression described in Sec. 2B2 is the parameter weighting vector, $\vec{\beta }$, which we then apply to data from an independent test subject (i.e., DOT data from the “leftover” subject). Such an application derives a predicted probability of malignancy for each voxel in the test subject.

Normalization of the test data set is slightly more complicated than that of the training data, as we must not assume knowledge of the cancer location in the test subject’s breast. We therefore empirically define the healthy region as those voxels in which both Hb_t and ${\mu }_s^{\prime }$ lie within the whole-breast mean and the whole-breast mean plus 2 standard deviations. Note that the results turned out to be only mildly sensitive to the particular choice of healthy criterion, as the cancers usually do not occupy a large fraction of the breast.

RESULTS

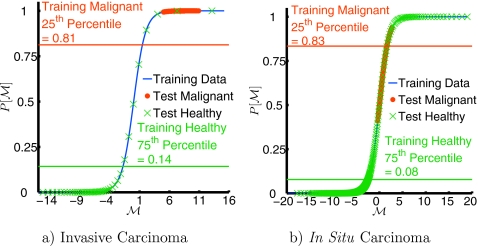
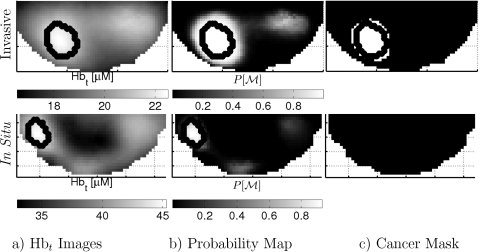
Figure 5 shows P vs M for two subjects; example slices through the center of the cancers for the same subjects are shown for rHb_t [Fig. 6a] and P[M] [Fig. 6b]. A probability cutoff is readily applied to the data (i.e., a horizontal line in Fig. 5) in order to provide a concrete criterion to create spatial masks of regions that are highly suspicious for malignancy [Fig. 6c]. One can then compare these masks to the gold standard malignant and healthy regions for each test subject.

Figure 5.

Example probability of malignancy (P[M]) calculated for two test subjects. The function P[M] (blue line) is derived from the training set, as described in Sec. 2B2. This function is then applied to the remaining test subject in each case; using the gold standard segmentation described in Sec. 2A, voxels are labeled as healthy (green crosses) or malignant (red dots). Image slices from the same subjects are shown in Fig. 6. For clarity, only every hundredth voxel is plotted. (a) Typical invasive cancer that shows very good separation between healthy and malignant regions. (b) Case study: In situ lesion; this lesion is not as well separated from the background healthy tissue. P[M] for this in situ lesion is more heterogeneous, with a lower average than the invasive lesion and more overlap between malignant and healthy tissue.

Figure 6.

Slices from 3D images of subjects in Fig. 5, showing total hemoglobin concentration [(a) Hb_t], probability of malignancy [(b) P[M]], and a binary cancer mask (c) using a cutoff of P[M]=0.95. This in situ lesion provides an interesting case study, with the P[M] falling between the malignant lesions and the healthy regions.

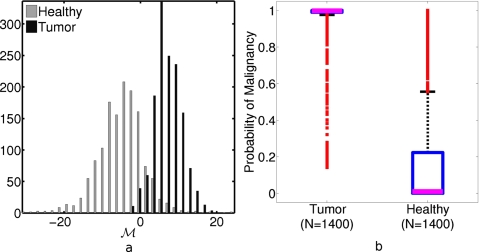
To quantify the quality of probability maps, such as those shown in Fig. 6b, we examine the distributions of M and P[M] for N_v=40 voxels in gold standard healthy and malignant regions across the entire set of test subjects; for this task, we use the same randomly selected voxels, as described in Sec. 2B1. Figure 7a shows a histogram of M drawn from test subject healthy and malignant regions in each iteration of the leave-one-out protocol; Fig. 7b is a box plot of the P[M] distributions. Notice that the voxels from the tumor region are distributed narrowly about P[M]∼1, but the distribution has a small tail of outliers. Similarly, the healthy region voxels are concentrated near P[M]∼0.1, but the central quartiles of the distribution extend from ∼0.01 to ∼0.2 and the fourth quartile extends to ∼0.6, with outliers up to ∼1. This wide distribution of values in the healthy region can also be seen in Fig. 5.

Figure 7.

(a) Histogram of M for the healthy and tumor regions of 35 test subjects, used to generate the box plot in (b). (b) Box plot of probability of malignancy (P[M]) of N_v=40 voxels from all test subjects (bold lines mark median values, boxes denote interquartile range, dashed lines indicate outer two quartiles, and squares mark outliers). See insets in Fig. 8 for a tabulation of mean classification rates at several values of P_cut. Median P[M]=0.998 for tumor voxels and 0.019 for healthy voxels.

We next impose a probability of malignancy cutoff, P_cut: Voxels with probability above P_cut are predicted to be malignant, those below P_cut are predicted to be healthy. Finally, we compare this prediction to the gold standard diagnosis. For each value of P_cut, some test subject voxels are malignant and correctly predicted to be malignant [true positive (TP)]; some test subject voxels are malignant, but incorrectly predicted to be healthy [false negative (FN)]; some test subject voxels are healthy, but incorrectly predicted to be malignant [false positive (FP)]; and some test subject voxels are healthy and correctly predicted to be healthy [true negative (TN)].

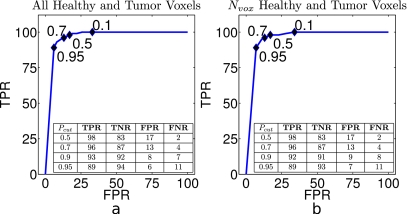
These quantities can be expressed as rates by dividing each of these classifications by the total number of voxels in the healthy or malignant regions. We can thus calculate true and false positive rates (TPR=TP∕(TP+FN), FPR=FP∕(TN+FP)) and true and false negative rates (TNR=TN∕(TN+FP), FNR=FN∕(FN+TP)) as functions of P_cut. The receiver operator characteristic (ROC) curve plots TPR against FPR; ROC curves are shown in Fig. 8. Note that these quantities are often referred to as sensitivity (TPR) and specificity (1−FPR). Rates are averaged over 35 permutations of our training∕test subjects. Average TPR, FPR, FNR, and TNR across all test subjects for several values of P_cut are tabulated in the insets of Fig. 8.

Figure 8.

(a) Average ROC curve for all healthy and tumor voxels for each of 35 test subjects. [(a), inset] Classification rates calculated using all voxels from cancerous and healthy tissue, as defined by our gold standard. Black diamonds mark TPR[P_cut] vs FPR[P_cut] values for P_cut given by the numeric labels. (b) Rates calculated only using the N_v=40 training voxels from each region in each subject. [(b), inset] Average classification rates calculated over N_v voxels. (Insets) Mean TPRs, FPRs, FNRs, and TNRs as a function of P_cut. Healthy voxels are defined as P[M]≤P_cut. Note that a low FNR is desirable for cancer diagnosis. Rates are averaged over all test subjects used in the leave-one-out protocol and given as percentages.

For the purposes of cancer detection, FNR is critical, as this determines how many cancers are missed. With the sample used in this analysis, a probability cutoff of P_cut=0.95 yields FNR of 11%. At the same cutoff, 89% of the voxels predicted to be cancerous are correctly classified (TPR) and 6% of the voxels in the healthy region are incorrectly predicted to be cancerous (FPR), while the remaining 94% of the healthy region voxels are correctly labeled. The cutoffs can be tuned to suit particular clinical needs (see insets in Fig. 8 for classification rates corresponding to other values of P_cut).

Since the Z-score is in “units” of standard deviation, we can directly compare the magnitudes of the derived coefficients $\vec{\beta }$ to determine the relative importance of each parameter for identifying malignancy. Averaging over 35 combinations of 34 subjects in the training set gives, ⟨β_zHb_t⟩=0.83±0.06, ⟨β_zStO₂⟩=−0.19±0.04, and $⟨{\beta }_{z{\mu }_s^{\prime }}⟩=2.68\pm 0.12$,³⁷ suggesting that of the three optical parameters, the difference in ${\mu }_s^{\prime }$ offers the strongest evidence of malignancy. It should be noted that the weights are coefficients derived from a logistic regression model and can be interpreted precisely in terms of changes in the log odds of malignancy. For example, a one unit change in $z{\mu }_s^{\prime }$ implies an estimated 2.7-fold increase in the log odds of malignancy for that voxel or, equivalently, a 14.9-fold increase in the odds of malignancy. However, when $\vec{\beta }$ is calculated across all 35 subjects, we find the significance (“p value”) of each element in $\vec{\beta }$ to be <0.005, suggesting that all three parameters should be retained in the model.

The analysis described above assumes that each 2×2×2 mm voxel in the 3D tomogram is independent of the others. However, it is well known that the spatial point spread function of light transport in tissue limits DOT spatial resolution to ∼0.5–1 cm (Refs. ^{32, 33, 34, 35}) in breast tissue at biological contrast levels. Furthermore, there are likely to be physiological correlations between different spatial locations in the breast (e.g., all voxels drawn from adipose tissue). We explored a simple model of correlated voxels, in which we identified “clumps” of the same size as the tumor in each breast and then compared the average value of the probability of malignancy in these clumps to that of the tumors. Interestingly, we found the distribution of P[M] to have fewer outliers than Fig. 7 and values in the confusion matrix to be within ∼±5% of the per-voxel values presented in the insets of Fig. 8 at P_cut=0.95.

DISCUSSION

This study suggests that multisubject, multivoxel, multiparameter statistical analysis of diffuse optical data is potentially quite useful. Using a relatively simple statistical classification approach, we have reproduced most of the results described in Ref. 15. Furthermore, a lengthy analysis by a skilled researcher was not required and several different cancer types were included (see Table 1). Initial results also suggest that this type of data analysis may be useful for suppression of image artifacts, but we have not yet systematically studied the issue. Interestingly, in the small number (3, see Table 1) of in situ cancers contained in our sample, we have noted a lower value of the malignancy parameter M than for the more common invasive cancers (see Fig. 5 for an example).

In Sec. 3, we noted $\left|⟨{\beta }_{z{\mu }_s^{\prime }}⟩\right|>\left|⟨{\beta }_{z{\text{Hb}}_t}⟩\right|>\left|⟨{\beta }_{z{\text{StO}}_2}⟩\right|$, and therefore $z{\mu }_s^{\prime }$ is the most important parameter for identification of malignancy, followed by zHb_t. The value of ${\beta }_{z{\mu }_s^{\prime }}$ and β_zHbt differed little between training sets. ⟨β_zStO₂⟩, on the other hand, was both smaller than the other coefficients and had a much larger variation between subjects (∼20% vs ∼5%). StO₂ is thus less important for differentiation of malignant regions in this data set, an observation consistent with earlier results.¹⁵

This preliminary study has several limitations. The most significant limitation is its small sample size. The current analysis uses a “leave-one-out” protocol. Future work with larger samples will use “leave-M-out,” for M>1, a better approach to probing the generalizability of the method.

A more subtle issue that deserves further exploration was our assumption that each voxel used in the training is independent. As we discussed at the end of Sec. 3, we expect spatial correlations from both biological sources and reconstruction artifacts from DOT mammography. The logistic regression classification scheme assumes independent measurements; future work will utilize more sophisticated classifiers to take advantage of the biological correlation (e.g., between voxels from glandular tissue) and minimize the effects of correlation arising from DOT (e.g., resolution limits). The use of correlated measurements in the training set will result in underestimation of the variance in $\vec{\beta }$; however, our classifier does not use this variance: We only apply the point estimate of $\vec{\beta }$, which is unbiased even when the data are correlated, to the test set. Therefore, the classification rates remain valid even though we did not explicitly take into account potential correlation between adjacent voxels.

We also explored possible effects on this analysis technique from DOT resolution limits by eliminating the smallest tumors from our data set. The smallest tumor included in the sample has a total volume of 1.1 cm³ (139 voxels). The median separation between the N_v=40 randomly chosen voxels in this tumor is 0.85 cm with an interquartile range (IQR) of 0.71 cm; this separation is within the expected ∼0.5–1 cm resolution of the optical reconstruction technique. For comparison, in the same subject, the median separation in the N_v=40 healthy tissue voxels was 4.5 cm and the IQR 3.5 cm. We then repeated the leave-one-out protocol described above on a sample of the 31 subjects with tumor volume greater than 2 cm³ (250 voxels). We found that the classification rates at P_cut=0.95 changed very little (i.e., ∼1%). Furthermore, $\vec{\beta }$ remained consistent within our calculated error. We also tested the possibility of overweighting small tumors through correlated measurements by extracting a fixed percentage (10%) of the total tumor voxels from each subject and using 10% of the total tumor voxels, up to a maximum of 40. These shifts in the training set selection changed the classification rates at P_cut=0.95 by only ∼2%. Alternately, we could select voxels from a sparse grid in the tissue regions to enforce a consistent or minimal voxel separation.

To test the effects of our random voxel selection, we repeated our analysis on the data sample five times, randomly selecting new training voxels with each iteration. The standard deviations of $\vec{\beta }$ extracted from the entire training set were σ_β0=2%, ${\sigma }_{{\beta }_{z{\mu }_s^{\prime }}}=6\mathrm{\%}$, σ_βzHbt=11%, and σ_βzStO2=29%. Recall that β_zStO2 had the smallest magnitude and most variation between different training sets (∼20%).

Another potential source of error is the imperfect tissue segmentation we relied upon as the gold standard for assignment of each voxel as healthy or cancerous. This segmentation relies upon both nonconcurrent clinical imaging (e.g., MRI) to locate the tumor and a region growing algorithm on each subject’s optical tomogram to define the tumor boundaries, therefore potentially introducing discrepancies in the tissue segmentation. We excluded a 2 cm thick boundary region about each tumor from the corresponding healthy region to reduce effects of errors in spatial localization of the tumor boundary on the training healthy tissue data.

Although the analysis includes more spatial data than typically used, most of the data were still discarded, i.e., N_v=40⪡4.5×10⁴ voxels drawn from the healthy region in each subject. We chose this limit for data selection in order to weight tumor and healthy regions equally and take only ∼30% of voxels from the smallest tumors. Furthermore, this choice permits a more intuitive interpretation of P[M] and improves quantification of classification accuracy. We are currently exploring other weighting schemes which permit use of all or most of the healthy tissue voxels. Additionally, no healthy subjects or benign lesions were included in the present sample; inclusion might raise false positive rates, as the relative optical properties of some benign tumors overlapped those of cancers in our previous work.¹⁵

Logistic regression is a fairly simple binary classification scheme, which permits use of both continuous and classification variables. The analysis presented here did not include other classification variables (menopausal status, age, etc.), as our total sample is fairly small. For the same reason, we did not attempt to separate cancer types; we will apply such analysis to larger samples in future work. More sophisticated classification techniques, for example, could include more than two output categories (e.g., image artifact, malignant, benign, and healthy regions); again, sufficiently large data sets will permit us to differentiate between types of benign and malignant lesions. Additionally, we will apply a variation in this technique to larger samples (e.g., nonimaging studies of many subjects) and more complete data sets (e.g., concurrent optical∕MR imaging). Finally, future work will implement classification approaches such as support vector machines or neural networks that have demonstrated better predictive capability in other applications, as in Klose et al.¹⁶

CONCLUSION

The potential for population-based statistical image processing of diffuse optical data using logistic regression of three optically measured physiological parameters (Hb_t, StO₂, and ${\mu }_s^{\prime }$) and a leave-one-out paradigm for 35 subjects was demonstrated. Our voxel-level diagnosis produced an average TPR of 89% and FPR of 11% with no human interpretation of test data set required. These results are a starting point for development of diffuse optical tomography CAD algorithms. Such multiparameter optical signatures of cancer may enhance the utility of an adjunct or standalone optical device in the clinical imaging environment.