Minimum Knowledge Base for Predicting Organ-at-Risk Dose-Volume Levels and Plan-Related Complications in IMRT Planning

Abstract

IMRT treatment planning requires consideration of two competing objectives: achieving the required amount of radiation for the planning target volume and minimizing the amount of radiation delivered to all other tissues. It is important for planners to understand the tradeoff between competing factors so that the time-consuming human interaction loop (plan-evaluate-modify) can be eliminated. Treatment-plan-surface models have been proposed as a decision support tool to aid treatment planners and clinicians in choosing between rival treatment plans in a multi-plan environment. In this paper, an empirical approach is introduced to determine the minimum number of treatment plans (minimum knowledge base) required to build accurate representations of the IMRT plan surface in order to predict organ-at-risk (OAR) dose-volume (DV) levels and complications as a function of input DV constraint settings corresponding to all involved OARs in the plan. We have tested our approach on five head and neck patients and five whole pelvis/prostate patients. Our results suggest that approximately 30 plans were sufficient to predict DV levels with less than 3% relative error in both head and neck and whole pelvis/prostate cases. In addition, approximately 30–60 plans were sufficient to predict saliva flow rate with less than 2% relative error and to classify rectal bleeding with an accuracy of 90%.

1. Introduction

Computerized planning for intensity-modulated radiation therapy (IMRT) is a complex process involving a large amount of input data and vast numbers of delivery variables whose calculation for a given patient may pose significant computational challenges. IMRT problems are further complicated by the fact that they are multi-objective and thus must take into account a trade-off between the competing goals of delivering the required radiation dose to the planning target volume (PTV) and minimizing the amount of radiation delivered to all other tissues. These dose distribution tradeoffs lead to one of the key limitations in current IMRT planning: the conventional IMRT treatment planning paradigm consists of an inefficient and time-consuming process of employing numerous plan-evaluate-modify cycles in a trial-and-error process. Successive planning cycles are based on conjecture rather than on explicit knowledge of the multi-dimensional plan surface (which reflects the behavior of plan properties as a function of planner input specifications).

Investigators have proposed the concept of generating a multitude of plans and sorting/ranking these plans through various metrics. Previous investigations in this area include Gopal and Starkschall (2002), which presents various two-dimensional plan comparison visualizations, Rosen et al (2005), which deals with conformal radiotherapy and emphasizes graphically-guided adjustments to base plans, Zhang et al (2006), which focuses on sensitivity analysis issues and, as in the earlier work by Yu (1997) and by Xing et al (1999) develops mechanisms for multi-parametric adjustments that seek to construct a sequence of treatment plans that converge to a pre-specified set of goals. Our own multi-plan framework provides the generation and ranking of many plans for a given patient without planner intervention between plans (Meyer et al 2007). Romeijn et al (2004) showed the mathematical equivalence of Pareto surfaces based on alternative metrics, and Craft et al (2007) discussed the invariance properties of Pareto surfaces. The Pareto surface approach is applied to IMRT cases by formulating the problem as multi-objective/multi-criteria optimization problem. A pre-calculated plan database can be generated using Pareto optimality and Pareto surface can be presented to a treatment planner to visualize/navigate through the plans (Küfer et al 2000, Schreibmann et al 2004, Thieke et al 2004, Aubry et al 2006, Hoffmann et al 2006). The question of how many plans are sufficient to appropriately model the Pareto surfaces was addressed by Craft and Bortfeld (2008). Das (2009) proposes a non-Pareto approach for generating optimized plan sequences in order to enable the planner to obtain a satisfactory plan and understand the trade-off between structures; generation of an optimal treatment plan for the patient is not guaranteed because dose-volume (DV) constraints are not handled explicitly.

A limitation in current treatment planning is that the relationship between the achieved plan dose or DV levels and the dose or DV constraint settings is not known apriori. The achieved DV levels for an organ-at-risk (OAR) are frequently not equal to the input DV constraint settings even in the case that the constraint settings for that OAR are met. Desired outcomes, such as achieved DV levels or plan-related complication levels, are not readily achieved by trial-and-error manipulations of the formulations of the objectives and constraints.

A further important aspect of treatment planning is the consideration of OAR complications following radiation therapy. Current planning systems typically rely on dose and dose-volume measures, which are surrogates for clinical complications. Zhang et al (2009) model achieved DV levels as a function of input dose and DV constraints, extending the multi-plan framework of Meyer et al (2007).

Being able to identify relationships between the input DV constraint settings and achieved plan DV levels apriori would eliminate the trial-and-error manipulations in treatment planning. However, the computational burden associated with modeling the IMRT plan surface is significant. Craft and Bortfeld (2008) have investigated the minimum knowledge base for Pareto surfaces. In this work we introduce an empirical approach to determine the minimum knowledge base (minimum number of computed treatment plans) required to build accurate representations of the IMRT plan surface in order to predict (via machine learning (ML)) OAR DV levels corresponding to a single OAR as a function of input DV constraint settings corresponding to all involved OARs. Further, we also seek to determine the minimum knowledge base associated with predicting plan-related OAR complications as a function of the input DV constraint settings, taking into account previously established relationships between OAR DV levels and complications. The IMRT plan surface created from this limited knowledge base allows plan quality to be pre-determined from input DV settings without the explicit generation of the corresponding plan.

2. Methods and Materials

Our approach to determining the knowledge needed to predict DV levels and plan-related OAR complications employs ML algorithms. We selected two commonly encountered IMRT treatment sites: (1) head and neck and (2) prostate.

2.1. Multi-Plan Framework Knowledge Base

A multi-plan framework was used to generate the full knowledge base, of which part was used in training (i.e., model development) and the rest in validation (i.e., establishment of accuracy measurements) of the prediction of one OAR DV level or complication as a function of DV constraints corresponding to all involved OARs in the case. This knowledge base was generated by varying the DV constraint settings for each OAR and computing an optimized treatment plan for each choice of settings. Our approach was tested on five head and neck and five whole pelvis/prostate cases. For each of the five cases of each disease site, the prescription dose and the collection of OAR DV constraint settings employed were the same.

One hundred twenty-five (125) plans comprising the full knowledge base were generated for each of the head and neck cases by varying the input DV constraints corresponding to the OARs (left parotid, right parotid and spinal cord). For each OAR, five separate sets of input DV constraints were considered. The input dose constraints for 33% and 66% of the parotids were varied from 26–38 Gy and 20–32 Gy, respectively in 3 Gy increments. Similarly the maximum dose constraint on the spinal cord was varied from 33–45 Gy. (Here we have 5 dose-volume levels and 3 OARs, 5³ = 125 plans). The prescription dose to the target was the protocol published by Lee et al (2007) for head and neck cases, which is 70 Gy to the gross tumor volume (GTV), 59.4 Gy to the high-risk clinical target volume (CTV) and 54 Gy to the low-risk CTV.

Two hundred fifty-six (256) plans were generated for each of the whole pelvis/prostate cases by varying the input DV constraints on the rectum, bladder and small bowel. At our institution, it is common practice to treat the whole pelvis to a dose of 45 Gy while the prostate dose is escalated to 75.6 Gy. DV constraint settings were prescribed according to the Radiation Therapy Oncology Group (RTOG) 0126 protocol. An initial set of 64 plans was generated in which the target involved the prostate plus nodal volumes (prescription dose of 45 Gy). The input dose constraints for 25% and 50% of the rectum were varied from 41–47 Gy and 35–41 Gy; 25% and 50% of the bladder were varied from 38–44 Gy and 31–37 Gy; 30% of the bowel were varied from 11–17 Gy respectively in 2 Gy increments. (Here we have 4 dose-volume levels and 3 OARs, 4³ = 64 plans). Subsequently a set of four boost plans were generated in which the target involved the prostate alone (prescription dose of 30.6 Gy). The input dose constraints for 25% and 50% of the rectum and bladder were varied from 29–30 Gy, 25–26 Gy, 27–28 Gy and 24–25 Gy, respectively in 1 Gy increments. (2 dose-volume levels and 2 OARs, 2² = 4 plans). The combination of all initial plus boost plans resulted in 256 possible plans.

The input constraint settings for head and neck and whole pelvis/prostate cases are summarized in Table 1 (Only unit weighting factors for each DV constraint setting are considered). In addition, homogeneity constraints, such as at most 5% of the tumor should receive 108% of the prescription, are also imposed. Minimum target dose is restricted at 95% of the prescription. This full knowledge base, generated through an automated script within the planning system (Pinnacle³, Philips Medical Systems, Cleveland, OH) without planner intervention, takes approximately 20–24 hour to be generated. We investigate if a much smaller knowledge base is adequate for the development of models that allow accurate predictions of achieved OAR DV values and complications for virtual plans that need not be generated unless their predicted properties are deemed satisfactory.

Table 1.

Dose ranges of constraint settings on different volume levels for head and neck and whole pelvis/prostate cases

Head/Neck	33% Left Parotid	66% Left Parotid	33% Right Parotid	66% Right Parotid	Max Cord
	26–38 Gy	20–32 Gy	26–38 Gy	20–32 Gy	33–45 Gy
Pelvis	25% Bladder	50% Bladder	25% Rectum	50% Rectum	30% Bowel
	41–47 Gy	35–41 Gy	38–44 Gy	31–37 Gy	11–17 Gy
Prostate	25% Bladder	50% Bladder	25% Rectum	50% Rectum
	29–30 Gy	25–26 Gy	27–28 Gy	24–25 Gy

2.2. Knowledge Base Investigation via Machine Learning (ML)

In this work, our goal is to find the minimum computational effort needed to identify the relationship between the inputs (DV constraint settings referred to as features) corresponding to all involved OARs and the outputs, such as achieved OAR DV levels and plan-related complications (referred to as properties). ML algorithms (Kotsiantis 2007, Zhang et al 2009) are employed to obtain functions F and G as follows,

$$\begin{array}{c}{\mathit{\text{DV Levels}}}_{\mathit{\text{OARi}}}=F({\mathit{\text{features}}}_{\mathit{\text{OAR}}1},{\mathit{\text{features}}}_{\mathit{\text{OAR}}2},\dots ,{\mathit{\text{features}}}_{\mathit{\text{OARn}}})\hfill \\ {\mathit{\text{Complications}}}_{\mathit{\text{OARi}}}=G({\mathit{\text{features}}}_{\mathit{\text{OAR}}1},{\mathit{\text{features}}}_{\mathit{\text{OAR}}2},\dots ,{\mathit{\text{features}}}_{\mathit{\text{OARn}}})\hfill \end{array}$$

where i corresponds to the OAR whose plan properties are being modeled and n corresponds to the number of involved OAR constraint settings.

The goal of ML in this work is to build and validate the numerical prediction or decision models from the knowledge base. The knowledge base is the collection of plans arising from our multi-plan framework coupled with properties of those plans.

2.3. Prediction of OAR DV Levels

IMRT treatment planning involves the specification of DV constraints, but differences between the DV values specified in the input to the treatment planning system and the actual DV values achieved in the resulting plans are difficult to estimate in the absence of a model that approximates the functional relationship between these two sets of values. We model the achieved plan DV levels as a function of the DV constraint settings by using a limited number of plans from the full knowledge base. The DV levels that we modeled such as D24 (dose received by 24% of the OAR), D33, D45 and D66 corresponding to the parotid glands in head and neck IMRT and D25 and D50 corresponding to the rectum in prostate IMRT were chosen because they correlated with complications in previous studies.

The achieved DV levels for a single OAR corresponding to the virtual plans were modeled as a function of the DV constraint settings corresponding to all involved OARs (including the OAR in question). Augmentation of input DV constraint-setting data is performed in order to obtain nonlinear functions of this data to be used in the ML framework. For example, if there are two input constraint settings referred as feature₁ and feature₂, five terms are input to the ML algorithm (feature₁, feature₂, ${\mathit{\text{feature}}}_1^2,{\mathit{\text{feature}}}_2^2$ and feature₁ · feature₂). We refer to these augmented data sets as a function of the input features, q(features). Then, referring to achieved DV levels in the virtual plans as plan properties, and DV constraint settings as features, the ML prediction process may be summarized mathematically as the construction of functional models f_i that approximate the relations:

$${\mathit{\text{Property}}}_{\mathit{\text{OARi}}}=f_i(q({\mathit{\text{feature}}}_{\mathit{\text{OAR}}1},{\mathit{\text{feature}}}_{\mathit{\text{OAR}}2},\dots ,{\mathit{\text{feature}}}_{\mathit{\text{OARn}}}))$$ (1)

where i corresponds to the OAR whose DV levels are being modeled and n corresponds the number of the involved OAR constraint settings.

2.4. Prediction of OAR Complications

Dose and DV measures are surrogates for OAR complications. Previous clinical trials have established relationships (derived retrospectively) between plan DV levels and OAR complications. We focused on the minimum knowledge base needed to predict two plan related OAR complications: xerostomia and rectal bleeding. Prior research on the relationship of achieved plan DV levels to these complications is summarized in the following sections, and serves as ground truth in our prediction models.

2.4.1. Prediction of Saliva Flow Rate

Doses corresponding to 66%, 45%, and 24% of parotid gland volumes were determined to be correlated with saliva flow rate (Eisbruch et al 1999, 2001). They also provide a EUD-exponential model to estimate saliva flow rate. We use this EUD-exponential model as ground truth for determining the saliva flow rate corresponding to all 125 IMRT treatment plans (full knowledge base) in each head and neck cases. The saliva flow rate (mL/min) is normalized relative to that before treatment. The model is

$$H=[\mathit{\text{exp}}(-A·{\mathit{\text{EUD}}}_L-B·{\mathit{\text{EUD}}}_L^2)+\mathit{\text{exp}}(-A·{\mathit{\text{EUD}}}_R-B·{\mathit{\text{EUD}}}_R^2)]/2$$ (2)

where A and B are fitted parameters, H is the expected resulting fractional saliva output, and EUD is the equivalent uniform dose to the left and right parotids.

The saliva flow rate corresponding to a virtual plan in this work was modeled as a function of the DV constraint settings:

$$\mathit{\text{Flow Rate}}=g(q({\mathit{\text{feature}}}_{\mathit{\text{OAR}}1},{\mathit{\text{feature}}}_{\mathit{\text{OAR}}2},\dots ,{\mathit{\text{feature}}}_{\mathit{\text{OARn}}}))$$ (3)

We used a sequential minimal optimization (SMO) algorithm (a ML algorithm) for training a support vector regression model in order to obtain the function used to predict this continuous value from the treatment input constraint settings. Details of the SMO algorithm as relevant to modeling saliva flow rate can be found elsewhere (Zhang et al 2009).

2.4.2. Prediction of Rectal Bleeding

Literature reviews by Jackson (2001) and Yorke (2003) suggest that the fraction of the rectum receiving doses from 50 Gy to 70 Gy are most correlated to rectal bleeding. Good categorical prediction accuracy was obtained in the prediction of this complication by using only the original input features in a model of the form:

$$\mathit{\text{RectalBleedingCategory}}=h({\mathit{\text{feature}}}_{\mathit{\text{OAR}}1},{\mathit{\text{feature}}}_{\mathit{\text{OAR}}2},\dots ,{\mathit{\text{feature}}}_{\mathit{\text{OARn}}})$$ (4)

The method employed to generate the binary classification function h is an optimized decision tree (see Zhang et al (2009) for details). We use a threshold of 25% rectal volume and 70 Gy for binary classification of rectal bleeding.

2.5. Empirical Determination of the Minimal Knowledge Base

We introduce an empirical approach to determine the minimal knowledge base size (minimum number of computed plans) needed to build accurate representations of the IMRT plan surface. Our approach involved successively reducing the size of the assumed explicitly computed knowledge base, referred to as the training data to build the machine learning model and then evaluating the model on the remaining data, referred to as the testing data. The training data is used to build the model (to obtain functions (see equations 1, 3 and 4)), and then the model is applied to the testing data to determine model accuracy. The size of the training data thus corresponds to the assumed computed knowledge base required to obtain the model. Knowledge bases of various sizes (comprising subsets of the full knowledge base) were used to determine the sizes needed to obtain accurate plan surface models and accurate complication predictions. The testing data consisted of the full knowledge base less the number of plans in the training data set. We used knowledge bases corresponding to 15, 30, 62, and 125 plans in the training data for the head and neck case and 16, 32, 64, 128, 256 plans for the whole pelvis/prostate case. Plans corresponding to DV constraint settings that defined the upper limits of constraints as well as plans corresponding to the lower limits were always included in the training data set.

To obtain accurate statistical measures of our method, for each training data size and each patient, fifty instances of random samples were tested and the results corresponding to the average, quartiles and confidence intervals over the testing data sets were determined. For example, when using 15 plans in the training data, a single sample consisted of 15 plans randomly selected from the total 125 plans to build the model. The model was tested on the rest of the 110 plans. This process was repeated 50 times (each time 15 different plans were randomly selected) to obtain the average result. Relative prediction error for continuous values (achieved DV levels and saliva flow rate) and correct prediction percentage for categorical values (grade 2 rectal bleeding complication) were analyzed, including mean, median, quartiles and confidence interval on medians.

3. Results

The results reported below for machine learning algorithms are the mean testing errors (for continuous variables) and the mean correct prediction percentages (for categorical variables) on the testing data sets. We summarize results of 250 trials (50 trials for each of the five patients) for each knowledge base size of the machine learning algorithm. If full knowledge base was used as training data (e.g. 125 plans for head and neck patients or 256 plans for prostate patients), the average of the modeling errors (only based on training data sets) of the five patients were reported.

3.1. Head and Neck Cases

3.1.1. Prediction Results of Parotid DV Levels

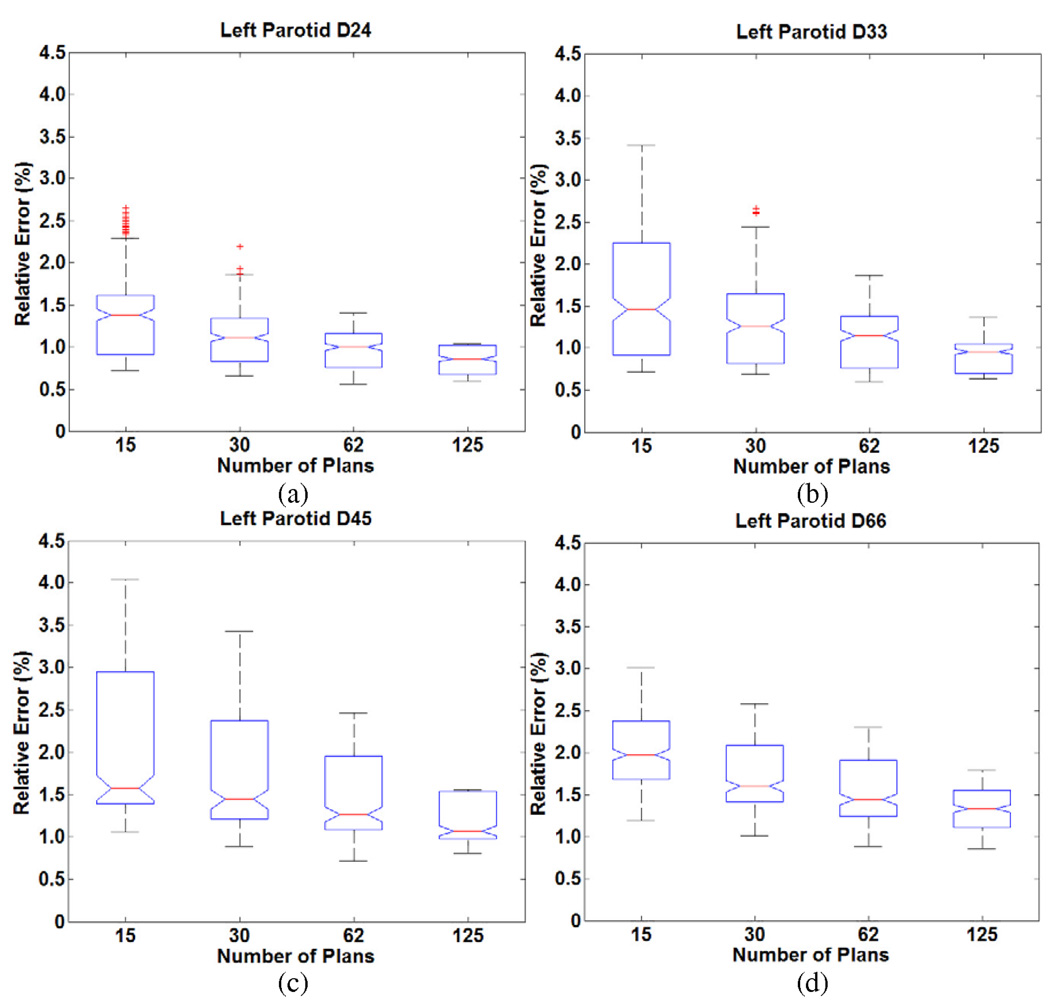
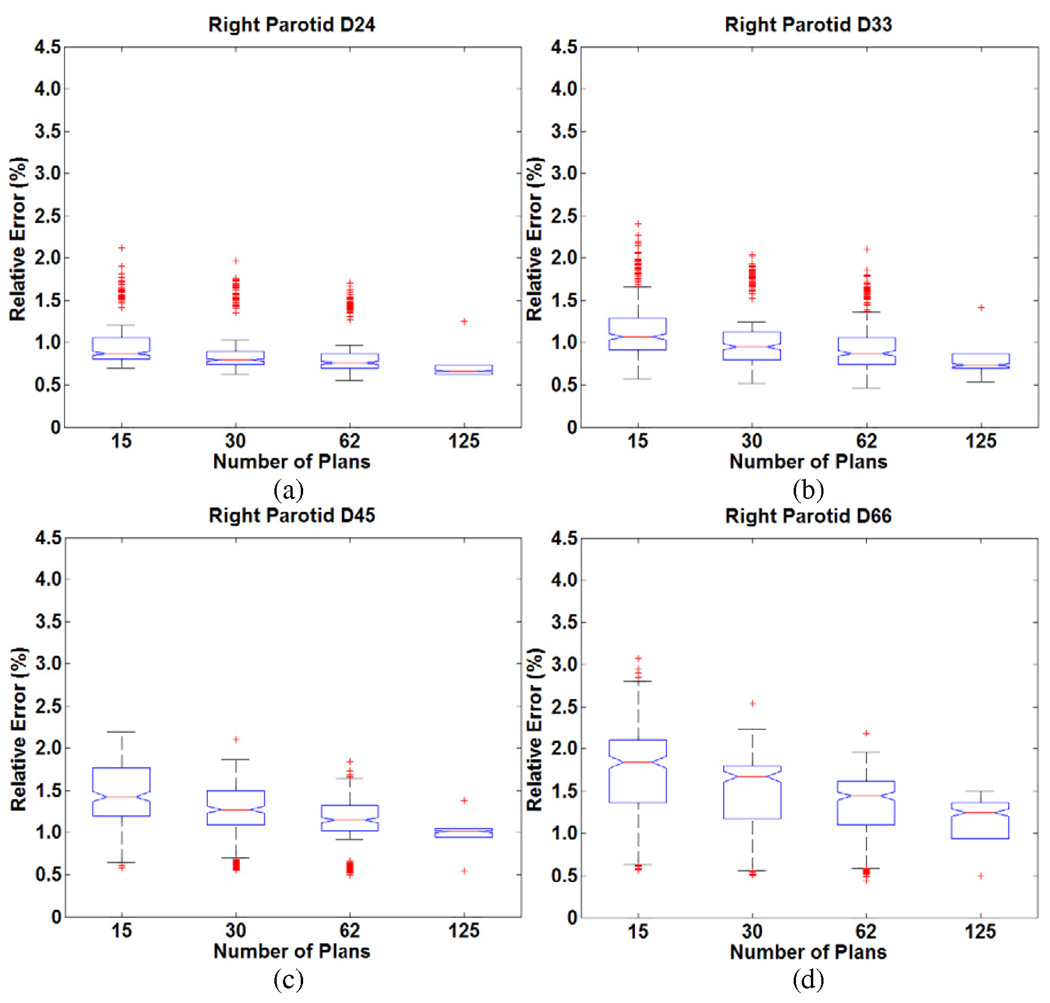
We consider the results for the five head and neck cases. Figure 1 and Figure 2 show the distribution of errors in predicting DV levels (D24, D33, D45, D66) of left and right parotid respectively. The line in the middle of each box in the figures is the median of the mean errors of the predictions, and the lower and upper edges of boxes represent 25% and 75% quartiles over the 50 runs in five cases. The whiskers are extreme ranges of the predictions (as explained below). The points outside the whiskers are outliers. The extreme ranges were decided as follow: points are shown as outliers if they are larger than 2q₃ − q₁ or smaller than 2q₁ − q₃, where q₁ and q₃ correspond to the 25th and 75th percentiles, respectively. The notches within the boxes are 95% confidence intervals on the median. The errors increase when the knowledge base sizes decrease, but remain acceptably small over a wide range of knowledge bases. For each head and neck patient, when using different knowledge base sizes, the errors ranged from less than 1% to slightly more than 3% in predicting DV levels of parotids. From patient to patient, the variation was ≤ 2%. Note that the ranges of errors also increase when the knowledge base sizes decrease. This means the model stability decreases for smaller knowledge bases. Overall, 30 plans were sufficient to predict achieved DV levels of parotid with less than 3% relative error.

Figure 1.

Distribution of relative errors in predicting DV levels (a) D24 (b) D33 (c) D45 (d) D66 for the left parotid in the head and neck cases as a function of knowledge base size. (The middle line is the median of the mean errors of the predictions; lower and upper edges of boxes represent 25% and 75% quartiles; whiskers are the extreme ranges of the predictions.)

Figure 2.

Distribution of relative errors in predicting DV levels (a) D24 (b) D33 (c) D45 (d) D66 for the right parotid in the head and neck cases as a function of knowledge base size.

3.1.2. Prediction Results of Saliva Flow Rate

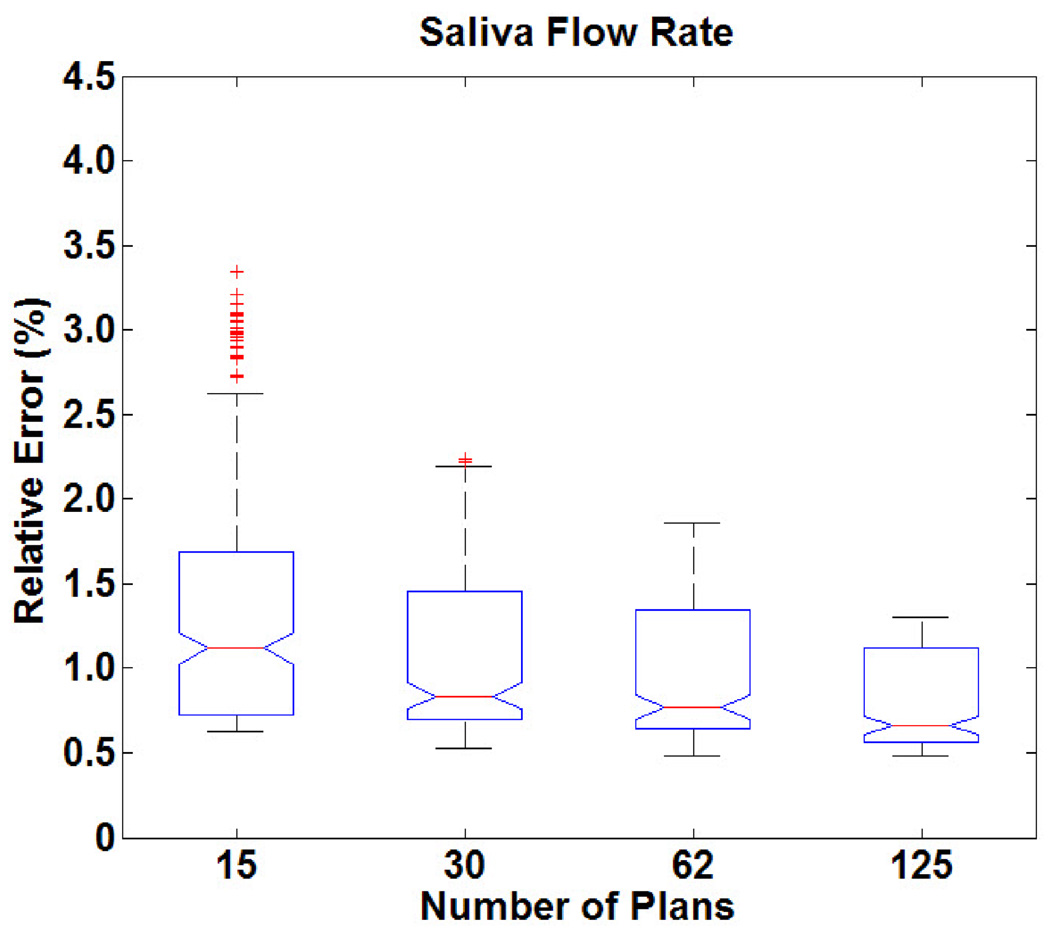
Figure 3 shows the distribution of errors when predicting saliva flow rate. The performance of our approach is very stable when predicting saliva flow rate (error always less than 2%). The variation from patient to patient was also ≤ 2%. From Figure 3, it is seen that when the knowledge base size decreases, there are more prediction outliers (more outlier occurrences in the model validation process). Our results suggest that 30 plans were sufficient to predict saliva flow rate with less than 2% relative error.

Figure 3.

Distribution of relative errors in predicting saliva flow rate as a function of knowledge base size.

3.2. Whole Pelvis/Prostate Cases

3.2.1. Prediction Results of Rectum DV Levels

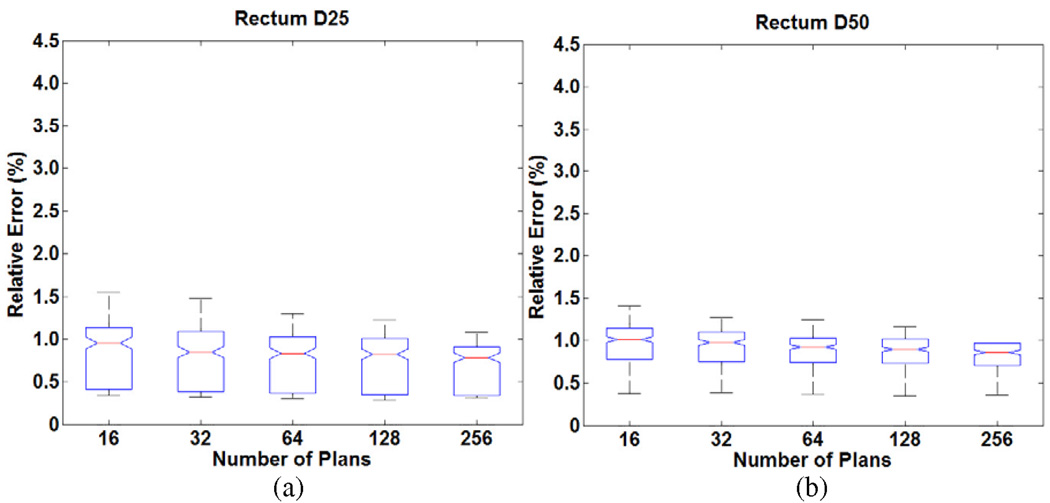
For the full set of five whole pelvis/prostate patients, Figure 4 shows the plot of distribution of prediction errors. The prediction results for rectum DV levels (D25 and D50) are very stable compared to predicting DV levels of parotids in the head and neck cases. The errors ranged from less than 1% to a little more than 1%. This range is tighter than predicting DV levels of the parotids, which means higher accuracy was achieved for the rectum than the parotid. 32 plans were sufficient to predict achieved DV levels of rectum with less than 2% relative error.

Figure 4.

Distribution of relative errors in predicting DV levels (a) D25 (b) D50 for the rectum in the prostate cases as a function of knowledge base size.

3.2.2. Prediction Results of Rectal Bleeding

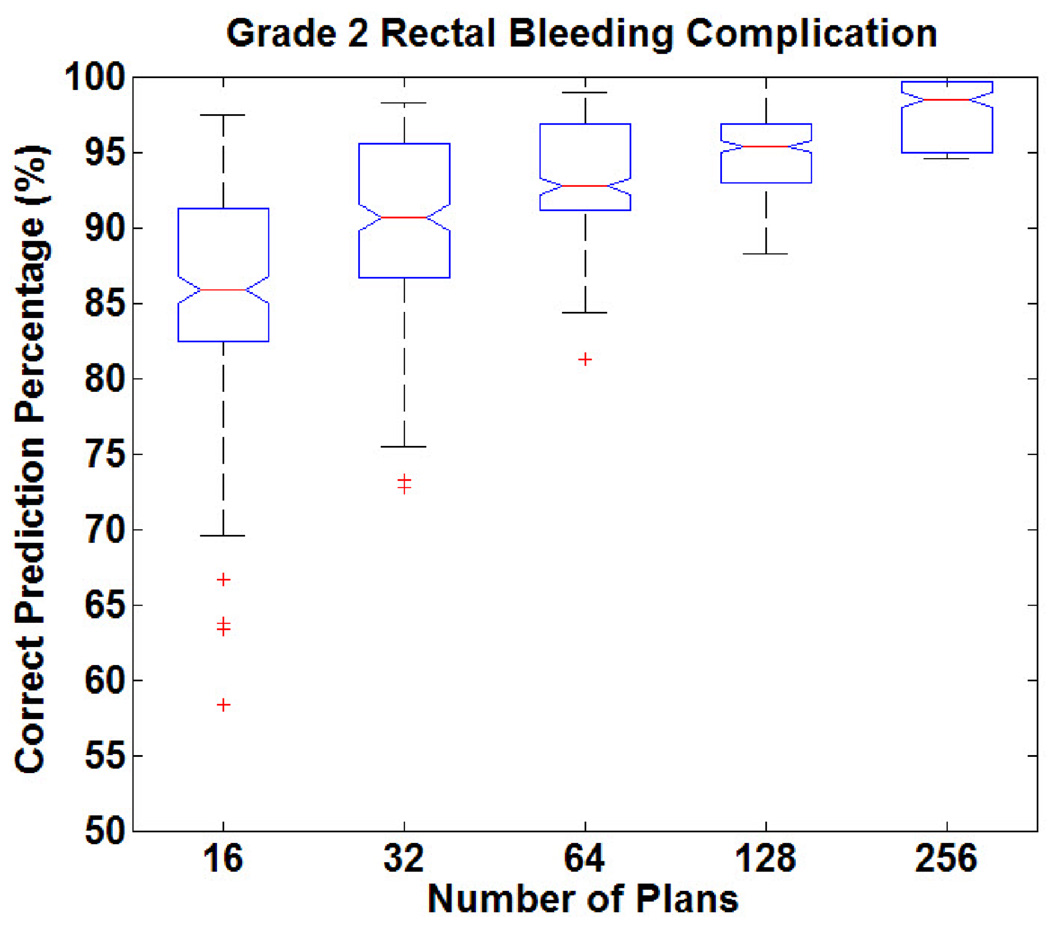
Figure 5 shows the distribution of prediction accuracy in predicting rectal bleeding complications (formulated as a binary classification). The correct prediction percentage for rectal bleeding (using previously established relationships between OAR complications and DV levels) as a function of DV constraint settings ranged from 80% to 98%. When the knowledge base decreases, not only does the accuracy decrease, but low-accuracy outliers (less than 70% correct prediction percentage) appear as well. Overall, rectal bleeding complications can be predicted with greater than 90% accuracy using 64 plans.

Figure 5.

Distribution of correct prediction percentages in classifying rectal bleeding as a function of knowledge base size in the prostate cases.

4. Discussion

The purpose of this work was to determine the minimal knowledge base of explicitly computed IMRT treatment plans needed in order to build accurate representations of the IMRT plan surface in order to predict OAR DV levels and complications corresponding to a single OAR as a function of input DV constraint settings corresponding to all involved OARs in the plan. Our results suggest that 30–60 explicitly computed plans are needed in order to model the plan surface and to obtain models that yield accurate prediction of OAR DV levels and plan-related complications. Following the generation of the plan surface, virtual plan data can be implicitly generated without actual plan computation.

The gains achieved by modeling via a small number of plans rather than the full knowledge base are the savings in computation times, especially considering the number of cases for which IMRT treatments are needed at any given time in a typical clinic. Reducing the computational burden makes extending this approach to a larger number of IMRT cases tenable. The tradeoff between competing OAR DV constraint settings can be evaluated by navigation of the virtual plan surface. With this decision support system, a planner can determine inputs that will lead to a desirable plan. Thus, repetitive plan-evaluate-modify cycles can be eliminated. In this work, we only consider unit weighting factors for each dose-volume constraint setting. Consideration of additional weighting factors will increase the dimensionality of the problem and we plan on investigating the minimum knowledge area with an increased number of features in future work.

It is known that the achieved DV levels for an OAR are frequently not equal to the DV constraint settings (Zhang et al 2009). Without a suitable knowledge base of plans for a given patient it is generally impossible to determine the DV constraint setting ranges for each OAR that will yield the desired output values (and consequently avoid OAR complications). Reese et al (2009) has shown that doses cannot be removed from the normal tissues surrounding the target when planning parameters are adjusted; they can only be redistributed among OARs while keeping the target dose constant. They highlight the point that when a treatment planner aims to lower the dose in a specific part of the patient there must be a commensurate increase in dose in another part of the patient. Our research determines the minimum knowledge base needed to determine the inter-relationship between DV constraint settings corresponding to the OARs and can help the planner obtain the knowledge of how the doses will be redistributed within the patient when he/she adjusting the input constraints.

Other investigators have used the Pareto surface to deal with the issue of multi-criteria IMRT optimization (Lahanas et el 1999, Küfer et al 2000, Cotrutz et al 2001, Craft et al 2005, Craft et al 2007, Craft and Bortfeld 2008). The Pareto surface is developed from optimal solutions of multi-objective optimization problem. Craft and Bortfeld (2008) show that approximately 75 plans in the knowledge base can limit the error in generating the Pareto surface to within 15%. The main difference between the Pareto surface and our plan surface is the object modeled by the surface. Each dimension of the Pareto surface corresponds to one of the objective terms of the overall multi-objective optimization problem, and the selection of these terms depends on the problem formulation. For our plan surface, each input dimension is one of the input DV constraint settings (more readily used and interpreted by treatment planners in clinical environments). The surface points of both approaches reflect the quality of the plans. Pareto surface points reveal the values of the multiple objective terms. The plan surface in this work describes the plan quality through achieved dose-volume levels and OAR complications of the virtual plans. While this work has focused on DV level and plan-related OAR complications, other quality measures such equivalent uniform dose or normal tissue complication probability can be incorporated into our formulation.

A limitation of the Pareto surface is that it requires each term of the multi-objective optimization problem and the feasible space to be convex so that the resulting Pareto surface is convex. This limits the formulation and DV constraints that could be applied to the optimization problem. Zhang et al (2009) have shown that plan surfaces may be non-convex in the case of plan-related rectal bleeding as a function of input DV constraint settings. Thus, our formulation of the plan surface in this work provides the flexibility of modeling non-convex surfaces. Generating either the Pareto surface or the plan surface can be time-consuming without utilizing high-throughput computing. Our results show that approximately 30–60 explicitly computed plans are sufficient to model the plan surface. We believe that with the introduction of multi-core and cluster hardware and eventually a multithreaded treatment planning infrastructure, the generation of this number of treatment plans will be readily accomplished in a 1–2 hour time frame or less.

In another approach, Das (2009) presents a fast (1–4 hour) non-Pareto approach for generating sequences of related plans and then combining plans to obtain a satisfactory plan. Each element of the plan sequence reduces dose to one OAR step-by-step until target coverage limits are violated. An advantage of the approach is efficiency because the optimization of each plan in the sequence is initiated from the solution of the previous solution in the sequence. In principle, this process is similar to the plan-evaluate-modify cycle, but is automated.

5. Conclusion

Approximately 30–60 explicitly computed IMRT treatment plans for a given case are sufficient to model the IMRT planning surface, i.e., the achieved OAR DV levels and plan-related OAR complications for an OAR as a function of the input DV constraint settings corresponding to all involved OARs in the plan, with relative errors of 2–3% or 90% classification accuracy.