Revealing Non-Covalent Interactions

Abstract

Molecular structure does not easily identify the intricate non-covalent interactions that govern many areas of biology and chemistry, including design of new materials and drugs. We develop an approach to detect non-covalent interactions in real space, based on the electron density and its derivatives. Our approach reveals underlying chemistry that compliments the covalent structure. It provides a rich representation of van der Waals interactions, hydrogen bonds, and steric repulsion in small molecules, molecular complexes, and solids. Most importantly, the method, requiring only knowledge of the atomic coordinates, is efficient and applicable to large systems, such as proteins or DNA. Across these applications, a view of non-bonded interactions emerges as continuous surfaces rather than close contacts between atom pairs, offering rich insight into the design of new and improved ligands.

1 Introduction

Chemical interactions between a protein and a drug, or a catalyst and its substrate, self-assembly of nanomaterials,^1,2 and even some chemical reactions,^3,4 are dominated by non-covalent interactions. This class of interactions spans a wide range of binding energies, and encompasses hydrogen bonding, dipole-dipole interactions, steric repulsion, and London dispersion.⁵ Molecular structure is governed by covalent, non-covalent, and electrostatic interactions, the latter two of which are the driving force in most biochemical processes. The three-dimensional molecular structure defines covalent bonds, however, non-covalent interactions are hidden within voids in the bonding network. Although there are several ways to view and analyze covalent and electrostatic interactions, an analogous method for non-covalent interactions is conspicuously missing. Such a method would aid understanding of the complex interactions between biomolecules, and the design of self-assembled materials and drugs, among others.⁶

In this work, we present an approach to map and analyze non-covalent interactions, requiring only molecular geometry information, which compliments existing methods for covalent and electrostatic interactions. Covalent bonds are intuitively represented using conventional Lewis structures.⁷ They can be visualized from properties of the electron density with modern quantum-mechanical models of bonding, such as the electron localization function (ELF)^8,9 and atoms-in-molecules (AIM) theory.^10–12 Also, purely electrostatic interactions can be analyzed using electrostatic potential maps.¹³ Non-covalent interactions are frequently visualized using distance-dependent contacts, generally without consideration of hydrogen atoms.^14–16 Hydrogen-bonds can be identified from the molecular geometry¹⁷ and from ELF,¹⁸ while grid-based calculations based on classical force fields are used to model other van der Waals interactions.¹⁹ Our approach outlined below, using the density and its derivatives, allows simultaneous analysis and visualization of a wide range of non-covalent interactions types as real-space surfaces and adds an important tool to a chemist's arsenal.

2 Theory

2.1 Background

The quantum-mechanical electron density, ρ, from which all chemical properties can, in principle, be obtained²⁰ is the key quantity in density functional theory (DFT). The reduced density gradient, coming from the density and its first derivative, ( $s=\frac{1}{2{(3{\pi }^2)}^{1/3}}\frac{\mid \nabla \rho \mid }{{\rho }^{4/3}}$) is a fundamental dimensionless quantity in DFT used to describe the deviation from a homogeneous electron distribution.^20–22 Properties of the reduced gradient have been investigated in depth in the process of developing increasingly accurate functionals.²³ In density tails (i.e. regions far from the molecule, in which the density is decaying to zero exponentially) the reduced gradient will have very large positive values. Conversely, the reduced gradient will assume very small values, approaching zero, for regions of both covalent bonding and non-covalent interactions.

2.2 Identifying Non-Covalent Interactions

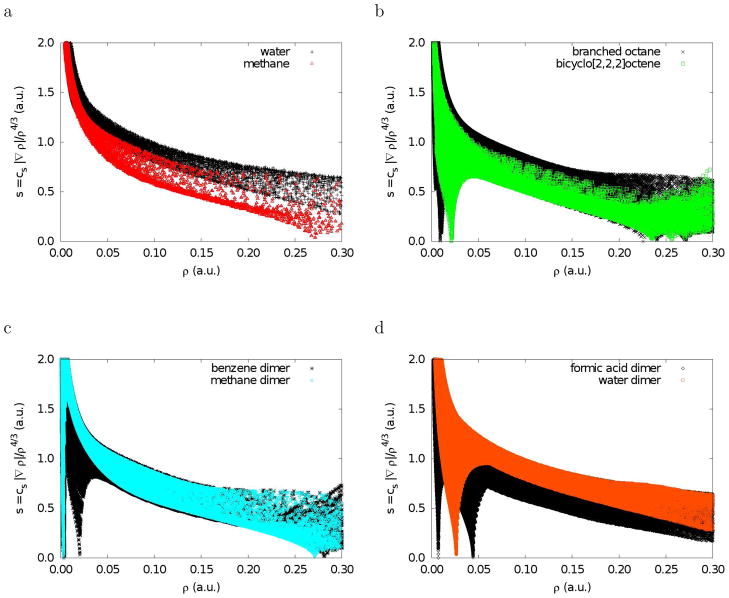
To explore the features associated with small reduced gradients, we first examine plots of s versus ρ (Figure 1). These plots were generated by evaluating the B3LYP^24,25 density and reduced gradients on cuboid grids, with a 0.1 au step size, for each molecule or dimer. To provide even more sampling of the small low-density, low-gradient regions in hydrogen-bonded complexes, additional calculations were performed for water and formic acid dimers with a much denser 0.025 au grid.

Figure 1.

Plots of the electron density and its reduced gradient for methane, water, branched octane, bicyclo[2,2,2]octene, and the homomolecular dimers of methane, benzene, water, and formic acid. The data was obtained by evaluating B3LYP/631G* density and gradient values on cuboid grids.

Plotting s versus ρ, as in Figure 1, reveals the basic pattern of intramolecular interactions. Methane (Fig. 1a) illustrates the typical covalent bond pattern. The top left-side points (small density and large reduced gradient) correspond to the exponentially-decaying tail regions of the density, far from the nuclei. The points on the bottom right side (density values of ca. 0.25 au and low reduced gradient) correspond to the C-H covalent bonds. Covalent bonds have a characteristic saddle point in the electron density (bond critical points^10–12), corresponding to s = 0. Regions near the nuclei have larger density values and appear beyond the right edge of the plot. The plot has an overall shape of the form aρ^−1/3 because atomic and molecular densities are piecewise exponential. The results for water are very similar, the only difference being that the covalent bonds lie at higher density values, past the edge of the plot. In Figure 1b-d, we consider six examples of chemical systems displaying various types of non-covalent interactions. Plots of s versus ρ for these systems all exhibit a new feature: one or more spikes in the low-density, low-gradient region, a signature of non-covalent interactions. The origin of this feature is made apparent by considering the formation of an intermolecular complex. The predominant change in the density-gradient profile occurs for the low-density region between the two monomers. The reduced gradient changes from very large values in the monomers to near zero upon dimer formation. This is the basis of our approach.

We also explored other ratios of density and gradient values. Indeed, the reduced gradient (regardless of the constant), the fundamental dimensionless variable in DFT, is also found to be the ratio of density and gradient values that most clearly isolates non-covalent interactions in real space (see supplementary information). In order for some ratio of the density and gradient of the form |∇ρ|/ρⁿ to be successful, it must distinguish between non-covalent interactions and the exponentially-decaying tails of the density that occur far from the molecular system. Both types of regions are characterized by low densities. In density tails, both the density and gradient approach zero exponentially. In regions of non-covalent interactions, the gradient will again approach zero and will be identically zero at the critical point.

To this point, we have found that non-covalent interactions can be isolated as regions with low density and low reduced gradient. The density values of the low-gradient spikes also appear to be an indicator of the interaction strength. However, very different types of interactions (i.e. hydrogen-bonding and steric crowding) appear in the same region of density/reduced-gradient space. To distinguish between these interactions, we consider second derivatives of the density.

2.3 Identifying Interaction Types

Although localizing low-density, low-gradient regions enables identification of weak interactions in a molecular system, more specific interaction types cannot be determined from the density values alone. Low density regions are obviously related to the weakest interactions, such as van der Waals, whereas those with higher densities will be related to stronger (either stabilizing or de-stabilizing) interactions.²⁶ Density derivatives can be used to this end.

The sign of the Laplacian of the density, ∇²ρ, is a widely used tool to distinguish between different types of strong interactions.²⁷ To understand bonding in more detail, the Laplacian is often decomposed into a sum of contributions along the three principal axes of maximal variation. These components are the three eigenvalues λ_i of the electron-density Hessian (second derivative) matrix, such that ∇²ρ = λ₁ + λ₂ + λ₃, (λ₁ ≤ λ₂ ≤ λ₃). Analysis of these components has been widely applied to chemical bonding.^11,27,28

At nuclei (or non-nuclear attractors), the density reaches a local maxima and all three eigen-values are negative. Interatomic regions between bonded atoms are characterized by the presence of one positive and two negative eigenvalues (λ₁ < 0; λ₂ < 0; λ₃ > 0). In the case of covalent interactions, the negative contributions are dominant and the resultant Laplacian is negative. For weaker, non-covalent interactions, the Laplacian in the interatomic region is dominated by the positive contribution,²⁷ independently of whether they are bonding or non-bonding. Bonding interactions can be identified by the negative sign of λ₂, as for the hydrogen-bond in the water dimer example. Conversely, if atoms are in non-bonded contact, λ₂ > 0 in the interatomic region (λ₃ > 0 and λ₁ can be either positive or negative). An example of this situation occurs in the center of the bicyclo[2,2,2]octene cage. Cases where several atoms interact, but are not bonded, correspond to steric crowding in the context of classical chemistry.

Therefore, we can utilize the sign of λ₂ to distinguish bonded (λ₂ < 0) from non-bonded (λ₂ > 0) interactions. Analysis of the sign of λ₂ thus helps to discern between different types of non-covalent interactions, whereas the density itself provides information about their strength. This is illustrated in Figure 2, which shows a modification of our earlier reduced gradient and density plots, such that the ordinate is now sign(λ₂)ρ. The figure shows data for the hydrogen-bonded water dimer, with the low-density, low-gradient spike now lying at negative values indicative of stabilizing interactions. Conversely, the low-density, low-gradient spike for the sterically-crowded bicyclo[2,2,2]octene molecule remains at positive values indicating the lack of bonding in the central area of this moleule. Finally, the low-density, low-gradient spike for the dispersion-bound methane dimer is very near zero, with slightly negative values, indicative of weak attraction.

Figure 2.

Plots of the reduced density gradient versus the electron density mulitplied by the sign of the second Hessian eigenvalue. Results are shown for bicyclo[2,2,2]octene, methane dimer, and water dimer. The data was obtained by evaluating B3LYP/631G* density (a) or promolecular density (b) and gradient values on cuboid grids.

There have been many previous studies of λ₂ in different bonding situations and attempts to rationalise it in terms of movements (accumulation/depletion) of the density, that is often understood as due to attractive/repulsive interactions.^11,27,28 For non-covalent interactions, the main features of the electron density and its derivatives appear clearly if the density is constructed from something as simple as a sum of atomic densities (see Section 4.3). Indeed, for all cases considered, results at the self-consistent and promolecular level are qualtiatively equivalent, which rules out any simple connection to accumulation or depletion of the density. However, when the effect of self-consistent calculations on the density and eigenvalues are analyzed, we find that some quantitative differences are introduced by density relaxation. As expected, the density-gradient peaks are shifted to more bonding regimes when comparing promolecular and self-consistent densities. Specifically, a large shift toward smaller density values is observed in the peak corresponding to non-bonded overlap, introducing less repulsion and greater stability.

To summarize, since non-covalent interactions are characterized by low density and reduced gradient values, they can be located by generating gradient isosurfaces enclosing the corresponding regions of real space. The interaction types can be further understood by the values of sign(λ₂)ρ in these regions. These isosurfaces are the basis of our non-covalent interaction method.

3 Computational Details

To obtain plots of the electron density (ρ) and reduced density gradient ( $s=\frac{1}{2{(3{\pi }^2)}^{1/3}}\frac{\mid \nabla \rho \mid }{{\rho }^{4/3}}$), density-functional theory calculations were performed for a selected set of small molecules and dimers. Calculations on methane, water, branched octane, bicyclo[2,2,2]octene, and the homo-molecular dimers of methane, benzene, water, and formic acid, were performed with the B3LYP functional^24,25 and the 6-31G* basis set, using the Gaussian 03 program.²⁹ Molecular geometries of methane, water, branched octane, and bicyclo[2,2,2]octene are the same as those used in the G3X procedure.³⁰ The geometries of the methane, water, and formic acid dimers were obtained from Ref.31 and the benzene dimer geometry was obtained from Ref.32 Additional B3LYP/6-31G* calculations were performed on Hobza's set of 22 bi-molecular complexes.³³ Diamond and graphite calculations were performed using the CRYSTAL program,³⁴ with the BPW91 functional^35,36 and modified 6-21G* basis sets optimized for diamond or graphite.³⁴

To generate approximate promolecular densities, fully-numerical, LSDA,³⁷ free-atomic densities were generated for the atoms H-Ar using the NUMOL program.^38,39 These densities were spherically averaged over space and summed over spins. Because atomic densities are piecewise exponential for each shell of electrons, they were then fit to one (H, He), two (Li-Ne), or three (Na-Ar) Slater-type functions of the form ρ^at = Σ_j c_je^(−r/ζ_j), with the c and ζ parameter values given in the supporting information. The use of simple exponential functions to construct the promolecular density also allows first and second derivatives to be obtained analytically.

To demonstrate our method for the interaction between a ligand and a protein active site, we apply it to a complex of a bacterial regulatory protein of the tetR family with a tetracycline inhibitor.⁴⁰ The geometry was obtained from the protein data bank⁴¹ (pdb file 2UXO, only chain B). All crystal waters were included in the calculations. Protonation states were determined by WhatIf.⁴² Hydrogens were added using the hbuild function in CHARMM.⁴³ The positions of the protein and water hydrogen atoms were optimized, followed by the positions of the ligand hydrogen atoms. In both these geometry optimizations, the positions of all other atoms were frozen. The protein was described with the CHARMM27 force field, the water molecules were described with TIP3 force field, and the ligand was described with the PM3 semi-empirical Hamiltonian. Since the exponential atomic densities die off fairly quickly, only atoms lying within 6 Å of the tetracycline inhibitor were used in calculation of the promolecular density and reduced gradient. For simplicity, all intramolecular interactions within the protein and ligand, as well as intermolecular interactions between the protein and water molecules, were omitted.

4 Results and Discussion

4.1 Small Molecules, Complexes, and Solids

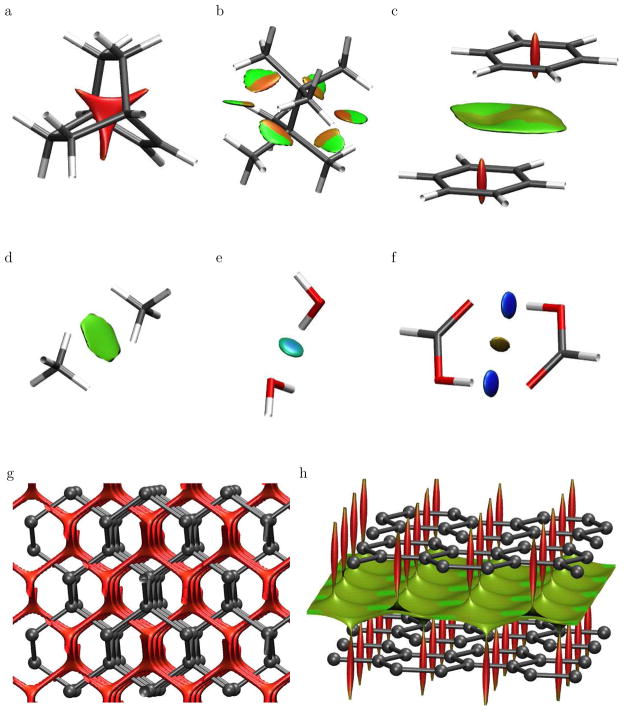
Figure 3 displays low-gradient (s = 0.5 au) isosurfaces, subject to the constraint of low density, for branched octane, bicyclo[2,2,2]octene, and the homomolecular dimers of methane, benzene, water, and formic acid. A density cut-off of ρ < 0.05 au was chosen since it encapsulates the non-covalent interaction region of interest (see Fig. 1). Other isovalues of the reduced gradient could be used as a diagnostic of non-covalent interactions. The choice of cut-off can be made objective by representing all points within the s versus ρ peaks (see Figs. 1 and 2). However, this more complicated algorithm is not necessary, since any cut-off that fulfills the requirements of lying within the peak values already provides the interaction information. Appropriate bounds on the density and reduced gradient should be selected to isolate the low-density, low-gradient peaks for each chemical system of interest. The locations of these peaks are sensitive to the atom types involved, the interaction strengths, and the level of theory used to obtain the density (self-consistent versus promolecular densities).

Figure 3.

Gradient isosurfaces (s = 0.5 au) for (a) bicyclo[2,2,2]octene, (b) branched octane, and the homomolecular dimers of (c) benzene, (d) methane, (e) water, and (f) formic acid. Gradient isosurfaces are also shown for cuboid sections of (g) diamond and (h) graphite. The surfaces are colored on a blue-green-red scale according to values of sign(λ₂)ρ, ranging from −0.04 to 0.02 au. Blue indicates strong attractive interactions and red indicates strong non-bonded overlap.

The gradient isosurfaces are colored according to the corresponding values of sign(λ₂)ρ, which is found to be a good indicator of interaction strength. Large, negative values of sign(λ₂)ρ are indicative of attractive interactions (such as dipole-dipole or hydrogen bonding); while if sign(λ₂)ρ is large and positive, the interaction is non-bonding. Values near zero indicate very weak, van der Waals interactions.

The gradient isosurfaces provide a rich visualization of non-covalent interactions as broad areas of real space, rather than simple pair-wise contacts between atoms. We first consider the sterically-crowded molecules bicyclo[2,2,2]octene (Fig. 3a) and the branched octane isomer (Fig. 3b). In the first case, the low-density, low-gradient region corresponds to the center of the cage, where steric repulsion between the bridgehead carbons is expected. For the branched octane isomer, the isosurface lies between the closely-interacting methyl groups on opposite sides of the central C-C bond. The interactions are repulsive nearer the C-C bond and weakly attractive between the hydrogen atoms. Dispersion and hydrogen bonding can also be clearly detected. In the benzene dimer (Fig. 3c), there is an area of non-bonded overlap located at the center of each benzene ring, resembling the isosurface for bicyclo[2,2,2]octene. There is another lower-density surface between the overlapping portions of the benzenes, where π-stacking is expected. In the dispersion-bound methane dimer (Fig. 3d), the isosurface forms a disc between the individual monomers. For the water dimer (Fig. 3e), the isosurface lies between a hydrogen donor and oxygen acceptor, characteristic of H-bonding. Finally, the formic acid dimer (Fig. 3f) reveals stronger H-bonds than in the water dimer, and also weak van der Waals interactions between the two closely-interacting acidic hydrogens.

Crystalline solids exhibit rich and challenging bonding patterns. We consider the prototypical examples of carbon in the diamond (Fig. 3g) and graphite (Fig. 3h) phases at their equilibrium geometries. In diamond, the carbon atoms are sp³ hybridized and are connected by strong covalent bonds that form a tridimensional, tetrahedral network. Fig. 3g shows a low-gradient, low-density isosurface for a cuboid section of the diamond crystal. The non-covalent surface extends through the voids of the structure, creating a network similar to that of the covalent bonds. Graphite in its α form (Fig. 3h) has a bidimensional, hexagonal lattice, with the carbon atoms sp² hybridized and covalently bonded to their three nearest neighbors. The low-gradient, low-density isosurface shows areas of non-bonded overlap at the center of the hexagonal rings, as seen previously in benzene. π – π stacking interactions between the graphene sheets are clearly manifested by the isosurfaces filling the interlayer spaces.

The use of DFT densities to visualize non-covalent interactions, including dispersion, may seem counter-intuitive. In the case of dispersion, predicted binding energies are highly sensitive to the choice of method. It is well known that most density-functional theory methods, including B3LYP, do not account for dispersion binding^44,45 and in fact predict no binding in the benzene and methane dimer cases. However, one of the main advantages of our approach is that it is based on properties of the electron density, the dominant features of which are quite insensitive to the choice of electronic structure method used in the computations, particularly for very weak interactions. As a side note, the main problem with DFT for dispersion is not in computing the density, but in extracting an accurate energy. Different computational methods give almost the same densities, but very different energetics. As two monomers form a dispersion-bound complex, the changes in density caused by the dispersion interaction are quite subtle. They vary depending on whether the method predicts dispersion binding or repulsion.⁴⁶ Nevertheless, they are quite small in magnitude in the inter-monomer region.

To test the validity of B3LYP densities for non-covalent interactions, we repeated our calculations for the test set of six small molecules and dimers with MP2/6-311++G**, which does predict dispersion binding. The MP2 results, with identical cut-offs, are given in the supporting information and are virtually indistinguishable from our B3LYP/6-31G* isosurfaces in Figure 3. Due to the reduced computational cost, DFT calculations with small basis sets are recommended over MP2 for practical visualization of non-covalent interactions.

To summarize, plotting low-gradient isosurfaces, subject to a further low-density constraint, allows real-space visualization of non-covalent interactions. In addition to the small test set of molecules considered above, the method was successfully applied to Hobza's set of 22 bi-molecular complexes;³³ these results are given in the supporting information. Our model discriminates between different types of weak interactions and allows for simultaneous visualization of all of them. Classification of the various non-covalent interaction types agrees with general chemical concepts. Surfaces with very low density values (i.e. ρ < 0.005 au) generally map to weaker dispersion interactions. Surfaces with slightly higher density values (i.e. 0.005 < ρ < 0.05 au) map to stronger non-covalent interactions, including both attractive H-bonding (negative λ₂) and steric clashes (positive λ₂).

Although not the focus of this paper, our method is also applicable to covalent bonds, which obviously appear at much larger density values than those considered above. This is possible since all covalent bonds have a saddle point in the density, where s = 0. The low-gradient isosurfaces are also distinctly different for single, double, and triple bonds; results are shown for the ethane, ethylene, acetylene series in supporting information.

This also highlights a limitation of our method. It assumes an equilibrium or near-equilibrium geometry, which is broadly applicable to most nanoscale or biomolecular systems. As molecular geometries are compressed, the density at which the reduced gradient approaches zero will shift to higher value, approaching that of covalent bonds. Also, the second eigenvalue remains negative, despite the repulsive nature of the interaction at compressed separations. This shortcoming has already been observed for other density-based bonding analyses, such as Atoms in Molecules.²⁸

4.2 Comparison with Quantum-Chemical Bonding Theories

Our method compliments existing quantum-chemical theories of bonding such as ELF and AIM. The electron localization function (ELF)^8,9 allows visualization of covalent bonds, electron lone pairs, and atomic shell structure from properties of the density. A comparison between isosurfaces generated using our approach and ELF is shown for the benzene dimer in the supporting information. With a 0.9 au isosurface, ELF clearly shows the core electrons of the carbon atoms, the aromatic C-C bonds, and the electrons localized on the hydrogen atoms. While the ELF surface does not show any interaction between the benzenes, the ELF values at critical points have been used to construct tree-diagrams that reflect weak binding in intermolecular complexes.¹⁸

The AIM molecular graph showing critical points and bond paths, obtained using the AIM 2000 program⁴⁷ is also shown in the supporting information. Note that the dispersion interaction appears as two bonds. AIM predicts low-density critical points and bond paths connecting the benzene rings via the two closest pairs of carbon atoms, capturing the π-stacking interaction between the two benzenes. Similar plots are shown in the work of Waller et al.⁴⁸ However, AIM is not an ideal method for visualization of non-covalent interactions, particularly for large chemical systems where the calculations become prohibitively expensive. Moreover, AIM depicts both covalent and non-covalent interactions as local, pair-wise contacts along the bond paths;⁴⁸ in large systems the vast number of AIM bond paths obscures non-local van der Waals interactions. Conversely, our approach manifests non-covalent interactions as broad surfaces between entire functional groups. This allows a much clearer and more intuitive visualization of interactions in complex systems.

4.3 Biological Systems

Biological macromolecules, such as proteins or DNA, are probably the most relevant systems for a visual representation of non-covalent interactions, which are the main driving forces in biological processes. Understanding of these interactions is crucial for the comprehension of their three-dimensional structure and biological activity required for drug design. However, calculation of the electron densities of these systems becomes extremely computationally expensive. A more effcient way to obtain s and ρ is required to display non-covalent interactions. It is well-known^49,50 that important topological features of the electron density are contained in the sum of atomic densities, termed the promolecular density, ${\rho }^{\mathit{pro}}={\sum }_i{\rho }_i^{at}$. A promolecular density obtained from simple exponential atomic pieces is able to predict low-density, low-reduced-gradient regions similar to density-functional results. The free atomic densities used in these calculations consist of one Slater-type function for each electron shell, fit to closely reproduce spherically-averaged, density-functional atomic densities.

Approximate promolecular densities were constructed by summing exponential atomic densities for branched octane, bicyclo[2,2,2]octene, and the homomolecular dimers of methane, benzene, water, and formic acid. Resultant plots of s^pro versus ρ^pro for these species show the same features seen in Fig. 1. Also, gradient isosurfaces generated from the promolecular density (see supporting information) are very similar to those obtained previously with self-consistent DFT and even MP2 densities (Fig. 3). Thus, our approach can be extended to very large systems by using an approximate promolecular density, from which the relevant isosurfaces are plotted. This allows rapid characterization of non-covalent interactions for biomolecules, with only the molecular geometry required as input.

For all cases considered, results at the self-consistent and promolecular level are qualitatively equivalent. Some quantitative differences are introduced in the promolecular calculations that, as expected, shift the s versus ρ peaks to more bonding regimes. This is illustrated in Fig. 2, which plots the reduced gradient versus sign(λ₂)ρ for both SCF and promolecular densities. The promolecular approach is expected to perform best for very weak or moderately attractive interactions, where there is minimal response of the density to the interaction. Because the density cannot adjust, the promolecular approximation gives the largest differences from SCF results for non-bonding interactions, as shown in Fig. 2. This explains why the largest differences between SCF and promolecular isosurfaces appear at the center of rings, such as bicyclo[2,2,2]octene and benzene.

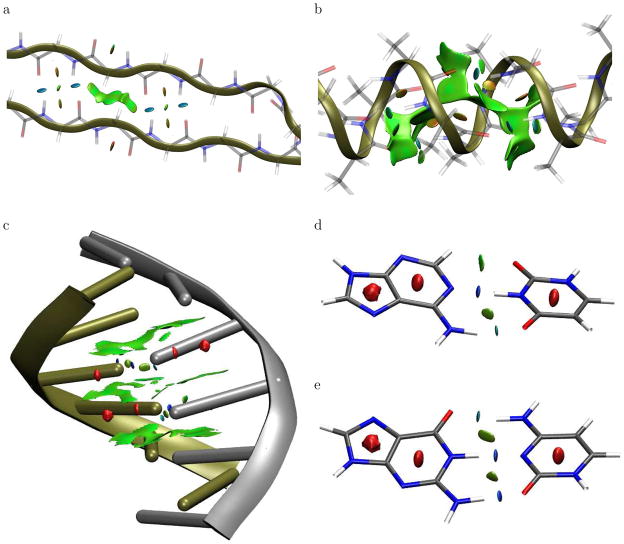
We first consider two model polypeptides: an α-helix consisting of 15 alanine residues and an anti-parallel β-sheet consisting of 17 glycine residues. Geometries of the polypeptides were obtained with the MMFF force field using the spartan program.⁵¹ Both were capped with COCH₃ and NHCH₃ groups. Figure 4 displays low-gradient isosurfaces for cuboid regions at the center of these polypeptides, colored according to the corresponding density values. For the β-sheet, the lowest-density portions of the gradient isosurface arise from hydrophobic, dispersion-dominated interactions, primarily involving the CH₂ groups of the glycines. The higher-density regions correspond to inter-residue hydrogen-bonds and repulsive interactions between the adjacent C=O and N-H groups. For the α-helix, the isosurface has a large, low-density region within the helix and between the side-chain methyl groups. The higher-density portions of the isosurface correspond to inter-residue hydrogen-bonds along the helix and repulsive interactions between adjacent N-H groups.

Figure 4.

Gradient isosurfaces (s^pro = 0.35) for cuboid sections of the (a) β-sheet and (b) α-helix polypeptides. Gradient isosurfaces (s^pro = 0.25) are also shown for the (c) B-form of DNA, and the (d) A-T and (e) C-G base pairs. The surfaces are colored on a blue-green-red scale according to values of sign(λ₂) ρ, ranging from −0.06 to 0.05 au. Blue indicates strong attractive interactions and red indicates strong non-bonded overlap.

We also considered the non-covalent interactions between nucleobases in the B-form of double-strand, six-base-pair (TGTGTG) DNA. The structure was obtained using the X3DNA program⁵² with ideal geometry parameters.⁵³ Figure 4c displays the low-gradient isosurface for a cuboid section in the center of the DNA helix, colored according to the sign(λ₂)ρ values. The calculated isosurface resembles that of graphite, with broad, low-density regions indicative of π-stacking between base-steps. The interactions between individual deoxyadenosine-deoxythymidine and deoxycytidine-deoxyguanosine pairs are shown in Fig. 4d,e. The isosurfaces show non-bonded overlap within the nucleobase rings, as in benzene and graphite, and hydrogen-bonding motifs similar to the formic acid dimer. The strong N-H – O and N-H – N hydrogen bonds can be clearly distinguished from the weaker, attractive C-H – O interaction by the density values, as shown in different colors.

The hydrogen-bonding surfaces in the DNA model have density values of ca. 0.065 au, compared to density values of ca. 0.035 au for the polypeptide hydrogen bonds. This is evident from the degree of blue shading for the hydrogen bonds in Fig. 4. Since density values at hydrogen-bond critical points correlate with the interaction strength,^12,54 our results indicate that the hydrogen bonds between nucleobase pairs are substantially stronger than between amino acids, in agreement with literature data.^55–57

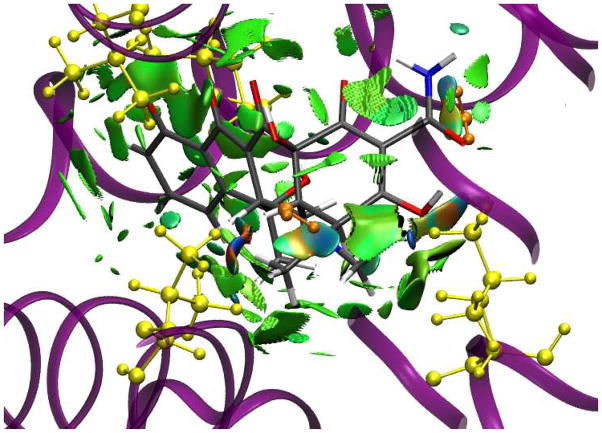
Let us now consider the interaction between a ligand and a protein active site. The low-gradient isosurface for a tetracycline inhibitor bound to the tetR protein in Fig. 5 shows a complex web of non-covalent interactions between the ligand and active site. Several other protein-ligands pairs have been tested, leading to the same conclusions. When analyzing non-covalent interactions in protein-ligand complexes, it is usually assumed that these interactions are due to a specific contact between two atoms.¹⁶ However, it is clearly seen in Fig. 5 that this assumption is only partly correct. Hydrogen bonds, such as those between the tetracycline amine groups and two water molecules (shown in orange), are directional and specific. Conversely, van der Waals, dipole-dipole, and hydrophobic interactions, such as those between the tetracycline and the Leu61, Val91, Ile136, and Val166 residues (shown in yellow), are not atom-specific and occupy broader regions in space. The figure reveals some steric clashes (orange and red regions of the isosurface) that must be offset by stronger, attractive interactions to give binding in this crystal structure. A ligand “fits” the geometry of the active site, and the interaction energy between the ligand and protein is comprised of many small contributions. When trying to design a new ligand to fit a specific active site, one should consider all such interactions.

Figure 5.

Gradient isosurfaces (s^pro = 0.35) for interaction between the tetR protein and tetracy-cline inhibitor. The surfaces are colored on a blue-green-red scale according to values of sign(λ₂)ρ, ranging from −0.06 to 0.05 au. Blue indicates strong attractive interactions and red indicates strong non-bonded overlap.

5 Summary

In conclusion, non-covalent interactions have a unique signature and their presence can be revealed solely from the electron density. Non-covalent interactions are highly non-local and manifest in real space as low-gradient isosurfaces with low densities. The sign of the second Hessian eigenvalue is used to give the type of interaction, and its strength can be derived from the density on the non-covalent interaction surface. This approach provides a rapid and rich representation of van der Waals interactions, hydrogen-bonds, and steric clashes, requiring only the atomic coordinates as input. This tool offers exciting possibilities for aiding design of ligands, self-assembled materials, catalysts, and other molecular systems. Of specific interest would be analysis of the interaction between two large bio-molecules, such as protein-protein and protein-DNA interfaces.