Effects of Healthy Aging and Early-Stage Dementia of the Alzheimer’s Type on Components of Response Time Distributions in Three Attention Tasks

Abstract

Objective

The characteristics of response time (RT) distributions beyond measures of central tendency were explored in three attention tasks across groups of young, healthy older adults and individuals with very mild dementia of the Alzheimer’s type (DAT).

Method

Participants were administered computerized Stroop, Simon, and Switching tasks, along with psychometric tasks that tap various cognitive abilities, and a standard personality inventory (NEO-FFI).

Ex-Gaussian (and Vincentile) analyses were used to capture the characteristics of the RT distributions for each participant across the three tasks, which afforded three components: Mu, Sigma (mean and standard deviation of the modal portion of the distribution), and Tau (the positive tail of the distribution).

Results

The results indicated that across all three attention tasks, healthy aging produced large changes in the central tendency Mu parameter of the distribution along with some change in Sigma and Tau (mean η_p²=.17, .08, and .04, respectively). In contrast, early stage DAT primarily produced an increase in the Tau component (mean η_p²=.06). Tau was also correlated with the psychometric measures of episodic/semantic memory, working memory, and processing speed, and with the personality traits of Neuroticism and Conscientiousness.

Structural equation modeling indicated a unique relation between a latent Tau construct (−.90), as opposed to Sigma (−.09) and Mu constructs (.24), with working memory measures.

Conclusions

The results suggest a critical role of attentional control systems in discriminating healthy aging from early stage DAT and the utility of reaction time distribution analyses to better specify the nature of such change.

There has been considerable interest in the cognitive performance of individuals who are in the earliest stage of dementia of the Alzheimer’s type (hereafter referred to as very mild DAT individuals). Studies have demonstrated that the pathological processes of the disease are present in the brain for years before the appearance of symptoms (e.g., Bennett et al., 2006; Morris et al., 1996; Petersen, 2004; Price et al., 2009; Rubin et al., 1998; Storandt, 2008), indicating that preclinical markers of the disease are likely to be present in some older adults who appear to be clinically “normal”. This highlights the need to reliably identify potential behavioral changes that could serve as additional early and antecedent markers for DAT. While episodic memory has been regarded as the primary predictor of the onset of dementia (e.g., Albert et al., 2007; Storandt et al., 2006), there is accumulating evidence for a breakdown in processes related to attention in healthy older adults and to a greater extent, in very mild DAT individuals across aspects of visual attention (Faust & Balota, 1997), divided attention (Duchek & Balota, 2005; Baddeley et al., 2001), task switching (Belleville et al., 2008), and selective attention (Balota & Duchek, 1991; Castel et al., 2007; Spieler et al., 1996).

Consider, for example, the Stroop task, a prototypical measure of attentional control (MacLeod, 1992). To successfully name the color on an incongruent trial (e.g., RED printed in blue), individuals have to maintain the task goals (naming the ink color instead of the word RED) throughout the task, activate the task-relevant information (the ink color blue), and control the highly active but irrelevant information (the word RED). As noted, there are clear increases in the size of the Stroop effect both in healthy older adults and in early stage DAT. Importantly, Balota et al. (in press) showed that the errors on incongruent trials were the best discriminator of those to convert vs those who do not convert to DAT over a 14-year period. Of course, breakdowns in attention are not localized but also influence other cognitive functions. For example, it is widely acknowledged that there is an intimate connection between attention and memory (e.g., Craik & Lockhart, 1972; Hasher & Zacks, 1988; Jacoby, 1991). In fact, there is accumulating evidence that breakdowns in attentional control systems contribute to memory loss in both healthy aging and early-stage AD (e.g., Baddeley et al., 2001; Balota et al., 1999, 2002; Perry & Hodges, 1999; Sommers & Huff, 2003; Tse et al., in press).

In most attention tasks, mean response time (RT) and error rate are the standard measures. There has been an increasing interest in measures of performance above and beyond the central tendency of RTs. For example, there is evidence for changes in variability across trials as a function of healthy aging and mild DAT (Hultsch et al., 2002; see Hultsch et al., 2008, for a review). Hultsch et al. (2002) found that RT variability was a better discriminator between healthy aging and mild DAT than mean RT performance. More recently, Duchek et al. (in press) reported that individual trial-by-trial RT variability (as reflected by the coefficient of variation, the standard deviation divided by the mean of the distribution) in three attention tasks (Stroop, Simon and Switching) was higher for very mild DAT individuals than healthy older adults and in turn, young adults. Duchek et al. argued that one possible cause for the increase in variability across age and DAT in these attention tasks was due to changes in the ability to maintain appropriate task sets across time. Of course, simple increases in RT variability across individuals can be produced by various changes in the underlying RT distributions. For example, the variance of the entire RT distribution could be increased in a multiplicative manner. Accounts which attribute age-related changes to general slowing (see e.g., Myerson et al., 1990) would suggest that older adults’ performance is simply a multiplicative function of young adults’ performance. This predicts that all components of the RT distribution change at the same rate across age groups. Alternatively, it is possible that some components may change more than others. For instance, the increase in variance could be entirely attributed to an increase in the slow end of the RT distribution, which is consistent with the evidence of increases in variability above and beyond mean performance (e.g., Duchek et al., Hultsch et al., 2002). Hence, it is important to pinpoint the change in specific components of the RT distribution that contribute to the observed changes in the overall RT variability.

The present study explored the influence of healthy aging and the earliest detectable form of DAT on components of RT distributions in three standard attention tasks (Stroop, Simon, and Switching). To capture the components of an individual’s RT distribution, we fit raw RTs of each participant to an ex-Gaussian distribution and estimated parameters that reflect whether the age-related and DAT-related changes in mean RT were due to shifting (Mu), scaling (Sigma) and/or an increased tail (Tau) of the RT distribution (see Balota et al., 2008, for a discussion). This approach allows one to specify whether the change in intraindividual variability as a function of age and/or DAT (Duchek et al., in press; Hultsch, et al., 2000, 2002) is due to general slowing, which is reflected by changes in all parameters, or more specific changes in Gaussian or exponential components of the distribution. We now turn to a brief description of RT distributional analyses.

RT Distribution Analyses

The characteristics of an RT distribution have been shown to capture important aspects of human cognition (Luce, 1986), including selective attention (e.g., Castel et al., 2007; Heathcote et al., 1991; Spieler et al., 1996, 2000), episodic memory (e.g., Hockley, 1984; Rohrer & Wixted, 1994), word recognition (e.g., Andrews & Heathcote, 2001; Balota & Spieler, 1999; Plourde & Besner, 1997; Yap & Balota, 2007; Yap et al., 2006) semantic priming (e.g., Balota et al., 2008; Lyons et al., 1995), and individual differences in cognition (Bub et al., 2006; McAuley et al., 2006; Yap et al., in press). In the current research, distributional analyses were carried out both by (a) fitting individual raw RTs to a theoretical ex-Gaussian distribution and (b) averaging RT distributions across participants, via Vincentile analyses. The ex-Gaussian distribution is a convolution of a Gaussian (normal) and an exponential distribution that closely approximates the empirical RT distribution (Ratcliff, 1979). The distribution is operationally defined by a three-parameter function. Mu and Sigma parameters reflect the mean and standard deviation, respectively, of the Gaussian component and the Tau parameter reflects any additional exponential contribution to the observed fit of the RT distribution. A change in Mu reflects the shifting of the RT distribution, whereas a change in Tau is more reflective of the tail of RT distribution. Because the algebraic sum of Mu and Tau is constrained to closely approximate the empirical distribution, one can partition the individual mean RT for a particular condition into distributional shifting and/or changes in the tail of the distribution. Importantly, even though two conditions may produce the same mean RT, the underlying RT distributions could be different due to counteracting effects of Mu and Tau (see Balota et al., 2008, for a discussion). This highlights the importance of conducting these fine-grained analyses on RT distributions.

Apart from the ex-Gaussian analyses, which assume that the empirical distribution can be captured by an ex-Gaussian distribution, we conducted Vincentile analyses to obtain converging evidence regarding the shape of the RT distributions. In Vincentile analyses, one first rank-orders all of the RTs within a participant, and then bins the rank-ordered data into a set of equal number of observations. For instance, to obtain eight Vincentiles, the RT data for a participant are first sorted (from fastest to slowest responses). The first 12.5% of the data is then averaged, followed by the second 12.5%, and so on. Individual Vincentiles are then averaged across participants. Unlike ex-Gaussian fitting, Vincentizing reflects the average shape of the RT distributions without strong assumption regarding the theoretical shapes of the RT distribution. Hence, it is important to demonstrate convergence across the two techniques.

RT Distribution, Attentional Control, and Cognition

According to the worst performance rule (Coyle, 2003; Larson & Alderton, 1990), the slower portion of participants’ RT in cognitive tasks accounts for a larger proportion of variance of general intelligence than the faster portion of their RTs. In attention tasks, given that individuals with impaired attentional control systems are less likely to maintain the task goal and to suppress irrelevant information, these individuals may be more likely to experience losses of control across time (cf., goal neglect; Duncan et al., 1996), and produce slower RTs and more errors than those who have more intact attentional control systems. Thus, deficits in attentional control would lead to a larger tail of the RT distribution (i.e., larger Tau). This would not be revealed if only central tendency measures, such as RT and errors, instead of the characteristics of the RT distribution, were considered. A longer RT in one group of participants could be due to a shift, rather than an increase in the size of the tail of their RT distribution, relative to other groups. The ex-Gaussian parameters have been used to differentiate groups of individuals who are high vs. low in attentional control abilities in developmental and aging research (e.g., Leth-Steensen et al., 2000; McAuley et al., 2006; Spieler et al., 1996; West et al., 2002). Similarly, the individual-difference approach used by Schmiedek et al. (2007) involved estimating the ex-Gaussian parameters in eight choice RT tasks. They showed that Tau, but not Mu or Sigma, for young adults were strongly related to working memory capacity, providing more direct evidence for the relationship between Tau and attentional control that had only been assumed in previous studies (e.g., Spieler et al.). In the present study, we used three attention tasks that induce stronger response competition between relevant pathways and hence more directly tap attentional control than Schmiedek et al.’s choice RT tasks do. The sensitivity of a task to one’s attentional control is critical in the current study because the deficit in attentional control can be quite subtle for individuals who are in the earliest stage of DAT.

Personality and RT Distribution

Personality has recently been found to serve as an early non-cognitive indicator of early onset DAT (Duchek et al., 2007; Wilson et al., 2003, 2007). For example, Duchek et al. found that very mild DAT individuals were higher in Neuroticism and lower in Conscientiousness than healthy older adults, even after taking into account the performance of psychometric tests. Also, Wilson et al. (2007) found that healthy older adults high in conscientiousness, compared to those low in conscientiousness, were less likely to later develop DAT in a longitudinal study. Indeed, Wilson et al. (2007) pointed out that “Conscientiousness refers to an individual’s tendency to control impulses and be goal directed” (p. 1204), suggesting that individuals who are high in Conscientiousness are more able to stay tuned to the task goal in the face of irrelevant information. Interestingly, Duchek et al. (2008) recently showed that high scores in Neuroticism and low scores in Conscientiousness for healthy older adults were associated with increased intraindividual variability in their RT performance in three attention tasks (see also Robinson & Tamir, 2005, for further evidence of a relationship between Neuroticism and RT variability in the Stroop task for young adults). However, as noted above, variability can reflect different components of the RT distribution, so it is important to examine specifically which aspects of the RT distribution change as a function of Conscientiousness/Neuroticism in both healthy aging and early-stage DAT. A priori, one would expect a negative correlation between Conscientiousness and Tau (i.e., the tail of the RT distribution), because individuals who are less conscientious experience more difficulty staying tuned to the task, such that they need to reinstate the task set more frequently and hence show a larger tail of their RT distribution. On the other hand, one might expect a positive correlation between Neuroticism and Tau because individuals who are more neurotic are more sensitive to non-goal oriented environmental stressors, such that they need to suppress the distracting information more frequently and hence show a larger tail in their RT distribution. Thus, the intriguing prediction is that one might correlations between Tau and both Conscientiousness and Neuroticism, but in opposite directions.

Present Research

The clinical dementia rating (CDR) scale was used in the present study to identify individuals at the earliest stages of DAT; CDR ratings are derived independently without considering psychometric test performance (Morris, 1993; Storandt et al., 2006), and have been shown to be highly predictive of pathology consistent with AD based on autopsy (Berg et al., 1998; Storandt et al.). This well-characterized sample of very mild DAT individuals can provide a more refined examination of the components of RT distribution as an early marker for the onset of DAT. It is noteworthy that the very mild DAT individuals in the current sample (CDR 0.5s) are high functioning, as reflected by their relatively high MMSE scores (29.0 for healthy controls and 26.6 for the CDR 0.5s).

There are four main predictions that highlight the role of attentional control in healthy aging and early-stage DAT. First, the age- and DAT-related differences in the Stroop effect and Simon effect should be found, replicating the findings of previous studies (e.g., Castel et al., 2007; Spieler et al., 1996). For the Switching task, we predicted a null age-related effect in local switch cost, as reported in previous studies (e.g., Kray & Lindenberger, 2000). However, for the DAT-related effect, one might expect a smaller local switch cost in RTs yet a larger local switch cost in errors for very mild DAT individuals, relative to healthy older adults, due to a deficit in their attentional control system. Specifically, because switching across two different task sets (odd/even vs. consonant/vowel) requires a well-tuned attentional control system that can activate one task set while suppressing the other throughout the task, individuals with a deficit in this system may be less likely to suppress the irrelevant task set across trials. The resultant simultaneous activation of both task sets reduces the local switch cost in RT while at the same time, may increase the local switch cost in errors because responses should be more error-prone when the activation of the irrelevant task set is not successfully suppressed.

Second, very mild DAT individuals should show a larger Tau than healthy older adults in all three attention tasks. An absence of the DAT-related effect in Mu and Sigma would suggest that the RT difference between healthy older adults and very mild DAT individuals can be attributed primarily to the latter group showing a larger number of slow RT trials.

Third, the correlation analyses for the ex-Gaussian parameters and composite scores extracted from scores in the psychometric battery (see below) should produce a robust negative correlation between Tau and other aspects of cognition that depend on attentional control systems, such as working memory and episodic memory (see McCabe et al., in press). In addition, we will attempt to replicate the intriguing finding by Schmiedek et al. (2007), indicating a specific relationship between a Tau construct and a working memory construct, via structural equation modeling.

Fourth, Conscientiousness and Neuroticism should be associated with Tau, due to their relationship with one’s attentional control abilities, but interestingly in opposite directions.

Methods

Participants

A total of 352 individuals participated in this study, with 246 non-demented (CDR 0) healthy older adults and 74 very mild DAT (CDR 0.5) individuals recruited from the Washington University Alzheimer’s Disease Research Center (ADRC) and 32 healthy young adults recruited from the Washington University undergraduate participant pool (see Table 1). Although part of this data set was recently reported in Duchek et al. (in press), the current paper includes new analytic procedures and a larger sample of participants. Because not all of the participants did all of the attention tasks, the sample sizes varied across tasks. There was a significant age difference between healthy older adults and very mild DAT individuals (see Table 1), and hence, we controlled for this variable in all of the following analyses that involved only these two groups. All ADRC participants were screened for depression, untreated hypertension, reversible dementia, and other disorders that could potentially produce cognitive impairment. The inclusion and exclusion criteria for DAT are consistent with the criteria for “probable AD” of National Institute of Neurological and Communications Disorders and Stroke—Alzheimer’s disease and Related Disorders Association (McKhann et al., 1984). The presence of dementia was assessed according to the Washington University CDR scale (Morris, 1993; Morris et al., 1988), with CDR 0, 0.5, 1, 2, and 3 representing no dementia, very mild dementia, mild dementia, moderate dementia, and severe dementia, respectively. The CDR is based on a 90-minute clinical interview that assesses the participants and obtains information from their family members. This interview assesses potential changes in participants’ cognitive and functional abilities in memory, orientation, home and hobbies, judgment and problem solving, community affairs, and personal care relative to previous behavior. The determination of a CDR status for each participant at baseline and at each annual assessment thereafter is made without reference to the psychometric performance of the individual. The recruitment and assessment methods permit the diagnosis of DAT in individuals who elsewhere may be characterized as MCI (i.e., mild cognitive impairment) (Berg et al., 1998; Morris et al., 2001; see http://alzheimer.wustl.edu/cdr/PDFs/CDR_OverviewTranscript-Revised.pdf for an online summary). Both the reliability of the CDR (Burke et al., 1988) and the validity of the diagnosis based upon autopsy by this research team have been excellent (93% accuracy), including those diagnosed with very mild DAT (Berg et al.; Storandt et al., 2006). This study was approved by the Institutional Review Board at Washington University School of Medicine and all participants provided their informed consents at the beginning of the study.

Table 1.

Psychometric, Span and Personality Measure Means (SD) as a Function of Group

	Young			Healthy Old (CDR 0)			Very Mild DAT (CDR 0.5)
	Mean	N	SD	Mean	N	SD	Mean	N	SD
Age	20.31 a	32	1.12	71.77 b	246	7.71	75.82 c	74	7.81
Years of Education	14.62 a	32	1.01	15.28 a	246	2.71	14.70 a	74	2.93
Mini-Mental State Exam	--	--	--	28.99 a	246	1.36	26.58 b	74	2.78
Logical Memory	--	--	--	13.28 a	230	5.17	8.45 b	74	4.76
WMS Associate Recall	--	--	--	14.71 a	230	3.78	10.42 b	73	4.14
WAIS Information	--	--	--	21.48 a	231	4.59	18.16 b	74	4.67
Animal Fluency	--	--	--	20.54 a	246	5.82	15.66 b	74	5.14
Reading Span	8.70 a	30	1.91	7.58 b	245	1.86	5.49 c	73	2.08
Rotation Span	11.80 a	30	3.07	8.94 b	240	3.33	5.53 c	66	3.59
Computational Span	12.73 a	30	4.04	8.72 b	244	3.66	5.97 c	70	3.15
Word Fluency S-P	--	--	--	31.46 a	224	10.81	26.42 b	74	10.71
WAIS Digit Symbol	--	--	--	49.51 a	223	10.79	37.59 b	73	12.34
Trail Making A	--	--	--	33.59 a	246	12.34	43.61 b	74	23.21
Trail Making B	--	--	--	85.09 a	245	34.61	127.92 b	74	52.56
Forward Digit Span	--	--	--	6.53 a	224	1.23	6.35 a	74	1.15
Backward Digit Span	--	--	--	4.80 a	224	1.28	4.19 b	74	1.09
Boston Naming	--	--	--	49.73 a	224	12.16	43.32 b	74	13.39
Crossing Off	--	--	--	168.31 a	224	58.77	144.97 b	74	36.73
Conscientiousness	--	--	--	34.45 a	228	5.59	31.57 b	70	4.94
Neuroticism	--	--	--	14.16 a	228	6.39	17.53 b	70	7.34

Note. The values within each row with different superscripts are significantly different with each other (p < .05, two-tailed). The analyses for healthy older adults vs. very mild DAT individuals were controlled for age.

Design and Procedures

Psychometric Testing

Each ADRC participant was administered a 2-hour psychometric battery in a separate testing session, by an examiner who was unaware of the participant’s CDR status. The battery includes Mini-Mental State Exam (MMSE, Folstein et al., 1975), forward and backward digit spans, Logical Memory, and Associate Memory subtests in Wechsler Memory Scale (WMS, Wechsler & Stone, 1973), Information and Digit Symbol subtests in Wechsler Adult Intelligence Scale (WAIS, Wechsler, 1955), Crossing Off (Botwinick & Storandt, 1973), Trail Making A and B (Armitage, 1946), Boston Naming (Goodglass & Kaplan, 1983), Animal Naming (Goodglass & Kaplan, 1983), Word Fluency Test S-P (Thurstone & Thurstone, 1949). In addition, all participants received three working memory span tasks (reading, rotation, and computation span, Engle et al., 1999) in the same session that the attention tasks were conducted. The group means and standard deviations for all of these measures are presented in Table 1. As expected, very mild DAT individuals performed worse than healthy older adults on most tests. Because young adults were not recruited via the ADRC, they did not receive the psychometric battery, although they did complete the three working memory span tasks. As shown in Table 1, their working memory performance was better than healthy older adults and very mild DAT individuals, as typically found in the literature (e.g., White & Murphy, 1998).

Personality Testing

Two hundred and twenty eight out of 246 healthy older adults and 70 out of 74 CDR 0.5 individuals completed the NEO-FFI (Costa & McCrae, 1992), a shortened version of the Revised NEO Personality Inventory (NEO-PI-R) that measures the five factors of Neuroticism, Openness, Extraversion, Agreeableness, and Conscientiousness. There are 60 items rated on a 5-point scale from strongly agree to strongly disagree. Administration of the scale takes about 10–15 minutes. This shortened scale has correlations of .77 to .92 with the five factor scales from the NEO-PI-R, and internal consistency values range from .68 to .86 (Costa & McCrae). The participants filled out the form after they finished the three attention tasks. If they were unable to fill out the form on their own, a trained research assistant orally administered the questionnaire. Because previous studies reported that Conscientiousness and Neuroticism are most relevant to attentional control and affected by DAT (e.g., Duchek et al., 2007; Wilson et al., 2003, 2007), we reported only these factors in the current article. As shown in Table 1, we replicated the findings that very mild DAT individuals yielded lower Conscientiousness and higher Neuroticism scores than healthy older adults.

Stroop Task

This task involved four color names (red, blue, green, and yellow) and four neutral words (bad, poor, deep, and legal). In the 36 congruent trials, each of the four color names appeared nine times in its corresponding color. In the 36 incongruent trials, each of the four color names appeared three times in each of the three nonmatching colors. In the 32 neutral trials, each of the four neutral words appeared twice in each of the four colors. These trial types were randomly intermixed for each participant. To familiarize the participants with the task and screen out any potential color-blind individuals, they were first presented with examples of colors and words to be used in the task. Prior to the actual trials, participants were presented with a block of 16 practice trials. Each trial began with a fixation stimulus “+++” displayed for 700 ms, following by a 50-ms blank-screen interstimulus interval. The word then appeared on a black background and remained on the screen until the participant read aloud its color. Once the voice-operated relay was triggered, the experimenter coded the response as correct, non-intrusion error (i.e., stutters, false starts, or other noises), or intrusion error (i.e., participant named the word or other color names).

Simon Task

The stimulus display in this task consisted of a white central fixation “+” and a white arrow (measuring approximately 4 cm in length and 2 cm in height) presented on a black background. The peripheral locations of the arrow (left and right) were situated 5° on the horizontal plane from the central fixation. Participants were told that they would be presented with an arrow pointing to either left or right on the screen and the arrow would appear on the left half, right half, or center of the screen. They were told to ignore the arrow location on the screen and respond according to its direction by pressing a key on either left (q key) or right side (p key) of the keyboard when the arrow was pointing left or right, respectively. In the 40 congruent trials, the arrow direction corresponded to the arrow location (e.g., left-pointing arrow on the left half of the screen). In the 40 incongruent trials, the arrow direction was opposite to the arrow location (e.g., left-pointing arrow on the right half of the screen). In the 40 neutral trials, the arrow appeared at the center of the screen. These trials were included to ensure that participants would keep fixated at the center of the screen. These trial types were randomly intermixed for each participant. Prior to the actual trials, participants were presented with a block of 12 practice trials. Each trial began with a 500-ms central fixation, followed by the onset of an arrow, which stayed on the screen until the participant made a response or until 5 s had elapsed. Once a response was made, the screen cleared and accuracy feedback was presented for 400 ms. After feedback, the next trial began 2 s later. Both RT and accuracy were recorded.

Switching Task

In this task (modified from Minear & Shah, 2008), participants engaged in two different tasks across trials. On each trial, a letter-number pair (e.g., A 3) appeared at the center of the screen with a cue appearing at the top of the screen indicating if it is a letter or number trial. On a letter trial, participants were told to decide whether the letter was a consonant or vowel (CV). On a number trial, they were told to decide whether the number was odd or even (OE). Participants pressed the d key when responding consonant/odd and the k key when responding vowel/even. They first received 10 practice trials with feedback, and then a block of 60 switch/nonswitch trials in an alternate runs sequence, CV, CV, OE, OE, CV, CV, OE, OE etc. in which a given task (e.g., consonant/vowel decision) was performed on successive trials, but then switched to a different task (e.g., odd/even decision). Hence, there were 30 switch trials (e.g., CV trial followed by OE trial) and 30 nonswitch trials (e.g., CV trial followed by CV trial). Feedback was not given on these trials. The letter-number pair remained on the screen until participants made a response and then the next pair appeared immediately. Participants were instructed to respond as quickly and as accurately as possible and keep track of the order of the trials, rather than rely on the cues at the top of the screen.¹

Results

We first present the mean RT and error data as a function of group and condition to insure we replicated the typical findings reported in Stroop, Simon and Switching studies. We also followed Faust et al.’s (1999) recommendation and performed z-transformed RT analyses to determine if the observed effects within condition were due to general slowing. The overall patterns of the zRT data were similar to those of the RT data. Hence, we report only the RT and error data here for the sake of brevity.

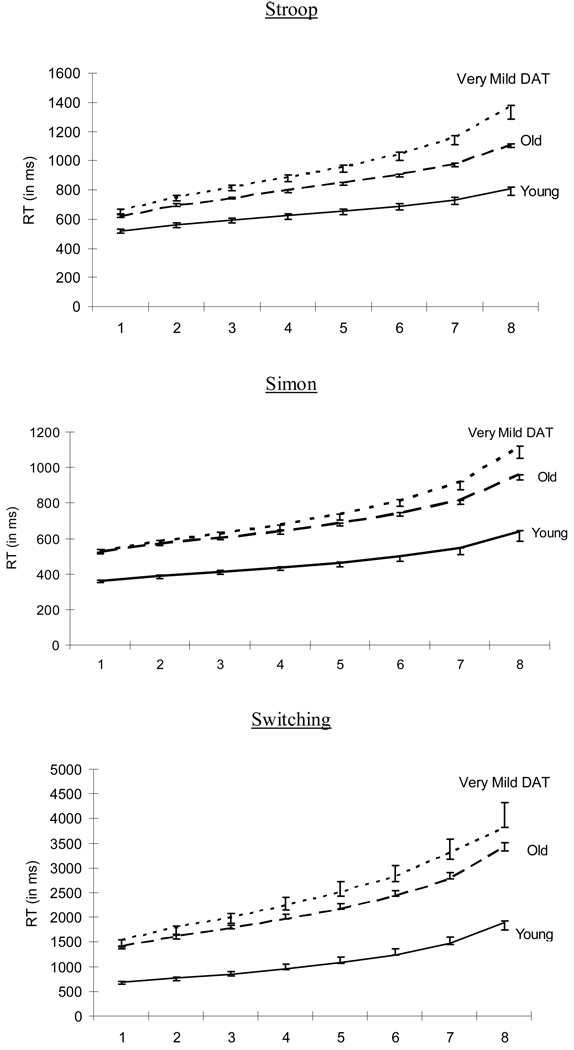
For the RT analyses, trials with incorrect responses and trials with correct-response RTs that were shorter than 200 ms and those that were above or below 3 SD of each participant’s mean RT were all removed, resulting in an elimination of 2–3% of correct-response trials for each group in each task. We only included the trials with correct responses in all of our RT analyses. The effect sizes of F statistics are represented by η_p². For each of the three tasks, we obtained the ex-Gaussian parameters for each participant for all trials within a task using quantile maximum likelihood estimation procedure in QMPE 2.18 (Cousineau et al., 2004; Heathcote et al., 2002). This procedure provides unbiased parameter estimates and has been shown to be more effective than continuous maximum likelihood estimation for small samples (Heathcote & Brown, 2004; Speckman & Rouder, 2004). All fits successfully converged within 500 iterations. Mean Vincentiles for the data were plotted, providing a graphical complement to the ex-Gaussian fits (see Figure 3). As noted earlier, Vincentizing averages RT distributions across participants to produce the RT distribution profile of a group of participants (Ratcliff, 1979).

Figure 3.

The Vincentile plot for Stroop, Simon, and Switching tasks as a function of group.

RT and Errors

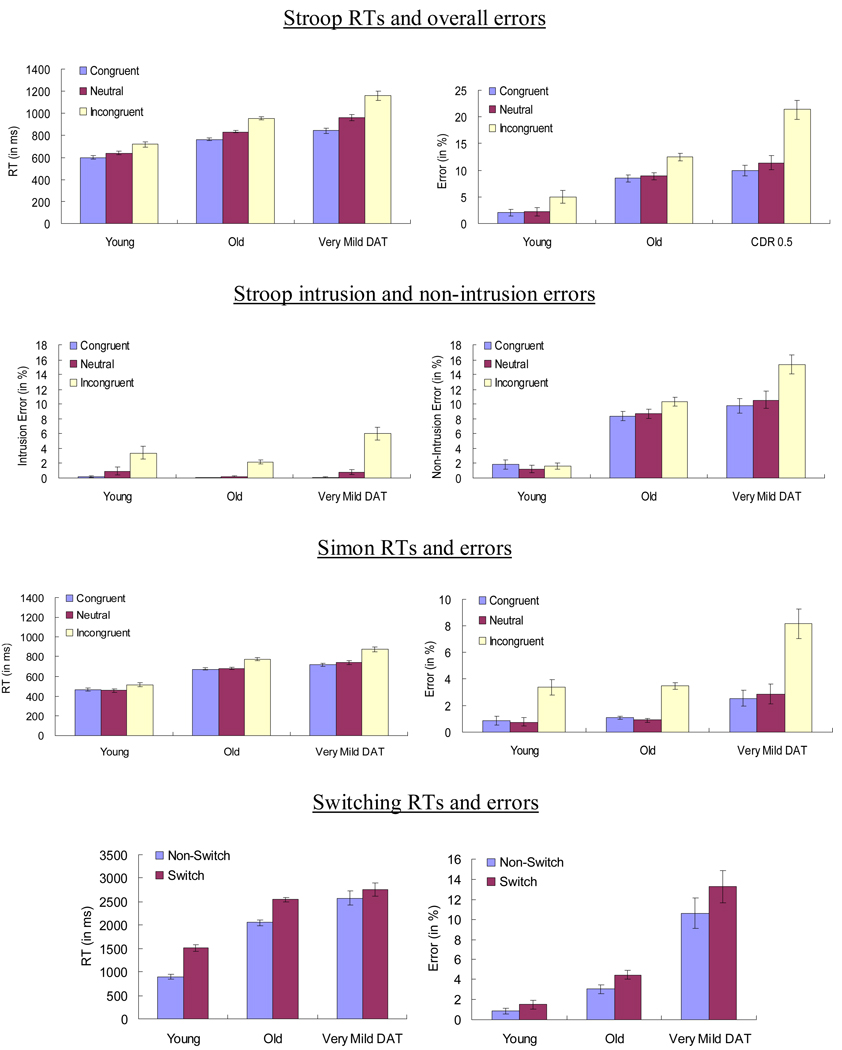
For the Stroop and Simon tasks, participants’ means were submitted to a 3 (group) × 3 (condition: congruent, neutral, or incongruent) mixed-factor ANOVA. For the Switching task, participants’ means were submitted to a 3 (group) × 2 (condition: switch or non-switch) mixed-factor ANOVA. For the Stroop task, we separately report the mean overall, intrusion and non-intrusion error rates. Figure 1 summarizes the mean RTs and errors by conditions in these three tasks. The statistics from these ANOVAs are listed in Table 2.

Figure 1.

Mean RTs and % errors in Stroop, Simon, and Switching tasks as a function of condition and group. Error bars indicate standard errors of means.

Table 2.

ANOVA Table for RT, error, and ex-Gaussian parameters in Stroop, Simon and Switching tasks

		df	F	MSE	p	ηp2
For Stroop RT	Main Effect of Group	(2,346)	44.03	85254	< .001	.20
	Main Effect of Condition	(2,692)	309.07	6221	< .001	.47
	Group × Condition Interaction	(4,692)	24.78	6221	< .001	.13
For Stroop Error	Main Effect of Group	(2,346)	16.13	248.98	< .001	.09
	Main Effect of Condition	(2,692)	60.92	32.29	< .001	.15
	Group × Condition Interaction	(4,692)	15.06	32.29	< .001	.08
For Stroop Intrusion Error	Main Effect of Group	(2,346)	13.52	14.20	< .001	.07
	Main Effect of Condition	(2,692)	81.96	8.54	< .001	.19
	Group × Condition Interaction	(4,692)	13.86	8.54	< .001	.07
For Stroop Non-Intrusion Error	Main Effect of Group	(2,346)	15.71	212.99	< .001	.08
	Main Effect of Condition	(2,692)	13.40	24.05	< .001	.04
	Group × Condition Interaction	(4,692)	5.93	24.05	< .001	.03
For Stroop Mu	Effect of Group	(2,346)	17.82	14097	< .001	.09
For Stroop Sigma	Effect of Group	(2,346)	16.51	2679	< .001	.09
For Stroop Tau	Effect of Group	(2,346)	30.02	15925	< .001	.15
For Simon RT	Main Effect of Group	(2,343)	32.28	69318	< .001	.18
	Main Effect of Condition	(2,686)	145.40	3586	< .001	.30
	Group × Condition Interaction	(4,686)	10.81	3586	< .001	.06
For Simon Error	Main Effect of Group	(2,343)	19.94	32.24	< .001	.10
	Main Effect of Condition	(2,686)	67.98	9.62	< .001	.17
	Group × Condition Interaction	(4,686)	9.19	9.62	< .001	.05
For Simon Mu	Effect of Group	(2,343)	48.24	6588	< .001	.22
For Simon Sigma	Effect of Group	(2,343)	16.10	491	< .001	.09
For Simon Tau	Effect of Group	(2,343)	20.35	11037	< .001	.11
For Switching RT	Main Effect of Group	(2,320)	34.82	1260786	< .001	.18
	Main Effect of Condition	(1,320)	143.77	107091	< .001	.31
	Group × Condition Interaction	(2,320)	12.63	107091	< .001	.07
For Switching Error	Main Effect of Group	(2,320)	34.23	107.72	< .001	.18
	Main Effect of Condition	(1,320)	16.16	12.65	< .001	.05
	Group × Condition Interaction	(2,320)	2.02	12.65	.14	.01
For Switching Mu	Effect of Group	(2,320)	17.69	525062	< .001	.10
For Switching Sigma	Effect of Group	(2,320)	6.76	109659	< .001	.04
For Switching Tau	Effect of Group	(2,320)	9.02	403709	< .001	.05

For the Stroop task, the main effects of Group and Condition and the Group × Condition interaction were all significant. Follow-up tests revealed that the Stroop effect (incongruent – congruent) was larger for very mild DAT individuals than for healthy older adults after controlling for age (RT: p < .001, η_p² = .12; overall errors: p < .001, η_p² = .09; intrusion errors: p < .001, η_p² = .06; non-intrusion errors: p < .001, η_p² = .04) and larger for healthy older adults than for young adults in RT (p < .001, η_p² = .05), but not in overall errors (p = .50, η_p² = .002), intrusion errors (p = .20, η_p² = .006) or nonintrusion errors (p = .11, η_p² = .009).

For the Simon task, the main effects of Group and Condition and the Group × Condition interaction were all significant. Follow-up tests revealed that the Simon effect (incongruent – congruent) was larger for very mild DAT individuals than for healthy older adults, after controlling for age (RT: p < .001, η_p² = .05; errors: p < .001, η_p² = .03), and larger for healthy older adults than for young adults in RT (p < .005, η_p² = .04), but not in errors (p = .87, η_p² = .00).

For the Switching task, the main effects of Group and Condition in both RT and errors and the Group × Condition interaction in RTs were all significant, but the interaction in errors was not. Follow-up tests revealed that the local switch cost (switch – nonswitch) in RT was smaller for very mild DAT individuals than for healthy older adults, after controlling for age (p < .001, η_p² = .05). The local switch cost in error rates was larger, albeit marginally so, for very mild DAT individuals than for healthy older adults, after controlling for age (p = .09, η_p² = .01). The cost did not differ for young and healthy older adults in RT (p = .18, η_p² = .01) or errors (p = .38, η_p² = .003), consistent with previous studies in task switching (e.g., Kray & Lindenberger, 2000). The smaller local switch cost in very mild DAT individuals was also in line with our prediction. That is, the deficit in attentional control system for these individuals made it less likely for them to suppress one of the task sets across trials in the Switching task. The activation of both task sets reduced the local switch cost in RT but at the same time, increased, albeit marginally, the local switch cost in errors as responses were more error-prone when the activation of the irrelevant task set were not successfully suppressed.²

The DAT-related reduction in local switch cost at first glance appears to be incompatible with the findings reported in previous studies examining individuals with DAT (e.g., Belleville et al., 2008) or with other attentional control problem (e.g., ADHD children in Cepeda et al., 2000). However, it should be noted that the methodological differences between these studies and the present study likely make direct comparisons problematic. For example, Belleville did not find any differences in local switch cost between their MCI individuals and their controls; however, their switching task involved a random intermixing of switch and nonswitch trials, as opposed to the AABBAA ordering used here. Hence, healthy controls may have been less tuned to the task constraints before hand in Belleville et al., thus producing great switch costs. In addition, Cepeda et al. used a numerical Stroop switching task, and observed larger switch costs in their ADHD children, compared to the control sample. It is possible that the selection based on the numerical Stroop task produced the increased difficulty for the ADHD participants. In fact, we have recently found that a Stroop switching task does indeed produce a much higher error rate in DAT individuals, compared to healthy controls (Hutchison, Balota & Duchek, submitted). Clearly, there are many characteristics of switching tasks that can influence between group comparisons of switch costs (see Logan & Gordon, 2001, for a review), and so one needs to be cautious about the comparisons across different switching tasks. The important emphasis in the present study is how early stage DAT influences the RT distributional characteristics in the present type of switching task, which we now turn.³

Ex-Gaussian Parameters and Vincentile Plots

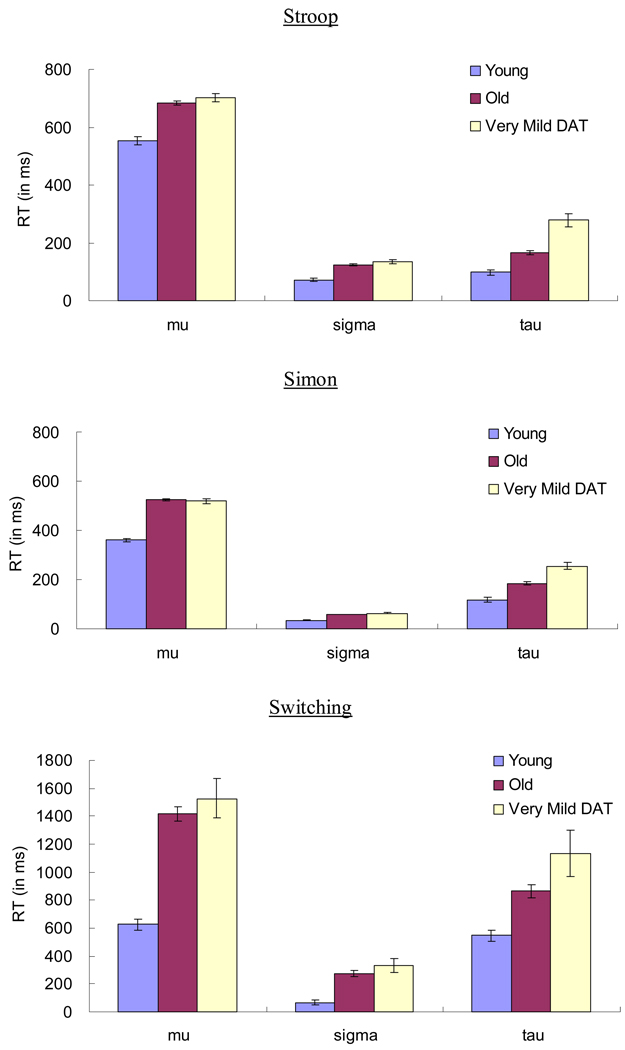
Figure 2 summarizes the mean ex-Gaussian parameters in these three tasks and Figure 3 presents the Vincentile plots in all of these tasks. For each plot, the empirical Vincentiles are represented by data points and standard error bars, while the Vincentiles for the respective best-fitting ex-Gaussian distribution are represented by lines. The theoretical Vincentiles were computed by line search on the numerical integral of the fitted ex-Gaussian distribution. The goodness of fit between the empirical and theoretical Vincentiles reflects the extent to which the empirical RT distributions are being captured by the ex-Gaussian parameters (see e.g., Andrews & Heathcote, 2001). The Greenhouse-Geisser correction was used in all analyses involving Vincentiles in order to avoid the potential violation of sphericity. The statistics of the one-way ANOVAs for the ex-Gaussian parameters are listed in Table 2. For the three attention tasks, all three ex-Gaussian parameters increased across groups. For the Stroop task, follow-up tests showed that all three ex-Gaussian parameters were higher for healthy older adults than for young adults (Mu: p < .001, η_p² = .11; Sigma: p < .001, η_p² = .10; Tau: p = .001, η_p² = .04). As noted earlier, an increase in all three parameters is consistent with a general slowing model of aging. Importantly, however, after controlling for age, Tau, but not Mu or Sigma, was higher for very mild DAT individuals than for healthy older adults (Mu: p = .68, η_p² = .001; Sigma: p = .22, η_p² = .005; Tau: p < .001, η_p² = .10). In the Vincentile plots, the increase in RT across the distributions was sharper for very mild DAT individuals than for healthy older adults after controlling for age [F (1.24, 392.92) = 56.14, MSE = 4104, p < .001, η_p² = .15] and for healthy older adults than for young adults [F (1.29, 353.10) = 37.79, MSE = 2476, p < .001, η_p² = .12].

Figure 2.

The ex-Gaussian parameters in Stroop, Simon, and Switching tasks as a function of group. Error bars indicate standard errors of means.

For the Simon task, all three ex-Gaussian parameters were higher for healthy older adults than for young adults (Mu: p < .001, η_p² = .27; Sigma: p < .001, η_p² = .10; Tau: p < .005, η_p² = .04). Again, after controlling for age, Tau, but not Mu or Sigma, was higher for very mild DAT individuals than for healthy older adults (Mu: p = .11, η_p² = .01; Sigma: p = .34, η_p² = .003; Tau: p < .001, η_p² = .05). In the Vincentile plot, the increase in RT across the distribution was sharper for very mild DAT individuals than for healthy older adults after controlling for age [F (1.11, 351.49) = 10.35, MSE = 4173, p < .001, η_p² = .03] and for healthy older adults than for young adults [F (1.12, 302.06) = 11.35, MSE = 3380, p < .001, η_p² = .04].

For the Switching task, all three ex-Gaussian parameters were higher for healthy older adults than for young adults (Mu: p < .001, η_p² = .13; Sigma: p < .001, η_p² = .05; Tau: p < .01, η_p² = .03). Once again, after controlling for age, Tau, but not Mu or Sigma, was higher for very mild DAT individuals than for healthy older adults (Mu: p = .44, η_p² = .002; Sigma: p = .27, η_p² = .004; Tau: p < .05, η_p² = .02). In the Vincentile plot, the increase in RT across the distribution was sharper for very mild DAT individuals than for healthy older adults after controlling for age [F (1.22, 354.46) = 9.52, MSE = 175189, p < .005, η_p² = .03] and for healthy older adults than for young adults [F (1.18, 309.01) = 18.21, MSE = 119719, p < .001, η_p² = .07]. It should be noted that even though the ex-Gaussian distributions were not always fitted very well in the slowest bin for all three attention tasks (see Figure 3), the overall pattern of Vincentile plots still clearly demonstrate that the DAT-related effect was particularly stronger in the last few bins of the RT distribution.

In sum, the results from the RT distributional analyses are remarkably clear. Whereas healthy aging has a consistent effect on Mu, Sigma, and Tau, early-stage DAT only influences the tail of the distribution, as reflected by changes in Tau. This pattern was replicated across all three attention tasks.⁴

Relationship between Ex-Gaussian Parameters and Psychometric/Span Measures

Because the overall patterns of Mu, Sigma and Tau were quite similar across the Stroop, Simon and Switching tasks, we conducted a confirmatory factor analysis to determine if these three variables loaded on three distinct latent factors, reflecting the three ex-Gaussian parameter estimates. Indeed, the results from this analysis yielded three latent variables with an excellent fitted model [χ²(15) = 21.17, p = .13, RMSEA = .04, CFI = .99], using a minimum criterion for acceptability of fit as a CFI > .90 (Hu & Bentler, 1995) and a RMSEA < .10 (Browne & Cudeck, 1993). We therefore computed a composite Mu, Sigma and Tau for the following correlation analyses. For each participant we computed the z-scores of Mu, Sigma and Tau (based on the overall mean and standard deviation across groups) for each of the three tasks and then averaged the z-scores of Mu, Sigma and Tau across all three tasks. These composite scores represent the mean (Mu) and standard deviation (Sigma) of the Gaussian distribution and the tail (Tau) of the RT distribution across the three attention tasks.

Table 3 summarizes the correlations between the composite Mu/Sigma/Tau and the psychometric/span/personality measures listed in Table 1. All 15 psychometric/span measures (except MMSE and personality measures) were first classified under three types of cognitive abilities: episodic/semantic memory, processing speed, and working memory. This classification was assessed by confirmatory factor analyses, with each type of cognitive ability represented by a latent factor.⁵ There were four outlier tasks that were not well fit by the model in this sample. For example, forward digit span did not load highly on any of the three latent factors. Moreover, although backward digit span, Crossing Off, and the Boston Naming Task loaded as expected, their loadings were not very strong (all < |.32|) and excluding them significantly improved the fit of the overall model, as reflected by the fit statistics. Hence, we did not include these three variables in our composite measures. In the final model, all loadings for the three latent variables were higher than |.44|, suggesting that the variables that contributed to each of these three latent variables should be representative enough for the cognitive abilities in a particular domain. To perform the following correlation analyses, we computed composite measures for working memory by averaging the z-scores of reading span, computation span and rotation span, for episodic/semantic memory by averaging the z-scores of logical memory, associate recall, WAIS information and Animal Fluency, and for processing speed by averaging the z-scores of word fluency S-P, WAIS Digit Symbol, Trail Making A and Trail Making B. These composite scores are analogous to the factor scores estimated in the confirmatory factor analyses.

Table 3.

Correlation between composite Mu/Sigma/Tau and Psychometric/Span/Personality Measures

	Healthy Old (CDR 0)			Very Mild DAT (CDR 0.5)			Overall Sample
	Mu	Sigma	Tau	Mu	Sigma	Tau	Mu	Sigma	Tau
Mini-Mental State Exam	−0.03	−0.06	−0.30**	−0.13	−0.06	−0.35**	−0.06	−0.05	−0.33**
Forward Digit Span	−0.06	−0.04	−0.14*	0.12	0.10	−0.11	0.02	0.02	−0.12*
Backward Digit Span	0.00	−0.05	−0.20**	0.07	−0.01	−0.24*	0.03	−0.03	−0.20**
Boston Naming	−0.05	−0.08	−0.15*	−0.18	−0.20^	−0.18	−0.08	−0.11^	−0.16*
Crossing Off	−0.19**	−0.08	−0.20**	−0.11	−0.14	−0.31*	−0.15*	−0.09	−0.21**
Conscientiousness	−0.15*	−0.15*	−0.17*	−0.05	0.00	−0.14	−0.12*	−0.11^	−0.15*
Neuroticism	−0.01	0.05	0.07	0.04	0.05	0.28*	0.02	0.06	0.15*
Working Memory	−0.10	−0.12	−0.38**	−0.02	0.04	−0.41**	−0.07	−0.07	−0.38**
Partial Correlation	0.05	−0.04	−0.17**	0.03	0.07	−0.09	0.04	0.00	−0.15**
Reading Span	−0.05	−0.09	−0.19**	−0.01	0.02	−0.35**	−0.04	−0.06	−0.24**
Computation Span	−0.07	−0.07	−0.29**	0.01	0.03	−0.28*	−0.05	−0.05	−0.27**
Rotation Span	−0.10	−0.14*	−0.36**	−0.16	−0.08	−0.33**	−0.13*	−0.13*	−0.34**
Episodic/Semantic Memory	−0.10	−0.08	−0.28**	0.01	0.07	−0.43**	−0.07	−0.04	−0.32**
Partial Correlation	0.04	0.01	−0.01	0.08	0.12	−0.17	0.03	0.04	−0.05
Logical Memory	−0.09	−0.14*	−0.15*	0.05	0.05	−0.26*	−0.05	−0.09	−0.17**
WMS Associate Recall	−0.09	−0.11	−0.26**	−0.11	0.02	−0.37**	−0.10^	−0.08	−0.29**
WAIS Information	−0.04	−0.05	−0.27**	0.16	0.15	−0.33**	0.03	0.01	−0.28**
Animal Fluency	−0.07	0.02	−0.17*	−0.10	−0.01	−0.34**	−0.09	0.00	−0.21**
Processing Speed	−0.28**	−0.17**	−0.49**	−0.25*	−0.22^	−0.59**	−0.25**	−0.18**	−0.53**
Partial Correlation	−0.27**	−0.13^	−0.35**	−0.27*	−0.28*	−0.48**	−0.24**	−0.17**	−0.40**
WAIS Digit Symbol	−0.29**	−0.25**	−0.41**	−0.23^	−0.17	−0.53**	−0.24**	−0.21**	−0.44**
Word Fluency S-P	−0.26**	−0.07	−0.35**	−0.15	−0.17	−0.27*	−0.20**	−0.09	−0.31**
Trail Making A	0.22**	0.17*	0.36**	0.12	0.11	0.44**	0.15*	0.13*	0.40**
Trail Making B	0.05	0.03	0.35**	0.25*	0.22^	0.53**	0.11^	0.09	0.44**

^{^}Note. p < .10,

^*p < .05,

^**p < .01.

The Mu, Sigma and Tau were based on the averaged z-score of Mu, Sigma and Tau in Stroop, Simon and Switching tasks. The composite scores of episodic/semantic memory, working memory, and processing speed were based on the averaged z-score of psychometric/span variables under the subheadings. The “Partial Correlation” row under each subheading indicates the correlation between the composite score in one domain (e.g., processing speed) and Mu/Sigma/Tau after controlling for the scores in other two domains (e.g., working memory and episodic/semantic memory). All correlation analyses for older adults and very mild DAT individuals were controlled for age and those for overall samples were controlled for age and CDR status.

We separately performed the correlation analyses for healthy older adults and for very mild DAT individuals, controlling for age. We also conducted the analyses for the overall sample, controlling for age and CDR status (0 vs. 0.5) (see Table 3). While Mu and Sigma were only correlated with processing speed, Tau was correlated with all three composite scores. The Pearson correlations were generally higher for working memory and processing speed than episodic/semantic memory. When we controlled for the effects of the other two composites scores, (a) all three ex-Gaussian parameters were no longer correlated with episodic/semantic memory, (b) processing speed was still correlated with all ex-Gaussian parameters, with all partial correlations being stronger for Tau, and more importantly, (c) working memory was still significantly correlated with Tau. We will return to the specific Tau/working memory relationship in the General Discussion section.

Relationship between Ex-Gaussian Parameters and Personality

All three ex-Gaussian parameters were negatively correlated with Conscientiousness for healthy older adults (see Table 3). Despite the small effect size, the relationship between Tau and Conscientiousness is consistent with previous studies (e.g., Duchek et al., 2007, 2008) which have provided suggested that Conscientiousness reflects the ability to maintain goals and to suppress irrelevant information in the attentional control system. It is noteworthy that the correlations in the overall sample are consistent with the prediction that Tau is positively correlated with Neuroticism and negatively correlated with Conscientiousness. The only other significant correlation in the overall sample is a negative correlation between Mu and Conscientiousness. Again, although these correlations are modest, these results clearly converge with recent evidence suggesting a relationship between variability in these attention tasks and personality traits (see Duchek et al., 2007; Robinson & Tamir, 2005), and point to the importance of the relatively slow RTs in producing the changes in variability.

Discussion

In the present research, we investigated the characteristics of the RT distribution in three attention tasks, Stroop, Simon and Switching, to better understand the changes that occur in healthy aging and in the earliest detectable changes in very mild DAT. These attention tasks have been shown to be sensitive to the effects of healthy aging and early-stage DAT (e.g., Castel et al., 2007; Spieler et al., 1996). We also examined how ex-Gaussian parameters were associated with various cognitive abilities, as measured by standard psychometric tasks, and with specific personality traits (Neuroticism and Conscientiousness) that likely tap attentional control systems. It is worth emphasizing that the current study provided a comparison of a well-characterized group of individuals in the earliest detectable stage of DAT with healthy older adults, free of any cognitive impairment. A designation of very mild DAT on the CDR scale (CDR 0.5) denotes cognitive impairment at a very comparable stage to MCI without dementia (Storandt et al., 2006).

The results are very straightforward. When examining the mean-level RT performance across groups in the three attention tasks, we found the typical age-related and DAT-related changes in the Stroop effect, Simon effect, and local switch cost, suggesting that healthy older adults and to a larger extent, very mild DAT individuals, had greater difficulty controlling the prepotent pathway when there was an incongruent mapping between a stimulus (e.g., RED presented in green color) and the appropriate response (e.g., green). This is consistent with the notion of a breakdown in attentional control in early-stage DAT (see also Balota & Faust, 2001; Castel et al., 2007; Duchek & Balota, 2005; Spieler et al., 1996). The analyses of ex-Gaussian parameters that estimate different components of participants’ overall RT distribution indicated that healthy aging affected all three components of RT distributions. Relative to young adults, healthy older adults demonstrated a shift (Mu), an increase of variability of the Gaussian component (Sigma) and an increased tail (Tau) of their RT distributions. Thus, all parameters appear to change, albeit to varying degrees. More importantly, only Tau, but not Mu or Sigma, is sensitive to the DAT-related change, indicating that the DAT-related increase in intraindividual variability in RT reported in prior research (e.g., Christensen et al., 2005; Dixon et al., 2007; Duchek et al., in press) may be due to very mild DAT individuals producing a larger tail of the RT distribution than healthy older adults. It is noteworthy that all of these findings were replicated in three attention tasks, attesting to the consistency of DAT-related changes in a specific component (i.e., the tail) of the RT distribution.

Before elaborating on the implications of the current findings, it is important to clarify a conceptual distinction between selective attention and response selection and to rule out three alternative interpretations. First, although we have labeled the tasks used as “attention” tasks, it is the case that they likely measure both selective attention (how well participants attend to the task-relevant information, e.g., ink color in the Stroop task) and response inhibition (how well they inhibit the task-irrelevant information, e.g., color name in the Stroop task, see Faust & Balota, 2007). Some researchers have found it very difficult to separate the influence of selective attention and response inhibition (Gorfein & MacLeod, 2007), while others have tried to tease apart their contributions to task performance. For example, by manipulating the cue-target interval and quantitatively modeling young and older adults’ performance in a task-switching paradigm, Meiran and Gotler (2001) found that the age-related effect was stronger for the duration of response initiation and selection than for attentional selection (i.e., the time it takes to adjust the attentional focus). However, because the purpose of the present study is to explore the general influence of attentional control on the characteristics of the underlying RT distributions for healthy older adults versus very mild DAT individuals, our three tasks were not designed to tease apart the influences of selective attention and response inhibition on participants’ RT performance. Given that we found robust age- and DAT-related differences in the tail of the RT distributions (i.e., Tau), future research should utilize specific paradigms (e.g., Meiran & Gotler, see also Yehene & Meiran, 2007) to further dissociate the roles of selective attention and response selection in these standard attention tasks.

Second, one could argue that very mild DAT individuals might have used a more stringent response criterion than young and healthy older adults. As shown by their psychometric performance (see Table 1), very mild DAT individuals produced worse performance than healthy older adults across various cognitive tasks. To compensate for a reduced reliability of their cognitive system, when making speeded responses, very mild DAT individuals might be biased toward awaiting the results of further processing to distinguish among the activated representations, rather than producing any available “well-formed” response, thus making slower responses more frequently than their healthy counterparts. If this is the case, one would expect that those individuals who were more accurate in their responses should yield larger Tau in all three attention tasks. However, we found negative correlations between composite Tau and overall accuracy for young adults (r = −.12, ns), healthy older adults (r = −.43, p < .01) and very mild DAT individuals (r = −.66, p < .01). Those who showed a larger tail in their RT distribution were in fact less accurate in their responses, suggesting that the age- and DAT-related differences in Tau were unlikely due to speed-accuracy tradeoffs.

Third, one could argue that the size of Tau in very mild DAT individuals might have been artificially inflated by their high error rates. Because these individuals made more errors in our attention tasks (see Figure 1) and RTs are typically slower following erroneous trials (e.g., Rabbitt, 1966), their larger Tau could be attributed to having more error trials, rather than producing a particularly large proportion of slower responses in the tasks. To address this possibility, we reanalyzed the estimates for Tau in all three attention tasks after excluding the trials that were preceded by errors. After averaging the findings across the three tasks due to their high similarity, Tau was still larger for very mild DAT individuals (613 ms) than for healthy older adults (446 ms), and in turn for young adults (269 ms) (all comparisons yielded ps < .01). If anything, the size of Tau was numerically larger when the trials with preceding errors were excluded from the analyses than when they were included (young: 255 ms, healthy old: 405 ms, and very mild DAT: 557 ms). Hence, the age-related and DAT-related differences in Tau are not likely due to the fact that very mild DAT individuals and healthy older adults produced more errors in the attention tasks.

Fourth, for the Switching task, it is possible that the difference in performance between healthy older adults and very mild DAT individuals could be partially attributed to their use of different strategies. Given that very mild DAT individuals have poorer working memory abilities (see Table 1), they might have difficulty keeping track of the predictable AABB sequence in the switching task and thus rely more on the cues presented at the top of the screen than healthy older adults. This could partially account for their larger tails of RT distribution (i.e., larger tau), relative to young and healthy older adults. Indeed, we measured the number of trials (out of 60) that participants looked at the cue during the Switching task (i.e., look-up frequency) for 70% of healthy older adults and very mild DAT individuals. Importantly, both groups were likely to look at the cues. There was no difference in the frequency between the two groups [45.8 vs. 45.3, t (224) = .19]. Nevertheless, to determine whether this variable affected the pattern of our results, we performed the same set of analyses on RTs, errors and ex-Gaussian parameters, with the frequency of looking at the cues and participants’ age being treated as covariates. The patterns were highly similar to those reported above. The local switch cost in RT was smaller for very mild DAT individuals than for healthy older adults (p < .001, η_p² = .05), although the local switch cost in error rates was not different between healthy older adults and very mild DAT individuals (p = .42, η_p² = .003). More importantly, the pattern of ex-Gaussian parameters was replicated. Only Tau, but not Mu or Sigma, was higher for very mild DAT individuals than for healthy older adults (Mu: p = .57, η_p² = .001; Sigma: p = .63, η_p² = .001; Tau: p < .05, η_p² = .03). The increase in RT across the distribution was sharper for very mild DAT individuals than for healthy older adults [F (1.15, 255.18) = 7.65, MSE = 1025595, p < .005, η_p² = .03]. Hence, the potential differences in participants’ strategies between healthy older adults and very mild DAT individuals did not significantly influence the pattern of our findings. Of course, this potential strategic difference could not account for why very mild DAT individuals also showed larger Tau in two other attention tasks either.

After ruling out all these alternative explanations, the important question then becomes why the very mild DAT individuals produced particularly slower RTs than healthy older adults in the slow tail of their RT distributions? Among various potential neurobiological/physiological mechanisms, such as neural transmission speed and fatigue, we believe that the larger Tau effect in early-stage DAT could be interpreted within an attentional control framework (see Balota & Faust, 2001). One of the major goals of a cognitive system is to flexibly tune itself to current task demands and stay tuned across time to those demands via attentional control mechanisms (see, e.g., Baddeley et al., 2001; Engle & Kane, 2004). As attentional control systems begin to deteriorate, these systems may no longer be as well tuned across time to the specific goals of the task (cf., Duncan et al., 1996). Hence, individuals in the earliest stage of DAT may more frequently take a longer time to avoid the distracting information, thereby demonstrating a larger tail in their RT distributions. This extends West’s proposal (e.g., West, 2001; West et al., 2002) that the age-related changes in cognitive performance are associated with the deterioration of an attentional control system that maintains the goals of a task across time and regulates competing pathways (see also Bunce et al., 2007, for a discussion of the connection between intraindividual variability in RT and white matter hyperintensities in the frontal lobe, one of the major anatomical areas implicated in attentional control).

In the present study, the relationship between Tau and the abilities to maintain their task goal over time was supported by our correlation analyses. We found that Tau, rather than Mu and Sigma, was correlated with various psychometric measures, in particular those that tap working memory and processing speed. It is intriguing that the relationship between Tau and working memory was still significant after controlling for participants’ age and CDR status, as well as their differential episodic/semantic memory or processing speed performance (cf. Engle et al., 1999.

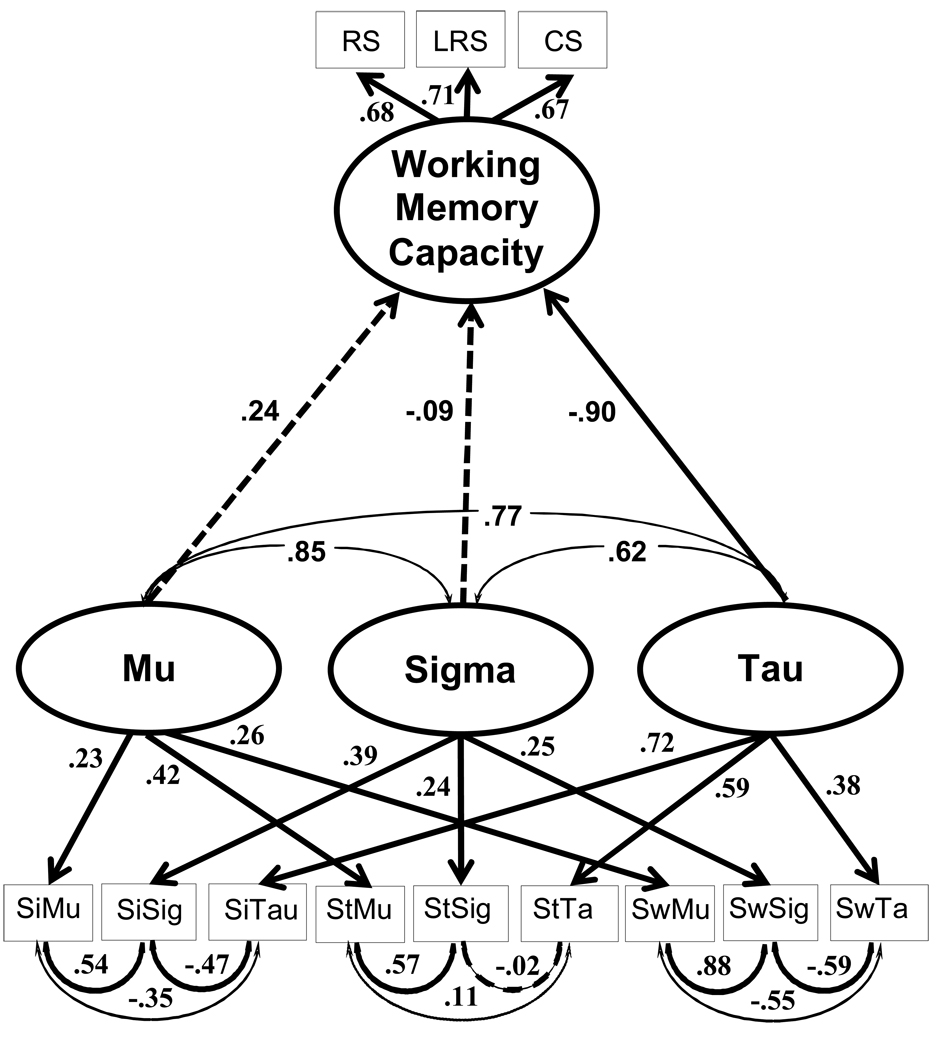
As noted earlier, Schmiedek et al. reported an interesting relationship between Tau, but not Mu and Sigma, and working memory constructs via structural equation modeling. Because we also had working memory measures available in the present study we attempted to replicate this theoretically important relationship in our sample. Hence, we computed a structural equation model using maximum likelihood estimation. Because the distributions of several variables were significantly skewed, the data were transformed in order to reduce skewness. For the Stroop Tau and Simon Mu parameters, the data were log transformed. For the Simon Sigma, Simon Tau, Switching Mu, Switching Sigma, and Switching Tau parameters, the data were square root transformed. Missing WMC data (for 8 healthy older adults and 9 very mild DAT individuals) and were replaced with the mean of each variable within each group (i.e., within the healthy older adult and DAT groups). The resulting model is shown in Figure 4. The model fit was excellent [χ²(39) = 47.38, p = .17, RMSEA = .03, CFI = .98], using a minimum criterion for acceptability of fit as a CFI > .90 (Hu & Bentler, 1995), and a RMSEA < .10 (Browne & Cudeck, 1993). Remarkably, as shown in Figure 4, the factor intercorrelation between the Tau construct and the working memory construct was very strong (−.90), whereas, the factor intercorrelations for both Mu and Sigma factors were much weaker (.24 and −.09, respectively). These data indicate that the pattern of relations reported by Schmiedek et al. in a young adult sample generalized to a sample of healthy older adults and DAT individuals, with more attention-demanding cognitive tasks. Because working memory capacity has been conceptualized as an attentional control ability required for goal maintenance (Engle & Kane, 2004; McCabe et al., in press), these data provide converging evidence demonstrating a role of goal maintenance in Tau.

Figure 4.

Model fit for the relationship between the latent construct of working memory and the latent construct of ex-Gaussian parameters.

Apart from the relationship between cognitive measures and ex-Gaussian parameters found in the attention tasks, we also explored the relationship between these parameters and personality traits. As previously mentioned, recent studies have reported that there was an increase in Neuroticism and a decrease in Conscientiousness in very mild DAT individuals relative to healthy older adults, which accounted for unique variance in discriminating these two groups, above and beyond standard neuropsychological tests (Duchek et al., 2007; see also Table 1). This is consistent with the claim that differences in these personality traits may serve as a “non-cognitive” indicator of the early onset of DAT (see also Wilson et al., 2003, 2007). In the current study, we found DAT-related differences in Conscientiousness and Neuroticism.⁶ For the overall participants controlling for age and CDR status, the larger Tau was associated with a higher score in Neuroticism and a lower score in Conscientiousness, supporting the notion that Tau, a specific component of the RT distribution, appears to be relatively more sensitive to the personality changes that occur with onset of the disease. As noted earlier, both Neuroticism and Conscientiousness could be easily tied to mechanisms that are related to attentional control.

Of course, there are alternative ways to capture RT distributions, such as the Weibull and ex-Wald models (see Luce, 1986; Van Zandt, 2002, for excellent reviews), and clearly there is some debate about which distribution is best. Cousineau et al. (2004, see also Balota et al., 2008) listed a number of guiding principles for considering an appropriate model for distributional analyses. First, parameters from a particular model should capture the manipulations in a useful manner. It is unclear if a RT distributional model provides any new information if all parameters are consistently changing across manipulations. In the current study, in contrast to healthy aging, only the exponential component captured DAT related changes. Second, the model should be parsimonious in the number of parameters that are used to describe the RT distribution. The relatively simple three-parameter ex-Gaussian would appear efficient by this criterion. In short, we have chosen the ex-Gaussian approach because of recent evidence suggesting it is useful in understanding changes across conditions within a task and across tasks, and also its relation to the standard mean analyses (i.e., the sum of Mu and Tau is the Mean). Ultimately, any RT distributional analyses should be coupled with specific computational models of a given task performance (see e.g., Balota & Spieler, 1999; Norris, 2009; Racliff et al., 2004), and so the present study and analyses should only be considered as the first descriptive account of both age related and DAT related changes in the RT distributions across standard attentional control tasks.

In conclusion, the current study supports the utility of examining the characteristics of RT distributions for capturing changes in variability that occur both in healthy aging and in early stage DAT. To our knowledge, this is the first study that uses three attention tasks (Stroop, Simon and Switching) and employs ex-Gaussian analyses to pinpoint the specific components of the RT distribution that were affected by healthy aging as well as early-stage of DAT. Of course, how well such variability actually predicts early-stage DAT conversion depends on a large scale longitudinal study of well-characterized healthy controls. We are currently engaged in such a study. Finally, we argue that a consistent increase in the tail of distribution for RT performance across three attention tasks in early-stage DAT is consistent with the notion of a breakdown in attentional control systems very early in the disease process.