Abstract
We describe an immersed boundary method for problems of fluid-solute-structure interaction. The numerical scheme employs linearly implicit timestepping, allowing for the stable use of timesteps that are substantially larger than those permitted by an explicit method, and local mesh refinement, making it feasible to resolve the steep gradients associated with the space charge layers as well as the chemical potential, which is used in our formulation to control the permeability of the membrane to the (possibly charged) solute. Low Reynolds number fluid dynamics are described by the time-dependent incompressible Stokes equations, which are solved by a cell-centered approximate projection method. The dynamics of the chemical species are governed by the advection-electrodiffusion equations, and our semi-implicit treatment of these equations results in a linear system which we solve by GMRES preconditioned via a fast adaptive composite-grid (FAC) solver. Numerical examples demonstrate the capabilities of this methodology, as well as its convergence properties.
Keywords: immersed boundary method, advection-electrodiffusion, local mesh refinement, implicit, fast adaptive composite, FAC
1 Introduction
Almost everything around us is moving in visible and invisible ways. Within a living organism, such motion invariably involves fluid-structure interaction. At the level of individual cells, the coupled motion of fluid and structure is linked also to the electrodiffusion of ions.
Ca2+ ion, in particular, acts as a signal which triggers the motion of cells and of subcellular components. Examples include the well known roles of Ca2+ in excitation-contraction in muscle [34]; in the fusion of vesicles to the plasma membrane during the process of exocytosis, for example within the presynaptic terminal of a neuron where the result is the release of neurotransmitter [46]; and in the dendritic spine, where Ca2+ triggers transient shape changes (“twitching spines”) and is thought to play a role in synaptic plasticity [35]. In the case of dendritic spines, it is particularly noteworthy that the dynamics of Ca2+ within the spine head is determined not only by diffusion but also by fluid flow [47], that flow being induced by the Ca2+-triggered contraction of the spine.
Osmotic phenomena also couple the motion of fluid to that of solute. In biology, on the cellular and subcellular scales, osmosis is the principal mechanism for the movement of water, and is therefore of fundamental importance. When the relevant solutes are charged, as is typically the case in the biological context, their motions, and therefore the motions of the water that they produce, are strongly influenced by electrical effects. These considerations are crucial in the control of cell volume [36], in the transport of water across epithelia [48], in the movement of water within cells [49], and therefore in cell locomotion [50].
The computer simulation of osmotic phenomena but with neutral solutes has previously been done by Atzberger and colleagues [51]. In common with the present work, these authors used an immersed boundary method [7], which involves an Eulerian description of the fluid and solutes together with a Lagrangian description of immersed boundaries. The case of charged solutes has been undertaken by Rhyham and colleagues [39], who, in contrast to the approach taken here, used a fully Eulerian, phase-field method.
Also related to the present paper is a much larger body of work on electrodiffusion [52] without fluid flow. In this field, we mention the pioneering work of van Roosbroek [53], which was done in the context of the invention of the transistor, and also the research of Eisenberg and colleagues [54] on the Poisson-Nernst-Planck (PNP) equations as applied especially to ion transport through membrane channels. Finally, in this category, we mention the related work of Mori et al. [40, 55], who use a finite-volume methodology [37, 38] to simulate electrodiffusion in the electroneutral limit, in which solute concentrations are constrained to satisfy local electroneutrality, and in which space charge layers are regarded as infinitely thin and are therefore incorporated into internal boundary conditions. In the present work, by contrast, space charge layers have a finite (i.e., nonzero) thickness, and approximate local electroneutrality outside of the space charge layers emerges as a consequence of the basic electrodiffusion equations without any limiting process being used to simplify those equations before undertaking their numerical solution. The present methods are therefore more suitable for smaller scale problems, in which it may be important to resolve the space charge layers, instead of treating them as infinitely thin. For larger scale problems, however, the methods of [40,55] are likely to be more efficient, precisely because they do not require the resolution of the space charge layer.
In the present work, we describe a version of the immersed boundary method for problems of fluid-solute-structure interaction, i.e., fluid-structure interaction problems which include the advection-diffusion of one or more species of solutes [1]. We impose smoothed chemical potential barriers along internal boundaries or membranes. By means of these chemical potential barriers, the permeability of each solute across a membrane can be separately controlled. Although we do not do so at present, the chemical potential barriers for the different solutes can be spatially inhomogenous, and in this way our framework allows for the simulation of localized ion-selective membrane channels. Similarly, the chemical potential barriers can have local time dependence to simulate the stochastic opening and closing of membrane channels. Because the membrane appears in our computation as a collection of smooth chemical potential barriers (one for each solute), there are no boundary conditions per se to be applied at the membrane, and we are able to use a Cartesian grid covering the entire domain, with possible local Cartesian mesh refinement. In our methodology, there is no sharp distinction between the interior and exterior domain.
The numerical scheme for fluid-solute-structure interaction introduced in this paper employs linearly implicit timestepping and Cartesian grid local mesh refinement. We use the block-structured Cartesian grid adaptive mesh refinement (AMR) approach of Berger and Oliger [2] and Berger and Collela [3], an approach that was introduced in the context of shock capturing methods for hyperbolic partial differential equations. In the present context, this approach makes it feasible to resolve the steep gradients associated with the space charge layers that develop on either side of the membrane in our computations, as well as the steep gradients associated with the chemical potential barriers that model the membrane itself. Low Reynolds number fluid dynamics are described by the time-dependent incompressible Stokes equations, which are solved by a cell-centered approximate projection method [4–6]. The dynamics of the chemical species are governed by the advection-electrodiffusion equations. We use a semi-implicit discretization of these equations which results in a linear system of equations for the updated solute concentrations. This linear system is solved at each timestep by GMRES preconditioned via a fast adaptive composite-grid (FAC) solver.
The paper is organized as follows: In Section 2, we present the continuous formulation of the immersed boundary method with advection-electrodiffusion. In Section 3, a uniform grid discretization with implicit timestepping is proposed for the governing equations. In Section 4, we describe the locally-refined formulation of the numerical scheme. In Section 5, we briefly discuss implementation details, including linear solvers for locally refined grids. In Section 6, we present the results of several illustrative computations involving diffusion, advection-diffusion, electrodiffusion, and advection-electrodiffusion with a single neutral solute or with two ionic species, with either a fixed or a moving boundary. In Section 7, we present a convergence test which demonstrates that the method of this paper is first-order accurate. Finally, in Section 8, we conclude and discuss some possible future applications of the methodology.
2 Mathematical formulation of the immersed boundary method with advection-electrodiffusion
In the present work, we consider a fixed two-dimensional physical domain filled with a viscous, incompressible fluid that contains dissolved solute, which may be neutral or charged. Immersed within the domain is a closed membrane, which may either be fixed in place or be mobile and elastic. In the latter case, we assume that the mass of the membrane may be neglected, so that the sum of the forces acting on any part of the membrane is always equal to zero. The membrane may be permeable or impermeable to solute, and the permeability is controlled in a graded manner by a chemical potential barrier.
Throughout this work, we employ the following constants:
Dk: diffusion coefficient of the kth solute species
q: the elementary electrical charge (charge on a proton)
qzk: charge of the kth species of solute
ε: dielectric constant of fluid medium
KB: Boltzmann constant
T: absolute temperature (degrees Kelvin)
ρ: fluid density
μ: fluid viscosity
The Eulerian domain and its variables are denoted as follows:
ΩE: Eulerian domain
x = (x1, x2) ∈ ΩE: fixed Eulerian physical coordinates
u(x, t) = (u1(x, t), u2(x, t)): fluid velocity
p(x, t): fluid pressure
Ψ(x): chemical potential kernel
ψk(x, t): chemical potential associated with the kth solute species
ck(x, t): concentration of the kth solute species
Jk(x, t): flux per unit area of the kth solute species
ϕ(x, t): electrical potential
ρe(x, t): electrical charge density
The Lagrangian domain and its variables are denoted in the following way:
ΩL: Lagrangian domain of the immersed membrane
s ∈ ΩL: moving Lagrangian material coordinate attached to the membrane
X(s, t) = (X1(s, t), X2(s, t)): position of Lagrangian point s at time t
E[X(·, t)]: internal elastic energy stored in the membrane
FE(s, t): Lagrangian force density applied by the membrane
Fms(s, t): Lagrangian force density applied by the membrane to the solute
Fmf(s, t): Lagrangian force density applied by the membrane to the fluid
Ak(s, t) ds: contribution of arc (s, s + ds) of membrane to chemical potential of kth solute species
In our formulation, chemical potentials are used to control the permeability of the membrane to the different solutes that may be present. The chemical potential of the kth solute species is expressed by
| (1) |
Here, X(s, t) is the configuration of the immersed membrane at time t, where s is a Lagrangian parameter. The function Ak(s, t) describes the contribution of the membrane at X(s, t) to the chemical potential barrier for the kth species. The chemical potential kernel Ψ(x) defines how the contribution Ak(s, t) ds is to be spread out in space in the neighborhood of X(s, t).
In general, any bell-shape function with compact support can be used to construct the chemical potential kernel. To construct Ψ, we use the four-point smoothed Dirac delta function φ(r) described by Peskin [7]. The function φ(r) is given by
| (2) |
where r ∈ IR. The two-dimensional chemical potential kernel is taken to be the tensor product of the one-dimensional smoothed delta functions, i.e.,
| (3) |
Here, ω is a scaling factor so that Ψω is supported on a 4ω × 4ω square centered at the origin.
The electrical potential is the solution of the Poisson equation
| (4) |
| (5) |
Here, ρe is the electrical charge density. Note that ρe is different from the fluid density ρ which appears below in the incompressible Stokes equations. In the present work, Eq. (4) is solved on a periodic box. Consequently, a necessary condition for the existence of a solution to Eq. (4) is that the integral of the right-hand side over the domain is zero, i.e., that the system as a whole be electrically neutral. Note, however, that electroneutrality can be violated locally.
Eq. (4) defines ϕ uniquely up to an additive constant. The choice of this constant has no significance since only potential differences have physical effects.
Each chemical species of solute satisfies the advection-electrodiffusion equation
| (6) |
| (7) |
Eq. (6) is the continuity equation for the kth solute species. In this equation, ck is the concentration and Jk is the flux per unit area of this solute. Eq. (7) gives the flux per unit area as a sum of four terms: diffusion, drift caused by chemical potential gradients, drift caused by electrical potential gradients, and advection by fluid flow. The advection component from fluid flow is uck, where the fluid velocity u is obtained from the solution of the Stokes equations, as described below. The Eqs. (6)–(7) are a spatially distributed form of Nernst-Plank equations [41]. The equations (4)–(7) are sometimes called the Poisson-Nernst-Plank (PNP) equations [54]. In seminconductor physics, essentially the same equations (but with recombination included) are called the van Roosbroeck equations [53]. A somewhat unusual feature of our formulation is the inclusion of the advection term, but note that this is also done in [39].
To describe the (low Reynolds number) fluid flow, we use the time-dependent Stokes equations,
| (8) |
| (9) |
where ρ is the fluid density and μ is the fluid viscosity. The immersed elastic membrane moves at the local fluid velocity,
| (10) |
This boundary advection equation is the no-slip condition of a viscous fluid. Note that this equation implies that the membrane is impermeable to fluid. (Allowing the boundary to be permeable to fluid, as is required to simulate, e.g., osmotic effects, requires a simple modification to the equation of motion for the boundary; see [1,8].)
The external force f that appears in the Stokes equations has two parts,
| (11) |
where fmf is the force applied by the membrane directly to the fluid in which it is immersed, and fb is the electrochemical force transmitted to the fluid by the solutes. These forces are of the form
| (12) |
| (13) |
In Eq. (12), Fmf(s, t) ds is the force applied by an element ds of the membrane to the fluid in its vicinity. The delta function expresses the local character of the fluid-structure interaction. Note that if we integrate Eq. (12) over an arbitrary physical region Ω ⊆ ΩE, we obtain
| (14) |
which simply is the statement that the force transmitted by the membrane to the fluid in the region Ω is equal to the force generated by the part of the membrane that lies within Ω.
In Eq. (13), the quantity −(∇ψk + qzk∇ψ(x, t)) is the force acting on one molecule of the kth species of solute at location x at time t. Multiplying by ck(x, t) and summing over k, we obtain the force per unit volume acting on all of the chemical species at location x at time t. This force is transmitted to the fluid by collisions between the fluid and solute molecules.
Because the membrane is massless, the elastic force applied by the membrane to the fluid and to the solute can be expressed in terms of the internal elastic energy E stored in the membrane,
| (15) |
where ℘/℘X is the variational derivative defined by
| (16) |
which holds for all Y. We use the symbol ℘ here for “perturbation” instead of the more conventional δ to avoid confusion with the Dirac delta function, which plays a prominent role in this work.
We may obtain an explicit expression for Fmf in terms of ℘E/℘X and Fms. Recalling that ψ is defined by Eq. (1), we derive Fms, the Lagrangian form of the chemical force applied to the solutes by the membrane, via
| (17) |
where fchemical is the body force resulting from the chemical potential barrier. Just as Eq. (14) implies that the Lagrangian and Eulerian elastic forces are equal, Eq. (17) states that the total chemical force transmitted to the fluid from the membrane is equal to total chemical force acting on the solutes. Because Eq. (17) is satisfied on any sub-domain of ΩL, we have that the Lagrangian chemical force is given by
| (18) |
Having obtained an expression for Fms, we may express the Lagrangian force applied by the membrane to the fluid as
| (19) |
Note that explicit formulae are available for each of the terms on the right-hand side of Eq. (19). The formula for Fms has been given above (Eq. (18)), and a formula for ℘E/℘X, which depends on the assumptions made about the elasticity of the membrane, will be be stated next.
In our examples, the immersed boundary is an elastic membrane with a stiffness coefficient Ks for which the internal elastic energy E is defined in terms of the configuration of the membrane X(·, t) via
| (20) |
from which we derive
| (21) |
where
| (22) |
| (23) |
In these equations, FT is the tension of the elastic membrane, τ is the unit tangent to the boundary, and FE ds is the elastic force per unit length (see the discussion of units near the beginning of Section 6) applied by the arc ds of the boundary to the fluid and solute.
3 Uniform grid discretization
In this section, we describe a linearly implicit, uniform grid discretization of the continuous governing equations of Section 2. In many cases, when explicit timestepping methods are used, the stiffnesses of the elastic boundaries and the large gradients in the chemical and electrostatic potentials across boundaries necessitates the use of small timesteps to obtain a stable numerical scheme. Implicit timestepping schemes offer an approach to alleviating the stability restrictions imposed by explicit schemes. To avoid solving a monolithic system of equations for the updated fluid, solute, and structure variables at each timestep, however, we use a timestep-splitting approach to obtain independent backward-Euler type systems of equations for the advection-electrodiffusion and immersed boundary/Stokes systems which are solved independently each timestep. It is important to emphasize that although our discretization gives rise to systems of equations for the advection-electrodiffusion and immersed boundary/Stokes systems which are solved independently within each timestep, these systems are nonetheless explicitly coupled between timesteps. Indeed, an important feature of our method is that the dynamics of the solute, fluid, and structure are fully coupled.
Eqs. (4)–(7) of the advection-electrodiffusion equations, and Eqs. (8)–(10) immersed boundary/Stokes equations are both discretized using a linearly implicit timestepping scheme. In particular, for the advection-electrodiffusion equation satisfied by each chemical species, the drift velocity is handled explicitly but the concentration is treated implicitly, resulting in a linear system of equations for the unknown concentrations cn+1. In the immersed boundary/Stokes equations, the force-spreading and velocity-interpolation operators are handled explicitly, as are the electrochemical body forces on the solutes, but the elastic forces, the boundary configuration, the fluid velocity, and the fluid pressure are all treated implicitly, i.e., we solve a linear system for Xn+1, un+1, and . (Earlier implicit treatments of the immersed boundary method for fluid-structure interaction have been described by Mayo and Peskin [9], Newren et al. [10, 11], and Mori and Peskin [12], among others, and our basic approach is similar to these earlier schemes.) Although our time discretization is not fully implicit, we are nonetheless able to take significantly larger timesteps with this scheme as compared to a fully explicit time discretization.
3.1 Eulerian discretization and finite difference approximations
The Eulerian physical domain is discretized using a uniform Cartesian grid which is periodic in each coordinate direction. The locations of the grid cell centers are denoted by
| (24) |
where h = Δx = Δy is the uniform Cartesian grid spacing. The value of a variable u(x, t) at cell center (i, j) at time t = nΔt is denoted by
| (25) |
The cell-centered finite difference discretizations of the divergence, gradient, and Laplacian are denoted by Dh ·, Dh, and Lh, and are defined by
| (26) |
| (27) |
| (28) |
which are all second-order accurate finite difference approximations.
Side-centered fluid velocities are used for the computation of the drift velocity in the advection-electrodiffusion equations. Side-centered values and are obtained by averaging adjacent cell-centered quantities, i.e.,
| (29) |
| (30) |
The discrete divergence of a side-centered vector field u = (u1, u2) is denoted by Dh/2 · and is defined by
| (31) |
which is also a second-order accurate finite difference approximation.
3.2 Lagrangian discretization, a smoothed version of the Dirac delta function, and Lagrangian-Eulerian interaction
The Lagrangian coordinate domain is taken to be periodic in the Lagrangian parameter s (since the membrane takes the form of a closed curve) and is discretized on a computational lattice with uniform mesh spacing Δs. The value of a variable F evaluated at a node s of the Lagrangian mesh at time t = nΔt is denoted by
| (32) |
Using the function φ(r) defined in Section 2, a one-dimensional regularized Dirac delta function is constructed as
| (33) |
The two-dimensional smoothed delta function is taken to be the tensor product of one-dimensional smoothed delta functions, i.e.,
| (34) |
Note that δh(x) is supported on the 4-by-4 grid box centered at the origin.
The Lagrangian force density is spread from the Lagrangian mesh onto the Cartesian grid at time t = nΔt via
| (35) |
where Σs denotes a sum over discrete values of s, i.e., over s = 0, Δs, 2Δs, …. Similarly, the Eulerian fluid velocity is interpolated from the Cartesian grid onto the Lagrangian mesh at time t = nΔt via
| (36) |
for s = 0, Δs, 2Δs,….
For notational convenience, we define the spreading operator Sn and the interpolation operator by
| (37) |
| (38) |
Note that Sn and are adjoint linear operators with respect to an inner product which may be interpreted as the power applied by the membrane to the fluid. A consequence of this is that the power comes out the same whether it is evaluated in Lagrangian or in Eulerian variables.
3.3 The discretized chemical and electrical potentials
The discretized chemical potential for the kth chemical species is expressed by
| (39) |
and the discretized Poisson equation for the electrical potential is
| (40) |
In our timestepping scheme, we evaluate by Eq. (39) once per timestep for each of the chemical species, and we solve Eq. (40) for ϕn once per timestep.
3.4 A semi-implicit discretization of the advection-electrodiffusion equations
The spatial discretization of the advection-electrodiffusion equations uses a second-order upwind method for the advection terms and a centered second-order accurate discretization for the diffusion terms. The time discretization employs a combination of forward and backward Euler. Consequently, the method is formally second-order accurate in space but only first-order accurate in time. The time discretization results in a linear system of equations with a non-compact 9-point finite difference stencil.
The semi-implicit time discretization of the advection-electrodiffusion equations for the concentration ci,j = (ck)i,j of the kth species of solute is defined by
| (41) |
| (42) |
| (43) |
| (44) |
| (45) |
In these equations, the chemical concentration c is treated implicitly whereas the net drift velocity U is treated explicitly. The net chemical flux J = (J1, J2) is computed at the x and y cell edges of the Cartesian grid via Eqs. (42) and (43), and the net drift velocity is computed at the x and y edges of the grid from the fluid velocity and the electrochemical drift via Eqs. (44) and (45).
The values of the concentrations at the cell edges are determined by a spatially second-order accurate upwind discretization,
| (46) |
An analogous formula is used to compute the values of the concentration on the y edges of the grid. Note that the choice of which formula to use in Eq. (46) is made using the net drift velocity, which is fixed throughout the timestep. Consequently, the system of equations which must be solved to compute is linear.
3.5 A semi-implicit discretization of the immersed boundary/Stokes equations
The discretized immersed boundary/Stokes equations are solved using a linearly implicit scheme which makes use of an approximate projection method [4,13,14] for the time-dependent incompressible Stokes equations. The approximate projection method used for the incompressible Stokes equations employs a Crank-Nicolson treatment of the viscous terms, and makes use of a lagged approximation to the pressure gradient.
Before we present the discretization of the immersed boundary/Stokes equations, we first define the approximate projection operator  used in this work, namely
used in this work, namely
| (47) |
In the uniform grid case, this approximate projection operator is the same as that introduced in [13], and in the locally-refined case described in Section 4, this operator is the same as that described in [15]. In either case,  can be seen to be a finite difference approximation to the continuous projection operator I − ∇ (∇2)−1 ∇ ·. Because Lh ≠ Dh · Dh, generally Dh · (
can be seen to be a finite difference approximation to the continuous projection operator I − ∇ (∇2)−1 ∇ ·. Because Lh ≠ Dh · Dh, generally Dh · ( u) ≠ 0, and thus
u) ≠ 0, and thus 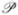 is not an “exact” projection operator. For any smooth vector field u, however, Dh · (
is not an “exact” projection operator. For any smooth vector field u, however, Dh · (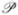 u) =
u) = 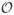 (h2), so that
(h2), so that 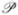 imposes the constraint of incompressibility to second order accuracy. For further details on projection methods for incompressible flows, see [16–18].
imposes the constraint of incompressibility to second order accuracy. For further details on projection methods for incompressible flows, see [16–18].
Our linearly implicit discretization of the immersed boundary/Stokes equations is based on the following nonlinearly implicit time discretization,
| (48) |
| (49) |
| (50) |
The foregoing system of equations defines un+1 and Xn+1 but not
To compute
, we note that the definition of 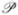 implies that
implies that
| (51) |
| (52) |
so that
| (53) |
Here, we are using a second-order accurate pressure-increment projection method; for further details, see [6]. Although the value of has no effect on the values of un+1 or Xn+1, the value of is used in the subsequent timestep and does affect the values of un+2 and Xn+2.
In the foregoing timestepping scheme, Eqs. (48)–(50), the quantity is the Lagrangian force derived from the stored elastic energy of the membrane and is to be computed from the unknown membrane configuration at the end of the time step Xn+1. This makes the above scheme implicit in the boundary force. In general, may be a nonlinear function of Xn+1. To simplify the task of solving the implicit equations, in practice we linearize the relationship between and Xn+1. In particular, the implicit elastic force term is linearized about Xn via
| (54) |
where is the Jacobian operator defined by
| (55) |
Replacing by in Eqs. (48)–(50) and algebraically rearranging terms, we obtain the following linear equation for (Xn+1 − Xn),
| (56) |
where
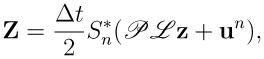 |
(57) |
| (58) |
| (59) |
| (60) |
Eq. (56) is a linear system which we solve for (Xn+1−Xn) via GMRES without preconditioning. The right-hand side Z is defined entirely in terms of quantities which are known at time level n. Once this linear system has been solved, we may evaluate u* as
| (61) |
Finally, un+1 and can be obtained from u* via Eqs. (51)–(53).
4 Local mesh refinement
In the immersed boundary method with advection-electrodiffusion, sti3 elasticity makes the tangential fluid velocity gradient large across the boundary. The gradients of the electrochemical potential are also steep near the boundary. To resolve these gradients efficiently, we employ local mesh refinement in the vicinity of the boundary. Previously, adaptive mesh refinement has been used in the context of the immersed boundary method by Roma et al. [19] and Griffith et al. [15,56]. In this section, we outline our approach to discretizing the governing equations on locally-refined grids.
In the block-structured local mesh refinement approach used in the present work, the Eulerian domain is described using a hierarchy of nested levels. Each level in the grid hierarchy is composed of the union of rectangular grid patches. All patches in a given level share the same uniform Cartesian grid spacing, and grid spacings on adjacent levels are related by an integer refinement ratio, which in this work is taken to be 2. Away from coarse-fine interfaces between levels of grid resolution, the standard uniform grid discretization is used. In the vicinity of such interfaces in grid resolution, however, additional care is required. Each grid patch possesses a layer of ghost cells which is adjacent to the patch boundary. Away from coarse-fine interfaces, ghost cell values are obtained by copying values from adjacent patches at the same level of refinement. At coarse-fine interfaces, ghost cell values on fine patches are computed by interpolating coarse and fine grid values. In the present work, we employ a linear interpolation strategy introduced by Ewing et al. [20] which makes use of both coarse and fine values in the vicinity of coarse-fine interfaces.
Following [5], our basic approach to computing cell-centered approximations to spatial differential operators on locally-refined grids is to define the discretization as the composition of three simpler operations: first, an operation which maps cell-centered quantities to cell edges; second, an operation which “synchronizes” values along the coarse-fine interfaces by averaging quantities defined on fine cell edges onto the overlying coarse cell edge; and third, an operation which maps edge-centered quantities back onto cell centers. For instance, the computation of the cell-centered gradient of a cell-centered quantity p is decomposed as (1) computing an edge-centered approximation to ∇p on each cell edge, (2) averaging the edge-centered approximation from finer levels onto coarser levels, and (3) interpolating the edge-centered approximation of ∇p back onto cell centers. Note that ghost cell values for p are only required by step (1), in which we compute an edge-centered approximation to ∇p using cell-centered data. These ghost cell values are determined via linear interpolation of coarse- and fine-grid values, as mentioned previously. For further details on the construction of the finite difference discretizations of ∇ ·, ∇, and ∇2 used in the present work, see [15,21]. The same approach is used to construct a composite-grid cell-centered discretization of the advection-electrodiffusion equations. Note that only one layer of ghost cells is required to evaluate our cell-centered approximations to the divergence, gradient, and Laplace operators, whereas two layers of ghost cells are required to evaluate the cell-centered approximation to the advection-electrodiffusion equations.
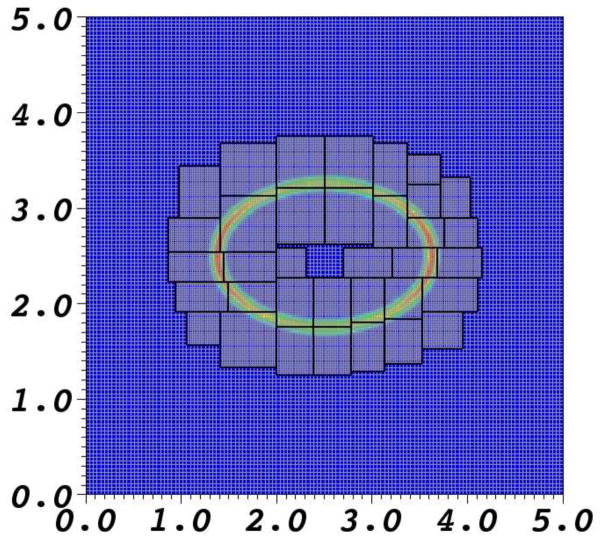
In the present work, the locally refined grid is constructed at the beginning of the simulation and is not adaptively updated as the simulation progresses. Grid patches are generated by tagging cells for refinement and applying the box-generation algorithm of Berger and Rigoutsos [22]. Cells are tagged for refinement within the support of the chemical potential barrier. An example of a locally refined mesh is shown in Fig. 1.
Fig. 1.
A locally refined grid comprised of two levels around the chemical potential barrier.
5 Implementation details
Our implementation of the foregoing numerical scheme employs several freely-available software libraries. Krylov subspace iterative methods such as GM-RES are provided by the PETSc library [23–25]. Grid generation and data management for locally refined grids is provided by the SAMRAI (Structured Adaptive Mesh Refinement Application Infrastructure) library [26–28].
To solve the immersed boundary/Stokes equations, we must solve Poisson problems resulting from the implicit treatment of the viscous terms and the application of the approximate projection operator. To solve the advection-electrodiffusion equations, we must solve one advection-electrodiffusion equation for each chemical species. In all cases, we employ a standard fast adaptive composite-grid (FAC) method [29] as a preconditioner for GMRES. (For details on the FAC algorithm used in this work, see [21].) We use the PFMG uniform-grid geometric multigrid solver [30,31] from the hypre library [32,33] as a bottom-solver in this FAC preconditioner. Note that the hypre geometric multigrid solvers are designed for finite difference, finite volume, or finite element discretizations with compact 5-point or compact 9-point stencils. Our discretization of the advection-electrodiffusion equation makes use of a non-compact 9-point stencil, however. Thus, for the multigrid bottom solver used by the FAC preconditioner, we replace the second-order upwind scheme described in Section 3.4 with a standard first-order upwind scheme, because such schemes require only a standard compact 5-point stencil. Note that we only use the first-order upwind scheme in the bottom solver for the FAC algorithm. In particular, our use of a lower-order discretization in the pre-conditioner does not affect the accuracy of our spatial discretization of the advection-electrodiffusion equations.
As convergence criteria, we choose a relative tolerance of 1.0e-12 and an absolute tolerance of 1.0e-15. In the multigrid algorithm, we apply only 3 sweeps of post-smoothing when solving Poisson equations, and we apply 3 sweeps of pre-and post-smoothing when solving the advection-electrodiffusion equations.
6 Numerical examples
Several numerical examples are presented to demonstrate the capabilities of the scheme. We consider the cases of one solute with an elastic membrane at rest, one solute with a moving elastic membrane, two ions with an elastic membrane at rest, and finally two ions with a moving elastic membrane.
The value of the stiffness constant Ks is chosen to be 1.0 × 10−5 N/m. In all cases, the viscosity of the fluid is 11.3 × 10−4 Pa s, and the density of the fluid is 998.0 kg/m3. The diffusion coefficients of solute and ions are 2.0 × 10−10 m2/s.
Note that we regard the plane of the computation as the cross-section of a three-dimensional physical problem in which all variables are independent of the coordinate whose axis is normal to the plane of the computation. The units are those of the three-dimensional problem, even though the computation is two-dimensional. In particular, the elastic “energy” E is actually the energy per unit length of the membrane, the length in question being normal to the plane of the computation. Other units, such as those of the stiffness coefficient Ks, follow from those of E.
6.1 One solute species with a membrane at rest
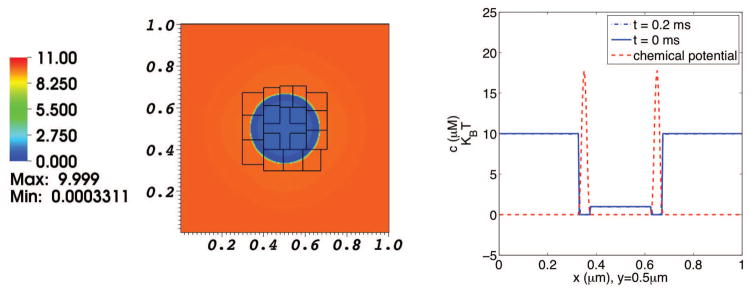
In our first example, we consider the diffusion of a single solute species which interacts with a circular membrane. The membrane is in mechanical equilibrium, and does not move in this computation. At the initial time, the concentration of the solute is 10 μM in the exterior region (i.e., exterior to the membrane) and 1 μM in the interior. The membrane is impermeable to solvent, and carries a chemical potential barrier to solute penetration. The width of the chemical potential barrier is 40 nm, and its height is about 17 KBT. The physical domain is a periodic box with a length of 1 μm in each coordinate direction. The elastic membrane is a circle centered at (0.5 μm, 0.5 μm) and with radius 0.15 μm. The concentration distributions are shown in Fig. 2.
Fig. 2. Concentration distribution in a simulation of the diffusion of one solute species interacting with a membrane at rest.
The left panel shows the solute concentration distribution on the composite grid at t = 0.2 ms. The right panel shows graphs of solute concentration (blue) and chemical potential (red) along the line y = 0.5 μm, which cuts through the center of the domain. The dotted blue curve depicts the initial solute concentration, and the solid blue curve depicts the solute concentration at t = 0.2 ms. Since the chemical potential barrier is high in comparison to KBT, there is little movement of solute.
6.2 One solute with a moving elastic membrane
In our second example, we again consider the dynamics of a single solute species interacting with an elastic membrane, but in this case, we initialize the membrane in a non-equilibrium configuration.
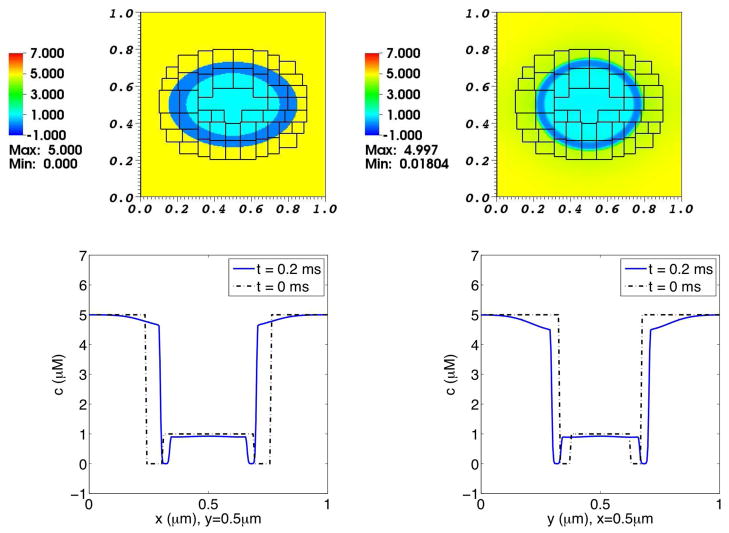
At the initial time, the concentration of the solute in the interior and exterior regions are 1.0 μM and 5.0 μM, respectively. The initial configuration of the membrane is an ellipse with major diameter and minor diameter in a ratio of 3: 2. As the simulation progresses, the elastic membrane undergoes damped oscillations about its circular equilibrium configuration. The resulting concentration distributions are shown in Fig. 3, and the pressure distribution is shown in Fig. 4.
Fig. 3. Concentration distribution in a simulation of the advection-diffusion of one solute species interacting with a moving elastic membrane.
The upper panels show the solute concentration distribution on the composite grid at times 0.0 ms (left) and 0.2 ms (right). The lower panels are graphs of solute concentration as a function of x at y = 0.5 μm (left), and as a function of y at x = 0.5 μm (right). In these lower panels, the broken curve shows the initial concentration profile for reference, and the solid curve shows the concentration profile at t = 0.2 ms. Note the inward displacement over time of the concentration profile plotted as a function of x (lower left panel), and the outward displacement over time of the concentration profile plotted as a function of y (lower right panel).
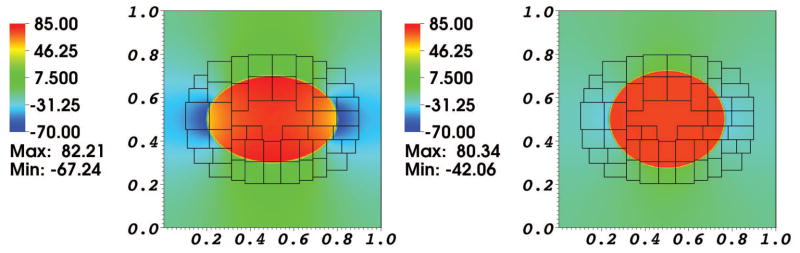
Fig. 4. Pressure distribution in a simulation of the advection-diffusion of one solute species interacting with a moving elastic membrane.
The left panel is at time t = 0.0 ms, and the right panel is at time t = 0.2 ms.
6.3 Two ionic species with a membrane at rest
Next, we simulate the electrodiffusion of two ionic species, Ca2+ and Cl−, interacting with an elastic membrane in a circular, equilibrium configuration. The physical domain is a periodic box with a length of 5 μm in each coordinate direction. The elastic membrane is a circle centered at (2.5 μm, 2.5 μm) and with radius 1.5 μm. At the initial time, the concentration of Ca2+ is 4 μM in the exterior region and 1 μM in the interior region, and the concentration of Cl− is 8 μM in the exterior region and 2 μM in the interior region, yielding an electroneutral configuration. The membrane is nearly impermeable to Ca2+ and freely permeable to Cl−. The Ca2+ and Cl− concentration distributions are shown in Figs. 5 and 6. The resulting electrical charge density and electrical potential are shown in Figs. 7 and 8.
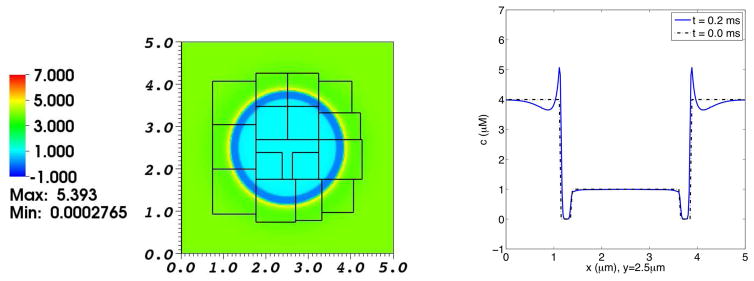
Fig. 5. Concentration distribution of Ca2+ in a simulation of the electrodiffusion of two ionic species interacting with a membrane at rest.
The left panel shows the Ca2+ distribution on the composite grid at t = 0.2 ms. The right panel is a graph of the Ca2+ concentration profile as a function of x along the line y = 2.5 μm, which goes through the center of the domain. The broken curve shows the initial Ca2+ concentration profile for reference, and the solid curve shows the Ca2+ concentration profile at t = 0.2 ms. At the initial time, the concentration of Ca2+ in the interior and exterior regions are 1.0 μM and 4.0 μM, respectively. Note the excess concentration of calcium ions near the outer side of the membrane at time t = 0.2 ms. There is a high chemical potential barrier to the diffusion of Ca2+ across the membrane, but the membrane is freely permeable to Cl− in this simulation.
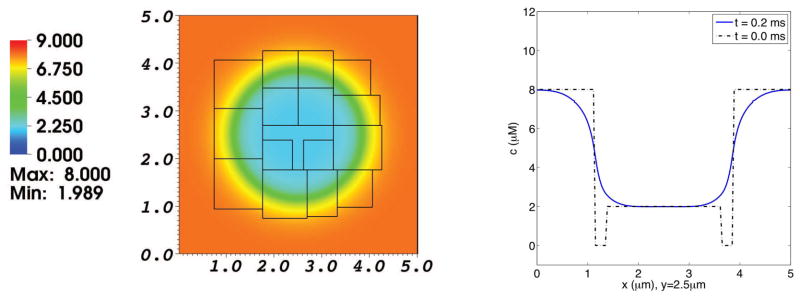
Fig. 6. Concentration distribution of Cl− in a simulation of the electrodiffusion of two ionic species interacting with a membrane at rest.
The left panel shows the Cl− distribution on the composite grid at t = 0.2 ms. The right panel is a graph of the Cl− concentration profile as a function of x along the line y = 2.5 μm, which goes through the center of the domain. The broken curve shows the initial Cl− concentration profile for reference, and the solid curve shows the Cl− concentration profile at t = 0.2 ms. At the initial time, the concentration of Cl− in the interior and exterior regions are 2.0 μM and 8.0 μM, respectively. The membrane is almost impermeable to Ca2+, but freely permeable to Cl−. Only enough Cl− crosses the membrane to set up space charge layers that generate an electrical potential difference across the membrane that is large enough to prevent further transmembrane flux of Cl−.
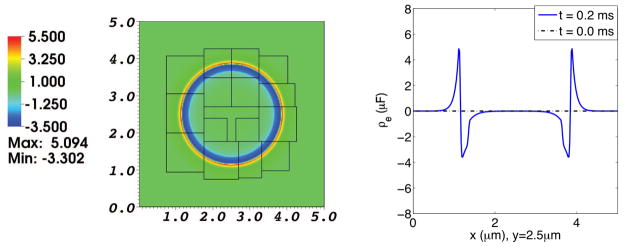
Fig. 7. Electrical charge density in a simulation of the electrodiffusion of two ionic species interacting with a membrane at rest.
The left panel shows the electrical charge density distribution on the composite grid at t = 0.2 ms. The right panel is a graph of the electrical charge density as a function of x along the line y = 2.5 μm, which goes through the center of the domain. The dotted line shows the initial charge density, which is identically zero. The solid line shows the charge density at t = 0.2 ms. Note the spontaneous formation of space-charge layers adjacent to the membrane. The net charge density organizes itself into a double layer, with equal and opposite charges on the inner and outer sides of the membrane, which therefore acts like a capacitor.
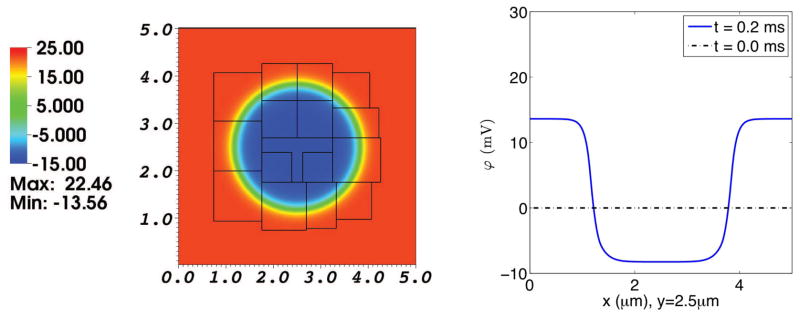
Fig. 8. Electrical potential in a simulation of the electrodiffusion of two ionic species interacting with a membrane at rest.
The left panel shows the electrical potential distribution on the composite grid at t = 0.2 ms. The right panel is a graph of the electrical potential as a function of x along the line y = 2.5 μm, which goes through the center of the domain. The dotted line shows the initial electrical potential, which is identically zero. The solid line shows the electrical potential profile at t = 0.2 ms. Note the emergence of a potential difference across the membrane. This is a consequence of the disparity between the membrane permeabilities of Ca2+ and Cl−. Recall that we have imposed a high chemical potential barrier to transmembrane Ca2+ diffusion, but no chemical potential barrier at all to transmembrane Cl− diffusion. Enough Cl− crosses the membrane to build up an electrical potential barrier sufficient to prevent further transmembrane flux of Cl−.
The thermodynamic relationship of the Nernst equation [45] in the steady state is satisfied by the permeable Cl− ion in the following way:
| (62) |
The computed values (to three digits accuracy) are the following:
| (63) |
| (64) |
where ϕout, cout are observed at (0, 2.5μm), and ϕin, cin are observed at (2.5μm, 2.5μm). That is, the electrical potential difference between the intracellular and extracellular domains in Fig. 8 is balanced by the concentration ratio of Cl− ion that can be seen in Fig. 6.
In this simulation we clearly see the difference between electrodiffusion and diffusion. Even though there is no chemical potential barrier to transmembrane movement of Cl−, only a small amount of Cl− actually crosses the membrane, enough to build up space charge layers which generate a potential difference that is strong enough to oppose further movement of Cl−. Away from the membrane, the system maintains local electroneutrality. The surface charge densities of the space charge layers just outside and just inside of the membrane are +6.46×10−17C/μm2 and −6.46×10−17C/μm2, respectively. These surface charge densities were evaluated from the computational result at the time t = 0.2ms in the following way. First integrate the net charge density (charge per unit volume) over that part of the plane of the computation for which the net charge density is positive. This gives a quantity with units of charge per unit length. Next, divide by the circumference of the membrane at the time of interest (9.42μm) to get the charge per unit area of the positive space charge layer. The same procedure with the integral being evaluated instead over that part of the plane of the computation for which the net charge density is negative yields the charge per unit area of the negative space charge layer. Note that the whole story of electroneutrality away from the membrane with space charge layers of equal magnitude and opposite sign on the two sides of the membrane [44] emerges here as a result of the computation instead of being postulated in advance.
6.4 Two ionic species with a moving elastic membrane
Finally, we simulate the advection-electrodiffusion of two ionic species, Ca2+ and Cl−, interacting with a moving elastic membrane. In this case, the physical domain is the same as in the case of two ions with a membrane at rest, but here the initial configuration of the membrane is an ellipse with a diameter ratio of 3:2. At the initial time, the concentration of Ca2+ is 4 μM in the exterior region and 1 μM in the interior region, and the concentration of Cl− is 8 μM in the exterior region and 2 μM in the interior region, yielding an electroneutral configuration. The membrane is weakly permeable to Ca2+ and freely permeable to Cl−.
Between t = 0.0 ms and t = 0.025 ms, the membrane is held fixed while the two ionic species undergo electrodiffusion. This gives the space charge layers time to develop. After t = 0.025 ms, the membrane is free to move and we can observe the evolution of the already developed space charge layers as the membrane deforms.
The Ca2+ and Cl− concentration distributions are shown in Figs. 9, 10. The resulting electrical charge density and electrical potential are shown in Figs. 11 and 12. The pressure distribution is shown in Fig. 13.
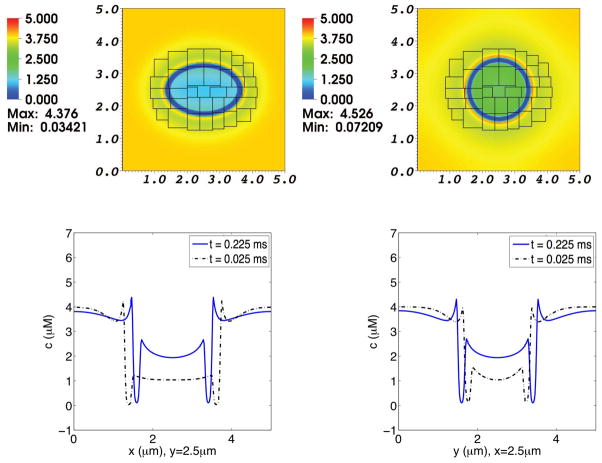
Fig. 9. Concentration distribution of Ca2+ in a simulation of the advection-electrodiffusion of two ionic species interacting with a moving elastic membrane.
The upper panels show the Ca2+ concentration distribution on the composite grid at time t = 0.025 ms (left) and at t = 0.225 ms (right). The lower panels show Ca2+ concentration profiles through the center of the domain. In each of these lower panels, the dotted curve shows the concentration profile at t = 0.025 ms, and the solid curve shows the concentration profile at t = 0.225 ms. In the lower left panel the concentrations at the two times are plotted as functions of x for fixed y, and in the lower right panel they are plotted as functions of y for fixed x. As the elliptical membrane becomes more circular, the concentration profiles shift accordingly. The membrane is only slightly permeable to Ca2+. Note the buildup of Ca2+ adjacent to the membrane, which contributes to the space-charge layer.
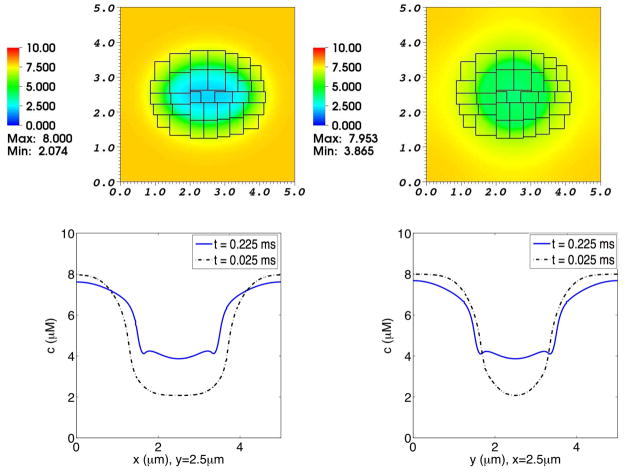
Fig. 10. Concentration distribution of Cl− in a simulation of the advection-electrodiffusion of two ionic species interacting with a moving elastic membrane.
The upper panels show the Cl− concentration distribution on the composite grid at time t = 0.025 ms (left) and at t = 0.225 ms (right). The lower panels show Cl− concentration profiles through the center of the domain. In each of these lower panels, the dotted curve shows the concentration profile at t = 0.025 ms, and the solid curve shows the concentration profile at t = 0.225 ms. In the lower left panel the concentrations at the two times are plotted as functions of x for fixed y, and in the lower right panel they are plotted as functions of y for fixed x. As the elliptical membrane becomes more circular, the concentration profiles shift accordingly. Even though the membrane is freely permeable to Cl−, the interior and exterior Cl− concentrations do not equalize because of the transmembrane electrical potential that develops as Cl− diffuses inward but Ca2+ is for the most part prevented by a chemical potential barrier from crossing the membrane.
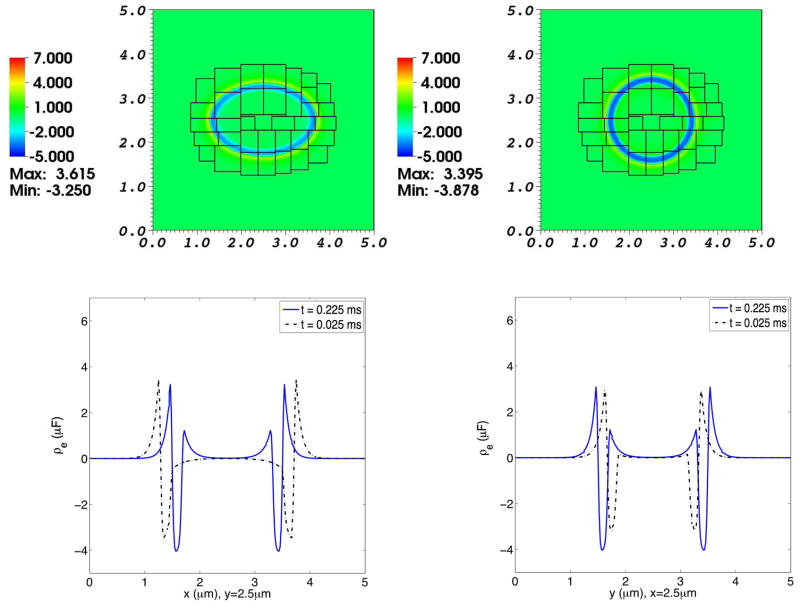
Fig. 11. Electrical charge density in a simulation of the advection-electrodiffusion of two ionic species interacting with a moving elastic membrane.
The upper panels show the charge density distribution on the composite grid at time t = 0.025 ms (left) and at t = 0.225 ms (right). The lower panels show charge density profiles through the center of the domain. In each of these lower panels, the dotted curve shows the charge density at t = 0.025 ms, and the solid curve shows the charge density at t = 0.225 ms. In the lower left panel the charge densities at the two times are plotted as functions of x for fixed y, and in the lower right panel they are plotted as functions of y for fixed x. As the elliptical membrane becomes more circular, the charge densities shift accordingly. Note the emergence of space charge layers adjacent to the membrane, and that the charge density remains near zero (local electroneutrality) except in these space charge layers.
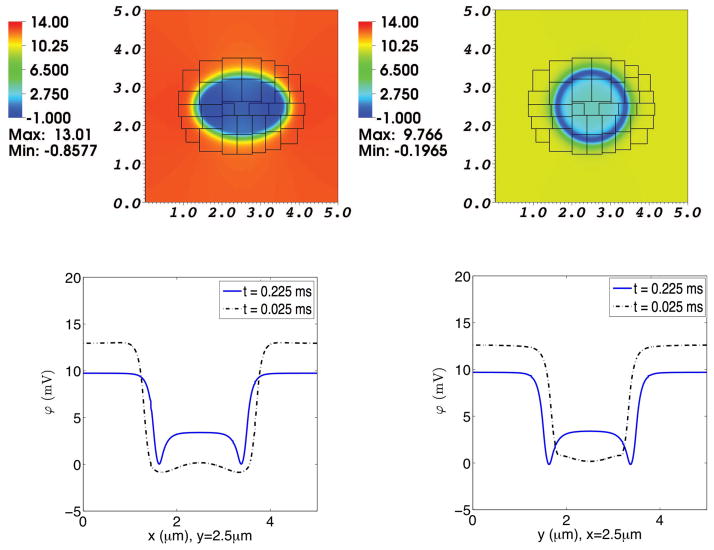
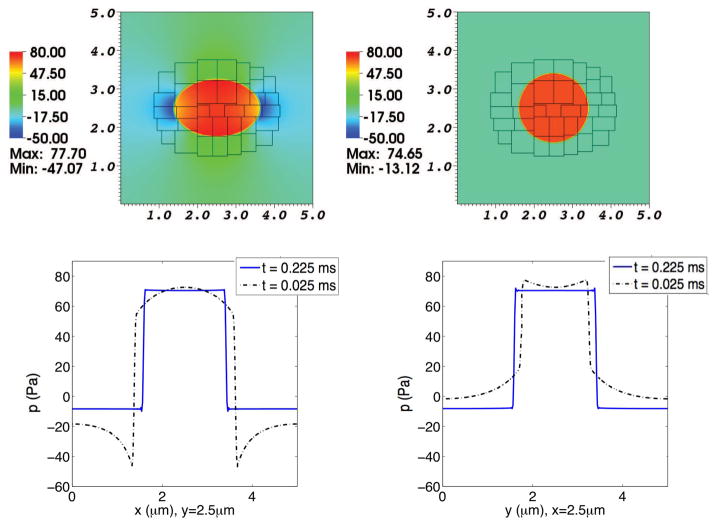
Fig. 12. Electrical potential in a simulation of the advection-electrodiffusion of two ionic species interacting with a moving elastic membrane.
The upper panels show the electrical potential on the composite grid at time t = 0.025 ms (left) and at t = 0.225 ms (right). The lower panels show electrical potential profiles through the center of the domain. In each of these lower panels, the dotted curve shows the electrical potential profile at t = 0.025 ms, and the solid curve shows the electrical potential profile at t = 0.225 ms. In the lower left panel the potentials at the two times are plotted as functions of x for fixed y, and in the lower right panel they are plotted as functions of y for fixed x. As the elliptical membrane becomes more circular, the electrical potential profiles shift accordingly. Notice, too, the development of local minima of potential just inside the membrane. This is related to the triphasic distribution of space charge across the membrane, as shown in the previous figure, which may in turn be a transient effect associated with the nonzero permeability of the membrane to Ca2+.
Fig. 13. Pressure in a simulation of the advection-electrodiffusion of two ionic species interacting with a moving elastic membrane.
The upper panels show the pressure on the composite grid at time t = 0.025 ms (left) and at t = 0.225 ms (right). The lower panels show pressure profiles through the center of the domain. In each of these lower panels, the dotted curve shows the pressure profile at t = 0.025 ms, and the solid curve shows the pressure profile at t = 0.225 ms. In the lower left panel the pressures at the two times are plotted as functions of x for fixed y, and in the lower right panel they are plotted as functions of y for fixed x. As the elliptical membrane becomes more circular, the pressure profiles shift accordingly. Besides the pressure jump across the membrane, which is present both early and late in the simulation, there are pressure gradients at the earlier time (broken curves) throughout the moving fluid. These pressure gradients disappear as the membrane settles into its circular equilibrium configuration and the pressure profiles become essentially piecewise constant (solid curves).
7 Convergence
We now assess the convergence properties of the algorithm on a sequence of two-level computational grids ΩN, where N is the number of Cartesian grid points in each coordinate direction on the coarse level of the the two-level locally-refined grid. Local mesh refinement is deployed in the vicinity of the chemical potential barrier in a manner described below.
Because analytic solutions are not available to assess the accuracy of the scheme, we employ standard methods to estimate the convergence rate of the algorithm. Briefly, we use a coarsening operator which averages quantities defined on Ω2N onto ΩN. Differences between solutions obtained on coarse and fine grids are measured using discrete Lp norms. These are defined for p = 1 or 2 by
| (65) |
where hl is the mesh width corresponding to level l of the locally refined grid, and where the valid grid cells on level l are precisely those grid cells which are not covered by grid cells on finer levels of the hierarchical grid. The error EN and convergence ratio RN in the discrete Lp norm are defined by
| (66) |
| (67) |
where uN is a quantity defined on computational domain ΩN, respectively. In the present convergence tests, we consider N = 64, 128, 256, and 512. The timestep duration ΔtN and Lagrangian mesh spacing ΔsN corresponding to ΩN are determined to keep ΔtN/hlmax and ΔsN/hlmax fixed, independent of N.
The problem setups are exactly the same as the previous numerical examples in Section 6. Tables 1, 2, and 3 show the convergence ratios obtained for the various problems at time t = 0.1 ms. The overall accuracy is essentially first order (corresponding to convergence ratios R ≈ 2), as expected.
Table 1. Convergence property for diffusion and advection-diffusion.
From the examples of Section 6.1 and Section 6.2, numerical error and convergence ratio are computed on the two-level locally refined grids ΩN with discrete Lp norms. For the diffusion of one species of solute with a membrane at rest, only solute concentration c0 is considered at t = 0.1 ms. When one species of solute does interact with a moving elastic membrane, both solute concentration c0 and fluid velocity u are employed at t = 0.1 ms.
| c0 without advection (μM) | c0 with advection (μM) | u (μm/s) | |||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
2.29e-3 | 1.26e-3 | 3.51e-4 | ||||||
|
|
|
1.31e-3 | 1.75 | 7.26e-4 | 1.74 | 1.18e-4 | 2.98 | ||
|
|
|
7.27e-4 | 1.80 | 3.87e-4 | 1.87 | 4.95e-5 | 2.38 | ||
|
|
7.40e-10 | 5.55e-10 | 2.39e-10 | ||||||
|
|
|
4.09e-10 | 1.81 | 3.15e-10 | 1.76 | 7.14e-11 | 3.35 | ||
|
|
|
2.10e-10 | 1.95 | 1.69e-10 | 1.86 | 2.96e-11 | 2.41 | ||
Table 2. Convergence property for electrodiffusion.
From the example of Section 6.3, numerical error and convergence ratio are computed on the two-level locally refined grids ΩN with discrete Lp norms. The concentrations of two species of Ca2+ and Cl−, electrical charge density ρe as well as electrical potential ϕ are employed at t = 0.1 ms.
| [Ca2+] (μM) | [Cl−] (μM) | ρe(μC) | ϕ (mV) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
7.62e-3 | 1.43e-2 | 2.884e-4 | 4.738e-6 | |||||||
|
|
|
4.43e-3 | 1.72 | 7.92e-3 | 1.81 | 1.658e-4 | 1.74 | 2.507e-6 | 1.89 | ||
|
|
|
2.40e-3 | 1.85 | 4.24e-3 | 1.87 | 8.865e-5 | 1.87 | 1.319e-6 | 1.90 | ||
|
|
2.25e-8 | 4.24e-8 | 6.482e-10 | 2.323e-10 | |||||||
|
|
|
1.28e-8 | 1.75 | 2.38e-8 | 1.78 | 3.466e-10 | 1.87 | 1.210e-10 | 1.92 | ||
|
|
|
6.90e-9 | 1.86 | 1.26e-8 | 1.89 | 1.815e-10 | 1.91 | 6.173e-11 | 1.96 | ||
Table 3. Convergence property for advection-electrodiffusion.
From the example of Section 6.4, numerical error and convergence ratio are computed on the two-level locally refined grids ΩN with discrete Lp norms. In addition to the concentrations of two species of Ca2+ and Cl−, electrical charge density ρe, and electrical potential ϕ, fluid velocity u is employed at t = 0.1 ms.
| [Ca2+] (μM) | [Cl−] (μM) | ρe (μC) | ϕ (mV) | u (μm/s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
5.82e-3 | 1.09e-2 | 2.778e-4 | 1.454e-5 | 4.347e-3 | ||||||||
|
|
|
3.40e-3 | 1.71 | 6.25e-3 | 1.75 | 1.561e-4 | 1.78 | 8.078e-6 | 1.80 | 1.469e-3 | 2.96 | ||
|
|
|
1.86e-3 | 1.83 | 3.36e-3 | 1.86 | 8.528e-5 | 1.83 | 4.438e-6 | 1.82 | 6.556e-4 | 2.24 | ||
|
|
1.33e-8 | 2.67e-8 | 4.756e-10 | 3.024e-11 | 1.167e-8 | ||||||||
|
|
|
7.16e-9 | 1.86 | 1.48e-8 | 1.81 | 2.571e-10 | 1.85 | 1.671e-11 | 1.81 | 3.752e-9 | 3.11 | ||
|
|
|
3.73e-9 | 1.92 | 7.89e-9 | 1.87 | 1.375e-10 | 1.87 | 8.793e-12 | 1.90 | 1.617e-9 | 2.32 | ||
8 Summary and Conclusions
This paper extends the application domain of the immersed boundary method from problems of fluid-structure interaction to problems of advection-electrodiffusion with fluid-structure interaction. In particular, we have introduced a computational method to solve the equations of advection-electrodiffusion of ionic (and/or neutral) solutes in a Stokes fluid containing an elastic membrane. In this paper, the membrane is impermeable to solvent, and solute permeability is controlled by a chemical potential barrier that may be chosen separately for each solute species and may also be varied spatially and/or temporally, e.g., to simulate localized channels that fluctuate open and closed. Membrane permeability to solvent may be added by following the methodology used to simulate a porous immersed boundary described in [1,8].
When the solute particles are charged, and the system as a whole is electrically neutral, we have seen that the methodology of this paper automatically produces the phenomena that are characteristic of electrodiffusion in the presence of a membrane, namely electroneutrality away from the membrane and the formation of space charge layers in the region immediately adjacent to the membrane, together with an electrical potential that varies rapidly as function of position across the membrane and the space charge layers, and only slowly elsewhere.
Although local electroneutrality outside of the space charge layers was not guaranteed but emerges to a good approximation as a result of our computations, global electroneutrality was enforced a priori by the use of periodic boundary conditions. We leave for future work the consideration of other boundary conditions that will allow the treatement of globally charged systems. The methods described in [56] for the use of non-periodic, physical boundary conditions in immersed boundary computations may be useful for this purpose.
An important feature of this work is that the fluid-structure interaction aspects of the problem are fully coupled to the solute dynamics. In particular, forces applied to the solute by the chemical potential barrier of the membrane are transmitted to the surrounding fluid, and these forces (with opposite sign) are likewise felt by the membrane itself. These mechanical aspects of membrane-solute interaction will be particularly important (once membrane permeability to solvent has been implemented) in the computer simulation of osmotic effects.
The numerical methodology of this paper employs Cartesian grid local mesh refinement in order to resolve efficiently the steep gradients in electrical potential, chemical potential, solute concentration, and hydrostatic pressure that occur near and across the elastic membrane. Local mesh refinement is here combined with a linearly implicit timestepping scheme that maintains stability without requiring excessively small time step durations. Such an implicit scheme is especially needed because local mesh refinement makes possible the introduction of especially fine grids, which would otherwise require especially small time steps. Convergence testing shows that the scheme is first-order accurate, which is the typical result when the immersed boundary method is applied to problems with sharp interfaces.
It is our belief that the methodology of this paper will be especially useful for biophysical problems at the subcellular level. Potential applications are those in which ionic fluxes are coupled to mechanical effects, either for osmotic reasons, or because the ionic concentration changes trigger contraction of cytoskeletal elements. Such processes are believed to occur, for example, in dendritic spines [42,47], which are the principal targets of synapses in the central nervous system, and also in the outer hair cells of the cochlea [43], which amplify the cochlear wave and sharpen auditory tuning as a consequence of their electromechanical activity. This paper provides a unified methodology for such biophysical problems.
Acknowledgments
PL was supported in part by a Go Abroad Scholarship from the Korea Science and Engineering Foundation (Grant Number M06-2003-000-10337-0). BEG was supported in part by an American Heart Association Postdoctoral Fellowship (Grant Number 0626001T). CSP was supported in part by the Systems Biology Center in New York through Grant Number P50GM071558 from the National Institute of General Medical Sciences.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Pilhwa Lee, Email: plee@uchc.edu, Department of Cell Biology, University of Connecticut Health Center, 263 Farmington Avenue, Farmington, CT 06030-3505.
Boyce E. Griffith, Email: boyce.griffith@nyumc.org, Leon H. Charney Division of Cardiology, Department of Medicine, NYU School of Medicine, 522 First Avenue, New York, New York 10016.
Charles S. Peskin, Email: peskin@courant.nyu.edu, Courant Institute of Mathematical Sciences, New York University, 251 Mercer Street, New York, New York 10012.
References
- 1.Lee P. PhD thesis. Courant Institute of Mathematical Sciences, New York University; 2007. The immersed boundary method with advection-electrodiffusion. [Google Scholar]
- 2.Berger MJ, Oliger J. Adaptive mesh refinement for hyperbolic partial-differential equations. J Comput Phys. 1984;53(3):484–512. [Google Scholar]
- 3.Berger MJ, Colella P. Local adaptive mesh refinement for shock hydrodynamics. J Comput Phys. 1989;82(1):64–84. [Google Scholar]
- 4.Almgren AS, Bell JB, Crutchfield WY. Approximate projection methods: Part I. Inviscid analysis. SIAM J Sci Comput. 2000;22(4):1139–1159. [Google Scholar]
- 5.Martin DF, Colella P. A cell-centered adaptive projection method for the incompressible Euler equations. J Comput Phys. 2000;163(2):271–312. [Google Scholar]
- 6.Brown DL, Cortez R, Minion ML. Accurate projection methods for the incompressible Navier-Stokes equations. J Comput Phys. 2001;168(2):464–499. [Google Scholar]
- 7.Peskin CS. The immersed boundary method. Acta Numer. 2002;11:479–517. [Google Scholar]
- 8.Kim Y, Peskin CS. 2-D parachute simulation by the immersed boundary method. SIAM J Sci Comput. 2006;28(6):2294–2312. [Google Scholar]
- 9.Mayo AA, Peskin CS. In: Cheer AY, van Dam CP, editors. An implicit numerical method for fluid dynamics problems with immersed elastic boundaries; Fluid Dynamics in Biology: Proceedings of an AMS-IMS-SIAM Joint Summer Research Conference, Vol. 140 of Contemporary Mathematics; Providence, RI, USA: American Mathematical Society; 1993. pp. 261–277. [Google Scholar]
- 10.Newren EP, Fogelson AL, Guy RD, Kirby RM. Unconditionally stable discretizations of the immersed boundary equations. J Comput Phys. 2007;222(2):702–719. [Google Scholar]
- 11.Newren EP, Fogelson AL, Guy RD, Kirby RM. A comparison of implicit solvers for the immersed boundary equations. Comput Meth Appl Mech Eng. 2008;197(25–28):2290–2304. [Google Scholar]
- 12.Mori Y, Peskin CS. Implicit second order immersed boundary methods with boundary mass. Comput Meth Appl Mech Eng. 2008;197(25–28):2049–2067. [Google Scholar]
- 13.Lai MF. PhD thesis. University of California at Berkeley; 1993. A projection method for reacting flow in the zero mach number limit. [Google Scholar]
- 14.Almgren AS, Bell JB, Szymczak WG. A numerical method for the incompressible Navier-Stokes equations based on an approximate projection. SIAM J Sci Comput. 1996;17(2):358–369. [Google Scholar]
- 15.Griffith BE, Hornung RD, McQueen DM, Peskin CS. An adaptive, formally second order accurate version of the immersed boundary method. J Comput Phys. 2007;223(1):10–49. [Google Scholar]
- 16.Chorin AJ. Numerical solution of the Navier-Stokes equations. Math Comput. 1968;22(104):745–762. [Google Scholar]
- 17.Chorin AJ. On the convergence of discrete approximations to the Navier-Stokes equations. Math Comput. 1969;23(106):341–353. [Google Scholar]
- 18.Bell JB, Colella P, Glaz HM. A second-order projection method for the incompressible Navier-Stokes equations. J Comput Phys. 1989;85(2):257–283. [Google Scholar]
- 19.Roma AM, Peskin CS, Berger MJ. An adaptive version of the immersed boundary method. J Comput Phys. 1999;153(2):509–534. [Google Scholar]
- 20.Ewing RE, Lazarov RD, Vassilevski PS. Local refinement techniques for elliptic problems on cell-centered grids I. Error analysis. Math Comput. 1991;56(194):437–461. [Google Scholar]
- 21.Griffith BE. PhD thesis. Courant Institute of Mathematical Sciences, New York University; 2005. Simulating the blood-muscle-valve mechanics of the heart by an adaptive and parallel version of the immersed boundary method. [Google Scholar]
- 22.Berger MJ, Rigoutsos I. An algorithm for point clustering and grid generation. IEEE Trans Syst Man Cybern. 1991;21(5):1278–1286. [Google Scholar]
- 23.Balay S, Buschelman K, Gropp WD, Kaushik D, Knepley MG, McInnes LC, Smith BF, Zhang H. PETSc Web page. 2009 http://www.mcs.anl.gov/petsc.
- 24.Balay S, Buschelman K, Eijkhout V, Gropp WD, Kaushik D, Knepley MG, McInnes LC, Smith BF, Zhang H. Tech Rep ANL-95/11 - Revision 300. Argonne National Laboratory; 2008. PETSc users manual. [Google Scholar]
- 25.Balay S, Eijkhout V, Gropp WD, McInnes LC, Smith BF. Efficient management of parallelism in object oriented numerical software libraries. In: Arge E, Bruaset AM, Langtangen HP, editors. Modern Software Tools in Scientific Computing. Birkhäuser Press; 1997. pp. 163–202. [Google Scholar]
- 26.SAMRAI: Structured Adaptive Mesh Refinement Application Infrastructure. http://www.llnl.gov/CASC/SAMRAI.
- 27.Hornung RD, Kohn SR. Managing application complexity in the SAMRAI object-oriented framework. Concurrency Comput Pract Ex. 2002;14(5):347–368. [Google Scholar]
- 28.Hornung RD, Wissink AM, Kohn SR. Managing complex data and geometry in parallel structured AMR applications. Eng Comput. 2006;22(3–4):181–195. [Google Scholar]
- 29.McCormick SF. Multilevel Adaptive Methods for Partial Differential Equations. Society for Industrial and Applied Mathematics; Philadelphia, PA, USA: 1989. [Google Scholar]
- 30.Ashby SF, Falgout RD. A parallel multigrid preconditioned conjugate gradient algorithm for groundwater flow simulations. Nucl Sci Eng. 1996;124(1):145–159. also available as LLNL Technical Report UCRL-JC-122359. [Google Scholar]
- 31.Falgout RD, Jones JE. Multigrid on massively parallel architectures. In: Dick E, Riemslagh K, Vierendeels J, editors. Multigred Methods VI, Vol. 14 of Lecture Notes in Computational Science and Engineering. Springer-Verlag; 2000. pp. 101–107. also available as LLNL Technical Report UCRL-JC-133948. [Google Scholar]
- 32.hypre: High performance preconditioners. http://www.llnl.gov/CASC/hypre.
- 33.Falgout RD, Yang UM. hypre: a library of high performance preconditioners. In: Sloot PMA, Tan CJK, Dongarra JJ, Hoekstra AG, editors. Computational Science - ICCS 2002 Part III, Vol. 2331 of Lecture Notes in Computer Science. Springer-Verlag; 2002. pp. 632–641. also available as LLNL Technical Report UCRL-JC-146175. [Google Scholar]
- 34.Bers DM. Cardiac excitation-contraction coupling. Nature. 2002;415:198–205. doi: 10.1038/415198a. [DOI] [PubMed] [Google Scholar]
- 35.Berridge MJ. Neuronal calcium signaling. Neuron. 1998;21:13–26. doi: 10.1016/s0896-6273(00)80510-3. [DOI] [PubMed] [Google Scholar]
- 36.Tosteson DC, Hoffman JF. Regulation of cell volume by active cation transport in high and low potassium sheep red cells. J Gen Physiol. 1960;44:169–194. doi: 10.1085/jgp.44.1.169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.LeVeque RJ. Finite volume methods for hyperbolic problmes. Cambridge University Press; 2002. [Google Scholar]
- 38.Calhoun D, Leveque RJ. A cartesian grid finite-volume method for the advection-diffusion equation in irregular geometries. J Comput Phys. 2000;157:143–180. [Google Scholar]
- 39.Ryham R, Liu C, Zikatanov L. Mathematical models for the deformation of electrolyte droplets. Discret Cont Dyn-B. 2007;8:649–661. [Google Scholar]
- 40.Mori Y, Jerome JW, Peskin CS. A three-dimensional model of cellular electrical activity. Bull Inst Math Acad Sinica. 2007;2:367–390. [Google Scholar]
- 41.Keener J, Sneyd J. Mathematical Physiology. Springer-Verlag; 1998. [Google Scholar]
- 42.Matus A. Growth of dendritic spines: a continuing story. Curr Opin Neurobiol. 2005;15:67–72. doi: 10.1016/j.conb.2005.01.015. [DOI] [PubMed] [Google Scholar]
- 43.Ruggero MA, Narayan SS, Temchin AN, Recio A. Mechanical bases of frequency tuning and neural excitation at the base of the cochlea: Comparison of basilar-membrane vibration and auditory-nerve-fiber responses in chinchilla. Proc Natl Acad Sci USA. 2000;97:11744–11750. doi: 10.1073/pnas.97.22.11744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Probstein RF. An Introduction. John Wiley and Sons; 1994. Physiocochemical Hydrodynamics. [Google Scholar]
- 45.Kandel ER, Schwartz JH, Jessel TM. Principles of Neural Science. McGraw-Hill Medical; 2000. [Google Scholar]
- 46.Neher E, Sakaba T. Multiple roles of calcium ions in the regulation of neurotransmitter release. Neuron. 2008;59:861–872. doi: 10.1016/j.neuron.2008.08.019. [DOI] [PubMed] [Google Scholar]
- 47.Holcman D, Schuss Z, Korkotian E. Calcium dynamics in dendritic spines and spine motility. Biophys J. 2004;87:81–91. doi: 10.1529/biophysj.103.035972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Weinstein AM. Sodium and chloride transport: proximal nephron. In: Giebisch G, Seldin D, editors. The Kidney: Physiology and Pathophysiology. 3. chapter 49. Raven Press; NY: 2000. pp. 1287–1332. [Google Scholar]
- 49.Leterrier JF. Water and the cytoskeleton. Cell Mol Biol. 2001;47:901–923. [PubMed] [Google Scholar]
- 50.Bottino D, Mogilner A, Roberts T, Stewart M, Oster G. How nematode sperm crawl. J Cell Sci. 2002;115:367–384. doi: 10.1242/jcs.115.2.367. [DOI] [PubMed] [Google Scholar]
- 51.Atzberger PJ, Isaacson S, Peskin CS. A microfluidic pumping mechanism driven by non-equilibrium osmotic effects. Phys D – Nonlinear Phenomena. 2009;238:1168–1179. [Google Scholar]
- 52.Rubinstein I. Electrodiffusion of Ions. SIAM; Philadelphia: 1990. [Google Scholar]
- 53.van Roosbroeck W. Theory of flow of electrons and holes in germanium and other semiconductors. Bell Syst Tech J. 1950;29:560–607. [Google Scholar]
- 54.Hollerback U, Chen DP, Eisenberg RS. Two- and three-dimensional Poisson-Nernst-Planck simulations of current flow through gramicidin A. J Sci Comput. 2001;16:373–409. [Google Scholar]
- 55.Mori Y, Peskin CS. A numerical method for cellular electrophysiology based on the electrodiffusion equations with internal boundary conditions at membranes. Commun Appl Math Comput Sci. 2009;4:85–134. [Google Scholar]
- 56.Griffith BE, Luo X, McQueen DM, Peskin CS. Simulating the fluid dynamics of natural and prosthetic heart valves using the immersed boundary method. Int J Appl Mech. 2009;1:137–177. [Google Scholar]