Running-specific prostheses limit ground-force during sprinting

Abstract

Running-specific prostheses (RSP) emulate the spring-like behaviour of biological limbs during human running, but little research has examined the mechanical means by which amputees achieve top speeds. To better understand the biomechanical effects of RSP during sprinting, we measured ground reaction forces (GRF) and stride kinematics of elite unilateral trans-tibial amputee sprinters across a range of speeds including top speed. Unilateral amputees are ideal subjects because each amputee's affected leg (AL) can be compared with their unaffected leg (UL). We found that stance average vertical GRF were approximately 9 per cent less for the AL compared with the UL across a range of speeds including top speed (p < 0.0001). In contrast, leg swing times were not significantly different between legs at any speed (p = 0.32). Additionally, AL and UL leg swing times were similar to those reported for non-amputee sprinters. We infer that RSP impair force generation and thus probably limit top speed. Some elite unilateral trans-tibial amputee sprinters appear to have learned or trained to compensate for AL force impairment by swinging both legs rapidly.

1. Introduction

Many physiological and biomechanical factors influence sprint-running performance. As sprinters with biological limbs run faster, their contact length plateaus, step frequency increases, and mean stance average vertical ground reaction forces (GRF) increase (Mero et al. 1992; Weyand et al. 2000). In general, research has shown that the ability to generate vertical force ultimately limits top speeds in humans with biological limbs (Weyand et al. 2000; Usherwood & Wilson 2006; Chang & Kram 2007).

The world-class 400 m running performances of a bilateral trans-tibial amputee, Oscar Pistorius, and subsequent scientific studies (Brüggemann et al. 2008; Weyand et al. 2009) have stimulated controversy surrounding the use of passive-elastic running-specific prostheses (RSP). RSP allow considerable elastic energy return (Brüggemann et al. 2008) and thus emulate the spring-like behaviour of biological limbs during running (Ker et al. 1987). However, unlike biological legs, passive prostheses cannot generate mechanical power de novo (Czerniecki et al. 1996), nor can the prosthesis’ stiffness be varied while running. At top speed, Oscar Pistorius had 22 per cent lower stance average vertical GRF than performance-matched intact sprinters (Weyand et al. 2009). Thus, RSP and/or residual leg weakness may impose a ground-force limitation. Amputee sprinters might compensate for these ground-force limitations by increasing step frequency via faster leg swing.

To better understand how RSP affect biomechanics during sprinting, we measured GRF and stride kinematics of elite unilateral trans-tibial amputee sprinters over a range of speeds up to top speed. Though there is some mechanical interdependence between limbs, we chose to study unilateral amputees because their affected leg (AL) could easily be compared with their unaffected leg (UL). To investigate whether greater prosthesis mass results in longer leg swing times, we also added mass to their prostheses.

First, we hypothesized that unilateral trans-tibial amputees using RSP would have lower stance average vertical GRF (F_avg) for the AL than the UL during sprint running. Second, we hypothesized that unilateral trans-tibial amputees using RSP would have shorter leg swing times for the AL compared with the UL during sprint running. Third, we hypothesized that adding mass to the RSP would increase leg swing times for the AL at top speed.

2. Material and methods

Six healthy unilateral trans-tibial amputee elite sprinters (table 1) gave informed written consent according to the Intermountain Healthcare IRB approved protocol. Each subject used his/her own sprint-specific RSP (table 1), which was either the same model of prostheses used by Oscar Pistorius (Ossur Cheetah) or very similar (Otto bock Sprinter and C-Sprint). All of the experiments were conducted at the Biomechanics Laboratory of the Orthopedic Specialty Hospital.

Table 1.

Subject characteristics. Demographic and anthropometric variables, treadmill top speeds, and 100 and 200 m personal records (PR) for each subject. Total mass includes RSP mass. Leg length equals the distance from the greater trochanter to the floor. AL length was determined when the prosthesis was not compressed.

	sex (M/F)	age (years)	height (m)	total mass (kg)	UL length (m)	AL length (m)	RSP (model)	RSP mass (kg)	top speed (m s−1)	100 m PR (s)	200 m PR (s)
1	M	36	1.842	79.9	0.985	1.030	Cheetah	1.6	9.0	11.02	22.83
2	M	25	1.854	71.0	1.005	1.025	Cheetah	1.2	9.0	12.28	24.79
3	M	27	1.753	69.3	0.930	0.970	Cheetah	1.5	9.3	11.93	22.96
4	M	29	1.867	109.1	0.985	1.065	C-Sprint	1.4	9.8	11.49	22.96
5	F	23	1.689	62.9	0.895	0.950	Sprinter	1.2	8.4	13.71	28.02
6	F	35	1.679	66.1	0.955	0.985	Cheetah	1.7	7.0	12.77	27.05

(a). Protocol

We measured each subject's height, mass, prosthesis mass and standing leg lengths. Leg length was defined as the vertical distance from the greater trochanter to the floor during standing. During AL length measurement, subjects stood with a block under their UL to unload the AL.

After warming up and accommodating to the treadmill, subjects performed a series of constant speed running trials on a custom, high-speed, 3D force sensing treadmill (Athletic Republic, Park City, UT). Each running trial consisted of at least 10 strides. Subjects started the series of trials at 3 m s⁻¹, each subsequent trial was incremented by 1 m s⁻¹ until subjects approached top speed, and then smaller speed increments were employed until subjects reached their top speed. Top speed was determined when subjects put forth maximal effort but could not maintain their position on the treadmill for eight strides (Weyand et al. 2000). Subjects were given as much time between trials as needed to recover fully.

(b). Added mass

Subjects then completed additional trials with 100 and 300 g lead strips attached distally over the forefoot region of their RSP. Some Paralympic sprinters regularly add 100–300 g during competition because they feel it helps them achieve a more symmetrical gait. We added a maximum of 300 g because a greater added mass would have increased the risk of socket disengagement during top speed sprinting. We again asked subjects to run at speeds up to and including top speed, as defined previously.

(c). Kinetics and kinematics

We collected GRF at 2400 Hz during all trials. Then, we used a custom software program to detect the instants of touch-down and toe-off from the raw vertical GRF data using a 40 N threshold and determined leg swing time (t_sw), aerial time (t_a), contact time (t_c) and step frequency (Step f) for 20 consecutive steps, 10 AL and 10 UL steps. Because the stance leg vertical impulse influences the subsequent aerial phase, we chose to define t_a for each leg as the flight time following the leg's contact phase. We acknowledge however, that due to the interaction between legs, it could be argued that the preceding aerial phase influences the subsequent stance phase impulse. Step f for each leg was assumed to equal 1/(t_c + t_a). We calculated contact length (L_c) using the equation, v_tm = L_c/t_c (McMahon & Greene 1978), where v_tm equals the treadmill speed. Then, we filtered the raw GRF data with a critically damped filter and determined F_avg and peak vertical GRF from 10 AL and 10 UL steps.

(d). Statistics

We compared each subject's AL and UL kinetic and kinematic variables using repeated measures ANOVAs with Tukey's HSD follow-up tests when warranted (p < 0.05).

3. Results

Our results support our first hypothesis. We found F_avg was approximately 9 per cent less for the AL compared with the UL across a range of speeds (figure 1) including top speed (p < 0.0001; table 2). At faster speeds, subjects increased step f in both the AL and UL, but the increase was more dramatic in the UL. Step f was 8 per cent greater for the UL than the AL at top speed (p = 0.04). Subjects increased L_c at faster speeds for both the AL and UL, but there were no significant L_c differences between legs.

Figure 1.

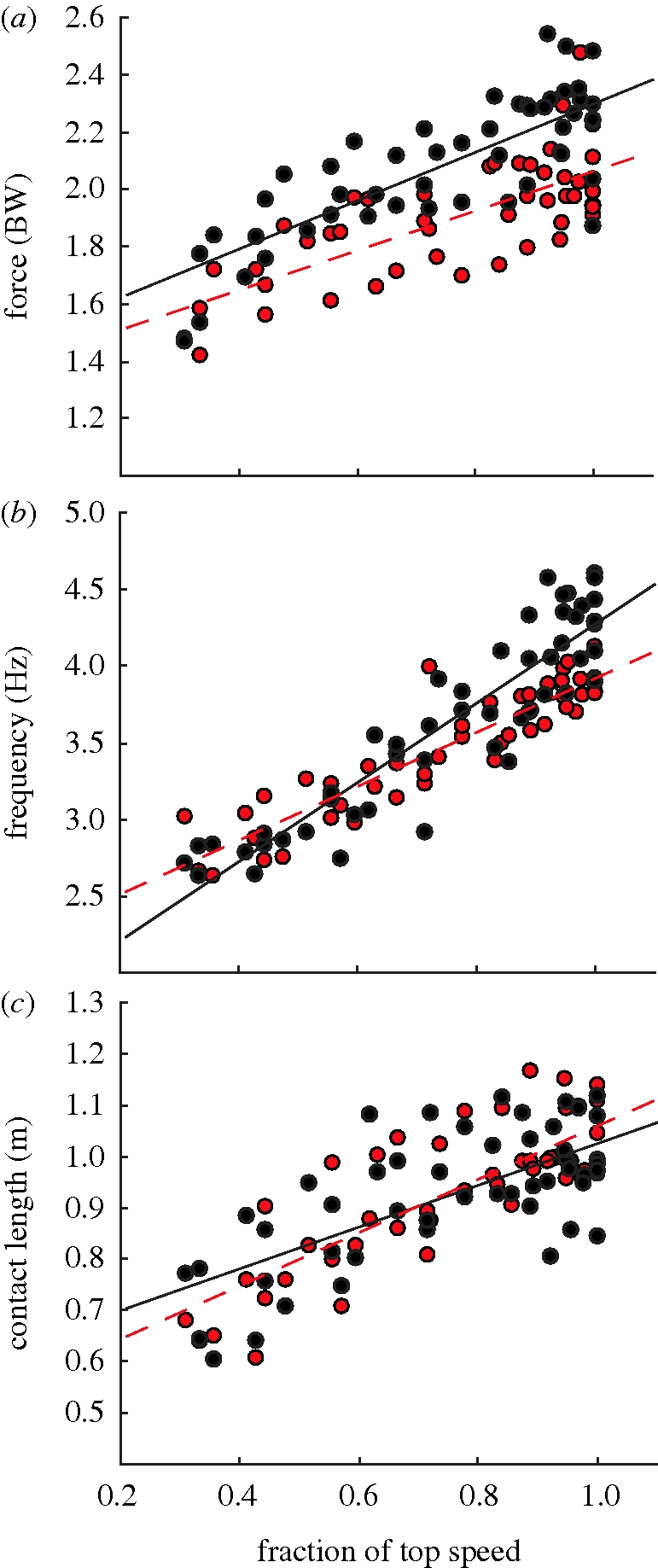
Biomechanical variables across speed for the UL and AL. Lines are linear regressions for the AL (dashed line) and UL (solid line). R² > 0.55 for each leg's (a) F_avg—stance average vertical GRF, (b) step f—step frequency and (c) L_c—contact length (filled black circle, UL; filled red circle, AL).

Table 2.

Top speed kinetic and kinematic variables. F_avg, peak vertical GRF (vGRF), step f, L_c, t_sw, t_a, and t_c at top speeds for the UL and AL without and with 100 and 300 g added to the prosthesis. BW is body weight. Data are mean ± s.d. Top speeds were not significantly different between conditions (n = 6). Individual kinetic and kinematic data across speed are provided in the electronic supplementary material.

condition	leg	Favg (BW)	peak vGRF (BW)	step f (Hz)	Lc (m)	tsw (s)	ta (s)	tc (s)
top speed	UL	2.19 ± 0.21	3.88 ± 0.22	4.31 ± 0.27	0.998 ± 0.095	0.370 ± 0.012	0.118 ± 0.007	0.115 ± 0.015
(8.8 ± 1.0 m s−1)	AL	2.02 ± 0.12*	3.34 ± 0.30*	3.98 ± 0.18*	1.039 ± 0.071	0.365 ± 0.017	0.133 ± 0.014	0.119 ± 0.011
top speed + 100 g	UL	2.22 ± 0.24	3.92 ± 0.21	4.06 ± 0.27	1.034 ± 0.086	0.380 ± 0.014	0.127 ± 0.008	0.122 ± 0.017
(8.4 ± 0.9 m s−1)	AL	1.97 ± 0.13*	3.24 ± 0.21*	3.95 ± 0.18*	1.034 ± 0.080	0.377 ± 0.020	0.133 ± 0.008	0.124 ± 0.012
top speed + 300 g	UL	2.22 ± 0.23	3.86 ± 0.42	4.04 ± 0.19	1.016 ± 0.092	0.381 ± 0.004	0.128 ± 0.009	0.121 ± 0.016
(8.5 ± 0.9 m s−1)	AL	1.96 ± 0.15*,**	3.26 ± 0.32*	3.96 ± 0.13	1.047 ± 0.088	0.378 ± 0.011	0.128 ± 0.012	0.125 ± 0.015

*Significant difference between legs (p < 0.05).

**Significant difference between added mass and no load conditions (p < 0.05).

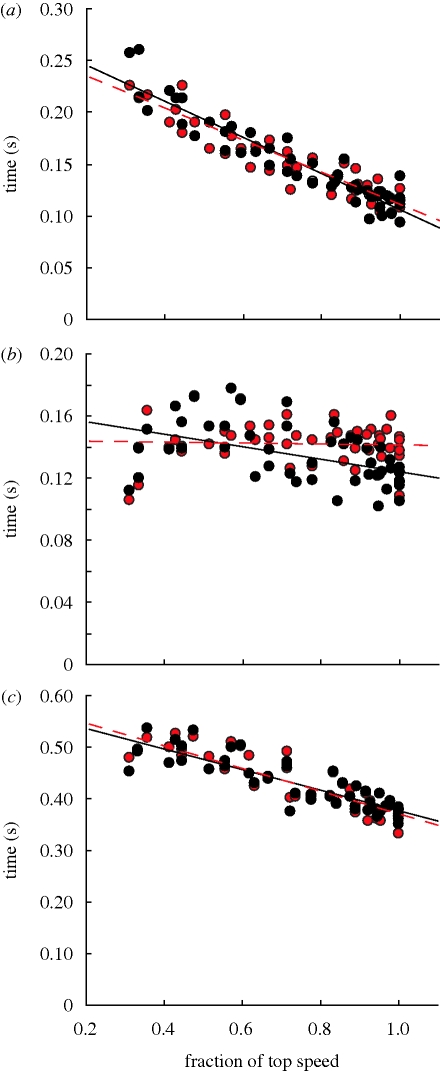
We reject our second hypothesis. Though step f was significantly faster for the UL compared with the AL at top speed, we found that t_sw was not significantly different between the AL and UL at any speeds, including top speed (p = 0.32; figure 2, table 2). Subjects swung both legs more quickly at faster speeds. Similarly, t_c decreased at faster speeds, but was not different between legs (p = 0.30). Thus, the significant difference in step f at top speed was probably due to shorter UL t_a (following the UL push-off) compared with the AL t_a (following the AL push-off) at faster speeds (p = 0.07). The AL t_a did not consistently change across speed.

Figure 2.

Plots of (a) t_c—contact time, (b) t_a—aerial time and (c) t_sw—leg swing time across speed for the UL and AL. Lines are linear regressions for AL (dashed line) and UL. R² = 0.85 & 0.89, 0.00 & 0.20, 0.80 & 0.77 for t_c, t_a and t_sw in the AL & UL, respectively (filled black circle, UL; filled red circle, AL).

Contrary to our third hypothesis, we found that adding mass to the prosthesis did not significantly change the AL or UL t_sw at top speed (100 g, p = 0.23 and 0.22 for the AL and UL; 300 g, p = 0.09 and 0.12 for the AL and UL). Adding 100 and 300 g to the AL did not result in significant changes to absolute top speed (p = 0.28 and 0.18, respectively), and just as we found for unloaded running, F_avg was significantly less in the AL compared with the UL with added loads (p = 0.02 and 0.01, respectively; table 2).

4. Discussion

Similar to previous studies that have analysed the mechanics of a bilateral amputee sprinter (Brüggemann et al. 2008; Weyand et al. 2009), our results show lower AL vertical GRF during top speed running while using RSP. Because the fastest non-amputee sprinters are those who can apply greater forces to the ground (Weyand et al. 2000), a significant force impairment for the AL probably limits the ability of amputees to achieve top speeds compared with non-amputee sprinters. Our data strongly suggest that the RSP or muscle weakness/impairment due to the prosthesis limit force production rather than some other physiological factor.

Faster step f might increase top speed by reducing the required vertical impulse during stance. Recalling that step f equals 1/(t_c + t_a), faster step f are realized by decreasing t_c and/or t_a. However, we found significantly greater step f for the UL than the AL at top speed (table 2). This result may seem counterintuitive because the AL had lower F_avg than the UL and nearly the same t_c, implying a softer AL vertical spring stiffness. A softer spring would produce a slower take-off velocity, thus one would expect a shorter t_a and faster step f (McMahon et al. 1987) for the AL if the take-off and landing height were the same. We verified that the AL had slower take-off velocities than the UL. Thus, the take-off height from the UL must have been lower than the landing height of the AL, thereby influencing the UL t_a. The difference in t_a may have resulted from a longer AL leg length (table 1), and/or the necessity for AL ground clearance, however a more detailed kinematic analysis is necessary to explain these results.

A faster t_sw could enhance top speed by increasing step f, but we did not find significant differences between the AL and UL t_sw at top speed. However, our number of subjects may have limited our statistical power. Amputees’ AL and UL mean t_sw at top speed were essentially the same as the mean t_sw for intact runners (0.373 ± 0.03 s) at top speed (Weyand et al. 2000). Added prosthesis mass did not significantly change top speed though t_a and step f became more symmetrical between legs when we added 300 g (table 2). Moreover, a greater AL mass and moment of inertia did not slow leg swing times.

To supplement our laboratory testing, we analysed high definition digital video recordings of the 2008 Beijing Paralympic Games men's T43/T44 events (obtained from the Universal Sports Network; frame rate = 30 Hz) to determine the t_sw for the top five 100 m and top two 200 m competitors. Competitors included one bilateral and five unilateral amputees. To capture top speeds, we analysed the last 50 m of the 100 m and last 100 m of the 200 m final races. The bilateral amputee's t_sw was 0.302 ± 0.003 s (mean ± SEM) and 0.318 ± 0.003 s for the 100 and 200 m events, respectively. The unilateral amputees had t_sw of 0.297 ± 0.008 s and 0.321 ± 0.005 s for their AL and UL, respectively. Four of the five unilateral amputees had shorter t_sw for their AL, but the second place finisher in the 200 m event actually had a longer AL t_sw (0.323 ± 0.004 s) than UL t_sw (0.304 ± 0.005 s). The leg swing times for the group were not significantly different between the AL and UL (p = 0.09), but the low number of subjects may have limited our statistical power.

We also analysed video from the 2008 Beijing Olympics (Beijing 2008 Highlights DVD, Ten Mayflower Productions). In the men's 100 m final, Usain Bolt set the world record and had an average t_sw of 0.328 ± 0.004 s during the last 50 m. The second and third place finishers had corresponding values of 0.305 ± 0.004 s and 0.274 ± 0.004 s. Like our laboratory data, the combined analysis of the Paralympic and Olympic videos suggest that the low mass and inertia of RSP do not facilitate unnaturally fast leg swing times, and we infer that fast leg swing times can result from learning and/or training.

Our results extend the understanding of prior published analyses of amputee sprint-runners and allow further insight into the biomechanical factors that limit the running speed of all terrestrial animal species. Some aspects of the mechanics of the AL and UL clearly differ over a range of speeds up to top speed, and there is probably interdependence between the mechanics of each leg. It has been proposed that using an RSP might enhance top speed by reducing the time required to reposition the limb (Weyand et al. 2009), but our results indicate that this is not the case. The impaired GRF observed during amputee running here and elsewhere (Brüggemann et al. 2008; Weyand et al. 2009) identify what may be a critical limitation for top speed (Weyand et al. 2000).