Replication in genome-wide association studies

Summary

Replication helps ensure that a genotype-phenotype association observed in a genome-wide association (GWA) study represents a credible association and is not a chance finding or an artifact due to uncontrolled biases. We discuss prerequisites for exact replication; issues of heterogeneity; advantages and disadvantages of different methods of data synthesis across multiple studies; frequentist vs. Bayesian inferences for replication; and challenges that arise from multi-team collaborations. While consistent replication can greatly improve the credibility of a genotype-phenotype association, it may not eliminate spurious associations due to biases shared by many studies. Conversely, lack of replication in well-powered follow-up studies usually invalidates the initially proposed association, although occasionally it may point to differences in linkage disequilibrium or effect modifiers across studies.

1. Introduction

Reproducibility has long been considered a key part of the scientific method. In epidemiology, where variable conditions are the rule, the repeated observation of associations between covariates by different investigative teams, in different populations, using different designs and methods is typically taken as evidence that the association is not an artifact, [1] for two principal reasons. First, repeated observation adds quantitative evidence that the association is not due to chance alone; second, replication across different designs and populations provides qualitative evidence that the association is not due to uncontrolled bias affecting a single study. Moreover, accumulated evidence can provide more accurate estimates of the effect measures of the risk factor being studied and their uncertainty.

Genetic epidemiology learned the importance of replication the hard way. Before the advent of genome-wide association (GWA) studies, most reported genotype-phenotype associations failed to replicate. There were a number of reasons for these conflicting results, including: inappropriate reliance on standard significance thresholds that did not take the low prior probability of association into account; small sample sizes; and failure to measure the same variant(s) across different studies.[2–4] In response, the field moved towards more stringent requirements for reporting associations, explicitly emphasizing replication.[5] Many high-profile journals now will not publish genotype-phenotype associations without concrete evidence of replication.[6]

In this article we review the requirements for replicating associations discovered via GWA studies in light of recent developments: in particular, the increasing role of consortia of multiple GWA studies. Prospective meta-analysis of multiple genome-wide studies (conducted by different investigative teams, in different populations, using different technologies and different designs) can satisfy the requirement for replication in the context of gene discovery, without the need to genotype yet more samples in yet further studies, as long as the combined evidence for association is strong and consistent.[7] This is an important point, since very large samples sizes are required to reliably identify common variants with modest effects, and formal replication of an association—i.e. genotyping the initially discovered genetic variant in a new, completely independent sample of sufficient size—may be too expensive in terms of time, money, and available samples. Indeed, for some rare diseases (e.g. Creutzfeldt Jakob disease) or relatively uncommon diseases (e.g., pancreatic cancer), most if not all samples with readily-available DNA may be genotyped as part of initial GWA studies used at the discovery stage.

We describe the goals of replication and statistical rules of thumb for distinguishing chance from true associations in the first section of this article. We then discuss the importance of exact replication—seeing a consistent association with the same risk allele using the same analytic methods across multiple studies—and describe analytic methods for combining evidence across multiple studies, along with their relative advantages and disadvantages. We close by discussing why an association may fail to replicate and place replication efforts in the wider picture of contemporary genetic epidemiology, with its focus on large-scale collaborations and data sharing.

2. Goals of replication

There are two primary reasons replication is essential to confirm associations discovered via GWA studies: to provide convincing statistical evidence for association, and to rule out associations due to biases. Another possible aim of replication is to improve effect estimation..

2.i. Convincing statistical evidence for association

To date most individual GWA studies do not have enough power to detect true associations at the conservative significance levels necessary to distinguish false positives from false negatives. This point has typically been made by referencing the large number of tests conducted in a GWA study and the consequent severe adjustment of the p-value threshold in order to control experiment-wide Type I error rate. Empirical estimates of the threshold needed to preserve the genome-wide Type I error rate in studies of European-ancestry subjects using current genotyping arrays range from 5×10⁻⁷ to 1×10⁻⁸. [8–11] These thresholds are different in other populations; for example, they are even lower in African or African-American samples, due to the greater genetic diversity in these populations. Even these stringent thresholds take into account only the complexity of the genetic architecture, and they do not adjust for the potential complexity of the phenotypic architecture, i.e. when targeting multiple phenotypes.

In the framework of the Bayes theorem, the probability that an observed association truly exists in the sampled population depends not only on the observed p-value for association, but also the power to detect the association (a function of minor allele frequency, effect size and sample size), the prior probability that the tested variant is associated with the trait under study, and the anticipated effect size. [3, 4, 12] We illustrate this in Figure 1, where we plot the Bayes Factor for association (versus no association) as a function of p-value, sample size, and minor allele frequency. [13] The Bayes Factor is the ratio of the probability of the data under the alternative hypothesis (association with the tested variant) to the probability of the data under the null hypothesis (no association). (Others define the Bayes Factor as the inverse of this ratio. [13]) The posterior odds of true association given the data are equal to the Bayes Factor times the prior odds of association. In Figure 1 the dashed line represents the Bayes Factor needed to achieve posterior odds for association of 3:1, assuming prior odds of association of 1:99,999 (i.e. roughly 100 out of 10,000,000 variants are truly associated with the studied trait).

Figure 1.

The relationship between the Bayes Factor and p-value for different sample sizes and minor allele frequencies (left panel: minor allele frequency of 40%; right panel: 5%). The dashed line represents the Bayes Factor necessary to achieve posterior odds in favor of association of 3:1 or greater, assuming the prior odds of association are 1:99,999. Bayes Factors were calculated for a case-control study with equal numbers of cases and controls, assuming the expected value of the absolute value of the log odds ratio is log(1.15), and assuming a “spike and smear” prior. Calculations use equations (4) and (5) from Ioannidis (2008),[13] with σ² = I_ββ⁻¹ − I_αβ⁻¹ [I_αα⁻¹]⁻¹I_βα⁻¹, where I is the Fisher information from simple logistic regression log(odds) = α + β G_additive calculated under the null (β=0).

Note that all p-values are not created equal: for a given p-value, the evidence for association increases with increasing sample size and depends on risk allele frequency. Increasing overall sample size not only increases power to detect common risk variants with modest effects, but it can increase the credibility of the observed associations. Differences in credibility by sample size for similar p-values are a consequence of the fact that these calculations take assumptions about the expected magnitude of the true allelic odds ratio into account. In particular, they assume that the true allelic odds ratio is unlikely (probability < 2.1%) to be smaller than 0.5 or bigger than 2. Since small p-values can only be achieved in small sample sizes if the estimated effect is large, these results are perceived to be less credible in this framework.

In other words, the Bayes Factor and thus the credibility of an association depends explicitly on what we assume for the typical magnitude of likely genetic effects. For example, if we assume that the average effect is not an odds ratio of 1.15 as in Figure 1, but an odds ratio of OR_av=1.5, then the prior odds of association will be less, because fewer variants—with larger effects than in the OR_av =1.15 scenario—would suffice to explain the genetic variability. A larger Bayes Factor would be needed to reach a 3:1 posterior. Moreover, large effects emerging from small studies will be more credible than in the OR_av =1.15 scenario, while very small effects emerging with similar p-values from large studies will be less credible.[13]

Conversely, if we assume that the average effect is an odds ratio of OR_av =1.02 (consistent with the theory of infinitesimal effects, each having an almost imperceptible contribution[14]), then the prior odds of association will be much higher, because a much larger set of (infinitesimally) associated variants are anticipated and a smaller Bayes Factor would be needed to reach a 3:1 posterior. Moreover, large effects emerging from small studies would be incredible, regardless of their p-value, while very small effects emerging with modest p-values from large studies would provide credible evidence for association.

We should acknowledge that the distribution of effect sizes of true associations is unknown, and there is no guarantee that they would be similar for different traits. The difficulty of arriving at the true causal variants (which may have larger effect sizes than their markers) adds another layer of complexity. Moreover, given simple power considerations, it is expected that a large proportion of the large effects have been identified, while only a small proportion of the smaller effects and a negligible proportion of the tiny and infinitesimal effects are already discovered. With these caveats, most evidence from GWA studies to-date is more compatible with the scenarios of OR_av being in the range of 1.15, [15] but the 1.02 scenario is not implausible, and for some traits the 1.5 scenario may be operating, but we still have not identified the true variants.

Many research groups cannot afford to genotype the large sample sizes needed to reliably detect genetic markers that are weakly associated with a trait using a genome-wide platform. This has sparked interest in multi-stage designs, where a subset of available samples are genotyped using the genome-wide platform, and then a subset of the “most promising” markers (typically those with lowest p-values) are genotyped using a custom platform. These designs are reviewed in more detail elsewhere in this issue.[16] We should note that the primary motivation of multi-stage designs is not to increase power by testing fewer hypotheses in the second stage samples, and hence paying a smaller penalty for multiple testing at the second stage. Rather the primary goal of multi-stage designs is to save genotyping costs or maximize power given a fixed genotyping budget. If genotyping costs were not an issue, then the multistage approach is less powerful than simply testing all markers in the entire available sample. [16–18] As genotyping costs decrease, and as more samples have been genotyped as part of previous GWA analyses, single-stage analyses become more common. [17]

The appropriate threshold for claiming association depends also on the context and the relative costs for false positive and false negative results. For example, re-sequencing a region and conducting in vivo and in vitro functional studies is quite expensive, and will require convincing evidence that the observed association is true. On the other hand, including a region in a predictive genetic risk score is relatively inexpensive, so a less stringent threshold might suffice. This approach to replication is intuitively Bayesian (although it need not use formal Bayesian methods): each successive study serves to update the prior for association in subsequent studies.

2.ii. Ruling out association due to artifact

Even when the initial association is unlikely to be a stochastic artifact due to multiple testing, it may still be an artifact due to bias. For common variants, the anticipated effects are modest—for binary traits, odds ratios smaller than 1.5; for continuous traits, percent variance explained less than 0.5%—and very similar in magnitude to the subtle biases that may affect genetic association studies—most notably population stratification bias. For this reason, it is important to see the association in other studies conducted using a similar (but not identical) study base. In principle, careful design and analysis should eliminate or greatly reduce bias due to population stratification in association studies using unrelated individuals [19–21]—and in practice these methods have effectively removed some worrying systematic inflation in association statistics. [22] Family-based designs can provide additional evidence that an observed association is not due to population stratification bias, but these designs are not cost-efficient, and have their own unique sources of bias. For example, non-differential genotyping error can inflate Type I error rates in some family-based analyses, although it does not change the Type I error rate. [23]

2.iii. Improving effect estimates

Another reason to conduct replication studies is to extend the generalizablity of the association. It is important to know if the association exists and has similar magnitude in different environmental or genetic backgrounds. It is particularly interesting to know how these associations play out in populations of non-European ancestry, considering most GWA studies to date have been conducted in European-ancestry samples. Differences in allele frequencies and local linkage disequilibrium (LD) patterns across populations present both challenges and opportunities for replication and fine mapping. On the one hand, a marker allele that is strongly associated with a trait in one population may not have a detectable association in another, as the allele frequency may be smaller or the LD with the (unknown) causal variant may be much weaker. Thus, initial replication studies should focus on populations with genetic ancestry similar to that sampled in the study that first observed the marker-trait association, using the exact strategy outlined in the next section. Once credible evidence for this association has been established, replication efforts in other populations should type not only the marker known to be associated in the original population, but other markers that “tag” common variation in a region surrounding the marker. For fine mapping, differences in LD patterns across populations—notably the lower levels of LD in African-ancestry populations—might lead to refined estimates of the position of causal variants. [24, 25]

Replication may also be useful in identifying a more reliable estimate of the effect size for the association. Signals selected based on statistical significance thresholds in underpowered settings are likely to have (on average) inflated effects due to the winner’s curse phenomenon. [26–30] Replication should take this into account during the sample size calculations for the replication efforts; the effect estimate from the initial study may be inflated, leading to an under-estimate of the number of subjects needed to reliably detect it. [26–29] Analytic methods are available to adjust for winner’s-curse bias, but studying the marker in additional samples (beyond those used to initially identify the marker) will help produce more unbiased estimates of the genetic effect. Accurate estimates of marker risks are important (even if the marker is only a surrogate for the as-yet unknown causal variant), as they may be used for personalized predictive purposes. [31, 32]

Finally, when there are several putative association signals in a region of high LD, dense genotyping in replication studies may help elucidate whether they represent independent loci, each with its own effect in the trait, or whether one or all are “passenger” markers, which have no effect conditional on the true underlying causal variant. Detailed discussion of fine mapping issues is beyond the scope of this review, but in light of the effort involved, such “fine mapping” efforts should arguably be reserved for loci with credible evidence for association, e.g. loci with markers that have been replicated exactly, as discussed in the next section. [33]

3. Prerequisites for exact replication of a putative association from a GWA study

One of the early difficulties in replicating genetic associations observed in candidate gene studies was the fact that different groups would study different markers in the same region. Because the LD among these markers was poorly understood, results from multiple studies could increase rather than decrease confusion. The initial study may have seen an association with SNP A, but the second study did not genotype that SNP, and instead saw an association with SNP B, which was not genotyped in the original study. As the number of SNPs typed per region increased, “moving the goalposts” in this fashion contributed to the problem of persistent false positives in the candidate gene literature; by chance some SNP in the region (not necessarily the SNP that was statistically significant in other studies) would have p<0.05, and this would be (incorrectly) proclaimed replication.[34] In response to this problem, guidelines for replication in genetic association studies now call for exact replication. The same marker—or, if technical difficulties preclude this, a perfect or near-perfect proxy for the original marker—should be genotyped across all studies and analyzed using the same genetic model. In this section we discuss prerequisites for exact replication. We use the term “exact replication” cautiously, recognizing that this is an unattainable goal in epidemiology (e.g. studies conducted by different investigators at different times let alone places will sample from different populations) and that in some sense it is the “inexactness” of replication studies that increases credibility of the observed association (it is less likely to be an artifact due to a bias that is unique to the initial study). We use the term to emphasize the danger of “moving the goalposts” so far that claims of replication carry little weight.

3.i. Test the same marker

This should be done preferably by directly genotyping this marker. Currently-available imputation methods are powerful and quite accurate for filling in information on missing common SNPs. [35–39] Even then, further conformation by direct genotyping would be very useful. (In fact, to rule out technical artifact, some have argued that an associated SNP should be genotyped using two different genotyping technologies, or that a second SNP in the region that is in [near-] perfect LD with the associated SNP be genotyped.[5]) Great caution is needed when “replicating” an association by finding an association with a (different) nearby marker: if the new marker does not have perfect or almost perfect LD with the previously discovered one, this cannot be considered replication. Moreover, even for markers with seemingly perfect LD in a given sample, the LD may be far less than perfect in a different population and it may break completely in populations of different ancestry. When a panel of markers spanning the whole locus is pursued (e.g. after resequencing and fine mapping), different markers and haplotypes may be found to be associated in different populations. Evidence from different markers and haplotypes should not be combined in the same meta-analysis. The consistency of each association can be formally assessed separately (see section on statistical heterogeneity).

3.ii. Use the same analytic methods

If the initial results found an increased risk per copy of, say, the A allele (additive model), then a significant increased risk for carriers of T allele (dominant model, in other direction), does not constitute replication. It is in principle possible that the direction of association can change due to differences in linkage disequilibrium across study populations. However, this “flip flop” phenomenon can occur only in very specific situations that are unlikely when the study populations have similar continental ancestry. [40] The burden of proof is on investigators to show evidence for how difference in LD in their study populations could produce a “flip flop” if they wish to claim replication, even though different alleles are associated with risk. Merely citing the possibility of “flipflopping” does not suffice.

Other analytical options include the statistical model (e.g. for a binary outcome, whether it is treated as simply yes/no or the time-to-event is also taken into account), the use of any covariates (e.g. for age, gender, or topic-specific variables), and the use of corrections for relatedness. Usually, the impact of these options is not major, but it can make a difference for borderline associations which may seem to pass or not pass a desired p-value threshold. This means that both for GWA studies and subsequent investigations, one should carefully report the methods in sufficient detail so they can be independently replicated by other researchers. [41]

Modeling can have a much more profound impact in more complex associations than go beyond single markers, e.g. with approaches that try to model dozens and hundreds of gene variants that form a “pathway.” [42, 43] Such complex models may be built by MDR, kernel machines, stepwise logistic regression, or a diversity of other methods and it is important for the replication process to use the same exact steps as the model building. Even then, because these models are so flexible, it is unclear whether a “significant” finding in a second data set constitutes replication; the association may be driven by different sets of SNPs in the different studies. Researchers who conduct complex model-selection/model-building analyses should report their “final” model in as much detail as possible, so other investigators can judge the fit of that model in other data sets.

3.iii. Try to use the same phenotype

For many traits, phenotype definitions may vary considerably across studies, or there may be many different options for defining the phenotypes of interest within each study. Some of this variability is unavoidable and results from differences in measurement protocols across studies. For example, disease may be self-reported in some studies or clinician-diagnosed in others; waist:hip ratios may be self-reported or measured in a clinic, using different operational definitions of “waist;” etc. Characteristics of studied phenotype may also differ across studies: for example, because of the widespread use of Prostate-Specific Antigen (PSA) screening in the United States since the early 1990s, the proportion of early-stage prostate cancer cases in the U.S. is higher than in Europe, where PSA screening is not as common. In the context of a prospective meta-analysis, study investigators can discuss these issues and reach consensus on how to define phenotype so as to maximize relevant information while ensuring as many studies can provide data as possible. In general, there is a trade off between more accurate (but more expensive and perhaps more invasive) measurements on fewer people and less accurate (but cheaper) measurements on more people. For example, although the Fagerstom Test may be a “gold standard” measure of nicotine dependence, currently only a few studies with available genome-wide genotype data have collected data on this test; on the other hand, many studies have collected information about the number of cigarettes smoked per day (a component of the Fagerstrom score). [44] To maximize sample size, investigators may agree to analyze cigarettes per day (which then raises further issues such as what scale to use; whether and how to transform the raw data; how to reconcile continuous with categorical data; etc.). Prospective meta-analyses for height, BMI, and fasting glucose have dealt with the issue of phenotype harmonization in a trait-by-trait basis. [45–48] Other consortia and projects such as the Public Population Project in Genomics (http://www.p3gconsortium.org/) and PhenX (www.phenx.org) aim to facilitate broad collaboration among existing and future genome-wide association studies by making recommendations for standard phenotyping protocols for many diseases and traits. Still, despite best efforts to harmonize measures, some measurement differences across studies will persist, and investigators should be aware of these as possible sources of heterogeneity (see Sections 4 and 5).

Requiring that replication studies use the same phenotype definition used in the initial study also helps avoid false positives due to “data dredging,” the temptation to generate small p-values by testing many different traits (different case subtypes, continuous traits dichotomize using different, arbitrary cut points, etc.). [4] When many phenotypes or phenotype definitions and analyses are used, there should be a penalty for multiple testing. Applying this penalty is not always straightforward, given that most of the phenotypes and analyses are usually correlated or even highly correlated. However, the danger exists for an association to be claimed replicated, after searching through repeated modifications of the phenotypes and analyses thereof. A p-value that has been obtained through such an iterative searching path is not the same as one that was obtained from a single main analysis of a single phenotype.

4. Replication methods and presentation of results

4.i. Statistical heterogeneity across datasets

There are several tests and metrics of between-dataset heterogeneity, borrowed from applications of meta-analysis in other fields. The most popular are Cochran’s Q test of homogeneity, [49] the I² metric (obtained by (Q-degrees of freedom)/Q), and the between-study variance estimator τ². [50] There are shortcomings to all of them. [51] The Q test is underpowered in the common situation where there are few datasets and may be overpowered when there are many, large datasets. There are now readily-available approaches that can be used to compute the power of the Q test to detect a given tau-squared. [52] When the Q test is underpowered, the I² metric has large uncertainty and this can be readily visualized by computing its 95% confidence intervals. [53] Similarly, estimates of τ² may have large uncertainty. One potentially useful approach may be to estimate the magnitude of between-study variability compared with the observed effect size θ, i.e. h=τ/θ. For a small effect size, even small τ² may question the generalizability of the conclusion that there is an association across all datasets. This conclusion would not be as easily challenged in the presence of a large effect size.

Some other caveats should be mentioned. The winner’s curse in the magnitude of the effect in the discovery phase may introduce spuriously inflated heterogeneity, when the discovery data are combined with subsequent replication studies. In such two-stage approaches, between-study heterogeneity should best be estimated excluding the discovery data. Conversely, if all datasets are measured with genome-wide platforms and GWA scan meta-analysis is performed in all gene variants, this is no longer an issue. In fact, if the GWA scan meta-analysis uses random effects (see below), the emerging top hits from the GWA scan meta-analysis are likely to have, on average, deflated observed heterogeneity compared with the true heterogeneity. This is because, underestimation of the between-study heterogeneity favors a variant to come to the top of the list, since it does not get penalized by wider confidence intervals in the random effects setting.

However, we caution that when the number of studies is relatively small, association tests based on random-effects meta-analysis may be deflated, as the between-study variance τ² will be poorly estimated. This is illustrated in Figure 2, which shows quantile-quantile plots for fixed-effect and random-effects meta-analyses of data from PanScan collaboration, which involves 13 studies in the initial GWAS scan. For the random effects analysis, the genomic-control “inflation factor” is in this case more aptly named a “deflation factor:” λ_GC=0.84, indicating that the random effects p-values are larger than expected under the assumption that the vast majority of SNPs are not associated with pancreatic cancer. Fixed-effect meta analysis is arguably more appropriate as an initial screening test for associated markers, although because fixed-effect analysis can be highly significant when only one (relatively large) study shows evidence for association, analyses that incorporate effect heterogeneity such as random effects meta-analysis should be reported for highly significant markers from fixed-effect analyses.

Figure 2.

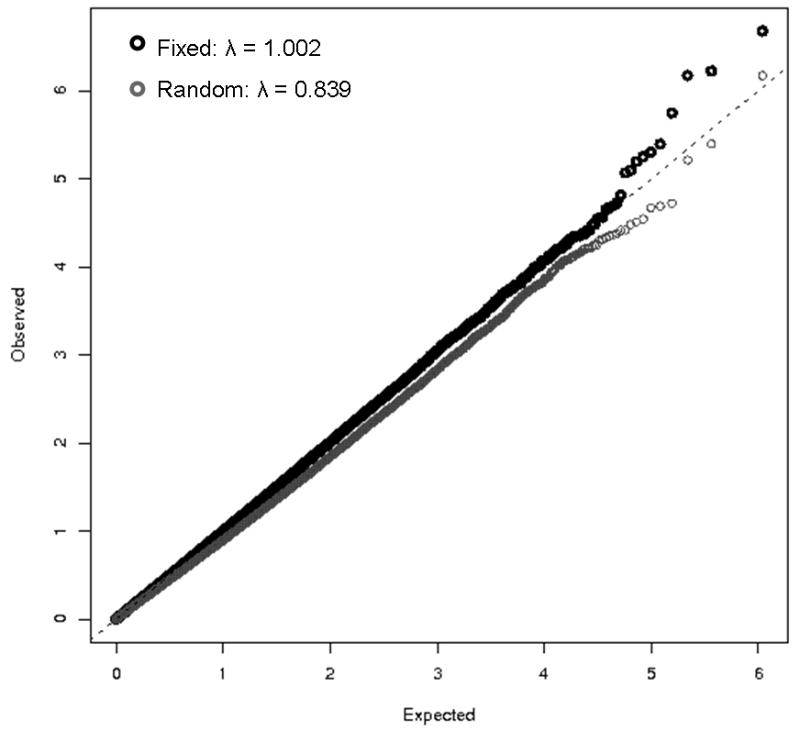
Quantile-quantile plots for fixed-effect and random-effect meta-analyses of the 13 studies in the initial PanScan genome-wide association study of pancreatic cancer. The genomic control inflation factors λ_GC for the fixed-effect and random effect analyses were 0.84 and 1.00, respectively. λ_GC was calculated as the median observed chi-squared test statistic divided by the median of a chi-squared distribution with one degree of freedom.

Finally, lack of demonstrable heterogeneity may be perceived as a criterion of credible replication. [54] However, one should note that tests and measures of heterogeneity address whether effect sizes across different datasets vary, not whether they are consistently on the same side of the null. Dataset-specific effects could vary a lot, but they may all still point to the same direction of effect. Given the potential diversity of LD structure across populations, and differences in phenotype definitions and measurements across studies, between-study heterogeneity should not dismiss an association because the effect sizes are not consistent, if the evidence for rejection of the null hypothesis is strong.

4.ii. Models for synthesis of data from multiple replication studies

Data across studies can be combined at the level of either p-values (probability pooler methods) or effect sizes (effect size meta-analysis). [36, 55, 56] When p-values are combined, at a minimum one should take into account also the direction of effects, but the magnitude of the effects is not taken into account. When effect sizes are used, there are several models that can be used, depending on whether between-study heterogeneity is taken into account or not, and if the former, how this is done. In general, fixed effects approaches that ignore between-study heterogeneity are better powered than random effects approaches and thus more efficient for discovery purposes. However, there is a trade-off for increased chances of false-positives. For effect estimation and predicting what effects might be expected in future similar populations, random effects are intuitively superior in capturing better the extent of the uncertainty. Commonly, random effects are estimated with a 95% CI that captures the uncertainty about the mean effect, but ideally one should also examine the uncertainty of the distribution of effects across populations. This is provided by the prediction interval. An approximate (1−α)% prediction interval for the effect in an unspecified study can be obtained from the estimate of the mean effect μ̂, its estimated standard error, and the estimate of the between-study variance τ̂² by

$$\widehat{\mu }\pm t_{k-2}^{\alpha }\surd \{{\widehat{\tau }}^2+\widehat{\text{SE}}{(\widehat{\mu })}^2\},$$

where $t_{k-2}^{\alpha }$ is the 100(1−α/2)% percentile of the t-distribution with k−2 degrees of freedom.[57] It becomes implicit that when an association has been probed in only a few datasets, then the prediction interval will be wider than the respective confidence interval, even if there is no demonstrable between-study variance (i.e. τ²=0). Table 1 summarizes some issues that arise in selecting, interpreting and comparing the properties and results of various commonly used meta-analyses methods.

Table 1.

Different methods for meta-analysis in the genome-wide association setting

Issues and caveats	P-value meta-analysis	Effect size meta-analysis
		Fixed effects	Random effects
Direction of effect is considered	In some methods	Yes	Yes
Effect size is considered	No	Yes	Yes
Summary p-value is obtained	Yes	Yes	Yes
Summary effect is obtained	No	Yes	Yes
Summary result can be converted to credibility based on priors for the anticipated effect sizes	No	Yes	Yes
Between-study heterogeneity can be taken into account	No	No	Yes
Between-study heterogeneity can be estimated/tested	No	Yes	Yes
Consensus on if/how datasets should be weighted	No	Yes	Yes
Commonly used weights	None, SQRT(N), N	Inverse variance	Inverse variance
Prior assumptions on the effect size can be used	No	In Bayesian meta-analysis	In Bayesian meta-analysis
Prior uncertainty on heterogeneity can be accommodated	No	No	In Bayesian meta-analysis
Prior uncertainty on the genetic model can be accommodated	No	In Bayesian M-A	In Bayesian meta-analysis
Normality assumptions typically made within each study	Yes	Yes	Yes
Normality assumptions within each study easily testable	Yes, rarely done	Yes, rarely done
Normality assumptions for distribution of effects across studies easily testable	No effects assumed	Single common effect assumed(assumption may be visibly wrong)	Not easily testable
Heavy-tail alternative methods exist	No	Yes, rarely used	Yes, rarely used
Use with uncommon alleles (small genotype groups, or even zero allele counts in 2 ×2 tables)	Need to use exact methods	Quite robust	Between-study variance estimation unstable
Power for discovery	Good	Good	Less than others
False-positives from single biased dataset	Susceptible	Susceptible	Less susceptible
False-positives when evidence from small studies is most biased	Susceptible	Susceptible	More susceptible
False-positives when evidence from large studies is most biased	Susceptible	Susceptible	Less susceptible
Can predict range of effect sizes in future similar populations	No	Too narrow confidence intervals	Appropriate with predictive intervals
Can convey uncertainty for practical applications (e.g. to be used in clinical prediction test)	Useless	Inappropriate	Most appropriate with prediction intervals

5. Reasons for non-replication

[T]here are often two or more hypotheses which account for all the known facts on some subject, and although, in such cases, men [sic] of science endeavour to find facts which will rule out all the hypotheses except one, there is no reason why they should always succeed.

— Bertram Russell[58]

A variant observed to be associated with a trait in an initial GWA may not be associated with the trait in subsequent studies, even though the originally association was (nearly) “genome-wide significant.” There are a number of potential reasons for this non-replication.

1. The original observation was a false positive due to sampling error. This is the default explanation, until proven otherwise. This is more likely for associations that were not (or just barely) “genome-wide significant” than for observations that were extremely statistically significant.

2. The follow-up study had insufficient power. This problem can be avoided by ensuring the follow-up study is large enough to reliably detect the observed effect (after accounting for inflation due to “winner’s curse”).[26–29] Moreover, if we consider the cumulative evidence (both the original data plus the follow-up data) as an updated meta-analysis, the cumulative evidence may still pass genome-wide significance or a sufficient Bayes Factor threshold, even though the follow-up data are not formally (highly) significant, when seen in isolation.

3. The genotypic coding used in the initial study may not accurately reflect the true underlying association, leading to a loss of power. Ideally the follow-up study should be well powered to detect associations based on different genetic models (e.g. recessive, dominant) that are consistent with the results observed in the first study.

4. The variant may be a poor marker for the trait due to differences in linkage-disequilibrium structure between the studies. This is more likely if the study populations have different ethnic background. When discussing this as a possible reason for non-replication, investigators should make a good-faith effort to provide empirical data on how linkage-disequilibrium patterns differ (e.g. using HapMap data) and how these differences would lead to inconsistencies across studies.

5. Differences in design or trait definition may lead to inconsistencies. See sections 6.i and 6.ii for examples of how different matching or ascertainment schemes can affect estimates of marker-trait association. Again, when citing this as a reason for non-replication, investigators should as far as possible present arguments for the likelihood and magnitude of differences due to design or measurement differences.

6. The absence of an association in the subsequent studies may be due to true etiologic heterogeneity. Sometimes, this may be driven by gene-gene or gene-environment interaction. If cases in the original study were required to have a family history of disease, for example, or required to have a relatively rare exposure profile (e.g. male lifetime never smokers), then subsequent studies that do not impose these restrictions may not see the association, if the association is restricted to subgroups with a particular genetic or exposure background. However, to-date gene-gene and gene-environment interactions have been notoriously difficult to document robustly.

For the last three explanations, it is useful to clarify if the explanation was offered a posteriori after observing the inconsistent results in different studies. Post hoc explanations for subgroup differences, interactions, and effect modification may be overfit to the observed data and may require further prospective replication in further datasets before they can be relied upon.

6. The wider picture of replication efforts: consortia, data availability, and field synopses

With the recent successes of GWA studies, the field has realized that increasingly large sample sizes are required to identify and replicate the increasingly small effect sizes at common variants that remain undetected. Even wider networks will be required to facilitate the study of variation at the lower end of the frequency spectrum (be it single base changes, copy number variants or otherwise). Collaboration and data sharing are invaluable tools in achieving the necessary sample sizes for well-powered replication studies. The past few years have witnessed a rapid rise in international consortium formation and collaboration has taken a most prominent role in conducting research. Consortia allow investigators to make some design choices up front (if only deciding which SNPs to attempt to replicate), and to work together to harmonize phenotypes and analyses. [7] Several examples of notable successes of consortium-coordinated efforts have started to emerge in the literature. [47, 59–62]

In silico replication of association signals has been further facilitated by initiatives making genetic association study results and/or raw data publicly available (or available through application to an access committee), for example the Wellcome Trust Case Control Consortium (www.wtccc.org.uk), dbGAP (http://www.ncbi.nlm.nih.gov/sites/entrez?db=gap) and the European Genotype Archive (EGA, http://www.ebi.ac.uk/ega). Several emerging considerations, for example with respect to the anonymity of data, [63] avenues for communication between primary investigators and secondary users to facilitate a better understanding of the datasets and their appropriate uses, and suitable accreditation of involved parties, require resolution in order to optimize the use of publicly available raw data.

Replication undoubtedly constitutes an evolving practice. The need to incorporate new data arising from further GWA scans, other replication studies, meta-analyses or all of the above, leads to the emerging paradigm of conglomerate analyses. Field synopses, for example, are efforts to integrate data from diverse sources (GWA studies, consortia, single published studies) in the published literature and to make them publicly available in electronic databases that can be updatable. Examples include the field synopses on Alzheimer’s disease (AlzGene database), schizophrenia (SzGene database) and DNA repair genes.[64, 65] The results of the meta-analyses on the accumulated data can then also be graded for their epidemiological credibility, e.g. as proposed by the Venice criteria.[54]

6.i. Example from the field of type 2 diabetes

Researchers in the field of type 2 diabetes (T2D) genetics were among the first to lead the way in distributed collaborative networks, exemplified by early efforts such as the International Type 2 Diabetes Linkage Analysis Consortium and the International Type 2 Diabetes 1q Consortium. [66–68] The advent of GWA scans was met by pre-publication data sharing between three large-scale studies, the WTCCC, DGI and FUSION scans, [9, 69–71] leading to the formation of the DIAGRAM Consortium (Diabetes Genetics Replication and Meta-analysis). By exchanging information on top signals, the three studies obtained in silico replication of individual scan findings and then further pursued de novo replication in additional sets of independent samples. This endeavour additionally highlighted examples of statistical heterogeneity across the studies, notably with respect to one of the WTCCC study’s strongest signals, residing within the FTO gene. [72] This inconsistency in observed associations could be ascribed to study design and, specifically, to matching cases and controls for BMI (DGI study). The FTO signal was quickly identified as the first robustly replicating association with obesity, mediating its effect on T2D through BMI. A truly genome-wide meta-analysis of the three scans ensued, with large-scale replication efforts in independent datasets of T2D cases and controls, all of European origin. This effort led to the identification of further novel T2D susceptibility loci. [59] Table 2 demonstrates the gains in power afforded by increasing sample size from a single scan to the synthesis of all three studies for a realistic common complex disease susceptibility locus.

Table 2.

Cumulative power to detect association (α=5×10⁻⁸) at a risk allele with frequency 0.20 and 0.40, and allelic odds ratios of 1.1 and 1.2, given sample sizes for the WTCCC, DGI and FUSION studies.

Studies	Risk allele frequency	Allelic odds ratio	Cumulative n cases	Cumulative n controls	power
WTCCC	0.20	1.10	1924	2938	0.0002
WTCCC+DGI	0.20	1.10	3388	4405	0.0011
WTCCC+DGI+FUSION	0.20	1.10	4549	5579	0.0033
WTCCC	0.40	1.10	1924	2938	0.0007
WTCCC+DGI	0.40	1.10	3388	4405	0.0054
WTCCC+DGI+FUSION	0.40	1.10	4549	5579	0.0166
WTCCC	0.20	1.20	1924	2938	0.0333
WTCCC+DGI	0.20	1.20	3388	4405	0.2078
WTCCC+DGI+FUSION	0.20	1.20	4549	5579	0.4426
WTCCC	0.40	1.20	1924	2938	0.1336
WTCCC+DGI	0.40	1.20	3388	4405	0.5468
WTCCC+DGI+FUSION	0.40	1.20	4549	5579	0.8219

6.ii. Anthropometrics and the analysis of “secondary traits”

The meta-analyses of body mass index and height conducted by the Genetic Investigation of ANthropometric Traits (GIANT) consortium raised additional issues. [45, 47, 73] Specifically, unlike the diabetes consortia, where each participating study was designed with diabetes as its primary outcome, the studies involved in GIANT were not originally designed to study determinants of BMI and height, rather they were originally case-control studies of diabetes, prostate and breast cancers, and other diseases. In principle, if the studied trait is associated with disease risk, then conditioning on case-control status can create a spurious association between a marker and the trait. [74, 75] In practice, only a small number of markers will have an inflated Type I error rate—namely, those markers that are associated with disease risk but not directly with the secondary trait—and the magnitude of the inflation depends on both the strength of the association between the secondary trait and disease (which could be modest or controversial, as in the case of smoking and breast or prostate cancer, or quite strong, as in the case of BMI and T2D or smoking and lung cancer) and the strength of the association between the marker and disease (typically relatively weak). [75, 76] Moreover, the risk of false positives may be further ameliorated by diversity of designs among the participating studies some may have originally been case-control studies of different diseases, others may have been cohort or cross-sectional studies. Although there are analytic methods that can eliminate spurious association or bias due to case-control ascertainment in particular situations and under particular assumptions, [74, 76] these should not replace careful consideration of potential biases and evaluation of heterogeneity in effect measures across studies with different designs.