Who benefits most from college? Evidence for negative selection in heterogeneous economic returns to higher education

Abstract

We consider how the economic return to a college education varies across members of the U.S. population. Based on principles of comparative advantage, positive selection is commonly presumed, i.e., individuals who are most likely to select into college benefit most from college. Net of observed economic and non-economic factors influencing college attendance, we conjecture that individuals who are least likely to obtain a college education benefit most from college. We call this theory the negative selection hypothesis. To adjudicate between the two hypotheses, we study the effects of completing college on earnings by propensity score strata using an innovative hierarchical linear model with data from the National Longitudinal Survey of Youth 1979 and the Wisconsin Longitudinal Study. For both data sources, for men and for women, and for every observed stage of the life course, we find evidence suggesting negative selection. Results from auxiliary analyses lend further support to the negative selection interpretation of the results.

Educational expansion is one of the most apparent, enduring, and consequential features of a modern society. Considering the significant educational expansion in the United States over the twentieth century, particularly at the post-secondary level, Fisher and Hout (2006) conclude that “the division between the less- and more-educated grew and emerged as a powerful determiner of life chances and lifestyles” (p. 247). The U.S. Census Bureau reported in 2007 that college graduates were earning on average about $55,000 compared to less than $30,000 for high school diploma recipients. As decades of research have confirmed the consequential role education plays in socioeconomic attainment and mobility (e.g., Blau and Duncan 1967; Hout 1988; Hout and DiPrete 2006), questions about access to and the impact of higher education have long occupied the attention of sociologists and economists. More concretely, scholars have asked (1) what family and individual attributes are associated with the attainment of higher education? and (2) what are the causal effects of higher education on subsequent socioeconomic outcomes?

In the rational-behavioral model for the choice of attaining higher education common to the economics literature, the questions posed above are intrinsically intertwined: individuals make decisions about whether or not to pursue higher education on the basis of cost-benefit analyses, doing so only if higher education enables them to earn more lifetime earnings, at least in expectation (Becker 1964; Card 1995, 2001; Heckman and Honore 1990; Manski 1990; Mincer 1974; Willis and Rosen 1979). In other words, barring imperfect information, borrowing constraints, or uncertainty, individuals choose college versus non-college according to expected economic returns, such that they attain college educations only if the economic returns outweigh the costs. While this utility maximization paradigm can in principle accommodate non-economic factors, scholars partial to this approach seldom pay much attention to such factors in determining higher education.¹ If economic factors are the main determinants of college attainment, it follows that individuals who are most likely to attend college would also benefit most from college (Carneiro, Hansen, and Heckman 2003; Carneiro, Heckman, and Vytlacil 2001, 2007; Heckman, Urzua, and Vytlacil 2006; Willis and Rosen 1979). We call this thesis the positive selection hypothesis.

In the sociological literature, the two research questions posed above are treated separately. This separation has been justified by the recognition that higher education is an achieved status subject to the influences of numerous factors (e.g., Boudon 1974; Bourdieu 1977; Bowles and Gintis 1976; Coleman 1988; DiMaggio 1982; Jencks et al. 1972; Lucas 2001; MacLeod 1989; Mare 1981; Morgan 2005; Sewell, Haller, and Ohlendorf 1970). A key theme that emerges from this literature is that many non-economic factors predict college attainment, as college-going behavior is governed not only by rational choice, but also by cultural and social norms and circumstances (Coleman 1988). As such, mechanisms influencing college attainment may differ by social background. For some persons of socially advantaged backgrounds, college is a culturally expected outcome and thus less exclusively and intentionally linked to economic gain than it is for people in less advantaged groups, for whom college education is a novelty that may well demand economic justification (Beattie 2002; Boudon 1974; Smith and Powell 1990). In addition, the earnings prospects for less-educated workers are bleak, particularly if they come from disadvantaged backgrounds. In contrast, for persons from advantaged backgrounds, the likelihood of going to college and earnings prospects are relatively high. Hence, once we partial out observed covariates that help predict college education, it is possible that, due to differential selection mechanisms and earnings prospects, individuals who are least likely to obtain a college education benefit most from college. We call this conjecture the negative selection hypothesis.

To adjudicate between the positive and the negative selection hypotheses, we conduct an empirical study analyzing data from two large U.S. longitudinal surveys: the National Longitudinal Survey of Youth 1979 cohort and the Wisconsin Longitudinal Study 157 cohort. Use of these two data sources enables us to curb relative strengths and weaknesses across the datasets, such as quality of available control variables; to establish robustness for our results; and to examine possible differences in returns over the life course across cohorts. As individuals invest in higher education with the expectation of obtaining economic benefits over the lifetime (Mincer 1974), it is important to consider variation in returns to higher education over the life course.

We utilize a three-step methodological approach. First, we invoke an ignorability assumption that, after we control for a rich set of observed covariates, there are no additional confounders between persons who do and do not complete college. Under the ignorability assumption, we summarize in estimated propensity scores systematic differences in covariates between college and non-college goers (Rosenbaum and Rubin 1983, 1984; Rubin 1997). Second, we estimate effects of college completion on earnings by propensity score strata and examine patterns of effects using a hierarchical linear model (Xie and Wu 2005). This innovative key step allows us to find either a positive or a negative pattern between the effects of a college education and the likelihood of obtaining a college education. Third, we revisit and challenge the ignorability assumption and conduct auxiliary analyses that aid our interpretation of the results. In a sensitivity analysis, we purposely omit several key covariates and explore the consequences of violating the ignorability assumption by omitting them. We conduct all analyses separately for men and women.

Theoretical And Methodological Issues In Assessing College Returns

Two Sources of Selection Bias

As is well known in the causal inference literature, but seldom acknowledged in empirical sociological research, there are actually two types of selection bias in observational data (Morgan and Winship 2007). The first type is due to heterogeneity in preexisting conditions or attributes that are associated with both the treatment condition and the outcome; in the case of economic returns to higher education, attributes such as mental ability and work habits may be positively associated with the likelihood of attaining both higher education and higher earnings. The second type is due to heterogeneity in treatment effects, i.e., systematic differences between those who do and those who do not attain a college education in the causal effect of a college education on earnings. Economic returns to higher education should vary across different members of a society (Card 1999), as it is implausible to assume that different members of the population respond identically to treatment. In this research, we depart from the population homogeneity assumption and focus on group-level variability by aggregating individuals according to their estimated propensity to complete college based upon observed attributes.² We ask whether persons who are more likely to attain college educations based on observed attributes receive higher or lower returns to college education relative to persons less likely to attain college educations. This approach allows us to explore the potential association between the two sources of population heterogeneity.

To illustrate the first source of bias, let us begin with a standard model in which the effect of a college education is homogeneous. For the i^th person, the following regression function decomposes the observed logged earnings into the sum of three additive parts (in addition to a constant term), i.e., the treatment effect of college education, a linear combination of covariates, and the residual:

$$y_i=\alpha +\delta d_i+\beta \prime X_i+U_i,$$ (1)

where y is the natural logarithm of earnings, d is a dummy variable representing whether or not the respondent completes college (d = 1 if yes; = 0 otherwise),X is a vector of earnings determinants that may also influence the probability of completing college, and U is the residual unexplained by the baseline model. The parameters β are regression coefficients measuring the change in log earnings associated with changes in the earnings determinants X, which typically include several measures of family socioeconomic status, geographic residence, academic achievement, and, in many studies, some measure of mental ability. The exponential transformation of the regression coefficient δ represents the multiplicative increase in earnings associated with the receipt of a college degree, ceteris paribus. Note that in equation (1) δ is assumed to be an unknown constant parameter, invariant across all members of the population. Extensions to this standard model may incorporate additional explanatory factors related to treatment such as institutional selectivity, academic major, and academic performance (e.g., Brewer, Eide, and Ehrenberg 1999; Dale and Krueger 2002; Thomas 2003; Thomas and Zhang 2005; Zhang 2005).

If homogeneity is true, the main threat to causal inference is that an ordinary least squares (OLS) regression of y on d, even controlling for X, is subject to the first source of selection bias due to a nonzero correlation between U and d (Griliches 1977). Under the homogeneity assumption, the conventional wisdom is that OLS estimates of the economic return to schooling are upwardly biased (Griliches 1977; Hauser and Daymount 1977), as factors such as unobserved ability and work ethics should positively affect both education and earnings. The actual direction of the bias, however, has not been empirically settled. For instance, Ashenfelter and Krueger (1994) contend that OLS estimates of the effect of education on earnings are downwardly biased because such estimates are often below instrumental variable (IV) estimates of returns to schooling. If we relax the unrealistic homogeneity assumption, however, there is no simple answer as to whether OLS estimates are biased upward or downward: the OLS estimate is essentially a weighted average of heterogeneous effects, some of which are necessarily higher, while others are lower, than the population average (Angrist and Kruger 1999; Morgan and Winship 2007). Under this more realistic conceptualization of underlying heterogeneity in the returns to education, individuals differ not only in background attributes but also in the economic benefits they reap from a college education.

To systematically study heterogeneous treatment effects of higher education on earnings, we adopt a simple and straightforward approach of using rich covariates and invoking ignorability, at least provisionally. This approach allows us to find empirical patterns of treatment effect heterogeneity as a function of observed covariates. A common way of studying heterogeneous treatment effects by observed covariates is to examine the interaction between education and specific factors that also influence the probability of attaining a college education and wages, such as race or gender (Barrow and Rouse 2005; Perna 2005; Welch 1973) or parents' education or occupation (Altonji and Dunn 1996; Hauser 1973; Olneck 1979). For the question of comparing returns to college between those who complete college and those who do not, however, the most meaningful interaction is between college education and the propensity of completing college (Heckman, Urzua, and Vytlacil 2006).³ We aggregate heterogeneous college effects to propensity score group-level mean effects and directly observe trends in effects (Xie and Wu 2005).⁴

The ignorability assumption (also called “unconfoundedness” or “selection on observables”) states that potential outcomes are uncorrelated with treatment status, conditional on observed covariates. The assumption can never be verified and indeed should not be taken as true in practice for observational data; its plausibility depends on the availability of observed covariates that differ between college graduates and non-college graduates and also influence earnings. It is reasonable to suspect that models that do not control for cognitive ability, for instance, do not satisfy ignorability. Still, measurement of meaningful confounders renders ignorability tentatively more plausible, though not necessarily true. While we do not think the ignorability assumption is true, analyses under this assumption are the most the data can tell us without additional unverifiable assumptions.⁵ Utilizing our strategy, we focus on group differences by the propensity to complete college and adjudicate between two potential patterns in observed heterogeneous effects of college completion on earnings: positive selection (persons most likely to benefit from college are most likely to complete) versus negative selection (persons most likely to benefit from college are least likely to complete).

Positive Selection versus Negative Selection

Human capital theory in economics has proven an influential explanation for educational acquisition (Becker 1964; Mincer 1974). The core idea of traditional human capital theory is that a gradation in earnings by education level reflects returns to individuals' rational investment in education. If we let λ represent the present-value of the lifetime economic return to college, and c the cost of college, attending college produces a net gain if λ > c, with the benefit thus defined as π = λ − c. The association between the returns to college and the decision to attend college is at the core of the more recent literature that links variation in returns to education to heterogeneous schooling behavior. Premised on principles of self-selection and comparative advantage, the thesis is that the most “college worthy” individuals, in the sense of having the highest returns to college, are the most likely to select into college (Averett and Burton 1996; Carneiro, Hansen, and Heckman 2003; Carneiro, Heckman, and Vytlacil 2001, 2007; Roy 1951; Willis and Rosen 1979) and are in a better position to cover the economic costs of a college education, particularly at high-cost institutions (Zhang 2005). Thus, a central conjecture from this literature is that there should be positive selection because individuals who benefit most from are most likely to select into college education.

The positive selection thesis is widely, albeit not universally, accepted in economics. In our view, it is more a theoretical argument than a proposition that can readily be subject to empirical tests. Empirical research in economics on choice has relied heavily on the revealed preference framework (e.g., Manski and Wise 1983; Train 2003). Applied to the research question on the returns to college education, the framework essentially states that the researcher can infer that λ > c, at least in expectation, if a person is observed to complete college education, and λ ≤ c otherwise. This research strategy was implemented by Willis and Rosen (1979) in their classic study, which applied Roy's (1951) model to the college education question, with the difference in expected utility between college education and high school education determining the likelihood of college education. More recently, Carneiro, Heckman, and Vytlacil (2007) also found evidence suggesting positive self-selection – i.e., persons for whom the returns are greatest are those who are most likely to attend college.

Sociologists have recognized heterogeneity in returns to college as well. Raftery and Hout (1993), for example, state that it “seems likely that the perceived benefit of education varies among individuals” as a function of individual attributes (p. 57). Like economists, sociologists infer that the choice of attending college can result from a cost-benefit analysis (Boudon 1974; Breen and Goldthorpe 1997; Raftery and Hout 1993); however, such scholars emphasize that the costs and benefits are not purely economic. For instance, in terms of costs, sociologists have considered heterogeneity in both the financial burden and the family pressure of deviating from cultural norms based on one's socioeconomic background (Boudon 1974; Raftery and Hout 1993).

Moreover, in contrast to the strictly economic cost-benefit model of college attendance, ample research indicates that college attendance is influenced by multiple actors and factors. Beginning with the Blau-Duncan model, sociologists have recognized the significance of numerous family background factors, such as parents' education and occupation, family structure (McLanahan, and Sandefur 1994), and sibship size (Blake 1981) for educational attainment.⁶ The “Wisconsin model” of status attainment further specified the concrete processes by which family background affects educational attainment, through occupational and educational aspirations affected not only by family socioeconomic status and measured ability but also by parents' and significant others' encouragement (Hauser, Tsai, and Sewell 1983; Sewell and Hauser 1975; Sewell, Haller, and Portes 1983; Sewell, Haller, and Ohlendorf 1970).⁷ Coleman (1988) also offered insight into why family background factors influence children's attainment via the concept of social capital, or the resource of social relationships consisting of expectations, information channels, and social norms. Encouragement, expectations, information, and norms differ by family background, generating differential mechanisms of selection into college (Morgan 2005).

In addition, sociological work has developed a neo-Marxist conflict perspective to educational attainment that helps explain differences in educational attainment by social background. For instance, cultural capital scholars stress the importance of family background for educational attainment, emphasizing general cultural background, knowledge, disposition and skills that are passed on from parents to their children, but further argue that schools systematically reward the cultural capital of the advantaged classes and devalue that of the lower classes (Bourdieu 1977; DiMaggio 1982; Lareau 2003). Social reproduction theorists further elaborate this theme, maintaining that primary and secondary schools train advantaged students to take up their positions at the top of the socioeconomic order, including pursuing post-secondary schooling, while conditioning the poor to accept their lower status in the class structure (Bowles and Gintis 1976; MacLeod 1989). In summary, this literature suggests that high social background individuals are likely to go to college even in the absence of a rational economic cost-benefit analysis, whereas low social background individuals must overcome considerable odds to attend college.

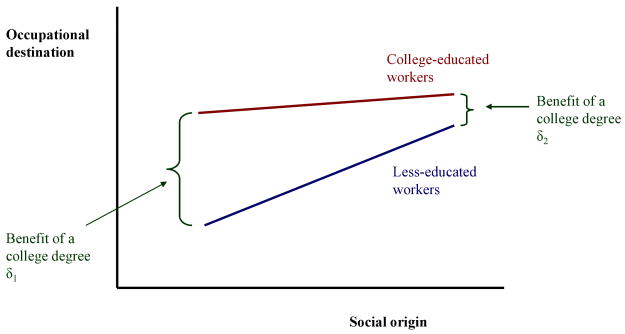
Moreover, past research in social stratification provides a compelling theoretical and empirical basis for postulating variation in the effects of education on earnings by social background. This research has shown that the direct relationship between social origin and destination (both measured by occupational status) is much weaker for college graduates than for workers without college degrees (Hout 1984, 1988). We depict this empirical pattern in Diagram 1. If we change the perspective and examine returns to schooling (Goldthorpe and Jackson 2008), i.e., the difference in destination between college-educated and less-educated workers, as a function of social origin, this interaction pattern yields a smaller difference by college education for individuals of high social origin (δ₂) than for individuals of low social origin (δ₁). In other words, individuals with relatively disadvantaged social backgrounds, or those with the lowest probability of completing college, benefit the most, rather than the least, from completing college. This pattern results from the particularly poor labor market prospects for workers with low levels of education combined with low levels of other forms of human, social, or cultural capital.⁸ This collective theoretical and empirical tradition leads us to formulate our negative selection hypothesis.

Diagram 1.

Hypothetical Model: Origin, Education, and Destination

We are not the first to discuss possible patterns of negative selection in the sociological literature (Brand and Halaby 2006; Bryk, Lee, and Holland 1993; Diprete and Engelhardt 2004; Hoffer, Greeley, and Coleman 1985; Morgan 2001; Tsai and Xie 2008). It has been shown, for example, that high school environment has a stronger effect on the marginal college attendee than on more advantaged students (Bryk, Lee, and Holland 1993; Hoffer, Greeley, and Coleman 1985). Direct empirical evidence in support of negative selection in higher education has also appeared in the economics literature. Heckman, Tobias, and Vytlacil (2001) find that a randomly chosen person might expect to receive a 9 percent increase in wages due to college education, while those actually selecting into college receive about a 4 percent increase. Additionally, studies that have used compulsory schooling laws, differences in the accessibility of schools, and similar features as instrumental variables have found larger economic returns than OLS estimates (Card 2001), i.e., suggesting larger returns to education for those individuals on the margin of school continuation.⁹

Behavioral Model

We now write out the behavioral model for college education as follows. Let d* represent the potential likelihood that the i^th person completes college, and d_i the observed outcome (d_i = 1 if yes; = 0 otherwise). It is customary to relate the two through a threshold measurement model:

$$\begin{array}{l}{d}_i=1\text{if}{d}_i^{\ast }>0;\\ d_i=0\text{otherwise}.\end{array}$$ (2)

We further specify that college attainment is determined by a weighted average of an economic component π_i and a non-economic component η_i, plus a residual (ε_i):

$$d_i^{\ast }=w_i{\pi }_i+(1-w_i){\eta }_i+{\varepsilon }_i,$$ (3)

where ε_i is assumed to be independent of π_i, η_i, and w_i, with 0 ≤ w_i ≤ 1. A key insight from the sociological literature is that the relative weight w_i given to the economic component may decrease with the non-economic determinant η_i, i.e. a negative correlation between the two in the population. We further assume π_i to be a linear function of observed covariates (λ₁'X) plus an unobserved component μ_i, and η_i to be a linear function of observed covariates (λ₂'X). We can rewrite (3) as:

$$d_i^{\ast }=w_i{\lambda }_1\prime X_i+(1-w_i){\lambda }_2\prime X_i+w_i{\mu }_i+{\varepsilon }_i.$$ (4)

The likelihood of completing college is high when $d_i^{\ast }$ is large. Writing out the model of equations (1)-(4) makes it easier to appreciate the key difference between the economic and non-economic factors influencing college attainment. In the traditional Roy-type college behavioral model, w_i = 1, and μ_i drives the college education decision, conditional on X (Willis and Rosen 1979). In most sociological literature, familial, personal, and institutional characteristics dominate (i.e., w_i is much smaller than 1), so that the decision rule is determined primarily by observed covariates X, with the self-selection component given the secondary role or sometimes ignored (i.e., w_iμ_i = 0).

Equation (4) is clearly non-estimable because it is unidentified. As a research strategy, we invoke the ignorability assumption and thus assume away the unobserved self-selection component (μ_i) as a first step of data analyses. We further simplify (4) into a misspecified but estimable reduced-form propensity score model:

$$d_i^{\ast }=\lambda \prime X_i+v_i,$$ (5)

We ask how the misspecification of equation (5) affects our ability to make inferences regarding propensity score-specific causal effects of college education on earnings. The sociological literature suggests that because w should be negatively correlated with the observed propensity score, the extent of misspecification caused by omitting μ declines with the observed propensity score; that is, the decision to go to college among children from high-status families is dictated less by rational choice and self-selection than that among children from low-status families. When a person who is not expected to go to college based on observed characteristics does go to college, there are strong unobserved factors involved, one of which may well be the economic incentive.

Statistical Models

To fix ideas, we adopt the potential outcome approach to causal inference. The potential outcome approach has early roots in experimental designs (Neyman 1923) and economic theory (Roy 1951) and has been extended and formalized for observational studies in statistics (e.g., Holland 1986; Rosenbaum and Rubin 1983, 1984; Rubin 1974), in economics (e.g., Heckman 2005; Manski 1995), and in sociology (e.g., Sobel 2000; Winship and Morgan 1999; Morgan and Winship 2007). The approach makes explicit the issues that concern the identification and estimation of causal effects. Let y be logged earnings and again let d be a variable scored d = 1 for an individual who completes college and d = 0 otherwise. We ask for individual i what earnings would be if he or she received the treatment, i.e., completed college, compared to not receiving the treatment, i.e., not completing college. As only one of the two earnings values, $y_i^1$ or $y_i^0$, is actually observed, causal inference is impossible at the individual level and thus always requires statistical analysis at the group level on the basis of some homogeneity assumption (Holland 1986).

To infer causality with observational data, it is necessary to introduce unverifiable assumptions. In this research, we first introduce the ignorability assumption:

$$E(y^0|X,d=1)=E(y^0|X,d=0)$$ (6a)

and

$$E(y^1|X,d=0)=E(y^1|X,d=1).$$ (6b)

Equation (6a) assumes the average earnings of college-educated workers had they not completed college are the same as the average earnings of non-college-educated workers, conditional on observed covariates; likewise, equation (6b) assumes the average earnings of non-college-educated workers had they completed college are the same as the average earnings of college-educated workers, conditional on observed covariates.

Models for Heterogeneous Treatment Effects

When treatment effects are heterogeneous, there can be two types of selection bias, as we discuss above: pre-treatment heterogeneity bias and treatment-effect heterogeneity bias. Both types of bias may threaten the validity of causal inference with observational data. Estimators such as fixed-effects and the difference-in-differences attempt to eliminate pre-treatment heterogeneity bias, but not treatment effect heterogeneity bias (Angrist and Krueger 1999).

If we allow the coefficient of treatment in equation (1) to be heterogeneous, we can, at least theoretically, write out the two types of heterogeneous components. Equation (1) becomes the following:

$$y_i={\alpha }_i+{\delta }_i{d}_i+\beta \prime X\prime +U_i,$$ (7)

In this specification, α_i represents pre-treatment heterogeneity while δ_i represents treatment-effect heterogeneity.¹⁰ If there is pre-treatment heterogeneity bias, correlation ρ(α, d) ≠ 0. If there is treatment-effect heterogeneity bias, correlation ρ(δ, d) ≠ 0 (Heckman, Urzua, and Vytlaci 2006; Winship and Morgan 1999). The individual-level heterogeneity model is not identifiable, as α_i and δ_i cannot be separated from U_i without further constraints; we invoke the ignorability assumption. In practice, conditioning on X, which is typically multi-dimensional, proves difficult due to the “curse of dimensionality”; we cannot often find both treated and untreated units with identical values on X if X is of a high dimension. However, the important work of Rosenbaum and Rubin (1983, 1984) shows that, given the ignorability assumption, it is sufficient to condition on the propensity score as a function of X. The propensity score is defined as the probability of assignment to the treatment group, i.e. college completion, given covariates X:

$$P=p(d_i=1|X)$$ (8)

In this study, we evaluate heterogeneity in treatment effects by decomposing δ in equation (7) into a nonparametric function of the propensity score and utilize a hierarchical linear model to reveal a pattern of returns.¹¹ The sociology and economics literatures inform us of a variety of family and personal attributes that we use to predict college attendance; thus, we can divide a population into subpopulations with similar predicted propensity scores to complete education based on observed attributes. We assess whether or not population heterogeneity in the propensity to complete college is associated with heterogeneity in returns to college; specifically, we ask if the estimated effect of college is positively or negatively associated with the estimated propensity to complete college.

Our analytic strategy proceeds in three steps: (1) We estimate binary logistic regressions predicting the probability of completing college and derive propensity scores for each individual in the sample; we group respondents into strata of estimated propensity scores to balance the distributions of the covariates between college graduates and non-college graduates (p<.001); (2) In level-1, we estimate the treatment effects specific to balanced propensity score strata using ordinary least squares regression; and (3) In level-2, we examine the heterogeneous results by propensity score strata, and summarize the trend in the variation of effects using a hierarchical linear model (Xie and Wu 2005). Our approach is similar to propensity score matching as respondents' observed differences are characterized by propensity scores. The two methods differ in how comparisons are constructed. In a typical propensity score matching setting, comparison by treatment status is first made on an individual basis and then averaged over the population or a subpopulation. In our approach, comparison by treatment status is first constructed for a relatively homogeneous group based on propensity scores and then examined across different groups of similar propensity scores through a hierarchical linear model.¹²

Data, Measures, And Descriptive Statistics

Data Description

To examine heterogeneous treatment effects of education on earnings, we utilize two large panel datasets containing extensive information about respondents' social backgrounds, abilities, and schooling experiences: the National Longitudinal Survey of Youth 1979 (NLSY)¹³ and the Wisconsin Longitudinal Study (WLS)¹⁴. Both samples are cohort-based. Single-cohort longitudinal surveys are advantageous in controlling for the potential confounding effect of cohort with experience. The NLSY is a nationally representative sample of 12,686 respondents who were 14-22 years old when first surveyed in 1979. These individuals were interviewed annually through 1994 and are now interviewed on a biennial basis. We restrict our sample to respondents who were 14-17 years old at the baseline survey in 1979 (n = 5,581), had not graduated from high school at the time the Armed Services Vocational Aptitude Battery (ASVAB) tests were administered (n = 3,885), had completed at least the 12^th grade as of 1990 (n = 3,034), and did not have any missing data on the set of covariates used in our analysis (n = 2,474). We set these sample restrictions to examine a cohort with little age variation, to ensure that all measures we use are pre-college, and to compare college graduates to those respondents who completed at least a high school education. We evaluate effects of completing college on earnings for respondents age 29-32 (in 1994), 33-36 (in 1998), and 37-40 (in 2002), i.e., from early to mid-career years.

The WLS is a regional panel study based on a random sample of 10,317 men and women who graduated from Wisconsin high schools in 1957. Past research has shown that for processes of socioeconomic attainment, patterns found in the WLS mirror those found in national probability samples (Sheridan 2001). We restrict our sample to respondents who did not have any missing data on the set of covariates used in our analysis (n = 7,905).¹⁵ Replication of the analysis through these data sources for two different cohorts allows us to check the robustness of the core findings. The two data sources are also complementary in their relative strengths and weaknesses. While the NLSY offers us national representation, the WLS contains a much larger sample of relatively homogeneous respondents with many well-measured pre-college covariates, notably a reliable measure of cognitive ability.

Variable Measurement

Table 1 lists the pre-college variables we use to construct propensity score strata for our two data sources. Most of these measures have figured prominently in sociological studies of educational and occupational attainment, and their measurement is straightforward. There are, however, a few differences across data sources in the measurement of these variables. Parents' income is measured as total net family income in 1979 dollars in the NLSY and as parents' income in 1957 dollars in the WLS. “Residence/proximity to college or university” indicates whether a respondent lived in an SMSA in 1979 in the NLSY and whether a respondent's high school was within 15 miles of a college or university in the WLS. College-track indicates whether or not the student was enrolled in a college-preparatory curriculum in the NLSY and had completed the requirements for UW-Madison in the WLS. The measurement of mental ability also differs across the data sources. In 1980, 94 percent of the NLSY respondents were administered the ASVAB, a battery of ten intelligence tests measuring knowledge and skill in areas such as mathematics and language. We follow the practice of Cawley et al. (1997) by first residualizing each of the ASVAB tests on age at the time of the test separately by race and gender, with the residuals standardized to have mean zero and variance one. We then combine the items (with equal loadings which sum to one) into a composite scale (Cronbach's α = 0.92). In the WLS, we use the 1957 Henmon-Nelson Test of Mental Ability scores. We use hourly wages as the outcome variable in the logarithm form.¹⁶ In the NLSY, our outcome is logged hourly wages and salary for the late 20s through the early 40s (in 1994, 1998, and 2002). In the WLS57, our outcome is logged yearly earnings at age 35 (in 1975) and logged hourly wages at age 53 (in 1993).¹⁷ We add a small positive constant ($0.50) before taking the logs. Unemployed workers are eliminated.¹⁸

Table 1. Descriptive Statistics of Pre-College Covariates.

	NLSY Means				WLS Means
	Men (n=1265)		Women (n=1209)		Men (n=3690)		Women (4215)
Variables	Non- College Grad.	College Grad.	Non- College Grad.	College Grad.	Non- College Grad.	College Grad.	Non- College Grad.	College Grad.
Race
Black	0.18	0.07	0.15	0.07	---	---	---	---
Hispanic	0.07	0.03	0.07	0.03	---	---	---	---
Social background
Parents' income*	17870	26538	18174	25991	5605	8123	5622	9262
Mother's education	11.26	13.32	11.18	13.37	10.15	11.56	9.94	12.02
Father's education	11.23	14.39	11.16	14.14	9.10	11.37	9.21	11.79
Intact family (0-1)	0.72	0.83	0.67	0.85	0.90	0.92	0.90	0.92
Number of siblings	3.29	2.34	3.40	2.45	3.45	2.61	3.51	2.40
Rural residence (0-1)	0.25	0.19	0.24	0.21	0.22	0.12	0.20	0.16
Urban res. / prox. to coll.*	0.77	0.78	0.75	0.80	0.42	0.50	0.50	0.53
Jewish (0-1)	0.00	0.03	0.00	0.04	0.00	0.02	0.00	0.03
Ability and academics
Class rank	---	---	---	---	35.76	65.49	53.78	79.51
Mental ability (IQ)*	-0.09	0.69	-0.04	0.64	97.03	111.75	98.67	112.00
College track (0-1)*	0.23	0.59	0.23	0.49	0.54	0.91	0.46	0.89
Social-psychological
Teachers' encouragement	---	---	---	---	0.35	0.75	0.36	0.77
Parents' encouragement	---	---	---	---	0.47	0.91	0.39	0.90
Friends' plans	0.42	0.79	0.48	0.81	0.22	0.66	0.30	0.76
Weighted Sample Proportion	0.76	0.24	0.77	0.23	0.69	0.31	0.82	0.18

Notes: Parents' income is measured as total net family income in 1979 dollars in the NLSY and in 1957 dollars in the WLS. “Urban res. / proximity to coll.” indicates whether a respondent lived in an SMSA in the NLSY and whether a respondent's high school was within 15 miles of a college or university in the WLS. Ability is measured with a scale of standardized residuals of the ASVAB in the NLSY and with the Henmon-Nelson IQ test in the WLS. College-track indicates whether the student was enrolled in a college-preparatory curriculum in the NLSY and whether the student completed the requirements for UW-Madison in the WLS.

Descriptive Statistics

A higher probability of attaining a college degree is among the most important causal mechanism for realizing the advantage associated with a high socioeconomic origin, a key finding of the classic Blau and Duncan (1967) study. As shown in Table 1, college graduates are more likely to come from families with high income, highly educated parents, intact family structure, and few siblings than non-college graduates. Also predictive of college education are high levels of secondary school academic success, high levels of cognitive ability, high levels of encouragement from teachers and parents to attend college, and friends who plan to attend college. These statistics suggest that many non-economic factors figure prominently in the educational attainment of youth. Finally, for multifaceted reasons (Kao and Thompson 2003), the likelihood of completing college varies by race and Hispanic origin, with whites and Asians being more likely to complete college than blacks and Hispanics.

Main Analysis And Findings

College Returns under the Assumption of Homogeneity

Table 2 provides the estimated effects of college completion on earnings, separately by sex, through regression analyses under the homogenous effect assumption, controlling for the full set of covariates at our disposal described above.¹⁹ For NLSY employed men, college completion yields a highly significant positive effect on logged hourly wages that steadily increases over time, from an 18 percent advantage in men's late 20s to early 30s to a 41 percent advantage in their late 30s to early 40s, consistent with the human capital model. Given the known increasing temporal trend in returns to college, it is not surprising that the effect of college completion is smaller in magnitude in the earlier WLS cohort. Still, results for WLS men indicate significant and increasing returns associated with a college degree over the life course.

Table 2. Effects of College Completion on Log Wages under the Assumption of Homogeneity.

	Men	Women
NLSY
1994 Wages	0.180***	0.276***
(age 29-32)	(0.047)	(0.051)
1998 Wages	0.296***	0.188***
(age 33-36)	(0.054)	(0.052)
2002 Wages	0.410***	0.216**
(age 37-40)	(0.069)	(0.075)
WLS
1975 Earnings	0.124†	0.380**
(age 35)	(0.067)	(0.113)
1993 Wages	0.302***	0.225***
(age 53)	(0.034)	(0.038)

Note: Numbers in parentheses are standard errors. Treatment effects are conditional upon the set of covariates for each data source described in Table 1. NLSY estimates further condition on age at baseline. NLSY results for women also condition on an indicator for married with children at age 25. All outcome variables indicate current hourly wages, except for WLS 1975 earnings, which indicate current yearly earnings. Unemployed workers are omitted.

^†p < .10

^*p <. 05

^**p < .01

^***p < .001 (two-tailed tests)

Results for NLSY employed women reveal a large, significant effect of college completion in their late 20s to early 30s, a smaller effect in their mid-30s relative to their early 30s, and a larger effect in their late 30s to early 40s relative to their mid-30s.²⁰ Differences in life course patterns between men and women may reflect the influences of traditional gender roles in the family and corresponding intermittent labor force attachment among women relative to men, particularly during childbearing years (Becker 1991; Bianchi 1995; Mincer and Polacheck 1974). That is, women's life-course pattern of effects may reflect the selection of some women out of the labor force or a lower additive return to college during childbearing years. In the WLS, the effect of a college degree also declines over the life course, but the effect is larger for WLS women than for NLSY women in their mid-30s. We speculate that sample selection may explain this somewhat peculiar finding: Women's labor force participation was much lower for the WLS cohort (57 percent of WLS women were employed at age 35 in comparison to 76 percent of NLSY women in their mid-30s), and thus more selective with respect to earnings than for the NLSY cohort.

Generating Propensity Score Strata

Our next objective is to examine the heterogeneous effects of college completion by propensity score strata. We estimate binary logistic regressions predicting the odds of completing college by the covariates described in Table 1 for each data source, separately by sex, and derive estimated propensity scores for each individual (Becker and Ichino 2002). Results for the logistic regressions are reported in Appendix A. We then generate balanced propensity score strata; balancing is satisfied when within each interval of the propensity score the average propensity score and the means of each covariate do not significantly differ between college and non-college graduates. We restrict the balancing algorithm to the region of common support, i.e., to regions of propensity scores in which both treated and control units are observed.²¹ To demonstrate the balance achieved within each stratum, we present covariate means by propensity score strata for NLSY men in Table 3.²² Inspection of Table 3 also elucidates the characteristics of a typical individual within each stratum. For instance, a person with parents who are both high school drop-outs, with three siblings, with low ability, enrolled in a non-academic track, and with friends who do not plan to go to college is characteristic of stratum 1. By contrast, a person with parents who had some college, with one sibling, with high ability, enrolled in an academic track, and with friends who plan to go to college is characteristic of stratum 5. Table 4 provides the number of cases in each stratum, separately by college attainment, gender, and data source. As expected, the frequency distributions for college and non-college educated individuals run in opposite directions: In the case of college-educated individuals, the frequency count increases with the propensity score, whereas in the case of non-college-educated individuals the count decreases with it. Still, we achieve overlap within each stratum; i.e., for each propensity score stratum there are individuals with d = 1 and other individuals with d = 0.²³

Appendix A. Logit Models Predicting College Completion for the Generation of Estimated Propensity Scores.

	NLSY		WLS
Variables	Men	Women	Men	Women
Black	-0.651* (0.268)	-0.208 (0.256)	---	---
Hispanic	-0.792* (0.335)	-1.100** (0.326)	---	---
Parents' income	0.000 (0.000)	0.000 (0.000)	0.000*** (0.000)	0.000* (0.000)
(Parents' inc.)2	0.000 (0.000)	0.000 (0.000)	0.000* (0.000)	0.000 (0.000)
Mother's edu.	-0.363* (0.162)	-0.407** (0.137)	-0.334*** (0.092)	-0.200† (0.109)
(Mother's edu.)2	0.020** (0.007)	0.021*** (0.006)	0.017*** (0.004)	0.018* (0.005)
Father's edu.	0.124** (0.037)	0.072* (0.036)	0.088*** (0.017)	0.055** (0.017)
Intact family	0.281 (0.236)	0.507* (0.230)	0.073 (0.169)	0.025 (0.185)
Num. of siblings	-0.089† (0.051)	-0.123* (0.050)	-0.018 (0.021)	-0.067** (0.025)
Rural res.	0.066 (0.251)	-0.098 (0.225)	-0.099 (0.143)	0.667*** (0.150)
Availability coll.	-0.419† (0.239)	-0.065 (0.228)	-0.092 (0.099)	0.092 (0.106)
Jewish	1.999† (1.032)	---	1.280* (0.609)	1.387** (0.409)
Class rank	---	---	0.028*** (0.002)	0.027*** (0.003)
Mental ability	1.984*** (0.298)	1.514*** (0.239)	0.023*** (0.004)	0.018*** (0.005)
(Mental ability)2	-0.386† (0.218)	-0.305† (0.176)	---	---
College track	0.603** (0.196)	0.514* (0.199)	0.618*** (0.132)	0.693*** (0.003)
Teachers' enc.	---	---	0.438*** (0.107)	0.565*** (0.117)
Parents' enc.	---	---	0.996*** (0.130)	1.323*** (0.146)
Friends' plans	0.992*** (0.209)	0.645** (0.204)	0.946*** (0.101)	0.723*** (0.116)
LR Chi-Sq.	445.23	304.11	1765.50	1429.10
Prob. > Chi-Sq.	0.00	0.00	0.00	0.00
Sample size	1265	1203	3690	4215

Note: Numbers in parentheses are standard errors.

^†p < .10

^*p <. 05

^**p < .01

^***p < .001 (two-tailed tests)

Table 3. Mean Covariate Values by Propensity Score Strata: NLSY Men.

	Propensity Score Strata
	[0.0-0.1)		[0.1-0.2)		[0.2-0.4)		[0.4-0.6)		[0.6-1.0)
Variables	Non- Coll. Grad.	Coll. Grad.	Non- Coll. Grad.	Coll. Grad.	Non- Coll. Grad.	Coll. Grad.	Non- Coll. Grad.	Coll. Grad.	Non- Coll. Grad.	Coll. Grad.
Black	0.37	0.25	0.21	0.40	0.23	0.23	0.19	0.12	0.15	0.07
Hispanic	0.18	0.30	0.12	0.08	0.12	0.09	0.12	0.09	0.07	0.05
Parents' income	13381	12253	17614	18482	19324	18422	23062	21348	23469	34702
Mother's edu.	10.31	10.05	11.67	12.16	11.98	12.21	12.71	12.54	13.67	14.79
Father's edu.	10.17	9.95	11.79	10.72	12.08	12.53	13.33	13.97	15.11	16.30
Intact family	0.63	0.55	0.63	0.80	0.74	0.67	0.85	0.80	0.85	0.91
Num. of siblings	3.84	4.05	3.04	3.04	2.64	2.47	2.88	2.46	2.04	2.17
Rural res.	0.21	0.30	0.26	0.20	0.21	0.21	0.19	0.12	0.11	0.20
Availability coll.	0.76	0.70	0.80	0.84	0.75	0.77	0.73	0.77	0.81	0.78
Jewish	0.00	0.00	0.00	0.00	0.01	0.00	0.00	0.02	0.04	0.08
Mental ability	-0.14	-0.01	0.31	0.48	0.62	0.57	0.79	0.76	0.90	1.05
College track	0.17	0.16	0.32	0.37	0.41	0.52	0.57	0.55	0.83	0.73
Friends' plans	0.35	0.55	0.61	0.52	0.66	0.74	0.90	0.85	0.93	0.93

Table 4. Frequency Counts per Propensity Score Stratum.

NLSY						WLS
Men			Women			Men			Women
P-Score	d=0	d=1	P-Score	d=0	d=1	P-Score	d=0	d=1	P-Score	d=0	d=1
[.00, .10)	454	20	[.00, .05)	573	12	[.00, .05)	931	28	[.00, .05)	1367	27
[.10, .20)	135	25	[.05, .10)	181	17	[.05, .10)	418	33	[.05, .10)	441	38
[.20, .40)	130	43	[.10, .20)	156	28	[.10, .15)	255	25	[.10, .20)	367	67
[.40, .60)	52	65	[.20, .40)	147	47	[.15, .20)	155	45	[.20, .40)	391	172
[.60, 1.00)	27	76	[.40, .60)	37	48	[.20, .40)	386	149	[.40, .60)	204	185
---	---	---	[.60, 1.00)	19	55	[.40, .60)	208	200	[.60, 1.00)	101	265
---	---	---	---	---	---	[.60, .70)	72	122	---	---	---
---	---	---	---	---	---	[.70, .80)	46	173	---	---	---
---	---	---	---	---	---	[.80, 1.00)	48	380	---	---	---

Heterogeneous College Returns

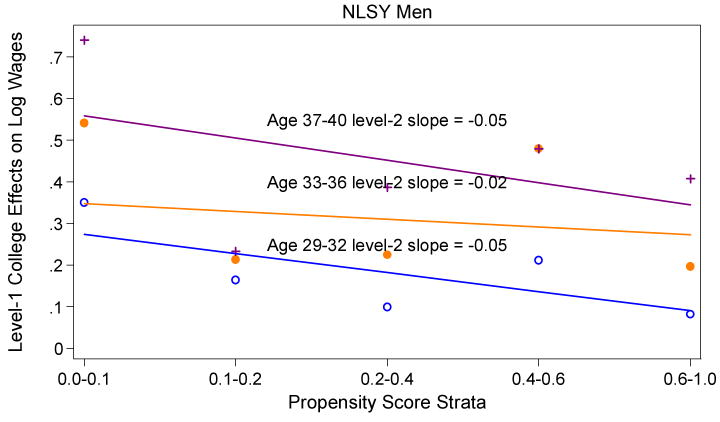
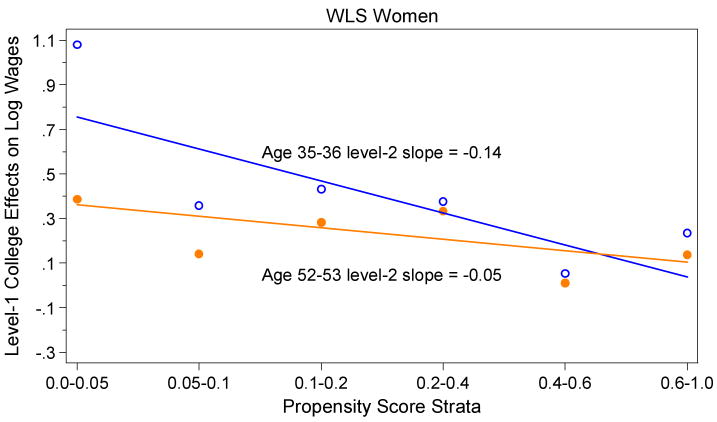
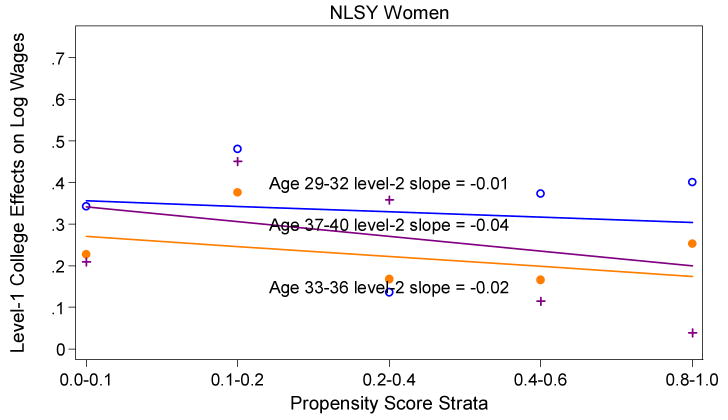
Figures 1-4 present the main results of our study. We first estimate treatment effects specific to propensity score strata and then detect the pattern of effects by propensity score with a hierarchical linear model (HLM). Points in Figures 1-4 represent estimates of stratum-specific effects of college completion on logged earnings. The linear plots and reported level-2 slopes included in the figures are based on the HLMs, i.e. level-2 variance-weighted least squares models estimated by level-1 college effects specific to propensity score strata regressed on propensity stratum rank. All point estimates and associated t-values corresponding to Figures 1-4 are provided in Appendix B.1 for the NLSY and B.2 for the WLS.

Figure 1.

HLM of Economic Returns to College

Figure 4.

HLM Model of Economic Returns to College

Appendix B.1. Effects of College Completion on Log Wages by Propensity Score Strata: NLSY.

	Level-1 Slopes					Level-2
	Stratum 1	Stratum 2	Stratum 3	Stratum 4	Stratum 5	Slopes
Men
1994 Earnings	0.351**	0.164	0.099	0.212*	0.082	-0.046
(age 29-32)	(0.123)	(0.121)	(0.107)	(0.104)	(0.082)	(0.038)
1998 Earnings	0.542***	0.214†	0.225*	0.479***	0.197	-0.019
(age 33-36)	(0.150)	(0.108)	(0.099)	(0.120)	(0.164)	(0.046)
2002 Earnings	0.740***	0.234	0.387**	0.479*	0.408*	-0.053
(age 37-40)	(0.163)	(0.191)	(0.133)	(0.188)	(0.178)	(0.055)
Women
1994 Earnings	0.343**	0.480***	0.137	0.373	0.401*	-0.013
(age 29-32)	(0.119)	(0.109)	(0.107)	(0.142)	(0.168)	(0.044)
1998 Earnings	0.228*	0.376**	0.169	0.167	0.253	-0.024
(age 33-36)	(0.103)	(0.121)	(0.114)	(0.140)	(0.265)	(0.047)
2002 Earnings	0.210	0.452*	0.359**	0.116	0.039	-0.035
(age 37-40)	(0.160)	(0.176)	(0.134)	(0.193)	(0.368)	(0.068)

Note: Numbers in parentheses are standard errors.

^†p < .10

^*p <. 05

^**p < .01

^***p < .001 (two-tailed tests)

Appendix B.2. Effects of College Completion on Log Wages by Propensity Score Strata: WLS.

	Level-1 Slopes									Level-2
	Stratum 1	Stratum 2	Stratum 3	Stratum 4	Stratum 5	Stratum 6	Stratum 7	Stratum 8	Stratum 9	Slopes
Men
1975 Earnings	0.175	-0.104	-0.243	0.195	0.288*	0.360*	-0.364	0.007	0.029	-0.003
(age 35)	(0.268)	(0.269)	(0.277)	(0.225)	(0.132)	(0.146)	(0.244)	(0.261)	(0.249)	(0.033)
1993 Earnings	0.444***	0.126	0.428*	0.374**	0.360***	0.255***	0.221†	0.188	0.285*	-0.017
(age 52)	(0.118)	(0.133)	(0.168)	(0.112)	(0.080)	(0.073)	(0.127)	(0.151)	(0.132)	(0.017)
Women
1975 Earnings	1.079*	0.358	0.433	0.376	0.053	0.235	---	---	---	-0.143†
(age 35)	(0.462)	(0.403)	(0.321)	† (0.208)	(0.223)	(0.329)				(0.087)
1993 Earnings	0.385**	0.141	0.283**	0.333***	0.011	0.138	---	---	---	-0.052†
(age 52)	(0.147)	(0.137)	(0.106)	(0.076)	(0.087)	(0.103)				(0.029)
WLS Men, Small Set of Covariates
1975 Earnings	0.181	0.031	0.392**	0.189	0.082	0.224	0.423†	---	---	0.031
(age 35)	(0.117)	(0.099)	(0.119)	(0.204)	(0.202)	(0.219)	(0.246)			(0.032)

Note: Numbers in parentheses are standard errors.

^†p < .10

^*p <. 05

^**p < .01

^***p < .001 (two-tailed tests)

Beginning with Figure 1, which depicts results for NLSY men's college effects on earnings at age 29-32 (in 1994), age 33-36 (in 1998), and age 37-40 (in 2002), the downward linear slopes illustrate the declining trend in effects with propensity stratum rank at every observed time period. For instance, for men in their late 20s to early 30s, a unit change in stratum rank is associated with a 5 percent reduction in the treatment effect, such that the predicted effect of college completion on earnings in stratum 1 is about 30 percent while the predicted effect in stratum 5 is about 10 percent. This means that an individual, for example, who has parents who are high school drop-outs and who himself has low measured ability benefits more from completing college, on the magnitude of an estimated 20 percent, than an individual whose parents went to college and who himself has high measured ability. We also find evidence suggesting a declining trend in college effects on earnings for men in their mid- and late 30s and early 40s. In the late 30s to early 40s, for instance, the 5 percent reduction in treatment effect per stratum rank again results in an estimated 20 percent difference between the lowest and highest strata, or between the least and most advantaged college goers. The level-2 slopes thus offer support for the negative selection hypothesis at each observed stage of the life course. We observe, as would be expected, that college completion is associated with an increasing economic return over the life course, and this is true across propensity score strata.

The results for NLSY women in Figure 2 are similar to those for men in suggesting negative selection at each observed stage of the life course. For instance, for women in their late 30s to early 40s, a unit change in stratum rank is associated with a 4 percent reduction in the treatment effect, such that the predicted effect of college completion on earnings is about 35 percent for stratum 1 women with disadvantaged socioeconomic backgrounds, versus about 20 percent for stratum 5 women with advantaged socioeconomic backgrounds. However, in contrast to men, we observe an oscillating return to college over the life course among women, as we discussed for results under the assumption of homogeneity. Again, differences in life course earnings returns between men and women likely reflect intermittent labor force attachment among women relative to men during childbearing years, and these family processes could impact women differently by propensity score strata.

Figure 2.

HLM of Economic Returns to College

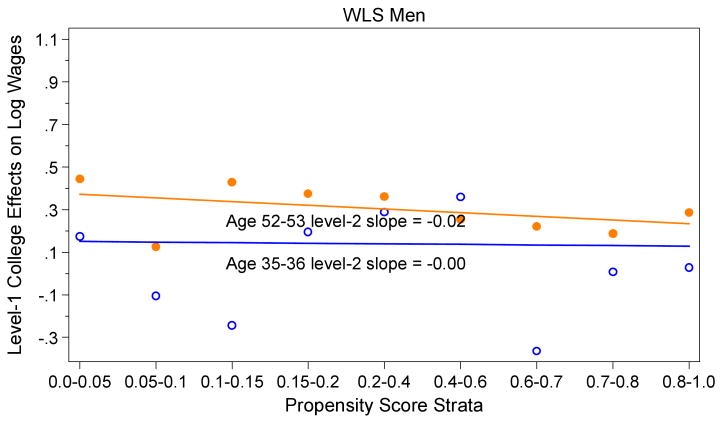
Results for WLS men and women are presented in Figures 3 and 4, respectively.²⁴ Figure 3 depicts results for WLS men's earnings at age 35 (in 1975) and age 53 (in 1993). Level-2 slopes in the WLS indicate a less than 1 percent reduction per stratum rank at age 35 (the flattest of the level-2 slopes we observe), and a 2 percent reduction per stratum rank at age 53. There are 9 strata in the WLS compared to 5 in the NLSY; thus, a 2 percent reduction per stratum rank at age 53 means an 18 percent decrease in the earnings return to college education for the highest stratum, i.e., the most advantaged men, relative to the lowest stratum, i.e., the most disadvantaged men. While we observe generally lower returns to education in the earlier cohort, the results from the WLS are consistent with those from the NLSY in lending support for negative selection. In both Figures 1 and 3, the level-2 slopes reveal that the benefit to completing college is greatest among men least likely to complete college at every observed stage in the life course.

Figure 3.

HLM of Economic Returns to College

For WLS women, we observe a much steeper downward slope at age 35 compared to NLSY women in their mid-30s, the result of a very high return among women in stratum 1. It is likely that women from disadvantaged social backgrounds who obtained college degrees in the early 1960s were particularly selective, generating an unusually high return. Such women may have been less likely to assume traditional family roles due to a lesser likelihood that they were married and/or married to men with economic resources sufficient for role-specialization within the family relative to their advantaged peers (Hill and Stafford 1974).

In summary of Figures 1-4, we have presented evidence for a systematic selection mechanism at work: When individuals with a low propensity of completing college, i.e., individuals from the most disadvantaged social origins and the lowest ability and achievement, actually complete college, they benefit the most from college. From Appendices B.1 and B.2, we see that the wage gap between the treatment and control groups (level-1 coefficient) is statistically significant within several, but by no means every, propensity score stratum. This facet of our findings is in fact consistent with the negative selection hypothesis: 8 out of the 10 estimated effects in stratum 1 are statistically significant, while only 3 out of the 10 estimated effects in the final stratum are significant. Still, there are few statistically significant level-2 slope coefficients. We note that level-2 slope coefficients are based on very few data points. There is no “population” of propensity score strata as true level-2 units of analysis. We fit the HLM model to provide an overall one-degree-of-freedom summary of the direction of the pattern of effect heterogeneity as a function of propensity score, and the direction is negative in every case. At the least, we can say that the selection patterns in Figures 1-4 are clearly not positive. While the evidence for the negative selection hypothesis is only suggestive for each case we present, we note that the core finding of a negative pattern holds true for two different data sources with varying quality of measures, at every observed life course stage for different cohorts, and for men and for women – a total of 10 distinct negative level-2 slopes. Moreover, we found the same pattern for another cohort-based U.S. longitudinal dataset (Brand and Xie 2007).²⁵ Nevertheless, our results should be taken as descriptive and suggestive, not definitive.

Auxiliary Analysis

Given the evidence suggesting negative selection, we now consider the question of causal mechanisms. It is plausible, indeed likely, that multiple mechanisms account for the pattern we observe. We first test the idea of differential selection mechanisms by propensity score strata with a measure of the value of a college education among high school seniors in the WLS. The variable “value of college” was created by Armer (1964); it is a weighted average of the scores in response to a series of 18 statements regarding perceptions of the value of going to college. The most highly weighted items include: “I would rather start earning money quickly, and learn on the job”; “learning on a job is more practical than most school learning”; and “going to college would be a waste of time for me.” (See WLS Memo 129 for further details on the items and the variable construction.) In Table 5, we examine values of college by propensity score strata and education among WLS men. We find a large differential between college graduates and non-college graduates in low propensity strata, with the former valuing college more than the latter, while the gap gradually decreases across propensity score strata to almost no difference among those in the highest propensity stratum. The atypically high value placed upon college by disadvantaged youth who actually completed college stands in contrast to the uniformly high value (i.e., undifferentiated by actual college completion status) placed upon college among advantaged youth. This result suggests, as we hypothesize, that mechanisms leading to college attainment differ by social background.

Table 5. Mean “Value of College” by Propensity Score Strata: WLS Men.

Propensity Score Strata
	[0.0-0.05)	[0.05-0.1)	[0.1-0.15)	[0.15-0.2)	[0.2-0.4)	[0.4-0.6)	[0.6-0.7)	[0.7-0.8)	[0.8-1.0)
Non-college grad.	45.12	54.55	63.29	66.09	74.82	82.52	84.90	88.73	85.36
College grad.	58.86	70.59	81.00	82.77	85.26	86.79	89.13	88.48	88.92

Note: The variable “value of college” is a weighted average of the scores in response to a series of 18 statements regarding perceptions of the value of going to college.

As the value of college variable encompasses both economic and non-economic incentives, we utilize an additional variable to determine whether low propensity college attendees are more economically driven than high propensity college attendees, for whom college attendance is a cultural expectation. As it is well known that field of study impacts earnings (Thomas and Zhang 2005), we examine stratum-specific college majors for college-educated men in the WLS. In Table 6 we observe that while low propensity students are more likely to concentrate in business and education, majors that yield immediate economic return, high propensity students are more likely to major in the sciences and humanities, subjects that require strong academic interests and are less likely to be motivated by immediate economic rewards.²⁶

Table 6. Proportion of College Majors for College-Educated Men by Propensity Score Strata: WLS.

Propensity Score Strata
College Major	[0.0-0.05)	[0.05-0.1)	[0.1-0.15)	[0.15-0.2)	[0.2-0.4)	[0.4-0.6)	[0.6-0.7)	[0.7-0.8)	[0.8-1.0)
physical science	0.00	0.06	0.04	0.02	0.03	0.05	0.05	0.04	0.05
math	0.00	0.06	0.04	0.02	0.06	0.09	0.08	0.04	0.05
biological science	0.11	0.03	0.04	0.02	0.09	0.09	0.11	0.07	0.12
engineering	0.04	0.06	0.13	0.12	0.06	0.14	0.13	0.23	0.22
pre-professional	0.00	0.00	0.00	0.00	0.00	0.01	0.01	0.01	0.02
computer science	0.04	0.00	0.04	0.00	0.01	0.02	0.01	0.01	0.01
business	0.19	0.27	0.17	0.19	0.16	0.15	0.10	0.11	0.10
social science	0.15	0.15	0.25	0.17	0.18	0.19	0.10	0.22	0.21
humanities	0.04	0.03	0.00	0.10	0.13	0.08	0.13	0.11	0.10
art and music	0.11	0.09	0.04	0.07	0.04	0.05	0.05	0.01	0.05
education	0.22	0.18	0.21	0.14	0.15	0.08	0.07	0.06	0.05
communications	0.04	0.03	0.00	0.02	0.06	0.01	0.01	0.04	0.01
agriculture	0.04	0.00	0.00	0.02	0.01	0.01	0.02	0.04	0.01
other	0.04	0.03	0.04	0.10	0.02	0.03	0.03	0.04	0.02
Number	27	33	24	42	145	196	120	171	375

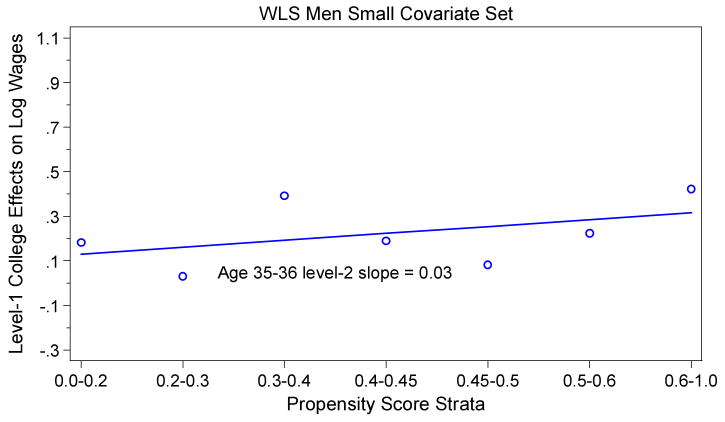
Our results suggesting negative selection raise a question: Why have some prior studies suggested empirical support for positive selection? We suspect that one reason lies in the choice, or availability, of covariates in the analyses. Empirical support for positive selection is at times based on models omitting key variables such as ability, high school academic performance, and/or parents' and teachers' encouragement. Omitting these important confounders may well introduce a distortion to the observed pattern of selection from negative to positive. To test this possibility, we now act as if we do not have access to the full set of covariates at our disposal and restrict covariates in the WLS to a set comparable to that used in Carneiro, Heckman, and Vytlacil (2001);²⁷, ²⁸ that is, we omit ability and academics, social-psychological variables, and religion from our models, highly significant factors in our expanded model reported in Appendix A. As expected, we find large mean differences in these covariates between college and non-college educated respondents within each propensity score stratum.

Figure 5 shows the revised results for WLS men at age 35 omitting the aforementioned variables. We observe that when we restrict models to a more limited set of covariates there is evidence for positive selection. Note that this figure should be compared to Figure 3, as the analysis is parallel for the same sample, the difference lying in the specification of covariates for the propensity model. Thus, the omission of these variables results not only in changing the overall size of the college effect (as in the case when effects are assumed to be homogeneous), but also in changing the direction of association between propensity of treatment and treatment effects. With the full set of covariates at our disposal, we observe a modest pattern of negative selection; when we trim covariates to a more limited set, we observe positive selection. We cannot attribute the change in direction to the omission of one single covariate; a detailed decomposition analysis modeled after Xie and Shauman (1998) shows that no single covariate can be held accountable.²⁹ Rather, the omission of the whole set of covariates (ability and academic achievement, aspirations, and encouragement) induces the observed change from a positive slope to a negative slope. This change comes out because these additional covariates exert greater power explaining college completion in a higher score propensity stratum than in a lower propensity stratum. This is consistent with our earlier discussion of equations (3) and (4), where we state that non-economic factors should play a greater role in predicting college education for persons who are likely to complete college based on observed attributes than their peers who are less likely to complete college.

Figure 5.

HLM of Economic Returns to College

Summary

Heterogeneity in response to a common treatment is a norm rather than an exception. Individuals differ not only in background attributes but also in how they respond to a particular treatment. An important task of sociological research is to summarize systematic patterns in population variability, a longstanding demographic tradition that Xie (2007) attributes to Otis Dudley Duncan. In this paper, we consider population heterogeneity in returns to schooling, examining the effects of completing college by propensity score strata in a hierarchical linear model. We first estimate effects of college for groups based upon the likelihood of a college education and then examine systematic heterogeneity in those group-specific effects. Our cross-group analysis provides a depiction of whether patterns of population heterogeneity reflect positive or negative selection, i.e., whether economic benefits of college are greater among persons most or least likely to complete college. We find evidence suggesting negative selection: Individuals who are most likely to benefit from a college education are the least likely to obtain one. This finding holds for both men and women, for every observed stage over the life course, and for two different cohorts.

Empirical patterns are generally consistent with our hypothesized interaction effect depicted in Diagram 1. While it is widely known that the increasing demand for educated workers alongside the decreasing demand for less-educated workers has resulted in an increase in the earnings differential between educated and less-educated workers (Farley 1996), we find that this differential is especially large among individuals with a low propensity of completing college. Therefore, a principal reason for a relatively large economic return experienced by low propensity college-educated workers is that their social position, coming from disadvantaged socioeconomic origins, is marked by substantial disadvantage. In the absence of a college degree, low propensity men and women have limited human, cultural, and social capital and hence particularly limited labor market prospects; in contrast, individuals of more advantaged social backgrounds, in the absence of a college degree, can still rely on their advantaged resources and abilities. Thus, the negative selection pattern emerges not because low propensity college goers earn more wages than high propensity college goers; they do not. Rather, the pattern emerges because low propensity non-college goers earn so little.

We have used the propensity score in identifying heterogeneous treatment effects. We realize this approach has serious limitations, as it relies on the ignorability assumption and overlooks heterogeneity due to unobserved variables. The plausibility of the ignorability assumption is specific to each research setting, depending on the richness of the observed covariates. We invoke the ignorability assumption because we wish to know what the observed data alone can reveal, knowing that we do have a set of rich covariates. However, we are keenly aware that there are always other unobservable causal factors or mechanisms. Nevertheless, we have shown several benefits in focusing on observable heterogeneity in treatment effects. Although treatment effect heterogeneity is potentially observable, as we have shown, it is seldom studied in empirical sociological research. With a focus on observable heterogeneity, we uncover an important finding indicating that the most disadvantaged individuals with respect to observed social background, achievement, and ability are the most likely to benefit from a college education. Auxiliary analyses lend further support to the negative selection hypothesis: individuals of disadvantaged social backgrounds who attend college may wittingly utilize the educational system as a means for economic mobility while those with advantaged social backgrounds, for whom college is a cultural norm, may be less purposively driven by economic rationale. Moreover, we present evidence suggesting that empirical support for positive selection in prior research may be a product of missing certain key variables.

We have several plans for future research. First, for simplicity, in this study we limited our focus to the earnings gap between individuals who complete college and those who complete only high school, which allowed us to easily borrow from the methodological literature on causal inference. While there is a well-documented difference between the two groups in the labor market (Grubb 1993; Kane and Rouse 1995; Mare 1981), it is clearly a simplification to treat education as a dichotomous treatment. In future studies, we will measure higher education more precisely by amount, quality, and major. Second, in this study, we noted some interesting differences between men and women patterned by propensity score strata across the life course, which we conjecture reflects differences across strata in women's labor market intermittency. Future research will analyze the heterogeneous effects of higher education on women's family formation patterns in greater depth.

Discussion and Conclusion

The widespread belief in the socioeconomic return to higher education has prompted policy efforts that expand educational opportunities for all Americans. While many if not most policy makers at least implicitly assume homogeneity in the return to schooling, potential heterogeneity in returns to schooling has been receiving more attention as many countries are experiencing rapid expansion in college enrollment, leading to a questioning of the relative costs and benefits of higher education for those who were not previously receiving it. Yet, in the presence of heterogeneous treatment effects, there is no simple summary statement that can be invoked as to the benefit of completing college, either for those already receiving higher education or for those who are likely to benefit from educational expansion. The average benefit depends on the composition at any given time of the group of students who complete college. One interpretation of our results is that a college education may be particularly beneficial among groups targeted by educational expansion efforts – those who are otherwise unlikely to attend college based on their observed characteristics.

Due to our simplifying methodological assumption, the above conclusion is only tentative. We cautioned earlier that no empirical researcher should accept the ignorability assumption without reservations. After all, the ignorability assumption is unverifiable and unlikely to be true in practice. The very pattern of heterogeneous treatment effects of college education on earnings by the propensity to complete college suggests an unobserved selection mechanism at work: among persons from disadvantaged social backgrounds, for whom college is not a culturally expected outcome, individuals overcome considerable odds to attend college and may be uniquely driven by the economic rationale. Thus, if educational expansion results in a larger number of college goers who are otherwise unlikely to attend college, unobserved selectivity due to economic motivation among them may go down. This would equalize the unobserved selectivity across the spectrum of the propensity to complete college and thus change the overall negative pattern we observed in this study to a flat one. Hence, an alternative interpretation of our results is that the observed pattern of negative selection is due to differential selectivity, with persons of low propensity to complete college more selective than persons of high propensity. While we cannot adjudicate between the two alternative interpretations in this study, we have produced an important empirical finding that individuals who are less likely to obtain a college education are observed to benefit more from college.

Biographies

Jennie E. Brand is Assistant Professor of Sociology at the University of California – Los Angeles. She is also a faculty affiliate at the California Center for Population Research. Her research focuses on the relationship between socioeconomic background, educational attainment, job conditions, and socioeconomic attainment and well-being over the life course. This substantive focus accompanies a methodological focus on causal inference and the application and innovation of statistical models for panel data. Current research projects include evaluation of heterogeneous effects of programs to assist disadvantaged students and higher education on socioeconomic outcomes, and the social consequences of job displacement.

Yu Xie is Otis Dudley Duncan Distinguished University Professor of Sociology and Statistics at the University of Michigan. He is also a Research Professor at the Population Studies Center and Survey Research Center of the Institute for Social Research, and a Faculty Associate at the Center for Chinese Studies. His main areas of interest are social stratification, demography, statistical methods, Chinese studies, and sociology of science. His recently published works include Women in Science: Career Processes and Outcomes (Harvard University Press 2003) with Kimberlee Shauman and Marriage and Cohabitation (University of Chicago Press 2007) with Arland Thornton and William Axinn.