Coherent reflection without traveling waves: On the origin of long-latency otoacoustic emissions in lizards

Abstract

Lizard ears produce otoacoustic emissions with characteristics often strikingly reminiscent of those measured in mammals. The similarity of their emissions is surprising, given that lizards and mammals manifest major differences in aspects of inner ear morphology and function believed to be relevant to emission generation. For example, lizards such as the gecko evidently lack traveling waves along their basilar membrane. Despite the absence of traveling waves, the phase-gradient delays of gecko stimulus-frequency otoacoustic emissions (SFOAEs) are comparable to those measured in many mammals. This paper describes a model of emission generation inspired by the gecko inner ear. The model consists of an array of coupled harmonic oscillators whose effective damping manifests a small degree of irregularity. Model delays increase with the assumed sharpness of tuning, reflecting the build-up time associated with mechanical resonance. When tuning bandwidths are chosen to match those of gecko auditory-nerve fibers, the model reproduces the major features of gecko SFOAEs, including their spectral structure and the magnitude and frequency dependence of their phase-gradient delays. The same model with appropriately modified parameters reproduces the features of SFOAEs in alligator lizards. Analysis of the model demonstrates that the basic mechanisms operating in the model are similar to those of the coherent-reflection model developed to describe mammalian emissions. These results support the notion that SFOAE delays provide a noninvasive measure of the sharpness of cochlear tuning.

INTRODUCTION

Sounds evoked from the ear, known as otoacoustic emissions (OAEs), provide a noninvasive window on the mechanics of hearing. In mammalian ears, two broad classes of OAE generation mechanisms—so-called “wave-fixed” and “place-fixed”—have been identified on the basis of emission phase-versus-frequency functions (Kemp and Brown, 1983; Shera and Guinan, 1999). The characteristics of place-fixed emissions—those with rapidly rotating phases or, equivalently, long phase-gradient delays—appear well described by the coherent-reflection model (Zweig and Shera, 1995; Talmadge et al., 2000; Shera et al., 2005). In this model, the emissions arise when pressure-difference waves traveling within the cochlear duct encounter intrinsic micromechanical irregularities in the organ of Corti. According to the cochlear model equations, mechanical irregularities give rise to a reverse energy flow through a process analogous to the scattering of waves by perturbations in the impedance of the medium (e.g., the scattering of light within a medium of variable refractive index). Place-fixed OAEs are therefore also known as “reflection-source” otoacoustic emissions.

Although the coherent-reflection model was developed to account for mammalian place-fixed OAEs, recent work shows that a similar place- versus wave-fixed distinction among OAE mechanisms also pertains in certain non-mammalian vertebrates such as the chicken and the gecko (Bergevin et al., 2008). The existence in lizards of OAEs with steep phase gradients and other characteristics of mammalian reflection-source OAEs presents a serious challenge. Although lizard ears evidently produce OAEs with spectral levels and phase gradients comparable to those found in many mammals (Bergevin et al., 2008), important aspects of their inner ear morphology and physiology are rather different. Most significantly for models of emission generation, lizards evidently lack a clear analog of the mammalian traveling wave (e.g., Peake and Ling, 1980; Manley, 1990), and their tonotopy is thought to arise micromechanically at the level of the hair-cell bundle (Manley et al., 1999; Aranyosi and Freeman, 2004). Despite these major functional differences between the inner ears of mammals and lizards, the striking similarities in their emission characteristics suggest that the underlying mechanisms of OAE generation are somehow equivalent (e.g., Köppl, 1995).

The following conundrum thus arises: If the coherent-reflection model applies in mammals, how can similar mechanisms be operating in the lizard, where there are no waves to be reflected? Alternatively, might some other as yet unidentified generation mechanism be operating in both cases? At a minimum, any candidate model must account for the long phase-gradient delays found in both mammalian and non-mammalian ears (typically 1–10 ms or longer, depending on stimulus frequency and intensity). These substantial delays are not due to middle-ear transmission, whose contribution amounts to only several tens of microseconds (e.g., Guinan and Peake, 1967; Rosowski et al., 1985; Manley et al., 1988). Inner-ear dimensions may play a role but can hardly be invoked to explain why geckos (whose basilar papilla measures 1.5–2 mm in length) have phase-gradient delays similar to those of cats (whose basilar membrane is some 15 times longer). Thus, although delays associated with wave propagation presumably contribute in mammals, the origin of the long delays in non-mammals, especially those lacking basilar-membrane (BM) traveling waves (or, as in amphibians, a flexible BM altogether), remains unclear.

In this paper, we address questions raised by the existence of long-latency reflection-source OAEs in lizard. In particular, we develop a simplified model inspired by the lizard inner ear to determine whether the basic principles and predictions of coherent-reflection theory might somehow apply even in the absence of traveling waves. In the process, we test the conjecture (Shera, 2003; Shera and Guinan, 2008) that the generation of realistic reflection-source OAEs requires nothing more than a slightly irregular array of tuned mechanical resonators.

A MODEL INSPIRED BY THE GECKO INNER EAR

To explore possible mechanisms of OAE generation, we adopt a highly simplified model inspired by the functional anatomy of the gecko inner ear (see Fig. 1). Detailed descriptions of the anatomy and physiology of the gecko ear are available elsewhere (e.g., Wever, 1978; Köppl and Authier, 1995; Manley et al., 1999; Bergevin et al., 2008). Briefly, the gecko inner ear consists of 1000–2000 hair cells sitting atop the relatively rigid basilar papilla. Although gecko hair cells lack the somatic motility characteristic of mammalian outer hair cells (Köppl et al., 2004), they presumably manifest mechanisms of active amplification within their bundles. Whereas the low-frequency portion of the papilla is covered by a continuous tectorial membrane, the hair cells sensitive to frequencies above ∼1 kHz are covered by discrete sections of tectorium (sallets), which couple small groups of hair cells together into a single radial row (Wever, 1978). Although gecko ears apparently lack analogs of BM traveling waves (Manley et al., 1999), they produce robust otoacoustic emissions (Manley et al., 1996; Bergevin et al., 2008) and have auditory-nerve fiber (ANF) responses with thresholds and frequency tuning comparable to many mammals (Eatock et al., 1981; Sams-Dodd and Capranica, 1994; Manley et al., 1999).

Figure 1.

Schematic cross-section of the model showing two chambers filled with incompressible fluid and separated by a rigid partition (papilla) attached to the left-hand wall by a stiff, lossy hinge (☉). An array of masses (bundles, n=1,…,N) sits atop the papilla, each coupled to the papilla through an elastic element. The bundles are arranged longitudinally, parallel to the x-axis. Vibration of the stapes induces a papilla rotation through the angle θ with the horizontal, which is taken parallel to the y-axis. In the small-angle limit, rotation of the papilla has two important effects: It moves the center of the basilar membrane (⊗) vertically (i.e., parallel to the z-axis) by an amount ξ_z≅rθ, where 2r is the papilla width, and it drags the bundles horizontally through the fluid. The total horizontal displacement of bundle n is denoted ξ_n. The elastic force on each bundle is taken proportional to its displacement relative to the top surface of the papilla (i.e., to ξ_n−ξ_y, where ξ_y≅hθ is the papilla displacement just below the bundle and h is the papilla height). Bundle motion is damped by viscous losses in the fluid. The resonant frequencies and quality factors of the bundle oscillators are taken to vary systematically along the papilla.

Since our purpose here is to explore the origin of long-latency OAEs in a mechanical system without basilar-membrane traveling waves, we simplify the analysis by boiling the many exquisite details of gecko functional anatomy down to a few idealized mechanical elements. Taken together, these elements provide perhaps the simplest realization of a mechanically tuned inner ear. Although the physical framework we adopt was inspired by the gecko—and appears isomorphic to other, more physically and biologically realistic models of the lizard inner ear (e.g., Weiss et al., 1985; Authier and Manley, 1995)—we make no attempt to faithfully represent the complex inner ear morphology or mechanics of any particular species. Although our model is therefore an abstract representation of lizard functional anatomy, it is not unphysical. The hydromechanical system we describe could, in principle, be built and experimented upon in the laboratory.

Figure 1 shows a schematic of the model, which consists of two rigid-walled cavities (the scala vestibuli and tympani) filled with incompressible fluid and separated by a rigid partition (papilla). Tuned mechanical elements representing hair bundles (or groups of hair bundles coupled by sallets) sit atop the papilla. The pressures in the two scalae (p_v and p_t) are driven by the motions of the stapes and round window, and are presumed uniform throughout their respective cavities. The papilla and the hair cells on its surface are represented as linear, passive resonators (e.g., Authier and Manley, 1995; Aranyosi and Freeman, 2004). The hair-cell resonators (hereafter referred to as “bundles”) are elastically coupled to the movement of the papilla. Much like the papilla in the alligator lizard (Frishkopf and DeRosier, 1983; Holton and Hudspeth, 1983), the model papilla rotates about a longitudinal axis. For simplicity, we locate the axis of rotation along one edge of the papilla, parallel to the x-axis. For small-angle motions,1 rotation about this axis can be regarded as the superposition of a bulk translational motion and a pure rotation about the center of the basilar membrane (⊗ in Fig. 1). The translational motion of the papilla produces a net vertical fluid displacement that couples to the motion of the stapes, and the rotational motion stimulates the bundles by dragging them horizontally through the fluid. Analogues of these two coupled modes of motion have been observed in the alligator lizard (Aranyosi and Freeman, 2005).

Motion of the papilla and the bundles

The model papilla rotates as a rigid body driven both by the pressure difference across its surface and by forces from the bundles. Although the spatial arrangement of the bundles is not important in the model (due to the rigidity of the papilla), we facilitate bookkeeping by assuming that the bundles are uniformly distributed along the papilla and are numbered in order of increasing distance from the apical end. Summing the forces on the papilla, including those from each of the N bundles, and applying Newton’s second law yields

$$I\ddot{\theta }+R\dot{\theta }+K\theta +h\sum _{n=1}^N{k}_n\left({\xi }_y-{\xi }_n\right)\cong rA\left(p_{\mathrm{v}}-p_{\mathrm{t}}\right),$$ (1)

where diacritical dots represent time derivatives. In this equation, the clockwise angular displacement of the papilla about its “hinge” at the left edge is denoted θ; the symbols I, R, and K represent the corresponding rotational mass (moment of inertia), damping, and stiffness of the papilla. The papilla has length L in the x direction, width 2r in the y direction, and height h in the z direction. Each of the N bundles acts through an elastic element (stiffness k_n) to produce a torque proportional to its horizontal displacement (ξ_n) relative to that of the top of the papilla (ξ_y). The effective moment arm is the papilla height h; in the small-angle limit, ξ_y≅hθ. The quantity rA(p_v−p_t) on the right represents the torque arising from the trans-papilla pressure. The moment arm r is the papilla half-width, and A is the effective area of the papilla in the xy-plane (A≅2rL). Note that vertical (or transverse) displacements of the papilla are defined as positive toward scala tympani (i.e., in the direction produced by stapes displacements into the inner ear).

Each bundle is a miniature harmonic oscillator driven by the elastic element that couples it to the horizontal motion (ξ_y) of the top of the papilla:

$$m_n{\ddot{\xi }}_n+r_n{\dot{\xi }}_n+k_n\left({\xi }_n-{\xi }_y\right)=0.$$ (2)

The effective mass of each bundle is denoted m_n. The damping force (proportional to r_n) is taken to be dominated by the viscous drag of the bundle as it moves back and forth through the fluid (assumed stationary in the horizontal direction). Exploiting the assumed linearity, we adopt harmonic time dependence and represent dynamical variables by Fourier coefficients (uppercase) at angular frequency ω=2πf [i.e., ξ_y(t)=Ξ_y(ω)e^iωt]. Equation 2 then simplifies to

$${\Xi }_n=\frac{{\Xi }_y}{1-{\beta }_n^2+i{\beta }_n∕Q_n},$$ (3)

where β_n is normalized frequency (i.e., β_n≡f∕CF_n, with ${\text{CF}}_n\equiv \sqrt{k_n∕m_n}∕2\pi$ representing the resonant frequency of bundle n) and Q_n is the quality factor of the resonance $\left(Q_n\equiv \sqrt{m_n{k}_n}∕r_n\right)$.

Equation 3 for the bundle response is consistent with previous studies in lizards (e.g., Weiss and Leong, 1985; Authier and Manley, 1995), which have found that the “micromechanical transfer function” (Ξ_n∕Ξ_y) is well approximated by a second-order system. Combining Eqs. 1, 3 and using the small-angle approximation (Θ≅Ξ_y∕h) yields

$${\Xi }_y\left[{\left(i\omega \right)}^{2}I+i\omega R+K+h^2\sum _{n=1}^N{k}_n\frac{-{\beta }_n^2+i{\beta }_n∕Q_n}{1-{\beta }_n^2+i{\beta }_n∕Q_n}\right]=rhA\left(P_{\mathrm{v}}-P_{\mathrm{t}}\right),$$ (4)

an equation that relates the horizontal displacement of the papilla beneath the bundle to the driving pressure force.

Coupling to the middle ear

The inner ear couples to the middle ear, and thereby to the external acoustic environment, through the motions of the oval and round windows. Conservation of mass requires that the volume velocity of the papilla equal that of the oval window,

$$i\omega A{\Xi }_z=U_{\text{ow}},$$ (5)

where U_ow is the volume velocity of the oval window (stapes) and Ξ_z≅rΘ is the mean vertical displacement of the papilla. Because of fluid incompressibility, the volume velocities of the oval and round windows are equal in magnitude but opposite in phase.

The mechanics of the papilla and its bundles can be represented by an acoustic impedance, defined as Z_ie=(P_v−P_t)∕U_ow, where the subscript stands for “inner ear.”2 Solving for Z_ie using Eqs. 4, 5 yields

$$Z_{\text{ie}}\cong Z_{\mathrm{p}}+\frac{1}{i\omega }{\left(\frac{h}{rA}\right)}^2\sum _{n=1}^N{k}_n\frac{-{\beta }_n^2+i{\beta }_n∕Q_n}{1-{\beta }_n^2+i{\beta }_n∕Q_n},$$ (6)

where Z_p=(K_p∕iω) $\left(1-{\beta }_{\mathrm{p}}^2+i{\beta }_{\mathrm{p}}∕Q_{\mathrm{p}}\right)∕A^2$ is the acoustic impedance of the papilla expressed in terms of its effective stiffness (K_p=K∕r²), normalized resonant frequency (β_p), and quality factor (Q_p). The summation over n implies that every bundle affects the impedance of the inner ear, and is thereby coupled to the middle and external ears. Equation 6 indicates that when tuning is sufficiently sharp any given bundle contributes maximally to the impedance Z_ie near the bundle’s resonant frequency (β_n≅1).

Bundle irregularity

Anatomical studies in tokay geckos and other lizards find spatial irregularities throughout the inner ear, including the width and thickness of the papilla, the number of hair cells in a given radial cross-section, and the heights of the hair bundles (e.g., Miller, 1973; Wever, 1978; Köppl and Authier, 1995). We parametrize these and other variations not so apparent in the anatomy by assuming that the mechanical properties of the bundles vary somewhat irregularly from row to row. A similar approach has been used to model the generation of reflection-source OAEs in the mammalian cochlea (Shera and Zweig, 1993; Zweig and Shera, 1995) and the production of spontaneous OAEs in the bobtail lizard (Vilfan and Duke, 2008). Specifically, we take the quality factors Q_n that characterize the tuning of the bundles to manifest small fractional deviations ϵ_n about some mean value that varies with location along the papilla. Thus, ${\tilde{Q}}_n=Q_n\left(1-{ϵ}_n\right)$, where Q_n varies smoothly with n and we have used the diacritical tilde to indicate the presence of mechanical irregularity. Although we have placed the effective mechanical irregularity in the bundle damping, based on the physical expectation that irregularities in this parameter will dominate near resonance, locating the irregularity in other mechanical properties of the bundle gives similar results.

Impedance and pressure changes

The effects of bundle irregularity on the impedance of the inner ear (now denoted ${\tilde{Z}}_{\text{ie}}$) can be quantified by computing the difference $\Delta Z={\tilde{Z}}_{\text{ie}}-Z_{\text{ie}}$, where Z_ie is the impedance of the corresponding “smooth” model (ϵ_n=0). Equation 6 implies that to first order in the irregularity ϵ_n,

$$\Delta Z\cong \frac{1}{\omega A^2}\sum _{n=1}^N\frac{{ϵ}_n{k}_n{\beta }_n∕Q_n}{{\left(1-{\beta }_n^2+i{\beta }_n∕Q_n\right)}^2}.$$ (7)

When transmitted through the middle ear, the impedance change ΔZ produces a change ΔP in the calibrated ear-canal pressure P. When the fractional changes ΔZ∕Z_ie and ΔP∕P are both small (as they are here), the two are proportional. To first order, the pressure change therefore has the form

$$\Delta P\cong G_{\text{me}}\left(\Delta Z∕Z_{\text{ie}}\right)P,$$ (8)

where G_me is the “proportionality constant.” Physically, G_me depends on both the acoustics of the stimulus source and the combined effects of forward and reverse middle-ear transmission. At any given frequency, the value of G_me can be found from explicit models of the transducer and middle ear (e.g., Rosowski et al., 1985) or, more generally, by representing the transducer by its Thevenin equivalent, and the middle ear as an acousto-mechanical two-port network characterized by a transfer matrix (e.g., Shera and Zweig, 1992; Puria, 2003; Songer and Rosowski, 2007).3

The pressure change ΔP given by Eq. 8 is the stimulus-frequency otoacoustic emission (SFOAE) produced by the model. As we demonstrate below, this computational definition of the SFOAE extracts what amounts to a delayed component from the total ear-canal pressure. In actual SFOAE measurements, the delayed component can be obtained using a variety of methods (e.g., by exploiting mechanical nonlinearity or by using signal-processing techniques to smooth the measured frequency response), all of which yield equivalent results, at least in humans (Kalluri and Shera, 2007).

Parameter values

Although the model simplifies the morphology of the gecko inner ear, we have chosen parameter values with an eye toward capturing some of the relevant physiology. Most important to the questions explored here are the parameters that characterize the frequency tuning of the bundles. On the supposition that peripheral tuning is predominantly mechanical in origin, we have selected the parameters of bundle tuning to match neurophysiological estimates of ANF tuning in the tokay gecko (Gekko gecko). Table 1 summarizes all parameters.

Table 1.

Parameter values used to compute model SFOAEs in gecko and alligator lizard. Values for alligator lizard (see Sec. 5B) are listed only when they differ from gecko.

		Gecko	Alligator lizard
Papilla length	L	1.7 mma	0.3 mmb c d, 1n3, d
Papilla area	A	0.15 mm2c	0.04 mm2c
Papilla resonant frequency	fp	1.5 kHze	2 kHzf
Papilla quality factor	Qp	2e	0.5f
Papilla volume compliance	Cp	0.57×10−6 mm3∕Pa g
Papilla stiffness	Kp	A2∕Cp
Papilla aspect ratio	h∕r	1.0c h, h	1.0j
No. of bundles (rows)	N	250h	130b c d, 1n3, d
Maximum bundle CF	CFmax	5 kHza	6 kHzb j, j
Tonotopic map space constant	ℓ	0.5 mma	0.16 mmb c d, 1n3, d
Bundle Q10 dB (at 1 kHz)	Q10 dB	2.3a	1.1b
Q10 dB power-law exponent		0.35a	0.55b
Bundle stiffness	kn	Kp∕N
Irregularity size	rms(ϵn)	0.03 (or 3%)
Round-trip middle-ear gain	Gme	0.25g
Stimulus pressure	P	20 dB SPLk

^aManley et al. (1999).

^bWeiss et al. (1976).

^cWever (1978).

^dManley (1990).

^eChiappe (2006).

^fPeake and Ling (1980).

^gRosowski et al. (1985).

^hKöppl and Authier (1995).

ⁱMulroy(1974).

^jInferred from SFOAE magnitudes, which fall off above about 6 kHz in alligator lizard.

^kBergevin et al. (2008).

We assume that the N∼250 bundles are spaced uniformly along the papilla, with spacing Δx=L∕N, where L is the length of the papilla (L≅1.7 mm giving Δx≅7 μm). In accord with ANF tracing experiments (Manley et al., 1999), which determine the characteristics of ANF tuning as a function of location along the papilla, we take the bundle resonant frequencies to vary exponentially with position. More precisely, CF_n=CF_maxe^−x_n∕ℓ, where CF_max=5 kHz, x_n=(n−1)Δx, and the distance ℓ≅0.5 mm is the space constant of the tonotopic map (Manley et al., 1999).4 Note that x is the distance from the apical end of the papilla; the gecko’s tonotopic map is reversed and fibers tuned to low frequencies innervate the basal end (Manley et al., 1999). The quality factors Q_n of the bundle resonators are assumed to vary with CF as Q_n=3Q_{10 dB}(CF_n), where Q_{10 dB}(CF)=2.3(CF∕kHz)^0.35 is a power-law fit to tokay gecko ANF tuning data (Manley et al., 1999). For internal consistency, we use tuning data from the same study that determined the tonotopic map (Manley et al., 1999). The factor of 3 that converts physiological Q_{10 dB} values to equivalent Q_n values is an approximation valid for second-order filters (e.g., Hartmann, 1998).

Although most of the other model parameters have little impact on our basic results—they primarily affect overall OAE amplitude, which we make no attempt to match due to the absence of active bundle amplification in the model—several do warrant mention. We used the papilla volume compliance reported in alligator lizard (Rosowski et al., 1985) to determine the stiffness K_p. We then arbitrarily set the stiffness of the individual bundles to the value k_n=K_p∕N, independent of n.5 Taking the bundle stiffness proportional to that of the papilla, but scaled down by a factor of N, compensates for the summation over bundles and guarantees that the papilla and the bundles make similar order-of-magnitude contributions to the inner ear impedance Z_ie. If this rough equality of impedances were grossly violated, specifically if the net bundle impedance were much smaller than that of the papilla, then the bundles would have negligible effect on ear-canal pressure and could not generate appreciable OAEs. For simplicity, and because delays introduced by middle-ear transmission are small compared to OAE delays, we assumed a constant value of round-trip middle-ear pressure gain G_me. Our value of G_me is roughly consistent with that predicted by the model of Rosowski et al. (1985) in alligator lizard. Finally, the irregularities ϵ_n were assumed to vary randomly from bundle to bundle. In the numerical simulations, values of ϵ_n were obtained by sampling from a Gaussian distribution with zero-mean and standard deviation 0.03; thus, the rms fractional irregularity was 3%. This value was chosen for consistency with that used in models of mammalian SFOAEs (e.g., Talmadge et al., 2000; Shera et al., 2005); the amount of irregularity may well be substantially larger in lizards. Because mean emission amplitudes vary in direct proportion to the size of the irregularities, the value of ϵ_n makes a significant contribution to overall OAE levels.

COMPARISON WITH GECKO EMISSIONS

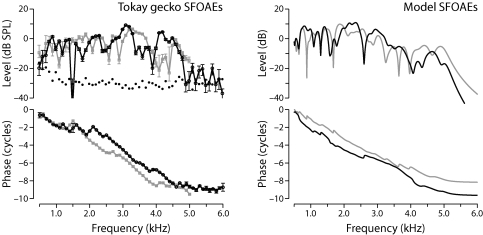
Figure 2 compares model simulations with representative SFOAEs measured in the tokay gecko (Bergevin et al., 2008). Model results for two different “ears” were obtained by using different patterns of irregularities. Despite the simplicity of the model, the simulated SFOAEs are in strong qualitative agreement with the data. An exception, of course, is the overall emission magnitude. With our choice of parameters, OAE levels are some 45 dB smaller than the measurements; including active mechanisms and∕or larger irregularities would presumably narrow that gap substantially. Both the measurements and the model manifest relatively broad spectral maxima, punctuated at irregular intervals by sharp notches. The model predicts that the spectral structure characteristic of a given measurement reflects the distinctive pattern of mechanical irregularity in that ear. At stimulus frequencies above the maximum CF represented along the papilla (∼5 kHz), both measured and model SFOAE magnitudes fall off sharply. The patterns of phase variation across frequency are also strikingly similar. In both cases, SFOAE phase rotates rapidly, accumulating a phase lag of 8–10 cycles over the operative 4.5 kHz span of the figure. Phase gradients vary with frequency but correspond, on average, to a delay of about 2 ms.

Figure 2.

Measured and model stimulus-frequency OAEs. Panel A: Representative SFOAEs at probe levels of 20 dB SPL in the tokay gecko (G. gecko) from the study of Bergevin et al. (2008). Black and gray lines show data from two different geckos. Error bars on the data points give the standard error of the mean (35 measurements at each frequency in each gecko). The dotted line shows the acoustic noise floor. Panel B: Simulated SFOAEs ΔP computed from Eq. 8 using random micromechanical irregularities and the parameter values given in Table 1. The emission magnitudes have been scaled up by 45 dB to approximate those of the measurements (see text). Black and gray lines show model results for two different “ears” (i.e., different irregularity patterns).

THE ORIGIN OF THE EMISSION PHASE GRADIENT

To explore the origin of the rapidly rotating OAE phase predicted by the model, we derive an approximate analytic expression for the emission phase-gradient delay. In a nutshell, the derivation indicates that the rapid rotation of OAE phase originates in mechanical phase shifts (delays) associated with the frequency tuning of the bundles. Because of their frequency selectivity, the bundles take time to respond, and the resulting delays are reflected in SFOAE phase gradients. At any given frequency, the delay associated with mechanical filtering by the bundle increases with the sharpness of tuning. As a result, we find that the predicted emission delay (expressed in periods of the stimulus frequency) is proportional to the quality factor of the resonance [Eq. 14 below]. The derivation sketched below generally parallels analysis of the coherent-reflection model; further discussion and technical details can be found in previous publications (e.g., Zweig and Shera, 1995; Talmadge et al., 2000; Shera and Guinan, 2008).

Analytic approximation for the delay

We begin the derivation by noting that the delay in the model arises predominantly from the factor ΔZ in Eq. 8; delays associated with the factors G_me and Z_ie are negligible. Approximating the finite array of resonators [Eq. 7 for ΔZ] by a continuum and converting the sum over bundles into an integral over position yields

$$\omega A^2\Delta Z\left(\omega \right)\cong {\int }_0^L\frac{ϵk\beta ∕Q}{{\left(1-{\beta }^2+i\beta ∕Q\right)}^2}dx,$$ (9)

where k is the bundle stiffness per unit length and all quantities in the integrand are regarded as functions of position. To simplify the derivation without any significant effect on the outcome, we henceforth assume that k and Q are constant. Using the exponential tonotopic map to rewrite the spatial integral in terms of β(x,f)=f∕CF(x) yields

$$\omega A^2\Delta Z\left(\omega \right)\cong \left(\ell k∕Q\right){\int }_{{\beta }_0}^{{\beta }_L}ϵ{\left[T{e}^{i\varphi }\right]}^{2}d\beta ,$$ (10)

where dx=ℓ(dβ∕β), ℓ is the space constant of the map, β_{0,L}≡f∕CF({0,L}), and Te^iϕ≡1∕(1−β²+iβ∕Q) is the transfer function of the harmonic oscillator [with magnitude T(β) and phase ϕ(β)].

Decomposing the irregularity function ϵ(x) into spatial-frequency components κ facilitates description of phase-cancellation effects between contributions to the emission arising from different spatial locations (Shera and Zweig, 1993; Zweig and Shera, 1995). Just as in the coherent-reflection model, not all spatial frequencies κ contribute equally to the emission. In particular, the integral in Eq. 10 is dominated by spatial frequencies in a relatively narrow range about an “optimal” value, denoted $\widehat{\kappa }$. For irregularities arrayed at this special spatial frequency, contributions from adjacent bundles tend to combine coherently rather than cancel one another. To see this, and find the value of $\widehat{\kappa }$, we consider the case of a single (unspecified) spatial frequency and take ϵ(x)→2 cos(κx)=e^iκx+e^−iκx. For κ>0, it suffices to consider only the term e^iκx,6 which can be written in the form e^{iκℓln(β∕β₀)}. The integral in Eq. 10 then becomes

$$e^{-i\kappa \ell \text{ln}{\beta }_0}{\int }_{{\beta }_0}^{{\beta }_L}{T}^2\left(\beta \right)e^{i\left[\kappa \ell \text{ln}\beta +2\varphi \left(\beta \right)\right]}d\beta .$$ (11)

When the oscillators are sharply tuned, the factor T²(β) is strongly peaked at some value $\widehat{\beta }$ near β≅1. The spatial frequency that yields the dominant contribution to the emission can be found by applying the principle of stationary phase and requiring that the phase of the integrand be constant near its magnitude peak at $\widehat{\beta }$. This yields

$$\frac{\partial }{\partial \beta }\left[\kappa \ell \text{ln}\beta +2\varphi \left(\beta \right)\right]{|}_{\widehat{\beta }}=0\Rightarrow \widehat{\kappa }=-2\widehat{\beta }{\widehat{\varphi }}^{\prime }∕\ell ,$$ (12)

where ${\widehat{\varphi }}^{\prime }={\phantom{|}\partial \varphi ∕\partial \beta |}_{\widehat{\beta }}$ is the slope of the transfer function phase at the magnitude peak.

To determine how the predicted emission phase varies with frequency, we exploit the “local scaling” manifest by the bundle responses in the model. Local scaling means that, at least near their magnitude peaks, the frequency responses depend on normalized frequency β=f∕CF, rather than on frequency and CF independently (Zweig, 1976). Local scaling applies in the model and also approximates the tip region of gecko ANF tuning curves (Manley et al., 1999). As a consequence of local scaling, the value of the integral in Eq. 11 does not depend strongly on frequency except at frequencies close to the ends of the tonotopic map (indeed, if the papilla were infinite, the integral over β would evaluate to a constant, independent of frequency). Consequently, the frequency dependence of the phase is determined principally by the argument of the phasor $e^{-i\widehat{\kappa }\ell \ln {\beta }_0}$ that multiplies the integral. The phase-gradient delay of ΔZ expressed in stimulus periods [succinctly expressed as −d(∠ΔZ∕2π)∕d ln f] is therefore well approximated by the value $\widehat{\kappa }\ell ∕2\pi$. Substituting the value of $\widehat{\kappa }$ from Eq. 12 and using $\widehat{\beta }\cong 1$ gives

$$N_{\text{SFOAE}}\cong -2\left({\widehat{\varphi }}^{\prime }∕2\pi \right),$$ (13)

where N_SFOAE is the emission delay in periods (the symbol N was chosen to denote the number of stimulus periods). Note that $-{\widehat{\varphi }}^{\prime }∕2\pi$ is just the peak phase-gradient delay of the harmonic oscillator transfer function expressed in periods of the characteristic frequency; N_SFOAE is twice this value.7

Computing N_SFOAE using the explicit form for Te^iϕ employed in the model gives

$$N_{\text{SFOAE}}\cong 2Q∕\pi =6Q_{10\text{dB}}∕\pi ,$$ (14)

where we have evaluated ϕ^′ for the harmonic oscillator at resonance $\left(\widehat{\beta }\cong 1\right)$ using the excellent approximation ϕ^′(β=1)≅−2Q. As discussed in Sec. 2E, the factor of 3 relating Q and Q_{10 dB} is valid for second-order filters. Although our derivation of Eq. 14 assumes, for simplicity, that Q is constant along the papilla, the result can be expected to hold so long as the change in Q over a distance corresponding to the bandwidth of the resonator remains small (i.e., so long as |d ln Q∕d ln CF|⪡1). According to this analysis, the mean value of N_SFOAE at any given frequency is directly proportional to the quality factor of the bundle tuning at that frequency: the sharper the tuning (higher the Q_{10 dB}), the longer the delay in periods (larger the value of N_SFOAE).

Computational validation

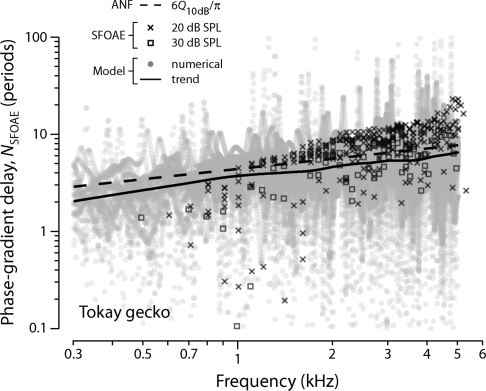
Figure 3 shows model simulations that verify the approximate proportionality between N_SFOAE and Q_{10 dB} predicted by Eq. 14. The dashed line in the figure is proportional to the empirical function Q_{10 dB}(CF) used to determine the model value of Q_n at each CF [Q_n=3Q_{10 dB}(CF_n)]. Recall that Q_{10 dB}(CF)=2.3(CF∕kHz)^0.35 is a power-law fit to ANF measurements of the sharpness of tuning in the tokay gecko (Manley et al., 1999). The gray dots and their trend (solid line) give the resulting model values of N_SFOAE versus frequency obtained from the phase-versus-frequency functions of simulated SFOAEs similar to those shown in Fig. 2. To improve the statistics, we computed and pooled the results for 25 different irregularity patterns (ears). Comparing the simulated SFOAE delays with the mean N_SFOAE values predicted by Eq. 14 shows that the analytic approximation 6Q_{10 dB}∕π correctly predicts the trend of the model results. Although at any given frequency, the approximate formula 6Q_{10 dB}∕π slightly overestimates the mean N_SFOAE value obtained from the model, it captures the slope of the variation across frequency almost exactly. A least-squares fit to the numerical values of N_SFOAE (gray dots) gives a power-law exponent of 0.355±0.01, where the uncertainty represents the 95% confidence interval computed using bootstrap resampling.8 The power-law exponent characterizing the relationship between SFOAE delay and frequency in the model is thus statistically indistinguishable from the value 0.35 used to set the quality factors of the bundle resonators (see Table 1). Evidently, model variations in the value of Q_{10 dB} along the length of the papilla produce corresponding changes in SFOAE delay, N_SFOAE.

Figure 3.

Measured and model SFOAE phase-gradient delays N_SFOAE versus frequency. Delays are expressed in periods of the stimulus frequency. The symbols × and ◻ show delays measured in the tokay gecko at probe levels of 20 dB SPL (ten ears) and 30 dB SPL (three ears), respectively (Bergevin et al., 2008). Data points whose corresponding SFOAE magnitudes fell within 10 dB of the noise floor are not shown. The gray dots show model N_SFOAE values obtained from numerical simulations of 25 different ears (i.e., irregularity patterns). The solid curve is a loess trend line (Cleveland, 1993) fit to the pooled model results. The dashed line gives the analytic approximation 6Q_{10 dB}∕π [Eq. 14], where Q_{10 dB}(CF) is a power-law fit to ANF data (Manley et al., 1999).

Why does the analytic approximation [Eq. 14] systematically overestimate the mean phase-gradient delay actually predicted by the model (compare the dashed and solid lines in Fig. 3)? By evaluating the phase-gradient delay −ϕ^′∕2π at the response peak $\left(\widehat{\beta }\right)$, the analytic formula assumes, in effect, that the entire emission originates at this point. In fact, however, the emission arises from a region about $\widehat{\beta }$, whose effective spatial extent depends on such things as the sharpness of tuning. Because the value of ϕ^′ varies somewhat over the peak region [with $\left|{\varphi }^{\prime }\left(\beta \right)\right|\le \left|{\widehat{\varphi }}^{\prime }\right|$ for the harmonic oscillator], the phase-gradient delay of the actual emission is smaller than that estimated from the analytic approximation. Numerical simulations verify that the accuracy of the analytic approximation improves when the spatial region about $\widehat{\beta }$ that contributes to the emission is artificially reduced by restricting the summation in Eq. 7 to bundles in the immediate vicinity of the peak.

Correlations between tuning and delay in the gecko

For comparison with the delays predicted by the model, Fig. 3 also plots values of N_SFOAE obtained from SFOAE measurements in the tokay gecko (Bergevin et al., 2008). Measured values of N_SFOAE are shown at probe levels of 20 and 30 dB sound pressure level (SPL), roughly corresponding to the typical thresholds for the auditory-nerve fibers used to determine the dependence of Q_{10 dB} on CF (Manley et al., 1999). The delays are slightly shorter at the higher stimulus level, consistent with the trend observed in humans (e.g., Schairer et al., 2006). Although our linear model does not explicitly capture this nonlinear effect, Eq. 14 reproduces the empirical trend when supplemented with the near ubiquitous observation that peripheral tuning broadens with increasing intensity.

The tokay SFOAE delays generally appear somewhat longer than those found in the model. Since the otoacoustic and neural measurements were made on different animals under different conditions, the discrepancy may reflect actual differences in the sharpness of tuning between the two groups. We note that tokay gecko ANF Q_{10 dB} values vary somewhat across studies (e.g., Eatock et al., 1981; Sams-Dodd and Capranica, 1994). At least in part, however, the discrepancy must reflect our choice to model the bundle resonators as harmonic oscillators, a form which is presumably too simple. Despite the model’s underestimation of absolute SFOAE delay, the frequency dependence of the empirical trend is well described by an approximate proportionality between N_SFOAE and Q_{10 dB}, as predicted by Eq. 14.

Empirical evidence for the proportionality between tuning and delay predicted by the model is especially clear above 1–2 kHz. Although the data below 1 kHz are limited, they hint at possible deviations from the trend established at higher frequencies. In particular, SFOAE delays appear systematically shorter than those predicted by the model. Interestingly, a similar low-frequency deviation between measured SFOAE delays and those predicted by the coherent-reflection model appears in chinchilla (Shera and Guinan, 2003; Siegel et al., 2005; Shera et al., 2008), where it may stem from mixing between OAEs generated by multiple source mechanisms. Like mammals, geckos show evidence for both place- and wave-fixed generation mechanisms (Bergevin et al., 2008); the present model describes only a place-fixed mechanism. In the gecko, possible correlates of the otoacoustic trend include a change in the morphology of the tectorial membrane near the 1 kHz location (Manley et al., 1999), suggesting a change in the coupling between bundles. Another possible explanation for the discrepancy at low frequencies is that tuning in this region of the papilla may be primarily electrical in origin, rather than mechanical (Eatock et al., 1991; Aranyosi, 2002). If so, the mechanisms of SFOAE generation at these frequencies may be quite different from those proposed here.

DISCUSSION

This paper addresses the observation that so-called reflection-source OAEs with phase-gradient delays comparable to those found in many mammals can readily be measured in nonmammalian species that lack any clear analog of the mammalian traveling wave (Bergevin et al., 2008). To keep the analysis tractable, we adopted a simplified model inspired by the functional anatomy of the gecko inner ear. Parameters were chosen to match the measured CF range and tuning of tokay gecko auditory-nerve fibers. The model described here thus serves to test the conjecture that realistic reflection-source OAEs can be produced by nothing more than a slightly irregular array of tuned oscillators (Shera, 2003; Shera and Guinan, 2008). Despite the simplicity of the assumptions—but consistent with the conjecture—the model produces SFOAEs with characteristics in qualitative and quantitative agreement (aside from a significant disparity in overall emission magnitude) with those measured in the tokay gecko. The unrealistically small emissions produced by the model result from the small coefficient of irregularity and the absence of any form of active amplification. In all other respects, however, the model reproduces the prominent features of tokay SFOAEs, including their overall spectral structure and the approximate value and frequency dependence of their phase-gradient delay.

Generality of the model results

The structure and assumptions of the present model are broadly consistent with the comprehensive model of Weiss et al. (1985), who developed a quantitative description of the entirety of the lizard auditory periphery, albeit for a species with free-standing stereocilia and minimal overlying tectorial membrane (the Southern alligator lizard, Elgaria multicarinata). Their model, summarized by mechanoelectric circuit analogs representing the various macro- and micro-mechanical stages (Rosowski et al., 1985; Weiss and Leong, 1985), was carefully derived from biophysical considerations and a wealth of physiological data. Whenever possible we employed this more comprehensive model of the lizard auditory periphery to probe the validity of the simplifying assumptions made here. For example, we used their model of the lizard middle ear (Rosowski et al., 1985) to validate our approximations regarding the round-trip middle-ear gain G_me. Most importantly, we note that the papilla and the hair bundles in the Weiss et al. (1985) model are represented, as they are here, by harmonic oscillators, that is, by second-order linear band-pass filters (Eatock et al., 1991). Because of the isomorphism between these superficially distinct model representations of the lizard inner ear, we are confident that our principal conclusions regarding SFOAE generation (e.g., the origin of the rapidly rotating OAE phase and the approximate proportionality between N_SFOAE and Q_{10 dB}) would survive if analogous OAE generation mechanisms were embedded in this more detailed and realistic model of the lizard ear.

Extension to the alligator lizard

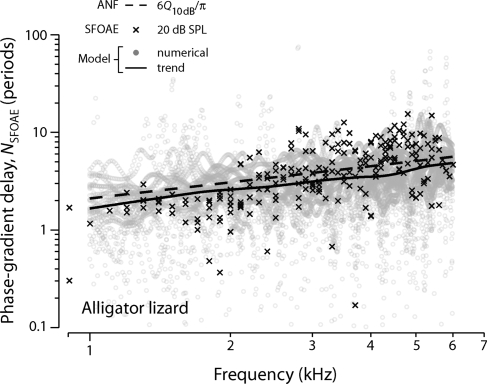
The structural similarity between our model, inspired by the gecko and models of other lizard ears, suggests that the approach might provide a quantitative account of SFOAE phase gradients measured in other species. To test this conjecture, we adapted the model parameter values to approximate the features of the high-frequency region of the alligator lizard papilla, where the hair bundles are free-standing rather than grouped into sallets as in the gecko (see Table 1). Figure 4 compares model results with measured SFOAE delays in alligator lizard (Bergevin et al., 2010). The overall agreement remains close; as predicted by the model, tuning and delay are strongly correlated. Note that both N_SFOAE and Q_{10 dB} are somewhat smaller in the alligator lizard than in the gecko. Although the inner ears of the gecko and alligator lizard manifest major morphological differences—including the presence or absence of tectorial sallets, the overall length of the papilla, and the slope and orientation of the tonotopic map—our results suggest that the most important parameters for reproducing SFOAE delays are those controlling the sharpness of tuning with CF.

Figure 4.

Measured and model SFOAE phase-gradient delays N_SFOAE versus frequency in alligator lizard. The format is the same as Fig. 3. The symbol × shows delays in stimulus periods measured at a probe level of 20 dB SPL (six ears) using methods described elsewhere (Bergevin et al., 2008). Data points within 10 dB of the noise floor are not shown. The gray dots show model N_SFOAE values obtained from numerical simulations of 25 different irregularity patterns. The solid curve is a loess trend line fit to the model results. The dashed line gives the analytic approximation 6Q_{10 dB}∕π [Eq. 14], where Q_{10 dB}(CF) is a power-law fit to ANF data (Weiss et al., 1976). Data are taken the study of Bergevin et al. (2010).

Robustness to changes in the bundle oscillators

Although we follow historical precedent and represent the hair bundles as harmonic oscillators, our main conclusions do not depend on this choice. For example, replacing the harmonic oscillators with gammatone filters9 modifies quantitative details of the relationship between N_SFOAE and Q_{10 dB}, but leaves SFOAE characteristics nearly unchanged. Similarly, replacing the model’s passive oscillators with active oscillators of the form derived from mammalian basilar-membrane data by Zweig (1991) complicates the analysis but does not affect our principal conclusions. The reason for the robustness of our results is not difficult to see: The analysis of the origin of the rapid rotation of SFOAE phase, culminating in Eq. 14 for N_SFOAE, depends in no essential way on the precise form of the underlying oscillators. We sought to emphasize the generality of the arguments following Eq. 10 by adopting the generic nomenclature T(β)e^iϕ(β) for the oscillator response. Similar arguments would apply, and similar results would be obtained, no matter what the detailed functional form of the excitation pattern and associated mechanical phase shifts, so long as the response remains strongly peaked somewhere along the papilla and the principle of stationary phase can be applied. To underscore this point, note that Eq. 14 for N_SFOAE is identical—modulo the entropy of changes in notation—to equations derived using models of the mammalian cochlea [e.g., Eqs. (51)–(53) of Zweig and Shera (1995)], where excitation patterns take the form of basilar-membrane traveling waves.

Coherent reflection by any other name

The analysis presented in Sec. 4 demonstrates that the mechanisms responsible for producing SFOAEs in the model are closely analogous to those of the coherent-reflection model. The only real difference is this: There are no basilar-membrane traveling waves. But the absence of traditional mammalian traveling waves in the gecko does not mean that there are no mechanical phase shifts between the responses of different bundles arrayed along the papilla. These mechanical phase shifts, and the fact that they couple back to the stapes via the papilla, come to play for the gecko the same role in the generation of reflection-source OAEs that traveling waves and their associated phase shifts play in the mammal.

Although the terminology of the coherent-reflection model derives from the mammalian case (Zweig and Shera, 1995), the basic mechanisms operating in the gecko model are fundamentally the same. In both models, the effects of intrinsic micromechanical irregularities couple back to the stapes, where they affect the impedance of the inner ear. In models of the mammalian cochlea, this coupling occurs via traveling pressure-difference waves. In the gecko model, the coupling between hair bundles and the stapes is mediated by the bulk motion of the papilla. In both models, contributions to the response at the stapes arise all along the partition, although the emission is usually dominated by contributions that arise near the peak of the mechanical response (the equations indicate that coupling to the stapes is strongest in this region).

Although the irregularities located within the peak region may be spatially “noisy” (i.e., the cell-to-cell variations in the mechanics may contain many different spatial-frequency components), their net contribution to the impedance is smoothed out by a filtering process whose analog in the mammal has been dubbed “coherent-reflection filtering” (Zweig and Shera, 1995). Filtering occurs because of phase-interference effects among contributions that arise from different locations within the peak region. The filtering process effectively eliminates contributions from all but a relatively narrow range of spatial frequencies (i.e., those near $\widehat{\kappa }$). Contributions from spatial frequencies near $\widehat{\kappa }$ combine coherently and can therefore sum up to a large value; all others effectively cancel one another out. This is why mechanically smooth cochleae do not produce appreciable reflection-source OAEs: The spatial variation of their mechanical properties does not contain significant spatial-frequency components near $\widehat{\kappa }$.

Because of the filtering, the net effect of the irregularities is to produce quasiperiodic spectral oscillations in the impedance Z_ie. (If no filtering occurred, the impedance would be a noisy function of frequency, mirroring the noisy spatial pattern of irregularities.) Interpreted in the time domain, quasiperiodic spectral oscillations in the impedance represent the addition of a delayed component (i.e., an echo or emission) to the pressure measured in the ear canal. At any given frequency, the mean delay is determined by the value of the dominant spatial frequency $\widehat{\kappa }$. As outlined in Sec. 4, stationary-phase analysis shows that $\widehat{\kappa }$ is determined by the gradient of the response phase near the magnitude peak [Eq. 12]. Filter theory indicates that this phase gradient is, in turn, proportional to the sharpness of tuning.

Invariance under spatial rearrangement of the bundles

Although our parameter values reflect the (reversed) exponential tonotopic organization of gecko hair cells (Manley et al., 1999), the model requires no ordered array of CFs. Indeed, the model predictions are invariant under spatial permutation of the bundles. [Addition is commutative, and the expression for ΔZ in Eq. 7 is a discrete sum over independent bundles.] Unlike in the mammalian cochlea, where the basilar membrane participates in the tuning and the driving pressure forces are spatially nonuniform (e.g., Olson, 2001), in the lizard, the supporting structure (papilla) that couples the bundles to one another and to the stapes moves approximately as a rigid body; consequently, all places along the papilla are created equal. In the model, the mechanical drive and response of any given bundle remain the same no matter where it may reside along the papilla and no matter who its neighbors happen to be. (Of course, the model simplifies the in-vivo physics; the actual papilla is not perfectly rigid and hydrodynamic coupling between adjacent salletal groups may sometimes be important.) Although concepts such as the “spatial pattern” or the “spatial-frequency content” of the irregularities are convenient for the analysis—and entirely appropriate in the tokay, where the tonotopy appears regular—they conceal the full generality of the model. What matters in the model is not the arrangement of the bundles or their irregularities with respect to spatial position, but their arrangement with respect to characteristic frequency (when the frequency-position map is smooth and monotonic, the two are simply related). Bundles are operationally “close” to one another if they have similar CFs, whether they reside in adjacent rows or at opposite ends of the papilla. The model therefore predicts that the principles of OAE generation operating in the normal lizard continue to apply even in some hypothetical mutant in which the regular exponential tonotopy of the papilla becomes radically, even randomly, reorganized during development.

Correlations between peripheral tuning and SFOAE delay

Independent of any model, the otoacoustic and neural data in Fig. 3 demonstrate an empirical correlation between measurements of N_SFOAE and Q_{10 dB} in geckos. The covariation of SFOAE phase-gradient delay and the sharpness of tuning established here in geckos provides a reptilian analog of correlations previously demonstrated in mammals (Shera et al., 2002; Shera and Guinan, 2003). Our model of SFOAE generation in the gecko accounts for this relationship [Eq. 14], just as coherent-reflection theory accounts for it in the mammalian ear (Zweig and Shera, 1995).

The model predicts that species differences in the sharpness of tuning among lizards should correlate with differences in SFOAE delay. For example, Manley et al. (1996) report species differences between tokay and leopard geckos (Gekko gecko and Eublepharis macularius) in the relative bandwidths of suppression tuning curves obtained by measuring the response of SOAEs to external tones. As reviewed by Manley et al. (1996), the properties of SOAE suppression tuning curves generally match those obtained from neural measurements. The authors report that the values of Q_{10 dB} in tokay geckos are generally larger than in leopard geckos by an average factor of 1.3–1.4. The biophysical origins of this species difference in the sharpness of gecko tuning are not known. But if the difference arises or is manifest mechanically, our model predicts that SFOAE phase-gradient delays should differ correspondingly [Eq. 14]. We test this prediction in Fig. 5, which compares values of N_SFOAE measured in the two gecko species (Bergevin et al., 2008). As predicted by the model, the emission data show that N_SFOAE is larger in tokay than in leopard geckos. Indeed, at frequencies above 2 kHz, where the SOAE suppression tuning curves were measured, the ratio of the SFOAE delays averages 1.4–1.5, in close agreement with reported ratios of tuning sharpness.

Figure 5.

SFOAE phase-gradient delays versus frequency in tokay and leopard geckos. The symbols × and ● show delays N_SFOAE (in periods) measured, respectively, in tokay (G. gecko, ten ears) and leopard geckos (E. macularius, 12 ears). The loess trend lines demonstrate that N_SFOAE values are generally larger in the tokay, consistent with the sharper tuning measured in this species (Manley et al., 1996). Emission data are taken from the study of Bergevin et al. (2008). Probe levels were 20 dB SPL. Data points whose corresponding SFOAE magnitudes fell within 10 dB of the noise floor are not shown.

Extending these ideas to other lizards, we note that previous studies have suggested that an overlying tectorial membrane, when present, may somehow act to enhance the frequency selectivity of mechanical tuning (Manley et al., 1988; Authier and Manley, 1995). If the presence of a tectorial membrane correlates with sharper tuning, then, all other things being equal (a significant caveat), our model predicts that SFOAE delays should generally be shorter in lizards that lack a tectorial covering over much of their papilla. If correlations between peripheral tuning and SFOAE delay hold more generally among vertebrates, then the frog may be an exception that tests the rule. At stimulus frequencies below 1–2 kHz (depending on species), frog SFOAE delays are significantly longer than those in geckos and many mammals (Meenderink and Narins, 2006; Bergevin et al., 2008). Despite their longer OAE delays, frogs appear to have broader ANF tuning (Ronken, 1991). Reconciling these observations with the correlations between tuning and delay observed in other species requires additional mechanisms in the frog—perhaps traveling waves on the tectorial curtain of the amphibian papilla (Hillery and Narins, 1984)—that contribute significant mechanical delay without a corresponding effect on the sharpness of tuning.

Although traveling waves along both the basilar and tectorial membranes (Ghaffari et al., 2007) also occur in mammals, the great bulk of the delay measured in mammalian cochlear mechanics and otoacoustic emissions appears well correlated with tuning (Shera et al., 2007). To put it another way, signal-front delays constitute a relatively small fraction of the total mechanical delay (Temchin et al., 2005), most of which is associated with “filter build-up.” Unlike the waves that may propagate along the tectorial curtain in frogs, traveling waves in mammals propagate along and are influenced by the tuned structure itself. Since the mechanical response builds up as the wave propagates, tuning and delay are inextricably linked in mammals, just as they appear to be in lizards.