Abstract
The active regulation of cellular forces during cell adhesion plays an important role in the determination of cell size, shape and internal structure. While on flat, homogeneous and isotropic substrates some cells spread isotropically, others spread anisotropically and assume elongated structures. In addition, in their native environment as well as in vitro experiments, the cell shape and spreading asymmetry can be modulated by the local distribution of adhesive molecules and topography of the environment. We present a simple elastic model, and experiments on stem cells to explain the variation of cell size with the matrix rigidity. In addition, we predict the experimental consequences of two mechanisms of acto-myosin polarization and focus here on the effect of the cell spreading asymmetry on the regulation of the stress-fiber alignment in the cytoskeleton. We show that when cell spreading is sufficiently asymmetric the alignment of acto-myosin forces in the cell increases monotonically with the matrix rigidity; however, in general this alignment is non-monotonic as shown previously. These results highlight the importance of the symmetry characteristics of cell spreading in the regulation of cytoskeleton structure and suggest a mechanism by which different cell types may acquire different morphologies and internal structures in different mechanical environments.
I. INTRODUCTION
Recent experiments have demonstrated that geometrical and mechanical properties such as the cell shape and the elastic rigidity of the environment play an essential role in the regulation of cellular processes including, cell proliferation, differentiation and apoptosis [1–9]. Interestingly, even when plated on isotropic and homogeneous substrates, human mesenchymal stem cells were shown to adopt distinct morphologies when the rigidity of these substrates was different [6]. In particular, on either very soft or very rigid substrates, the cells adopted more isotropic morphologies, while on substrates with intermediate rigidities, the cells adopted polarized (elongated) structures. Another typical observation is that the spread area of cells increases monotonically with the rigidity of the environment [3, 4, 10]. The fact that the size and shape of spreading cells depends on the rigidity of the environment suggests that these properties may be determined by a mechanical balance of forces resulting from the elastic deformation of both the cell and its environment.
Indeed, cell adhesion is accompanied by the generation of isometric tension in the cytoskeleton [11–13]. This tension is created by various mechanisms (that operate simultaneously) including the active polymerization of the actin network that pushes the cell front during cell spreading and the concurrent acto-myosin forces that locally compress the cytoskeleton [14, 15]. The rigidity of the cell and the surroundings, as well as the cell shape, play an essential role in the determination of the elastic stress and strain and the force balance in the cytoskeleton. In general, a more rigid external matrix can support more tension in the cytoskeleton, suggesting that cells may possess more stretched configurations in more rigid environments, as observed in experiments [3, 4, 10]. Somewhat less intuitive is the effect of the shape and spreading symmetry of cells on the balance of forces and its effect on the internal structure of the cytoskeleton; this is the subject matter of the present paper.
The isometric tension developed during cell adhesion does not reach a steady-state when the cell is fully spread on the surface. Rather, experiments show that on a time scale of tens of minutes to hours, the cell continues to remodel its cytoskeleton to establish a distribution of acto-myosin fibers, called stress-fibers, that span the cytoskeleton and terminate at localized protein complexes called focal-adhesions [16]. The number of stress-fibers formed and their orientational distribution in the cell is likely to depend on the magnitude and symmetry characteristics of the elastic stress in the cell [17–20]. We have recently shown, both theoretically and experimentally, that an early-time anisotropy in the shape of a cell may direct the spontaneous alignment of the stress-fibers along the long axis of the cell, even if the forces exerted by the cell are isotropic; we have also demonstrated that the stress-fiber alignment caused by this mechanism depends non-monotonically on the matrix rigidity [20]. While recent evidence indicates that isolated cells plated on flat, homogeneous and isotropic surfaces spread isotropically on a surface [14], cell spreading does not always occur in an istropic environment. In both the native environment, and in-vitro experiments, cells often spread in anisotropic geometries. For example, this can occur when a cell spreads on a thick but long collagen fiber in the extracellular matrix (a phenomenon known as contact guidance [21, 22]) or when the cell shape and spreading are artificially manipulated by the topography of the substrate or the distribution of adhesive ligands on the surface [17, 18, 23, 24]. The anisotropy of cell spreading in these situations affects the elastic stress in the cytoskeleton and may therefore govern the polarization of stress-fibers in the cell.
In this paper, we study both theoretically and experimentally, the elastic consequences of cell spreading that dictate the dependence of cell size on the rigidity of the surroundings and the regulation of stress-fiber polarity in the cell. We present a simple elastic model that predicts the variation of cell size (area) with the matrix rigidity and experiments on stem cells that support our model. In addition, we study the effects of the adhesion-induced stress on the polarization of stress-fibers in the cell. While the complete dynamics of cell spreading is not considered here, we do focus on the symmetry characteristics of the elastic forces that the cell exerts during cell adhesion and predict how these forces feed back on the regulation of the stress-fiber orientation in the cell. We model the cell as an active elastic inclusion that pulls on its surroundings and generates an elastic stress in both the cell and its environment; the surroundings are treated as an infinite isotropic and homogeneous elastic medium and we consider both 2D and 3D geometries. The model includes both the elastic forces resulting from cell spreading as well as the contractile forces originating from myosin motors in the cytoskeleton. We use approaches from continuum mechanics to quantify the elastic stress created by these forces, for different cell shapes, for different levels of spreading asymmetry and for different rigidities of the environment. We then couple the changes in the elastic stress in the cell to the initial, active modulation of the acto-myosin forces in the cell (both in magnitude and orientation) that is likely to be an important first step in the global orientation and polarization of stress-fibers in the cell.
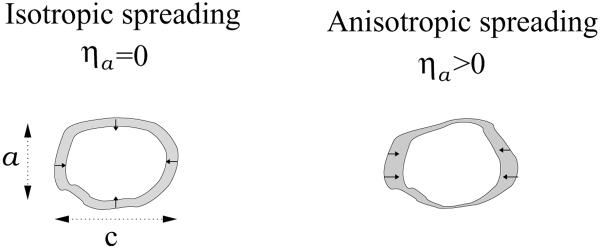
Our model allows us to distinguish two fundamentally different mechanisms that drive the polarization of stress-fibers in cells, see Fig. 1. One mechanism, which is the focus of the present work, results from the anisotropy of elastic stresses within the cell that can arise from asymmetric cell spreading; for brevity, we shall call this the asymmetry that arises from cell spreading. This can occur even for symmetrically shaped cells if the surface properties that govern cell spreading are anisotropic. The other mechanism, treated in Ref. [20], arises from the early-time anisotropy of the cell shape. We showed in [20] that even if a cell spreads isotropically on a substrate the elastic stress produced by the cell can be anisotropic if the cell shape is already anisotropic at early times. Thus, both the early time shape of the cell and the anisotropy of cell spreading may result in an anisotropic stress in the cytoskeleton, that in turn, may govern the orientation of stress-fibers in the cell. However, while the stress-fiber polarization resulting from the anisotropy of the cell shape depends non-monotonically on the matrix rigidity, the polarization resulting from the anisotropy of cell spreading increases monotonically with the matrix rigidity. This distinction leads us to suggest that different cell types with different spreading characteristics can show qualitatively different behaviors of stress-fiber polarization in different mechanical environments.
Figure 1.
Schematic illustration of cell spreading symmetry. The blank and shaded domains shows a top view over the cell shape before and after cell spreading, respectively; small arrows indicate the direction of the consequent elastic, restoring forces. On the left we illustrate a cell whose early-time shape on the substrate is slightly anisotropic but its spreading is isotropic. In this case, as explained in the text, the stress in the cell need not be isotropic due to the early time shape of the cell, and as a consequence, we predict that the stress-fibers polarize spontaneously parallel to the long axis of the cell. Our calculations show that dependence of this alignment on the matrix rigidity is non-monotonic. In contrast, we find that the polarization resulting in the case of anisotropic cell spreading, as illustrated in the right panel, increases monotonically with the matrix rigidity, in response to the increasing stress-anisotropy.
II. THEORETICAL MODEL
The anchoring of a cell to the extracellular matrix as well as the active spreading of cells on a surface involve a shape and volume deformation of the cell that produces elastic stresses in both the cell and the matrix [11–13, 25]. A similar effect occurs in a solid when some part of it, an elastic inclusion, undergoes a shape or volume transformation, due to a phase transition, thermal expansion, or other chemical change and thereby produces a stress field in both the solid and the inclusion [26]. The theory presented here shows how the rigidity of the environment and its coupling to the symmetry of cell spreading, dictate the elastic stress in the cell, that in turn, feeds back on the acto-myosin forces in the cell and governs their density and orientation. We consider a sparse distribution of cells and focus on the elastic interaction of an isolated cell with its surrounding matrix. To calculate the elastic stress produced by an active cell we use approaches from solid mechanics and generalize the well-known inclusion problem [26, 27] to include the “live” nature of the cell, that is, its ability to actively regulate its forces. Our theory is applicable for both 2D and 3D systems; for clarity we focus first on a 3D system that is applicable to cells in tissues. The formalism we use here is similar to that used in Ref. [20] but for clarity we review it here in detail and focus on the change in cell area and on the effects of spreading asymmetry.
We focus on the early stages of cell adhesion where the actin cytoskeleton is still in the isotropic gel state, the myosin motors are dispersed in the cell and both have not yet assembled in organized, anisotropic stress-fibers. Thus, for simplicity, the cell and surrounding matrix are each modeled as a continuum, isotropic (linear) elastic medium and are respectively characterized by the (fourth rank) elastic moduli tensors Cc and Cm [51]. We use bold face letters to designate fourth-rank tensors and a product of the form A gij to denote Aijkl gkl, and similarly AB gij = AijmnBmnkl gkl, where summation over repeated indices is implied (in the 2D model the summation is restricted to the x – z plane).
Experiments show that the spreading area of cells increases monotonically with the matrix rigidity reaching maximal values when placed on rigid substrates such as plastic or glass coverslips [3, 4]; similarly in a 3D collagen gel cells were shown to assume larger sizes when the gel was fixed to the culture dish than when it was floating in solution [10]. This leads us to suggest that the dependence of the cell size on the rigidity of the environment is dictated by an elastic balance of forces between the cell and the matrix. To calculate this dependence we first focus on the maximally stretched state of the cell as it exists when the cell is fully spread and anchored to an infinitely rigid matrix. We define the state in which the cell is fully stretched, but where the matrix is in its equilibrium, (as yet) undeformed, state as the state of zero displacement. This provides the reference state from which all strains defined hereafter are measured [26, 27]. If now the cell is removed from the matrix and placed in solution, it undergoes the free transformation strain, , and reverts back to its original, elastically undeformed and more compact size. Conversely, , is the strain associated with the anchoring and spreading of the (initially undeformed) cell in an infinitely rigid matrix. Thus, in its fully stretched state the cell exerts inward restoring forces Cc that tend to contract the cell; is the unit vector that denotes the outward normal to the cell surface. We now consider the more general case where the cell spreads and anchors to an elastic matrix with finite rigidity.
After some initial spreading of the cell, adhesion of the cell and matrix develops - this couples the cell and the matrix elastically; once this happens, the actively generated tension in the cytoskeleton, that (at least) in part originates from the early-time isotropic pulling forces of myosin motors, deforms the matrix. To calculate how these effects dictate the elastic state of the cell in matrices of different rigidities, we assume that the cell first (actively) stretches to its maximum size, as it would in a rigid environment that cannot deform, and then calculate the actual strain that develops in the cell, , once the forces are allowed to relax in both the cell and the matrix. To calculate the equilibrium strain , and stress, , in the cell, we follow the usual treatment of inclusions in solids. To simplify the calculation we model the cell as an ellipsoidal, homogeneous and isotropic, inclusion in an infinite 3D matrix. In this case, an important simplification applies: the strain distribution within the inclusion is uniform [26, 27]. For the simple case that Cm = Cc we have: , where S is the well-known Eshelby tensor that is calculated for models of passive, elastic inclusions. This tensor is a known function of the inclusion shape and the Poisson ratio of the matrix [26, 27]. For the more general case where the cell and the medium have different elastic properties one denotes S by Sm and generalizes the original Eshelby result to give [26, 28, 29]:
| (1) |
with . Here, I, denotes the fourth-rank identity tensor ; the subscript in Sm implies that the Eshelby tensor is a function of the Poisson ratio of the matrix; the fourth-rank tensor, A, is often termed the strain-concentration tensor [28, 30]. Since (by definition) and are measured relative to the state where the cell is fully stretched (and where the matrix is undeformed), and since is the free transformation of the cell to its undeformed state, the difference, , measures the cellular deformation relative to the undeformed state of the cell; thus is the elastic stress in the cell.
We now propose that this initial elastic state of the cell provides a mechanical cue that directs the development and alignment of stress-fibers in the cell. The active forces that act on the cell surface arise from a distribution of equal and opposite forces within the cell volume that are locally exerted on the actin fibers by myosin. These elastic, “force dipoles” [31–33] each occupy a very small volume on the scale of the cell and we assume that the cell contains a uniform distribution of these dipoles. The elastic dipoles are tensor quantities that have units of energy since the dipole magnitude is given by the product of the force exerted and the distance between the two points (related to the size of the myosin molecule), that produce the equal and opposite forces. One index of this tensor signifies the direction of the force and the other index signifies the direction of the vector that represents the two points at which the myosin exerts its forces along the stress-fiber [32]. We define the average dipole per unit volume, 〈pij〉, (equivalent to a force per unit area) exerted by the acto-myosin elastic, dipolar forces in any volume element within the cell. We assume that these force-dipoles polarize in response to the local stress in the cell, and thus change their magnitude and orientation compared with their average initial value . We thus propose a feedback response of the form:
| (2) |
where, , is the polarization tensor. The tensor α determines the response of the cell to the mean cytoskeleton stress, given by: . The cytoskeleton stress, is the steady-state stress that is a result of both: (i) the matrix forces that act on the cell and (ii) the polarization of the acto-myosin forces in the cell that develop after the initial cell adhesion. It must thus be calculated in a self-consistent manner. The tensor α is termed the cell polarizability tensor, because it determines the extent of cell polarization in response to strains within the cell that arise from forces external to the cell, in our case, due to the matrix elasticity. In general, α is a fourth-rank tensor whose elements may be cell-type specific. We argue below that since the polarization response begins when the cytoskeleton is still in an isotropic gel state [34, 35] the polarizability tensor, α, can be approximated by an isotropic tensor that is characterized by two independent parameters αv and αs, corresponding respectively, to global, volume and shape (shear) deformations of the cell. In the results section we discuss the elastic polarizability tensor in more detail.
In the cell, both the active forces (per unit volume) due to acto-myosin activity, , and the passive elastic forces (per unit volume), , are linearly related to the strain in the cytoskeleton, we can thus define a set of effective material quantities that combine the passive and active cell response. To do this, we note that for an ellipsoidal cell, the elastic field and consequently the polarization are uniform. This allows us to write the force balance equation at the cell/matrix interface: ; where are the (surface) polarization forces analogous to the so-called polarization charges in electrostatics [36]. By use of Eq. 2 and the relationship between the active force and the dipole strength, , we may rewrite this boundary condition as follows:
| (3) |
with
| (4) |
For comparison, immediately after cell adhesion, when the long-term, active polarization response of the cell has not yet been established, there are no feedback effects; this is equivalent to setting α = 0 in Eq. 4. In this early time regime, the boundary conditions that relate the matrix and cell stresses at the cell boundary are those of passive inclusions in an elastic matrix: . Thus, the effective elastic moduli, C̃c, renormalize the passive moduli, Cc, of the cell to include the active (linear) polarization response of the force dipoles.
We are now in position to write formal expressions for the mean strain in the cell, , that drives the reorganization of the stress-fibers and focal adhesions, as well as for the increase in the mean value of the local, elastic force dipole per unit volume (force per unit area) that are produced by active cells in 3D matrices. Making use of Eqs. 1– 2, and replacing Cc by the effective moduli C̃c we obtain:
| (5) |
with . This allows us to calculate the mean cellular dipole via the feedback relation of Eq. 2, and we find:
| (6) |
This equation predicts how the early-time polarization of the acto-myosin dipoles in the cytoskeleton is governed by the cell shape (via the Eshelby tensor S), and the elastic moduli of the cell and the matrix. On the right hand side, , is the early-time strain that results from cell spreading and from the compressional forces exerted by the isotropic distribution of myosin motors in the cytoskeleton. In the results section we shall discuss the symmetry characteristics of and the properties of the polarizability tensor, α, and demonstrate how these affect the polarization of stress-fiber in the cell.
The formalism presented above is also applicable to an active, elliptical cell embedded in an infinite 2D sheet of matrix under conditions of generalized plane-stress [37]. This is defined in a geometry in which the cell and the matrix are in the x – z plane, with zero stress boundary conditions in the perpendicular direction: σyy = σxy = σzy = 0. Thus while the problem is two-dimensional the cell is free to deform in and out of the x – z plane. As in the 3D case, the elastic field in the cell is uniform and Eqs. 1–6 hold but with a 2D version of the Eshelby tensor, which is a known function of the cell shape and matrix Poisson ratio [38]. This allows us to solve the problem analytically and to compare the polarization response of cells in two- and three-dimensions. The 2D, plane-stress model applies to substrates whose thickness is smaller than the cell size. The experimental situation is therefore intermediate between our 2D and 3D calculations. However, as shown in [20] we find the same, generic, qualitative dependence of the acto-myosin polarization on the matrix rigidity in both 2D and 3D.
III. RESULTS AND DISCUSSION
A. The spreading area of cells and its dependence on the matrix rigidity
Perhaps the clearest indication that the elastic tension in the cell governs its geometry is the well known observation that the area of cells that spread on a surface depends on, and generally increases with the rigidity of the environment [3, 4, 10]. Our model allows us to estimate how the cell area (in 2D) or volume (in 3D) vary with the matrix rigidity. This estimate is based on the assumption that the variation of cell size with the matrix rigidity is dictated by the elastic balance between the cell and matrix forces. We denote by u0 and uc the respective traces of and . Noting that in 3D, u0 ≈ (VR – V0)/V0, and uc ≈ (Vc – V0)/V0, where VR is the cell volume in its relaxed state, V0 is the cell volume in its fully stretched state, as it exists in an infinitely rigid matrix, and Vc is its equilibrium size in a compliant matrix, we have (Vc – VR)/(V0 – VR) ≈ (uc −u0)/(−u0). Similarly, in 2D we find an expression for the change in the cellular area, (Ac – AR)/(A0 – AR) ≈ (uc − u0)/(−u0).
Using Eq. 5 to expand this ratio in powers of the cell aspect ratio, r, around r = 1, and assuming that the cell spreads isotropically, we find the following expression for the area variation of the cell with the matrix rigidity:
| (7) |
where , with νc and νm, the Poisson ratios of the cell and matrix respectively. In 3D we find a similar expansion for the relative volume change of the cell in powers of the cell aspect ratio. In this case, the second term in the expansion scales as (r − 1)3/2. In addition, the effective Young's modulus of the cell is given by: . In the incompressible limit, νc → 1/2, diverges and consequently no volume change is possible in the cell. Eq. 7 shows that the cell area is rather insensitive to the cell shape; the next higher order term in the above expansion is quadratic in the deviation of r from unity. It is known in continuum mechanics [26, 39] that for Cm = Cc and for an isotropic dilatational (eigen)strain, , the strain inside the inclusion is independent of the inclusion shape. The inset of Fig. 2 shows the effect of cell shape on the area. For an equal Poisson ratio of the cell and the matrix, in all these limits, Em → 0, Em → Ec and Em → ∞ the cell shape has zero effect. In addition, we note that the variation of the cell area as a function of the matrix rigidity depends on the polarizability parameters, particularly on αv (the other factor, αs enters via the r-dependent terms). This reflects the effect of the polarization of the cellular forces on the cell area. Inspection of the parameter shows that the polarizability of the cell causes it to appear effectively more rigid with a Young's modulus that scales as ~ (1+αv)Ec. Below, we discuss the polarization response and the polarizability factors in more detail.
Figure 2.
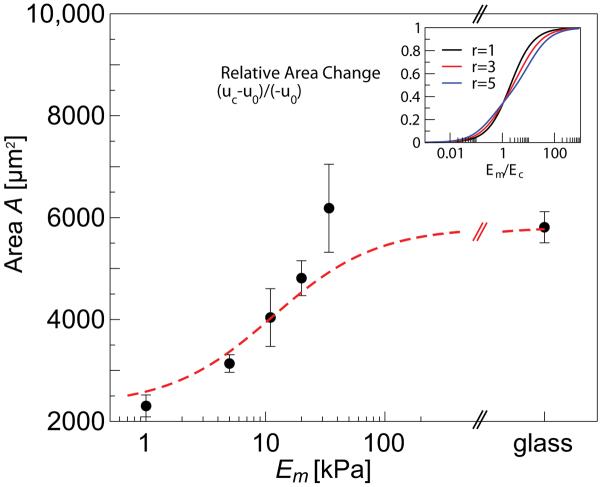
Modulation of cell spreading area with matrix rigidity. Main panel shows a quantitative fit of the model Eq. 7 to our experimentally measured values for human mesenchymal stem cells; the fit was obtained with the value and did not include the point corresponding to Em = 34 kP a due to its large error. The inset shows how the modulation of cell area varies with the cell shape and the rigidity fraction, Em/Ec. This plot is for ηa = αv = αs = 0; cell and matrix Poisson ratios are νc = 0.3 and νm = 0.45 respectively. For finite values of αv and αs the cell area decreases. Finite values of spreading asymmetry, ηa (see Eq. 8 below), have only a small effect on these results.
Finally, Eq. 7 predicts a very simple functional dependence of the area (or volume) dependence on the matrix rigidity. In the main panel of Fig. 2 we show a quantitative fit of our model to the measured area changes of human mesenchymal stem cells that were plated on substrates of various rigidities. A similar functional form was used empirically by Engler et al.[3]. This good agreement of theory and experiment supports our assumption that the modulation of cell area with the matrix rigidity is indeed dictated by a simple elastic balance of cell and matrix forces.
B. Stress-fiber polarization
Experiments show that the spontaneous, active spreading of cells on flat, homogeneous, and isotropic substrates is isotropic [14]. Even in this case, however, the elastic stress in the cell (and the matrix) can be anisotropic if the early-time shape of the cell on the surface is somewhat anisotropic [20]. The symmetry and topography of the native cellular environment, however, is also often strongly anisotropic and rough on the scale of the cell size (≳ 10μm). Thus cell spreading may often be biased by the local asymmetry of the environment. This is seen for example in the anisotropic spreading of cells along collagen fibers, a phenomenon known as contact guidance [21, 22]. A common practice in cell adhesion research is the use of artificially designed substrates to control the cell shape and spreading on a surface [18, 23, 24]. Thus, the asymmetry of cell-matrix interaction may arise from either an anisotropy of the initial cell shape as treated in Ref. [20], or from anisotropic stresses due to the anisotropy of cell spreading; as shown in Fig. 1, a cell may start round but spread anisotropically (right panel) due to anisotropy of the spreading forces, or it may possess some early-time shape anisotropy, and spread isotropically (left panel). In this paper we do not treat elastic anisotropy, but rather show how even in an isotropic medium, the symmetry (or asymmetry) of cell spreading may govern the polarization of stress-fibers in the cell; this is applicable for example, to experiments where the distribution of adhesive ligands can be varied to govern cell spreading, or where the cell type is such that there is an intrinsic (e.g., genetically controlled) tendency that determines whether the cell spreads either symmetrically or asymmetrically in a given environment. We show below that the cell shape, and the symmetry of cell spreading have independent effects on the polarization of stress-fibers in the cytoskeleton, and that the dependence on the rigidity of the surroundings is qualitatively different.
To study the effect of cell-spreading asymmetry on the polarization of stress-fibers in the cell we assume for simplicity, that the early-time stress imposed by the cell on its surroundings, , is biased along one direction, say the z-direction, we thus write:
| (8) |
The first term is the isotropic contribution due to the early-time distribution of acto-myosin dipoles in the cytoskeleton; the second term is an anisotropic contribution arising due to an asymmetric spreading of the cell [52]. The elastic field that governs the increase in the polarization of the force-dipoles from their initial value, , to their steady-state value, 〈pij〉, is given by Eq. 5. This field includes the contribution of both terms on the right hand side of Eq. 8 as well as the contribution arising from the anisotropic polarization of the acto-myosin forces in the cytoskeleton, ; Eqs. 5, 6 thus provide a self-consistent solution of the problem.
The early-time polarization of acto-myosin dipoles in the cytoskeleton (that on longer times results in anisotropic stress-fiber formation), is phenomenologically described by the (fourth-rank) polarizability tensor, α, that couples the change in the acto-myosin forces to the stress developed in the cytoskeleton, , as in Eq. 2. We now examine the properties of the polarizability tensor and the possible polarization mechanisms it reflects. The polarization response begins when the cytoskeleton is still in an isotropic gel state [20, 34, 35] and hence the polarizability tensor, α, can be approximated by an isotropic tensor that is characterized by two independent parameters [26], as follows:
| (9) |
where, d = 2, 3 is the dimensionality, Iijkl = (δikδjl + δilδjk)/2 is the fourth rank identity tensor, and δij is the Kronecker delta function. This form of α is characteristic of fourth-rank isotropic tensors including the elastic moduli tensor, C, of isotropic materials [26]. The two parameters αv and αs reflect respectively, the mean response of the dipoles to stresses resulting from pure volume (area in 2D) and shear deformations. Equivalently, the polarizability tensor can be expressed in terms of the parallel and perpendicular components αiiii = α∥ and αiijj = α⊥.
The diagonal components of the polarizability tensor, αiiii = α∥, describe a parallel response in which an axial stretch gives rise to the additional formation of stress-fibers and the strengthening of focal adhesions in that direction; conversely, a weakening of the force causes disassembly of focal adhesions and stress-fibers in that direction. The off-diagonal elements of the polarizability tensor, αiijj = α⊥, describe the response in the perpendicular direction (that occurs along with the parallel response), in which a given stress or strain also affects the focal adhesions and stress-fibers in the perpendicular direction. This may arise due to global conservation constraints on the total dipolar force, for instance, due to a limit in the total myosin or ATP content in the cell. In that case, we would expect α∥ and α⊥ to have opposite signs (see below). Such conservation constraints and the possibility that this results in different polarization responses have thus far not been studied experimentally but as shown theoretically below, these have important implications on the polarization of stress-fibers in the cell.
We therefore analyze two extreme limits of the polarization mechanisms (and hence values of the components of the polarization tensor) that we term, axially induced polarization and orientational polarization, in analogy to the polarization of non-polar and polar molecules by an electric field, respectively [36]. In the limit of axially induced polarization, stress-fibers and focal adhesions assemble/dissassemble in the direction of the local stress, with no coupling between the different directions; this happens when αiijj = α⊥ = 0 or equivalently when αs = αv = αiiii = α∥, see Eq. 9. In the limit of purely orientational polarization, the enhancement of force, due to formation of additional acto-myosin dipoles in the stress direction is compensated by a reduction of the force in the perpendicular direction due to loss of an equivalent amount of such dipoles. This describes a situation in which the early-time acto-myosin dipoles in the cytoskeleton effectively “rotate” in the direction of the stress but their total number is conserved. This situation occurs when α∥ = (1 − d)α⊥ or when the polarizability parameter αv is zero; this is because a symmetric, hydrostatic pressure (that controls the volume of the cell) can only cause a symmetric increase (decrease) in the number or magnitude of the dipoles (if αv ≠ 0) but cannot result in a net orientation of the dipoles. This is similar to the Poisson effect of isotropic materials. In the incompressible limit, where the compressibility modulus drops to zero, 1/κ → 0, the volume is conserved and thus a stretch in one direction results in an equivalent narrowing in the perpendicular directions.
Fig. 3 shows a calculation of the 2D, orientational order parameter of the force dipoles S = 〈cos(2θ)〉 = 〈pzz − pxx〉/p as a function of the ratio of the Young's modulus of the matrix, Em, and the cell, Ec; where, θ is the angle between each stress-fiber and the z axis; and p = 〈pxx〉 + 〈pzz〉. The two elements of the dipole tensor are given by 〈pxx〉 = p 〈sin2θ〉 and 〈pzz〉 = p 〈cos2θ〉 [40]; these are proportional to the number of force-dipoles in the x and z direction, respectively. We plot S for increasing values of the spreading asymmetry parameter, ηa, and for the two limiting cases of the polarization mechanism described above. The figure is plotted for an elliptical cell in an infinite, homogeneous and isotropic 2D sheet. We note that when a cell spreads anisotropically its aspect ratio changes. However, the relevant shape that dictates the elastic field in the cell, is the shape of the cell in its stretched configuration. We thus choose r (= 3 in the figure) to be the aspect ratio of the cell in its maximally stretched configuration and before the long range elastic stresses in the matrix have been established or relaxed [53]. We set the long (short) axis of the cell to be parallel to the z-axis (x-axis), and r = c/a is the ratio of the long to short axis.
Figure 3.
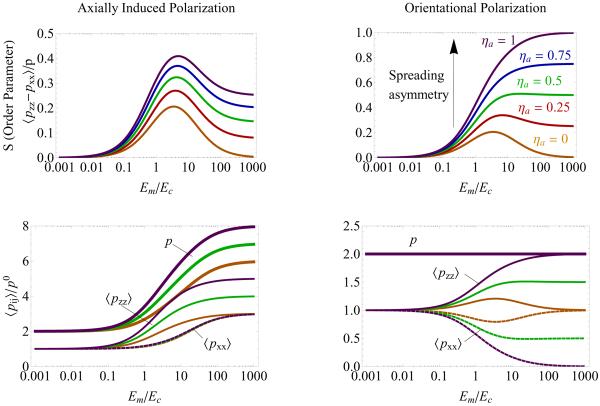
Dependence of acto-myosin polarization on the spreading asymmetry ηa for two possible polarization mechanisms, shown for the 2D system; left and right panels are for the two limits of axially-induced and orientational polarization mechanisms, respectively. Upper two panels show the 2D orientational order parameter, S as a function of the Young's moduli ratio, Em/Ec; plotted for various values of the spreading asymmetry parameter, ηa. These plots show that as ηa increases, the qualitative shape of S(Em/Ec) changes; this change is more prominent in the orientation mechanism but for large enough values of ηa the curves become non-monotonic also in the axially-induced mechanism (not shown). The figure shows that the acto-myosin alignment is more highly developed for the orientational mechanism for the same value of ηa. The bottom panels show the separate components of the dipole tensor 〈pxx〉 (dashed), 〈pzz〉 (thin), and the trace, p = 〈pxx〉 + 〈pzz〉 (bold), for several choices of ηa = 0, 0.5, 1.0. Color coding is the same in all plots. Parameters used for this plot: cell aspect ratio, r = 3; cell and matrix Poisson ratios, νc = 0.3 and νm = 0.45 respectively; here, αs = αv = 2 for the left panels, αs = 2 and αv = 0 for the right panels.
Fig. 3 shows how the asymmetry of cell spreading, as expressed via the parameter ηa affects the dependence of the orientational order parameter, S, on the matrix rigidity. When the cell spreads isotropically, ηa = 0, the orientation of the force-dipoles in the cytoskeleton is solely a consequence of the early-time shape of the cell (see Fig. 1 left panel). We find that in this case, the orientational order parameter, S, depends non-monotonically on the matrix rigidity. As shown in Ref. [20], the explanation for this intriguing phenomenon is that in both very rigid and very soft environments the elastic field developed in the cell is isotropic and is independent of the cell shape. In a very rigid environment the isotropic cellular tractions are opposed by isotropic, equal and opposite forces in the surrounding matrix; thus no breaking of symmetry occurs. In a very soft environment, the matrix resistance, and hence the stress in the cell drops to very small values in all directions; since the feedback depends on the stress in the cell, no feedback occurs and the stress fibers in the cell are not polarized. In between these limits, the cellular forces increase with different dependencies on the matrix rigidity. Consequently, the order parameter shows a maximum for some intermediate value of the matrix rigidity.
In contrast to the effects of cell shape, the anisotropy of cell spreading (ηa > 0) introduces, an additional, asymmetric contribution to the elastic stress. This axial force increases monotonically with the matrix rigidity and its magnitude depends on the extent of the asymmetric stretching (spreading) of the cell as given by ηa. The reason for the monotonic increase of the axial force with the matrix rigidity is that the magnitude of the elastic stresses in the cell increases with the matrix rigidity. As a result also the anisotropy of the elastic stress in the cell increases with the matrix rigidity and via the feedback effect on the acto-myosin anisotropy, so does the stress-fiber polarity. This behavior may explain the observation that cells often polarize even on rigid substrates such as glass [18, 23, 41, 42]. In this case, it is the axial stretch of the cell that results from its biased, asymmetric spreading that “induces” the formation of stress-fibers in that direction.
As noted above, the polarization of stress-fibers in the cell depends on whether the dipoles merely orient themselves in response to the change in the local stress or whether they also change in magnitude and number. Fig. 3 compares the two limiting cases of axially-induced (αv = αs = α∥, α⊥ = 0) and orientational (αv = 0 or α∥ = (1 − d)α⊥) polarization, as described above; where d = 2, 3 is the dimensionality. We find that in the limit of the orientational polarization, the stress fiber alignment is much more sensitive to the stress-asymmetry (non-zero value of ηa) induced by cell spreading. The bottom two panels allow us to simultaneously track the variation in the polarization along the x and z directions and their sum as a function of the matrix rigidity. In the limiting case of orientational polarization (right panel), the total force is conserved. Polarization of the dipoles along the z-axis results in an increase of 〈pzz〉 from its isotropic value p0 and in an equivalent decrease in the force along the x-axis. For su±ciently high values of ηa, and the Young's moduli ratio, Em/Ec, all dipoles orient parallel to the z-axis. We note that the restriction that both 〈pxx〉/p0 and 〈pzz〉/p0 are positive quantities (since these are proportional to the number of acto-myosin dipoles in the cell) sets a limit on the accuracy of our linear model. We find that in the limit of orientational polarization, αs is therefore constrained to values that obey, αs < d/ηa. For sufficiently high values of the spreading asymmetry, ηa, all the acto-myosin dipoles in the cell would polarize along the z-axis. If αs were greater than d/ηa, this would require the disassembly of dipoles along the x-direction (and their reassembly along the z-direction). However, due to the finite number of dipoles (and the conservation requirement in the limit of orientational polarization), there are no additional dipoles in the x-direction, and this process cannot occur. For ηa → 0, the polarization saturates once all the dipoles orient along the z-axis and therefore αs may assume any value. In the axially induced polarization limit we find no such restriction since 〈pij〉/p0 is always positive and increases monotonically with Em; there is no limit on the number of dipoles. In the limit of axially-induced polarization, there is therefore no conservation-induced coupling between the z and x directions; since we assume that the asymmetry is directed along the z-axis (cf. Eq. 8), only the polarization along the z axis increases with ηa (as seen in the bottom-left panel of Fig. 3). This figure also shows that the total polarization 〈pxx + pzz〉 increases with the matrix rigidity. Clearly, for intermediate values of the polarizability parameters, αs and αv, we find values for the polarization and its behavior as a function of the matrix rigidity that are intermediate between those shown on the left and right panels of Fig. 3.
Finally, we present an analytical argument that explains the general behavior of the curves seen in Fig. 3. While the exact expression for S is a complicated function of Em/Ec we find simplified expressions in the limit of small aspect ratios, r, and the spreading asymmetry factor, ηa. Expanding S in powers of both ηa and r around ηa = 0 and r = 1 we find:
| (10) |
where A,B and C have the following dependence on the ratio , , and [54]; the parameters a1, a2 · ·· are positive functions of the two polarizability parameters, αs and αv, the Poisson ratios of the cell and the matrix and the dimensionality (See Appendix B). The first term in Eq.10 has a Lorentzian-type of form. This term is the only one involved in the polarization of the stress-fibers in cells that isotropically spread (ηa = 0) on a substrate. The polarization in this case is driven by the stress anisotropy that results from the early-time shape asymmetry of the cell and by the feedback effect described earlier. The stress-fibers polarize along the long axis of the cell. Interestingly, the dependence of this polarization on the matrix rigidity is non-monotonic (the function A has a non-monotonic dependence on the scaled matrix rigidity, em), attaining a maximal value when the cell and matrix rigidity are comparable (em ≈ 1). The second term in Eq. 10 is the leading term in the polarization that is due to the spreading asymmetry (ηa not equal to zero). Unlike the previous contribution, that results solely from the cell shape-anisotropy, this contribution (given by B above) increases monotonically with the matrix rigidity up to a saturation value that is given by αs ηa/(d + d αv). This agrees with the curves shown in Fig. 3, that demonstrate that the stress-fiber alignment is higher in the limit of orientational polarization (αv = 0) compared with the limit of axially induced polarization (αs = αv). It is also consistent with our previous theoretical prediction [20] that the polarization of stress-fibers is more prominent in 2D geometries. Finally, the third term in Eq. 10 (given by C above) couples the effects of both the cell shape and spreading asymmetry. This term, like the first one, varies non-monotonically with the matrix rigidity.
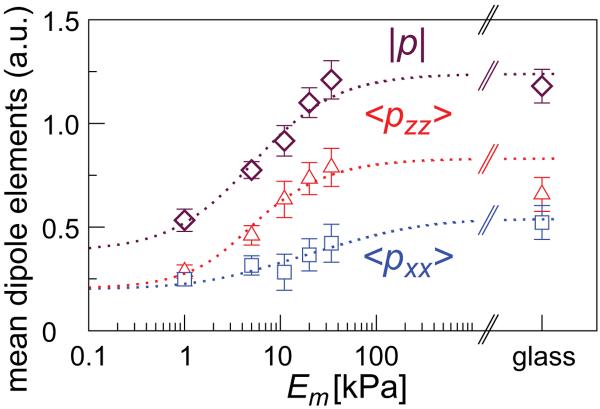
In Ref. [20] we reported the experimentally measured non-monotonic dependence of the stress-fiber order parameter, S, on the matrix rigidity in adult mesenchymal stem cells that were (sparsely) grown on substrates of varying rigidities and sorted by their aspect ratio; we use this information here to calculate the elements of the polarization tensor, 〈pxx〉 and 〈pzz〉 and the trace, p = 〈pzz + pxx〉 for the group of cells whose aspect ratio is relatively small r = 1.5. We choose this group since in this case we find most pronounced differences between the two polarization elements 〈pxx〉 and 〈pzz〉. Consistent with our model, the order parameter shows a non-monotonic dependence on the matrix rigidity [20]. Fig. 4 shows the results of our experimental measurement of the total amount of myosin in stress-fibers in the cells; the experimental procedures are described in detail in the appendix. The fluorescence intensity corresponding to the total myosin in stress-fibers is likely to scale with the average dipole strength, p. To estimate the separate components, 〈pxx〉 and 〈pzz〉 we used the fact that S ~ 〈pzz − pxx〉 and p = 〈pzz + pxx〉. Our measurement of the total myosin incorporated in acto-myosin stress-fibers in the cell as a function of matrix rigidity suggests that the cell produces a stronger overall force on the more rigid substrates. This is consistent with a recent direct measurement of the force exerted by fibroblasts on a pillared surface of varying rigidity [43]. This trend is consistent with the behavior seen in the left panels of Fig. 3, that correspond to the induced polarization limit.
Figure 4.
Experimental measurement of the total amount of stress-fibers in human mesenchymal stem cells as a function of the substrate rigidity. The figure shows the total myosin content that scales with the mean-dipole strength, p = 〈pxx + pzz〉, and the corresponding elements, 〈pxx〉 and 〈pzz〉, calculated from S and p, see text. Theory curves obtained from the expansions of S and p (cf. Eq. 10) are shown to guide the eye (dashed curves).
IV. CONCLUDING REMARKS
Our results predict two fundamentally different mechanisms for stress-fiber polarization in cells. One mechanism is driven by the anisotropy of cell spreading (finite values of ηa). Anisotropic cell spreading can occur due to an uneven distribution of ligands on a surface, or due to a topographic constraint such as the presence of a thick but long collagen fiber in the extracellular matrix; this produces an axial stretch of the cytoskeleton of the cell. In this paper we studied the consequences of asymmetric stresses within the cell that can arise from asymmetric cell spreading in an isotropic elastic medium. Our calculations show that in this case, the polarization of the stress-fibers along the stretch direction increases monotonically with the matrix rigidity. This explains the observation that cells, whose spreading is restricted to being elongated (e.g., via the asymmetry of the adhesive pattern on a substrate), show polarized stress-fibers even when plated on rigid substrates such as glass [18, 42]. In contrast to the monotonic dependence on rigidity predicted for anisotropic spreading, our experiments [20] with human mesenchymal stem cells, grown on flat, isotropic and homogeneous substrates show that the polarization of stress-fibers, as well as the level of cell elongation (aspect ratio) [6], depend non-monotonically on the matrix rigidity. Our theory predicts that a non-monotonic dependence of stress-fiber polarization on the matrix rigidity is expected when a cell, whose early time shape is non-isotropic, spreads isotropically on the substrate (ηa = 0). Such a pure shape effect is another cause of stress-fiber polarization. However, unlike the previous case, this shape-induced stress-fiber polarization diminishes to zero in both very high and very low matrix rigidities where the stress inside the cell becomes isotropic. Thus, a maximum in the polarization anisotropy 〈pzz − pxx〉 is expected as a function of the matrix rigidity. These findings suggest that the dependence of stress-fiber polarization on the matrix rigidity may be governed by the symmetry of the adhesive pattern on a substrate and/or its topography, and can therefore be manipulated (in vitro) by various fabrication technics [17, 18, 23, 24].
In addition, the distinction between stress fiber polarization anisotropy determined by spreading anisotropy and by initial shape anisotropy, raises the possibility that different cell types might be governed by different inherent mechanisms of cell spreading. Consequently, even when plated on flat, isotropic and homogeneous substrates, different cell types may show either a maximum or monotonic behavior of their stress fiber polarization as the matrix rigidity is increased, depending on whether that particular cell type is governed by shape anisotropy or spreading anisotropy. Engler et al. [6] have shown that while the level of stem cell elongation on a substrate depends non-monotonically on the matrix rigidity, smooth muscle cells do not show this dependence; these cells adopt elongated morphologies (characteristic of muscle cells) even when plated on glass surfaces. It is tempting to speculate that the variability of stem cell shapes, internal structure and differentiation in different mechanical environments depends on their inherent tendency to spread isotropically in their environment; perhaps this greater level of symmetry is important for providing these cells with the larger structural and developmental variability they possess.
We are grateful to the Israel Science Foundation, the Clore Center for Biological Physics, the Schmidt Minerva Center and an EU Network grant for their support. F.R. gratefully acknowledges financial support through the Feodor Lynen fellowship of the Alexander von Humboldt foundation. D.E.D. thanks NFS and NIH. A.E.X.B. was supported by a scholarship from the Natural Sciences and Engineering Research Council of Canada.
APPENDIX A: EXPERIMENTAL METHODS
The cells used in this study were human mesenchymal stem cells (hMSCs) from the bone marrow obtained from Lonza and cultured in standard tissue culture treated plastic flasks (Corning). The MSC growth medium consisted of low glucose DMEM (Invitrogen) with 10 % fetal bovine serum (Sigma) and 1 % penicillin/streptomycin (Invitrogen)). In order to have only isolated cells, 500 cells per cm2 were plated on collagen coated PA gels.
After 24 hours the cells were fixated using a 10 % solution of formaldehyde (Sigma) in PBS and subsequently permeabilized with a 0.5 % solution of Triton X 100 (Sigma) in PBS. To obtain a clear outline of the cell, F-actin was visualized using rhodamine-phalloidin (Fluka) and the nucleus was stained with a Hoechst dye (#33342, Invitrogen) to ensure that only healthy cells were recorded. Non-muscle myosin IIa was immuno-stained with a primary antibody raised in rabbit (# M8064, Sigma) followed by a fluorescent secondary IgG antibody (#A-21206, Invitrogen). Fluorescence images were taken with an inverted microscope (IX 71, Olympus) using a 20× phase contrast objective and a 1.6 × post magnification lens. Unbiased cell images were obtained by searching for single nuclei that looked healthy and had no close neighbors. The cell spreading area was determined with NIH ImageJ [44].
As tunable elastic substrates, collagen-I (BD Biosciences) coated polyacrylamide (PA) gels with a Young's elastic modulus Em of 1, 5, 11, 20, and 34 kPa were prepared as reported elsewhere [6, 45, 46]. The elastic Young's modulus was verfied for each batch of gels by force-indentation measurements using a atomic force microscope (MFP-3D, Asylum Research, Santa Barbara).
To determine the total myosin content in the the stress fibers, fluorescence images were segmented using a simple fiber-finding algorithm [20]. Raw images were first convolved with a series of elongated Laplace of Gaussian filters with different angular orientations. The resulting images were collapsed into one by taking the maximum at each pixel over all the filtered images as the intensity of a new `maximum response image'. The maximum response image is then thresholded using the Otsu method [47] and used as a mask for the original image, leaving only regions in the original that are judged to be fibers by the algorithm. This procedure eliminates the contribution of the surrounding background intensity and intensity due to labeled cytosolic myosin that is not incorporated into stress fibers giving a better estimate for the force-generating structures than using the total myosin fluorescence intensity of the cell.
APPENDIX B: ORDER PARAMETER EXPANSION
In this section we detail the expressions for the elements in the expansion of the order parameter in powers of r − 1 and ηa in the 2D system.
| (B1) |
| (B2) |
| (B3) |
References
- [1].Chen CS, Mrksich M, Huang S, Whitesides GM, Ingber DE. Geometric control of cell life and death. Science. 1997;276:1425–1428. doi: 10.1126/science.276.5317.1425. [DOI] [PubMed] [Google Scholar]
- [2].McBeath R, Pirone DM, Nelson CM, Bhadriraju K, Chen CS. Cell shape, cytoskeleton tension, and RohA regulate stem cell lineage commitment. Developmental Cell. 2004;6:483–495. doi: 10.1016/s1534-5807(04)00075-9. [DOI] [PubMed] [Google Scholar]
- [3].Engler AJ, et al. Myotubes differentiate optimally on substrates with tissue-like stiffness: pathological implications for soft or stiff microenvironments. J. Cell Biol. 2004;166:877–887. doi: 10.1083/jcb.200405004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Yeung T, et al. Effects of substrate stiffness on cell morphology, cytoskeletal structure, and adhesion. Cell Motil. Cytoskeleton. 2005;60:24–34. doi: 10.1002/cm.20041. [DOI] [PubMed] [Google Scholar]
- [5].Discher DE, Janmey P, Wang Y. Tissue cells feel and respond to the stiffness of their substrate. Science. 2005;310:1139–1143. doi: 10.1126/science.1116995. [DOI] [PubMed] [Google Scholar]
- [6].Engler AJ, Sen S, Sweeney HL, Discher DE. Matrix elasticity directs stem cell lineage specification. Cell. 2006;126:677–689. doi: 10.1016/j.cell.2006.06.044. [DOI] [PubMed] [Google Scholar]
- [7].Georges PC, Miller WJ, Meaney DF, Sawyer ES, Janmey PA. Matrices with compliance comparable to that of brain tissue select neuronal over glial growth in mixed cortical cultures. Biophys. J. 2006;90:3012–3018. doi: 10.1529/biophysj.105.073114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Ruiz SA, Chen CS. Emergence of patterned stem cell differentiation within multicellular structures. Stem Cells. 2008;26:2921–2927. doi: 10.1634/stemcells.2008-0432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Discher DE, Mooney DJ, Zandstra PW. Growth factors, matrices, and forces combine and control stem cells. Science. 2009;324:1673–1677. doi: 10.1126/science.1171643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Grinnell F. Fibroblast-collagen-matrix contraction: growth-factor signalling and mechanical loading. Trends in Cell Biology. 2000;10:362–365. doi: 10.1016/s0962-8924(00)01802-x. [DOI] [PubMed] [Google Scholar]
- [11].Wang N, et al. Cell prestress. i. stiffness and prestress are closely associated in adherent contractile cells. Am. J. Physiol. Cell Physiol. 2002;282:C606–C616. doi: 10.1152/ajpcell.00269.2001. [DOI] [PubMed] [Google Scholar]
- [12].Kumar S, et al. Viscoelastic retraction of single living stress fibers and its impact on cell shape, cytoskeletal organization, and extracellular matrix mechanics. Biophys. J. 2006;90:3762–3773. doi: 10.1529/biophysj.105.071506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Griffin MA, et al. Patterning, prestress, and peeling dynamics of myocytes. Biophys. J. 2004:1209–1222. doi: 10.1016/S0006-3495(04)74195-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Dubin-Thaler BJ, et al. Quantification of cell edge velocities and traction forces reveals distinct motility modules during cell spreading. PLOS One. 2008:e3735. doi: 10.1371/journal.pone.0003735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Gov NS, Gopinathany A. Dynamics of membranes driven by actin polymerization. Biophys. J. 2006;90:454–469. doi: 10.1529/biophysj.105.062224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Bershadsky A, Kozlov M, Geiger B. Adhesion-mediated mechanosensitivity: a time to experiment, and a time to theorize. Curr. Opin. Cell Biol. 2006;18:472–481. doi: 10.1016/j.ceb.2006.08.012. [DOI] [PubMed] [Google Scholar]
- [17].Wang N, Ostuni E, Whitesides GM, Ingber DE. Micropatterning tractional forces in living cells. Cell Motil. Cyto. 2002;52:97–106. doi: 10.1002/cm.10037. [DOI] [PubMed] [Google Scholar]
- [18].Théry M, Pépin A, Dressaire E, Chen Y, Bornens M. Cell distribution of stress fibres in response to the geometry of the adhesive environment. Cell Motil. Cytoskeleton. 2006;63:341–355. doi: 10.1002/cm.20126. [DOI] [PubMed] [Google Scholar]
- [19].Deshpande VS, McMeeking RM, Evans AG. A bio-chemo-mechanical model for cell contractility. Proc. Natl. Acad. Sci. 2006;103:14015–14020. doi: 10.1073/pnas.0605837103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Zemel A, Rehfeldt F, Brown AEX, Discher DE, Safran SA. Optimal matrix rigidity for stress fiber polarization in stem cells. Nat. Phys. doi: 10.1038/nphys1613. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Kemkemer R, Neidlinger-Wilke C, Claes L, Gruler H. Cell orientation induced by extracellular signals. Cell Biochem. Biophys. 1999;30:167–195. doi: 10.1007/BF02738066. [DOI] [PubMed] [Google Scholar]
- [22].Walboomers XF, Monaghan W, Curtis ASG, Jansen JA. Attachment of fibroblasts on smooth and microgrooved polystyrene. J. Biomed. Mat. Res. 1999;46:212–220. doi: 10.1002/(sici)1097-4636(199908)46:2<212::aid-jbm10>3.0.co;2-y. [DOI] [PubMed] [Google Scholar]
- [23].K. Kurpinski CH, Chu J, Li S. Anisotropic mechanosensing by mesenchymal stem cells. Proc. Natl. Acad. Sci. 2006;103:16095–16100. doi: 10.1073/pnas.0604182103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Liu WF, Chen CS. Cellular and multicellular form and function. Adv. Drug Deliv. Rev. 2007;59:1319–1328. doi: 10.1016/j.addr.2007.08.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Chicurel ME, Chen CS, Ingber DE. Cellular control lies in the balance of forces. Curr. Opin. Cell Biol. 1998;10:232–239. doi: 10.1016/s0955-0674(98)80145-2. [DOI] [PubMed] [Google Scholar]
- [26].Mura T. Micromechanics of defects in solids. Kluwer Academic Publishers; 1991. [Google Scholar]
- [27].Eshelby JD. The determination of elastic field of an ellipsoidal inclusion, and related problems. Proc. Roy. Soc. A. 1957;241:376–396. [Google Scholar]
- [28].Benveniste Y. A new approach to the application of mori-tanaka's theory in composite materials. Mechan. Matr. 1987;6:147–157. [Google Scholar]
- [29].Zemel A, Safran SA. Active self-polarization of contractile cells in asymmetrically shaped domains. Phys. Rev. E. 2007;76:021905. doi: 10.1103/PhysRevE.76.021905. [DOI] [PubMed] [Google Scholar]
- [30].Tucker CL, Liang E. Stiffness predictions for unidirectional short-fiber composites: review and evaluation. Comp. Sci. Tech. 1999;59:655–671. [Google Scholar]
- [31].Siems R. Mechanical interactions of point defects. Physica Status. Solidi. 1968;30:645–658. [Google Scholar]
- [32].Schwarz US, Safran SA. Elastic interactions of cells. Phys. Rev. Lett. 2002;88:048102. doi: 10.1103/PhysRevLett.88.048102. [DOI] [PubMed] [Google Scholar]
- [33].Carlsson AE. Contractile stress generation by actomyosin gels. Phys. Rev. E. 2006;74:051912. doi: 10.1103/PhysRevE.74.051912. [DOI] [PubMed] [Google Scholar]
- [34].Chrzanowska-Wodnicka M, Burridge K. Rho-stimulated contractility drives the formation of stress fibers and focal adhesions. J. Cell Biol. 1996;133:1403–1415. doi: 10.1083/jcb.133.6.1403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Burridge K, Chrzanowska-Wodnicka M. Focal adhesions, contractility, and signaling. Ann. Rev. Cell Develop. Biol. 1996;12:463–519. doi: 10.1146/annurev.cellbio.12.1.463. [DOI] [PubMed] [Google Scholar]
- [36].Kittel C. Introduction to solid state physics. 6th edn John Wiley and Sons; 1986. [Google Scholar]
- [37].Landau LD, Lifshitz EM. Theory of elasticity, vol. 7 of Course of theoretical physics. 3rd edn Reed Educational and Professional Publishing Ltd; 1986. [Google Scholar]
- [38].Jaswon MA, Bhargava RD. Two-dimensional elastic inclusion problems. Proc. Comb. Phil. Soc. 1961:669–680. [Google Scholar]
- [39].Eshelby JD. The elastic field outside an ellipsoidal inclusion. Proc. Roy. Soc. A. 1959;252:561–569. [Google Scholar]
- [40].Zemel A, Bischofs IB, Safran SA. Active elasticity of gels with contractile cells. Phys. Rev. Lett. 2006;97:128103. doi: 10.1103/PhysRevLett.97.128103. [DOI] [PubMed] [Google Scholar]
- [41].Théry M, et al. Anisotropy of cell adhesive microenvironment governs cell internal organization and orientation of polarity. Proc. Natl. Acad. Sci. 2006;103:19771–19776. doi: 10.1073/pnas.0609267103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Curtis A, Aitchison G, Tsapikouni T. Orthogonal (transverse) arrangements of actin in endothelia and fibroblasts. J. R. Soc. Interface. 2006;3:753–756. doi: 10.1098/rsif.2006.0132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Ghibaudo M, et al. Traction forces and rigidity sensing regulate cell functions. Soft Matt. 2008;4:1836–1843. [Google Scholar]
- [44].Rasband WS. ImageJ. U. S. National Institute of Health; Bethesda, Maryland, USA: http://rsb.info.nih.gov/ij/,1997–2007. [Google Scholar]
- [45].Pelham RJ, Wang YL. Cell locomotion and focal adhesions are regulated by substrate flexibility. Proc. Natl. Acad. Sci. USA. 1997;94:13661–13665. doi: 10.1073/pnas.94.25.13661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Engler AJ, Rehfeldt F, Sen S, Discher DE. Microtissue elasticity: measurements by atomic force microscopy and its influence on cell differentiation. vol. 83. Academic Press; 2007. pp. 521–545. [DOI] [PubMed] [Google Scholar]
- [47].Otsu N. Threshold selection method from gray-level histogrames. IEEE Transactions on Systems Man and Cybernetics. 1979;9:62–66. [Google Scholar]
- [48].Storm C, Pastore JJ, MacKintosh FC, Lubensky TC, Janmey PA. Nonlinear elasticity in biological gels. Nature. 2005;435:191–194. doi: 10.1038/nature03521. [DOI] [PubMed] [Google Scholar]
- [49].Gardel ML, et al. Prestressed f-actin networks cross-linked by hinged filamins replicate mechanical properties of cells. Proc. Natl. Acad. Sci. 2006;103:1762–1767. doi: 10.1073/pnas.0504777103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Koenderink GH, et al. An active biopolymer network controlled by molecular motors. Proc. Natl. Acad. Sci. 2009;106:15192–15197. doi: 10.1073/pnas.0903974106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].This neglects non-linear and anisotropic elastic effects that become more important as the force exerted by the cell increases and prominent stress-fibers fill the cytoskeleton [48–50].
- [52].An additional, isotropic term, ηsδij, arising from cell spreading can be included but this merely renormalizes the value of p0 and can be eliminated.
- [53].We note that this calculation overrides the dynamics of cell spreading and the accompanying shape change with time. Rather, for any given cell shape, and stress, , that would develop in an infinitely rigid matrix, we calculate the corresponding elastic field that results in a compliant matrix with finite rigidity; in principle, our calculation holds for any instant of cell adhesion but this analysis goes beyond the scope of the present paper.
- [54].In 3D the function C is a ratio of a 3-order polynomial to a 4-order polynomial