Probing Surface Charge Fluctuations with Solid-State Nanopores

Abstract

We identify a contribution to the ionic current noise spectrum in solid-state nanopores that exceeds all other noise sources in the frequency band 0.1–10 kHz. Experimental studies of the dependence of this excess noise on pH and electrolyte concentration indicate that the noise arises from surface charge fluctuations. A quantitative model based on surface functional group protonization predicts the observed behaviors and allows us to locally measure protonization reaction rates. This noise can be minimized by operating the nanopore at a deliberately chosen pH.

As nanodevices are increasingly used for single-molecule detection and manipulation in the time domain, their noise characteristics at kHz frequencies gain additional significance. In the case of protein nanopores, noise has elucidated both pore and analyte dynamics [1–3]; in solid-state nanopores to date, noise has simply interfered with detection of DNA and proteins [4–9]. Previous work has described a variety of noise sources in solid-state nanopores and typical measuring apparatus [10–12].

In this Letter, we identify a new source of current noise in solid-state nanopores that is dominant in the frequency range from 0.1–10 kHz. A simple analysis of the noise dependence on pH and the electrolyte ionic strength, based on a few general assumptions, suggests that the noise originates from surface charge fluctuations. Finally, we develop a quantitative model based on protonization of surface functional groups [1] and compare it to the experimental results. Our technique is sensitive to a few tens of active surface groups in the nanopore, allowing us to observe variations in local surface properties from nanopore to nanopore and to guide optimization of single-molecule detectors.

Nanopores were fabricated with a transmission electron microscope [13] in a thin film of low-stress, amorphous silicon nitride, resulting in single, roughly hourglass-shaped [14] channels ~55 nm long and ~4 nm in diameter at the smallest point. The silicon nitride film containing the nanopore separates two reservoirs of potassium chloride electrolyte in a sealed fluidic cell; current measurements were made between Ag/AgCl electrodes in each reservoir (Fig. 1). Noise measurements on different nanopores show the same general features and pH spectral shapes, while the sensitivity and local nature of the technique reveals sample-to-sample variability [15]. The noise sources we observe appear to be intrinsic to the silicon nitride nanopore surface and are not as variable as 1/f noise [12].

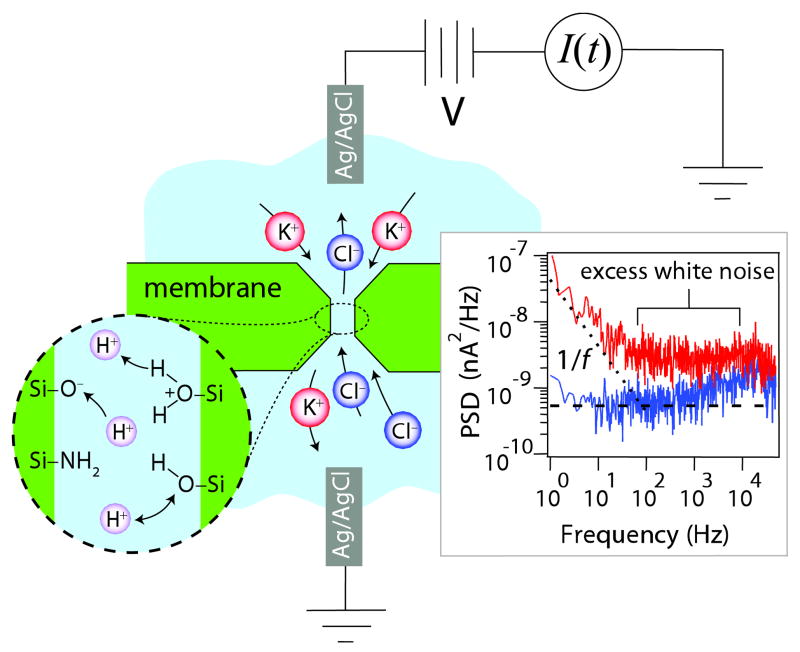
FIG. 1.

(color online). A nanopore is a narrow channel in a thin Si_3.5N₄ membrane. A current of electrolyte ions flows through the nanopore in response to an applied voltage. Detail: surface protonization reactions. Inset: Typical current noise spectra at 0 mV (lower trace) and 150 mV (upper trace) applied voltage at 1 M KCl and neutral pH.

The power spectral densities (PSDs) of typical current recordings (Fig. 1, inset) demonstrate various expected noise sources: with no applied voltage bias (lower spectrum), only thermal (Johnson) noise (thick dashed line) and high-frequency capacitive noise driven by the preamplifier input are present. With applied voltage bias across the nanopore device (upper spectrum), conductance fluctuations such as 1/f noise (dotted line) become apparent. We also observe the appearance of an additional frequency-independent (“white”) noise between 0.1 kHz and our RC filter cutoff at 20 kHz. In the inset to Fig. 2(b), this excess white noise, averaged over the 1–8 kHz band, is plotted as a function of mean nanopore current. The average noise (closed circles) scales with the square of the dc current, indicating that the excess white noise derives from a conductance fluctuation. For an Ohmic system of conductance G, flowing current I, the PSDs of the current fluctuations S_I and the conductance fluctuations S_G are related by S_I = (S_G/G²)I². The parabolic coefficient S_G/G² contains all the relevant physics of the intrinsic system fluctuations. A simple RC system of similar conductance and capacitance (500 MΩ, 33 pF) shows no excess white noise (open circles), demonstrating that the noise source is not the electronics or analysis used to obtain our results; likewise, a long capillary with Ag/AgCl electrodes of similar conductance and capacitance yields no excess white noise, indicating that the electrodes are also not a source of noise.

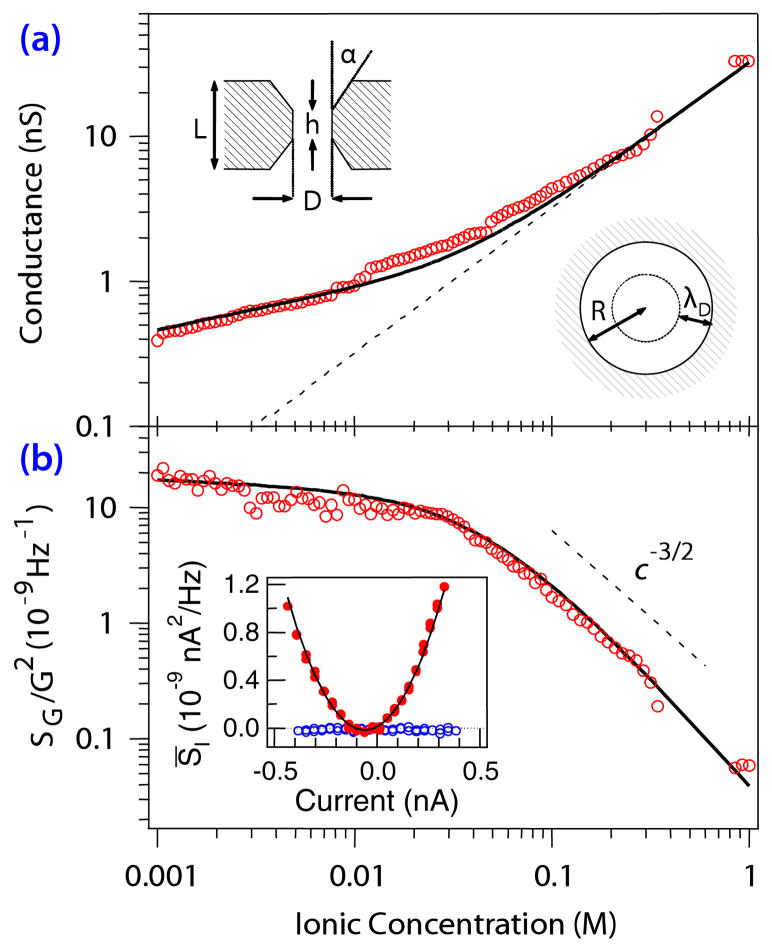
FIG. 2.

(color online). (a) Dependence of the ionic conductance through the nanopore on bulk electrolyte concentration (open circles), with a fit to the Poisson-Boltzmann model (solid line). Insets: (upper left) A schematic of the geometry [14] used for the Poisson-Boltzmann model, (lower right) The effect of surface fluctuations over the Debye length λ_D, predicting the c^−3/2 dependence of the noise level. (b) Conductance fluctuations vs bulk ionic concentration (open circles). The solid line is the fit, using the same parameters as in (a), to the charge fluctuation model outlined in the text. Inset: Parabolic dependence of the frequency-averaged PSD of S_I (closed circles) on current, with fit (solid line).

To determine the physical source of the excess white noise, we measured the PSD as a function both of electrolyte concentration [Fig. 2(b)] near neutral pH, and of pH [Fig. 3(b)] at constant ionic strength (110 mM unbuffered KCl), using a fluidic cell capable of preparing gradient concentration flows and an in situ pH-sensitive half-cell [15]. For each point, full I-V and S_I-V curves were collected; the conductance is determined from the slope of the I-V curve at zero bias, while the conductance fluctuation S_G/G² is determined from the parabolic fit of the excess white noise vs the current [Fig. 2(b), inset].

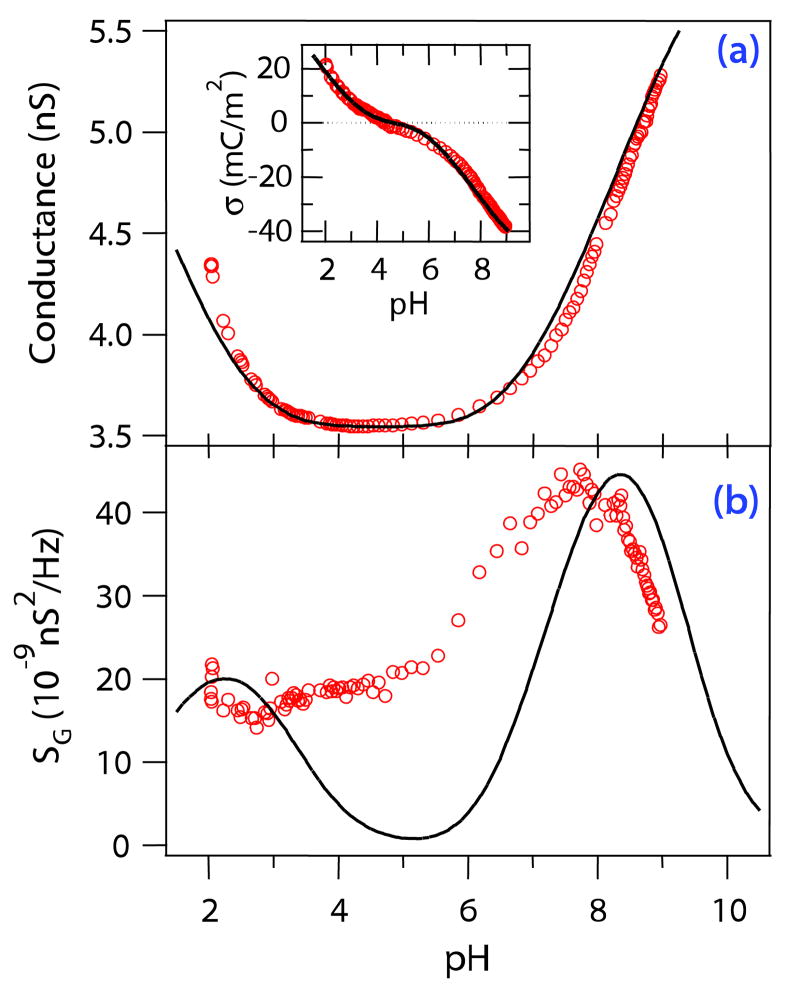
FIG. 3.

(color online). (a) Measured conductance (open circles) vs pH at constant 110 mM ionic strength. The minimum at pH ~ 4.1 corresponds to the point of zero charge. The solid line represents the predicted conductance from a fluctuating 3-level system. Inset: Surface charge as induced from the data (open circles) and as predicted by the model (solid line). (b) Experimental noise spectral density (open circles) vs pH. The solid line is a fit to the charge fluctuation model presented in the text. Both curves are modeled by the same set of parameters that was used to fit the variable electrolyte concentration data (see Fig. 2).

There are two distinct regimes of the noise as a function of electrolyte concentration c [Fig. 2(b)]. At high concentrations, the noise varies as c^−3/2 (dotted line), while the conductance is proportional to c [Fig. 2(a), dashed line]. Below about 100 mM KCl, both the noise and the conductance deviate strongly from their high-c behavior. This effect can be understood by considering Debye screening in the context of fluctuating surface charges on the walls of the nanopore, which for simplicity we assume to be cylindrical. For high electrolyte concentrations, the Debye screening length (λ_D ~ c^−1/2) is smaller than the radius of the nanopore R_p. When λ_D ≪ R_p, the number of charge carriers affected by the fluctuating charges [Fig. 2(a), inset] is given by

$$c·A_{\text{ring}}=c\pi (2{\lambda }_D{R}_p-{\lambda }_D^2)\sim c{\lambda }_D\sim c^{1/2}.$$ (1)

Conductance is proportional to the concentration in this regime, so S_G/G² ~ c^−3/2.

At low concentrations, the Debye length becomes comparable to or larger than the radius of the nanopore, and ions in the entire cross section of the nanopore are affected by the fluctuations of the electric field originating from the surface charge. In the simplest approximation, the local ion concentration—and hence the conductance—should be independent of the bulk concentration and proportional to the surface charge required to maintain charge neutrality inside the nanopore. Because the surface charge itself slightly decreases with electrolyte dilution, the concentration dependence of the noise is bounded between the limit of constant surface charge (S_G = const, G = const) and the limit of no surface charge effects (S_G ~ c, G ~ c). To summarize,

$${(S_G/G^2)}_{\text{surface}}\sim \{\begin{array}{ll}{c}^{-3/2}\hfill & \text{for}{\lambda }_D\ll R_p\hfill \\ c^{-\gamma },0\le \gamma <1\hfill & {\lambda }_D\gtrsim R_p\hfill \end{array}.$$ (2)

Despite the simplicity of our model, it agrees very well with the experimental results in Fig. 2(b). For the high-concentration regime, we also note that for geometric fluctuations at the surface (such as those postulated for polymer nanopores [16]), and for volume fluctuations (as suggested by the Hooge relation for 1/f noise [17]), S_G would scale with c, so S_G/G² ~ c⁻¹. Only for surface-bound electrical potential fluctuations does the normalized PSD scale as c^−3/2.

Excess white noise varies with pH [Fig. 3(b)]. The noise peaks at pH 7.5 with a long tail extending to pH 2. The conductance has minimum at pH 4.1, but there is no obvious correspondence between the noise and conductance curves. A noise level peak similar to that depicted in Fig. 3(b) has been observed in single OmpF channels [3]. Bezrukov and Kasianowicz, working with α-hemolysin protein ion channels [1], attribute the peak to protonization reactions of individual protein residues in the ion channel and calculate the number of ionizable residues and the reaction kinetics of the protein channel.

The silicon nitride surface consists of a large fraction of amphoteric silicon oxide groups [18,19], which are known to be active in the experimentally accessible pH range. The minimum of the conductance corresponds to the pH at which the densities of positive and negative surface groups are equal, the so-called point of zero charge. At low or high pHs, respectively, either positive or negative surface groups dominate, increasing the local concentration of charge carriers and hence the total conductance. The relevant reactions are

$${\text{SiO}}^{-}+{\text{H}}^{+}\underset{k_D}{\overset{k_R}{\rightleftarrows }}\text{SiOH}$$ (3)

$$\text{SiOH}+{\text{H}}^{+}\underset{l_D}{\overset{l_R}{\rightleftarrows }}{\text{SiOH}}_{\text{2}}^{+}.$$ (4)

The equilibrium constants of these reactions are defined by

$$\begin{array}{l}K\equiv k_D/k_R=\frac{N_{{\text{SiO}}^{-}}{[{\text{H}}^{+}]}_0}{N_{\text{SiOH}}}\equiv {10}^{-pK}\\ L\equiv l_D/l_R=\frac{N_{\text{SiOH}}{[{\text{H}}^{+}]}_0}{N_{{\text{SiOH}}_{\text{2}}^{+}}}\equiv {10}^{-pL}\end{array}$$ (5)

where [H⁺]₀ is the hydrogen ion activity at the surface and N_i is the density of surface sites in state i. The hydrogen ion activity at the surface is related to the bulk pH by [H⁺]₀ = [H⁺]_bulk exp(−β e ψ₀), where [H⁺]_bulk = 10^−pH, ψ₀ is the electrical potential at the nanopore surface, β = (kT)⁻¹ is the thermodynamic factor, and e is the unit of elementary charge, and β e ψ₀ is the energy cost for a positively charged ion to approach a charged surface. For example, if the surface has a net negative surface charge, hydrogen ions are attracted to the nanopore walls, resulting in a lower local pH. Combining the above expressions with Eq. (5), and taking Γ = ΣN_i to be the total surface density of active sites and σ to be the surface charge density, we obtain a generalized form of the Behrens-Grier equation [20]:

$$\begin{array}{l}{10}^{pL-p\text{H}}(\sigma -e\mathrm{\Gamma })exp(-2\beta e{\psi }_0)\\ +\sigma exp(-\beta e{\psi }_0)+{10}^{p\text{H}-pK}(\sigma -e\mathrm{\Gamma })=0.\end{array}$$ (6)

The basic Stern model relates the potential at the nanopore surface to the potential at the double layer, ψ_D, by the Stern capacitance C_s, which captures the dielectric properties and effective thickness of the water-solid interface: ψ₀ − ψ_D = σ/C_s. Finally, the surface charge as a function of double layer potential is approximated by the Grahame equation [21]:

$$\sigma ({\psi }_D)=\frac{2\epsilon {\epsilon }_0}{\beta e{\lambda }_D}sinh\left(\frac{\beta e{\psi }_D}{2}\right).$$ (7)

Solving Eqs. (6) and (7) self-consistently, we obtain σ and the surface density of each species N_i as a function of pH, electrolyte concentration, and the four chemical parameters Γ, C_s, pK, and pL. A plot of σ vs pH is given in the inset to Fig. 3(a).

To model the conductance data in Figs. 2(a) and 3(a), we calculate G(σ) from the numerical solution of the Poisson-Boltzmann equation in a cylindrically symmetric hourglass geometry. Access resistance is small enough to be subsumed into the geometric parameters of the nanopore. A thorough investigation of the conductance of the nanopore is beyond the scope of this Letter and will be published elsewhere.

The set of coupled chemical reactions 3 and 4 define a 3-level protonization system. To calculate the spectral density, we note that L ≪ K, allowing us to decouple these reactions into two independent 2-level systems defined by the individual reactions. The contribution to the spectral density from each chemical reaction is calculated by combining the solution to the Kolmogorov equations for a discrete 2-level Markov system [1,22,23] with the chemical equilibrium and surface proton activity Eqs. (3)–(7), yielding the expression

$$S_G^{(\alpha )}(p\text{H},c)=S_0\frac{{10}^{p{K}_{\alpha }-p\text{H}}exp(-\beta e{\psi }_0)}{{[1+{10}^{p{K}_{\alpha }-p\text{H}}exp(-\beta e{\psi }_0)]}^3}.$$ (8)

This is a generalization of the Bezrukov-Kasianowicz equation for protonization noise in protein channels [1]. The additional surface potential factor ψ₀(pH, c) combines contributions from all species and is responsible for the dependence of the noise on ionic strength.

The solid curves in Figs. 2 and 3 are calculated using geometric parameters (determined from conductance measurements and transmission electron microscope imaging) R_p = 3.3 nm, L = 54 nm, h = 7 nm, and α = 30°, and the chemical parameters pL = 2.7, pK = 6.6, C_s = 0.7 F/m², and Γ = 0.4 nm⁻², corresponding to ~150 protonizable surface sites in the cylindrical region of the nanopore. The chemical parameters are consistent with those cited in the literature for SiO₂ surfaces (see [24] and references within).

We note an excellent general correspondence between the experimental data and the theoretical dependence of measurables on electrolyte concentration. For the pH-dependence, the model correctly predicts the noise peak close to pK, with two discrepancies: the relative positions of peaks of experimental and modeled data are shifted by ΔpH ≈ 0.5, and we cannot account for the increased experimental noise level between pH ~ 4 and pH ~ 6. These deviations could have various origins. The basic Stern model may not be sophisticated enough to explain the details of the S_G(pH) curve: additional effects, such as incorporation of electrolyte ions into the Stern layer, or the high surface curvature in the nanopore, might be significant [25]. Additional contributions to the conductance fluctuations may interfere with the low-pH peak, particularly charge carrier number fluctuations [26]. It is also likely that the protonizable chemical sites have a distribution of equilibrium constants (pKs), due to variations in the local chemistry and the existence of species involving both N and O atoms, multiple Si atoms, and multiple O atoms. The conductance measurements with pH support this idea, as the two-peak model underestimates the conductance (and hence the surface charge) between pHs 4 and 6 and overestimates the conductance above pH 7.

Nanopore noise measurement is a sensitive local probe, not only for surface composition, but also for surface charge fluctuations at time scales much shorter than the electronic measurement bandwidth. The chemical dynamics information is contained in the normalization factor [1] of Eq. (8), $S_0^{(K)}=4{\sum }_i{(\mathrm{\Delta }{g}_i)}^2{k}_D^{-1}\simeq 4{(\mathrm{\Delta }G)}^2{N}^{-1}{k}_D^{-1}$, where Δg_i is the fractional change of conductance due to protonization of an individual chemical site i, N is the total number of protonizable sites, and ΔG is the maximum enhancement of the ionic conductance due to the surface reactions 3 and 4. Using the geometric and chemical parameters of the nanopore, we obtain reaction parameters k_D = 1.8 × 10⁵ s⁻¹ and k_R = 7 × 10¹¹ M⁻¹ s⁻¹ for reaction 3. The mean lifetime of the proton bonding in SiO-H, ${\tau }_{\text{SiOH}}=k_D^{-1}=5.6\mu \text{s}$, is comparable to, though smaller than, the proton binding lifetime in a protein channel [1], perhaps due to additional conformational changes induced in the protein upon protonization. Equivalently, we deduce reaction parameters for reaction 4: l_D > 3.9 × 10⁵ s⁻¹ and l_R > 2 × 10⁸ M⁻¹ s⁻¹. Because we cannot actually resolve this peak from the background, l_D and l_R must be interpreted as lower bounds on the low-pH reaction kinetics.

Practically, surface charge fluctuations will decrease the signal to noise ratio of nanopore biosensing devices. Our experiments demonstrate that there are large, predictable variations in excess white noise over broad pH ranges. The results suggest that the nanopores can be used as a sensitive local probe of detailed surface dynamics and chemistry: to establish such a technique, experimental evaluations of multiple films and conditions will be performed. This study establishes the importance of mitigating interference from protonization noise by the selection of appropriate surface materials and operating conditions for dynamic nanoscale devices.