Steric, Quantum, and Electrostatic Effects on S_N2 Reaction Barriers in Gas Phase

Abstract

Biomolecular nucleophilic substitution reactions, S_N2, are fundamental and commonplace in chemistry. It is the well documented experimental finding in the literature that vicinal substitution with bulkier groups near the reaction center significantly slows the reaction due to steric hindrance, but theoretical understanding in the quantitative manner about factors dictating the S_N2 reaction barrier height is still controversial. In this work, employing the new quantification approach that we recently proposed for the steric effect from the density functional theory framework, we investigate the relative contribution of three independent effects, steric, electrostatic, and quantum, to the S_N2 barrier heights in gas phase for substituted methyl halide systems, R₁R₂R₃CX, reacting with fluorine anion where R₁, R₂, and R₃ denote substituting groups and X=F or Cl. We found that in accordance with the experimental finding, for these systems the steric effect dominates the transition state barrier, contributing positively to barrier heights, but this contribution is largely compensated by the negative, stabilizing contribution from the quantum effect due to the exchange-correlation interactions. Moreover, we find that it is the component from the electrostatic effect that is linearly correlated with the S_N2 barrier height for the systems investigated in the present study. In addition, we compared our approach with the conventional method of energy decomposition in density functional theory, as well as examined the steric effect from the wavefunction theory for these systems via the natural bond orbital analysis.

I. Introduction

The biomolecular nucleophilic substitution, S_N2, is one of the most common and best understood reactions in chemistry.¹ It occurs at an aliphatic sp³ carbon center with an electronegative leaving group directly attached. The nucleophile enters on the opposite side of the carbon to the leaving group, leading to a trigonal bipyramidal transition state. The breaking of the carbon – leaving group bond and the formation of the new carbon – nucleophile bond occur simultaneously, so the reaction is second order overall, involving both leaving and entering groups in the slow and rate-determining step. Many factors have been found to affect the S_N2 reaction rate, such as the basicity of the leaving group, the size of the nucleophile, the polarity of the solvent, etc. ^2-5

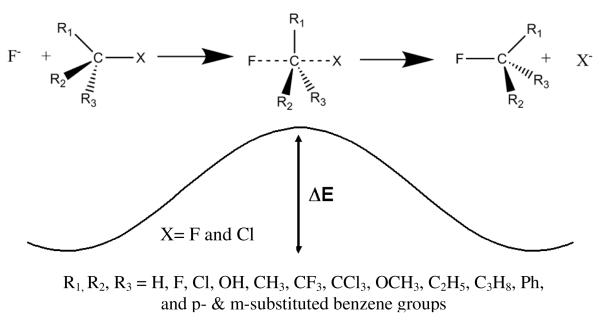
The steric effect from substituents of the carbon at the reaction center has been a well-known factor that considerably influences the S_N2 reaction rate in solutions.^2-9 Originated from the steric hindrance, bulkier substituents for R₁, R₂, or R₃ groups in Scheme 1 significantly slows the reaction because larger groups effectively block the backside approach of the incoming nucleophile. Experimental data in the gas phase are limited but available data indicate the same ordering as in solution.^10-15 Much has been devoted to understand steric hindrance of these reactions earlier,^16,17 but it is still of considerable research interest in the recent literature.^18,19 One of the reasons for the continuous investigation and controversy about them in our opinion is that no better approach to quantify steric effect has been available until very recently.

Scheme 1.

The steric effect is one of the most widely used concepts in chemistry. It originates from the fact that each atom in a molecule occupies a certain amount of space. When atoms are brought together, hindrance will be induced at the expense of shape, energy, reactivity, etc. Weisskopf²⁰ originally attributed the steric effect to the “kinetic energy pressure”. Since no physically observable variable is associated with the steric effect, quantum mechanically speaking, there is no unique way to define it. Two approaches of quantifying steric effect are available in the literature thus far, one from the wavefunction theory ²¹ and the other from density functional theory (DFT).²²

The wavefunction approach of quantifying the steric effect employs the Pauli Exclusion Principle. When two electrons are parallel in spin, the Principle dictates that they move apart, thus occupying more space and yielding larger steric effect than when the spins are anti-parallel. One problem with this quantification is that no dynamic electron correlation effect is included so this definition cannot be extended to post Hartree-Fock methods such as MP2 and coupled-cluster methods. The dynamic correlation between anti-parallel spin electrons is also repulsive, and thus contributes to the steric effect as well. Another concern is that the kinetic energy contribution from the Pauli Exclusion Principle is not included either.^23-27 Also, it is well known that for the kinetic energy, there is not only an exchange component, termed the Pauli energy, but also a dynamic correlation ingredient, T_c.^28-34 In addition, there is no distinction between quantum and pure steric effects with the present wavefunction approach of steric effect description.

Recently, we proposed a new approach of quantifying the steric effect from DFT.²² Assuming that the total energy comes from the independent contribution of three effects, steric, quantum and electrostatic, we have established that the energy component from the steric effect is precisely defined by the Weizsäcker kinetic energy.³⁵ Physically, it represents the minimal space of a hypothetical state occupied by the electrons when all of them are placed in the lowest orbital. Several appealing properties have been disclosed such as exclusiveness, repulsiveness and extensiveness. It is consistent with Weisskopf’s attribution that the steric effect is kinetic in nature. It is extendable to any level of theory besides DFT, because only the electron density and its gradient are needed to compute the quantity. More importantly, our approach can be extended to atomic and functional group concepts if Bader’s atoms-in-molecules (AIM) approach ³⁶ is adopted. Then, atoms attain balanced steric repulsion by sharing a zero steric repulsion interface when they form a molecule. We have applied this new quantification to understand molecular conformation changes,^37-41 and also compared this new theoretical scale with the experimental scale of steric effect by Taft⁴² with reasonable agreement between the two observed.⁴³

In this work, we apply our scheme of energy decomposition to S_N2 reactions in gas phase in order to unravel different energy contributions, steric, electrostatic, and quantum, to their reaction barrier height. We find that in most cases steric effect is indeed the dominant factor, contributing positively to the energy difference between the transition state and reactants, but its contribution is largely compensated by the negative, stabilizing contribution from the quantum effect, with the correlation coefficient R² between the two larger than 0.99. It is the contribution from the electrostatic effect that is found to be linearly proportional to the barrier height of S_N2 reactions investigated in this study. The correlation coefficient R² is 0.95. Comparisons of our scheme with other approaches, the steric effect description from the wavefunction theory using the Pauli Exclusion Principle and the conventional method of the total energy partition in DFT, have also been carried out.

II. Methods and Computations

In DFT,⁴⁴ the conventional energy difference ΔE between the transition state and reactants, is as follows^37-41

$$\Delta \mathrm{E}=\Delta {\mathrm{T}}_{\mathrm{s}}+\Delta {\mathrm{E}}_{\mathrm{e}}+\Delta {\mathrm{E}}_{\mathrm{xc}},$$ (1)

where T_S, E_e and E_xc are the non-interacting kinetic, the electrostatic, and the exchange-correlation energy density functionals, respectively, and

$$\Delta {\mathrm{E}}_{\mathrm{e}}=\Delta {\mathrm{V}}_{\mathrm{ne}}+\Delta \mathrm{J}+\Delta {\mathrm{V}}_{\mathrm{nn}}$$ (2)

with V_ne, J, and V_nn defining the nuclear-electron attraction, classical electron-electron Coulomb repulsion, and nuclear-nuclear repulsion energies, respectively.

In the new energy decomposition scheme,^22,45 we assume that the energy difference comes solely from three independent effects, steric, electrostatic, and quantum (due to the exchange-correlation interaction),

$$\Delta \mathrm{E}\equiv \Delta {\mathrm{E}}_{\mathrm{s}}+\Delta {\mathrm{E}}_{\mathrm{e}}+\Delta {\mathrm{E}}_{\mathrm{q}}$$ (3)

where the steric contribution is found to be the Weizsäcker kinetic energy³⁵

$$E_s\equiv T_W=\frac{1}{8}\int \frac{{\mid \nabla \rho \left(\mathbf{r}\right)\mid }^2}{\rho \left(\mathbf{r}\right)}d\mathbf{r}$$ (4)

and the contribution from the quantum effect is the following

$${\mathrm{E}}_{\mathrm{q}}={\mathrm{E}}_{\mathrm{xc}}+{\mathrm{E}}_{\text{Pauli}}={\mathrm{E}}_{\mathrm{xc}}+{\mathrm{T}}_{\mathrm{S}}\text{-}{\mathrm{T}}_{\mathrm{W}}.$$ (5)

The main difference between Eqs. (1) and (3) is the identification of the Pauli component in the kinetic energy,^23-27 E_Pauli ≡ T_S - T_W, which must be included as part of the contribution to the quantum effect.

The physical meaning of this description of steric effect in the framework of density functional theory is the introduction of a hypothetical reference state, where electrons are assumed to be Bosons. Physically, Eq. (4) represents the minimal space of the hypothetical state occupied by the electrons when all of them are placed in the lowest orbital. This picture is in contrast with the wavefunction quantification of the steric effect where the Pauli Exclusion Principle was employed, which applies only to the same-spin electrons to account for their static (exchange) correlation.

Two points need to be clarified about the quantum effect. First, because of the above reference state using bosons, it is more appropriate to call the quantum effect in Eq. (5) “fermionic effect” or “fermionic quantum effect”.⁴⁶ Secondly, the contribution from the quantum effect, E_q, is due to the exchange-correlation interactions among electrons. It is fundamentally different from Exc in Eq. (1) because E_q defined in Eq. (5) contains exchange-correlation energy contributions from the kinetic energy whereas Exc is purely a potential energy component.

From the information theory perspective, Eq. (4) is nothing but the Fisher information (without a multiplying factor 1/8).^38,40,46 The Fisher information is a measure of the narrowness or sharpness or heterogeneity of the density distribution. Equation (4) is then a measure of the compactness of the system and thus must have to do with the effect from the spacious viewpoint. Notice that the intrinsic relationship between Shannon entropy and Fisher information for atomic and molecular systems has recently been revealed by one of the authors.³⁸

In the present work, we consider the energy difference between the transition state and the reactant complex in the gas phase for 59 self-exchange S_N2 reactions of R₁R₂R₃C-F reacting with fluorine anion, where R₁, R₂, and R₃ represent substituting groups including H, F, Cl, OH, CH₃, CF₃, OCH₃, C₂H₅, C₃H₈, Ph, and para- and meta-substituted benzene groups (Scheme 1). The S_N2 reaction in the gas-phase is known to proceed via a pre-transition state association type of complex. We computed all energy differences in above equations with respect to this complex. To confirm what we have found for the self-exchanging S_N2 reaction, we also considered R₁R₂R₃C-Cl systems reacting with fluorine and the same number of central-carbon substitutions (Scheme 1). We represent these systems in terms of three substituted groups in the format of (R₁R₂R₃). The central purpose of this study is to understand the nature of S_N2 reaction barriers in terms of the three independent effects, steric, electrostatic and quantum, and with special focus on the impact of the steric effect to dictate the S_N2 reaction rate in a quantitative manner.

All calculations were performed at the DFT B3LYP/6-311+G(d) level of theory.⁴⁷ Calculations of the reactions paths were performed with Gaussian 03 package version E02⁴⁸ with tight SCF convergence and ultra fine integration grids. For transition-state structure searches, the quadratic synchronous transit approach⁴⁹ was employed and single-point frequency calculation was followed to ensure that the final structure obtained has only one imaginary frequency and that the vibration mode of the negative frequency corresponds to the bond formation that is anticipated. In addition, an intrinsic reaction coordinate⁵⁰ run was ensued to verify the relevance of transition-state structures. The new energy decomposition analysis has been implemented in the NWChem suite ⁵¹ of software at the same level of theory. NWChem Version 5.0 ⁵² as developed and distributed by Pacific Northwest National Laboratory, P. O. Box 999, Richland, Washington 99352 USA, and funded by the U. S. Department of Energy, was used. The single point calculation was also done at the DFT B3LYP/6-311+G(d) level of theory. We have shown earlier ³⁷ that the new energy decomposition scheme does not qualitatively depend on the choice of either basis set or density functionals. As a comparison, we also calculated the steric energy from the wavefunction theory using natural bond orbitals for all the systems. The NBOFILE keyword in NWChem was used to create an input file to be used as the input for the stand-alone natural bond orbital analysis code, NBO version 5.0. ⁵³ We term the result from this calculation as the NBO steric energy thereafter with the difference denoted by ΔNBOSteric.

III. Results and Discussion

Table 1 shows the results from the two energy decomposition analyses, Eqs. (1) and (3), together with the steric energy difference result from the wavefunction theory for the 59 self-exchange S_N2 reactions of substituted methyl halide systems, R₁R₂R₃CX, with F⁻ and R₁, R₂, and R₃ = H, F, Cl, OH, CH₃, CF₃, OCH₃, C₂H₅, C₃H₈, Ph, and para- and meta-substituted benzene groups. Gas-phase S_N2 barrier height data from both computational and experimental studies have been reported elsewhere. ^14,16,54-56 For example, for CH₃F (i.e., the HHH species in Table 1), the experimental value of the barrier height in enthalpy difference is about 13.3 kcal/mol, ¹⁴ our results are 9.22 kcal/mol in energy difference and 13.8 kcal/mol in enthalpy difference, indicating that our results are in general in reasonable agreement with the experimental data. Nevertheless, we notice that earlier studies have shown that to accurately reproduce the experimental data, high-level computational approaches at the G2, G3, or even higher level of theory are required.^52-54 Since the main purpose of this work is to qualitatively understand the nature of the barrier height in terms of energy decomposition schemes, the high accuracy and agreement with experimental data are not our major concern in this work.

Table 1.

S_N2 energy barrier heights for 59 systems investigated in this study together with their energy decomposition analyses based on Eqs. (1) and (3). For the comparison purpose, the steric energy difference from the NBO analysis is also tabulated for the systems. Units are in kcal/mol.

Models (R1R2R3)	ΔE	ΔEs	ΔEq	ΔEe	ΔTs	ΔExc	Δ(NBOSteric)
HHH	9.22	89.40	−93.73	13.56	−22.84	18.50	−30.17
CH3HH	14.67	122.83	−130.24	22.08	−27.92	20.51	−15.58
CH3CH3H	19.66	145.01	−155.68	30.33	−35.80	25.12	−17.15
CH3CH3CH3	27.13	148.69	−161.12	39.55	−40.53	28.10	−7.15
PhCH3CH3	29.42	158.89	−168.47	39.00	−38.99	29.41	−27.96
C2H5C2H5C2H5	24.90	126.99	−136.16	34.06	−37.23	28.07	−0.92
C2H5C2H5CH3	25.52	134.71	−144.12	34.92	−37.98	28.57	−11.23
C2H5CH3CH3	26.21	139.65	−150.60	37.15	−39.22	28.27	−9.40
PhPhCH3	30.75	154.87	−166.14	42.03	−42.89	31.62	−23.87
PhPhPh	24.48	150.45	−160.59	34.62	−43.22	33.08	−52.53
PhCH3H	21.66	170.70	−178.00	28.96	−34.16	26.87	−27.65
PhHH	16.36	161.63	−170.21	24.93	−32.82	24.25	−10.39
C2H5HH	13.79	118.08	−125.34	21.05	−27.67	20.41	2.60
C3H8C2H5C2H5	24.84	126.33	−135.31	33.82	−37.06	28.08	−1.67
C3H8C3H8C2H5	26.80	108.45	−119.76	38.11	−39.46	28.15	−4.42
C3H8C3H8C3H8	26.69	106.40	−118.04	38.33	−39.70	28.06	−6.39
CCl3HH	18.98	9.08	−8.21	18.11	−18.11	18.99	5.13
CF3CH3H	20.93	90.78	−99.76	29.91	−32.06	23.08	−42.65
CF3HH	17.28	89.53	−98.54	26.29	−27.97	18.96	−28.41
ClClCl	13.05	−5.54	0.12	18.47	−31.60	26.18	−93.70
ClClH	32.43	32.34	−55.72	55.81	−36.52	13.14	−44.86
ClHH	20.40	85.25	−97.26	32.41	−29.52	17.51	−32.41
FClCl	13.31	−20.49	14.76	19.04	−29.09	23.36	−98.20
FFCl	14.19	−41.23	32.61	22.81	−28.13	19.50	−97.11
FFF	15.94	−61.09	49.61	27.43	−27.12	15.64	−64.78
FFH	28.80	14.14	−34.51	49.18	−37.73	17.35	−19.86
FHH	17.15	70.32	−80.97	27.80	−29.37	18.72	−13.49
OCH3FH	25.35	25.67	−42.07	41.76	−35.27	18.87	−7.90
OCH3HH	19.01	116.61	−127.03	29.43	−33.06	22.64	7.07
OHFF	74.78	49.10	−81.88	107.56	−62.89	30.12	−24.67
OHHH	38.98	231.56	−241.01	48.43	−34.06	24.60	39.86
OHOHH	34.38	127.41	−138.82	45.79	−25.27	13.85	22.60
p-Ph(CCH)CH3H	20.87	168.74	−175.35	27.48	−33.14	26.52	−25.42
p-Ph(CCH)HH	8.32	98.10	−99.58	9.79	−18.41	16.94	−6.23
p-Ph(CH3)CH3H	21.73	171.60	−179.70	29.82	−35.09	26.99	−25.89
p-Ph(CH3)HH	16.47	162.07	−170.01	24.41	−32.12	24.17	−10.33
p-Ph(CN)CH3H	20.33	166.21	−172.50	26.62	−31.90	25.61	−24.90
p-Ph(CN)HH	8.87	114.41	−114.39	8.85	−16.81	16.83	−0.85
p-Ph(Cl)CH3H	21.82	169.25	−177.44	30.00	−34.16	25.97	−25.35
p-Ph(Cl)HH	16.61	162.14	−171.20	25.67	−32.47	23.40	−9.33
p-Ph(F)CH3H	22.06	171.41	−179.11	29.77	−34.20	26.50	−26.78
p-Ph(F)HH	16.81	160.44	−169.92	26.29	−33.24	23.76	−8.50
p-Ph(NH2)CH3H	22.51	179.26	−186.69	29.94	−34.92	27.49	−22.16
p-Ph(NH2)HH	17.18	161.93	−170.73	25.98	−32.96	24.16	−1.00
p-Ph(NO2)CH3H	19.31	161.15	−168.39	26.55	−32.01	24.77	−32.81
p-Ph(NO2)HH	1.53	39.39	−33.55	−4.30	5.38	0.45	26.40
p-Ph(OCH3)CH3H	23.83	213.73	−218.29	28.39	−34.90	30.34	−28.18
p-Ph(OCH3)HH	18.58	198.18	−204.76	25.16	−33.66	27.09	−3.51
p-Ph(OH)CH3H	22.96	177.50	−185.49	30.95	−35.41	27.42	−20.94
p-Ph(OH)HH	17.69	160.60	−170.22	27.31	−33.71	24.09	−8.68
m-Ph(CCH)HH	16.69	162.38	−171.31	25.63	−33.24	24.30	−5.73
m-Ph(CH3)HH	16.72	162.60	−171.73	25.85	−33.43	24.30	−7.66
m-Ph(CN)HH	16.57	163.93	−172.32	24.96	−32.48	24.09	−12.21
m-Ph(Cl)HH	16.36	161.20	−170.71	25.86	−33.57	24.07	−11.04
m-Ph(F)HH	16.21	162.07	−170.57	24.70	−32.44	23.94	−12.59
m-Ph(NH2)HH	29.37	247.74	−256.66	38.29	−35.94	27.02	10.45
m-Ph(NO2)HH	16.69	162.80	−172.22	26.11	−33.79	24.37	−9.59
m-Ph(OCH3)HH	20.07	176.82	−187.73	30.99	−36.02	25.11	−0.32
m-Ph(OH)HH	16.52	162.71	−171.26	25.07	−32.69	24.14	−12.11

From the Table, it is seen that (i) the S_N2 reaction barrier height, defined as the energy difference between the reactant complex and the transition state (Scheme 1), is always positive, ranging from 1.53 kcal/mol for p-Ph(NO₂)HH to 74.78 kcal/mol for OHFF; and (ii) the steric energy difference ΔE_s is positive in almost all cases (except ClClCl, FClCl and ClFF systems) indicating that steric effect generally contributes positively to the barrier height. That is, the larger the steric effect, the higher the S_N2 reaction barrier, and thus the slower the chemical reaction, consistent with the experimental finding. Moreover, looking at the general trend of the energy difference from three effects, steric ΔE_s, electrostatic ΔE_e and quantum ΔE_q, we find that ΔE_q is generally negative, contributing in stabilizing the transition state of S_N2 reactions. The quantity of ΔE_e is positive but much less than ΔE_s in magnitude, suggesting that in most cases the steric effect ΔE_s is the dominant factor controlling the barrier height.

As examples, let us look at the first five systems in Table 1. When R₁ changes from the hydrogen atom to the spaciously larger, methyl group with R₂ and R₃ fixed to H, the steric energy contribution increases from 89.40 to 122.83 kcal/mol. When R₂ and R₃ are subsequently altered also to the methyl group, ΔE_s keeps increasing to 145.01 and then to 148.69 kcal/mol, respectively. Notice that the amount of each steric hindrance increase from one methyl group to two to three methyl groups, 33.4, 22.2, 3.7 kcal/mol, respectively, is quickly decreased. This is because the vicinal substituted methyl groups rapidly occupy all available space near the reaction center, leading to that the steric hindrance becomes saturated. Furthermore, when one of the three methyl groups is replaced by a bulkier benzene group, the steric energy contribution gets even larger, becoming 158.89 kcal/mol. These results exhibit that not only the steric effect is the dominant factor of the S_N2 barrier, but it is also proportional the barrier height in some cases. For these five systems, the correlation coefficient R² between ΔE_s and ΔE is 0.88.

This relationship between ΔE_s and ΔE however is not universal, as is witnessed by many examples in the Table. For instance, from CH₃CH₃CH₃ to C₂H₅C₂H₅C₂H₅, both ΔE_s and ΔE are decreased, so are the differences from PhCH₃CH₃ to PhPhPh. Again, the same as for the above methyl substitution case, this is because the bulkier groups quickly occupied all available spaces around the reaction center and thus the repulsion due to the steric hindrance promptly becomes saturated. Even though in almost all cases ΔE_s is positive and dominantly contributes to ΔE, the overall correlation between ΔE_s and ΔE for all data points in Table 1 is statistically insignificant.

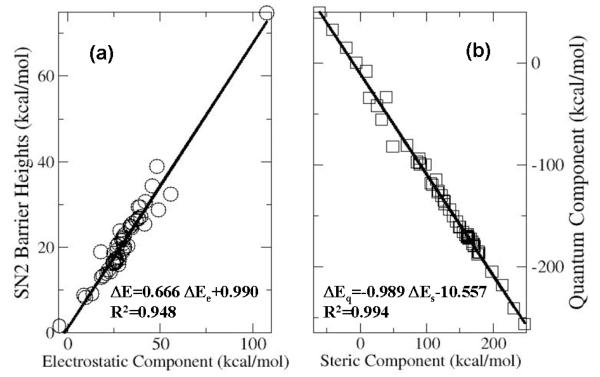
In contrast, we find that there exists a strong linear relationship between the barrier height ΔE and the electrostatic energy difference ΔE_e, as shown in Fig. 1a, with the correlation coefficient R² equal to 0.95. Removing the point with the largest barrier height (OHFF) does not change the fitting statistics. Also shown in Fig. 1 is the even stronger correlation between ΔE_s and ΔE_q, Fig. 1b, with R² = 0.99 for the 59 data points in Table 1. Notice that though much smaller in magnitude than ΔE_s, ΔE_e is positive as well in most cases in the Table, except p-Ph(NO₂)HH, and thus also contributes positively to the barrier height in S_N2 reactions. Taken together, these results suggest that (i) the steric effect dominates the S_N2 reaction barrier height; (ii) steric and quantum effects are mutually compensated; and (iii) it is the electrostatic effect that is linearly correlated with the barrier height.

Figure 1.

Strong linear correlations (a) between the transition state barrier height ΔE and the total electrostatic energy difference ΔE_e and (b) between the steric energy difference ΔE_s and the quantum energy difference ΔE_q for the S_N2 reactions of CR₁R₂R₃F with fluorine anion and 59 substituted groups investigated in this study. See discussion in detail in the text.

The above strong correlation between the two components, ΔE_s and ΔE_q, in Eq. (3) is seemingly in contradiction with the assumption that they represent the contribution from independent physiochemical, steric and quantum, effects. This is not the case. First, the relationship exists only at the solution point, not universal in general. If the two quantities, defined separately in Eqs. (4) and (5), were intrinsically related, the much harder quantum contribution E_q in Eq. (5) involving two most difficult quantities in DFT, non-interacting kinetic energy density functional T_S and exchange-correlation energy density functional E_xc, would then have a much simpler explicit solution from Eq. (4). Secondly, similar correlations such as viral theorems also exist in the solution point for other quantities. Thirdly, although this relationship existed for some of the systems in our early work on conformational changes, ³⁹ it was not observed in others cases. More importantly, we found that the correlation between E_s and E_q before the difference between the reactant and S_N2 transition state is taken is much less statistically significant. For both reactants and transition state of the R₁R₂R₃C-F system, the correlation coefficient R² between E_s and E_q is only 0.71, whereas R² of the difference correlation, ΔE_s vs. ΔE_q, between the two systems is 0.99. Based on these arguments, we conclude that the strong correlation between ΔE_s and ΔE_q is not universal.

The quantity ΔE_e is also included in Eq. (1), the conventional energy decomposition scheme in DFT. ^44,57,58 Does there exist any correlation between ΔT_S and ΔE_xc as well? The answer is no, based on the data in Table 1. Also, the last column of the Table tabulates the steric energy Δ(NBOSteric) computed from the wavefunction approach where the Pauli Exclusion Principle is employed as a measure of the steric repulsion. From the Table, it is seen that in almost all cases (except C₂H₅HH, CCl₃HH, OCH₃HH, OHHH, OHOHH and m-Ph(NH₂)HH systems), its contribution to the S_N2 barrier is negative, meaning that the steric description from the wavefunction theory gives that the larger the vicinal substituted group, the smaller the barrier height, which is in apparent contradiction with the well-documented experimental findings. In addition, no statistically significant correlation between Δ(NBOSteric) and other quantities in Table 1 has been observed.

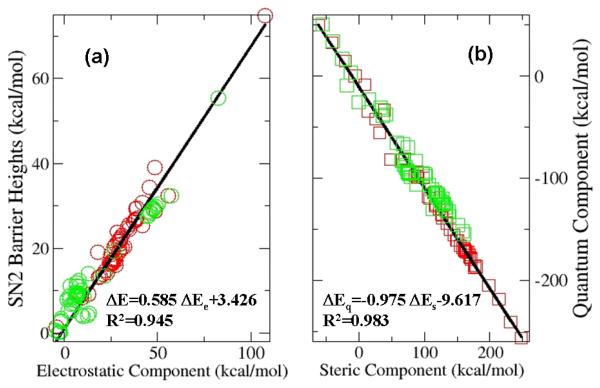
To confirm our findings from the self-exchange S_N2 reaction for R₁R₂R₃C-F and exclude the possibility that these results are not generally applicable, we then considered the S_N2 reaction of R₁R₂R₃C-Cl with fluorine anion and the same number of substitutions. Part of the results (in green color) for these systems together with those (in red color) from R₁R₂R₃C-F are shown in Fig. 2, where it is seen that these two kinds of systems give similar results and the least-square-fitting statistics of the two systems is similar in accuracy as well. Again, the contribution from the steric effect is dominant but largely compensated by the stabilizing contribution from the quantum effect. A strong correlation between the electrostatic effect and the barrier height is observed. No correlation between ΔT_S and ΔE_xc or between Δ(NBOSteric) and any other quantity is distinguished. One noticeable difference from the R₁R₂R₃C-F system is that there are more (62%) species within the R₁R₂R₃C-Cl system whose Δ(NBOSteric) values turned positive, indicating that for this system, the wavefunction quantification approach of the steric effect also predicts its positive contribution to the barrier height for a majority of the species considered in this study. In addition, the experimental barrier height in enthalpy of CH₃Cl is 2.9 kcal/mol ¹⁴, much smaller than that of CH₃F, and our computational barrier height result in enthalpy for the CH₃Cl S_N2 reaction is 1.8 kcal/mol, in reasonable agreement with the experimental data.

Figure 2.

Strong linear correlations (a) between the transition state barrier height ΔE and the total electrostatic energy difference ΔE_e and (b) between the steric energy difference ΔE_s and the quantum energy difference ΔE_q for S_N2 reactions of 59 substituted CR₁R₂R₃F (red color) and CR₁R₂R₃Cl (green color) systems reacting with fluorine anion investigated in this study. See discussion in detail in the text.

Finally, we mention in passing that we have also considered possible correlations of the S_N2 barrier heights for these systems with structural and electronic properties on the reaction center as well as other theoretical quantities from DFT or conceptual DFT frameworks such as changes in bond lengths, NBO charges, molecular electrostatic potential,^59,60 natural atomic bond energies, chemical potential, hardness, electrophilicity, etc.^44,45 No statistically significant correlation of the S_N2 barrier height with any of these examined quantities has been identified for the entire data set of these species. In addition, to determine the main atomic or functional group interactions that contribute to the quantities shown in Figs. 1 and 2, that is, to find out which atom or group contributes most to the total and component energy differences and whether or not it is the interaction between the nucleophile and the carbon atom on which the leaving group is attached, we will make use of the steric energy partition scheme that we recently reported.⁴³ This and other works along the line will be investigated and presented elsewhere.

IV. Conclusions

The biomolecular nucleophilic substitution, S_N2, is one of the most common and best understood reactions in chemistry. Though the reaction is fundamentally important in chemistry, factors dictating its barrier height are still not quantitatively well understood. In this contribution, we employ the energy decomposition scheme that we recently proposed to investigate the relative contributions from three independent effects – steric, electrostatic and quantum – for 118 S_N2 reactions in gas phase. The present study becomes possible, because new insight into and quantification of the steric effect have recently been accomplished within the framework of density functional theory. We found that while the steric effect dominates the barrier height, in accordance with the well documented experimental findings in the literature, it is largely compensated by the opposing, stabilizing contribution from the quantum effect. Moreover, we found that it is the positively contribution from the electrostatic effect that is best correlated with the S_N2 barrier height for the two types of systems that we investigated in this study, R₁R₂R₃C-F and R₁R₂R₃C-Cl reacting with fluorine anion with R₁, R₂, and R₃ as substituting groups. Comparisons with the conventional approach of energy decomposition in density functional theory as well as with the quantitative description of the steric effect from the wavefunction theory have been carried out and discussed. This work offers new thoughts and insights to a fundamental class of chemical reactions and can similarly be applied to other categories of chemical reactions as well.