Some statistical properties of differencing schemes for baseline correction of sedimentation velocity data

Abstract

For the detailed analysis of sedimentation velocity data, the consideration of radial-dependent baseline offsets is indispensable. Two main approaches are data differencing (‘delta-c’ approach), and explicit inclusion of baseline parameters (‘direct boundary model’ of the raw data). The present work aims to clarify the relationships between the two approaches. To this end, a simple model problem is examined. We show that the explicit consideration of the baseline in the model is equivalent to a differencing scheme where from all data points their average value is subtracted. Pair-wise differencing in the ‘delta-c’ approach always results in higher parameter uncertainty. For equidistant time points, the increase is smallest when the reference points are taken at intervals of 1/3 or 2/3 of the total number of time points. If the difference data are misinterpreted to be statistically independent samples, errors in the calculation of the parameter uncertainties can occur. Contrary to claims in the literature, we observe there is no distinction in the approaches regarding their ‘model-dependence’: both approaches arise from the integral or differential form of same model, and both can and should provide explicit estimates of the baseline values in the original data space for optimal discrimination between macromolecular sedimentation models.

Introduction

In the last decade, sedimentation velocity analytical ultracentrifugation (SV) has made great progress in the level of detail that can be reliably extracted from the experiment through the mathematical data analysis. This has been exploited in many biophysical studies of macromolecular interactions and multi-protein complexes, fiber formation, macromolecular shapes and size-distributions, as well as applications in other fields, among them protein pharmaceuticals and nanoparticles. For reviews, see [1–3]. One key element of this progress was the development of techniques to account for the baseline profiles that are invariant with time and superimposed to the measured macromolecular sedimentation signals [4, 5] (often referred to as ‘TI noise’). For the Rayleigh interference optics, these baseline offsets are typically between 10 – 100 fold the magnitude of the statistical error of data acquisition, often similar in magnitude to the signal from the sedimenting macromolecular species of interest, and therefore essential to be accounted for. When using the absorbance optical system, the time-invariant profile is smaller but still usually of similar magnitude as the statistical noise [5]. With the pseudo-absorbance method [6], where data from samples in both centerpiece sectors can be recorded, data with similar noise structure as the interference optical data are obtained.

An efficient approach to address this problem directly was the time-derivative method g(s*) introduced by Stafford in 1992 [7]. Radial-dependent, time-invariant baseline profiles were eliminated by forming a time-difference Δc/Δt r,t^* (attributed to a particular effective time point t^* between t and t + Δt) serving as an approximation of the time-derivative dc/dt r,t. Numerically this involved the division of the even number of total scans N into two sets, and pair-wise subtraction according to Δc_j(r) = c_j(r) − c_(N/2)+j(r) with j = 1…N/2 [8]. This step is followed by averaging, rescaling, and transformation along s^* = ω²t^*−1 log r^*/m into to apparent sedimentation coefficient distributions g(s*) [8]. The elimination of time-invariant baseline offsets through differencing brought unprecedented sensitivity to SV analysis and was widely applied at the time. However, the differencing of time-points and the determination of the effective time t^* has non-trivial consequences for the resolution and accuracy of the dc/dt method, and ultimately causes significant limitations in the total number of scans that can be included in the analysis [9–11], thus not fully exploiting the experimental data and causing bias due to the pre-selection of scans [12]. However, such complications are absent, in principle, in the ‘delta-c’ approach where the same scheme for differencing of scans is used solely to remove the time-invariant baseline offsets from the data and similarly the model [13].

In 1999, a different approach to address the baseline problems in SV analysis was introduced that consists simply of the idea of accounting for all unknown baseline parameters rigorously by introducing the corresponding parameters explicitly as unknowns into the model [5]. Although there are many such parameters across the radial baseline profile, it was shown that, based on the principle of separation of linear and non-linear parameters [14], the baseline parameters are trivial to optimize analytically and independently of all other parameters, without causing significant computational overhead. This was termed the ‘algebraic noise elimination’ method. This is the standard method of accounting for baseline offsets in the ‘direct boundary modeling’ approach, and is applied widely, for example, in the software SEDFIT in conjunction with the diffusion-deconvoluted sedimentation coefficient distributions c(s) [15, 16], multisignal sedimentation coefficient distributions c_k(s) [17], size-and-shape distributions [18], as well as Lamm equation models for reacting systems in SEDPHAT [19]. In addition to allowing the full exploitation of the signal/noise ratio of the raw data and allowing the comparison of data and fitted model in the raw data space, it provides an explicit estimate of the baseline profile that may be compared with the expected baseline profiles as measured from water blanks. After the fit, the estimated baseline profile can be subtracted from the data to visualize directly the macromolecular sedimentation profiles for inspection [20]. This strategy was initially described only for scans with equal radial ranges, but recently generalized to non-overlapping radial ranges in ‘partial boundary modeling’ [12]. The same strategy was shown to be highly useful also in the analysis of sedimentation equilibrium data [21].

The relationship between the two methods has not yet been rigorously examined. Distinctions were perceived and proposed to guide the choice of analysis strategy. For example, the differencing method is sometimes referred to as being ‘model-independent’ [22–24], in contrast to the direct boundary model approach, where the results (and in particular the baselines) are characterized as ‘model-dependent’ and of more limited “validity” [25]. On the other hand, the dogma that no data processing step can increase information would lead one to fit an explicit model in the raw data space. The goal of the present work is to clarify these attributes and to better characterize the different approaches with regard to their statistical implications for the data analysis.

One difficulty in this task is the problem that the error surfaces are quite complex, even for simple models, due to the dimensionality of the raw data sets and due to the non-linear nature of the macromolecular sedimentation parameters. To circumvent this difficulty, we instead examine here a much simpler, linear problem, to which the concepts of differencing or direct boundary modeling can be applied. In this way, the implicit and explicit assumptions as well as the statistical consequences can become more transparent. In particular, we consider data points that have the form

$$y_i={at}_i+b+{\sigma }_i$$ (Eq. 1)

(with a representing a slope, b a baseline offset, and σ_i normally distributed noise), which are to be fitted by least-squares with the straight line

$$f(t)=at+b$$ (Eq. 2)

with unknown values for the slope and an unknown offset. We can apply both ideas of data differencing and direct modeling to account for the baseline offset. The linear nature of the model allows easily determining the resulting properties of these models. Some of the results are well-known from text-book examples [26], however, most are not previously considered in this context.

There are obvious differences to SV analysis, including: (i) Rather than single data points, in SV we would measure a whole scan at each time-point, and rather than a single baseline there would be a complete baseline profile across the whole cell; (ii) The parameters of primary interest in SV are often sedimentation coefficients, which are non-linear parameters in the model that depend in a more complex way on the evolution of the profiles, rather than being simply a slope from the propagation with time; and (iii) the number and spacing of time-points differ. In spite of this, we believe that the insights from this simple model does still reflect some salient features of the time-differencing in comparison with the direct boundary modeling approach in SV analysis. At the very least, we hope that the analysis presented here will clarify the discussion and focus on the question in which way any aspects of real SV analysis could possibly cause properties of the differencing schemes fundamentally different from those exhibited here in the simpler context.

Method

The theoretical analysis is based on basic statistical principles, as described by Bevington [26]. Due to the linearity of the model, all aspects can be analytically solved. Results were confirmed analytically using the symbolic math toolbox of MATLAB (The Mathworks, Natick, MA), and key statistical quantities were compared with the result of Monte-Carlo analyses, based on normally distributed samples with between 100 and 100,000 data points, typically using 10,000 to 100,000 iterations.

Outline of the Analysis Approaches

When applied to the classical text-book problem of fitting a straight line, some aspects of the approaches discussed here may appear trivial. Nevertheless, this is a worthwhile exercise that can clarify the concepts and relationships in light of the analogy to SV analysis. Further, it will lead to interesting results which have to our knowledge not yet been considered in this context.

Direct boundary modeling

Here, we directly consider the original problem (Eq. 1) and (Eq. 2) in the raw data space, explicitly accounting for all unknowns (in the SV problem typically including baselines, concentration factors, sedimentation coefficients and diffusion coefficients, but here only represented by a and b). This leads to the minimization problem

$$\underset{a,b}{\mathit{Min}}\sum _{i=1}^N{y}_i-{at}_i-b^2\equiv \underset{a,b}{\mathit{Min}}{S}_1(a,b)$$ (Eq. 3)

where S₁(a, b) denotes the error surface formed by the sum of squared deviations in the original data space that depends on the two unknowns a and b. For simplicity, we assume all data points have equal weight.

As introduced in [5], the direct boundary modeling approach proceeds in applying the principle of “separation of linear and non-linear parameters” [14]. This separates out the linear parameters (e.g. the concentration factors and baselines in SV), and finds a formula for its optimum as a function of the remaining nonlinear parameters. In our fitting analogy, all parameters are linear. Nevertheless, we can apply the same technique and first optimize for b, a linear parameter, and defer the calculation of the slope a to the separate optimization in a second stage. In the present context, it is irrelevant how the second stage optimization takes place (non-linear regression in SV, analytically here), and therefore this separation can be viewed analogous to that in real SV analyses.

To this end, the original problem $\underset{a,b}{\mathit{Min}}{S}_1(a,b)$ is split it up into

$$\underset{a,b}{\mathit{Min}}{S}_1(a,b)=\underset{a}{\mathit{Min}}\underset{b}{\mathit{Min}}{S}_1(a,b)$$ (Eq. 4)

and we can define a second error surface S₂ which is of lower dimension than S₁ and arises from S₁ by choosing for each point a the best-possible b(a)

$$S_2(a)\equiv \underset{b}{\mathit{Min}}{S}_1(a,b).$$ (Eq. 5)

For the first problem $\underset{b}{\mathit{Min}}{S}_1$, a necessary condition for optimality is dS₁/db = 0, which leads to

$$b=\frac{1}{N}\sum _{j=1}^N{y}_i-a\frac{1}{N}\sum _{j=1}^N{t}_i\equiv \overline{y}-a\overline{t}.$$ (Eq. 6)

This solves $\underset{b}{\mathit{Min}}{S}_1$ unambiguously. When this result is inserted in S₁, it follows that

$$S_2(a)=\underset{b}{\mathit{Min}}{S}_1=\sum _{i=1}^N(y_i-\overline{y})-a{(t_i-\overline{t})}^2$$ (Eq. 7)

We are left then with the remaining problem $\underset{a}{\mathit{Min}}{S}_2$:

$$\underset{a,b}{\mathit{Min}}{S}_1(a,b)=\underset{a}{\mathit{Min}}{S}_2(a)=\underset{a}{\mathit{Min}}\sum _{i=1}^N(y_i-\overline{y})-a{(t_i-\overline{t})}^2$$ (Eq. 8)

We denote the best estimate of a obtained in this way as a_d (with the subscript ‘d’ for direct modeling). Once we have determined a_d, we go back to (Eq. 6), use our knowledge b(a) of the dependence of the optimal b given any a, and calculate the best-fit b.

‘Delta-c’ approach

Here, the goal is also to obtain a best-fit estimate for the slope a, but without explicitly calculating the baseline b. To this end, the data y_i(t_i) are ‘transformed’ to Δy_i(Δt_i),

$$\mathrm{\Delta }{y}_i=y_i-y_{i-\mathrm{\Delta }N},\text{and}\mathrm{\Delta }{t}_i=t_i-t_{i-\mathrm{\Delta }N}$$ (Eq. 9)

such that the pair-wise differencing removes b from the correspondingly ‘transformed’ model: Now, we can fit the ‘transformed’ data with the new function

$$g_{\mathrm{\Delta }}(\mathrm{\Delta }{t}_i)=f(t_i)-f(t_{i-\mathrm{\Delta }N})=a\times (t_i-t_{i-\mathrm{\Delta }N})$$ (Eq. 10)

resulting in the minimization problem

$$\underset{a}{\mathit{Min}}{S}_{\mathrm{\Delta }}(a),\mathit{where}{S}_{\mathrm{\Delta }}(a)\equiv \sum _{i=\mathrm{\Delta }N+1}^N\mathrm{\Delta }{y}_i-a\mathrm{\Delta }{t_i}^2$$ (Eq. 11)

where S_Δ(a) is defined here as the sum of squared deviations of the ‘transformed’ data and model, i.e. the error surface. Let us denote a_Δ the best-fit slope based on (Eq. 11).

Comparison

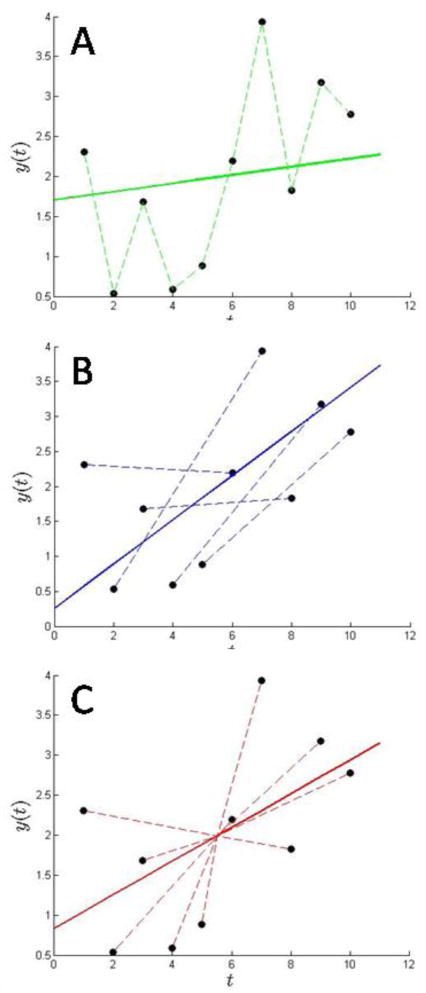
Figure 1 shows a graphical illustration of the approaches, for the case of N = 10 noisy data points. The ‘delta-c’ approach is depicted in green (Panel A) and blue (Panel B): the slope a_Δ (solid line) is the average of the slopes from the pair-wise differences (dotted lines), with ΔN = 1 (green, Panel A) and ΔN = N/2 (blue, Panel B). The former provides more lines with higher fluctuation, the latter has fewer lines with less fluctuation. The slope a determined with the direct boundary approach is shown by the red line (Panel C). Its slope is the average of the slopes between each data point and the average ȳ at the average time t̄.

Figure 1.

Illustration of different schemes for estimating the baseline and slope of noisy data points. Circles show 10 points calculated as y = 0.2t + 1 superimposed with normally distributed noise with σ = 1.0. The best-fit models based on pair-wise differencing are shown with ΔN = 1 and ΔN = 5, with the dashed lines indicating the slopes of the individual data point pairs, yielding 9 differences (Panel A, green) and 5 differences (Panel B, blue), respectively. Their average slope determines the slope of the best-fit results (solid lines). Their implicit baseline offset was calculated by (Eq. 13). In red is shown the best-fit model from the direct fit (Panel C, solid red line), which has a slope that is determined by the average between the differences (10 dashed red lines) of each data point and the mean signal ȳ at t̄, as indicated by the intersection of the solid lines.

Despite the fact that b does not occur explicitly in the formulas of the ‘delta-c’ approach, it is important to realize that this approach still implies that there can be a baseline offset in the original data, and that this baseline is unknown but constant with time. (Even though hypothetical functions for straight lines without offsets, f^*(t) = at, would lead to the same expression rhs of (Eq. 10) for their time-difference, use of (Eq. 10) and (Eq. 11) does not imply the model f^*.)

We note that S₂ and S_Δ are very much alike: both do not depend on b. Both arise from differencing the data. Interestingly, just like the differencing scheme in (Eq. 9) was postulated without further justification, one could have guessed different starting points for a ‘delta-c’ approach. In particular, based on the notion that the average scan will certainly represent the baseline at least equally well as any particular scan, one could have arbitrarily taken the more refined form of (Eq. 8) upfront.

Although the current ‘delta-c’ implementations in SV choose to leave the baseline undetermined, once we estimate a_Δ from minimizing S_Δ, we can go back and ask the new question of what b might be. For this, however, we have to go back into the original data space, minimizing S₁ given a_Δ. (Certainly we should believe that a_Δ is an excellent estimate for the value of a.) The result was already given above in (Eq. 6), and we can define

$$b_{\mathrm{\Delta }}=\overline{y}-a_{\mathrm{\Delta }}\overline{t}$$ (Eq. 12)

This has been proposed, for example, for calculating TI profiles from g(s*) analyses [27]. In SV practice, this is an important step, as it allows one to compare the baseline profile implicit in the particular boundary interpretation with the expected TI noise profile from water blanks or from the profiles at the start of sedimentation.

Having determined a_Δ and b_Δ, we can make explicit the model that was silently underlying the ‘delta-c’ approach, and trace the fitted function in the original data space

$$f_{\mathrm{\Delta }}(t)=a_{\mathrm{\Delta }}t+b_{\mathrm{\Delta }}=a_{\mathrm{\Delta }}t-\overline{t}+\overline{y}$$ (Eq. 13)

Likewise, we can insert for the ‘direct modeling’ (Eq. 6) into the model (Eq. 2)

$$f_d(t)=a_{d}t-\overline{t}+\overline{y}$$ (Eq. 14)

which is identical except for the possible difference in the estimated slope (Figure 1). Thus, just like the two approaches lead to optimization problems of similar structure in the ‘transformed’ data space (just with different referencing), they are also equivalent in the raw data space once the analytically optimized baseline is inserted. Since the baseline offsets are always linear parameters, their analytical optimization and elimination can be achieved easily for any real SV model.

Solving the Problems

Since we chose at the outset to study a problem where all parameters are linear, we can analytically solve the problems. First, for the direct boundary approach, the problem (Eq. 8) can be solved by requiring that dS₂/da = 0, leading to

$$a_d=\frac{{\displaystyle \sum _{i=1}^N}(y_i-\overline{y})(t_i-\overline{t})}{{\displaystyle \sum _{i=1}^N}{(t_i-\overline{t})}^2}$$ (Eq. 15)

We can insert here in (Eq. 15) the definitions of the averages (Eq. 6), which after reordering leads to

$$a_d=\frac{N{\displaystyle \sum _{i=1}^N}{t}_i{y}_i-{\displaystyle \sum _{i=1}^N}{t}_i{\displaystyle \sum _{i=1}^N}{y}_i}{N{\displaystyle \sum _{i=1}^N}{t_i}^2-{\left({\displaystyle \sum _{i=1}^N}{t}_i\right)}^2}$$ (Eq. 16)

The latter expression is the well-known standard expression for the slope resulting from least-squares fit of a straight line (see, e.g., Eq. 6.12 in [26], noting the switched terminology of a and b). We can rewrite this under the assumption of equidistant time points, t_i = t₁ + (i − 1) δt, as

$$a_d=\frac{{\displaystyle \sum _{i=1}^N}(y_i-\overline{y})i-(N-1)/2}{N\delta t{N}^2-1/12}$$ (Eq. 17)

For the delta-c approach, we solve Eq. (Eq. 11) by requiring that dS_Δ/da = 0. This leads to

$$a_{\mathrm{\Delta }}=\frac{{\displaystyle \sum _{i=\mathrm{\Delta }N+1}^N}\mathrm{\Delta }{y}_i\mathrm{\Delta }{t}_i}{{\displaystyle \sum _{i=\mathrm{\Delta }N+1}^N}\mathrm{\Delta }{t_i}^2}$$ (Eq. 18)

For equidistant time-points it is (t_i − t_i−ΔN) = ΔNδt, and

$$a_{\mathrm{\Delta }}=\frac{1}{\mathrm{\Delta }N\delta t}\frac{1}{(N-\mathrm{\Delta }N)}\sum _{i=\mathrm{\Delta }N+1}^N{y}_i-y_{i-\mathrm{\Delta }N}$$ (Eq. 19)

or

$$a_{\mathrm{\Delta }}=\frac{\overline{\mathrm{\Delta }y}}{\mathrm{\Delta }N\delta t}$$ (Eq. 20)

i.e., a_Δ is the average slope (compare Figure 1), or the average difference in y divided by the corresponding time-difference. Not surprisingly, the best-fit estimate a_d (Eq. 17) is different from a_Δ (Eq. 20).

Statistical Error Estimates

A key question is the statistical accuracy of the different estimates. We can determine the errors of the estimates a_Δ and a_d by applying the standard error propagation formula for determining the error σ_p of a parameter p (Eq. 6.19 of [26]). If the data points all have the same errors σ, this takes the form

$${\sigma }_p^2={\sigma }^2\sum _{n=1}^N{\left(\frac{dp}{{dy}_n}\right)}^2$$ (Eq. 21)

(we assume only errors in y, not in t).

For the error of a_d the resulting value ${\sigma }_{a,d}^2$ from applying (Eq. 21) to (Eq. 16) has been reported by Bevington ([26] Eq. 6.23) as

$${\sigma }_{a,d}^2=\frac{N{\sigma }^2}{N{\displaystyle \sum _{i=1}^N}{t_i}^2-{\left({\displaystyle \sum _{i=1}^N}{t}_i\right)}^2}$$ (Eq. 22)

In the case of equidistant time points, t_i = t₁ + (i − 1) δt, this simplifies to

$${\sigma }_{a,d}^2=\frac{{\sigma }^2}{{(\delta t)}^2}\frac{12}{N{N}^2-1}$$ (Eq. 23)

If one were interested in the uncertainty of the baseline parameter, once we know σ_a,d a convenient approach is via (Eq. 6) applying (Eq. 21) (assuming equidistant time points):

$${\sigma }_{b,d}^2={\sigma }_{a,d}^2{\left(\frac{db}{da}\right)}^2+{\sigma }^2\sum _{i=1}^N{\left(\frac{db}{{dy}_i}\right)}^2={\sigma }_{a,d}^2{\overline{t}}^2+\frac{1}{N}{\sigma }^2.$$ (Eq. 24)

We can compare the errors σ_a,d with those that would occur if there was no baseline offset. In this case, ${a_d}^{\ast }={\sum }_{i=1}^N{y}_i{t}_i/{\sum }_{i=1}^N{t_i}^2$, and in the case of δt = 1 and t₁ = 1 simplifies to

$${\sigma }_{a^{\ast },d}^2={\sigma }^2\frac{6}{N2N^2+3N+1}$$ (Eq. 25)

As one might expect, this is much smaller than (Eq. 23).

For the error of a_Δ, we apply (Eq. 21) to (Eq. 19). For ΔN ≤ N/2, contributions with ΔN < n ≤ N − ΔN cancel out, which leads to

$${\sigma }_{a\mathrm{\Delta }}^2=\frac{{\sigma }^2}{{(\delta t)}^2}\{\begin{array}{ll}\frac{2}{\mathrm{\Delta }N{(N-\mathrm{\Delta }N)}^2}\hfill & \mathit{for}\mathrm{\Delta }N\le N/2\hfill \\ \frac{2}{{(\mathrm{\Delta }N)}^2(N-\mathrm{\Delta }N)}\hfill & \mathit{for}\mathrm{\Delta }N>N/2\hfill \end{array}$$ (Eq. 26)

The dependence of the error of a_Δ on the choice of ΔN is illustrated in Figure 2. For example, if we assume ΔN = N/2 (for even N), this is

Figure 2.

Dependence of the uncertainty ${\sigma }_{a\mathrm{\Delta }}^2$ of the slope a_Δ in the pair-wise differencing scheme on the choice of ΔN, following Eq. (Eq. 26). The value of ${\sigma }_{a\mathrm{\Delta }}^2$ is normalized relative to the uncertainty of the slope parameter ${\sigma }_{a,d}^2$ from the direct fit Eq. (Eq. 23). The discontinuity and symmetry relative to the point ΔN/N = 1/2 arises from the cancellation of errors from statistically non-independent difference data Δy. If they were independent data points the error would follow the dashed line Eq. (Eq. 29).

$${\sigma }_{a\mathrm{\Delta }}^2=\frac{{\sigma }^2}{{(\delta t)}^2}\frac{16}{N^3}$$ (Eq. 27)

This is not the best choice for ΔN, since (Eq. 26) has minima for ΔN = N/3 and ΔN = 2N/3, both of which would lead to only

$${\sigma }_{a\mathrm{\Delta }}^2=\frac{{\sigma }^2}{{(\delta t)}^2}\frac{13.5}{N^3}$$ (Eq. 28)

These seem to be a better compromise between the signal/noise ratio of the Δy_i in (Eq. 9) and the number of ‘transformed’ data points available.

In the case of ΔN < N/2, each original data point may participate in two pairs (making positive and negative contributions). Therefore, the pair-wise differences are not all independent data points, and instead subject to serial autocorrelation. However, data points to be statistically independent observations is a pre-requisite of the error analysis based on standard χ² and F-statistics [28]. In this case, if one would make a mistake to regard the differences Δy simply as our (pre-processed) new data points, each having an uncertainty σ_Δ² = 2σ², the apparent error σ_aΔ′ would follow

$${\sigma }_{a{\mathrm{\Delta }}^{\prime }}=\frac{{\sigma }^2}{{(\delta t)}^2}\frac{2}{\mathrm{\Delta }{N}^2(N-\mathrm{\Delta }N)},$$ (Eq. 29)

which is indicated in Figure 2 as the dashed line. This coincides with the true error (Eq. 26) only for ΔN ≥ N/2. The Monte-Carlo approach to determine parameter uncertainties does not suffer from this potential difficulty.

Thus, in summary, the ‘delta-c’ approach with the differencing scheme at ΔN = N/2 will have a 15 % larger error (factor $\sqrt{16/12}$) than the ‘direct modeling’ approach. If the ‘delta-c’ approach was conducted with differences of ΔN = N/3 or ΔN = 2N/3, the loss in precision would only be 6%. This is independent of the number of data points.

Effect of Systematic Deviations

Although the baseline stability in SV is remarkably good, it is certainly not absolute. For example, the ‘aging’ procedure that the cell components are customarily subjected to prior to sedimentation equilibrium experiments with interference optical detection aims to mechanically stabilize the cell assembly and prevent baseline shifts, possibly arising from the compression of the window cushions [29]. Whether such baseline changes may occur continually during the long time-range of the sedimentation experiment, or accompany a relatively sudden collapse of a window cushion, or occurs during rotor acceleration and deceleration, is unclear. Also, unmatched buffer salts can contribute signals that appear as continuous shifts in the baseline, if unaccounted for in the model of the sedimenting species (manuscript submitted). Finally, periodic oscillations of the baseline patterns can occasionally be discerned in the residual bitmaps of SV experiments, possibly arising from temperature fluctuations [13], or rotor precession [25].

Therefore, we ask if there is any difference in the two approaches in the extent to which systematic errors in the model may go undetected and/or may bias the outcome of the analysis. Often when analyzing experimental data, a fit with a simpler model is tested against a more complex model and statistical criteria are applied whether the fits are significantly different and justify inclusion of the additional parameter.

For example, we can simulate data that have a small quadratic component, i.e., y_i = ct_i² + at_i + b + σ as a model for data with a slight baseline drift b_drift = b + ct_i², and fit these with the same model as above, y = at + b or Δy = aΔt, respectively. We observed the increase in the χ² value of the fit with increasing c. When the change in χ² relative to the correct case c = 0 reaches the Δχ² = 1 level [26], inclusion of corrective terms would be justified and the more complex behavior could possibly be correctly recognized. To this end, we determined the critical level of c by 10⁴ Monte-Carlo simulations for data sets of N = 10⁴ equidistant data points from t = 1 to 1000 with normally distributed noise of σ = 1. For the quadratic model, we obtained a critical value of c = 5.57×10⁻⁷ for a possible detection of a quadratic term the direct modeling approach. For the ‘delta-c’ approach we assumed ΔN = N/2 and evaluated the quality of fit from S_Δ(a) in (Eq. 11), i.e. treating the difference data as if they were the data points to be modeled. This yielded a critical value of 5.71×10⁻⁷, i.e. only 2.5% higher than the direct modeling approach.

For other systematic disturbances the two methods exhibit larger differences in their potential for detection. As an extreme example, when an offset in the middle of the time-interval occurs in the form of a step-function, cH t − t_max/2, the direct boundary approach offers possible detection at c > 0.071, whereas it obviously cannot be detected at all in the ‘delta-c’ approach with ΔN = N/2 for any c, as it can be fully compensated by corresponding offsets in a_Δ.

For periodic systematic disturbances c sin 2πt/τ, resembling a baseline oscillation, a strong dependence of the critical value of c on the period τ is observed for the ‘delta-c’ approach (see Figure 3), whereas nearly uniform value of ~0.025 were found for the direct modeling approach.

Figure 3.

Critical amplitude c for an oscillatory signal offset c sin 2πt/τ to create a significant decrease in the quality of the best-fit straight line. The critical amplitude was determined as the value that causes an increase χ² of the fit by an amount Δχ² = 1, which could make it potentially detectable. 10,000 data points were simulated with constant time-interval Δt = 1 and normally distributed noise with σ = 1.0. The critical amplitude is nearly independent of the period of oscillation for the ‘direct modeling’ approach (solid line), but shows sharp maxima for the ‘delta-c’ approach calculated at ΔN/N = 1/2 (crosses and interpolated dotted line).

Discussion

The unknowns in SV analysis can be divided in macromolecular parameters and baseline parameters. The baseline parameters often make very large signal contributions, but they are linear and therefore easy to eliminate. This can be accomplished either analytically in the original data space through the procedure termed ‘algebraic noise decomposition’ (allowing ‘direct boundary modeling’), or the model can be ‘transformed’ into a differential form where the constant baseline terms disappear. Both have corresponding models in the original data space and in the ‘transformed’, differenced data spaces.

For the direct boundary modeling approach, it is key to understand that the baselines are analytically pre-optimized, such that for the macromolecular parameters the error surface represents a subspace S₂ of the original error surface S₁, in which the baseline parameters are locally optimal for each macromolecular parameter combination. This simplification is possible due to the fact that analytical solutions for the baseline parameters can be derived algebraically as a function of macromolecular parameters.¹ The workflow consists first of the optimization of the macromolecular parameters in the pre-optimized subspace S₂, and then, as a second step, in S₁ the analytical determination of the baseline values that belong to (i.e. are optimal for) the estimated macromolecular parameters.

Interestingly, once in the subspace of algebraically pre-optimized baselines, S₂, the direct boundary modeling approach appears to be a differencing scheme that fits differences of data points. However, it is distinct from the ‘delta-c’ approach in that the difference is not taken between pairs of data points, but rather between each data point and the average signal from data points (at averaged position). This has significant statistical advantages, as it suppresses the noise-amplification inherent in the pair-wise subtraction. However, it is otherwise very similar to the ‘delta-c’ approach in the fact that both the optimal values of macromolecular parameters as well as their error estimates are completely independent of the values of the baseline parameters (the latter being eliminated in the subspace S₂).

Vice versa, we note that the differencing scheme of the ‘delta-c’ approach could not be conceived without implying the existence of a baseline term and the constancy of the latter. (Obviously, we know it has direct physical meaning). Therefore, just like differential equations can define the solution to a problem only up to integration constants, any differencing scheme allows for calculating the macromolecular sedimentation parameters but leaves the baseline parameters undetermined. Explicit values for b can be determined, though, by going back to S₁. This allows us trivially to calculate the least-squares best-fit values of the baseline for any set of macromolecular parameter estimates, which is a very useful step (see below).

The fact that the baseline parameters have not been determined in the historic delta-c based analysis approaches changes nothing about the existence of these unknown baseline parameters, and the effect that they exert on the error surface (as demonstrated here for S_Δ and S₂ in our linear analogue). The delta-c based historic methods simply do not completely determine the parameters of the sedimentation model in the raw data space. The differencing step does rephrase the problem in a way that is independent of the baseline value, but leaves it an unknown. This is a property that all differencing schemes share.

Just like the pair-wise differencing with ΔN = N/2 was postulated as a model, taken among many possible differencing schemes, one could have guessed upfront that the differences between particular and average scans would give statistical advantages. If one would postulate the latter differencing model directly for use in the differenced data space, without explicitly deriving it from its root in the raw data space (and ignore the determination of baselines), we would arrive at the same (Eq. 8), whether or not the baseline parameters are subsequently made explicit. Again, our choice to restrict the analysis to the parameters that appear in the differenced data space does not affect the true mathematical relationship of the model with its integral form in the raw data space.

The premise of the present contribution is that the linear model retains key properties of the differencing schemes of SV data. Clearly the higher dimensionality of the SV data, which requires typically hundreds of baseline parameters (one at each radial point), and the complex macromolecular sedimentation model, which exhibits non-linear parameters in the solution of the Lamm equation, present a different problem. However, we believe that the differencing of the data a(r, t_i) to model Δa = a(r, t_i) − a(r, t_i−ΔN) in the ‘delta-c’ approach exhibits similar statistical properties, even though it would appear as an array of one-dimensional problems (side-by-side for each radius value, all sharing the non-linear macromolecular parameters describing the evolution of signal at each radius). Likewise, we have shown previously that for any sedimentation model in SV the direct boundary fitting problem allows for the algebraic elimination of baseline parameters, and the optimization of the sedimentation parameters in a sub-space of the original error surface, completely analogous to the strategy outlined for the straight line problem. In particular, for any macromolecular sedimentation model M_rt({p}) (generally depending on the macromolecular parameter set {p}), it is

$$\underset{b_i,\{p\}}{\mathit{Min}}\sum _r\sum _t{a}_{rt}-M_{rt}(\{p\})-{b_r}^2=\underset{\{p\}}{\mathit{Min}}\sum _r\sum _t\left[a_{rt}-{\overline{a}}_r\right]-{\left[M_{rt}(\{p\})-{\overline{M}}_r(\{p\})\right]}^2$$ (Eq. 30)

where pre-optimization of all time-invariant noise parameters b_r from the original error surface $S_1^{(SV)}$ (lhs of (Eq. 30)) leads to an error surface $S_2^{(SV)}$ (rhs of (Eq. 30)), in which the data a_rt and the model M_rt({p}) appear as difference to their respective time-averaged scans, ā_r and M̄_r ({p}) [12]. Eq. (Eq. 30) amounts to fitting differences $a(r,t_i)-\overline{a(r)}$, similar to those examined here in the straight line model, except for the extension of the single baseline to an array of baseline values b_r. It is difficult to see how these differences between the SV problem and the straight line problem could fundamentally change the relationships between the ‘delta-c’ and the ‘direct modeling’ approach.

Therefore, we conclude that also for the case of SV there are no ‘philosophical’ differences or differences in the ‘model-dependence’ between the ‘delta-c’ and ‘direct boundary modeling’ approaches, which were suggested previously [22–25]. Just like for the straight line problem outlined above, both approaches are equally model dependent, as they are based on the same model and only expressed in either differential or integral form. Unfortunately, the step of explicitly calculating the baseline parameters that are implied by the macromolecular sedimentation model is sometimes ignored, and, to the author’s knowledge, it is currently not implemented in software packages such as SEDANAL and DCDT+. With the exception of differences in the error surface arising from noise amplification and possible distortions from data transformations [12], essentially the same models will fit the data similarly in both integral and differential formulations. This specifically includes models that, due to correlations of the sedimentation and baseline parameters, would imply baselines we would dismiss as unreliable (along with the sedimentation model) once available for inspection. Examples are strongly curving baseline profiles inconsistent with the usually relatively flat fringe profile of a well-aligned interference optics with empty cells. One should not be misled by merely the neglect to explicitly calculate the baseline, and the lack of its display, not to recognize that the baseline does constitute an unknown parameter that increases the flexibility of the fit. Vice versa, Stafford’s suggestion [25] that offering this information about the implicit baselines for inspection would affect the “validity” of the model or cause higher parameter correlation is erroneous. To the contrary, the ability to discern from the value of the explicit baseline that a certain model is invalid is an important advantage as an additional diagnostic information when searching for true macromolecular parameters.

The ‘delta-c’ approach has historical roots in the time-derivative method for SV to determine an apparent distribution of non-diffusing particles g(s*) [7] that relies on time-difference to approximate the rate dc/dt. However, distributions of non-diffusing particles can be determined also directly [11]. Similarly, models using explicit Lamm equation solutions can be naturally phrased in the raw data space, and there is no particular justification for the differencing approach. There is no other biophysical technique besides SV where a differential form of the fitting function is advocated to provide less parameter correlation and greater ‘model-independence’ due to the ‘elimination’ of the baseline parameters. If such an advantage were to exist, one should exploit the same advantage also in sedimentation equilibrium (SE) analytical ultracentrifugation, where baseline correlations can be very significant, and one would consequently be led to proceed fitting the pair-wise signal differences at different radii a(r_i) − a(r_j), rather than the raw equilibrium profiles a(r). Yet, despite the many decades long study of the baseline problem in the SE literature, to our knowledge such a strategy has not been proposed (for obvious reasons).

While the approaches are based on the same underlying model and assumptions, the integral and differential forms differ significantly in performance. Partly, this arises from the fact that differencing leads to noise amplification. In our simple model, for the pair-wise averages, the loss of precision of the estimate of the slope depends on the time-interval. Obviously, longer time-intervals Δt = t_i − t_j provide for smaller relative errors of the difference data Δy = y_i − y_j. This is balanced by the fact that only fewer difference data points are possible at longer time intervals. Shorter time intervals are not as bad as they may appear at first sight, since two difference data points that share the same raw data point (once positive and once negative) are not statistically independent. In our linear model with equidistant time-point, equally optimal choices were time-intervals of 1/3 and 2/3 of the total observation time. The choice of dividing the total number of data points in half [8] (this is the default choice in SEDANAL, DCDT+) exhibits a local maximum of the error amplification. In contrast, the best choice is differencing between each point and the average, y_i − ȳ, since the statistical precision of ȳ improves with the number of data points. We believe this is the optimal out of any possible differencing schemes, noting that the latter scheme arises directly as a computational result from the direct boundary modeling, and following the axiom that to fit the raw data is optimal.

In our simple model, we could also demonstrate a lower potential of the pair-wise differencing for the possible detection of systematic deviations of the data from the model. For example, it appears that a greater flexibility of the pair-wise differencing model can arise when data pairs from different segments of the experiment yield similar slopes but imply different baselines. Specifically, there appears to be a high susceptibility to oscillations, since addition of an arbitrary periodic offset z that fulfills z(t_i) = z(t_i−ΔN) leaves the Δy_i = y_i − y_i−ΔN data completely invariant. Similar effects may be relevant in SV in practice considering the possibility of signal oscillations from the vibration of optical components or rotor precession. This is not the case for ‘direct modeling’ approach, which is therefore a more stringent model.

A problem arises in SV analysis that the data suffer not only from time-invariant baseline profiles, but also from radial-invariant but time-dependent noise contributions β_t, which play in the time-domain the same role as the b_r in the spatial domain. We have shown previously that the same principle of separation of linear and non-linear variables can be applied, and equations equivalent to (Eq. 30) can be found in the presence of radial-invariant offsets β_t, as well as for simultaneous b_r and β_t baseline offsets [5]. In contrast, the ‘delta-c’ approach does not seem to allow the equivalent treatment of these orthogonal baseline parameters. In conjunction with the ‘delta-c’ approach, it is required to empirically eliminate the temporal offsets by ‘aligning’ the scans in small regions either outside the solution column or where the solutes are believed to be depleted. Clearly, this is a source of potential bias.

In the practice of SV analytical ultracentrifugation, the higher statistical errors for the ‘delta-c’ approach should be relevant for solving problems such as the determination of trace aggregates in protein pharmaceuticals [30–35], or the estimation of kinetic rate constants from sedimentation profiles of reacting systems [13, 19], both problems where the boundary shapes need to be assessed to a level of detail where signal/noise ratio becomes limiting. However, perhaps the most important conclusion of the present work is that there is no difference in the ‘model-dependence’ of the two approaches, but that making explicit the baseline profiles that are equally part of both approaches provides a useful diagnostic tool. The theoretical difference in their statistical performance may be small compared to the increase in parameter uncertainty arising from the arbitrary exclusion of data from considerations (subset analysis), and from sources of systematic error such as convection, un-accounted hydrodynamic non-ideality, signal offsets from buffer mismatch (Zhao et al., submitted), bias from constraining the meniscus parameter to incorrect values, and/or systematic errors arising from unaccounted time-resolution of the absorbance scanner [12].