Mechanical strain enhances survivability of collagen micronetworks in the presence of collagenase: implications for load-bearing matrix growth and stability

Abstract

There has been great interest in understanding the methods by which collagen-based load-bearing tissue is constructed, grown and maintained in vertebrate animals. To date, the responsibility for this process has largely been placed with mesenchymal fibroblastic cells that are thought to fully control the morphology of load-bearing extracellular matrix (ECM). However, given clear limitations in the ability of fibroblastic cells to precisely place or remove single collagen molecules to sculpt tissue, we have hypothesized that the material itself must play a critical role in the determination of the form of structural ECM. We here demonstrate directly, using live, dynamic, differential interference contrast imaging, that mechanically strained networks of collagen fibrils, exposed to collagenase (Clostridium histolyticum), degrade preferentially. Specifically, unstrained fibrils are removed ‘quickly’, while strained fibrils persist significantly longer. The demonstration supports the idea that collagen networks are mechanosensitive in that they are stabilized by mechanical strain. Thus, collagen molecules (together with their complement enzymes) may comprise the basis of a smart, load-adaptive, structural material system. This concept has the potential to drastically simplify the assumed role of the fibroblast, which would need only to provide ECM molecules and mechanical force to sculpt collagenous tissue.

1. Introduction

Nature builds structures that resist dissipation. In multicellular plants and animals, material is placed on the path of applied loads and it persists. The natural entropic force that tends to separate individual cells is defeated, allowing groups of cells to function in intricately connected colonies. Such multicellular formations are advantageous, as they have obviously enjoyed phenomenal evolutionary success. In animals, the rise of metazoans appears to be closely linked with the evolution of collagen (Exposito et al.2000, 2002). In vertebrate animals, the load-bearing molecules of choice are fibrillar collagens (types I, II, III, V and XI), which can be found distributed extensively in the musculoskeletal system (bone, ligament, tendon, cartilage, intervertebral disc (IVD)) in skin and in highly specialized load-bearing tissues such as the cornea. Though the fundamental bauplan of the vertebrate skeleton has remained consistent across taxonomies for more than 500 million years (Langille & Hall 1989), there are massive scale differences and form-factor alterations distributed across vertebrate species that exceed three orders of magnitude in linear dimension (consider the female Paedocypris micromegethes of length approx. 0.008 m and the blue whale Balaenoptera musculus of length approx. 30 m). Given that evolutionary genetic changes are constrained to be incremental, it is possible that small genotype changes are readily amplified to produce the observed massive scalability in musculoskeletal phenotypes. This idea is supported by a recent work which determined that the difference in the size scale of dogs (spanning two orders of magnitude) is principally because of changes in a single allele: IGF-1 (Sutter et al. 2007). As fibrillar collagen provides the principal structural element for the myriad of diverse vertebrate forms, it is instructive to consider how it (as a potentially intelligent biomaterial) could enhance the ability of fibroblastic cells to produce organized, load-bearing structures over many length scales.

Birk & Trelstad (1984), while examining the development of nascent chick corneal structure, suggested that collagen is produced and organized within cell surface crypts or fibripositors. This concept was extended to developing tendons by Canty & Kadler (2005). The fibripositor idea was adopted by Prof. Hay and was incorporated into her classic text on Cell biology of extracellular matrix (Birk et al. 1991). Thus, fibripositor-mediated assembly of collagen has generally become the standard model to explain the initial production of highly anisotropic, load-bearing collagenous arrays. The fibripositor model implies that cells individually direct the production and placement of collagen fibrils. The implication is that fibroblastic cells must individually ‘weave’ the complex structures required to support the massive loads produced in the mechanically disadvantaged musculoskeletal system (MS) of vertebrate animals.

An alternative model suggests that, during development, organized arrays of fibrillar collagen form not by direct deposition, but by the condensation of fibrils from highly concentrated ‘liquid crystalline’ solutions of collagen monomer (Trelstad 1982; Giraud-Guille 1996; Giraud-Guille et al. 2003). That liquid crystal collagen might be involved in the morphogenesis of the highly organized corneal stromal matrix formation was proposed by Trelstad, who noted the lack of bilateral symmetry in the rotation of the lamellae in chick primary corneal stroma and concluded that physical forces (rather than biological) were at play (Trelstad 1982). In our laboratory, we have readily formed alternating arrays of aligned collagen fibrillar structures that are surprisingly similar in organization to the fibrils found in the native corneal stroma simply by confining concentrated solutions of monomer between two featureless surfaces (Ruberti & Zieske 2008). If collagen assembly and organization occurs at a distance from the cell surface via liquid crystal ordering, it simplifies the process of matrix assembly. The cells would need only to organize themselves into an appropriate confining geometry, provide low-energy guidance cues (e.g. filopodia) and then secrete collagen monomer (and auxilliary extracellular matrix (ECM) molecules). This is consistent with the observations of corneal stromal development (Hay & Revel 1969; Cintron et al. 1983).

Regardless of how the initial template or anlagen is produced, it must then grow. There are currently few fundamental, physically based models that explain the subsequent growth and maintenance of the organized structures in the vertebrate MS. As engineers, we are not only interested in how biology solves the difficult problem of growing a load-bearing structure, we are also interested in how this can be accomplished in synthetic systems. There is simply no engineering analogue for a cable (tendon) that extends axially and radially while continually supporting heavy body weight during growth.

The maturation of the MS anlage into the fully loaded adult MS is thought to proceed under both genetic and epigenetic control (reviewed in Carter & Beaupre (2001)). Certainly, it has been known, for over a century, that portions of the MS must adapt epigenetically to more efficiently carry the applied mechanical stress (Wolff 1891). There is also substantial evidence suggesting that mechanical force is necessary to produce appropriately formed MS components in utero (reviewed in Carter & Beaupre 2001; Carter & Orr 1992; Chalmers & Ray 1962). However, the mechanism by which loads are transduced into a stable morphological change in tissue, which must counter dissipation under applied stress, is not yet understood. While most investigations into mechanotransduction in connective tissue ECM have focused on the genetic and proteomic response of fibroblastic or myofibroblastic cells (Robbins et al. 1997; Bishop & Lindahl 1999; Parsons et al. 1999; Majima et al.2000a,b; Blain et al. 2001; Altman et al. 2002), there has been little progress in explaining how the synthesized ECM components are assembled to produce a load-adapted structure. We have postulated that mechanotransduction events leading to ECM load adaptation not only occur at the level of the cells, but also occur directly at the level of the matrix molecules (discussed in detail in Ruberti & Hallab (2005)).

This manuscript will focus on the idea that strain is protective of collagen networks when they are exposed to an aggressive catabolic enzyme. Experimental support of the idea of strain-stabilized collagen has been scant. Huang & Yannas (1977) reported on the strain altered degradation rates in reconstituted collagen tapes. Nabeshima et al. (1996) found that collagen under tensile mechanical load in native tendon was protected from bacterial collagenase attack. Ruberti & Hallab (2005) demonstrated that bacterial collagenase preferentially degraded unloaded control fibrils in mechanically strained, native corneal tissue. This experiment demonstrated that exposure to collagenase and tensile mechanical strain could be used to sculpt or re-model native collagenous matrix. However, the latter two papers (Nabeshima et al. 1996; Ruberti & Hallab 2005) examined the response of native tissue to degradation with all its inherent complexities, including proteoglycan (PG) interactions, collagen crosslinking and released cellular contents. In the current investigation, we have isolated the effect of bacterial collagenase (and in limited trials, matrix metalloproteinases (MMPs)) on loose type I collagen gels, without tissue-specific enzyme/molecular interactions or diffusion/sieving effects. In addition, the differential interference contrast (DIC)/edge-detection method described here directly captures the dynamics of collagen degradation, which was not possible in our previous paper.

Ruberti & Hallab suggested that loss of stabilizing strain could be the root cause of a number of pathological conditions, including osteoarthritis and IVD degeneration. Indeed, in a recent paper, it has been shown that the degradative response of collagen lamellae in rat IVD is mitigated by applied tensile loads and exacerbated by compressive load in an in vivo injury model (Lotz et al. 2008). Taken together, these mechanochemical studies suggest that collagen–enzyme reaction kinetics could be a function of the state of strain or strain energy density in the system. If this is true, the strain-dependent relationship between collagen and its complementary catabolic enzymes could have far reaching implications across biology (connective tissue development, growth, homeostasis and pathology), materials science (smart, self-optimizing material systems) and tissue engineering (construction of organized collagenous tissue de novo).

The mechanism by which collagen appears to be protected or stabilized by the applied mechanical load is not yet understood, but a similar effect has been noted in systems where collagen fibrils under load also resist thermal denaturation (Bass et al. 2004). In addition, the mere packing of collagen monomers into fibrils has been shown to improve their resistance to both thermal and enzymatic degradation (Jeffrey 1998; Tiktopulo & Kajava 1998; Leikina et al. 2002). It has been suggested that the improved molecular stability obtained by packing monomers into fibrils is due to a decrease in the configurational entropy of the collagen molecules possibly enhancing inter or intrachain bonding (Miles & Ghelashvili 1999). It is possible that tensile mechanical load enhances stability by a similar mechanism. Potentially, straining the collagen monomer could alter the geometry of the enzyme binding site (making binding more difficult) or that strain alters the relative positions of the three alpha-chains (making cleavage more difficult).

Regardless of the mechanism by which protection from enzymatic attack is effected, it is important to isolate the kinetics of enzyme-mediated degradation of mechanically loaded collagen fibrils. It is also important to demonstrate whether or not the activity of physiologically relevant MMPs is affected by the applied mechanical forces. We have developed methods to allow simultaneous, direct optical assessment of strained and unstrained collagen fibril degradation kinetics in a thermally controlled microenvironmental chamber. In this investigation, we demonstrate the ability of our mechano-optical enzyme assay to extract small differences in the degradation rates of collagen that is unstrained or under tension following exposure to bacterial collagenase (an aggressive cleaver of the collagen triple helix at multiple locations). We also demonstrate the utility of the microchamber in evaluating the degradation rates of MMP-8 on strained collagen and the effects of strain on the preferential incorporation of monomers into fibrils.

2. Materials and methods

In this series of experiments, the hypothesis that strain enhances the survivability of collagen fibrils exposed to enzyme will be tested. The null hypothesis to be rejected is that cleavage of loaded molecules should occur faster than unloaded molecules to release strain energy. An environmentally controlled reaction microchamber to allow the direct optical imaging of the kinetics and pattern of enzymatic degradation in strained, reconstituted collagen micronetworks has been constructed. The total volume of the microchamber is less than 60 μl with a 20 μl reaction volume. Such a small reaction volume allows the testing of multiple collagen/enzyme systems (including MMPs that are prohibitively expensive to use on a large scale).

(a). Microenvironmental chamber

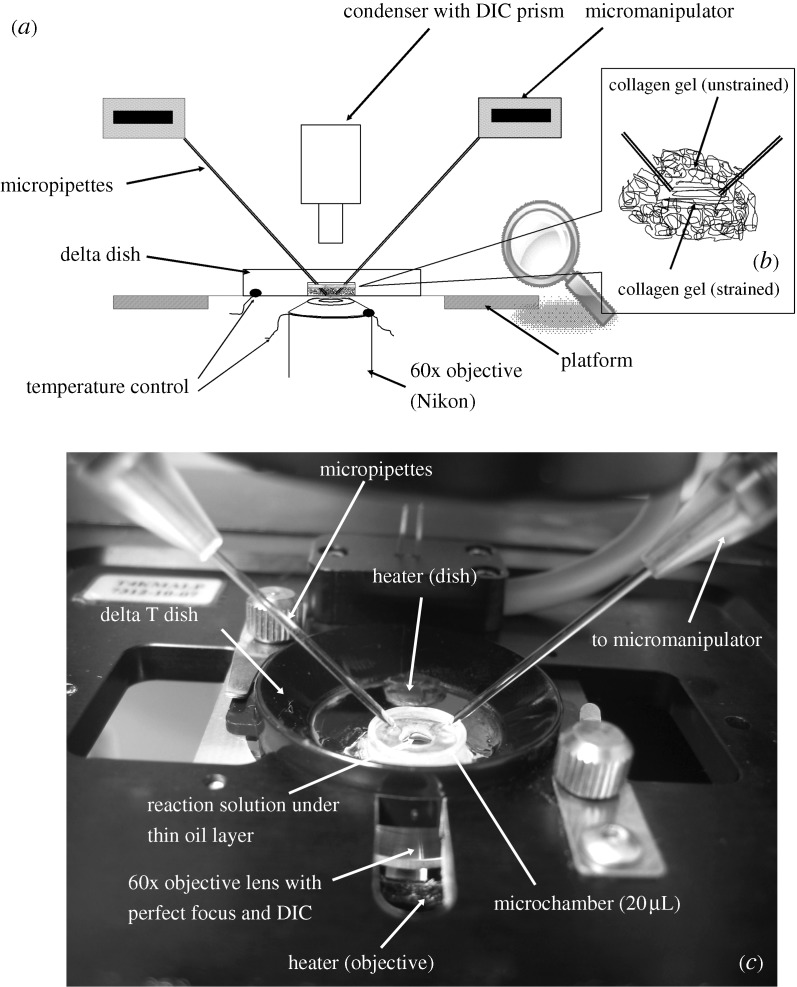
Figure 1 depicts the microenvironmental chamber constructed on the surface of a Bioptechs Delta T4 (Bioptechs, Butler, PA, USA) system comprising a Delta T dish (0.17 mm, 04200415B), triple plate stage adapter (PN 0402-6-02), Delta T4 culture dish temperature controller (PN 0420-4-03) and objective heater controller (PN 0420-4-03). Affixed to the Delta T4 glass surface is a small cylinder (height, 2.2 mm; inner diameter, 3.5 mm). The initial reaction volume is created by placing 10 μl of collagen solution into the cylinder and then covering it with objective oil (Cargille, non-drying, type A, viscosity 150; Cedar Grove, NJ, USA) to prevent evaporation. The final reaction volume is obtained by dropping an additional 10 μl of collagenase solution through the oil.

Figure 1.

(a) Schematic of the experimental setup used to carry out degradation of strained collagen under DIC microscopy. (b) Micropipette position and collagen gel in strained and unstrained form inside the microchamber. (c) Image of microchamber in situ. The design of the chamber permits manipulation of a small reaction volume.

(b). Enzyme and substrate

Commercially available, pepsin-extracted, bovine, type I, atelo-collagen monomers at a concentration of 3.0 mg ml⁻¹ were used in all experiments (PureCol; INAMED, Fremont, CA, USA). Extracted collagen monomers can be kept from aggregating by storage in cold, acidic solution, but will readily form fibrils when warmed and neutralized. Collagen in fibrillar form is generally resistant to most proteinases; however, it is susceptible to cleavage via bacterial collagenase (Clostridium histolyticum), members of the zinc-dependent MMP family and cathepsin K. In the main series of experiments, commercially available bacterial collagenase (crude; Sigma-Aldrich C0130, lot 016K1251) was used.

(c). Optical imaging

DIC or Nomarski microscopy is a beam-shearing interference method that detects gradients in the index of refraction (optical path). Reconstituted type I collagen fibrils are well resolved by DIC that has been used to study cell/matrix interaction in collagen gels (Petroll & Ma 2003). In addition, video-enhanced DIC has been used to estimate the diameter of biological filaments and structures well below the optical diffraction limit (Gelles et al. 1988; Schnapp et al. 1988). Thus, we surmised that the loss of monomer from degrading collagen fibrils would likely be reflected in the DIC signal, even when the fibril diameters become very small. DIC optics were mounted to a Nikon TE2000E (Nikon, Tokyo, Japan) inverted microscope equipped with a 60×, 1.45 NA Plan Apochromat objective and a digital camera (CoolSNAPHQ2 1394; Photometric, Pleasanton, CA, USA). The microscope was also outfitted with a Perfect Focus interference feedback stage controller that was capable of controlling vertical drift to less than 50 nm (Nikon).

(d). Formation and micromanipulation of reconstituted collagen micronetworks

To generate micronetwork strain, a pair of micropipettes was fitted to Eppendorf TransferMan NK2 micromanipulators (Eppendorf, North America) mounted on the stage (H101A, Proscan II; PRIOR Scientific, Rockland, MA, USA) of the Nikon TE2000E. Prior to mounting, the tips of the pipettes (fire-polished borosilicate with filament, outside diameter 1.0 mm, inside diameter 0.50 mm) were custom manufactured for minimum taper using a P-97 Flamming/Brown micropipette puller (Sutter Instrument Company, Novato, CA, USA) with a five-step programme setting (heat=712,pull=40,vel=15,time=150). To facilitate binding of collagen to the pipette tips, they were first plasma cleaned (PDC-32G; Harrick Plasma, Ithaca, NY, USA) for 0.5 min at 50 W and 26.7 Pa and then functionalized by silanization (3-mercaptopropyl-trimethoxysilane) followed by N-(γ-maleimidobutyryl-oxy)succynimide ester treatment. The functionalized micropipettes were positioned via a micro manipulator, such that they could be observed in close proximity (about 20 μm apart) at 60×. Collagen monomers were prepared for fibrillogenesis according to the packet insert (by gentle mixing of buffer (PBS 10×), NaOH (0.1 M) and the collagen solution (3.0 mg ml⁻¹) in parts of 8:1:1). To produce a fibrillar network or gel, 10 μl of neutralized collagen in buffer was added to the Delta TPG dish, covered with the immersion oil and the temperature raised to 37^°C. A sparse gel micronetwork formed both around and between the pipettes. The micromanipulators were then adjusted to produce a network strain of up to 50 per cent based on initial pipette separation.

In general, it is nearly impossible to produce a uniform strain field in the gel micronetwork. This was due to the fact that the initial conditions were variable and there were routinely different length fibrils between the pipettes. In some cases, the strain was created by simply moving the pipettes apart; in other experiments, the pipettes had to be manipulated significantly to produce observably strained fibrils. In all cases, we attempted to maximize the strain on the micronetwork, and the pipettes were separated until the network was beginning to fail or close to failure (determined by the experience of A. P. Bhole). It must be stated that the amount of realized ‘strain’ at the level of the fibrils was not known. First, even if a full, affine displacement field were calculated, it would not be accurate in predicting the strain on each monomer because the reconstituted fibrils are not cross-linked, and monomers can slide relative to one another within a fibril. Second, because the micronetwork initial strain conditions are variable, the final strain on each fibril in the micronetwork is likely to be different. Previous tensile mechanical testing on reconstituted 3.0 mg ml⁻¹ collagen gels at moderate levels of strain (6%) yielded an equilibrium modulus of approximately 1500 Pa (Krishnan et al. 2004). Reconstituted collagen gels (1.5 mg ml⁻¹) failed at 10 per cent in another series of tensile experiments (Ozerdem & Tozeren 1995). In our system, we routinely exceeded these strain values without frank mechanical failure or significant observable relaxation of the micronetwork between the pipettes. Thus, at least initially, we expect stresses at the micronetwork boundaries well in excess of 1000 Pa (assuming a nonlinear and increasing stress/strain relationship). However, it is known that bulk collagen gels exhibit viscoelastic and indeed liquid-like behaviour (Barocas et al. 1995); thus, it is likely that, following the initial pipette separation, some relaxation will occur.

In light of the complex and uncertain mechanical state of the gel, we were relegated to the demonstration of the existence of an effect of the displacement, rather than development of a specific relationship between strain and degradation rate.

(e). Collagen network degradation

Immediately following micropipette repositioning, 10 μl of 0.025 M bacterial collagenase in Dulbecco’s modified eagle medium (DMEM) was dropped through the oil to permit interaction with the strained micronetwork. In this way, timing of collagenase addition was well controlled to account for stress relaxation. However, the time for the enzyme to reach the pipettes could be variable, so it is possible that some creeping occurred (though little creep was observed following the initial repositioning). The final concentration of enzyme to monomer resulted in a 3.125 : 1 ratio, assuring the presence of more enzyme molecules than available collagen monomers at all times in the chamber.

(i). Diffusion delays

Because the solution could not be stirred, there is an expected and variable delay in the achievement of uniform concentration of enzyme. We anticipate that this is reflected in the variable onset to the initial degradation of the collagen. It is also possible that the enzyme first attacks unpolymerized collagen in the chamber. Because the observable focal plane is extremely thin (approx. 300 nm) diffusion delays in the z-direction would be extremely short. However, the distance between the analysed regions in the strained and unstrained matrix could be much larger (>50 μm), and diffusion delays might be significant. To rule out a systematic effect of diffusion delay on the calculated degradation rates, experiments were visually screened for unequal degradation onsets in the unstrained fibrils on either side of the strained fibrils. Further, a conservative set of statistical comparisons between the calculated degradation rates of the unstrained and strained fibrils were carried out to normalize for delay in the onset of degradation of the strained fibrils. The timing of collagenase addition was well controlled by consistent addition immediately following pipette repositioning.

(ii). Matrix compaction

Traction applied to fibrillar collagen networks in cell populated collagen gels (Barocas & Tranquillo 1997) has been shown to lead to matrix compaction and alignment. Strain-induced gel compaction in our initially sparse matrices was appreciable in some cases owing to attempts to produce a tensile strain field on the micronetwork between the pipettes. Compaction/alignment effects could potentially change the measured degradation time in our system. However, the effect of compaction on collagenase accessibility can be reduced if there is adequate collagenase to ensure that all of the available surface collagen monomers are occupied. In a surface erosion problem, prior to the filling of all available enzyme binding sites, the surface of the collagen will act as an enzyme sink, increasing transport into the denser fibrillar arrays (Tzafriri et al. 2002). Nonetheless, to address the potential effect of matrix compaction on monomer accessibility, we ran several experiments where the tensile strain field was carefully applied to prevent appreciable compaction of the matrix (7 of the 10 datasets).

(f). Image signal processing

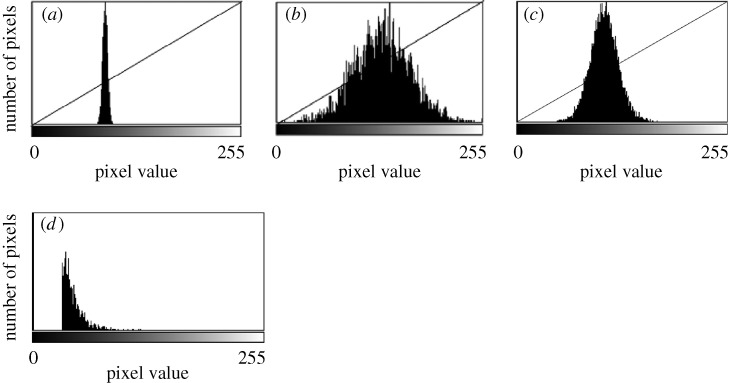
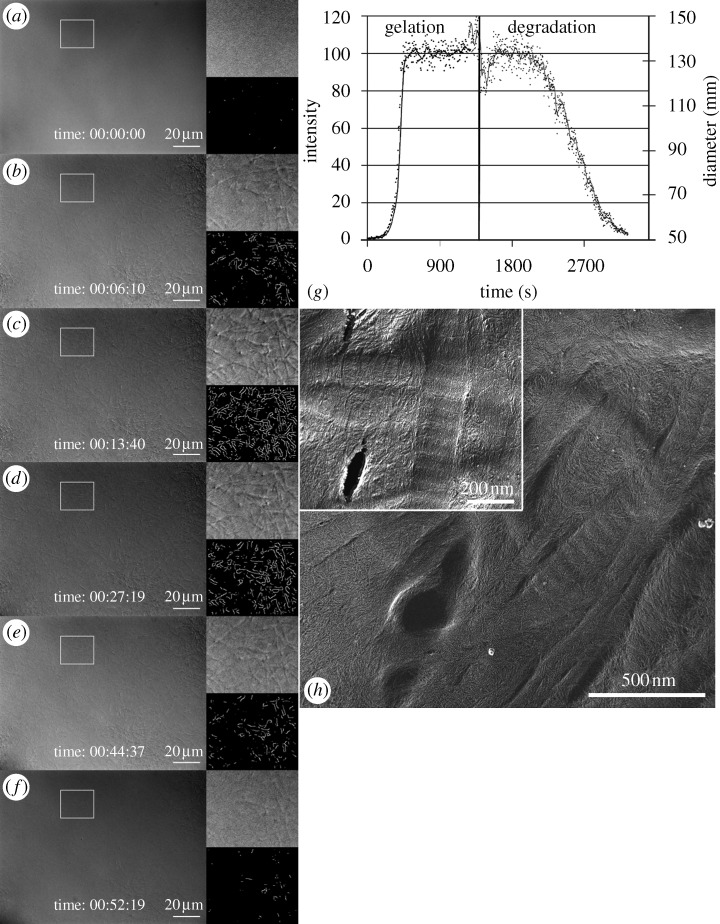
The DIC images extracted during the experiment were subjected to region of interest (ROI)-based edge detection for quantifying collagen degradation rates. Because there can be intensity variations across the large field of view, smaller regions of interest were chosen for analysis to minimize the effect of spatial contrast variation on the edge detection algorithm. The contrast for each strained and unstrained ROI was adjusted to a fixed-width gamma line in Matlab (The Math Works, Inc., Natick, MA, USA) to normalize fibril edge sharpness across time, as shown in figure 2. The initial gamma-line width was determined by the first image taken in the ROI and held constant for the remaining data in the image sequence. The contrast normalized images were then smoothed using a Gaussian filter by a small value (R=1) to reduce the background noise. Edge detection was performed on the temporal stack of strained and unstrained ROI images using a Canny–Deriche edge detection algorithm (α=0.5) in ImageJ software (NIH, Bethesda, MD, USA). The edge-detected 32 bit greyscale image output was converted to 8 bit, and the background noise (corresponding to fibril-free areas within each ROI) was subtracted using Matlab, as shown in figure 2. The summation of all of the pixel intensities (which reflect DIC gradient strength and thus diameter) in an image was assumed to represent the integration of fibril length (detected-edge length)×fibril diameter (gradient intensity), and thus represents a measure of the remaining fibril volume. Summation values for each ROI were normalized to percentages by dividing all values by the maximum value obtained for that ROI during the run. Thus, the values obtained (which we interpreted as the percentage of remaining fibril volume in the two-dimensional slice) were plotted against time for both the strained and unstrained regions. The resulting plots tracked the rate of fibril volume loss due to enzymatic degradation of each of the collagen fibril populations in the ROIs. To illustrate the method, figure 3 depicts the time sequence images of the gelation and degradation of self-assembled fibrils under no strain. Figure 3a–f shows the raw DIC image sequence of matrix gelation followed by degradation. Accompanying insets show the high-magnification DIC of an ROI and the associated processed edge-detected images. Limitations of this approach include the inability to correlate the processed edge strength precisely to fibril diameter and artefact introduced by ‘unmasking’ of edges during degradation events in dense networks. These limitations are mitigated by restricting our analysis to differences in the rate of change of signal strength and by the fact that the DIC imaging method has a very thin focal plane (approx. one collagen fibril thick).

Figure 2.

Contrast normalization and background noise removal. (a) Original histogram distribution in the image taken from the initially captured ROI. (b) Contrast enhancement is accomplished by stretching the lower value of the histogram to 0 and the higher value of the histogram to 255. (c) The width of the gamma line is kept constant about the mean value (brightness) of the histogram in all subsequent images. Thus, the contrast of all subsequent fibril edge strengths will be normalized to that of the initial fibrillar array. (d) The range of contrast noise in the histogram taken from a ‘fibril’-free area was typically subtracted from the histograms following edge detection. In this case, the noise floor was removed by ‘zeroing’ all pixel values below 32.

Figure 3.

Time-series DIC and edge-detected ROI during both gelation and degradation of collagen. (a–f) Larger image in each figure is the DIC of the entire field of view at 600×. The upper right image is a high magnification view of the ROI delineated by the white box to the left. The lower right image is the edge-detected signal, which is scaled to reflect the intensity of the DIC gradient. (g) Graph of the integration of the edge-detected ROI during the experiment. Each point on the plot represents the summation of all pixel intensities within the ROI. Because the pixel intensity is related to the diameter of a fibril in DIC (below the diffraction limit), each point on the plot is a scaled representation of the volume of fibrils within the focal plane in the ROI. (h) Transmission electron microscopy image of a quick-freeze, deep-etched gel sample from control (no pipettes) fibrillogenesis experiment, showing both banded and unbanded fibrils, along with a network of, presumably, much smaller fibrils. Mean fibril diameters are 121 nm (s.d.=18 nm) for banded fibrils and 64 nm (s.d.=11 nm) for unbanded fibrils. Scale bar, 20 μm (a–f); 500 nm (h); 200 nm ((h) inset).

(g). Edge detection method validation

To validate the edge-intensity image processing method used to determine relative fibrillogenesis and degradation rates at least qualitatively, an ideal network of constant-diameter fibrils was simulated for a range of diameters and then evaluated using the same image processing method. Collagen fibrils are modelled as infinite cylinders in the plane of observation, where the light scattering effects can be calculated by solving the cylindrical wave equation, as shown by Bohren & Huffman (1983). While the orientation of fibrils in reconstituted networks is random, DIC microscopy has excellent out-of-plane rejection and thus in-plane fibrils will dominate the intensity data. Forward scatter intensity profiles can be generated for a range of fibril diameters and in-plane angles with respect to incident light polarization, θ_P. A constant-diameter fibril network was simulated by randomly superimposing generated profiles for different values of θ_P with noise added. The DIC image of this simulated network was calculated to produce the final expected image.

(i). Quick-freeze deep-etch imaging

Morphology preserving quick-freeze deep-etch imaging was used to evaluate the initial polymerized condition of the fibrillar networks. Formed collagen gels were slam frozen at −196^°C on copper blocks with a portable cryogun (Delaware Diamond Knives, Wilmingdale, DE, USA). The samples were transferred under liquid nitrogen into a custom CFE-40 freeze-fracture/freeze-etch device (Cressington, Watford, UK). They were then etched at 95^°C for 45 min and rotary shadowed at −130^°C with 2 nm platinum and carbon at 20^° angle and backed by 90^° angle carbon. Replicas were picked up on grids and imaged digitally at 70 kV on a Jeol JEM-1000 (JEOL, Tokyo, Japan).

(h). Data analyses and statistics

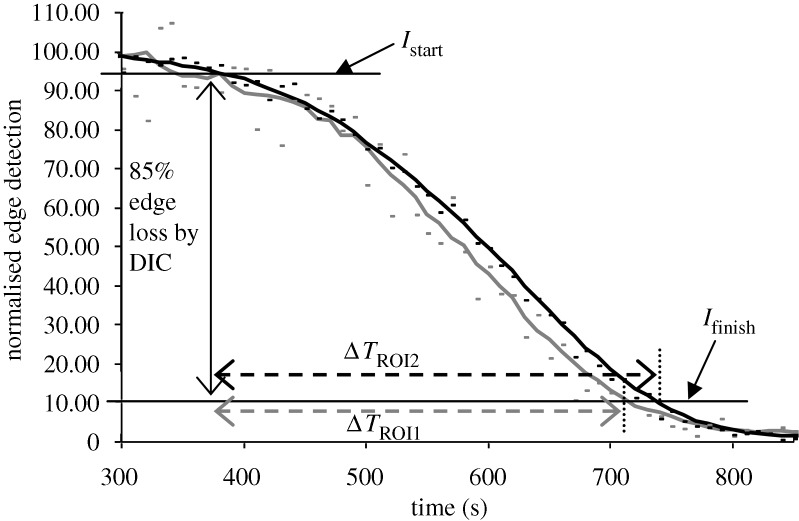
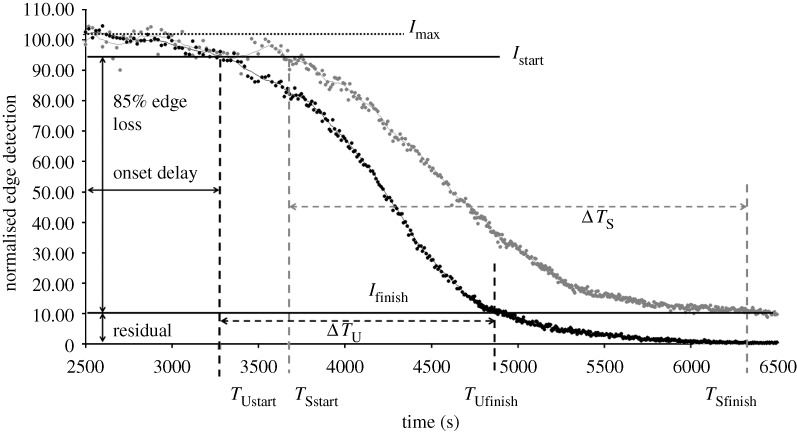
Degradation times within specified ROIs were extracted from the curves produced by the image-processing algorithm described above. The measured ‘degradation’ time was defined as the time interval between 95 per cent (I_start) and 10 per cent (I_finish) of 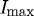(figure 4). The lower bound was conservatively chosen to be 10 per cent of 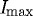. We considered the lower cutoff value conservative, as there were multiple strained fibril digestion experiments that did not reach 5 per cent of 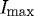prior to the end of the experiment. Degradation times from experimental runs were analysed for normality (Shapiro–Wilks test), skewness and kurtosis, and outliers were removed using SPSS15. A paired, two-tailed Student’s t-test (Excel, Microsoft) was used to assess the statistical significance (p≤0.05) in the processed datasets (n=10) and control experiments (n=2).

Figure 4.

Representative plot showing quantification of edge loss against digestion time ΔT in control sample (no strain), where I_start is 95 per cent of 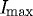(maximum edge detection intensity), I_finish is 10 per cent of 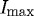and ΔT is the time (s) between. The small difference in the finishing times between the two unstrained ROIs within the same experiment is likely due to diffusion delay coupled with the inherent error in the optical edge-detection algorithm. Grey line, unstrained ROI1; black line, unstrained ROI2.

3. Results of comparative studies of collagen mechanochemistry

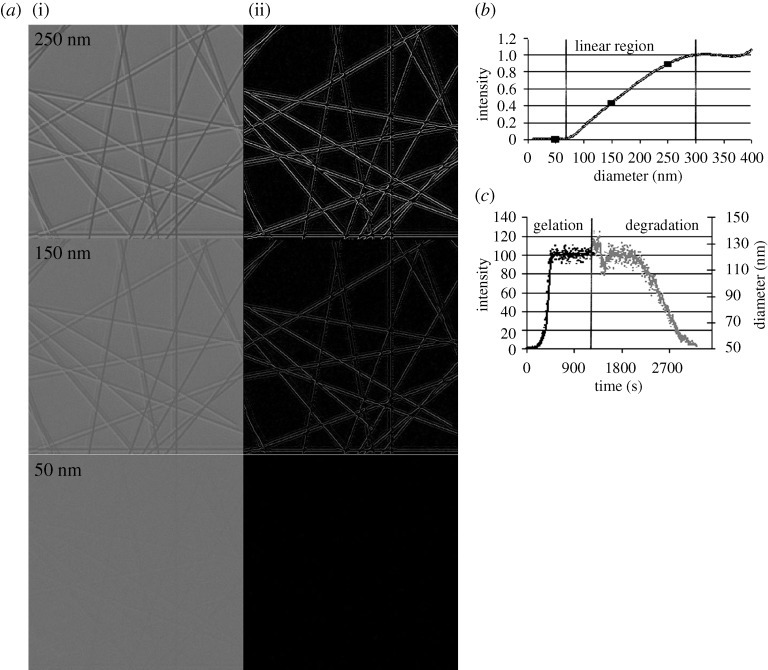
Figures 5 and 6 depict DIC sequences and their corresponding high-magnification and edge-detected ROIs for two different representative experiments. In these (and in all other) experiments, it was possible to discern that strained fibrils survive the enzymatic attack longer than unstrained fibrils. The video-enhanced and edge-detected DIC clearly elucidate the surviving structures. Initial evaluation of simulated edge intensities using the image-processing method described in §2f shows a linear relationship between fibril diameter and DIC edge intensity for fibril diameters of 60–250 nm (figure 7). Within this range, edge intensity provides a good qualitative, and potentially quantitative, method for evaluation of relative fibril diameter. Outside of this range, the edge intensity does not seem to vary much with diameter (figure 7c).

Figure 5.

DIC and edge-detected ROIs. (a) Intial strain on a heavily manipulated network of collagen fibrils. ROIs are strained (S) or unstrained (U). The translucent circle demarcates an area where collagen fibrils have been heavily compacted by our attempt to tension fibrils. The series of four boxes to the right of each large image represent: (upper left) high magnification of strained ROI, (upper right) corresponding detected edges, (lower left) high magnification of unstrained ROI and (lower right) corresponding edge-detected images. (b,c) Follow-on images showing the degradation sequence. Scale bar, 20 μm (a–c).

Figure 6.

DIC and edge-detected ROIs. (a) Initial strain on a gently manipulated network of collagen fibrils. ROIs are located under light tensile strain (S) or no observable strain (U). The four boxes to the right of each large image represent: (vertical boxes) high-magnification DIC and edge-detected signal, (horizontal boxes) high-magnification DIC and edge-detected signal. (b,c) Follow-on images in the sequence showing the pattern of degradation. Unstrained fibrils are removed significantly faster than fibrils loaded in tension. Scale bar, 20 μm (a–c).

Figure 7.

(a) Simulated fibril images (i) for diameters of 50, 150 and 250 nm and the result of the edge detection algorithm for each (ii). Note that the current edge-detection algorithm, in order to deal with noise, normalizes against a fibril-free image. The result of this normalization is a loss of some of the edge information, as can be seen by comparing detected edges with original images. (b) Normalized intensity versus fibril diameter. Note the linear relationship between intensity and diameter for 60–250 nm. (c) Normalized edge intensity and fibril radius in nanometres versus time during formation and enzymatic degradation of collagen fibrils (shown in figure 3).

Figure 8 provides a temporal plot of the integration of detected edge strength, which we interpret as being directly reflective of fibril volume, from two ROIs (strained or unstrained fibrils). Analysis of the data demonstrated that normalized degradation times for unstrained and strained fibrils were statistically different. Moreover, in every experiment, degradation was consistent: ΔT_S>ΔT_U. Quantitatively, the magnitude of the loss of detected edges between I_start and I_finish in strained and unstrained fibrils is ΔT_S=1113±260 and ΔT_U=654±149 s (time±standard error; p=0.0071). This significant difference includes a conservative allowance for the ‘delay’ in the onset of degradation that could be attributed to diffusion differences across the experimental domain. However, it must be stated that the delay in the onset of degradation was consistent in that it only affected the strained fibrils. The effect of strain was efficiently isolated by the presence of control (unstrained) fibrils microns away from the strained ROI; therefore, the reproducibility of the initial gel state is unlikely to skew our analysis. Comparison of the average ‘onset’ time for degradation (as we have defined it: 95% of 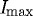) (mean±standard error) was, for strained fibrils, T_Sstart=723±357 s and, for unstrained fibrils, T_Ustart=586±323 s. T_finish also increased under strain; with a mean±standard error of 1836±587 s, compared with an unstrained mean±standard error of 1240±454 s. The large standard error associated with these values could reflect diversity in enzyme activity (from an unknown crude bacterial collagenase cocktail) or from differences in collagen susceptibility across samples.

Figure 8.

Representative plot showing quantification of edge loss against digestion time ΔT, where I_start is 95 per cent of 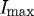(maximum edge detection), I_finish is 10 per cent of 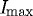and ΔT is the time (s) between. Multiple analyses were completed to consider differences in digestion time based on I_start and I_finish of strained (S) and unstrained (U) fibrils. The residual strained fibril population that persists despite prolonged degradation is marked below 10 per cent 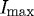. Grey line, strained; black line, unstrained.

We also compared the total loss of strained fibrils during the time it took for unstrained fibrils to fully degrade, as defined by I_Ustart and I_Ufinish (a total of 85% edge-detection loss). The loss of strained fibrils was significantly smaller during this period (mean fibril loss±standard error, 63±4%; p=0.0002). If fibril degradation is considered to begin when the unstrained fibrils reach 95 per cent of 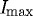(I_Ustart) and if degradation ends when each set of fibrils reaches 5 per cent of 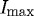(I_Sfinish) (mean±standard error, ΔT_S=1250±306 s and ΔT_U=654±149 s), a highly significant difference in degradation time remains, p=0.0078. Control experiments were also undertaken, where fibrils in the reconstituted matrix (including those between the functionalized pipette tips) were unstrained. Mean±standard error digestion time ΔT (between pipette tips)=510±180 s and, in the surrounding matrix, ΔT_U=565±215 s, a non-significant difference with p=0.5250, implying that the strain can be attributed as the causative factor in degradation-time differences.

4. Discussion and further evidence supporting collagen/enzyme mechanochemistry

The data demonstrate that DIC imaging in combination with an environmentally controlled microchamber enables direct observation of differences in the rate of degradation of strained and unstrained fibrils (permitting quantitative analysis of both control and strained fibrils in the same experiment). In all cases, strained fibrils between the pipettes took longer to degrade. The difference in the time to degradation between unstrained and strained fibrils was statistically significant by a number of measures (including following compensation for onset delay). Additionally, there were a number of experiments that demonstrated complete loss of unstrained fibrils, while strained fibrils persisted visibly for extended periods; thus, the quantitative data matched what we were able to see directly. Therefore, the null hypothesis of faster degradation in strained collagen fibrils has been rejected.

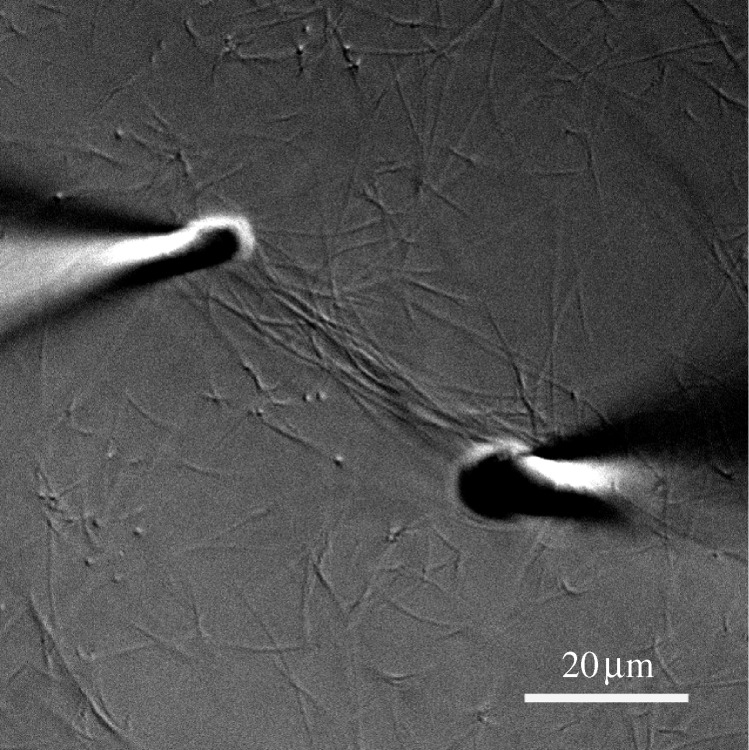
Because bacterial collagenase is readily available and is an aggressive collagen catalytic agent, the results suggest that it might be possible to use bacterial collagenase to rapidly ‘sculpt’ collagenous matrices. Through judicious application of mechanical strain and enzyme, strain-optimized or highly aligned structures might be produced. Figure 9 demonstrates this idea quite nicely. This effect could be useful for tissue engineers attempting to produce anisotropic materials for scaffoldings. In addition to the investigation of the mechanochemistry of collagen/bacterial collagenase, we have begun a series of similar experiments using MMP-8 as the catabolic enzyme. MMPs are one of the few known families of mammalian enzymes capable of cleaving the native collagen triple helix (reviewed extensively in Jeffrey (1998)). Unlike bacterial collagenase, MMPs are very specific with regard to their action on both collagen and on the surrounding matrix molecules. The existence of a mechanochemical relationship between collagen and MMPs could explain numerous biological phenomena. Although these data are preliminary, figure 10 provides the first direct evidence that mechanical strain affords substantial protection from the activity of a physiologically relevant collagen catabolic enzyme (MMP-8, also known as neutrophil collagenase). In all of the preliminary experiments conducted thus far (five), strained collagen was protected against MMP-8 catalytic activity in comparison to unstrained fibrils. The ability to conduct experiments with MMP-8 demonstrates that our microenvironmental, opto-mechanical assay system can handle delicate enzymes with low activity rates at very low concentrations (0.0007 mM). The consequences associated with a strain-dependent mechanochemical relationship between collagen and MMPs would have major implications for our understanding of development, growth, remodelling, homeostasis and pathology of load-bearing collagenous tissue under strain. For example, it is difficult to overstate the impact of diseases such as osteoarthritis on the United States economy and quality of life (Buckwalter et al. 2004), yet the aetiology of the disease remains elusive. However, the idea that mechanical strain protects collagen is consistent with the initiation and progression of diseases such as osteoarthritis (Arokoski et al. 2000). In normal cartilage, the type II collagen network is held in tension by the resident PGs (Maroudas 1972). High compressive mechanical loads (that produce strains in excess of 25 per cent (Maroudas 1972)), loss of PGs, or both, would cause fibrils in the collagen network to ‘slacken’ locally, possibly making them more susceptible to enzymatic breakdown (if enzymes are present). The progression of osteoarthritis may be explained by locally high compressive loads that can occur near existing or incurred defects in cartilage. In these areas, collagen fibrils would experience less stabilizing tensile strain and thus be more susceptible to degradation leading to further loss of mechanical strength (possibly via glycosaminoglycan release secondary to collagen fibrolysis). IVD degeneration typically follows the reduction in tensile mechanical load in the collagen lamellae in the anulus fibrosus after a general decrease in swelling pressure secondary to PG loss (Lyons et al. 1981; Urban & Roberts 2003). The loss of hydrophilic molecules effectively ‘deflates’ the disc and the load on the anulus changes from a mix of torsion, compressive and tensile loads to a primarily compressive load. This loss of tension is followed by degeneration of the anulus and could be explained by the loss of stabilizing tensile load on the collagen. This precise effect has been recently demonstrated by experiments in which intentionally differentially loaded IVDs (half of the disc in compression and half in tension) in a disc degeneration model (Lotz et al. 2008). There are numerous other phenomena where a mechanochemical relationship between collagen and MMP may have relevance, including the instability of unloaded collagen implants (Burke et al.1983, 1985; Donald 1986) and the documented loss of bone and ligament strength in microgravity (Vailas et al. 1990; Zerath 1998). It is also interesting to consider exactly why fibroblasts, upon entering a randomly self-assembled collagen gel, contract the matrix (Bell et al. 1979). By the strain-stabilization theory, it is possible that the fibroblasts are simply attempting to ‘stabilize’ the collagen in the matrix by putting tension on it. The same could be said for contraction of wound matrix by invading myofibroblast cells (for an extensive review, see Jester et al. (1999)). Mechanical loads are also reported to improve organization and strength in other engineered connective tissues (Juncosa-Melvin et al. 2006; Duty et al. 2007) and growth (through intraocular pressure) in the developing chick cornea (Neath et al. 1991). Soft-tissue compensation and growth during cosmetic osteogenesis distraction is clearly an epigenetic response to the applied tensile load. Finally, strain, stretch time and relaxation time have all been reported to determine the mechanical properties of collagen based media equivalents (Isenberg & Tranquillo 2003). In short, there are many phenomena that appear to be consistent with the idea that collagen removal and possibly fibril growth is affected by tensile mechanical strains.

Figure 9.

DIC images of the rapid degradation of the initially strained network shown in figure 2c. (a) Network of collagen fibrils after 3 min of exposure to bacterial collagenase. (b) After 8 min of exposure, fibrils loaded in tension are preserved while unloaded fibrils are preferentially removed from the field of view. Scale bar, 10μm (a,b).

Figure 10.

DIC and edge-detected ROIs in a similar experiment using MMP-8. (a) Initial strain on collagen fibrils formed between pipettes. ROIs are located as described previously, where S denotes a strained region and U denotes an unstrained region. The series of four boxes to the right of each large image are represented as described previously. Follow-on images (b,c) show the pattern of degradation as a function of time. These are preliminary unpublished results. Scale bar, 10 µm (a–c).

5. Concluding remarks and proposal of smart matrix model

The mounting evidence supporting a collagen/enzyme mechanochemical relationship that protects fibrils strained under tension combined with evidence that collagen monomers can organize spontaneously from dense monomer solutions to produce load-bearing structures has compelled us to reassess our view of load-bearing ECM morphogenesis, growth, homeostasis and pathology. It appears that collagen (with its complementary catabolic enzymes) may comprise the basis of smart engineering material and may not simply play the role of a ‘dumb rope’ that must be ‘positioned’ by resident cells. In fact, there is very little evidence supporting the idea that the cells can directly control the placement of each and every monomer at all times during the development, growth and maintenance of load-bearing ECM. By rejecting the notion that cells fully control collagen monomer placement and accepting the idea that collagen is cooperative and mechanoresponsive, a model of how load-bearing structures might be readily constructed starts to emerge. The model requires three components: (i) guided (not directed) assembly of organized collagen arrays possibly from dense monomer solutions, (ii) a strain-dependent relationship between collagen and its complement catabolic enzymes, and (iii) strain-dependent monomer/microfibril incorporation. We propose that these three phenomena may combine to form a smart, simply controlled, scalable, self-optimizing structural system. Load-bearing tissues may form in the following way. An initial collagenous template is first ‘condensed’ from liquid crystal concentrations of monomer that conforms to cell-produced confining geometries and guidance cues (genetic). Second, following the production of the initial template with reasonably appropriate structure, the template is then stabilized and refined by the application of mechanical loads combined with strain-dependent monomer cleavage (epigenetic). Thus, the role of the cells in initial template morphogenesis is greatly simplified. To establish initial structure, fibroblasts would merely need to self-organize (to control the space in which the collagen monomers are concentrated), provide low-energy guidance cues (filopodia, surface proteins, integrin attachments, spindle shape, etc. to direct the collagen monomer orientation) and synthesize molecules. Following the establishment of structure, mechanical loading in the presence of enzyme would help optimize the nascent collagen arrays to their mechanical environment via the strain-stabilization mechanism.

At this point, however, our theory runs into the problem of growth. There is currently no explanation for how load-bearing tissue grows without loss of mechanical integrity. To address this difficulty, we must introduce the hypothesis that free collagen monomers or microfibrils incorporate preferentially into fibrils that are strained in tension. This is the third component of the ‘smart’ matrix theory. Strain-induced polymerization has been observed in other self-assembling biopolymeric systems such as fibronectin (Zhong et al. 1998; Baneyx & Vogel 1999). Figure 11 shows a single experiment in our microenvironmental chamber where the pipettes serendipitously drifted apart by about 100 per cent of the initial distance during collagen fibril self-assembly. We note that some of the fibrils that were bound to both pipettes before they drifted apart became longer and retained their prominent DIC signal (suggesting that they did not thin). Additionally, there appears to be a general accumulation of collagen fibrils in the strained area between the pipettes. Though the data do not yet constitute proof of preferential monomer incorporation (as it could not be directly observed), the concept is supported by the results. Interestingly, if there is preferential monomer incorporation into loaded fibrils, it could lead to a tip in the balance between cleavage and aggregation in the strained micronetwork. Presently, we cannot discount that this may be responsible for the longevity of strained fibrils in our experimental setup.

Figure 11.

DIC image showing what appears to be a substantial accumulation of assembled collagen fibrils in the area of applied tensile strain on the network between the pipettes. The increase in distance between the pipettes from the initial value was approximately 100 per cent. Scale bar, 20 µm.

The ‘smart matrix’ model for load-bearing tissue morphogenesis, growth and homeostasis is reductionist in that it suggests that, if collagen has the intrinsic capacity to self-organize and then adapt in response to the most relevant local control signal (mechanical strain), the role of the matrix-producing fibroblastic cell is profoundly simplified. Fibroblasts would then need only to proliferate, organize themselves into an appropriate guiding geometry and then manufacture the collagen (and auxiliary ECM molecules) that would subsequently self-organize and adapt to carry the applied loads. Load-directed self-organization and growth would result from a balance of strain-directed collagen monomer incorporation into loaded fibrils and preferential removal of unstrained monomers and fibrils. This idea is supported by the fact that both matrix-degrading (MMPs) and matrix-building molecules (collagen monomers, PGs, etc.) can be found simultaneously in developing and remodelling connective tissue in vivo and in vitro (Moses et al. 1996; Robbins et al. 1997; Prajapati et al. 2000; Riley et al. 2002; He et al. 2004; Koskinen et al. 2004). In closing, we suggest that, without such cooperative and load-adaptive engineering material at their disposal, it is difficult to understand how the myriad of scalable, load-bearing structures could be produced by the most mechanically advanced metazoans: the vertebrates.