Abstract
Evolving constituent composition and organization are important determinants of the biomechanical behaviour of soft tissues. In arteries, vascular smooth muscle cells and fibroblasts continually produce and degrade matrix constituents in preferred modes and at altered rates in response to changing mechanical stimuli. Smooth muscle cells similarly exhibit vasoactive changes that contribute to the control of overall structure, function and mechanical behaviour. Constrained mixture models provide a useful framework in which to quantify arterial growth and remodelling for they can account for cell-mediated changes in individual structurally significant constituents. Our simulations show that the combined effects of changing mass density turnover and vasoactivity, as well as the prestretch at which constituents are incorporated within extant matrix, are essential to capture salient features of bounded arterial growth and remodelling. These findings emphasize the importance of formulating biologically motivated constitutive relations in any theory of growth and remodelling and distinct advantages of the constrained mixture approach, in particular.
Keywords: vasoactivity, collagen turnover, smooth muscle phenotype, deposition stretch, stress
1. Introduction
It is well accepted that arteries grow and remodel via cell and matrix turnover, and different constituents, possessing different natural configurations and mechanical properties, exhibit different (although likely intricately linked) rates of turnover that can change with mechanical stimuli. Thus, in addition to complex instantaneous nonlinear mechanical behaviours, time-varying changes in composition resulting from mass turnover are important determinants of arterial biomechanics. Rodbard (1975) introduced the concept of coupled vasoactivity and matrix remodelling via a two-phase process of acute changes in vasoactive tone followed by long-term entrenchment. This hypothesis has since been substantiated by numerous observations and is summarized well by Dajnowiec & Langille (2007). Experimental observations (Kelleher et al. 2004; Meshel et al. 2005; Kozel et al. 2006) reveal further that cells achieve such growth and remodelling (G&R) by actively manipulating structural proteins during and following deposition. That is, mechanical forces exerted by synthetic cells during deposition or reorganization contribute to the unique mechanical properties exhibited by the extracellular matrix, which, in general, can lead to residual stresses in unloaded tissues and thus optimal states of stress in vivo (cf. Cardamone et al. in press). Indeed, it appears that new constituents are deposited at preferred (homeostatic) stretches, which need not be equal for all constituents. In short, myriad studies, observed over diverse conditions in as many contexts (cf. Humphrey 2002; Humphrey & Rajagopal 2002), strongly suggest that mechano-controlled variable mass turnover, vasoactivity and preferred constituent deposition stretches are important fundamental mechanisms in arterial G&R. The goal of this paper is to explore numerically the individual and coupled roles of these different adaptive mechanisms via null hypothesis testing.
2. Background
Arterial homeostasis is a stable dynamic process that varies mass production and removal to optimize structure and function. Consideration of normal situations allows a heuristic investigation of some key concepts. Consider a healthy artery, with no loss of vasoactivity or elastin, that must maintain a constant geometry (radius, thickness and unloaded length) in response to an unchanging steady-state transmural pressure and flow despite continual turnover of collagen and smooth muscle; we call this tissue maintenance. The normal half-life of arterial collagen is approximately 70 days, for example, and smooth muscle turns over at <0.06 per cent per day (Langille 1993; Stenmark & Mecham 1997). If load-bearing ‘old’ collagen is degraded and replaced with new fibres that are stress free, that is, having a 0 per cent deposition stretch, then, because of the nonlinear properties, it is intuitive that smooth muscle would need to contract more to maintain the original inner radius in response to unchanging pressure and flow. This accommodation would be energetically unfavourable, however, and could reduce the vessel’s vasoactive range. Mechanistically, this suggests that cells should be capable of depositing or arranging new extracellular matrix fibres within extant matrix to have a stretch greater than unity. In this way, synthetic cells could effectively solve the problem of tissue maintenance without the need for an elevated and sustained exertion of active force by smooth muscle cells and the associated energy expenditure required to maintain circumferential equilibrium and an optimal luminal radius. However, it shall prove useful below to consider this situation numerically.
Our group has employed continuum-based constrained mixture models to investigate arterial G&R (Gleason et al. 2004; Gleason & Humphrey 2004, 2005; Baek et al. 2007; Valentín et al. 2009). These studies represent progressively more detailed implementations of the same general theoretical framework; they have captured salient trends by qualitatively (and in some cases quantitatively) predicting important experimental observations. A unique strength of the constrained mixture approach stems from its ability to include effects of fundamental cellular behaviours that contribute to mechanically driven G&R. Although the innovative concept of kinematic growth (Skalak 1981; Rodriguez et al. 1994; Rachev et al. 1998; Taber 1998) approximates the consequences of underlying mechanisms, it assumes that growth occurs in fictitious stress-free configurations, which it does not, and it does not account for basic cellular production (synthesis) and removal (degradation) of matrix. In this work, we aim to provide a more robust level of model verification (cf. Anderson et al. 2007) by scrutinizing the basic hypotheses upon which constrained mixture models are built and by showing that the currently implemented framework faithfully captures theoretical expectations and exhibits many observed consequences of arterial G&R.
3. Methods
(a). General continuum framework
Employing two-dimensional wall mechanics for a cylindrical segment of an artery, two equilibrium equations can be written in terms of the mean circumferential and axial stresses, namely
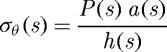 |
3.1 |
and
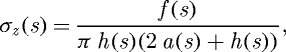 |
3.2 |
where P is the transmural pressure, a is the deformed inner radius, h is the deformed wall thickness and f is the applied axial force, each defined at G&R time s. Note that these two equations are not sufficient to solve for the three primary geometric variables: a, h and axial length l. Together with a constancy of mass density ρ(s)≡ρ(0), however, prescribing l(s) allows us to solve for a(s) and h(s), two variables of particular importance in flow- and pressure-induced adaptations.
The total Cauchy stress, including contributions from multiple passive constituents and active smooth muscle, can be computed as
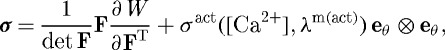 |
3.3 |
where F is the deformation gradient tensor, W is the homogenized strain energy function for the mixture and σact is the active muscle contribution (ultimately a function of intracellular calcium ion concentration [Ca2+] and muscle fibre stretch λm(act)) in the direction eθ. Employing a rule of mixtures approach, this strain energy function can be conceptualized as the sum of constituent contributions 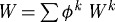 , where ϕk are the constituent mass fractions and Wk are the strain energy functions for each structurally significant constituent (e.g. collagen, elastin, smooth muscle). More generally, however, one can account for changing mass fractions by following changing mass densities. Evolving constituent mass densities Mk, defined per unit area, can be computed as (cf. Baek et al. 2006)
, where ϕk are the constituent mass fractions and Wk are the strain energy functions for each structurally significant constituent (e.g. collagen, elastin, smooth muscle). More generally, however, one can account for changing mass fractions by following changing mass densities. Evolving constituent mass densities Mk, defined per unit area, can be computed as (cf. Baek et al. 2006)
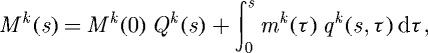 |
3.4 |
where Qk(s)∈[0,1] are survival fractions for constituents deposited before time s=0, mk(τ) are variable mass density production rates and qk(s,τ)∈[0,1] are survival fractions for constituents deposited at time τ∈[0,s] that survive to current G&R time s. The possibly evolving constituent strain energy functions, also defined per reference area, can thus be written as (cf. Baek et al. 2006)
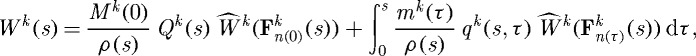 |
3.5 |
where ρ(s) is the mass density of the mixture, which is assumed to be constant (Rodriguez et al. 1994; Humphrey & Rajagopal 2002), and 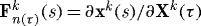 , with xk(s)=x(s) constraining all constituents to deform together and Xk(τ) reflecting different evolving natural configurations for constituents k when produced at time τ. In other words, subscripts n(0) and n(τ) denote individual natural configurations associated with times of deposition (at s=0 or before, versus τ∈[0,s]). These configurations facilitate the tracking of evolving constituent properties from the time of deposition. Additional details of the basic framework can be found in Baek et al. (2006) and Valentín et al. (2009).
, with xk(s)=x(s) constraining all constituents to deform together and Xk(τ) reflecting different evolving natural configurations for constituents k when produced at time τ. In other words, subscripts n(0) and n(τ) denote individual natural configurations associated with times of deposition (at s=0 or before, versus τ∈[0,s]). These configurations facilitate the tracking of evolving constituent properties from the time of deposition. Additional details of the basic framework can be found in Baek et al. (2006) and Valentín et al. (2009).
(b). Fundamental hypotheses
(i). Deposition stretch
The stretches at which constituents are deposited within extant extracellular matrix and the target homeostatic mechanical states for cells and matrix represent central assumptions within constrained mixture models of G&R (cf. Humphrey 2008a). The basic hypothesis that synthetic cells deposit new fibrillar proteins (such as collagens types I and III) at a preferred (homeostatic) stretch and that smooth muscle cells remodel to maintain a target state of stretch is married to the constrained mixture approach through a sequence of multiplicative deformations. For example, the total stretch experienced at G&R time s by a fibre deposited at time τ is (Baek et al. 2006)
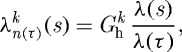 |
3.6 |
where 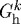 is the homeostatic deposition stretch for the kth constituent and λ(s) and λ(τ) are potentially measurable stretches experienced by the mixture at times s and τ, respectively. This result follows directly from the assumption that constituent motions follow those of the artery, despite having individual natural (stress-free) configurations, which is fundamental to the idea of a constrained mixture, as proposed by Humphrey & Rajagopal (2002). Letting
is the homeostatic deposition stretch for the kth constituent and λ(s) and λ(τ) are potentially measurable stretches experienced by the mixture at times s and τ, respectively. This result follows directly from the assumption that constituent motions follow those of the artery, despite having individual natural (stress-free) configurations, which is fundamental to the idea of a constrained mixture, as proposed by Humphrey & Rajagopal (2002). Letting 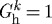 thus allows us to simulate consequences of disallowing fibroblasts and synthetic smooth muscle cells to endow fibrillar collagens (Meshel et al. 2005; Kozel et al. 2006) or cytoskeletal proteins (Na et al. 2008) with a homeostatic stretch at deposition time τ.
thus allows us to simulate consequences of disallowing fibroblasts and synthetic smooth muscle cells to endow fibrillar collagens (Meshel et al. 2005; Kozel et al. 2006) or cytoskeletal proteins (Na et al. 2008) with a homeostatic stretch at deposition time τ.
(ii). Smooth muscle contractility
Arteries possess the ability to constrict or dilate rapidly in response to a range of decreasing or increasing volumetric blood flow (i.e. wall shear stress). This vasoactivity is achieved via a [Ca2+]-mediated actin–myosin contractile mechanism, which can be abstracted as a product of two functions: a chemical dose response function, modulating the maximum force developed, and a length-dependent force generation envelope that relates to the degree of actin and myosin filament overlap (Ruch & Patton 1966; Guyton & Hall 1997). Briefly, diverse substances such as nitric oxide (NO), endothelin-1 (ET-1), norepinephrine (NE) and acetylcholine (ACh) control vasoactivity. For example, subjecting endothelial cells to increased shear stress upregulates the production of NO, a potent vasodilator. For a given level of [Ca2+], smooth muscle develops peak force at an optimal length 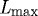 and diminished forces as
and diminished forces as 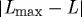 increases.
increases.
These two separate mechanisms were elucidated experimentally in Price et al. (1981) for canine anterior tibial arteries, with dose-response curves exhibiting roughly sigmoidal behaviour and force–length curves exhibiting the familiar inverse parabolic behaviour characteristic of skeletal muscle (cf. Rachev & Hayashi 1999). Force–length behaviour was reported only for one constrictor dose (corresponding to 50% maximum contraction), but one can imagine a family of force–length curves for varying constrictor dosages. The combined effect of these two mechanisms can be generalized conceptually as
| 3.7 |
where 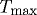 is a scaling factor with units kPa, C is a net ratio of constrictors to dilators and λm(act) is a measure of active smooth muscle fibre stretch, which can be related to
is a scaling factor with units kPa, C is a net ratio of constrictors to dilators and λm(act) is a measure of active smooth muscle fibre stretch, which can be related to 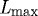 . Letting
. Letting  kPa eliminates the active response.
kPa eliminates the active response.
(iii). Variable mass turnover
Tissue maintenance requires balanced basal rates of mass production and removal to preserve normal structure and function. The vasculature must also accommodate changing physiological demands through functional adaptations, which may require deviations from basal turnover rates (Nissen et al. 1978; Sluijter et al. 2004). Numerous studies have investigated relationships between mechanical stimuli and changing synthetic and degradative behaviour (Humphrey 2008a). Consistent with this idea, mass density production rates can be conceptualized as (cf. eqn 1 in Fung 1991)
| 3.8 |
where 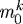 is a basal production rate, Δσ is a normalized difference between the current and target value of an appropriate scalar measure of intramural stress, Δτw is a normalized difference between the current and target values of the magnitude of the luminal wall shear stress, and
is a basal production rate, Δσ is a normalized difference between the current and target value of an appropriate scalar measure of intramural stress, Δτw is a normalized difference between the current and target values of the magnitude of the luminal wall shear stress, and  , which recovers the basal rate. Note that this basal production rate corresponds to normal conditions in maturity (homeostatic constituent deposition stretches and full vasoactive capability) and yields a constant geometry and mechanical properties (i.e. tissue maintenance provided balanced removal via qk), as long as there are no mechanical perturbations. Allowing mk to vary with changing mechanical stimuli enables the vessel’s geometry and properties to adapt so as to maintain τw, σθ and σz near homeostatic values while maintaining a preferred mechanical state. Forcing
, which recovers the basal rate. Note that this basal production rate corresponds to normal conditions in maturity (homeostatic constituent deposition stretches and full vasoactive capability) and yields a constant geometry and mechanical properties (i.e. tissue maintenance provided balanced removal via qk), as long as there are no mechanical perturbations. Allowing mk to vary with changing mechanical stimuli enables the vessel’s geometry and properties to adapt so as to maintain τw, σθ and σz near homeostatic values while maintaining a preferred mechanical state. Forcing 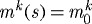 effectively renders the vessel incapable of modulating its G&R response to changes in mechanical environment.
effectively renders the vessel incapable of modulating its G&R response to changes in mechanical environment.
(c). Illustrative functional forms
In contrast to the general functional forms introduced above, specific forms are needed to illustrate numerically the consequences of fundamental characteristics of wall maintenance and adaptation. Many different functional forms have been or could be postulated based on the available data, and there is a pressing need for more research in this area. Nevertheless, we use the same specific functional forms and parameter values for the basilar artery as in Valentín et al. (2009), which were found to give rise to well-behaved G&R. That is, we use a neo-Hookean stored energy function for elastin and Fung exponentials for fibrillar collagen and passive smooth muscle. Moreover, a specific form of equation (3.7) can be written as (cf. Price et al. 1981; Rachev & Hayashi 1999)
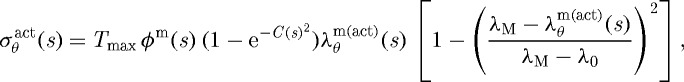 |
3.9 |
where ϕm is the mass fraction of active smooth muscle, λM and λ0 are the stretches at which the force-generating capacity is maximum and zero, respectively, and λm(act)θ(s)=a(s)/am(act)(s), where am(act)(s) evolves via a first-order rate equation. Towards this end, note that Murray (1926) led others (Rodbard 1975; Zamir 1977) to the conclusion that blood vessels change calibre to maintain a target wall shear stress. For fully developed laminar flow of a Newtonian fluid in a rigid tube, the mean wall shear stress can be approximated as τw=4μQ/πa3, where μ is the viscosity of blood, Q is the volumetric flow rate and a is the luminal radius. The ratio of constrictors to dilators C(s) is thus ultimately a function of wall shear stress
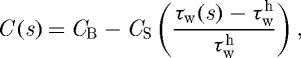 |
3.10 |
where CB is the basal ratio, CS is a scaling factor for shear-stress-induced changes and 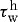 is the homeostatic (target) wall shear stress. Note that increases in τw above homeostatic tend to increase the production of NO (a vasodilator) by the endothelium, whereas decreases in τw below homeostatic give rise to ET-1 (a vasoconstrictor) production.
is the homeostatic (target) wall shear stress. Note that increases in τw above homeostatic tend to increase the production of NO (a vasodilator) by the endothelium, whereas decreases in τw below homeostatic give rise to ET-1 (a vasoconstrictor) production.
Mass density production of collagen (synthesis) and smooth muscle (proliferation) is known to vary with changes in smooth muscle cell stretch/stress (Leung et al. 1976; Wilson et al. 1993; Li et al. 1998), as well as with changes in the endothelial release of NO and ET-1 (Rizvi et al. 1996; Rizvi & Myers 1997; Dooley et al. 2007). For illustrative purposes, let production be prescribed as a linear function of mechanical stimuli (cf. Taber 1998; Rachev 2000)
| 3.11 |
where k denotes individual families of fibrillar collagen or contractile smooth muscle, σ is a scalar measure of intramural stress and 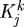 are rate parameters that govern the stress-mediated production rates. Degradation of structural proteins and cell apoptosis appear to be well described by first-order type kinetics, with appropriate half-lives (Niedermüller et al. 1977; Cho et al. 1995). Hence, let the survival functions be (cf. Baek et al. 2007; Valentín et al. 2009)
are rate parameters that govern the stress-mediated production rates. Degradation of structural proteins and cell apoptosis appear to be well described by first-order type kinetics, with appropriate half-lives (Niedermüller et al. 1977; Cho et al. 1995). Hence, let the survival functions be (cf. Baek et al. 2007; Valentín et al. 2009)
| 3.12 |
where  are rate-type parameters for mass removal with units of days−1. These rate parameters, in turn, are prescribed as
are rate-type parameters for mass removal with units of days−1. These rate parameters, in turn, are prescribed as 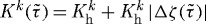 , where
, where 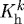 is a basal value (inverse the half-life),
is a basal value (inverse the half-life),  is the difference in fibre tension from its homeostatic value and ζk(τ) is the level of tension on fibre family k that was produced at time τ. Note that elastin is assumed to be highly stable under non-pathological conditions (Langille 1996) and produced exclusively during early development, thus Qe(s)≡1 and me(s)≡0
is the difference in fibre tension from its homeostatic value and ζk(τ) is the level of tension on fibre family k that was produced at time τ. Note that elastin is assumed to be highly stable under non-pathological conditions (Langille 1996) and produced exclusively during early development, thus Qe(s)≡1 and me(s)≡0  in maturity.
in maturity.
(d). Solution procedure
Assumptions of quasi-static two-dimensional wall mechanics reduce the equilibrium equations to nonlinear algebraic equations (cf. equations (3.1) and (3.2)), which are solved easily for the proposed G&R framework (cf. equation (3.5)) by equating them with Cauchy membrane stress resultants Ti for the principal directions i=z,θ (Valentín et al. 2009), namely
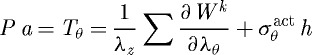 |
3.13 |
and
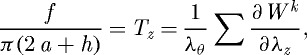 |
3.14 |
where λθ and λz are stretches experienced by the mixture in the circumferential and axial directions, respectively. Note also that 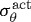 is a function of inner radius via equations (3.9) and (3.10) and
is a function of inner radius via equations (3.9) and (3.10) and  . Prescribing in vivo axial length l, transmural pressure P and luminal flow Q at all G&R times s permits one to solve for the inner radius via equation (3.13). At each computational time step δ, we can solve for aδ such that
. Prescribing in vivo axial length l, transmural pressure P and luminal flow Q at all G&R times s permits one to solve for the inner radius via equation (3.13). At each computational time step δ, we can solve for aδ such that
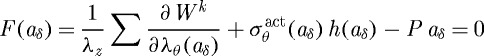 |
3.15 |
via the Newton–Raphson method. The resulting intramural stresses, stretches and wall shear stresses control mass production (equation (3.11)), mass removal (equation (3.12)) and vasoactivity (equations (3.9) and (3.10)). Finally, consistent with Valentín et al. (2009), illustrative values of the material parameters represent a normal basilar artery (table 1).
Table 1.
Material parameters and their values for a representative mature basilar artery under homeostatic conditions.
| role | value |
|---|---|
| vessel geometry | ah=1.42 mm, hh=0.176 mm |
| initial loads | P=93 mmHg, Q=3.075 ml s−1 |
| constituent mass fractions | 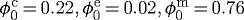 |
| homeostatic kinetics |
 day−1, day−1, 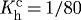 day−1 day−1
|
| vasoactive parameters |
 kPa, λM=1.1,λ0=0.4, CB=0.68,CS=20 CB kPa, λM=1.1,λ0=0.4, CB=0.68,CS=20 CB
|
| target stresses |
σh=100 kPa,  Pa Pa |
| deposition stretches | 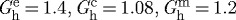 |
Although two-dimensional equations do not allow one to consider transmural differences in G&R, including associated experimental findings from histology, immunohistochemistry or opening angle tests (cf. Cardamone et al. in press), they enable one to examine clinically relevant changes in calibre and structural stiffness, including reasons for the latter. Moreover, we emphasize that the constrained mixture model enables one to incorporate significant biological information, including mechano-stimulated rates of matrix production or cell proliferation (Leung et al. 1976; Wilson et al. 1993; Li et al. 1998), known degradation kinetics and half-lives (Niedermüller et al. 1977; Nissen et al. 1978; Stenmark & Mecham 1997), the possibility of different deposition stretches for different constituents (Meshel et al. 2005; Kozel et al. 2006) and different mechanical properties for different constituents (Dorrington & McCrum 1977; Lanir 1983; Holzapfel et al. 2000). There are, of course, many other types of models possible for arterial G&R (e.g. Rachev et al. 1998, 2000; Taber 1998; Rachev 2000; Fridez et al. 2001; Driessen et al. 2004; Hariton et al. 2007; Kuhl et al. 2007; Menzel 2007; Tsamis & Stergiopulos 2007; Alford et al. 2008), but our focus herein is on constrained mixture models.
4. Illustrative results
(a). Deposition stretch
We have conjectured that constituents are deposited at preferred (homeostatic) values of stretch in maturity that render them optimally stressed when first incorporated within the extant matrix; these stretches are necessarily greater than unity, but differ considerably in basilar arteries for elastin (e.g. 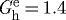 ), collagen (e.g.
), collagen (e.g. 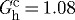 ) and smooth muscle (e.g.
) and smooth muscle (e.g. 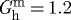 ). Note that elastin is probably deposited at a smaller value during development, but owing to its long half-life, it is stretched further by normal maturation; we consider here the net effect of these two processes, thus it can be thought of more as a net prestretch rather than a deposition stretch (cf. Cardamone et al. in press). One way to test the consequences of such an assumption numerically is to let
). Note that elastin is probably deposited at a smaller value during development, but owing to its long half-life, it is stretched further by normal maturation; we consider here the net effect of these two processes, thus it can be thought of more as a net prestretch rather than a deposition stretch (cf. Cardamone et al. in press). One way to test the consequences of such an assumption numerically is to let 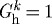 for k=c and m for all G&R times
for k=c and m for all G&R times 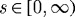 . Simulations show that this results in suboptimal tissue maintenance or remodelling (figure 1). To appreciate this, recall that mean values of the homeostatic (target) wall shear stress and circumferential stress are
. Simulations show that this results in suboptimal tissue maintenance or remodelling (figure 1). To appreciate this, recall that mean values of the homeostatic (target) wall shear stress and circumferential stress are
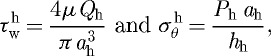 |
4.1 |
thus with sustained step changes in flow and pressure given by Q=ϵ Qh and P=γ Ph, respectively, the idealized expected radius and wall thickness are a=ϵ1/3 ah and h=γ ϵ1/3 hh (Humphrey 2008b). In all cases considered (ϵ,γ=0.9,1.0,1.1), the artery with 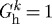 exhibited modest increases from the expected inner radius (<1%), but wall thicknesses that were far greater (approx. 720%) than expected based on a simple force balance. Figure 2 shows that increased production of smooth muscle accounted for this hypertrophy. Increased smooth muscle contractility was required to generate greater circumferential stresses (figures 3 and 4) in an attempt to offset the trend of enlargement owing to increased collagen and smooth muscle deposition at
exhibited modest increases from the expected inner radius (<1%), but wall thicknesses that were far greater (approx. 720%) than expected based on a simple force balance. Figure 2 shows that increased production of smooth muscle accounted for this hypertrophy. Increased smooth muscle contractility was required to generate greater circumferential stresses (figures 3 and 4) in an attempt to offset the trend of enlargement owing to increased collagen and smooth muscle deposition at  ; this compensatory mechanism is perhaps best appreciated in the case of increased pressure wherein increased contractility is needed to maintain wall shear stress, despite the distending action of pressure. Nevertheless, this overall finding is consistent with the idea that, if collagen is replaced with initially stress-free fibres, the only way that the artery can maintain its calibre is to increase active force generation by increasing the total mass of smooth muscle, increasing the contraction of extant active muscle, or some combination of both. Coupled with the decreased wall shear stress due to passive distension (which would probably induce ET-1 production and thus increase C), an increase in smooth muscle stress worked to increase the mass density production rate of smooth muscle (see equations (3.10) and (3.11)). Indeed, this already muscular basilar artery numerically gained much more smooth muscle than expected as it remodelled to maintain equilibrium.
; this compensatory mechanism is perhaps best appreciated in the case of increased pressure wherein increased contractility is needed to maintain wall shear stress, despite the distending action of pressure. Nevertheless, this overall finding is consistent with the idea that, if collagen is replaced with initially stress-free fibres, the only way that the artery can maintain its calibre is to increase active force generation by increasing the total mass of smooth muscle, increasing the contraction of extant active muscle, or some combination of both. Coupled with the decreased wall shear stress due to passive distension (which would probably induce ET-1 production and thus increase C), an increase in smooth muscle stress worked to increase the mass density production rate of smooth muscle (see equations (3.10) and (3.11)). Indeed, this already muscular basilar artery numerically gained much more smooth muscle than expected as it remodelled to maintain equilibrium.
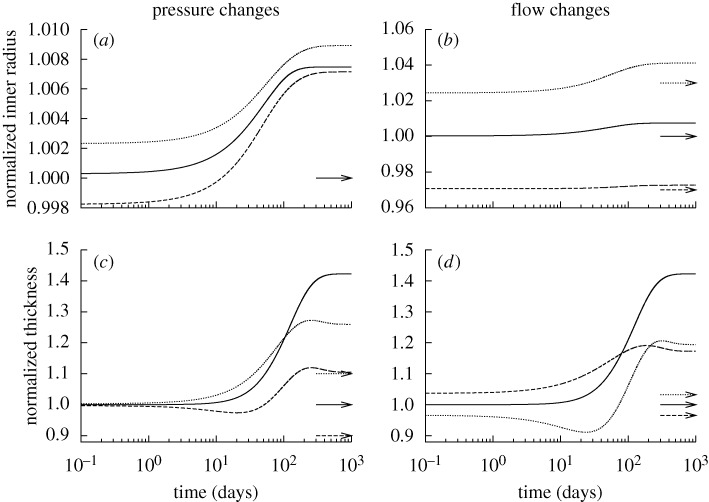
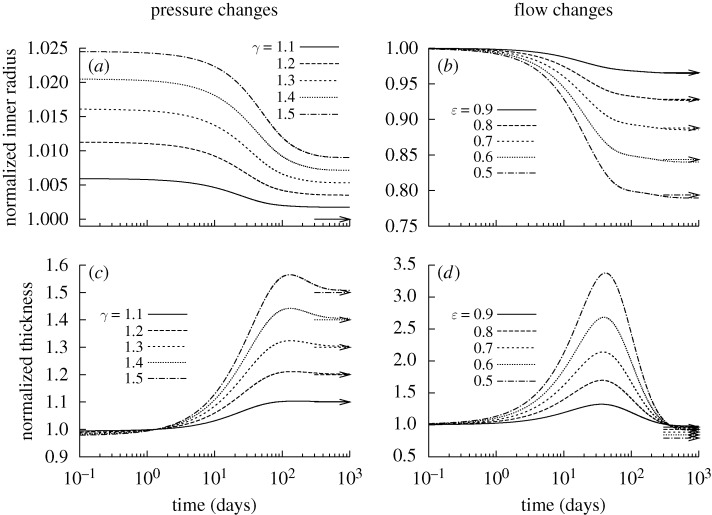
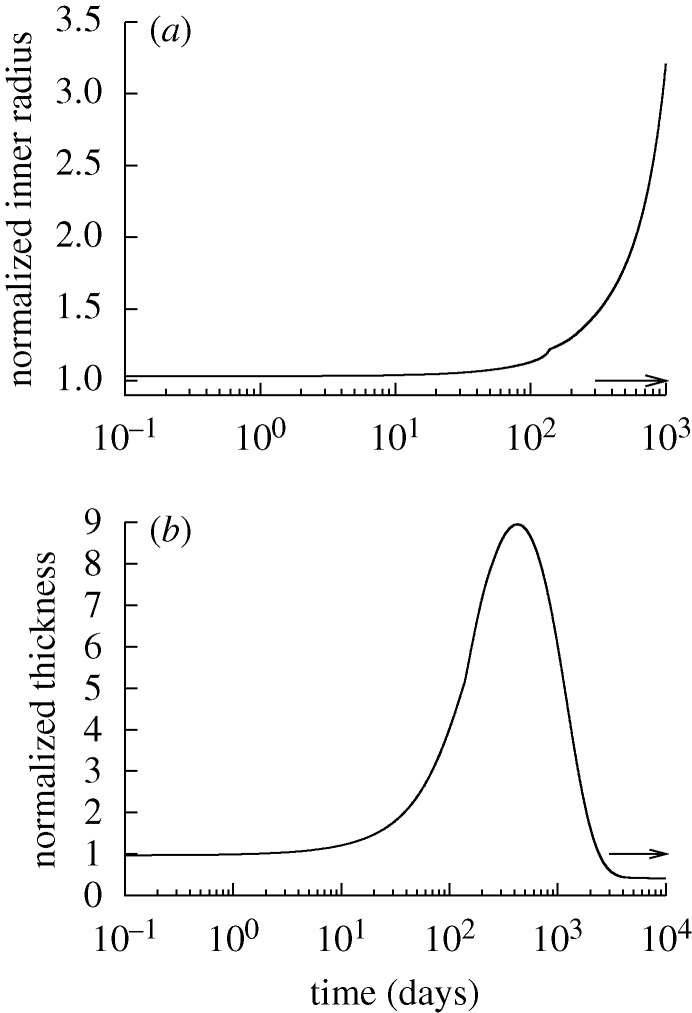
Figure 1.
Time courses of changing inner radius (a,b) and wall thickness (c,d) for changes in pressure (left) and flow (right) of −10% (dashed) and +10% (dotted) from the homeostatic value (solid) with  ∀s∈[0,1000] days. Expected values (cf. equation (4.1)) are indicated by corresponding arrows on the right ordinate. Although the vessel could neither maintain nor attain expected geometries, these changes stabilized asymptotically after long periods. Note the predicted large increase in wall thickness for all cases, suggesting the need for excessive deposition of sub-optimal material to compensate for the loss of the originally optimally deposited material. All quantities normalized with respect to homeostatic values at time s=0. These results can be compared to those in Valentín et al. (2009), which show ‘normal’ evolution towards expected values.
∀s∈[0,1000] days. Expected values (cf. equation (4.1)) are indicated by corresponding arrows on the right ordinate. Although the vessel could neither maintain nor attain expected geometries, these changes stabilized asymptotically after long periods. Note the predicted large increase in wall thickness for all cases, suggesting the need for excessive deposition of sub-optimal material to compensate for the loss of the originally optimally deposited material. All quantities normalized with respect to homeostatic values at time s=0. These results can be compared to those in Valentín et al. (2009), which show ‘normal’ evolution towards expected values.
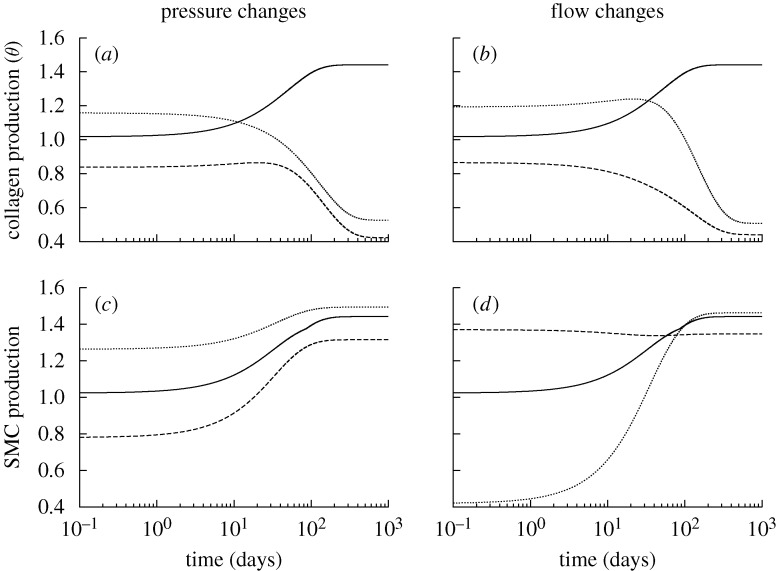
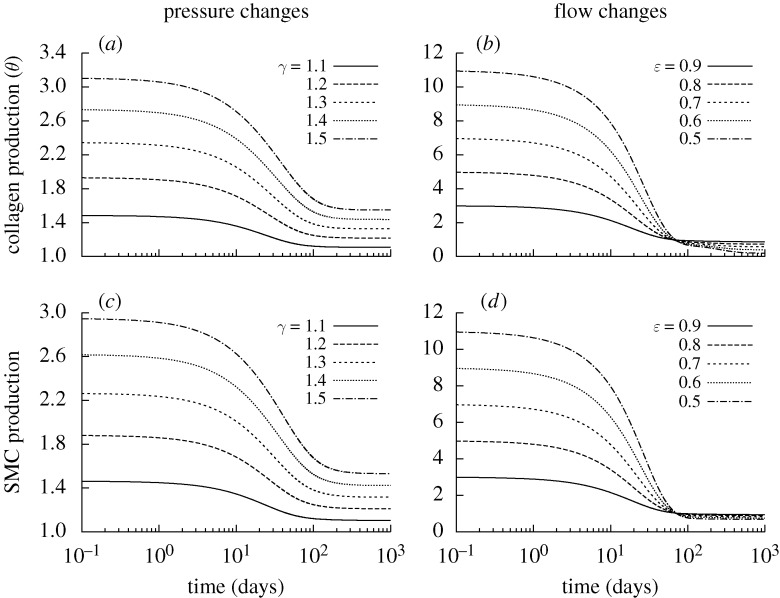
Figure 2.
Time courses of rates of mass density production for circumferential collagen (a,b) and smooth muscle (c,d), normalized with respect to homeostatic rates at s=0, for changes in pressure (left) and flow (right) of −10% (dashed) and +10% (dotted) from the homeostatic (solid) value where 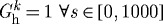 days. Note the predicted large and sustained increases in smooth muscle production. SMC is smooth muscle cell.
days. Note the predicted large and sustained increases in smooth muscle production. SMC is smooth muscle cell.
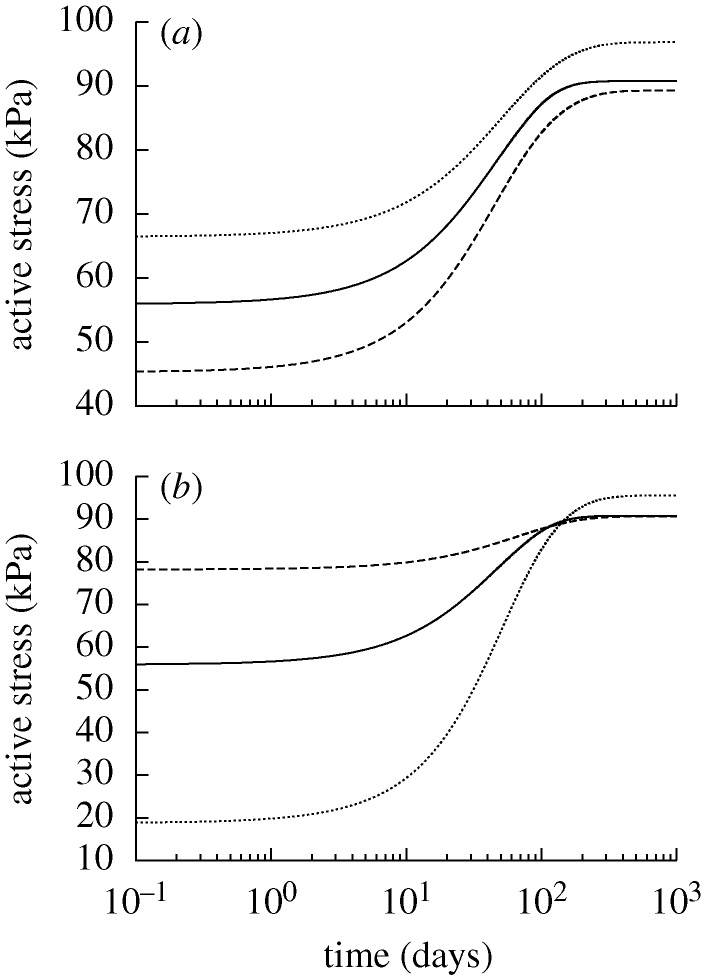
Figure 3.
Time courses of actively generated stress for changes in pressure (a) and flow (b) of −10% (dashed) and +10% (dotted) from the homeostatic (solid) value where  days. Initial decreases in active stress in the cases of decreased pressure and increased flow resulted from decreasing C as the vessel compensated for an increase in τw. Subsequent increases in active stress resulted from the enhanced need for active muscle to compensate for the diminished ability of the original prestretched constituents to contribute to circumferential equilibrium as they degraded and were replaced by constituents without a preferred deposition stretch.
days. Initial decreases in active stress in the cases of decreased pressure and increased flow resulted from decreasing C as the vessel compensated for an increase in τw. Subsequent increases in active stress resulted from the enhanced need for active muscle to compensate for the diminished ability of the original prestretched constituents to contribute to circumferential equilibrium as they degraded and were replaced by constituents without a preferred deposition stretch.
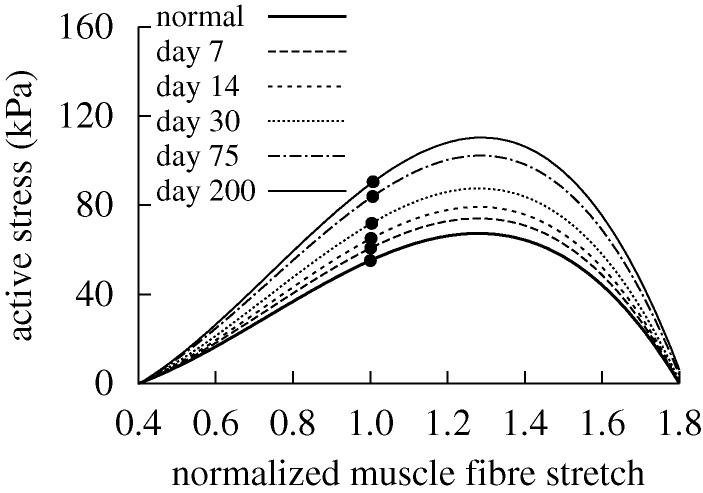
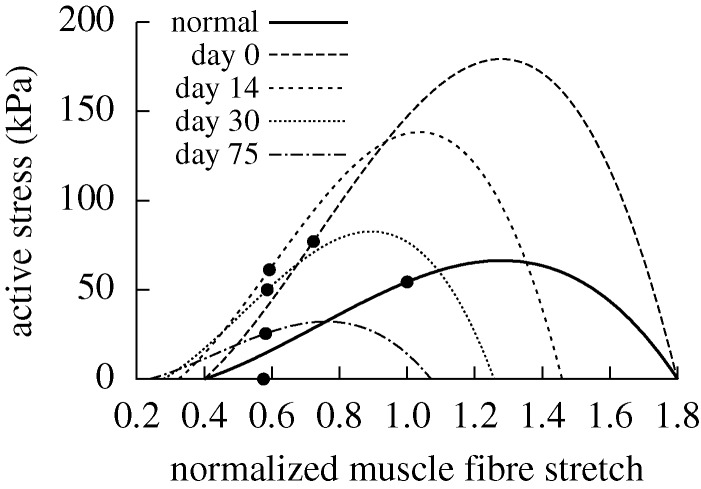
Figure 4.
Evolving active muscle response due to G&R for the case of 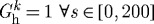 days, P=Ph and Q=Qh. The bold curve represents the active response before any perturbation. Solid points represent the state of activity for the vessel at the corresponding time. The abscissa ‘normalized muscle fibre stretch’ is expressed as a range of values for
days, P=Ph and Q=Qh. The bold curve represents the active response before any perturbation. Solid points represent the state of activity for the vessel at the corresponding time. The abscissa ‘normalized muscle fibre stretch’ is expressed as a range of values for  . Note the gradual increase in active stress from the time of perturbation (day 0) as the vessel becomes more muscular. While active muscle stress increased irreversibly, which would be energetically unfavourable, the vessel was able to maintain vasoactive function.
. Note the gradual increase in active stress from the time of perturbation (day 0) as the vessel becomes more muscular. While active muscle stress increased irreversibly, which would be energetically unfavourable, the vessel was able to maintain vasoactive function.
Increases in transmural pressure resulted in passive distension and thus increased fibre tensions and decreased τw. These effects worked to temporarily increase rates of collagen production. As extant collagen was subjected to increased tension, however, its removal rate accelerated (see equation (3.12) and Willett et al. (2007)). Because new fibres were deposited at 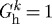 , the stresses borne by newly deposited collagen fibres were much lower than the homeostatic value, which initially prevented new collagen from attaining the high levels of stress experienced by original collagen (which was offset closer to the stiffer portion of the Fung exponential response curve) and provided a negative input for the rate of collagen production. Eventually, collagen production fell while smooth muscle production increased. An exception occurred when transmural pressure and fluid flow remained unperturbed (figure 2a,b, solid curves). In this case, the decrease in τw as the vessel passively distended was able to outweigh the changes in fibre stress, thus resulting in a sustained increase in collagen production. Figure 5 shows that, in addition to the increasing active contribution by smooth muscle cells, increased collagen and smooth muscle deposition rates resulted in irreversible passive stiffening. Similar stiffening trends were predicted for cases of changed pressure and flow (not shown).
, the stresses borne by newly deposited collagen fibres were much lower than the homeostatic value, which initially prevented new collagen from attaining the high levels of stress experienced by original collagen (which was offset closer to the stiffer portion of the Fung exponential response curve) and provided a negative input for the rate of collagen production. Eventually, collagen production fell while smooth muscle production increased. An exception occurred when transmural pressure and fluid flow remained unperturbed (figure 2a,b, solid curves). In this case, the decrease in τw as the vessel passively distended was able to outweigh the changes in fibre stress, thus resulting in a sustained increase in collagen production. Figure 5 shows that, in addition to the increasing active contribution by smooth muscle cells, increased collagen and smooth muscle deposition rates resulted in irreversible passive stiffening. Similar stiffening trends were predicted for cases of changed pressure and flow (not shown).
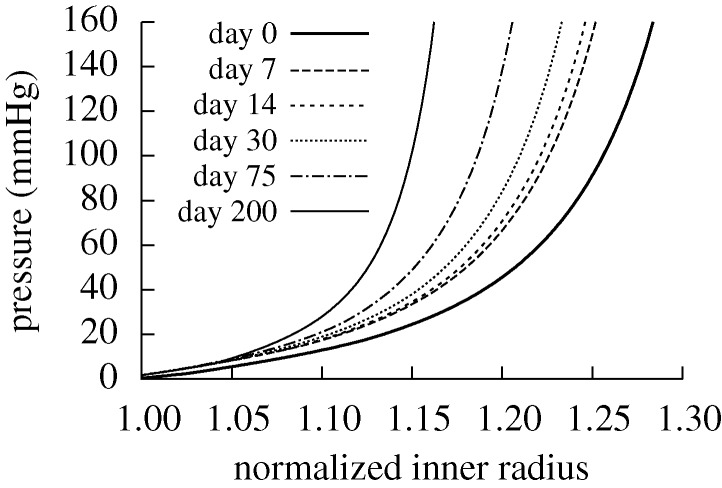
Figure 5.
Evolving passive response due to G&R for the case of 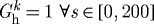 days, P=Ph and Q=Qh. The abscissa ‘normalized inner radius’ is expressed as the ratio of the current deformed inner radius to the current unloaded inner radius. The bold curve represents the passive response before any perturbation. Note the marked leftward shift, indicating increasing passive structural stiffening.
days, P=Ph and Q=Qh. The abscissa ‘normalized inner radius’ is expressed as the ratio of the current deformed inner radius to the current unloaded inner radius. The bold curve represents the passive response before any perturbation. Note the marked leftward shift, indicating increasing passive structural stiffening.
(b). Vasoactivity
Whereas letting 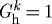 prevented the artery from maintaining, or when perturbed attaining, an expected geometry, removing vasoactivity (i.e.
prevented the artery from maintaining, or when perturbed attaining, an expected geometry, removing vasoactivity (i.e. 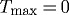 kPa) primarily delayed the artery from approaching optimal inner radii for cases of increased pressure or reduced flow (figure 6b; cf. figures 1b and 7b wherein changes in radius are not delayed). Increased transmural pressure initiated a G&R sequence independent of Rodbard’s phase 1 (i.e. vasoactivity). Because the artery experienced only modest passive distension, there was comparatively little stimulus to return to the expected inner radius (figure 6a). Passive distension and the associated increase in fibre stresses and decrease in wall shear stress stimulated increased mass productions as the wall approached its expected thicknesses (figure 6c). The most obvious limitation, however, was the inability to respond instantaneously to changes in flow (figure 6b). Although the artery could not constrict instantaneously in response to decreased flow, increases in flow-induced wall shear stress resulted in positive inputs to the mass production rate (figure 8b,d); that is, while vasoactivity no longer influenced vessel geometry, wall shear stress still influenced G&R via equation (3.11).
kPa) primarily delayed the artery from approaching optimal inner radii for cases of increased pressure or reduced flow (figure 6b; cf. figures 1b and 7b wherein changes in radius are not delayed). Increased transmural pressure initiated a G&R sequence independent of Rodbard’s phase 1 (i.e. vasoactivity). Because the artery experienced only modest passive distension, there was comparatively little stimulus to return to the expected inner radius (figure 6a). Passive distension and the associated increase in fibre stresses and decrease in wall shear stress stimulated increased mass productions as the wall approached its expected thicknesses (figure 6c). The most obvious limitation, however, was the inability to respond instantaneously to changes in flow (figure 6b). Although the artery could not constrict instantaneously in response to decreased flow, increases in flow-induced wall shear stress resulted in positive inputs to the mass production rate (figure 8b,d); that is, while vasoactivity no longer influenced vessel geometry, wall shear stress still influenced G&R via equation (3.11).
Figure 6.
Time courses of evolving inner radius (a,b) and wall thickness (c,d) for indicated changes in pressure P=γ Ph (left) and flow Q=ϵ Qh (right) where 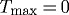 kPa ∀s∈[0,1000] days. Expected values are indicated by corresponding arrows on the right ordinate. Note the delayed change in inner radius for cases of reduced flow (b), due to the vessel’s inability to instantaneously vasoregulate after the perturbation. This is consistent with the observation that arteries are insensitive to changes in flow when denuded of endothelium ().
kPa ∀s∈[0,1000] days. Expected values are indicated by corresponding arrows on the right ordinate. Note the delayed change in inner radius for cases of reduced flow (b), due to the vessel’s inability to instantaneously vasoregulate after the perturbation. This is consistent with the observation that arteries are insensitive to changes in flow when denuded of endothelium ().
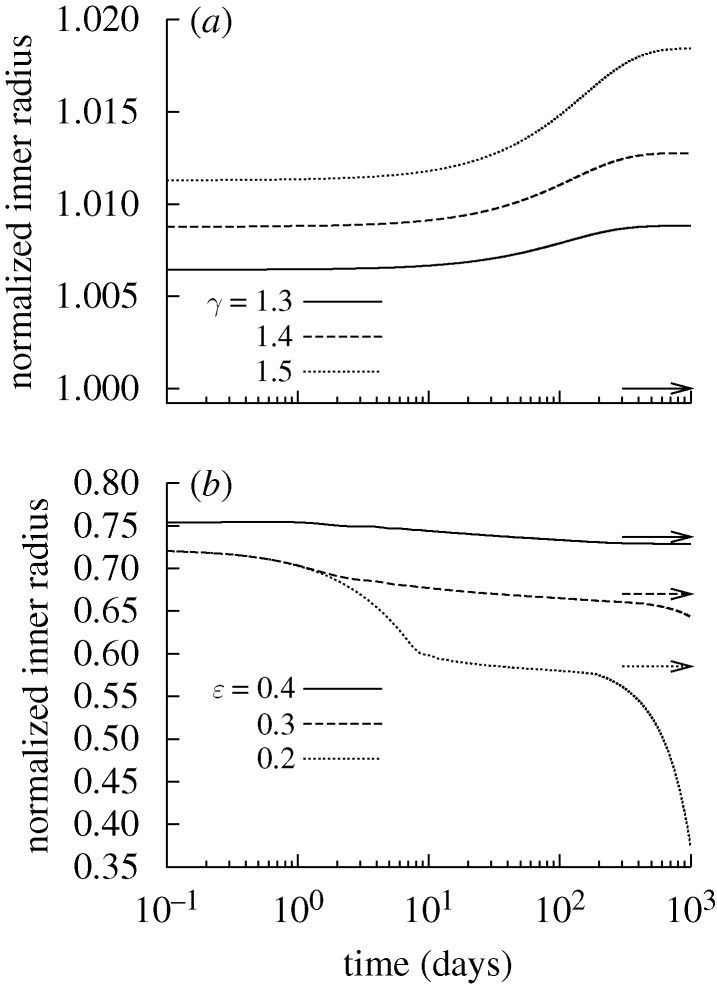
Figure 7.
Time courses of evolving inner radius for indicated changes in pressure P=γ Ph (a) and flow Q=ϵ Qh (b) where  and
and  days. Expected values (cf. equation (4.1)) are indicated by corresponding arrows on the right ordinate. Note that, for the cases of decreasing flow, the stable evolution range lies within the vessel’s instantaneous vasoactive range; note, too, the strongly diverging behaviour near day 200 for the case of ϵ=0.2, which suggests a sudden inability to regulate inner radius.
days. Expected values (cf. equation (4.1)) are indicated by corresponding arrows on the right ordinate. Note that, for the cases of decreasing flow, the stable evolution range lies within the vessel’s instantaneous vasoactive range; note, too, the strongly diverging behaviour near day 200 for the case of ϵ=0.2, which suggests a sudden inability to regulate inner radius.
Figure 8.
Time courses of rates of mass density production for circumferential collagen (a,b) and smooth muscle (c,d), normalized with respect to homeostatic rates for indicated changes in pressure P=γ Ph (a,c) and flow Q= ϵ Qh (b,d) where  kPa ∀s∈[0,1000] days. Note the high levels of production, especially for cases of reduced flow. SMC is smooth muscle cell.
kPa ∀s∈[0,1000] days. Note the high levels of production, especially for cases of reduced flow. SMC is smooth muscle cell.
The degree to which changes in flow and pressure affected G&R depended upon their respective rate parameters 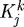 . For example, the artery could only attain expected thicknesses for changes in flow where
. For example, the artery could only attain expected thicknesses for changes in flow where 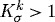 (fig. 5 in Valentín et al. 2009). Reducing Q while maintaining transmural pressure constant effectively renders inner radius as the primary geometric variable; the artery will rapidly remodel a towards its new expected value, possibly at the expense of not reaching an optimal thickness (figure 6d), that is, such G&R is driven primarily by τw, which depends only on a(s) and Q(s). Conversely, increased transmural pressure renders wall thickness as the primary geometric variable; the artery will rapidly remodel h towards its new expected value while not attaining the expected inner radius.
(fig. 5 in Valentín et al. 2009). Reducing Q while maintaining transmural pressure constant effectively renders inner radius as the primary geometric variable; the artery will rapidly remodel a towards its new expected value, possibly at the expense of not reaching an optimal thickness (figure 6d), that is, such G&R is driven primarily by τw, which depends only on a(s) and Q(s). Conversely, increased transmural pressure renders wall thickness as the primary geometric variable; the artery will rapidly remodel h towards its new expected value while not attaining the expected inner radius.
(c). Basal turnover
Restricting 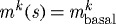 and
and 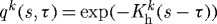 is, in many ways, opposite to the case of
is, in many ways, opposite to the case of  kPa. Because turnover was constant, with
kPa. Because turnover was constant, with 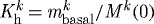 , the artery had a constant mass
, the artery had a constant mass 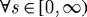 , and all motions were isochoric. The simulated artery was thus capable of vasoactively adjusting its inner radius instantaneously in response to changes in pressure and flow (figure 7), but its long-term G&R capabilities were limited seriously. Simulations predicted that the artery could not achieve expected values for inner radius (figure 7a) or thickness (not shown) for cases of increased pressure. Whereas an artery would normally maintain the homeostatic inner radius and accumulate additional mass to reach a new (greater) optimal thickness, this vessel could not accumulate any additional mass. As inner radius increased, the simulated artery only reached G&R stability because of increased vasoactivity (not shown) and elevated passive stiffness provided by extant (non-degrading) elastin at higher stretches.
, and all motions were isochoric. The simulated artery was thus capable of vasoactively adjusting its inner radius instantaneously in response to changes in pressure and flow (figure 7), but its long-term G&R capabilities were limited seriously. Simulations predicted that the artery could not achieve expected values for inner radius (figure 7a) or thickness (not shown) for cases of increased pressure. Whereas an artery would normally maintain the homeostatic inner radius and accumulate additional mass to reach a new (greater) optimal thickness, this vessel could not accumulate any additional mass. As inner radius increased, the simulated artery only reached G&R stability because of increased vasoactivity (not shown) and elevated passive stiffness provided by extant (non-degrading) elastin at higher stretches.
The artery could only achieve the expected inner radius for cases of reduced flow, and even then, only within a limited range (figure 7b). Thicknesses (not shown) were far greater than the expected values. Initially, vasoactivity increased in response to increased C, thus reducing the inner radius and returning τw to its homeostatic value. If the expected inner radius was within the normal vasoactive range, then the vessel could maintain a stable configuration. As the vessel remodelled in this state, however, the active stresses eventually decreased to some new steady state due largely to an excess accumulation of mass at the reduced calibre. In contrast, if the optimal inner radius was below the instantaneous vasoactive range, the active muscle stress eventually fell to zero (figure 9). At this time, the geometry changed in an unbounded manner; that is, the growth was unstable. The unrelenting deposition of collagen and passive muscle (with deposition stretches >1) tended to narrow the artery further. Once C reached 0, there was no longer a mechanism to stop this trend; muscle could only generate tensile stresses, and elastin was not stiff enough to resist compression.
Figure 9.
Evolving active muscle response due to G&R for a change in flow where ϵ=0.2 and 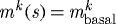 and
and 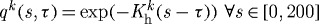 days. The bold curve represents the active response before any perturbation. Solid points represent the state of activity for the vessel at the corresponding time. The abscissa ‘normalized muscle fibre stretch’ is expressed as a range of values for
days. The bold curve represents the active response before any perturbation. Solid points represent the state of activity for the vessel at the corresponding time. The abscissa ‘normalized muscle fibre stretch’ is expressed as a range of values for 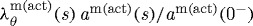 . Note the dramatic increase in active stress at the time of perturbation (day 0) and the gradual leftward shift as the active muscle remodels around a reduced inner radius. Also note the gradual reduction in vasoactivity after day 0 and eventual cessation by day 200, as denoted by the solid point on the abscissa. This loss of vasoactivity, coupled with constant collagen and smooth muscle deposition rates, resulted in the unbounded reduction of lumen caliber beginning near day 200 (figure 7b).
. Note the dramatic increase in active stress at the time of perturbation (day 0) and the gradual leftward shift as the active muscle remodels around a reduced inner radius. Also note the gradual reduction in vasoactivity after day 0 and eventual cessation by day 200, as denoted by the solid point on the abscissa. This loss of vasoactivity, coupled with constant collagen and smooth muscle deposition rates, resulted in the unbounded reduction of lumen caliber beginning near day 200 (figure 7b).
(d). Combined/synergistic effects
Figure 10 shows results of forcing both constant turnover 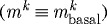 and no vasoactivity (
and no vasoactivity (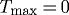 kPa). Although changing flow rate could then never affect vessel geometry (not shown), even small changes in transmural pressure resulted in unbounded changes in geometry. This suggests that, although the artery exhibited stable G&R behaviour at P=Ph, this was actually a meta-stable G&R equilibrium condition. Following an increase in transmural pressure, the artery distended and was unable to maintain its inner radius. Subsequently, new material was unrelentingly deposited in newly distended states. Although this new material was deposited with a deposition stretch >1, the artery could not accumulate mass and achieve the expected thickness. Coupled with the inability to increase actively generated stress, this thinning resulted in unbounded distension.
kPa). Although changing flow rate could then never affect vessel geometry (not shown), even small changes in transmural pressure resulted in unbounded changes in geometry. This suggests that, although the artery exhibited stable G&R behaviour at P=Ph, this was actually a meta-stable G&R equilibrium condition. Following an increase in transmural pressure, the artery distended and was unable to maintain its inner radius. Subsequently, new material was unrelentingly deposited in newly distended states. Although this new material was deposited with a deposition stretch >1, the artery could not accumulate mass and achieve the expected thickness. Coupled with the inability to increase actively generated stress, this thinning resulted in unbounded distension.
Figure 10.
Time courses of evolving inner radius for changes in pressure of −10% (dashed) and +10% (dotted) from the homeostatic (solid) value for 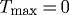 kPa,
kPa,  and
and  days. Note the diverging behaviour, suggesting a departure from a state of meta-stable G&R equilibrium.
days. Note the diverging behaviour, suggesting a departure from a state of meta-stable G&R equilibrium.
Reduced transmural pressure initially resulted in a modest decrease in calibre. This perturbation initiated a subsequent uncontrolled decrease in inner radius, however. As in the case of large decreases in flow for constant turnover, the artery experienced an unbounded decrease in calibre as newly deposited material compressed extant constituents. Without an initial level of vasoactivity and the associated ability to vasodilate, the artery could not recover the expected inner radius, thus resulting in uncontrolled G&R.
Figure 11 shows effects of restricting both 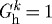 and
and 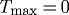 kPa
kPa  . Even for P=Ph and Q=Qh, the vessel exhibited unbounded distension; the artery could not maintain any inner radius, suboptimal or otherwise. As constituents were replaced at
. Even for P=Ph and Q=Qh, the vessel exhibited unbounded distension; the artery could not maintain any inner radius, suboptimal or otherwise. As constituents were replaced at 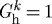 , the vessel tended to distend and without the ability to vasoconstrict, the artery could not reverse this trend. Although the wall could increase mass production in response to decreasing τw (not shown), the lack of a preferred deposition stretch and the relatively small amounts of compliant elastin prevented the artery from halting this distension. The model predicted substantial accumulation of new mass and thickening, but as the artery continued to distend, wall thickness decreased and eventually stabilized. Continued distension and increasing mass deposition eventually achieved a balance by which wall thickness stabilized.
, the vessel tended to distend and without the ability to vasoconstrict, the artery could not reverse this trend. Although the wall could increase mass production in response to decreasing τw (not shown), the lack of a preferred deposition stretch and the relatively small amounts of compliant elastin prevented the artery from halting this distension. The model predicted substantial accumulation of new mass and thickening, but as the artery continued to distend, wall thickness decreased and eventually stabilized. Continued distension and increasing mass deposition eventually achieved a balance by which wall thickness stabilized.
Figure 11.
Time courses of changing inner radius (a) and wall thickness (b) for the case of  and
and 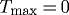 kPa ∀s∈[0,10 000] days. Transmural pressure and flow are unchanged from homeostatic. Expected values (cf. equation (4.1)) are indicated by corresponding arrows on the right ordinate. The model predicts an unbounded monotonic increase in inner radius (shown only to 1000 days) and an initial increase, followed by a gradual decrease and eventual stabilization of wall thickness.
kPa ∀s∈[0,10 000] days. Transmural pressure and flow are unchanged from homeostatic. Expected values (cf. equation (4.1)) are indicated by corresponding arrows on the right ordinate. The model predicts an unbounded monotonic increase in inner radius (shown only to 1000 days) and an initial increase, followed by a gradual decrease and eventual stabilization of wall thickness.
5. Discussion
We submit that deposition of constituents at preferred prestretches, vasoactivity and mechano-stimulated variable mass production and removal rates represent three fundamental ways by which vascular cells control overall geometry and biomechanical behaviour. Contractile smooth muscle can actively change the calibre in response to various constrictors and dilators, many of which are produced by endothelial cells in response to hemodynamic loads (Davies 1995), whereas synthetic smooth muscle cells and fibroblasts can change apparent mass densities of smooth muscle and collagen fibres, also as a function of mechanical and chemical stimuli. Moreover, for a pressurized vessel to maintain constant geometry, apparent mass densities and muscle activity under even homeostatic conditions, new collagen fibres and smooth muscle must be deposited having stretches greater than unity. Accounting for these three mechanisms is essential to capturing salient G&R trends and approximating diverse observed behaviours, including (biologically stable) tissue maintenance.
Vasoactivity is a well understood and widely appreciated vascular characteristic, and many models have incorporated this behaviour in diverse implementations (Rachev & Hayashi 1999; Humphrey & Wilson 2003; Zulliger et al. 2004; Stålhand et al. 2008). The concept of ‘deposition stretch’ has seen more limited attention despite increasing biological evidence for its existence (Alberts et al. 2002; Meshel et al. 2005; Kozel et al. 2006). This study suggests, however, that preferred deposition stretches are at least as important as active muscle in maintaining a stable and optimal geometry under normal conditions as well as enabling effective adaptations to altered loads. Indeed, we have shown that, whereas 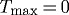 kPa does not preclude the vessel from approaching its expected geometry, an artery endowed with
kPa does not preclude the vessel from approaching its expected geometry, an artery endowed with 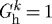 cannot achieve the expected geometry. Furthermore, this study suggests that, while both vasoactivity and deposition stretches are important individually, these two characteristics complement each other and endow arteries with the ability both to maintain stable geometric configurations and to adapt to diverse situations.
cannot achieve the expected geometry. Furthermore, this study suggests that, while both vasoactivity and deposition stretches are important individually, these two characteristics complement each other and endow arteries with the ability both to maintain stable geometric configurations and to adapt to diverse situations.
Variable mass density turnover is another fundamental cellular behaviour, clearly operative from development to maturity (Stenmark & Mecham 1997), without which the model artery could not appropriately compensate for large changes in transmural pressure or flow. For example, forcing constant mass production and removal rates resulted in unstable G&R for large reductions in flow. Our findings that effective arterial adaptations require mechanically mediated changes in the rates of production and removal of structural constituents are consistent with many recent findings (e.g. Eastwood et al. 1998; O’Callaghan & Williams 2000; Swartz et al. 2001; Jackson et al. 2002) and confirm the long-standing speculation of Wolinsky (1970) that ‘the high degree of correlation between the amounts of medial elastin and collagen and calculated levels of tension found in these studies is the first such relation described and is compatible with the possibility that tension, either directly or indirectly, provides the stimulus for elaboration of these fibrous proteins’. Moreover, Wolinsky suggested that ‘it would appear that the rates of accumulation of elastin and collagen … are linearly related to the degree of tension elevation’, which appears to be a reasonable first approximation of the likely nonlinear relation.
An artery may achieve a stable, albeit suboptimal, geometry for cases of either no deposition stretch (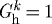 ) or no vasoactivity (
) or no vasoactivity (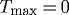 kPa). Similarly, an artery may be able to achieve a stable but suboptimal geometry for limited ranges of pressures and flows if mass density turnover (
kPa). Similarly, an artery may be able to achieve a stable but suboptimal geometry for limited ranges of pressures and flows if mass density turnover (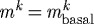 ) is constant. This degree of fault tolerance is typical of biological systems, which employ what amounts to multiple redundant or complementary systems to promote homeostasis. Combining constant mass density turnover and
) is constant. This degree of fault tolerance is typical of biological systems, which employ what amounts to multiple redundant or complementary systems to promote homeostasis. Combining constant mass density turnover and 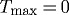 kPa resulted in a vessel that was, in effect, in a state of unstable G&R equilibrium, even under normal conditions. That is, any small perturbation in transmural pressure resulted in diverging, unbounded enlargement. Also, for cases in which
kPa resulted in a vessel that was, in effect, in a state of unstable G&R equilibrium, even under normal conditions. That is, any small perturbation in transmural pressure resulted in diverging, unbounded enlargement. Also, for cases in which 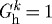 and
and  kPa, the vessel exhibited an unbounded change in geometry, even for the case of homeostatic transmural pressure and volumetric flow rate. In other words, although preferred deposition stretch, vasoactivity and variable constituent turnover rates are individually important to maintaining optimal or near optimal geometry and function, they work together. Hence, arteries cannot maintain G&R stability or function without any two of these mechanisms.
kPa, the vessel exhibited an unbounded change in geometry, even for the case of homeostatic transmural pressure and volumetric flow rate. In other words, although preferred deposition stretch, vasoactivity and variable constituent turnover rates are individually important to maintaining optimal or near optimal geometry and function, they work together. Hence, arteries cannot maintain G&R stability or function without any two of these mechanisms.
In summary, continuum-based constrained mixture models are well suited for simulating arterial G&R, for they allow one to account for biological characteristics that are fundamental to both tissue maintenance and adaptation: individual and variable mass density production/removal of constituents, individual preferred deposition stretches, vasoactivity with evolving reference configurations and so forth. Moreover, it is seen that such models are well suited to basic hypothesis generation and testing, not just parameter estimation or standard solutions to initial-boundary problems. Herein we effectively simulated, via what may be described as ‘numerical knockout models’, the consequences of possible biological phenotypes that were found to be problematic individually but likely catastrophic when coexisting, not unlike many mouse knockouts and double knockouts. We submit that it is not necessarily a large number of values of material parameters that is most important to enable continuum biomechanical models to describe and predict in vivo behaviours; rather, it is the biological appropriateness of the fundamental hypotheses that enables a model to capture and predict salient features of the biomechanics and mechanobiology. Hence, because of their inherent complexity, future fluid–solid-growth (FSG) models of the vasculature (Humphrey & Taylor 2008) should be based on physically reasonable and biologically appropriate constitutive relations that reflect underlying cell-mediated mechanisms.
Acknowledgements
This work was supported, in part, via NIH grants HL-64372, HL-80415 and HL-86418.
Footnotes
One contribution of 12 to a Theme Issue ‘Mechanics in biology: cells and tissues’.
References
- Alberts B., Johnson A., Lewis J., Raff M., Roberts K., Walter P. 2002. The molecular biology of the cell, 4th edn New York, NY: Garland Science. [Google Scholar]
- Alford P. W., Humphrey J. D., Taber L. A. 2008. Growth and remodeling in a thick-walled artery model: effects of spatial variations in wall constituents. Biomech. Model Mechanobiol. 7, 245–262. ( 10.1007/s10237-007-0101-2) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson A. E., Ellis B. J., Weiss J. A. 2007. Verification, validation and sensitivity studies in computational biomechanics. Comput. Methods Biomech. Biomed. Eng. 10, 171–184. ( 10.1080/10255840601160484) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baek S., Rajagopal K. R., Humphrey J. D. 2006. A theoretical model of enlarging intracranial fusiform aneurysms. J. Biomech. Eng. 142–149. ( 10.1115/1.2132374) [DOI] [PubMed] [Google Scholar]
- Baek S., Valentí n A., Humphrey J D. 2007. Biochemomechanics of cerebral vasospasm and its resolution: II. Constitutive relations and model simulations. Ann. Biomed. Eng. 35, 1498–1509. ( 10.1007/s10439-007-9322-x) [DOI] [PubMed] [Google Scholar]
- Cardamone L., Valentí n A., Eberth J., Humphrey J. In press Origin of axial prestretch and residual stress in arteries. Biomech. Model. Mechanobiol. 0237–008. ( 10.1007/s10237-008-0146-x) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cho A., Courtman D. W., Langille B. L. 1995. Apoptosis (programmed cell death) in arteries of the neonatal lamb. Circ. Res. 76, 168–175. [DOI] [PubMed] [Google Scholar]
- Dajnowiec D., Langille B. L. 2007. Arterial adaptations to chronic changes in haemodynamic function: coupling vasomotor tone to structural remodelling. 113, 15–23. ( 10.1042/CS20060337) [DOI] [PubMed] [Google Scholar]
- Davies P. F. 1995. Flow-mediated endothelial mechanotransduction. Physiol. Rev. 75, 519–560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dooley A., Gao B., Shi-Wen X., Abraham D. J., Black C. M., Jacobs M., Bruckdorfer K. R. 2007. Effect of nitric oxide and peroxynitrite on type I collagen synthesis in normal and scleroderma dermal fibroblasts. Free Radic. Biol. Med. 43, 253–264. ( 10.1016/j.freeradbiomed.2007.04.017) [DOI] [PubMed] [Google Scholar]
- Dorrington K., McCrum N. 1977. Elastin as a rubber. Biopolymers 16, 1201–1222. ( 10.1002/bip.1977.360160604) [DOI] [PubMed] [Google Scholar]
- Driessen N. B., Wilson W., Bouten C. C., Baaijens F. T. 2004. A computational model for collagen fibre remodelling in the arterial wall. J. Theor. Biol. 226, 53–64. ( 10.1016/j.jtbi.2003.08.004) [DOI] [PubMed] [Google Scholar]
- Eastwood M., McGrouther D. A., Brown R. A. 1998. Fibroblast responses to mechanical forces. Proc. Inst. Mech. Eng., H 212, 85–92. ( 10.1243/0954411981533854) [DOI] [PubMed] [Google Scholar]
- Fridez P., Rachev A., Meister J. J., Hayashi K., Stergiopulos N. 2001. Model of geometrical and smooth muscle tone adaptation of carotid artery subject to step change in pressure. Am. J. Physiol. Heart Circ. Physiol. 280, H2752–H2760. [DOI] [PubMed] [Google Scholar]
- Fung Y. C. 1991. What are the residual stresses doing in our blood vessels?. Ann. Biomed. Eng. 19, 237–249. ( 10.1007/BF02584301) [DOI] [PubMed] [Google Scholar]
- Gleason R. L., Humphrey J. D. 2004. A mixture model of arterial growth and remodeling in hypertension: altered muscle tone and tissue turnover. J. Vasc. Res. 41, 352–363. ( 10.1159/000080699) [DOI] [PubMed] [Google Scholar]
- Gleason R. L., Humphrey J. D. 2005. Effects of a sustained extension on arterial growth and remodeling: a theoretical study. J. Biomech. 38, 1255–1261. ( 10.1016/j.jbiomech.2004.06.017) [DOI] [PubMed] [Google Scholar]
- Gleason R. L., Taber L. A., Humphrey J. D. 2004. A 2-D model of flow-induced alterations in the geometry, structure, and properties of carotid arteries. J. Biomech. Eng. 126, 371–381. ( 10.1115/1.1762899) [DOI] [PubMed] [Google Scholar]
- Guyton A. C., Hall J. E. 1997. Human physiology and mechanisms of disease, 6th edn Philadelphia, PA: Sanders. [Google Scholar]
- Hariton I., de Botton G., Gasser T. C., Holzapfel G. A. 2007. Stress-driven collagen fiber remodeling in arterial walls. Biomech. Model Mechanobiol. 6, 163–175. ( 10.1007/s10237-006-0049-7) [DOI] [PubMed] [Google Scholar]
- Holzapfel G. A., Gasser T. C., Ogden R. W. 2000. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J. Elasticity 61, 1–48. ( 10.1023/A:1010835316564) [DOI] [Google Scholar]
- Humphrey J. D. 2002. Cardiovascular solid mechanics: cells, tissues, and organs. New York, NY: Springer-Verlag. [Google Scholar]
- Humphrey J. D. 2008a. Vascular adaptation and mechanical homeostasis at tissue, cellular, and sub-cellular levels. Cell. Biochem. Biophys. 50, 53–78. ( 10.1007/s12013-007-9002-3) [DOI] [PubMed] [Google Scholar]
- Humphrey J. D. 2008b. Mechanisms of arterial remodeling in hypertension. Coupled roles of wall shear and intramural stress. Hypertension 52, 195–200. ( 10.1161/HYPERTENSIONAHA.107.103440) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphrey J. D., Rajagopal K. R. 2002. A constrained mixture model for growth and remodeling of soft tissues. Math. Models Methods Appl. Sci. 12, 407–430. ( 10.1142/S0218202502001714) [DOI] [Google Scholar]
- Humphrey J. D., Taylor C. A. 2008. Intracranial and abdominal aortic aneurysms: similarities, differences, and need for a new class of computational models. Annu. Rev. Biomed. Eng. 10, 221–246. ( 10.1146/annurev.bioeng.10.061807.160439) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphrey J. D., Wilson E. 2003. A potential role of smooth muscle tone in early hypertension: a theoretical study. J. Biomech. 36, 1595–1601. ( 10.1016/S0021-9290(03)00178-7) [DOI] [PubMed] [Google Scholar]
- Jackson Z. S., Gotlieb A. I., Langille B. L. 2002. Wall tissue remodeling regulates longitudinal tension in arteries. Circ. Res. 90, 918–925. ( 10.1161/01.RES.0000016481.87703.CC) [DOI] [PubMed] [Google Scholar]
- Kelleher C. M., McLean S. E., Mecham R. P. 2004. Vascular extracellular matrix and aortic development. Curr. Top. Dev. Biol. 62, 153–188. ( 10.1016/S0070-2153(04)62006-0) [DOI] [PubMed] [Google Scholar]
- Kozel B. A. 2006. Elastic fiber formation: a dynamic view of extracellular matrix assembly using timer reporters. J. Cell. Physiol. 207, 87–96. ( 10.1002/jcp.20546) [DOI] [PubMed] [Google Scholar]
- Kuhl E., Maas R., Himpel G., Menzel A. 2007. Computational modeling of arterial wall growth. Biomech. Model Mechanobiol. 6, 321–331. ( 10.1007/s10237-006-0062-x) [DOI] [PubMed] [Google Scholar]
- Langille B. L. 1993. Remodeling of developing and mature arteries: endothelium, smooth muscle, and matrix. J. Cardiovasc. Pharmacol. 21, S11–S17. [DOI] [PubMed] [Google Scholar]
- Langille B. L. 1996. Arterial remodeling: relation to hemodynamics. Can. J. Physiol. Pharmacol. 74, 834–841. ( 10.1139/cjpp-74-7-834) [DOI] [PubMed] [Google Scholar]
- Lanir Y. 1983. Constitutive equations for fibrous connective tissues. J. Biomech. 16, 1–12. ( 10.1016/0021-9290(83)90041-6) [DOI] [PubMed] [Google Scholar]
- Leung D. Y., Glagov S., Mathews M. B. 1976. Cyclic stretching stimulates synthesis of matrix components by arterial smooth muscle cells in vitro. Science 191, 475–477. ( 10.1126/science.128820) [DOI] [PubMed] [Google Scholar]
- Li Q., Muragaki Y., Hatamura I., Ueno H., Ooshima A. 1998. Stretch-induced collagen synthesis in cultured smooth muscle cells from rabbit aortic media and a possible involvement of angiotensin II and transforming growth factor-β. J. Vasc. Res. 35, 93–103. ( 10.1159/000025570) [DOI] [PubMed] [Google Scholar]
- Menzel A. 2007. A fibre reorientation model for orthotropic multiplicative growth. Biomech. Model Mechanobiol. 6, 303–320. ( 10.1007/s10237-006-0061-y) [DOI] [PubMed] [Google Scholar]
- Meshel A. S., Wei Q., Adelstein R. S., Sheetz M. P. 2005. Basic mechanism of three-dimensional collagen fibre transport by fibroblasts. Nat. Cell. Biol. 7, 157–164. ( 10.1038/ncb1216) [DOI] [PubMed] [Google Scholar]
- Murray C. D. 1926. The physiological principle of minimum work. I. The vascular system and the cost of blood volume. Proc. Natl Acad. Sci. USA 12, 207–214. ( 10.1073/pnas.12.3.207) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Na S., Trache A., Trzeciakowski J., Sun Z., Meininger G. A., Humphrey J. D. 2008. Time-dependent changes in smooth muscle cell stiffness and focal adhesion area in response to cyclic equibiaxial stretch. Ann. Biomed. Eng. 36, 369–380. ( 10.1007/s10439-008-9438-7) [DOI] [PubMed] [Google Scholar]
- Niedermüller H., Skalicky M., Hofecker G., Kment A. 1977. Investigations on the kinetics of collagen-metabolism in young and old rats. Exp. Gerontol. 12, 159–168. ( 10.1016/0531-5565(77)90001-8) [DOI] [PubMed] [Google Scholar]
- Nissen R., Cardinale G. J., Udenfriend S. 1978. Increased turnover of arterial collagen in hypertensive rats. Proc. Natl Acad. Sci. USA 75, 451–453. ( 10.1073/pnas.75.1.451) [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Callaghan C. J., Williams B. 2000. Mechanical strain-induced extracellular matrix production by human vascular smooth muscle cells: role of TGF-β1. Hypertension 36, 319–324. [DOI] [PubMed] [Google Scholar]
- Price J. M., Davis D. L., Knauss E. B. 1981. Length-dependent sensitivity in vascular smooth muscle. Am. J. Physiol. 241, HS57–HS63. [DOI] [PubMed] [Google Scholar]
- Rachev A. 2000. A model of arterial adaptation to alterations in blood flow. J. Elasticity 61, 83–111. ( 10.1023/A:1010800703478) [DOI] [Google Scholar]
- Rachev A., Hayashi K. 1999. Theoretical study of the effects of vascular smooth muscle contraction on strain and stress distributions in arteries. Ann. Biomed. Eng. 27, 459–468. ( 10.1114/1.191) [DOI] [PubMed] [Google Scholar]
- Rachev A., Stergiopulos N., Meister J. J. 1998. A model for geometric and mechanical adaptation of arteries to sustained hypertension. J. Biomech. Eng. 120, 9–17. ( 10.1115/1.2834313) [DOI] [PubMed] [Google Scholar]
- Rachev A., Manoach E., Berry J., Moore J. J. 2000. A model of stress-induced geometrical remodeling of vessel segments adjacent to stents and artery/graft anastomoses. J. Theor. Biol. 206, 429–443. ( 10.1006/jtbi.2000.2143) [DOI] [PubMed] [Google Scholar]
- Rizvi M. D., Myers P. R. 1997. Nitric oxide modulates basal and endothelin-induced coronary artery vascular smooth muscle cell proliferation and collagen levels. J. Mol. Cell. Cardiol. 29, 1779–1789. ( 10.1006/jmcc.1996.0480) [DOI] [PubMed] [Google Scholar]
- Rizvi M. D., Katwa L., Spadone D. P., Myers P. R. 1996. The effects of endothelin-1 on collagen type I and type III synthesis in cultured porcine coronary artery vascular smooth muscle cells. J. Mol. Cell. Cardiol. 28, 243–252. ( 10.1006/jmcc.1996.0023) [DOI] [PubMed] [Google Scholar]
- Rodbard S. 1975. Vascular caliber. Cardiology 60, 4–49. ( 10.1159/000169701) [DOI] [PubMed] [Google Scholar]
- Rodriguez E. K., Hoger A., McCulloch A. D. 1994. Stress-dependent finite growth in soft elastic tissues. J. Biomech. 27, 455–467. ( 10.1016/0021-9290(94)90021-3) [DOI] [PubMed] [Google Scholar]
- Ruch T. C., Patton H. D. 1966. Physiology and biophysics, Howell and Fulton's 19th edition Philadelphia, PA: W. B. Saunders Company. [Google Scholar]
- Skalak R. 1981. Growth as a finite displacement field. In Proc. IUTAM Symp. Finite Elasticity (eds Carlson D. E., Shield R. T.), pp. 347–355, The Hague: Martinus Nijhoff [Google Scholar]
- Sluijter J. G., Smeets M. B., Velema E., Pasterkamp G., de Kleijn V. 2004. Increase in collagen turnover but not in collagen fiber content is associated with flow-induced arterial remodeling. J. Vasc. Res. 41, 546–555. ( 10.1159/000081972) [DOI] [PubMed] [Google Scholar]
- Stålhand J., Klarbring A., Holzapfel G. A. 2008. Smooth muscle contraction: mechanochemical formulation for homogeneous finite strains. Prog. Biophys. Mol. Biol. 96, 465–481. ( 10.1016/j.pbiomolbio.2007.07.025) [DOI] [PubMed] [Google Scholar]
- Stenmark K. R., Mecham R. P. 1997. Cellular and molecular mechanisms of pulmonary vascular remodeling. Annu. Rev. Physiol. 59, 89–144. ( 10.1146/annurev.physiol.59.1.89) [DOI] [PubMed] [Google Scholar]
- Swartz M. A., Tschumperlin D. J., Kamm R. D., Drazen J. M. 2001. Mechanical stress is communicated between different cell types to elicit matrix remodeling. Proc. Natl Acad. Sci. USA 98, 6180–6185. ( 10.1073/pnas.111133298) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taber L. A. 1998. A model for aortic growth based on fluid shear and fiber stresses. J. Biomech. Eng. 120, 348–354. ( 10.1115/1.2798001) [DOI] [PubMed] [Google Scholar]
- Tsamis A., Stergiopulos N. 2007. Arterial remodeling in response to hypertension using a constituent-based model. Am. J. Physiol. Heart Circ. Physiol. 293, H3130–H3139. ( 10.1152/ajpheart.00684.2007) [DOI] [PubMed] [Google Scholar]
- Valentín A., Cardamone L., Baek S., Humphrey J. D. 2009. Complementary vasoactivity and matrix remodelling in arterial adaptations to altered flow and pressure. J. R. Soc. Interface 6, 293–306. ( 10.1098/rsif.2008.0254) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willett T. L., Labow R. S., Avery N. C., Lee J. M. 2007. Increased proteolysis of collagen in an in vitro tensile overload tendon model. Ann. Biomed. Eng. 35, 1961–1972. ( 10.1007/s10439-007-9375-x) [DOI] [PubMed] [Google Scholar]
- Wilson E., Mai Q., Sudhir K., Weiss R. H., Ives H. E. 1993. Mechanical strain induces growth of vascular smooth muscle cells via autocrine action of PDGF. J. Cell. Biol. 123, 741–747. ( 10.1083/jcb.123.3.741) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolinsky H. 1970. Response of the rat aortic media to hypertension. Morphological and chemical studies. Circ. Res. 26, 507–522. [DOI] [PubMed] [Google Scholar]
- Zamir M. 1977. Shear forces and blood vessel radii in the cardiovascular system. J. Gen. Physiol. 69, 449–461. ( 10.1085/jgp.69.4.449) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zulliger M. A., Rachev A., Stergiopulos N. 2004. A constitutive formulation of arterial mechanics including vascular smooth muscle tone. Am. J. Physiol. Heart Circ. Physiol. 287, H1335–H1343. ( 10.1152/ajpheart.00094.) [DOI] [PubMed] [Google Scholar]