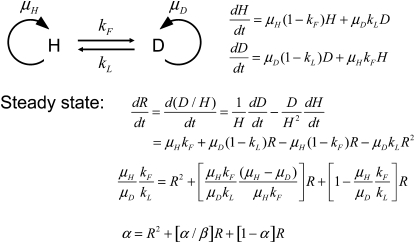Abstract
Tandem duplications are among the most common mutation events. The high loss rate of duplication suggested that the frequency of duplications in a bacterial population (1/1000) might reflect a steady state dictated by relative rates of formation (kF) and loss (kL). This possibility was tested for three genetic loci. Without homologous recombination (RecA), duplication loss rate dropped essentially to zero, but formation rate decreased only slightly and a steady state was still reached rapidly. Under all conditions, steady state was reached faster than predicted by formation and loss rates alone. A major factor in determining steady state proved to be the fitness cost, which can exceed 40% for some genomic regions. Depending on the region tested, duplications reached 40–98% of the steady-state frequency within 30 generations—approximately the growth required for a single cell to produce a saturated overnight culture or form a large colony on solid medium (109 cells). Long-term bacterial populations are stably polymorphic for duplications of every region of their genome. These polymorphisms contribute to rapid genetic adaptation by providing frequent preexisting mutations that are beneficial whenever imposed selection favors increases in some gene activity. While the reported results were obtained with the bacterium Salmonella enterica, the genetic implications seem likely to be of broader biological relevance.
TANDEM genetic duplications are probably the most common mutation type in terms of their rate of formation and their frequency in an overnight culture. Roughly 10% of cells in an unselected laboratory culture of Salmonella enterica carry a duplication of some chromosomal region and 0.005–3% have a duplication of a specified gene (Anderson and Roth 1977). The situation may be even more extreme in humans, whose genomes contain hundreds of copy number variations (CNVs) (Sharp et al. 2005; Korbel et al. 2007; Kidd et al. 2008). The phenotypes caused by duplications can be detected by selection and contribute to fitness whenever growth is limited by quantity or activity of a particular protein (Sonti and Roth 1989; Tlsty et al. 1989; Andersson et al. 1998). Selected increases in gene copy number can enhance the likelihood of point mutations that further increase fitness by providing more targets for change (Roth et al. 2006; Sandegren and Andersson 2009; Sun et al. 2009).
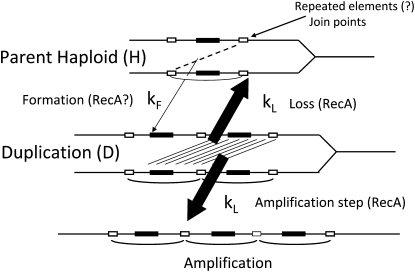
Little is known about duplication formation or why duplications are so frequent in unselected populations. Duplications form frequently between separated sequence repeats, suggesting a role for homologous recombination (Figure 1, top). For example, the most frequently duplicated regions of the chromosome of S. enterica are those between copies of the rrn cistrons, with 6.5 kb of nearly identical sequence (Anderson and Roth 1981). In contrast, less common duplications arise between regions with little or no sequence homology, whose formation seems unlikely to require recombination (Kugelberg et al. 2006). The role of recombination in duplication formation has been difficult to assess because previous duplication assays depended on recombination proficiency. New assays described here suggest that duplications can form without homologous recombination even when extensive sequence repeats serve as junction points. Duplication loss occurs at ∼1% per generation and is essentially eliminated in recA mutant strains (Anderson and Roth 1981), which lack a catalyst of strand invasion that is essential to homologous recombination in otherwise normal strains. Exchanges like those leading to duplication loss can also further amplify gene copy number (Figure 1, bottom).
Figure 1.—
Formation and loss of duplications. Duplications are thought to arise by exchanges between separated elements on sister chromosomes. These elements vary in size from several base pairs to multiple kilobases. Once a duplication is in place, the extensive sequence repeats are subject to unequal recombination events between sister chromosomes that can lead to loss of the duplication (reversion) or to further increases in copy number (amplification). Both loss and further amplification are expected to occur at the same rate (kL).
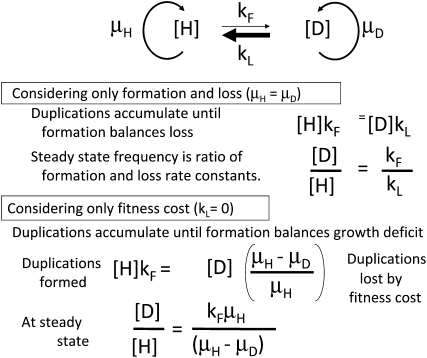
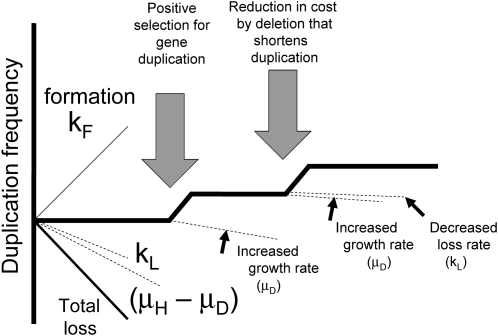
This study was initiated to test the possibility that duplication frequency in a population might reach a steady state dictated by the relative rates of formation (kF) and loss (kL), as diagrammed in Figure 2 (top). Initially, the fitness cost (growth deficit) of duplications was assumed to be small and was not considered. If rates of formation and loss dictate the steady-state duplication frequency (and fitness cost is negligible), steady state is expected when formation and loss are equivalent. This extreme situation is diagrammed at the top of Figure 2.
Figure 2.—
Conditions maintaining a steady-state duplication frequency. (Top) Every chromosomal region is subject to duplication that converts a haploid cell (H) to one with a duplication (D). The concentrations of H and D cells increase with growth rate constants μH and μD. Haploid cells give rise to duplications with rate constant kF and diploids lose their duplication with the rate constant kL. (Middle) When growth rates of haploid and diploid cells are equal, duplication frequency is dictated by rates of formation and loss, since kF ≪ kL. (Bottom) When duplications cannot be lost by reversion (kL= 0), a steady state can be reached if duplication strains grow less rapidly than haploids and formation rate balances growth deficit.
The contribution of fitness cost to steady states can be seen if one eliminates duplication loss by setting kL close to zero (as in a recA mutant). Under these extreme conditions (Figure 2, bottom), the duplication frequency can come to steady state if the duplication-bearing cell grows more slowly than the parent haploid. At this steady state, the formation of new duplications just compensates for decreases in duplication frequency due to the growth deficit.
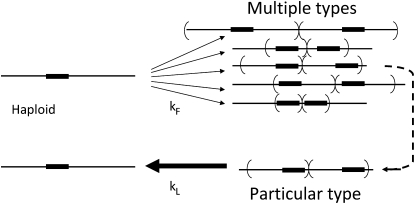
In discussing these predictions, one must realize that independent duplications of a particular locus may differ in endpoints and amounts of included flanking material (see Figure 3). The measured duplication formation rate for some locus is thus the sum of these separate rates. In contrast, loss rate is measured for an isolated mutant with one particular duplication type. The results described here suggest that for most regions, the variety of duplication types is small enough that one can use the aggregate formation rates and average loss rate in predicting the approach of duplication frequency to steady state.
Figure 3.—
Measured events in duplication formation and loss. The rate of duplication formation describes a variety of different events that provide two copies of the assayed locus. The rate of duplication loss is assayed for a particular duplication, which may or may not be typical of the whole collection.
The variability in size and fitness cost of duplications predicts that during prolonged growth, the new duplications added to the population will represent the full gamut of types and those with the greatest fitness cost will be lost preferentially. Thus with time, even near steady state, the frequency of lower-cost duplications will increase at the expense of those causing a slower growth rate. If small duplications have lower cost, the average duplication size should drop with time.
Results presented here suggest unexpected features of duplications. Homologous recombination contributes weakly to duplication formation but is almost essential for loss. Duplications can have a high fitness cost that contributes heavily (with formation and loss rates) to rapid establishment of steady-state frequencies. The growth required for a single cell to produce a saturated 1-ml liquid culture or a large colony on solid medium (109 cells) allows duplication frequency to approach steady state. The steady-state duplication frequency (typically 0.1% for any locus) can be considered a stable polymorphism that provides frequent copy number variants. These variants can contribute to rapid genetic adaptation whenever selection conditions favor increased gene activity. We expect that the general conclusions regarding steady-state duplication frequencies will apply to copy number variation in any organism. A proposal for rapid evolution of new genes by means of selective gene amplification has been described previously (Bergthorsson et al. 2007).
MATERIALS AND METHODS
Strains and media:
All strains were derivatives of S. enterica (Typhimurium) strain LT2. Primary strains are listed in Table 1. Rich medium was Luria broth (LB) with antibiotics as described below. The chromogenic β-galactosidase substrate 5-bromo-4-chloro-3-indolyl-β-d-galactopyranoside (X-gal) was obtained from Diagnostic Chemicals, Oxford, CT and used in plates at 40 μg/ml.
TABLE 1.
Strains used in this study
| Strain | Genotypea | Source or reference |
|---|---|---|
| TR10000 | Wild-type S. enterica (serovar Typhimurium) LT2 | Lab collection |
| TT22240 | recA643∷Tn10dTc | Williams et al. (2006) |
| TT25467 | his-644(ΔOGDCBHAF) pro-621/F′128pro+lacI4650∷Ka(sw, KnS), lacZY+/pSIM5(CmR) | This report |
| TT25468 | his-644(ΔOGDCBHAF) pro-621 recA650∷Gnt(sw)/F′128pro+lacI4650∷Ka(sw, KnS), lacZY+ /pSIM5(CmR) | This report |
| TT25469 | his-644(ΔOGDCBHAF) pro-621 recA651∷Rif(sw)/F′128pro+lacI4650∷Ka(sw, KnS), lacZY+/pSIM5(CmR) | This report |
| TT25478 | pyrD2266∷Tn10(TcSKn)/pSIM5(CmR) | This report |
| TT25479 | pyrD2266∷Tn10(TcSKn) recA650∷GntR(sw)/pSIM5(CmR) | This report |
| TT25486 | argH1823∷Tn10(TcSKn)/pSIM5(CmR) | This report |
| TT25487 | argH1823∷Tn10(TcSKn) recA650∷Gnt(sw)/pSIM5(CmR) | This report |
| TT25706 | argH1823∷Tn10(T-Recs) recA650∷Gnt(sw) | This report |
| TT25707 | pyrD2266:Tn10(T-Recs) recA650∷Gnt(sw) | This report |
| TT25791 | Wild-type LT2/F′128lacI4650∷Ka(sw, KnS), lacZY+ | This report |
| TT25792 | recA651∷Rif(sw)/F′128lacI4650∷Ka(sw, KnS), lacZY+ | This report |
| TT25794 | leuD21 proB1657∷Tn10 recA650∷Gnt(sw)/F′128 pro+ IS3C∷Rif(sw) ΔlacIZ4652∷KnR(sw) lacA4653∷(CmR, OcrecA+) | This report |
| TT25996 | argH1947∷Lac[lacI4650∷Ka(sw,KnS), lacZY+]/pSIM5(CmR) | This report |
| TT25997 | argH1947∷Lac[lacI4650∷Ka(sw,KnS), lacZY+] recA650∷Gnt(sw)/pSIM5 (CmR) | This report |
| TT26002 | pyrD2827∷Lac[lacI4650∷Ka(sw,KnS), lacZY+]/pSIM5 (CmR) | This report |
| TT26003 | pyrD2827∷Lac[lacI4650∷Ka(sw,KnS), lacZY+] recA650∷Gnt(sw)/pSIM5 (CmR) | This report |
| TT26046 | argH1947∷Lac[lacI4650∷Ka(sw,KnS), lacZY+] pyrD2826∷Kan recA650∷Gnt(sw)/pSIM5 (CmR) | This report |
| TT26047 | argH1947∷Lac[lacI4650∷Ka(sw,KnS), lacZY+] purH2378∷Kan recA650∷Gnt(sw)/pSIM5 (CmR) | This report |
| TT26049 | pyrD2827∷Lac[lacI4650∷Ka(sw,KnS), lacZY+] purH2378∷Kan recA650∷Gnt(sw)/pSIM5 (CmR) | This report |
| TT26050 | pyrD2827∷Lac[lacI4650∷Ka(sw,KnS), lacZY+] hisC10309∷Kan recA650∷Gnt(sw)/pSIM5 (CmR) | This report |
| TT26056 | his-644(ΔOGDCBHAF) proAB670∷sw-SpcRrecA650∷Gnt(sw)/F'128pro+ lacI4650∷Ka(sw,KnS), lacZY+] IS3A∷Kan(sw)/pSIM5(CmR) | This report |
| TT26057 | his-644(ΔOGDCBHAF) proAB1657(TcR) recA650∷Gnt(sw)/F′128pro+ lacI4650∷Ka(sw,KnS), lacZY+] IS3A∷Kan(sw)/pSIM5(CmR) | This report |
| TT26059 | his-644(ΔOGDCBHAF) proAB670(SpR) recA650∷Gnt(sw)/F′128pro+ DUP2066[lacI4650∷Ka(sw,KnS), lacZY+]–IS3ACjoin–[ΔlacIZ4652∷Kan(sw)]/pSIM5(CmR) | This report |
| TT26061 | his-644(ΔOGDCBHAF) proAB1657(TcR) recA650∷Gnt(sw)/F′128pro+ DUP2066[lacI4650∷Ka(sw,KnS), lacZY+]–IS3ACjoin–[ΔlacIZ4652∷Kan(sw)]/pSIM5(CmR) | This report |
| TT26065 | his-644(ΔOGDCBHAF) proAB1657(TcR) recA650∷Gnt(sw) /F'128pro+ DUP2067[lacI4650∷Ka(sw,KnS), lacZY+]–REP25/REP32/17 join –[ΔlacIZ4652∷Kan(sw)]/pSIM5(CmR) | This report |
| TT26066 | his-644(ΔOGDCBHAF) proAB670(SpR) recA650∷Gnt(sw)/F′128pro+ DUP2067[lacI4650∷Ka(sw,KnS), lacZY+]–REP25/REP32/17 join –[ΔlacIZ4652∷Kan(sw)]/pSIM5(CmR) | This report |
| TT26069 | his-644(ΔOGDCBHAF) proAB1657(TcR) recA650∷Gnt(sw)/F′128pro+ DUP2068[lacI4650∷Ka(sw,KnS), lacZY+]–REP26/REP32/17 join–[ΔlacIZ4652∷Kan(sw)]/pSIM5(CmR) | This report |
| TT26070 | his-644(ΔOGDCBHAF) proAB670(SpR) recA650∷Gnt(sw)/F′128pro+ DUP2068[lacI4650∷Ka(sw,KnS), lacZY+]–REP26/REP32/17 join—[ΔlacIZ4652∷Kan(sw)]/pSIM5(CmR) | This report |
| TT26073 | his-644(ΔOGDCBHAF) proAB1657(TcR) recA650∷Gnt(sw)/F′128pro+ DUP2069[lacI4650∷Ka(sw,KnS), lacZY+]–IS3BCjoin–[ΔlacIZ4652∷Kan(sw)]/pSIM5(CmR) | This report |
“sw” designates alleles in which the normal sequence was replaced by a drug resistance determinant. “T-Recs” designates a derivative of Tn10 with a CmR determinant and a constitutive (Oc) recA+ allele inserted into the middle of the Tn10 tetA gene, rendering the strain sensitive to tetracycline and resistant to chloramphenicol. “lacI4650∷Ka(sw, KnS)” refers to a lacI gene replaced by a promoterless kanamycin resistance determinant. “TcSKn” designates a Tn10dTc element in which a KnR determinant is inserted in the tetA gene, rendering the strain sensitive to tetracycline and resistant to kanamycin. The “pSIM5(CmR)” plasmid carries the recombination genes (red) of phage lambda.
Determining increases in duplication frequency during extended growth periods:
Three duplication assay methods are described in appendix a. The Ka-Kan assay was used for reported experiments, but its results were confirmed by both the T-Recs and the drug-in-drug assays. For the Ka-Kan assay, all strains carried a lacZ+ allele at the test locus (e.g., inserts in the chromosomal argH and pyrD genes and the standard lacZ locus on F′128). This lacZ gene was expressed constitutively due to an insertion in the repressor gene (lacI) of a promoterless kanamycin resistance determinant (Ka). All strains carried a plasmid (pSIM5) with repressed genes (Red) for lambda recombination (Court et al. 2002). The seven strains used in these assays are listed in Table 1 (TT25467, -25468, -25469, -25996, -25997, -26002, and -26003) and the material inserted at the test locus is diagrammed in appendix a.
To determine the duplication frequency after 33 generations, a 3-ml culture in LB was grown overnight at 30° to maintain repression of the Red recombination functions. One aliquot of a saturated culture was used to assay cell number and another to determine duplication frequency by transformation. Transformations were done after 15 min at 42° to induce Red genes. Recombinants were selected on LB kanamycin X-gal plates. Each transformant that acquired KanR simultaneously lost the adjacent lacZ+ gene. White (Lac−) transformant colonies indicated a haploid recipient cell; blue (Lac+) colonies indicated a recipient with a duplication of the test locus. A third aliquot from the overnight culture was used to inoculate a continuous growth chamber containing 40 ml of fresh LB medium.
A continuous growth chamber (turbidostat) was used to follow accumulation of duplications over extended time periods. Rich LB medium with chloramphenicol (to maintain the Red plasmid) was pumped continuously into a 40-ml culture vessel (and culture allowed to flow out) to maintain a constant volume and cell population size (i.e., cell loss by dilution balanced gain by growth.) Cultures grew at 30° with stirring at 200 rpm and continuous flushing with hydrated air. The medium flow rate was adjusted to maintain midlog phase (OD650 ∼ 0.2), well below saturation level (OD650 = 1.1). The number of cell generations was calculated from the flow rate (i.e., one generation per 40 ml removed). Wild-type cells grew ∼60 generations per day (24 min/generation). At various times, samples were removed and assayed for duplication frequency.
Fitness cost measurements:
All strains carried a recA mutation to prevent duplication loss and a plasmid (pSIM5) encoding phage lambda recombination functions (Red), which were repressed during growth and induced during the final duplication assay. It was assumed that, while a recA mutation reduces all growth rates slightly, it did not affect the relative fitness of duplication and haploid strains. Control experiments showed that recA effectively prevented duplication loss. Over the entire growth period, <3% of cells lost the lac duplication on F′128 and <0.001% of cells lost chromosomal duplications. The haploid control strain carried a chromosomal KanR insertion to ensure that differences in growth rate were not due to the KanR. Overnight cultures were diluted 800-fold into 6 wells of a 96-well plate containing LB with 10 μg/ml chloramphenicol (to maintain the repressed Red plasmid) and growth rates were measured using a Synergy HT plate reader (Bio-Tek). The culture plate was incubated at 30° with continuous shaking and absorbance at 650 nm was read at 15-min intervals. For each strain, the growth rate measurement was repeated for a minimum of three independent clones. The standard deviation of the relative rates was <0.02.
The small fitness costs of lac duplications on plasmid F′128 were also determined by the more sensitive method of direct growth competition between each of four duplication strains and the haploid parent strain (Figure 4). Strains to be compared were made recA to minimize duplication loss during growth and each was genetically tagged with either a tetracycline or a spectinomycin resistance cassette inserted into the chromosomal proAB genes. Results were the same with reversed tags. Five 3-ml tubes of LB medium containing 10 μg/ml chloramphenicol were inoculated with 106 cells of each of the two strains to be competed. After an overnight growth cycle, the culture was diluted and the process repeated for multiple passages. After each cycle, samples were plated for single colonies on LB plates, which were then printed to a tetracycline and a spectinomycin plate, to determine the ratio of the two cell types.
Figure 4.—
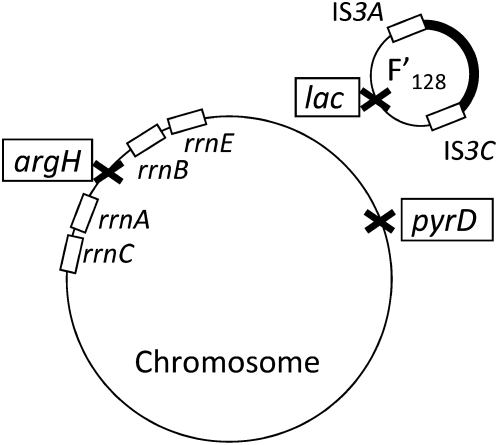
Three genomic loci assayed for duplication accumulation. The argH locus is between direct-order copies of the 6.5-kb rrn genes. The lac locus lies between repeated direct-order copies of the IS3 element (∼131 kb apart) on a low copy conjugative plasmid (F′128), whose transfer replication origin is responsible for intense recombination on the plasmid (Seifert and Porter 1984b; Syvanen et al. 1986; Carter et al. 1992). The chromosomal pyrD locus is not flanked by major repeats and is likely to be typical of most regions of the chromosome.
The relative fitness was calculated using a spreadsheet simulation in which virtual populations were started at the input ratios used in the actual experiment. In the simulation, haploids and diploids were allowed to double at distinct rates (μD and μH). The duplication formation rate (kF) was set to zero because recA duplication strains produce essentially no haploid cells from which new duplications could form. In the experiment, new duplications were also ignored in that the haploid cells were counted without regard to any new copy number variants, which would be rare and growth impaired. The duplication loss rate (kL) was essentially zero due to recA, but was set to the low rate measured for the specific duplications being analyzed. To determine relative fitness, the relative growth rate of haploid and diploid cells (μD/μH) was varied in the simulation, until a value was found that predicted the ratio of cell types determined in the experiment. The ratio of growth rates or relative fitness (μD/μH) allowed estimation of the duplication growth rate (μD).
Determining duplication loss rate (kL):
Assayed cells carried a duplication trapped using the Ka-Kan method and thus had a (KanR)(Lac+) phenotype. The loss rate of the KanR or Lac+ phenotype was measured in single colonies growing at 30° on nonselective plates of solid LB medium containing X-gal. Each colony served as an individual culture in which the observed frequency of cells losing the duplication was converted to loss rate by corrections for the different growth rates of haploids and duplication-bearing strains. Five single colonies were analyzed for each trapped duplication strain.
Small colonies appearing overnight (∼23 generations) were plugged using the wide end of a sterilized Pasteur pipette and cells were suspended in 1 ml of minimum medium (NCE) in a 1.5-ml Eppendorf tube. Cells were serially diluted in NCE medium and plated on LB–X-gal to determine total cell number and the fraction that was Lac+. The plates were replica printed to LB–kanamycin–X-gal plates to determine the number of duplication-bearing cells—KanR Lac+—and the fraction of cells that retained KanR, but had lost their Lac+ copy. The frequency of duplication loss was the sum of frequencies of cells that had lost either the KanR or the Lac+ phenotype. The total generations of nonselective growth were calculated from the total cell number in the colony.
To determine the loss rate constant, kL, a spreadsheet simulation was run in which a virtual single duplication-bearing cell grew and produced new haploid segregants. The simulation used previously measured growth rates of parent duplication cells and derived haploids (μD and μH). The spreadsheet keeps track of the entire population of haploid and duplication cells. Haploids were assumed never to reach a frequency sufficient to contribute significantly to formation of new diploids. The value of kL in this spreadsheet was varied until the simulation predicted the frequency of haploid cells that was observed experimentally (after a number of generations equal to that measured for the experimental colony).
Both the experiment and the spreadsheet simulation ignored formation of new diploids, assuming that the small size of the haploid segregant population and the low duplication rate made this negligible. In this experimental assay, any new duplication arising from haploid segregants would retain the haploid phenotype, either KanR Lac− or KanS Lac+, and would not be scored as a duplication (KanR)(Lac+). Jackpots were not an issue in the simulation since fractional numbers of haploids were allowed. In the colonies, jackpots were minimal because segregation rates were so high. The median kL value among five colonies was taken as the kL value for that strain; these values showed very little variance.
Predicting kF and the steady-state frequency on the basis of frequency after 33 generations:
The kF value was estimated from the rate at which duplications accumulate in a culture grown from a single haploid cell. This value was the most difficult to determine because newly formed duplication cells grew more slowly than the parent and were rapidly lost by segregation (kL is typically ∼1000-fold higher than kF). In addition, our methods for determining duplication frequency required ∼109 cells, which necessitates ∼30 generations of growth before the first measurement could be made. The value of kF was estimated using a simulation in which a virtual colony was grown from a single haploid cell dividing at measured rate μH and producing diploids that grew at measured rate μD. Duplications formed and disappeared at rates kF (unknown) and kL (described above). At each haploid generation, the number of haploid and duplication-bearing cells was calculated. The value kF was varied until the frequency of duplications predicted for haploid generation 33 of the simulation equaled that observed at the corresponding point in the actual culture. The value of kF determined in this was used as one estimate for the strain being tested. Essentially, the simulation used the measured values of kL, μH, and μD with the measured duplication frequency (D/H) at generation 33 to estimate kF and the expected steady-state frequency for the particular duplication. The simulation avoided Luria–Delbruck fluctuations by using fractional cell numbers. The solid lines in Figure 5 indicate the trajectory of duplication frequency based on this simulation. The trajectory was set to agree with the measured frequency at generation 33. The values obtained using the spreadsheet simulation are verified quantitatively below.
Figure 5.—
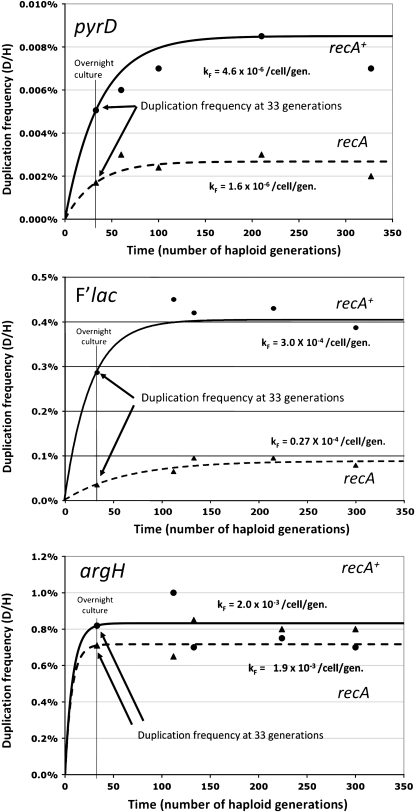
Accumulation of duplications in long-term cultures. Cultures initiated with a single haploid cell grew in LB with constant dilution to maintain the culture in midlog phase. The duplication frequency was determined using the Ka-Kan assay. Circles are for a recA+ haploid parent and triangles are for a recA mutant parent. Since the duplication assay required a large population size, the earliest time point at which an assay could be made was 33 generations. The plotted lines describe the duplication accumulation predicted by a spreadsheet simulation using the measured D/H (at 33 generations) and the measured fitness cost and duplication loss rate. Measurement of these values is described in the text.
RESULTS
Genomic regions assayed:
Duplications described here affected three sites: two in the chromosome and one on plasmid F′128 (see Figure 4). The argH gene is located between direct repeats of the 6.5-kb rrn repeats and is among the most frequently duplicated sites in the chromosome (>1% in unselected cultures) (Anderson and Roth 1981). The pyrD gene is far away from any rrn locus and has a low duplication frequency of ∼0.005% in an overnight culture. The lac operon of Escherichia coli on plasmid F′128 was chosen because amplification of this region plays a major role in reversion of lac under selection in the Cairns system (Cairns and Foster 1991; Hendrickson et al. 2002; Slechta et al. 2003; Kugelberg et al. 2006). Like the argH gene, the plasmid lac region is flanked by large repeats (IS3; 1258 bp) and by clusters of shorter (30-bp) Rep elements (Bachellier et al. 1999; Kofoid et al. 2003). The lac locus is duplicated in ∼0.2% of cells in an unselected culture.
Duplication frequency approached a steady state in both recA+ and recA− strains:
During prolonged growth of recA+ strains, the frequency of duplications reached a steady-state level for all of the three regions tested as seen in Figure 5 (see data points for recA+ strains). The data for recA mutant strains is described later. The solid lines describe the duplication accumulation predicted from a simulation that takes into account fitness costs and measured rates of duplication formation and loss. The close fit between experimental data and predicted accumulation should be noted; the simulation is described later.
All three loci were assayed in unselected cultures grown for extended periods in rich medium with continuous dilution to maintain a constant cell density (turbidostat). The several assay methods used are described in appendix a. The duplication frequency data presented were obtained using the Ka-Kan method and results for individual strains were confirmed by the other tests (T-Recs and drug-in-drug); all three methods gave closely comparable frequencies. In the Ka-Kan method, each tested strain has a copy of the lacI-Z region at the test site (inserted at argH or pyrD or present on F′128 lac). The lacI gene was replaced by a kanamycin resistance determinant lacking both a promoter and an initiation codon (Ka), leaving cells phenotypically KanS and Lac+ (expressed constitutively). A duplication of this site was identified by a Red-mediated transformation in which an introduced single DNA strand provided a promoter and initiation codon for Ka and thereby conferred drug resistance (KanR). Inheritance of the promoter fragment also generated a deletion extending into the lacZ gene, causing a Lac− phenotype. In identifying duplications, haploid Ka recipient cells (KanS, Lac+) gave rise to KanR Lac− transformants. Recipient cells with a duplication of the tested region gave rise to KanR transformants that remain Lac+ by virtue of their second copy of the region: (KanR Lac−) (KanS Lac+). This method can be used in either recA+ and recA− strains since recombination mediated by the Red functions of phage lambda (recombineering) is independent of RecA (Court et al. 2002).
The Ka-Kan assay required that strains carry genes for the Red recombination system of phage lambda. These genes were repressed during growth of the population and were induced only immediately before duplication trapping. To be certain that these Red functions did not contribute to duplication formation or loss (especially in recA mutant strains), measured duplication frequencies were confirmed using a transduction-based duplication assay, T-Recs (see appendix a).
In the T-Recs assay, an otherwise wild-type recA mutant is grown nonselectively to allow accumulation of duplications of any of the test loci (pyrD+, argH+, or lac+). Cells with a duplication were identified by a P22-mediated transduction cross that introduced a chloramphenicol resistance gene (CmR) insertion into the locus being tested (pyrD∷CmR, argH∷ CmR, or lac∷ CmR). The element carrying CmR (T-Recs) also includes a constitutively expressed functional recA+ gene. The RecA function produced from the transduced fragment allows the donor allele to recombine with the chromosome of the recA mutant recipient. Recipient (recA) cells with no duplication gave CmR transductants that were defective for the function of the test locus (Pyr−, Arg−, or Lac−). Recipient cells with a duplication formed during pregrowth gave CmR transductants that inherited the donor insertion allele in one copy of the test locus but retained a functional test allele in the other. Using this assay, duplications were found to accumulate at the same rate as that inferred using the Ka-Kan assay. A third assay, (drug-in-drug; appendix a) also confirmed the results in Figure 5. The steady-state frequency of the lac duplications was also independently confirmed by quantitative PCR amplification of the predominant duplication junction fragment (between IS3C and IS3A).
Use of the T-Recs assay gave further evidence that Red functions (used in the Ka-Kan assay) do not contribute to duplication formation. The duplication accumulation measured by T-Recs after 30 generations of a recA strain was the same with and without the Red plasmid. (A brief induction of Red functions at 42°, as used in the Ka-Kan assay, caused no increase in the assayed duplication frequency.) Thus Red functions appear to make no contribution to duplication formation even when fully induced.
The rate of duplication loss was also not affected by Red functions. Duplication strains with a recA mutation showed essentially no duplication loss (described below) and this negligible rate was not increased by a plasmid providing the repressed Red genes (lambda recombination functions) even after a 15-min period of induced Red expression. Thus the Red functions carried by strains for the Ka-Kan assay did not contribute to either formation or loss of duplications. The ability of Red to contribute to efficient transformation but not internal rearrangement is expected since Red-mediated transformation seems to require a high concentration of input fragments (Court et al. 2002).
Estimating the duplication loss rate (kL):
Independent duplications of a particular locus can include different amounts of material within which an exchange can lead to loss (Figures 1 and 3). Therefore, one might expect different duplications to show different loss rates. These rates were measured for a series of independent duplications of each locus, trapped using the Ka-Kan transformation method described above (see also appendix a). Five single colonies of each duplication strain (KanR, Lac+) were tested for the loss of either the Lac+ or the KanR phenotype during colony formation growth (∼23 generations) on nonselective LB plates (see materials and methods). After growth, the entire colony was plugged and used to estimate total cell number and frequency of accumulated haploid cells. The frequency was used to estimate loss rate (kL), using a spreadsheet simulation (see materials and methods). The magnitude of the correction made by this simulation varies with the growth rate of each particular duplication tested, which can be very different even for two duplications of the same locus. In each case the fitness defect of the particular strain was used in estimating its loss rate. In general, fitness costs were greatest for duplications of argH where the uncorrected kL value was two- to sevenfold higher than the value obtained taking fitness into consideration. For all other loci the corrections were less than twofold.
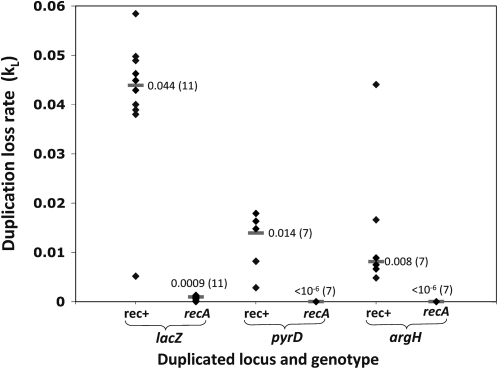
The duplications described in Figure 6 were isolated and tested for loss rate in the same genetic background (either recA or recA+), because rates of duplication loss will be used to assess the approach to steady state in strains with and without RecA. The duplications whose loss rate is shown in Figure 6 appeared to be structurally similar regardless of their origin. All duplications tested show a loss rate that is highly dependent on RecA (see below).
Figure 6.—
Estimated rate constants for duplication loss (kL). Duplication loss was measured during growth of single colonies on LB medium. Each data point represents one independently isolated duplication mutant and is the median value of five subclones of that mutant (SD < 38%). The data show the variation between different duplications. The bars indicate the median loss rate of the different assayed duplication mutants, followed (in parentheses) by the total number of duplications assayed.
Role of homologous recombination (RecA) in duplication loss:
The homologous recombination function RecA has been shown repeatedly to be important for the exchange events leading to duplication loss (Anderson and Roth 1979). This was confirmed by the observation that duplications isolated in a recA mutant background showed a very low loss rate (Figure 6), while those isolated in recA+ strains showed a rather high but variable loss rate (0.003–0.06/cell/generation). All of these duplications, regardless of their origin (recA+ or recA−), seem to be qualitatively the same. That is, the unstable duplications isolated in recA+ strains become stable when a recA allele is added and conversely stable duplications arising in recA strains show a typical high loss rate when a recA+ allele is provided. Furthermore, duplication formation rates are similar in recA+ and recA− backgrounds (see below). The primary effect of RecA is on duplication loss.
For the chromosomal argH and pyrD loci, no case of duplication loss was observed in the absence of RecA (<10−6/cell/division). The few cases of recA-independent loss of a lac duplication on F′128 (9 × 10−4) may reflect deletions arising on the plasmid, which has a very high rate of genetic rearrangement stimulated by its conjugative replication origin (Silver et al. 1980; Seifert and Porter 1984a,b; Tlsty et al. 1984; Carter and Porter 1991; Carter et al. 1992).
Estimating the rate constant for duplication formation (kF):
At early points in the growth of haploid strains, duplication frequency is low and therefore the number of duplications lost is negligible. This should in principle allow an estimate of duplication formation rate based on the initial accumulation rate. However, because available assay methods require a large population, the earliest time in the growth period at which a frequency could be measured was ∼30 generations. The measured frequency of duplications at this time point (33 generations) is marked on the curves in Figure 5. At this point, duplication frequency estimates can be seriously influenced by duplication loss and growth rate differences (duplication fitness cost).
To assess kF, the measured frequency at 33 generations was corrected for effects of duplication loss and growth rate differences. The correction was made using a spreadsheet simulation in which a virtual haploid cell was allowed to grow (at rate μH) and form duplications at rate kF (not yet determined). The simulation uses determined growth rates for haploid and diploids (see below) and the estimated loss rate kL (determined above). The unknown formation rate (kF) was varied in that simulation until the duplication frequency (D/H) at 33 generations equaled that experimentally determined frequency at this point in the growth period. The kF values for the three loci are presented in Figure 5 (see solid curves). By running the simulation past the 33-generation point, the approach to steady-state frequency can be predicted.
Figure 5 shows that the simulation predicts a trajectory and a steady-state duplication frequency that matches the experimentally measured increase in the frequency of duplications. This agreement suggests that the four parameters (kF, kL, μH, and μD) are sufficient to explain the observed accumulation of duplications. As expected if these four variables dictate accumulation, different loci (whose duplications behave differently) show distinct values of kF and attain different steady states at distinct rates. For example, lac duplication frequencies in recA strains reached only 40% of the steady-state value after 33 generations, while argH duplication frequencies in recA+ strains reached 98% of the steady-state value. The relationship between the approach to steady state and the four parameters also agrees with the analytical treatment of duplication accumulation seen below.
Role of RecA in duplication formation:
Table 2 shows average rates of duplication formation for each locus and the effect of RecA. It was surprising that duplication rates dropped so little in a recA mutant. The recA mutation essentially eliminates homologous recombination in otherwise normal strains and was seen above to eliminate duplication loss at all three loci (Figure 6). This raises a question regarding the mechanisms underlying duplication formation.
TABLE 2.
| Duplication formation rate (kF)a based on frequency after 33 generations |
RecA effect on duplication formation (Rec+/Rec−) | ||
|---|---|---|---|
| Duplicated locus | recA+ | recA− | |
| pyrD | 4.6 × 10−6 | 1.6 × 10−6 | 2.9 |
| lacZ | 30.0 × 10−5 | 2.7 × 10−5 | 11.1 |
| argH | 2.0 × 10−3 | 1.9 × 10−3 | 1.1 |
This kF value is based on the duplication frequency after 33 generations corrected for growth rate differences and kL using a spreadsheet simulation.
The pyrD locus lacks major flanking sequence repeats and may be typical of most chromosomal loci; pyrD shows the lowest duplication formation rate and a rather low dependence on RecA. The lac locus (with flanking 1.3-kb repeats) shows a nearly 100-fold higher duplication rate (in recA+), but only slightly higher dependence on RecA. The high duplication rate for lac may reflect both the presence of the IS3 repeats and the stimulatory effect on recombination of DNA ends generated by the plasmid conjugative transfer origin. Most surprising is the behavior of the argH locus, which lies in the midst of four direct-order rrn repeats (each 6.5 kb). The duplication rate for argH is 1000-fold higher than that of pyrD and but shows essentially no dependence on RecA. The high rate of argH duplication is consistent with the presence of large, direct-order rrn repeats (see Figure 4), but the lack of dependence on recombination suggests that exchanges between rrn loci may often arise without standard recombination.
Attaining a steady-state duplication frequency in the absence of RecA:
Initially it was expected that the steady-state duplication frequency would be dictated entirely by relative rates of formation and loss (kF/kL). This expectation is contradicted by the effects of a recA mutation seen in Figure 5 (see data points for recA mutant strains). The recA mutation had a minor effect on formation (kF) and essentially eliminated loss (kL). If the initial expectation had been correct, then a recA mutation should have caused a great increase in the steady-state duplication frequency (kF/kL) by severely reducing kL and modestly reducing kF. The reverse is seen in Figure 5: the recA mutation reduced steady-state duplication frequency for all tested loci. This suggested that another factor must contribute to establishment of the steady state.
Role of fitness cost in approach to steady state:
The fitness cost of duplications appears to be the missing contributor to attainment of steady state. If duplication strains grew more slowly than the haploid parent, then the frequency of duplications could reach a steady state, even when there is essentially no reversion (kL = 0). This is described in Figure 2 above. Steady-state frequency can be reached when increases caused by de novo duplication formation counterbalance decreases caused by slower growth of the duplication strains. Under conditions that allow both reversion rate and fitness cost to contribute, a steady state is expected when the formation rate balances the combined effects of duplication loss rate and growth deficit. The approximate relationship is that steady-state frequency (D/H)∞ = formation rate/(loss rate + fitness cost). To test this, duplications were first tested for fitness cost.
Fitness costs of duplications:
Growth rates were measured for independently formed duplications of each of the three genomic regions being tested (see Figure 7). Some of those duplications were isolated in a recA mutant background and others in a recA+ parent strain as described above. All those from the recA+ strain received a recA mutation just before the growth rate test to prevent duplication loss during growth. Without this stabilization, haploid segregants (with higher growth rates) quickly overgrew cultures and obscured the effect of the duplication on growth rate. In estimating duplication fitness effects in recA mutants, it is assumed that, even though the recA mutation reduced growth rate slightly, the ratio of growth rates for diploid and haploid strains was independent of recombination. Relative fitness was the ratio of the growth rate of a duplication strain (μD) and that of the isogenic haploid parent (μH).
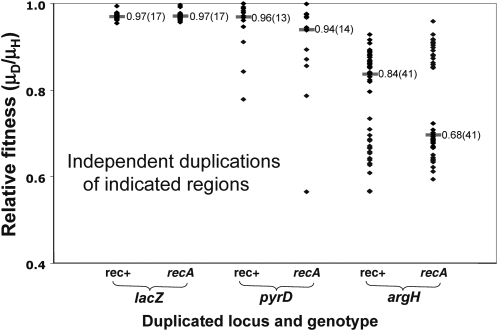
Figure 7.—
Fitness costs of duplications. Relative fitness is defined as the ratio of the growth rates of a duplication strain to that of its haploid parent (μD/μH). All tested duplications were isolated by the Ka-Kan selection (appendix a) and had a duplication with KanR Lac− in one copy and KanS Lac+ in the other. Each point represents one independently isolated duplication mutant, whose presented relative growth rate is the average of three or more determinations (SD < 0.02). The median for each group of duplications is represented by a horizontal bar; the total number of different duplications assayed is in parentheses. Some duplications arose in recA+ cells and others in recA mutants. To minimize duplication loss during growth, rate measurements were made after addition of a recA mutation, which reduces growth slightly but is assumed to have no effect on the relative fitness of haploid and duplication-bearing strains.
In Figure 7, it can be seen that strains with duplications of lac on the F′ plasmid are nearly as fit as the haploid parent (median cost is ≤3%). This might be expected since the plasmid carries no essential genes. Of the 17 lac duplication strains tested, 14 extend between the IS3A and IS3C elements and include 131 kb of F′ plasmid material (see Figure 3); these duplications have a fitness cost near 3%. Three lac duplications contained only ∼20 kb of material (1 was isolated in recA+ and 2 in recA− parents); these smaller duplications have a lower (1%) fitness cost. Duplications of both types have been described previously (Kugelberg et al. 2006). The low fitness cost of small lac duplications helps explain why cells with such a duplication quickly amplify and show rapid growth under selection for increased lacZ activity (Cairns and Foster 1991; Roth et al. 2006).
Duplications of the pyrD locus show a wide range of fitness costs. This is likely to reflect a variety of endpoints and sizes, but the exact extent of these duplicated regions has not been determined. The argH duplications form between various pairs of the flanking rrn loci, two on each side of argH (Figure 3). These duplications vary in fitness cost and seem to fall into two general classes, which may reflect repeated use of these few prominent rrn endpoint sequences. The regions between rrn loci encode a variety of highly expressed housekeeping proteins, which may explain the high fitness cost of some of these duplications.
Can fitness cost and relative rates of formation and loss explain steady-state duplication frequencies?
Duplication frequency seems to attain a steady state due to the combined effects of formation and loss rates and the fitness cost of a duplication relative to its haploid parent. The general contribution of the two effects to steady state is (D/H)∞ = formation rate/(loss rate + fitness cost).
An exact mathematical description of the accumulation process is derived in appendix b. The expression in Equation 1 describes the relationship between the four variables measured (kF, kL, μH, and μD) and the steady-state ratio R∞ = D/H, where D is the number of duplication-bearing cells and H is the number of haploid parent cells in a culture,
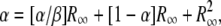 |
(1) |
where
 |
and
 |
The term “α” represents the ratio of new duplications formed to duplications lost by segregation and thus describes the contribution of formation and loss to the steady-state R value. This rate depends on growth because it is assumed that formation and loss events occur during chromosome replication and should be expressed per cell division. The correction for different growth rates is relatively small in most cases. The term “β” relates the formation rate to dilution rate attributable to fitness costs. Thus, it represents the contribution of fitness cost to the steady-state value.
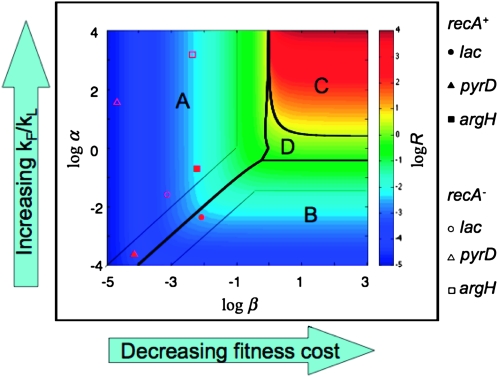
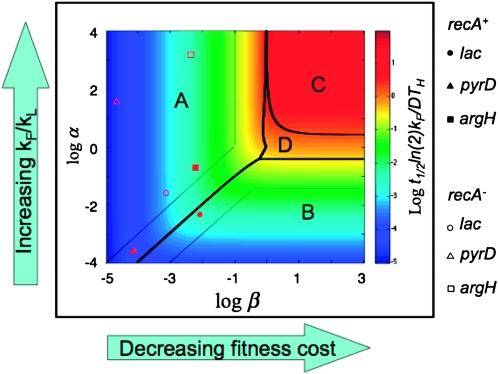
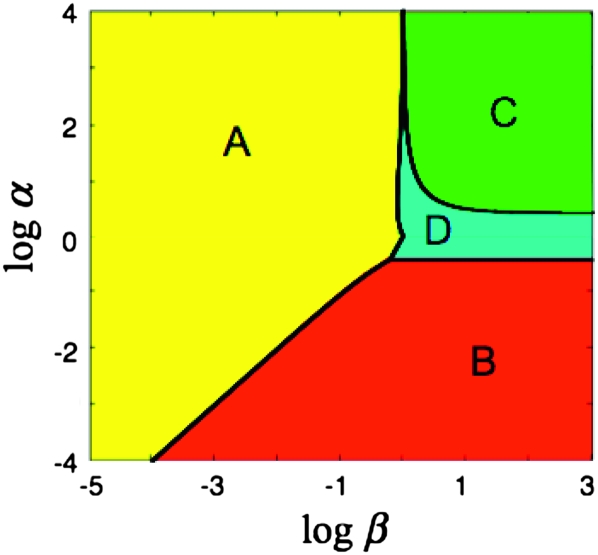
To visualize how formation/loss rates and fitness cost contribute to the steady state, one can plot “log α” vs. “log β” and examine steady state and time to half steady state, t1/2, expected for each point in this design space (Savageau et al. 2009). In Figure 8, the value of log R∞ is represented by color as described at the right. The sensitivity of R∞ to changes in α and β defines four regions (regions A–D in Figure 8). In region A, the value of R∞ depends heavily on relative fitness (μD/μH) and less on formation/loss rates (on changes in β and less on changes in α). In region B, R∞ depends heavily on formation/loss rates (α) but less on fitness cost (β).
Figure 8.—
Design space diagram for visualizing effects of fitness and formation/loss on steady-state duplication frequency.
Also shown in Figure 8 are the positions in this space of the loci assayed here. The experimental values for the argH region in a RecA+ strain place the point in region A of the design space, showing that fitness cost (β) is the major determinant of the steady-state duplication frequency. That is, the steady state rises as fitness cost decreases, but steady state is not sensitive to changes in the formation/loss rates. The pyrD and lac regions in RecA+ strains are located in regions A and B, respectively, but near the boundary between these regions. Thus, these strains exhibit a mixed contribution from both fitness cost (β) and formation/loss rates (α). In recA mutant strains (open symbols), all regions tested fall within region A, where R∞ is dictated by fitness cost (β). These results suggest that our initial focus exclusively on formation and loss rates was incorrect—fitness cost is a major factor in determining steady-state duplication frequency.
The time required to reach steady state can also be plotted as a heat map in the α−β design space (see Figure 9). Again all loci tested have values that fall into region A or B. In region A, time required to reach half steady state (t1/2) increases as fitness cost (β) is reduced. That is, the time required to reach steady state is shortened by increasing fitness cost, but is not affected by the ratio of formation and loss rates (α) for the regions studied here. In region B, changes in fitness cost (β) have little effect on t1/2, and the approach to steady state is accelerated primarily by the fitness cost of the duplication. That is, the approach to steady state is accelerated primarily by decreases in the ratio of formation rate (kF) to loss rate (kL).
Figure 9.—
Design space diagram for visualizing effects of relative fitness (β) and formation/loss rates (α) on time required for duplication frequency (R) to reach one-half of the final steady state (t1/2).
The values for the parameters summarized in Figures 8 and 9 are presented in Table 3 with the R∞ values and the time to half steady state (t1/2) predicted by the mathematical analysis (appendix b). Table 3 compares values of R∞ and t1/2 estimated in various ways. This agreement between these approaches shows that the mathematical description fits well with unprocessed experimental data and with approximations made using the spreadsheet simulation. A very similar dependency of steady-state duplication frequency on the four parameters was obtained when the process of duplication accumulation was modeled using a Monte Carlo simulation (data not shown). The concordance of several approaches suggests that the behavior of duplication frequency is well explained by the combination of relative fitness (μD/μH) and relative rates of formation and loss (kF/kL).
TABLE 3.
Comparison of observed and analytical values for duplication steady state
| Locus tested | RecA genotype | R33 = D/H ratio after 33 generations (×104)a | Loss rate kL (×103)b | Relative fitness μD/μH (average)c | Formation rate kF (×105) |
Steady-state frequency R∞= D/H (×104) |
Time to one-half steady state (t1/2) (in generations) |
||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rawd | Simulatione | Analyticf | Rawg | Simulationh | Analytici | Rawj | Simulationk | Analyticl | |||||
| pyrD | recA+ | 0.51 | 14.0 | 0.96 | 0.31 | 0.46 | 0.39 | 0.70 | 0.85 | 0.72 | 23 | 25 | 18.7 |
| recA− | 0.17 | <0.001 | 0.94 | 0.10 | 0.16 | 0.14 | 0.20 | 0.27 | 0.23 | 20 | 23 | 16.7 | |
| F′ lac | recA+ | 28.7 | 44.0 | 0.97 | 17.4 | 29.9 | 25.7 | 38.7 | 40.3 | 35.4 | 22 | 19 | 13.8 |
| recA− | 3.5 | 0.9 | 0.97 | 2.12 | 2.69 | 2.13 | 7.9 | 8.7 | 6.9 | 37 | 45 | 32.4 | |
| argH | recA+ | 81.8 | 8.0 | 0.77 | 50.0 | 198.5 | 193.0 | 75.0 | 83.4 | 82.4 | 15 | 6 | 4.27 |
| recA− | 71.0 | <0.001 | 0.74 | 43.4 | 192.5 | 184.0 | 80.0 | 74.0 | 71.3 | 18 | 6 | 3.87 | |
These values were determined directly.
These kL values were determined with the aid of a spreadsheet simulation to correct for growth rate differences.
Duplications described were isolated in either a recA or recA+ as indicated. Relative fitness was determined in recA mutant derivatives using a spreadsheet to correct for loss rate. For the pyrD and lac loci, each presented value is the median value for several independent duplication strains. Because the argH duplications fell into two classes, the average value is presented.
This value uses the determined R33 to define an uncorrected initial rate.
This kF value was determined using a spreadsheet simulation. After 33 generations in the simulation, this kF value produces a duplication frequency equal to that observed after 33 generations of growth.
This kF value was calculated using the mathematical description (appendix b) and solving for kF using measured values of fitness and kL with the measured values of R after 33 generations.
This value of R∞ is determined by direct observation of the data points in Figure 5, without any corrections.
This value of R∞ is predicted by the spreadsheet simulation using a kF that produces the observed frequency at generation 33 (see plot in Figure 5).
This value of R∞ is calculated using the mathematical description (appendix b), the “raw” unmanipulated value of R33, and the assayed values of kL and relative fitness.
This is estimated on the basis of an approach to the raw steady-state frequency and the raw kF.
This is estimated on the basis of the trajectory of the spreadsheet simulation obtained using the corrected kF and the measured relative fitness.
This value is calculated using the mathematical description and on the basis of unmanipulated values of R33, kL, and relative fitness.
DISCUSSION
The results presented here reveal several unexpected properties of duplication mutations:
Duplication formation (kF) depends only weakly on recombination, even when junctions reflect exchanges between rather extensive separated sequence repeats (1–6.5 kb). This observation suggests that mechanisms other than homologous recombination can underlie duplication formation (even when long repeats are involved). We suggest that this occurs by a stepwise process initiated by a tandem inversion duplication, in which deletion events generate the junctions found in the final simple duplication (Kugelberg et al. 2006; E. Kugelberg, unpublished results).
Duplication loss rate (kL) depends heavily on recombination, probably because exchanges occur between very long sequence repeats (>40 kb). Loss is frequent because of the length of these sequences and the use of an active system of homologous recombination. Longer duplications are expected to have higher loss rates since they present larger targets for recombination.
Duplications have a surprisingly high, but locus-dependent fitness cost. Most previous discussion of bacterial duplication frequency in rich medium has assumed neutrality, but the steady states described here depend heavily on fitness costs as well as high formation rates. The fitness cost of duplication has been recognized for higher organisms since the advent of genome sequences (Emerson et al. 2008; Conrad et al. 2009). The variability of cost for different duplications suggests that cost is due to toxicity of particular gene products when overproduced or when present in an inappropriate ratio to the levels of other products. One may expect that in general larger duplications will have higher costs simply because they are more likely to include toxic genes. We cannot exclude the possibility that the growth deficits measured here for duplications are due to occasional lethality of duplication-bearing strains. The fitness costs were estimated in strains with a recA mutation, which is known to cause some cell death. It is possible that the recA defect causes more frequent cell death in duplication cells than in haploid cells.
Duplication frequency comes to a steady state dictated by a high formation rate (kF) balanced in part by a high loss rate (kL), but primarily by the high fitness cost of duplications. During the period of 30 generations required for a single cell to form a saturated 1-ml culture or a large colony on solid medium (109 cells), duplication frequency for a particular locus reaches >40% of the steady-state level.
Duplications can form between extensive repeats without RecA:
Duplications form frequently even without the benefit of recombination (RecA). This is true even for regions between fairly extensive repeats such as the chromosomal argH locus flanked by repeated rrn loci (6.5 kb) and the lac locus flanked by IS3 sequences (1.3 kb) on plasmid F′128. At least some duplications of these regions have hybrid rrn or IS3 sequences at their junction (data not shown). A model for RecA-independent formation of duplications between large and small sequence repeats will be described in detail elsewhere. In this model, a RecA-independent mechanism generates frequent large deleterious structures (symmetrical tandem inversion duplications, sTID) of the form ABCDD′C′B′A′ABCE (where each letter represents a block of sequence). These sTID structures are usually lost, but can be stabilized by join point deletions (Kugelberg et al. 2006; E. Kugelberg, unpublished results). Deletions extending between different points in the flanking direct repeats remove both inversion junctions and generate a new junction of a simple duplication. Duplication formation can be RecA independent regardless of the nature of the junction sequences, because RecA is not needed for either the initial sTID or the deletions that generate the ultimate duplication junction.
Stable polymorphisms in bacterial populations:
The process by which duplication frequency reaches steady state should, in principle, affect all mutations. That is, mutation frequency increases due to formation and drops due to reversion and counterselection. However, point mutations arise and revert at very low rates and steady state is expected only after extensive growth periods. The steady-state duplication frequency should be viewed as a stable genetic polymorphism. Roughly 1% of cells in an unselected population have a duplication of a region flanked by the most closely located rrn loci (rrnC, -A, -B, and -E) and ∼0.1% have a duplication of any particular gene outside of this region (Anderson and Roth 1981). About 10% of cells in an unselected population have a duplication of some unspecified chromosomal region. The region of F′128 that includes lac is duplicated in ∼1 in 500 cells and this polymorphism contributes to the rapid accumulation of lac+ revertants during selective growth of a strain carrying a lac mutation on F′128 lac (Roth et al. 2006).
The steady-state duplication frequency described here is predicted to also apply to higher copy number variants of the affected locus. Recombination events that cause duplication loss can also generate higher levels of repeat amplification (Figure 2) and are expected to occur at the same rate (∼10−2/cell/division). The mathematical treatment described here can predict the steady-state frequency of cells with higher copy numbers. If one assumes that fitness costs of added copies accrue by a constant factor, it is estimated for the lac region of F′128 that in an unselected steady-state population, one cell in 106 would have eight or more lac copies. Thus when 108 cells are plated on medium selecting for increases in lac level, 100 of those cells are expected to have many lac copies at the moment of plating.
Implications of duplication polymorphisms for the effect of selection on bacterial populations:
Point mutations that increase the level of a particular enzymatic activity are rare, arising at perhaps 10−9/cell/division (affecting a few base pairs of the relevant gene). Yet increases in the level of that activity are easily achieved by the copy number changes discussed here, whose formation rates are 1000- to 106-fold higher. In addition, the polymorphisms described above provide a high frequency of potentially beneficial duplications to even a very small population. Such variants are already present at a substantial frequency when selective conditions are first imposed. Selection detects small improvements and causes an exponential increase in mutant frequency. Since further copy number increases occur at such a high rate (order of 10−2/cell/division), amplification is quickly favored as the population expands. The fitness cost of duplications, noted here, does not prevent these selective effects.
As diagrammed in Figure 10, positive selection for increased copy number causes an increase in duplication frequency even if the benefit provided under selection is less than the underlying fitness cost of the duplication. That is, duplication steady-state frequency prior to selection is a balance between net formation rate (relative to loss) and fitness cost. When selective conditions allow extra copies to provide a growth improvement, duplication frequency is expected to increase (due to the offset of general cost). Further increases in the steady-state frequency can be enabled by deletions that reduce the size of the duplicated region, but leave the positively selected gene. Deletions shorten the repeated unit and thereby reduce both fitness cost and the rate of duplication loss. This selective remodeling of duplications has been described previously (Kugelberg et al. 2006).
Figure 10.—
Effects of selection and duplication remodeling on steady-state frequency. The steady-state duplication frequency is determined (at left) by a balance between rate of formation (kF) on one hand and combined rates of loss (kL) and counterselection on the other hand. This steady-state frequency is expected to increase if conditions change so that some gene in the duplicated region provides a fitness increase. The frequency increase is expected even if the benefit is smaller than the cost, because cost is offset by formation. Frequency is also expected to increase if the size of the repeated unit is reduced by deletions, which should both reduce fitness cost and the rate of duplication loss kL.
Acknowledgments
We thank Allan Campbell, who pointed out that our initial thinking about steady-state duplication frequency was numerically unsanitary. We believe that inclusion of fitness cost will satisfy his concerns. A.B.R. thanks Rosemary Redfield for instruction in use of spreadsheet simulations in the study of bacterial populations. J.R.R. thanks Richard Lewontin for asserting (30 years ago) that bacteria are boring subjects for population genetics because there can be no stable polymorphisms without sex and diploidy. His comment has been worrisome, ever since, but perhaps the steady states described here will help fill the bacterial polymorphism gap. This work was supported by National Institutes of Health grant GM27068.
APPENDIX A: ASSAYS FOR DUPLICATION FREQUENCY
Three distinct assay methods were used to determine the frequency of cells in a population that carry a duplication of a particular locus. Each of these assays can be used in strains that are deficient in recombination ability (recA). While most reported data were obtained using the Ka-Kan assay, congruent results were obtained with the others.
The T-Recs assay:
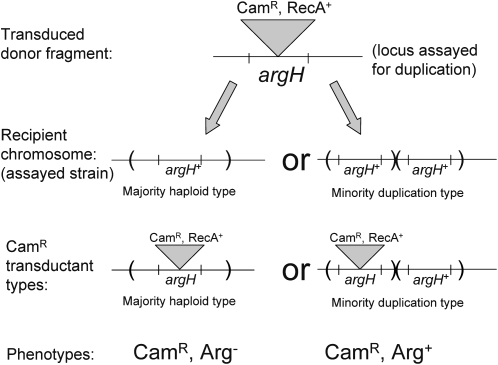
This assay is an improved version of an earlier method in which a transductional cross traps preexisting duplications in the recipient cell population (Anderson and Roth 1981). In the modified version, the Tn10 is replaced by variant element (T-Recs) that includes a recA+ gene and a chloramphenicol resistance (CamR) cassette. The recA+ gene is constitutively expressed due to a point mutation in its operator region. An inserted T-Recs element can be transduced into a recipient strain lacking RecA function. The transduced fragment carrying the T-Recs element expresses the RecA protein required for recombination with the chromosome. Thus a recA mutant population, grown without RecA function, can be assayed for accumulated duplications by selecting CamR of T-Recs and scoring the fraction of transductants that retain both the functional recipient allele and the defective donor allele. Recombination ability is restored only during the period of the assay.
The chromosomal genes analyzed for duplication formation are ones required for growth on minimal medium (argH and pyrD). The plasmid gene lacZ is required for growth on lactose. The donor strains carried a T-Recs (CamR, RecA+) element inserted into the assay locus (e.g., argH, pyrD, or lacZ). Transductants resistant to chloramphenicol (CamR) are selected on LB–chloramphenicol medium (see Figure A1). Duplications were detected by replica printing the transduction plates to minimal chloramphenicol medium. Most recipient cells are haploid for the assayed locus and inherit with CamR the growth defect of the donor (Arg−, Pyr−, or Lac−). Recipient cells with a duplication of the assayed locus inherit CamR but remain phenotypically Arg+, Pyr+, or Lac+ by virtue of the unaffected second copy. Such trapped duplications can be selectively maintained on minimum medium with chloramphenicol. The CamR transductants that do not acquire the metabolic defect of the donor are scored as duplications. As originally done, this assay requires recombination-proficient (RecA+) cells to support the transduction cross that traps the duplication, but the use of T-Recs insertions allows the assay to be done in a recA mutant recipient.
Figure A1.—
The T-Recs method for detecting duplications in a recA mutant strain. A transduction cross introduces a copy of the argH region with an inserted CamR marker (T-Recs). This insertion includes a recA+ gene in addition to the determinants for chloramphenicol resistance. When transduced into a recA mutant recipient, this element expresses RecA, which can support the recombination needed for acquisition of the donor insertion mutation. The duplication frequency is the fraction of CamR transductants that remain Arg+.
To assay duplication of lac on plasmid F′128, the donor carried a KanR replacement of lacIZ and a T-Recs (CamR RecA+) element inserted in lacA. Transductants were selected on rich medium containing kanamycin and X-gal. The duplication frequency was determined by counting the number of blue (duplications) and white colonies (haploids).
The T-Recs assay may slightly underestimate duplication frequencies, since occasional transductants into a duplication-bearing recipient may inherit the donor CamR(RecA) element in place of both copies of the duplicated region. This problem seems to be small since very similar duplication frequencies are inferred when this assay is compared to those described below.
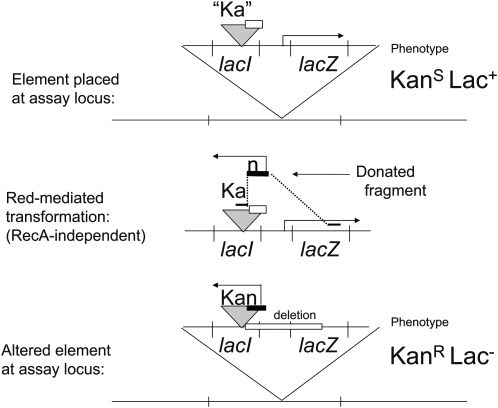
The Ka-Kan assay:
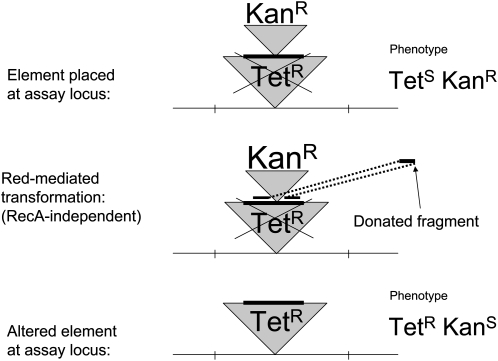
This assay detects duplications using a transformation cross, mediated by the recombination (Red) functions of phage lambda (recombineering), provided by a plasmid (pSIM5) that is carried (with repressed Red genes) by all strains being assayed (Court et al. 2002). The strategy is described in Figure A2. The locus whose duplication frequency is to be tested is disrupted by insertion of a lac operon whose lacI gene has an inserted kanamycin-resistance determinant lacking a promoter (this is designated Ka to indicate lack of expression). A strain carrying this insertion expresses LacZ constitutively due to its repressor defect. The donated fragment carries a promoter for the Ka gene flanked on one side by sequence within the Ka determinant and on the other side by sequence in the middle of the lacZ gene. Inheritance of the donor promoter generates a KanR phenotype and simultaneously creates a lacZ deletion (as diagrammed in Figure A2).
Figure A2.—
The Ka-Kan assay: a Red-mediated transformation to detect duplications in the absence of RecA. In this assay, a donated fragment includes a promoter for the Kan resistance gene and flanking homology to the Kan gene on the left and to the lacZ gene on the right. Inheritance of this fragment converts a KanS Lac+ allele to a KanR Lac− allele. Recipients with two copies of the lac region acquire KanR (in one copy) without loss of the Lac+ phenotype (provided by the other copy).
In a recipient cell that is haploid for the test locus, this transformation generates selectable KanR transformants with a Lac− phenotype. In recipient cells with a duplication of the test locus, the recombination event produces the KanR lacZ deletion in one copy, while the undisturbed other copy provides a Lac+ phenotype. Thus the fraction of Lac+ cells among the KanR transformants indicates the frequency of lac duplications in the recipient population.
Since Red-mediated transformation (recombineering) does not require RecA function, this assay can be used in recA mutant cells. This assay requires that the cells being tested carry a plasmid encoding the Red functions. These functions are not expressed during growth of the culture and duplication accumulation, but are induced in the course of the transformation cross used to detect duplications. The Red functions are not expected to contribute to duplication formation or loss (even if induced) since induction of these functions does increase duplication segregation in recA+ strains or allow segregation in strains carrying a recA mutation. The frequency of transformants observed following Red induction seems to depend heavily on the high copy number of the introduced fragment.
This assay was done using a synthesized 130-base single-stranded donor fragment. On the basis of work of Court and colleagues, these crosses appear to affect a single replication fork region and thus are not expected to remove preexisting duplications as can occur in the transduction assays above (Yu et al. 2003). In this assay, the duplication is not selectively held, since selection is made for KanR and the Lac phenotype is scored visually. It is possible that this assay misses duplications that happen to be lost early in the growth of the transformant clone, leading to underestimation of duplication frequency. This problem is avoided in the next assay, in which both copies are held selectively.
The drug-in-drug assay:
This assay detects and holds duplications selectively from the moment of the assay transformation. As in the Ka-Kan assay, duplications are trapped by a Red-mediated recombineering cross. The essence of the assay (see Figure A3) is that the assay site carries a resistance determinant for tetracycline (TetR) that is inactivated by insertion of a kanamycin-resistance determinant (KanR). Thus the assay strain is phenotypically KanR TetS. To assay duplication frequency, a short single-strand fragment (80 bases) is introduced that restores TetR by excising the KanR determinant from the test locus. A haploid recipient cell will become TetR, KanS.
Figure A3.—
The drug-in-drug assay for detecting duplications in recA mutant strains. The locus to be assayed carries an inserted TetR gene that is disrupted by a KanR cassette. The assay strain carries this compound allele and a plasmid that encodes the Red functions of phage lambda (Yu et al. 2003). The assay consists of a transformation cross in which a single-stranded donor fragment is electroporated into the recipient assay strain. This fragment displaces the KanR determinant and repairs the TetR determinant, thereby converting a KanR, TetS allele into a KanS, TetR allele. Recipients with a duplication of the test locus gain TetR (in one copy of the region) while retaining the KanR phenotype (provided by the other copy).
However, a recipient with a duplication of the test locus will acquire TetR by an exchange in one allele and remain KanR by virtue of the unaffected second copy of the test locus. The transformed culture was plated on tetracycline medium to reveal the total transductant number. After overnight growth these plates were replica printed to medium with both tetracycline and kanamycin to reveal the fraction of the total that carry duplications. The counted duplications were kept under selection and have little opportunity to lose the duplication before they can be counted. In some assays, the recipient TetR locus was the TetA, TetR region of a Tn10 insertion, and in others the tetA tetR genes were PCR amplified from Tn10 and inserted directly into the test locus.
APPENDIX B: MATHEMATICAL MODELING OF DUPLICATION ACCUMULATION
The process of duplication accumulation was described, making the assumption that events of duplication formation or loss occur in a replication-dependent way and thus will depend on the relative growth rates of haploid and duplication-bearing strains. The basic model is described in Figure A1.
The equations describing the temporal behavior of the populations in Figure A1 are the following:
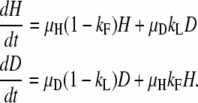 |
These can be used to characterize the duplication frequency as a function of time.
By combining the above equations, one obtains
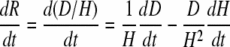 |
or
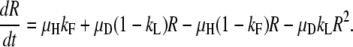 |
At steady state, dR/dt=0, and the resulting expression can be written as
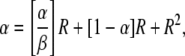 |
where
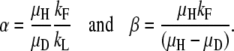 |
The parameter α describes the contribution of duplication formation and loss kF/kL to the steady state if corrected for relative growth rates (μH/μD). The extreme is the situation on the bottom right in Figure A2 when there is negligible fitness cost and there is a significant rate of duplication loss. The parameter β describes the contribution of fitness cost of a duplication to the steady state. The extreme is the situation on the top left in Figure B1 when kL is near zero (as in a recA mutant strain) and there is a large fitness cost. The steady-state duplication frequency (R∞) can exist in several different regions of this “design space,” depending on the values of the two aggregate parameters α and β. In each of these regions, the value of R shows a characteristic sensitivity to changes of the several parameters. These regions are described below and then graphed.
Figure B1.—
The diagrammed process shows the number of haploid cells (H) increases by growth (μH) and when a duplication-bearing cell loses its duplication (μDkL). Haploid cells can be lost when a duplication arises (μHkF). Duplication cell number (D) increases by growth (μD) and when a duplication forms in a haploid cell (μHkF). Duplications can be lost by reversion (i.e. recombination between repeats) as diagrammed in Figure 2 (μDkL). The duplication frequency (R = D/H) rises to a steady state (R∞) at which point the difference between duplication formation and loss is balanced by the differences between diploid and haploid growth rates.
In region A, steady-state duplication frequency depends most heavily on fitness cost:
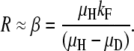 |
The boundaries of the region in which this form of R is dominant are
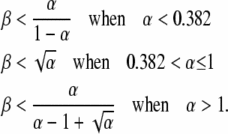 |
In region B, steady-state duplication frequency depends most heavily on relative rates of formation and loss:
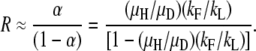 |
The boundaries of the region in which this form is dominant are
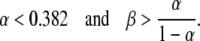 |
In region C, steady-state duplication frequency again depends most heavily on relative rates of formation and loss:
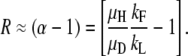 |
The boundary in this case is
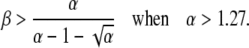 |
Finally, in region D, steady-state duplication frequency depends on yet a different form of expression involving the aggregate parameter α,
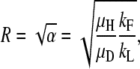 |
and the boundaries are given by
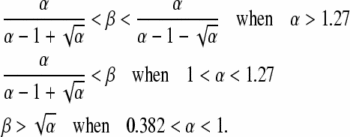 |
The four regions are diagrammed in Figure B2. In the body of this article, Figure B2 is repeated with R values represented in a heat map and the position of each locus studied here indicated in the plot. This graphical method has been described previously (Savageau et al. 2009).
Figure B2.—
Graphical representation of the design space (Savageau et al. 2009) for the model in Figure A1. The horizontal axis represents the contribution of fitness cost (proportional to 1/β) to the steady-state duplication frequency. The vertical axis represents the contribution of duplication formation and loss (proportional to α) to the steady-state duplication frequency. The boundaries between regions in which the steady-state duplication frequency R is dominated by different forms of the solution are shown as heavy black lines.
References
- Anderson, P., and J. Roth, 1981. Spontaneous tandem genetic duplications in Salmonella typhimurium arise by unequal recombination between rRNA (rrn) cistrons. Proc. Natl. Acad. Sci. USA 78 3113–3117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson, R. P., and J. R. Roth, 1977. Tandem genetic duplications in phage and bacteria. Annu. Rev. Microbiol. 31 473–505. [DOI] [PubMed] [Google Scholar]
- Anderson, R. P., and J. R. Roth, 1979. Gene duplication in bacteria: alteration of gene dosage by sister-chromosome exchanges. Cold Spring Harbor Symp. Quant. Biol. 43(Pt. 2): 1083–1087. [DOI] [PubMed] [Google Scholar]
- Andersson, D. I., E. S. Slechta and J. R. Roth, 1998. Evidence that gene amplification underlies adaptive mutability of the bacterial lac operon. Science 282 1133–1135. [DOI] [PubMed] [Google Scholar]
- Bachellier, S., J. M. Clement and M. Hofnung, 1999. Short palindromic repetitive DNA elements in enterobacteria: a survey. Res. Microbiol. 150 627–639. [DOI] [PubMed] [Google Scholar]
- Bergthorsson, U., D. I. Andersson and J. R. Roth, 2007. Ohno's dilemma: evolution of new genes under continuous selection. Proc. Natl. Acad. Sci. USA 104 17004–17009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cairns, J., and P. L. Foster, 1991. Adaptive reversion of a frameshift mutation in Escherichia coli. Genetics 128 695–701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carter, J. R., and R. D. Porter, 1991. traY and traI are required for oriT-dependent enhanced recombination between lac-containing plasmids and lambda plac5. J. Bacteriol. 173 1027–1034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carter, J. R., D. R. Patel and R. D. Porter, 1992. The role of oriT in tra-dependent enhanced recombination between mini-F-lac-oriT and lambda plac5. Genet. Res. 59 157–165. [DOI] [PubMed] [Google Scholar]
- Conrad, D. F., D. Pinto, R. Redon, L. Feuk, O. Gokcumen et al., 2009. Origins and functional impact of copy number variation in the human genome. Nature October 7, 2009 doi: 10.1038/nature08516. [DOI] [PMC free article] [PubMed]
- Court, D. L., J. A. Sawitzke and L. C. Thomason, 2002. Genetic engineering using homologous recombination. Annu. Rev. Genet. 36 361–388. [DOI] [PubMed] [Google Scholar]
- Emerson, J. J., M. Cardoso-Moreira, J. O. Borevitz and M. Long, 2008. Natural selection shapes genome-wide patterns of copy-number polymorphism in Drosophila melanogaster. Science 320 1629–1631. [DOI] [PubMed] [Google Scholar]
- Hendrickson, H., E. S. Slechta, U. Bergthorsson, D. I. Andersson and J. R. Roth, 2002. Amplification-mutagenesis: evidence that “directed” adaptive mutation and general hypermutability result from growth with a selected gene amplification. Proc. Natl. Acad. Sci. USA 99 2164–2169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kidd, J. M., G. M. Cooper, W. F. Donahue, H. S. Hayden, N. Sampas et al., 2008. Mapping and sequencing of structural variation from eight human genomes. Nature 453 56–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kofoid, E., U. Bergthorsson, E. S. Slechta and J. R. Roth, 2003. Formation of an F′ plasmid by recombination between imperfectly repeated chromosomal Rep sequences: a closer look at an old friend (F′(128) pro lac). J. Bacteriol. 185 660–663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korbel, J. O., A. E. Urban, J. P. Affourtit, B. Godwin, F. Grubert et al., 2007. Paired-end mapping reveals extensive structural variation in the human genome. Science 318 420–426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kugelberg, E., E. Kofoid, A. B. Reams, D. I. Andersson and J. R. Roth, 2006. Multiple pathways of selected gene amplification during adaptive mutation. Proc. Natl. Acad. Sci. USA 103 17319–17324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roth, J. R., E. Kugelberg, A. B. Reams, E. Kofoid and D. I. Andersson, 2006. Origin of mutations under selection: the adaptive mutation controversy. Annu. Rev. Microbiol. 60 477–501. [DOI] [PubMed] [Google Scholar]
- Sandegren, L., and D. I. Andersson, 2009. Bacterial gene amplification: implications for the evolution of antibiotic resistance. Nat. Rev. Microbiol. 7 578–588. [DOI] [PubMed] [Google Scholar]
- Savageau, M. A., P. M. B. M. Coelho, R. Fasani, D. Tolla and A. Salvador, 2009. Phenotypes and tolerances in the design space of biochemical systems. Proc. Natl. Acad. Sci. USA 106 6435–6440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seifert, H. S., and R. D. Porter, 1984. a Enhanced recombination between lambda plac5 and F42lac: identification of cis- and trans-acting factors. Proc. Natl. Acad. Sci. USA 81 7500–7504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seifert, H. S., and R. D. Porter, 1984. b Enhanced recombination between lambda plac5 and mini-F-lac: the tra regulon is required for recombination enhancement. Mol. Gen. Genet. 193 269–274. [DOI] [PubMed] [Google Scholar]
- Sharp, A. J., D. P. Locke, S. D. McGrath, Z. Cheng, J. A. Bailey et al., 2005. Segmental duplications and copy-number variation in the human genome. Am. J. Hum. Genet. 77 78–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silver, L., M. Chandler, H. E. Lane and L. Caro, 1980. Production of extrachromosomal r-determinant circles from integrated R100.1: involvement of the E. coli recombination system. Mol. Gen. Genet. 179 565–571. [DOI] [PubMed] [Google Scholar]
- Slechta, E. S., K. L. Bunny, E. Kugelberg, E. Kofoid, D. I. Andersson et al., 2003. Adaptive mutation: general mutagenesis is not a programmed response to stress but results from rare coamplification of dinB with lac. Proc. Natl. Acad. Sci. USA 100 12847–12852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sonti, R. V., and J. R. Roth, 1989. Role of gene duplications in the adaptation of Salmonella typhimurium to growth on limiting carbon sources. Genetics 123 19–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun, S., O. G. Berg, J. R. Roth and D. I. Andersson, 2009. Contribution of gene amplification to evolution of increased antibiotic resistance in Salmonella typhimurium. Genetics 182 1183–1195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Syvanen, M., J. D. Hopkins, T. J. T. Griffin, T. Y. Liang, K. Ippen-Ihler et al., 1986. Stimulation of precise excision and recombination by conjugal proficient F′ plasmids. Mol. Gen. Genet. 203 1–7. [DOI] [PubMed] [Google Scholar]
- Tlsty, T. D., A. M. Albertini and J. H. Miller, 1984. Gene amplification in the lac region of E. coli. Cell 37 217–224. [DOI] [PubMed] [Google Scholar]
- Tlsty, T. D., B. H. Margolin and K. Lum, 1989. Differences in the rates of gene amplification in nontumorigenic and tumorigenic cell lines as measured by Luria-Delbruck fluctuation analysis. Proc. Natl. Acad. Sci. USA 86 9441–9445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams, P. A., R. J. Ingebretsen and R. J. Dawson, 2006. 14.6 mT ELF magnetic field exposure yields no DNA breaks in model system Salmonella, but provides evidence of heat stress protection. Bioelectromagnetics 27 445–450. [DOI] [PubMed] [Google Scholar]
- Yu, D., J. A. Sawitzke, H. Ellis and D. L. Court, 2003. Recombineering with overlapping single-stranded DNA oligonucleotides: testing a recombination intermediate. Proc. Natl. Acad. Sci. USA 100 7207–7212. [DOI] [PMC free article] [PubMed] [Google Scholar]