Abstract
In diploid populations, indirect benefits of sex may stem from segregation and recombination. Although it has been recognized that finite population size is an important component of selection for recombination, its effects on selection for segregation have been somewhat less studied. In this article, we develop analytical two- and three-locus models to study the effect of recurrent deleterious mutations on a modifier gene increasing sex, in a finite diploid population. The model also incorporates effects of mitotic recombination, causing loss of heterozygosity (LOH). Predictions are tested using multilocus simulations representing deleterious mutations occurring at a large number of loci. The model and simulations show that excess of heterozygosity generated by finite population size is an important component of selection for sex, favoring segregation when deleterious alleles are nearly additive to dominant. Furthermore, sex tends to break correlations in homozygosity among selected loci, which disfavors sex when deleterious alleles are either recessive or dominant. As a result, we find that it is difficult to maintain costly sex when deleterious alleles are recessive. LOH tends to favor sex when deleterious mutations are recessive, but the effect is relatively weak for rates of LOH corresponding to current estimates (of the order 10−4−10−5).
ALTHOUGH sex is a costly (and often risky) enterprise, most eukaryotes engage in sex at least sometimes during their life cycle (reproduction being exclusively sexual in many species). Different theoretical models (reviewed in Agrawal 2006; Otto 2009) have explored the possible evolutionary advantages of sex due to its effects on genetic variation. Whether such benefits can maintain high rates of sex despite its important costs remains unclear, but modern computers allow more and more quantitative predictions to be obtained from simulation programs representing selection occurring at large numbers of loci (e.g., Keightley and Otto 2006; Salathé et al. 2006). Eukaryotic sex is the combination of two complementary events—meiosis and syngamy—resulting in the alternation of a diploid and a haploid phase during the life cycle. In diploids, sex affects genetic variation through two effects: segregation and recombination. The genetic effect of recombination is to erode linkage disequilibrium (LD) among loci, and different models have explored the strength and direction of selection for recombination under various possible sources of LD: epistasis between beneficial or deleterious alleles (Charlesworth 1990, 1993; Barton 1995; Otto and Feldman 1997; Roze and Lenormand 2005); fluctuating epistasis over time, generated, for example, by host–parasite interactions (Barton 1995; Peters and Lively 1999; Otto and Nuismer 2004; Gandon and Otto 2007; Salathé et al. 2008), spatial heterogeneity in selection (Pylkov et al. 1998; Lenormand and Otto 2000); and LD generated by the interplay between selection and genetic drift, known as the Hill–Robertson effect (Felsenstein and Yokohama 1976; Otto and Barton 1997, 2001; Iles et al. 2003; Barton and Otto 2005; Keightley and Otto 2006; Martin et al. 2006; Roze and Barton 2006).
The possible benefits of segregation have been studied more recently. “Segregation” in the strict sense involves the separation of homologous chromosomes at meiosis. However, following others (e.g., Otto 2003; Agrawal 2006), we use the term segregation to refer to the whole process of separation of homologous chromosomes at meiosis into separate gametes along with the eventual fusion (fertilization) of gametes taken from different individuals (outcrossing). In this article we consider only outcrossing and do not study selfing or other aspects of the mating system. In the same way as recombination “shuffles” alleles at different loci, eroding linkage disequilibria, segregation with outcrossing shuffles alleles at the same locus and brings populations closer to Hardy–Weinberg (HW) equilibrium. A first possible source of departure from HW equilibrium is dominance between alleles at a selected locus (in particular when sex is rare). Several models have explored the effect of dominance on selection for sex due to the segregation effect, in infinite populations. Uyenoyama and Bengtsson (1989) derived conditions for invasion of a modifier gene increasing the rate of sexual (vs. clonal) reproduction, when a recurrent lethal mutation occurs at a second locus. They found that under random mating, intermediate rates of sex are favored when the dominance coefficient h of the lethal mutation is < 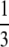 , while complete sex is favored when h >
, while complete sex is favored when h > 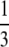 . Otto (2003) considered a similar model, with arbitrary strength of selection at the second locus, and showed that the parameter range where sex is favored shrinks dramatically when selection becomes weak (in particular, deleterious mutations have to be nearly additive). Both Uyenoyama and Bengtsson (1989) and Otto (2003) studied the effects of partial self-fertilization, which generates departures from HW equilibrium (excess of homozygotes), and showed that selfing increases the parameter range where sex is favored. The effects of host–parasite coevolution on selection for segregation have been investigated by Agrawal and Otto (2006), who found that coevolutionary dynamics are less favorable to segregation than they are to recombination. Finally, Agrawal (2009) showed that spatial heterogeneity may favor segregation whenever locally beneficial alleles tend to be dominant, because of the excess homozygosity caused by spatial selection.
. Otto (2003) considered a similar model, with arbitrary strength of selection at the second locus, and showed that the parameter range where sex is favored shrinks dramatically when selection becomes weak (in particular, deleterious mutations have to be nearly additive). Both Uyenoyama and Bengtsson (1989) and Otto (2003) studied the effects of partial self-fertilization, which generates departures from HW equilibrium (excess of homozygotes), and showed that selfing increases the parameter range where sex is favored. The effects of host–parasite coevolution on selection for segregation have been investigated by Agrawal and Otto (2006), who found that coevolutionary dynamics are less favorable to segregation than they are to recombination. Finally, Agrawal (2009) showed that spatial heterogeneity may favor segregation whenever locally beneficial alleles tend to be dominant, because of the excess homozygosity caused by spatial selection.
The effect of finite population size (or population structure) on selection for sex due to segregation has been little explored. Kirkpatrick and Jenkins (1989) showed that beneficial mutations may generate an advantage for sex in diploid populations, since mutations remain in the heterozygous state in asexuals (until a second mutation occurs), while in sexuals segregation quickly generates homozygotes for the beneficial allele (note that this benefit of sex does not occur in infinite populations, because a small proportion of double mutants would be produced every generation). Haag and Roze (2007) compared the equilibrium mutation load in sexual and asexual finite diploid populations and showed that the load may be far greater in asexuals in the parameter range where deleterious mutations reach fixation in the heterozygous state in asexuals, while they are still eliminated efficiently in sexuals due to segregation. However, the fate of a modifier affecting the rate of sex in such a system was not investigated. Finite population size may have stronger effects on selection for segregation than it has on selection for recombination: indeed in the case of recombination, linkage disequilibrium between loci is generated by the interplay between random drift and selection (Hill–Robertson effect) and should be of order sAsB/N between two loci A and B, where sA and sB measure the strength of selection acting at these loci and N is population size (e.g., Barton and Otto 2005; Martin et al. 2006). By contrast, finite population size tends to generate an excess of heterozygotes (particularly in partially clonal populations) even in the absence of selection (e.g., Balloux et al. 2003; Haag and Roze 2007), and the resulting departure from Hardy–Weinberg equilibrium should thus be of order 1/N. However, the relative forces of selection for segregation and recombination in finite diploid populations have never been explored.
Another potentially important factor affecting selection for segregation is mitotic gene conversion and/or recombination, which occur as a consequence of DNA repair and tend to generate homozygosity (e.g., Mandegar and Otto 2007). A double-strand break (DSB) is perhaps the most serious damage that can happen to a DNA molecule. Eukaryotes use two main pathways to repair such damage: nonhomologous end joining (NHEJ) involves the detection and ligation of the two broken ends, but is prone to error and chromosomal aberrations, while homologous recombination (HR) uses an homologous sequence as a template for repair, preferentially from the sister chromatid if the chromosome is replicated or from the homologous chromosome if the cell is diploid (Liang et al. 1998; Pâques and Haber 1999; Johnson and Jasin 2001; Helleday 2003; Aylon and Kupiec 2004). Note that HR may also occur in response to DNA lesions other than DSBs (Lettier et al. 2006). Indeed, one of the potential advantages of HR as a repair process is that in principle HR can cope with any kind of DNA damage. A consequence of HR is that a small fragment of the genome is transferred from the donor template to the repaired chromosome with heteroduplex DNA being generated to either side of the break, and this process may cause gene conversion when the template is the homologous chromosome. Another possible consequence of HR is crossing over (exchange of chromosome arms between homologs). Although HR occurs during both meiosis and mitosis, there are important differences between meiotic and mitotic HR: for example, the length of gene conversion tracts may differ: in yeast mitotic gene conversion tracts are often >4 kb (Judd and Petes 1988), longer than meiotic tracts (∼1–2 kb), while in mammals mitotic tracts are usually short, ∼200 bp−1 kb (Chen et al. 2007). Furthermore, a large proportion of meiotic HR events result in crossing over [up to 66% in yeast (Prado et al. 2003)], while this proportion is usually a lot smaller in the case of mitotic HR [<8% in several model systems (Richardson et al. 1998; Virgin et al. 2001; Ira et al. 2006; Chen et al. 2007)]. Crossing over occurring at mitosis (hereafter called “mitotic recombination,” MR) may render daughter cells homozygous over large portions of the chromosome (Mandegar and Otto 2007). Such loss of heterozygosity (LOH) events represent a frequent step in oncogenesis (Gupta et al. 1997; Tischfield 1997; Hagstrom and Dryja 1999; Holt et al. 1999; Sieber et al. 2002), which may partly explain why mitotic crossing over is suppressed. Nevertheless, mitotic recombination is thought to occur at rate ∼0.8 × 10−4 per cell per generation in yeast (Mandegar and Otto 2007 and references therein), while LOH is often observed at a frequency of 10−4–10−5 in normal cells in vivo, in mice and in humans (Tischfield 1997; Holt et al. 1999; Shao et al. 1999; Carr and Gottschling 2008). Furthermore, Chamnanpunt et al. (2001) measured rates of mitotic gene conversion ranging from 3 × 10−2 to 10−5 in hybrids of the oomycete Phytophthora sojae. Finally, LOH has been estimated to occur at rate ∼10−4 per locus per generation in an experiment involving mutation-accumulation lines of asexual Daphnia (Omilian et al. 2006).
To our knowledge, the only model studying the effect of mitotic recombination on selection for sex was done by Mandegar and Otto (2007), who showed that the benefit of sex described in Kirkpatrick and Jenkins (1989) (creation of homozygotes for beneficial alleles, by segregation) disappears in the presence of a low rate of mitotic recombination (which allows homozygotes to be generated in asexuals). Loss of heterozygosity due to HR is also a central component of the DNA repair and mutation complementation hypothesis for the evolution of sex (Bernstein et al. 1985, 1988). This hypothesis distinguishes between the recombinational and the outcrossing (segregational) aspects of sex, because it assumes that these two aspects of sex have different adaptive functions. According to this hypothesis, the main function of recombination, in the sense of breakage and rejoining of DNA molecules, is to repair DSBs and other kinds of DNA damage, while the function of segregation with outcrossing is to restore heterozygosity lost by the repair process (LOH across large portions of the genome leads to the expression of recessive deleterious alleles). This hypothesis has been criticized, notably because recombination without (or with little) crossing over is possible (mitotic HR only rarely leads to crossing over) and because double-strand breaks are actively generated during the initiation of meiotic recombination, making it doubtful that the main role of meiosis is to repair DSBs (Maynard Smith 1988; Keeney et al. 1997; Barton and Charlesworth 1998; Keeney and Neale 2006). Nevertheless, loss of heterozygosity occurring within mitotic lineages may generate a selective force for segregation and outcrossing (due to the expression of recessive deleterious mutations). Quantifying this force (which has never been done) is one of the goals of our study.
In this article, we use a two-locus analytical model to explore the effects of finite population size and of mitotic recombination on selection for outcrossed sex and segregation, focusing on the effect of recurrent deleterious mutations. This model shows that finite population size generates a selective pressure on a modifier affecting the rate of sexual vs. asexual reproduction, mainly due to the fact that drift tends to generate an excess of heterozygotes in the population (in particular when the rate of sex is low). This selective force is often stronger than the deterministic force that has been described in the case of infinite, randomly mating populations (Otto 2003), in particular when deleterious alleles remain at low frequency. Furthermore, we show that loss of heterozygosity (due to mitotic gene conversion and recombination) may have important positive effects on selection for sex if it occurs sufficiently frequently (at rate ≥ ∼10−3 per generation), while rates of LOH ≤ 10−4 have little effect. We then extend our model to introduce a second selected locus and show that selection for sex due to the interaction between selected loci may become important when the deleterious mutation rate is sufficiently high. These results are confirmed by multilocus simulations in which deleterious mutations occur at a large number of loci and where the rate of sex is free to evolve. Finally, from these simulation results it appears unlikely that deleterious mutations alone can allow the maintenance of high rates of sex when the cost of sex is twofold.
ANALYTICAL MODEL
General setting:
Table 1 summarizes the different parameters and variables of the model. We consider two loci M and A in a diploid population with nonoverlapping generations. At the start of a generation, the population consists of N adults. These adults produce a large number of juveniles, with different fecundities depending on their genotype at locus A. We assume that two alleles A and a segregate at this locus and that genotypes aa, Aa, and AA have (relative) fecundities 1, 1 – hs, and 1 – s (where fecundity is simply the number of juveniles produced). Allele A is thus deleterious, and we assume that mutations from a to A occur at a rate u per generation and back mutations occur at rate v. Note that uppercase letters do not refer to dominant alleles, as we consider the case where A is recessive (h <  ) and the case where it is dominant (h >
) and the case where it is dominant (h >  ). Locus M controls the proportion of juveniles produced sexually and asexually: two alleles M and m segregate at this locus, and individuals of genotype mm, Mm, and MM produce a proportion σ, σ + hMδσ, and σ + δσ of offspring sexually, respectively, and the remainder asexually (i.e., by mitosis). Locus M is thus a modifier locus affecting the rate of sex (Otto 2003), δσ measures the modifier effect, and hM the dominance of allele M. Sexual reproduction involves gamete production by meiosis (we call r the recombination rate between loci M and A), gamete release in the environment, and random union of gametes in the whole population. Except in the simulations, we assume no direct cost of sex, so that individuals bearing the same genotype at locus A produce the same number of juveniles, whatever their genotype at locus M (the modifier has no direct effect on fitness). Finally, N individuals are sampled randomly among the large number of juveniles produced to form the next adult generation. To incorporate effects of mitotic recombination, we assume that a proportion γ of juveniles produced asexually have undergone (unbiased) gene conversion at locus A: therefore, a proportion γ/2 of offspring produced asexually by Aa heterozygotes are AA homozygotes, while a proportion γ/2 are aa homozygotes. Although gene conversion occurs at much higher rates during meiosis than during mitosis (Chen et al. 2007), meiotic gene conversion would not affect the dynamics (as long as it is not biased) because it would have no effect on the frequencies of homozygotes and heterozygotes among offspring. Loss of heterozygosity does not affect the modifier locus in the analytical model, but it will do so in the simulations representing mitotic recombination, as explained in the next section.
). Locus M controls the proportion of juveniles produced sexually and asexually: two alleles M and m segregate at this locus, and individuals of genotype mm, Mm, and MM produce a proportion σ, σ + hMδσ, and σ + δσ of offspring sexually, respectively, and the remainder asexually (i.e., by mitosis). Locus M is thus a modifier locus affecting the rate of sex (Otto 2003), δσ measures the modifier effect, and hM the dominance of allele M. Sexual reproduction involves gamete production by meiosis (we call r the recombination rate between loci M and A), gamete release in the environment, and random union of gametes in the whole population. Except in the simulations, we assume no direct cost of sex, so that individuals bearing the same genotype at locus A produce the same number of juveniles, whatever their genotype at locus M (the modifier has no direct effect on fitness). Finally, N individuals are sampled randomly among the large number of juveniles produced to form the next adult generation. To incorporate effects of mitotic recombination, we assume that a proportion γ of juveniles produced asexually have undergone (unbiased) gene conversion at locus A: therefore, a proportion γ/2 of offspring produced asexually by Aa heterozygotes are AA homozygotes, while a proportion γ/2 are aa homozygotes. Although gene conversion occurs at much higher rates during meiosis than during mitosis (Chen et al. 2007), meiotic gene conversion would not affect the dynamics (as long as it is not biased) because it would have no effect on the frequencies of homozygotes and heterozygotes among offspring. Loss of heterozygosity does not affect the modifier locus in the analytical model, but it will do so in the simulations representing mitotic recombination, as explained in the next section.
TABLE 1.
Parameters and variables
| N | Population size |
| s | Strength of selection against allele A |
| h | Dominance of allele A |
| u | Mutation rate from allele a to allele A |
| v | Back mutation rate (from A to a) |
| r | Rate of recombination between loci A and M |
| σ | Baseline rate of sex in the population |
| δσ | Effect of the modifier (allele M) on the rate of sex |
| hM | Dominance of allele M |
| γ | Rate of mitotic gene conversion |
| χ | Rate of mitotic crossing over (in simulations) |
| U | Deleterious mutation rate per chromosome (in simulations) |
| L | Average number of crossovers at meiosis (in simulations) |
| c | Cost of sex (in simulations): relative fitness of asexuals in the absence of deleterious mutation |
| σinit | Initial rate of sex (in simulations) |
| pA, pM | Frequencies of alleles A and M |
| qA, qM | Frequencies of alleles a and m |
| DA,A | Departure from Hardy–Weinberg equilibrium (excess of homozygotes) at locus A |
| DMA,A | Association between the modifier and homozygotes at locus A |
| DMA, DM,A | Association between the modifier and the deleterious allele at locus A, on the same (DMA) or on the homologous chromosome (DM,A) |
| 〈X〉t | Expected value of random variable X at time t |
The population is described in terms of allele frequencies and genetic associations. We call pA and pM the frequencies of alleles A and M, respectively, and qA, qM the frequencies of alleles a and m. Genetic associations measure covariances in allelic state between genes present at different loci and/or on different chromosomes of an individual (Barton and Turelli 1991; Kirkpatrick et al. 2002). They are represented by variables DU,V, where U and V are sets of loci present on the first and second haplotypes of a diploid individual. In the context of the present model, one of the most important association is DA,A, measuring the covariance in allelic state between the two genes at locus A in an individual,
 |
(1) |
where pAA is the frequency of AA homozygotes in the population (and 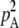 is the probability of sampling two A alleles with replacement from the population). When DA,A = 0, the population is at Hardy–Weinberg equilibrium, while a positive (negative) value of DA,A indicates an excess (deficit) of homozygotes in the population (note that DA,A and the more widely used inbreeding coefficient F are linked by the relation DA,A = FpAqA). Because population size is finite, allele frequencies and genetic associations are random variables. In the following, we use the notation
is the probability of sampling two A alleles with replacement from the population). When DA,A = 0, the population is at Hardy–Weinberg equilibrium, while a positive (negative) value of DA,A indicates an excess (deficit) of homozygotes in the population (note that DA,A and the more widely used inbreeding coefficient F are linked by the relation DA,A = FpAqA). Because population size is finite, allele frequencies and genetic associations are random variables. In the following, we use the notation 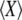 to denote the expected value of random variable X. A method for obtaining recursions over the different phases of the life cycle (selection, gene conversion, reproduction, and drift) for expected values of allele frequencies, genetic associations, and moments of allele frequencies and associations is presented in supporting information, Appendix SA—note that this method differs from the method used by Barton and Otto (2005) and by Martin et al. (2006) in that it does not assume that the population remains close to a deterministic trajectory; however, we assume that population size is large. Recursions for the different moments that affect the change in frequency of the modifier are given in Appendix SB. Throughout, we assume that selection is weak, gene conversion is rare, and population size is large: s, γ, and 1/N are all of order ɛ, where ɛ is a small term (in the simulations, we explore cases where s,
to denote the expected value of random variable X. A method for obtaining recursions over the different phases of the life cycle (selection, gene conversion, reproduction, and drift) for expected values of allele frequencies, genetic associations, and moments of allele frequencies and associations is presented in supporting information, Appendix SA—note that this method differs from the method used by Barton and Otto (2005) and by Martin et al. (2006) in that it does not assume that the population remains close to a deterministic trajectory; however, we assume that population size is large. Recursions for the different moments that affect the change in frequency of the modifier are given in Appendix SB. Throughout, we assume that selection is weak, gene conversion is rare, and population size is large: s, γ, and 1/N are all of order ɛ, where ɛ is a small term (in the simulations, we explore cases where s, 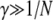 ). We also assume that the rates of sex and recombination (σ, r) are not too small. Under these conditions, it can be shown that the population quickly reaches a state of quasi-equilibrium, where expected values of genetic associations are small and change very slowly over time (Nagylaki 1993; Bürger 2000; see Appendix SA). In that case, associations can be expressed as functions of allele frequencies and of the different parameters of the model (e.g., Barton and Turelli 1991; Kirkpatrick et al. 2002). Finally, we assume that the modifier has only a small effect on the rate of sex (δσ small) and calculate terms to the first order in δσ only (we thus neglect terms in δσ2, δσ3, …). These different assumptions are relaxed in the simulation program presented in the next section.
). We also assume that the rates of sex and recombination (σ, r) are not too small. Under these conditions, it can be shown that the population quickly reaches a state of quasi-equilibrium, where expected values of genetic associations are small and change very slowly over time (Nagylaki 1993; Bürger 2000; see Appendix SA). In that case, associations can be expressed as functions of allele frequencies and of the different parameters of the model (e.g., Barton and Turelli 1991; Kirkpatrick et al. 2002). Finally, we assume that the modifier has only a small effect on the rate of sex (δσ small) and calculate terms to the first order in δσ only (we thus neglect terms in δσ2, δσ3, …). These different assumptions are relaxed in the simulation program presented in the next section.
Departure from Hardy–Weinberg equilibrium:
Most of the results of the model can be understood by the effects of different forces generating departure from Hardy–Weinberg equilibrium at the selected locus (measured by DA,A); indeed, the main effect of increasing sex in our model is to bring the population closer to HW equilibrium. From Appendix SB, the expected value of DA,A at quasi-equilibrium (measured after selection and gene conversion), to the first order in ɛ, is given by
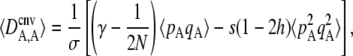 |
(2) |
where “cnv” indicates that the association is measured after selection and gene conversion (see Appendix SA). Equation 2 isolates the effects of three forces generating departure from HW equilibrium: selection, gene conversion, and random drift. As was shown previously (Otto 2003; Agrawal 2009), selection generates an excess of heterozygotes (negative DA,A) whenever h <  (that is, when the deleterious allele is partly recessive): indeed in that case, the fitness of heterozygotes at locus A is higher than the average fitness of homozygotes. When the deleterious allele is partly dominant (h >
(that is, when the deleterious allele is partly recessive): indeed in that case, the fitness of heterozygotes at locus A is higher than the average fitness of homozygotes. When the deleterious allele is partly dominant (h >  ), however, selection generates an excess of homozygotes (positive DA,A). Because gene conversion generates homozygotes from heterozygotes, it produces a positive DA,A (term in γ in Equation 2). Finally, drift tends to generate an excess of heterozygotes (negative DA,A), through the term in 1/(2N) (note that this term does not involve s and is thus not equivalent to the Hill–Robertson effect). This effect can be understood by noting that DA,A can also be written as freq(AA)freq(aa) − [freq(Aa)/2][freq(Aa)/2]. Random sampling from a population initially at HW equilibrium (without selection) may generate an excess either of homozygotes or of heterozygotes; however, when one homozygote (say AA) is oversampled, the effect on DA,A is weakened by the fact that the other homozygote (aa) is likely to be rarer due to the oversampling of AA. By contrast, when Aa is oversampled, both terms of the second part of the expression of DA,A equally contribute toward negative DA,A. This may be seen most easily by considering a fully asexual population in which A and a are neutral, and mutation rates are so small that the population is fixed most of the time for one of the three genotypes: DA,A = 0 when AA or aa is fixed, while DA,A = −0.25 when Aa is fixed (and thus DA,A is negative, on average). Note that this asymmetry is not present with LD between two loci, because the two halves of LD = freq(AB)freq(ab) – freq(Ab)freq(aB) both involve two different haplotypes (we are grateful to Sally Otto for offering this explanation). Finally, Equation 2 also indicates that when the deleterious allele remains rare (pA small), so that the term
), however, selection generates an excess of homozygotes (positive DA,A). Because gene conversion generates homozygotes from heterozygotes, it produces a positive DA,A (term in γ in Equation 2). Finally, drift tends to generate an excess of heterozygotes (negative DA,A), through the term in 1/(2N) (note that this term does not involve s and is thus not equivalent to the Hill–Robertson effect). This effect can be understood by noting that DA,A can also be written as freq(AA)freq(aa) − [freq(Aa)/2][freq(Aa)/2]. Random sampling from a population initially at HW equilibrium (without selection) may generate an excess either of homozygotes or of heterozygotes; however, when one homozygote (say AA) is oversampled, the effect on DA,A is weakened by the fact that the other homozygote (aa) is likely to be rarer due to the oversampling of AA. By contrast, when Aa is oversampled, both terms of the second part of the expression of DA,A equally contribute toward negative DA,A. This may be seen most easily by considering a fully asexual population in which A and a are neutral, and mutation rates are so small that the population is fixed most of the time for one of the three genotypes: DA,A = 0 when AA or aa is fixed, while DA,A = −0.25 when Aa is fixed (and thus DA,A is negative, on average). Note that this asymmetry is not present with LD between two loci, because the two halves of LD = freq(AB)freq(ab) – freq(Ab)freq(aB) both involve two different haplotypes (we are grateful to Sally Otto for offering this explanation). Finally, Equation 2 also indicates that when the deleterious allele remains rare (pA small), so that the term 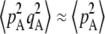 is small relative to
is small relative to 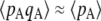 , the effect of selection on the departure from HW equilibrium may be negligible relative to the effects of drift and/or gene conversion. In particular,
, the effect of selection on the departure from HW equilibrium may be negligible relative to the effects of drift and/or gene conversion. In particular, 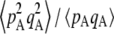 should roughly scale with u/(sh) when h > 0 and
should roughly scale with u/(sh) when h > 0 and 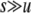 , 1/N, so that the relative importance of the three effects should depend on the relative magnitude of 1/(2N), γ, and u(1 – 2h)/h.
, 1/N, so that the relative importance of the three effects should depend on the relative magnitude of 1/(2N), γ, and u(1 – 2h)/h.
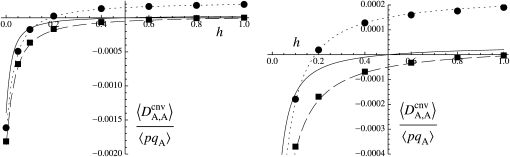
Figure 1 shows the equilibrium value of 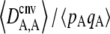 predicted from Equation 2, in the case of an infinite population (no drift) and γ = 0 (solid curve), with drift (N = 20,000) but no gene conversion (dashed curve), and with both drift and gene conversion (N = 20,000 and γ = 10−4, dotted curve). In the last two cases, the value of
predicted from Equation 2, in the case of an infinite population (no drift) and γ = 0 (solid curve), with drift (N = 20,000) but no gene conversion (dashed curve), and with both drift and gene conversion (N = 20,000 and γ = 10−4, dotted curve). In the last two cases, the value of 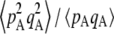 is obtained by numerical integration over Wright's distribution of allele frequency at mutation–selection–drift equilibrium (note that partial asexual reproduction does not affect this distribution as long as the rate of sex is not too small, and DA,A is of order ɛ). Figure 1 also shows results from a simulation program, in which the effects of selection, mutation, gene conversion, reproduction, and drift on the frequencies of the three genotypes at locus A are iterated over a large number (109) of generations,
is obtained by numerical integration over Wright's distribution of allele frequency at mutation–selection–drift equilibrium (note that partial asexual reproduction does not affect this distribution as long as the rate of sex is not too small, and DA,A is of order ɛ). Figure 1 also shows results from a simulation program, in which the effects of selection, mutation, gene conversion, reproduction, and drift on the frequencies of the three genotypes at locus A are iterated over a large number (109) of generations, 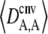 and
and 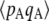 being measured every 100 generations. These simulation results show that Equation 2 provides accurate predictions of the average departure from HW equilibrium.
being measured every 100 generations. These simulation results show that Equation 2 provides accurate predictions of the average departure from HW equilibrium.
Figure 1.—
Average departure from Hardy–Weinberg equilibrium at the selected locus, after selection and gene conversion, divided by the average genetic variance at the same locus, as a function of the dominance coefficient of deleterious mutations h (the right side is a blow-up of the left). Curves correspond to analytical predictions from Equation 2 for different parameter values. Solid curve, deterministic limit (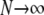 ), no gene conversion (γ = 0), the value of pA at mutation–selection equilibrium is obtained by solving –spA[h + (1 – 2h)pA] + u = 0; dashed curve, N = 20,000, γ = 0; dotted curve, N = 20,000, γ = 10−4. For both the dashed and dotted curves, 〈pqA2〉/〈pqA〉 is obtained by numerical integration over Wright's distribution,
), no gene conversion (γ = 0), the value of pA at mutation–selection equilibrium is obtained by solving –spA[h + (1 – 2h)pA] + u = 0; dashed curve, N = 20,000, γ = 0; dotted curve, N = 20,000, γ = 10−4. For both the dashed and dotted curves, 〈pqA2〉/〈pqA〉 is obtained by numerical integration over Wright's distribution, 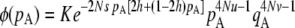 , where K is a constant. Squares and circles: simulation results for N = 20,000, γ = 0 (squares) and N = 20,000, γ = 10−4 (circles). Other parameter values: s = 0.05, σ = 0.5, u = 10−5, v = 10−6.
, where K is a constant. Squares and circles: simulation results for N = 20,000, γ = 0 (squares) and N = 20,000, γ = 10−4 (circles). Other parameter values: s = 0.05, σ = 0.5, u = 10−5, v = 10−6.
Selection on the modifier: weak selection:
From the methods of Appendix SA, one obtains that the expected change in frequency of the modifier at generation t, to leading order in ɛ, is given by
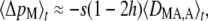 |
(3) |
where DMA,A measures the association between allele M and the two alleles of the same individual at locus A. In Appendix SC, we show that at quasi-equilibrium this association is positive whenever the frequency of allele M is higher in homozygotes at locus A than in heterozygotes, while DMA,A is negative whenever the frequency of M is higher in heterozygotes than in homozygotes. Noting that –s(1 – 2h) is proportional to the difference between the average fitness of homozygotes and the fitness of heterozygotes at locus A, Equation 3 can be understood easily: allele M can be favored either when homozygotes have a higher fitness than heterozygotes [h >  , so that –s(1 – 2h) > 0] and allele M tends to be associated with homozygotes (DMA,A > 0) or when heterozygotes have a higher fitness than homozygotes (h <
, so that –s(1 – 2h) > 0] and allele M tends to be associated with homozygotes (DMA,A > 0) or when heterozygotes have a higher fitness than homozygotes (h <  ) and allele M tends to be associated with heterozygotes (DMA,A < 0). Note that Equation 3 takes the same form in an infinite population (Agrawal 2009).
) and allele M tends to be associated with heterozygotes (DMA,A < 0). Note that Equation 3 takes the same form in an infinite population (Agrawal 2009).
In the following, we focus on the case of an additive modifier (hM =  ); however, expressions for arbitrary hM are given in Appendix SB. Using the quasi-equilibrium approximation, we can derive an expression for
); however, expressions for arbitrary hM are given in Appendix SB. Using the quasi-equilibrium approximation, we can derive an expression for 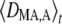 as a function of the parameters and moments of allele frequencies. One obtains
as a function of the parameters and moments of allele frequencies. One obtains
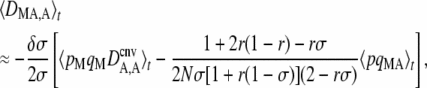 |
(4) |
where pqMA = pMqMpAqA. The first term of Equation 4 is equivalent to the expression obtained in the case of an infinite population: in that case, DMA,A is generated by the modifier effect (δσ) and by the departure from HW equilibrium (DA,A). This simply stems from the fact that a modifier increasing sex tends to bring the population closer to HW equilibrium; therefore if DA,A > 0 (excess of homozygotes in the population), a modifier allele increasing sex tends to create more heterozygotes and thus tends to be more frequent in heterozygotes than in homozygotes (DMA,A < 0 if δσ > 0). If DA,A < 0 (excess of heterozygotes in the population), a modifier increasing sex creates more homozygotes and is thus more frequent among homozygotes (DMA,A > 0 if δσ > 0). The second term of Equation 4 is generated by drift and by the modifier effect and involves associations other than DA,A (in particular, associations 〈DMA2〉, 〈DM,A2〉 and 〈DMADM,A〉, see Appendix SB). This extra effect comes from the fact that drift generates random associations between alleles M and A at some generations and between M and a at other generations. Because individuals carrying M engage in sex more often (assuming δσ > 0), these random associations translate into an excess of homozygotes at locus A among individuals carrying M.
Replacing the first term of Equation 4 by its expression at quasi-equilibrium, one obtains
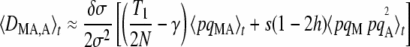 |
(5) |
with
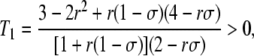 |
(6) |
which simplifies to T1 = (6 – σ)/(4 – σ) when r =  (free recombination). Note that from Equations 3 and 5, the change in frequency of the modifier is of order δσɛ2. These equations predict that under weak selection (so that the quasi-equilibrium approximation holds), increased sex should never be favored in the absence of drift and gene conversion, as was found previously (e.g., Agrawal 2009): when h <
(free recombination). Note that from Equations 3 and 5, the change in frequency of the modifier is of order δσɛ2. These equations predict that under weak selection (so that the quasi-equilibrium approximation holds), increased sex should never be favored in the absence of drift and gene conversion, as was found previously (e.g., Agrawal 2009): when h <  , increasing sex tends to produce homozygotes, but homozygotes have a lower fitness than heterozygotes, while when h >
, increasing sex tends to produce homozygotes, but homozygotes have a lower fitness than heterozygotes, while when h >  , increasing sex tends to produce heterozygotes, but heterozygotes have lower fitness. We see in the next section that sex can nevertheless be favored through terms in δσɛ3 that may become relatively strong when dominance is weak and/or sex is rare (the parameter window favoring sex opening up as selection becomes stronger). From Equations 3 and 5, drift causes a modifier increasing sex to be associated with homozygotes at the selected locus, which favors sex whenever deleterious mutations are dominant (h >
, increasing sex tends to produce heterozygotes, but heterozygotes have lower fitness. We see in the next section that sex can nevertheless be favored through terms in δσɛ3 that may become relatively strong when dominance is weak and/or sex is rare (the parameter window favoring sex opening up as selection becomes stronger). From Equations 3 and 5, drift causes a modifier increasing sex to be associated with homozygotes at the selected locus, which favors sex whenever deleterious mutations are dominant (h >  ), but disfavors sex when deleterious mutations are recessive (h <
), but disfavors sex when deleterious mutations are recessive (h <  ). Finally, gene conversion favors sex when mutations are recessive (as increasing sex tends to mask mutations that have become homozygous due to gene conversion), but disfavors sex when mutations are dominant.
). Finally, gene conversion favors sex when mutations are recessive (as increasing sex tends to mask mutations that have become homozygous due to gene conversion), but disfavors sex when mutations are dominant.
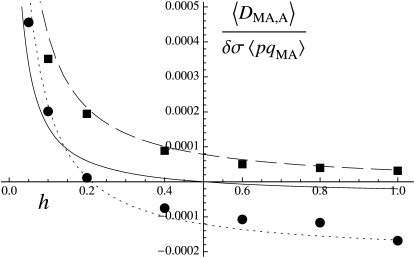
Figure 2 shows a test of Equation 5 against simulations. The simulation program iterates the effects of selection, mutation, gene conversion, reproduction (including a sex modifier), and drift on the 10 two-locus diploid genotype frequencies (initial population without deleterious mutation and the modifier being in frequency 0.5) until the modifier frequency is >0.95 or <0.05, measuring DMA,A and pqMA every 10 generations. The whole process is repeated until 109 points have been obtained. To generate the curves of Figure 2, we neglected any correlation in genetic variance at the two loci (pAqA and pMqM) and thus replaced 〈pqM pq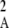 〉/〈pqMA〉 by 〈p
〉/〈pqMA〉 by 〈p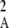 q
q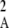 〉/〈pAqA〉, which is again obtained by numerical integration over Wright's distribution.
〉/〈pAqA〉, which is again obtained by numerical integration over Wright's distribution.
Figure 2.—
Average association DMA,A between the modifier and homozygotes at the selected locus (additive modifier), divided by the modifier effect δσ and the average product of genetic variances at both loci, as a function of the dominance coefficient of deleterious mutations h. Parameter values are the same as for Figure 1, with r = 0.5, δσ = 0.05.
Selection on the modifier: weak dominance:
The term on the right-hand side of Equation 3 becomes vanishingly small as h tends to  ; in that case, other terms affecting the change in frequency of the modifier become predominant. In Appendix SB, we calculate these terms when both s and h –
; in that case, other terms affecting the change in frequency of the modifier become predominant. In Appendix SB, we calculate these terms when both s and h –  are of order ɛ (“weak dominance,” where “weak” is relative to the strength of selection s). In that case, the change in frequency of the modifier is given by
are of order ɛ (“weak dominance,” where “weak” is relative to the strength of selection s). In that case, the change in frequency of the modifier is given by
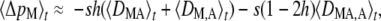 |
(7) |
which again takes the same form as in an infinite population (Agrawal 2009). The first term of Equation 7 represents selection on the modifier due to its association with the deleterious allele, either on the same chromosome (DMA) or on the other chromosome of the same individual (DM,A). As shown in Appendix SC, a positive value of DMA + DM,A means that the frequency of M is higher in individuals in which the frequency of the deleterious allele A is higher (which selects against the modifier). Conversely, when DMA + DM,A < 0 the frequency of M is lower in individuals carrying the deleterious allele, which favors the modifier through the first term of Equation 7. Quasi-equilibrium values of 〈DMA〉t and 〈DM,A〉t are given by
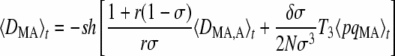 |
(8) |
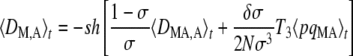 |
(9) |
with
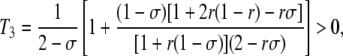 |
(10) |
which simplifies to T3 = 3/(4 – σ) when r =  . The first term within the brackets of Equations 8 and 9 is equivalent to the expression obtained in the case of an infinite population: in this case, 〈DMA〉 and 〈DM,A〉 have the opposite sign to 〈DMA,A〉 at quasi-equilibrium. Indeed, when the frequency of homozygotes at locus A is higher in the subset of the population that carries allele M (that is, when DMA,A > 0), selection against the deleterious allele is more efficient in that subset (because the variance in fitness is higher). This generates a negative association between allele M and the deleterious allele A (DMA, DM,A < 0, meaning that the frequency of the deleterious allele is lower in individuals carrying the modifier allele). The magnitude of this effect increases as r and σ decrease, so that the benefit of better purging remains confined to individuals carrying allele M. Conversely, when the frequency of heterozygotes at locus A is higher in the subset of the population that carries allele M (DMA,A < 0), purging becomes less efficient in that subset, generating positive associations DMA and DM,A between the modifier and the deleterious allele. The second term within the brackets of Equations 8 and 9 is an effect of finite population size, which tends to generate negative values of DMA and DM,A for a modifier increasing sex (δσ > 0). As shown in Appendix SB, this term is generated by the association 〈DMA,M〉, which is itself generated by the combined action of selection and drift and is positive at quasi-equilibrium. Indeed, drift generates random associations between the deleterious allele A and homozygotes at locus M at some generations (DMA,M > 0) and between A and heterozygotes at locus M at other generations (DMA,M < 0). In the first case, selection increases the genetic variance at locus M (because it increases the frequency of heterozygotes at locus M), while in the second case it decreases the variance. Because DMA,M is higher in absolute value when there is more genetic variance, the average value of DMA,M after selection is positive. On average, the deleterious allele A is thus more frequent in homozygotes at locus M than in heterozygotes; however, the fact that MM individuals engage in sex more often with Mm heterozygotes (in which A is less frequent) than mm individuals (assuming δσ > 0) tends to create a negative association between M and A. Unfortunately we could not test Equations 8 and 9 by simulation, because the expected values of DMA and DM,A are very small (of order δσɛ2), while the variance of these terms is much larger (of order ɛ, see Appendix SB). Finally, note that the first term of Equation 7 may be relatively strong even when dominance is not weak, in particular when the rate of sex is low (indeed, the first term scales with 1/σ3 while the second term scales with 1/σ2) and/or selection is sufficiently strong.
. The first term within the brackets of Equations 8 and 9 is equivalent to the expression obtained in the case of an infinite population: in this case, 〈DMA〉 and 〈DM,A〉 have the opposite sign to 〈DMA,A〉 at quasi-equilibrium. Indeed, when the frequency of homozygotes at locus A is higher in the subset of the population that carries allele M (that is, when DMA,A > 0), selection against the deleterious allele is more efficient in that subset (because the variance in fitness is higher). This generates a negative association between allele M and the deleterious allele A (DMA, DM,A < 0, meaning that the frequency of the deleterious allele is lower in individuals carrying the modifier allele). The magnitude of this effect increases as r and σ decrease, so that the benefit of better purging remains confined to individuals carrying allele M. Conversely, when the frequency of heterozygotes at locus A is higher in the subset of the population that carries allele M (DMA,A < 0), purging becomes less efficient in that subset, generating positive associations DMA and DM,A between the modifier and the deleterious allele. The second term within the brackets of Equations 8 and 9 is an effect of finite population size, which tends to generate negative values of DMA and DM,A for a modifier increasing sex (δσ > 0). As shown in Appendix SB, this term is generated by the association 〈DMA,M〉, which is itself generated by the combined action of selection and drift and is positive at quasi-equilibrium. Indeed, drift generates random associations between the deleterious allele A and homozygotes at locus M at some generations (DMA,M > 0) and between A and heterozygotes at locus M at other generations (DMA,M < 0). In the first case, selection increases the genetic variance at locus M (because it increases the frequency of heterozygotes at locus M), while in the second case it decreases the variance. Because DMA,M is higher in absolute value when there is more genetic variance, the average value of DMA,M after selection is positive. On average, the deleterious allele A is thus more frequent in homozygotes at locus M than in heterozygotes; however, the fact that MM individuals engage in sex more often with Mm heterozygotes (in which A is less frequent) than mm individuals (assuming δσ > 0) tends to create a negative association between M and A. Unfortunately we could not test Equations 8 and 9 by simulation, because the expected values of DMA and DM,A are very small (of order δσɛ2), while the variance of these terms is much larger (of order ɛ, see Appendix SB). Finally, note that the first term of Equation 7 may be relatively strong even when dominance is not weak, in particular when the rate of sex is low (indeed, the first term scales with 1/σ3 while the second term scales with 1/σ2) and/or selection is sufficiently strong.
In summary, we have seen that selection on the modifier involves two effects: the effect of the modifier on the frequencies of homozygotes and heterozygotes—term –s(1 – 2h)〈DMA,A〉 of 〈ΔpM〉, hereafter called “selection through effect on genotype frequencies”—and the effect of the modifier on the frequency of the deleterious allele—term –sh(〈DMA〉 + 〈DM,A〉) of 〈ΔpM〉, hereafter called “selection through effect on allele frequencies” (we prefer these terms over the commonly used “short-term” and “long-term” effects, as we think that they are more explicit). When selection is weak (s very small), the second effect is expected to be negligible unless h is close to  or sex and recombination are low. Table 2 shows how these two terms are affected by gene conversion, by finite population size, and by the departure from HW equilibrium caused by selection, assuming that the modifier increases sex (δσ > 0). In the case of recessive deleterious mutations (h <
or sex and recombination are low. Table 2 shows how these two terms are affected by gene conversion, by finite population size, and by the departure from HW equilibrium caused by selection, assuming that the modifier increases sex (δσ > 0). In the case of recessive deleterious mutations (h <  ), finite population size and the effect of selection on DA,A both disfavor sex through the effect on genotype frequencies but favor sex through the effect on allele frequencies, while gene conversion has opposite effects. When mutations are dominant (h >
), finite population size and the effect of selection on DA,A both disfavor sex through the effect on genotype frequencies but favor sex through the effect on allele frequencies, while gene conversion has opposite effects. When mutations are dominant (h >  ), gene conversion and the effect of selection on DA,A disfavor sex through both effects, while finite population size favors sex through both effects.
), gene conversion and the effect of selection on DA,A disfavor sex through both effects, while finite population size favors sex through both effects.
TABLE 2.
Effect of the departure from HW equilibrium generated by selection, gene conversion, and finite population size on the two components of indirect selection acting on the modifier
| Selection through effect on genotype frequencies |
Selection through effect on allele frequencies |
|||
|---|---|---|---|---|
h < 
|
h > 
|
h < 
|
h > 
|
|
| DA,A generated by selection | − | − | + | − |
| Gene conversion (term in γ) | + | − | − | − |
| Finite population size (term in 1/N) | − | + | + | + |
A “ + ” indicates a positive effect on the term −s(1 − 2h)〈DMA,A〉 of the change in frequency of the modifier (selection through effect on genotype frequencies) or on the term −sh(〈DMA〉 + 〈DM,A〉) (selection through effect on allele frequencies), in the case of a modifier increasing sex (δσ > 0). A “ − ” indicates a negative effect.
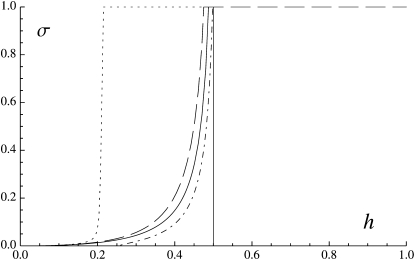
The evolutionarily stable rate of sex (that is, the rate of sex toward which the population should evolve, if evolution proceeds by small-step mutations) can be computed by replacing associations in Equation 7 by their expression at quasi-equilibrium and finding the values of σ for which 〈ΔpM〉 = 0. Solutions at which the derivative of 〈ΔpM〉 with respect to σ is negative (positive) correspond to stable (unstable) equilibria. Figure 3 shows these equilibria as a function of h, in three different cases. In the deterministic limit (N tends to infinity) and in the absence of gene conversion (γ = 0), the rate of sex converges to a stable equilibrium line when h <  (solid curve), while it converges to σ = 0 when h >
(solid curve), while it converges to σ = 0 when h >  . For N = 20,000, still in the absence of gene conversion, the situation is similar when h <
. For N = 20,000, still in the absence of gene conversion, the situation is similar when h <  (dashed curve, corresponding to a stable equilibrium line), while the rate of sex converges to 1 when h >
(dashed curve, corresponding to a stable equilibrium line), while the rate of sex converges to 1 when h >  . Finally, for N = 20,000 and a rate of gene conversion γ = 10−4, a stable equilibrium line appears for low values of h (dotted curve) at low values of σ, with a sharp increase around h = 0.2, while an unstable equilibrium line appears at higher values of h (∼0.25–0.5, dashed-dotted curve). Starting between the dotted and dashed-dotted curves, the rate of sex should thus increase to 1, while starting on the right of the dashed-dotted curve (or below), the rate of sex should decrease toward zero. For γ = 10−3 and γ = 10−2, the part of the stable dotted curve at σ = 1 extends to h = 0, while the dashed-dotted unstable curve becomes indistinguishable from the solid curve. In that case, the population should thus evolve toward complete sex (σ = 1) from any initial value located above the solid curve and toward no sex starting on the right or below the solid curve.
. Finally, for N = 20,000 and a rate of gene conversion γ = 10−4, a stable equilibrium line appears for low values of h (dotted curve) at low values of σ, with a sharp increase around h = 0.2, while an unstable equilibrium line appears at higher values of h (∼0.25–0.5, dashed-dotted curve). Starting between the dotted and dashed-dotted curves, the rate of sex should thus increase to 1, while starting on the right of the dashed-dotted curve (or below), the rate of sex should decrease toward zero. For γ = 10−3 and γ = 10−2, the part of the stable dotted curve at σ = 1 extends to h = 0, while the dashed-dotted unstable curve becomes indistinguishable from the solid curve. In that case, the population should thus evolve toward complete sex (σ = 1) from any initial value located above the solid curve and toward no sex starting on the right or below the solid curve.
Figure 3.—
Long-term evolution of the rate of sex (analytical prediction from the additive modifier model), as a function of the dominance of deleterious mutations h. Deterministic case ( ), no gene conversion: σ converges to the solid curve when h <
), no gene conversion: σ converges to the solid curve when h <  and to zero when h >
and to zero when h >  . N = 20,000, γ = 0: σ converges to the dashed curve (which is at σ = 1 for h >
. N = 20,000, γ = 0: σ converges to the dashed curve (which is at σ = 1 for h >  ). N = 20,000, γ = 10−4: the dotted curve is a stable equilibrium line, while the dashed-dotted curve is an unstable equilibrium line; σ thus converges to a very low value when h < 0.2, while it converges to one starting between the dotted and the dashed-dotted curves and to zero starting on the right of the dashed-dotted curve. When γ = 10−3 or γ = 10−2, the part of the stable dotted curve at σ = 1 extends to h = 0, while the unstable dashed-dotted curve becomes indistinguishable from the solid curve for h <
). N = 20,000, γ = 10−4: the dotted curve is a stable equilibrium line, while the dashed-dotted curve is an unstable equilibrium line; σ thus converges to a very low value when h < 0.2, while it converges to one starting between the dotted and the dashed-dotted curves and to zero starting on the right of the dashed-dotted curve. When γ = 10−3 or γ = 10−2, the part of the stable dotted curve at σ = 1 extends to h = 0, while the unstable dashed-dotted curve becomes indistinguishable from the solid curve for h <  (σ still converges to zero when h >
(σ still converges to zero when h >  ). Parameter values are the same as for Figures 1 and 2.
). Parameter values are the same as for Figures 1 and 2.
The results discussed so far assume additivity at the modifier locus (hM =  ). Expressions for arbitrary hM are given in Appendix SB. Analyzing these expressions shows that in many cases, the direction of selection at the modifier locus depends both on hM and on allele frequency at the modifier locus, which may lead to stable polymorphic equilibria (results not shown). Such situations (which may involve more than two modifier alleles being present simultaneously in the population) are not dealt with by our simple biallelic model (note that effects of dominance at the modifier locus have been explored by Otto 2003 in the deterministic case). However, in the next section we discuss effects of introducing modifier dominance into our multilocus simulations.
). Expressions for arbitrary hM are given in Appendix SB. Analyzing these expressions shows that in many cases, the direction of selection at the modifier locus depends both on hM and on allele frequency at the modifier locus, which may lead to stable polymorphic equilibria (results not shown). Such situations (which may involve more than two modifier alleles being present simultaneously in the population) are not dealt with by our simple biallelic model (note that effects of dominance at the modifier locus have been explored by Otto 2003 in the deterministic case). However, in the next section we discuss effects of introducing modifier dominance into our multilocus simulations.
Three-locus model:
When deleterious mutations segregate at a large number of loci, interactions between selected loci may become an important component of selection for sex (in particular, through the fact that sex allows recombination between loci). To quantify the relative effect of interactions between pairs of selected loci on selection for sex, we extended our model to include a second selected locus (denoted locus B). Two alleles b and B segregate at this locus; we assume that B is deleterious (with the same selection and dominance coefficients as allele A) and that selection is multiplicative across loci (no epistasis). In such a model, different genetic associations between loci A and B are generated by drift and selection. In particular, negative linkage disequilibrium DAB between alleles A and B due to the combined action of drift and selection (the Hill–Robertson effect, e.g., Hill and Robertson 1966; Barton and Otto 2005) generates a selective force for increased sex and recombination. Furthermore, genetic drift generates a correlation in homozygosity between loci A and B (measured by association DAB,AB). Sex tends to break this correlation (decreasing the frequency of double homozygotes and double heterozygotes), which is disadvantageous whenever h ≠  : indeed, genotypes homozygous at one selected locus and heterozygous at the other have a lower fitness than the average of double heterozygotes and double homozygotes when h ≠
: indeed, genotypes homozygous at one selected locus and heterozygous at the other have a lower fitness than the average of double heterozygotes and double homozygotes when h ≠  (e.g., Roze 2009). Other types of associations between loci A and B are also generated by selection and drift. Results from the three-locus model (for the case of an additive modifier) are presented in Appendix SD. These results show that although the selective force on sex generated by the interaction between two selected loci is smaller in magnitude than the selective force generated by each locus separately, the overall effect of interactions between loci may become important when the deleterious mutation rate U is high, so that many loci segregate for deleterious alleles: indeed in that case, the number of pairs of segregating loci may by greater than the number of loci by several orders of magnitude.
(e.g., Roze 2009). Other types of associations between loci A and B are also generated by selection and drift. Results from the three-locus model (for the case of an additive modifier) are presented in Appendix SD. These results show that although the selective force on sex generated by the interaction between two selected loci is smaller in magnitude than the selective force generated by each locus separately, the overall effect of interactions between loci may become important when the deleterious mutation rate U is high, so that many loci segregate for deleterious alleles: indeed in that case, the number of pairs of segregating loci may by greater than the number of loci by several orders of magnitude.
To leading order in ɛ, the change in frequency of the modifier at quasi-equilibrium is given by
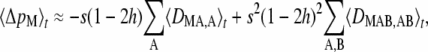 |
(11) |
where the first sum is over all segregating loci, and the second sum is over all pairs of loci. The association 〈DMAB,AB〉 is negative for a modifier increasing sex, reflecting the fact that sex tends to break correlations in homozygosity between loci A and B (as discussed above). Note that associations 〈DMA,A〉 are also affected by interactions among pairs of loci, this effect also disfavoring sex whenever h ≠  (see Appendix SD). As a result, one obtains that when h ≠
(see Appendix SD). As a result, one obtains that when h ≠  , sex becomes less favorable when selection becomes weaker and the mutation rate U higher, so that the number of segregating loci becomes larger (see figures in Appendix SD). Note that when U is sufficiently large, it is likely that higher-order associations (such as DMABC,ABC, DMABCD,ABCD, …) would also become important; however, it seems difficult to obtain general predictions about the effects of such associations.
, sex becomes less favorable when selection becomes weaker and the mutation rate U higher, so that the number of segregating loci becomes larger (see figures in Appendix SD). Note that when U is sufficiently large, it is likely that higher-order associations (such as DMABC,ABC, DMABCD,ABCD, …) would also become important; however, it seems difficult to obtain general predictions about the effects of such associations.
When dominance is weak, the change in frequency of the modifier is affected by many associations (given in Appendix SD), among which is the linkage disequilibrium 〈DAB〉 generated by the Hill–Robertson effect. Again, one obtains that the overall effect of these associations increases with U and may widen the parameter range in which sex is favored (in particular as the strength of selection increases and as rates of sex and recombination decrease). Interestingly, linkage disequilibrium 〈DAB〉 seems to be only a minor component of selection for sex due to interactions between selected loci (see Figure D3 in Appendix SD), as many other associations produced by selection and drift generate selection for sex (see Appendix SD for further details).
MULTILOCUS SIMULATIONS
Description of the program:
Our simulation program (written in C++ and available upon request) uses a similar setting as in Roze (2009). The population is made of N diploids, each possessing two copies of one chromosome. Values of N chosen in the simulations (between 10,000 and 50,000) were sufficiently large so that they appear realistic at least for some species, while sufficiently small so that execution time of the program remains reasonable. Each chromosome is represented by a table of real values between 0 and 1, indicating the positions of deleterious mutations present on the chromosome (0 and 1 corresponding to the chromosome ends); the number of loci at which mutation can occur is thus effectively infinite. Each generation, the number of new mutations occurring on a given chromosome is sampled from a Poisson distribution with parameter U (and the position of each mutation is sampled in a uniform distribution). A sex modifier locus is located at the midpoint of the chromosome (in position 0.5); alleles at this locus are represented by real values between 0 and 1. At the start of a generation, each individual becomes either fully sexual (that is, all of its offspring will be produced sexually) or fully asexual, the probability of becoming sexual being given by the average of the values of its two alleles at the modifier locus (in the following we also consider dominance effects between modifier alleles). Note that this scenario is slightly different from our analytical model, where a given individual may reproduce both sexually and asexually. The next generation is produced as follows. For each of the N individuals of the next generation, an individual is sampled randomly among the present generation; if a random value between 0 and 1 is <w/wmax, where w is the fecundity of the individual and wmax the maximal fecundity in the population, the sampled individual is chosen to be the mother of the new individual (otherwise, another individual is sampled, until the test is satisfied). Fecundity is given by
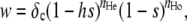 |
(12) |
where nHe and nHo are the numbers of deleterious mutations present in the heterozygous and homozygous state in the individual, and where δc = 1 in sexuals, while δc = c ≥ 1 in asexuals. The parameter c allows us to introduce a direct cost of sex: for example, in an oogamous hermaphroditic species, and under random mating, individuals are expected to invest half of their resources into male gametes that do not bring any resource to the next generation. In this case (and all else being equal) an asexual female may thus produce twice as many eggs as an hermaphrodite (in which case c = 2). If the mother is sexual, then a second individual is sampled among all sexuals of the present generation using the procedure described above, to serve as a father. Recombinant chromosomes are then produced in both mother and father: the number of crossovers occurring at meiosis is sampled from a Poisson distribution with parameter L (genome map length), the position of each crossover being random. If the mother is asexual, in the absence of gene conversion the genotype of the offspring is exactly the same as the mother's genotype. With gene conversion (γ > 0), each mutation present in the heterozygous state becomes homozygous for one of the two alleles with probability γ/2 (gene conversion thus occurs independently at the different loci). We also considered the case of mitotic crossing over (in a separate program): in that case, we assume that every time an individual is produced asexually, a mitotic crossover occurs with probability χ per chromosome (its position along the chromosome being random). If a crossover occurs, the offspring becomes homozygous for all loci located between the crossover position and the distal part of the chromosome (we assume that the centromere is located at position 0.25), including the modifier locus. Which of the two parental chromosomes is used as a template is random (note that the parameter χ is thus really the rate of mitotic crossovers that lead to loss of heterozygosity). Gene conversion is not implemented in the program that includes mitotic crossing over (note that the analytical model presented in the previous section does not differentiate between gene conversion and mitotic crossing over, as it represents only a single selected locus).
Each parameter combination is run one time. During the first 2000 generations of a run, all individuals have the same allele at the modifier locus, coding for a rate of sex σinit. These 2000 generations are generally sufficient to reach mutation–selection–drift balance, except when σinit is too low and mutations accumulate (these cases will be discussed). Then, during the next 2 × 106 generations, mutations occur at rate 10−4 per generation at the modifier locus. When a mutation occurs, with probability 0.5 the rate of sex coded by the new allele is sampled in a uniform distribution between 0 and 1, while with probability 0.5 it is sampled in a uniform distribution between σold – 0.1 and σold + 0.1, where σold is rate of sex coded by the parent allele. The average rate of sex in the population (average value of modifier alleles), average fitness, number of mutations per chromosome, and number of fixed mutations are recorded every 100 generations. Because we assume no back mutation, fixed mutations do not contribute to selection on the modifier locus and are removed from the population to increase execution speed. The evolutionarily stable rate of sex is then obtained by averaging over the last 1.9 × 106 generations (averaging over the last 106 generations yields very similar results). Error bars are computed using Hastings' (1970) batching method, dividing the 1.9 × 106 generations into 10 batches and calculating the standard error over the 10 averages (these error bars are often of similar size as the symbols used in the figures). In the absence of selection (U = 0, c = 1), we checked that the average rate of sex at equilibrium is 0.5 (results not shown).
General results:
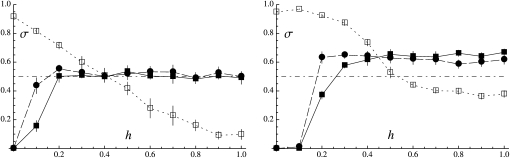
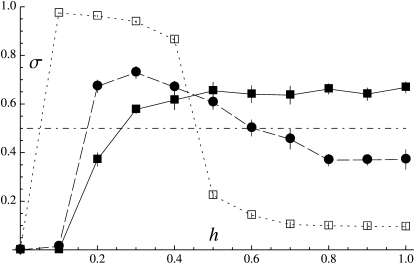
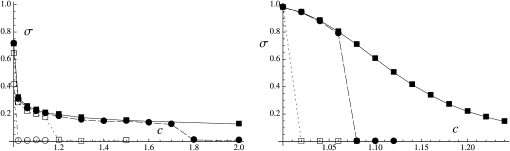
Figure 4 shows the effects of the dominance coefficient of deleterious mutations (h) and the rate of mitotic gene conversion (γ) on the average rate of sex at equilibrium (σ) starting from σinit = 1, for U = 0.05 (left) and U = 0.5 (right). In the absence of gene conversion (solid squares in Figure 4), the rate of sex evolves toward zero when deleterious alleles are completely (or nearly completely) recessive (h ∼ 0–0.1); deleterious mutations then accumulate in the heterozygous state, and the simulation is stopped before 2 × 106 generations, as the program becomes very slow. Higher values of h lead to greater rates of sex, σ reaching a plateau when 0.3 ≤ h ≤ 1. For U = 0.05 (Figure 4, left), the average rate of sex does not depart from the neutral expectation (dashed-dotted line) when h ≥ 0.2; in this case, the selective pressure for sex is very weak unless σ is very small, and dynamics at the modifier locus are mainly driven by random drift. Because Figure 4 does not inform us about selection for sex when h ≥ 0.2, we used a modified version of the program to obtain an estimate of this selective force when only two alleles segregate at the modifier locus and obtained results that are compatible with predictions from our two-locus model (see Appendix SE). When U = 0.5 (Figure 4, right), the rate of sex evolves toward relatively high values when h ≥ 0.3, while the two-locus model predicts that high rates of sex should not be favored unless h ≥ ∼0.45 (Figure 3, dashed line). This discrepancy does not come from the fact that Figure 3 was assuming free recombination: indeed, modifying the program to have free recombination among loci has only very little effect on the results (not shown). Rather, selection for sex when 0.3 ≤ h ≤ 0.45 is probably a consequence of interactions between selected loci: indeed, our three-locus model (Appendix SD) indicates that the effect of such interactions is relatively important when U = 0.5 and that it tends to widen the range of values of h for which high rates of sex are favored. Furthermore, we modified our simulation program to eliminate benefits of recombination (by keeping the σL product constant among individuals) and obtained that sex was not favored unless h > 0.4 in this modified program (see Figure F2 in Appendix SF). Note that our three-locus model still does not predict that σ should be >0.5 when 0.3 ≤ h ≤ 0.4 (Figure D4 in Appendix SD, with U = 0.5, s = 0.05); this may be due to the fact that we computed some three-locus associations under the assumption that dominance is weak (see Appendix SD) and the resulting expressions may thus not be precise when h < 0.4; alternatively, it may be an effect of interactions among more than two selected loci.
Figure 4.—
Average rate of sex observed in multilocus simulations, as a function of the dominance coefficient of deleterious mutations (h) and for different rates of mitotic gene conversion (γ): solid squares, solid lines, γ = 0; solid circles, dashed lines, γ = 10−4; open squares, dotted lines, γ = 10−3 (note that lines simply connect simulation results and do not correspond to analytical predictions). Left, U = 0.05; right, U = 0.5. Other parameter values: N = 20,000, s = 0.05, L = 10 (this high value is chosen to mimic multiple chromosomes), σinit = 1, c = 1 (no direct cost of sex). The dashed-dotted line represents the average rate of sex in the absence of selection (direct or indirect) at the modifier locus (σ = 0.5).
It can be noted that the average rate of sex reaches a plateau at σ ∼ 0.6 when h ≥ 0.5 (for U = 0.5 and γ = 0), while both the two- and three-locus models predict an evolutionarily stable rate of sex at σ = 1 in this case. This difference is likely to be due to the fact that the strength of selection for sex decreases very fast as σ increases (selection through effect on genotype frequencies decreases as 1/σ2, while selection through effect on allele frequencies decreases as 1/σ3). For example, the three-locus model predicts a selection gradient for sex [measured by 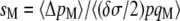 ] ∼5 × 10−5 when h = 0.5 and σ = 0.5 (under free recombination and other parameters as in Figure 4, right) and ∼3 × 10−6 when σ = 1. Selection between alleles coding for different, high rates of sex is thus extremely weak, and the change in frequencies of these alleles will be dominated by random drift (this is confirmed by the fact that the rate of sex fluctuates widely over the course of a simulation, as shown in Appendix SF). Drift at the modifier locus thus prevents the average rate of sex from reaching 1 (reducing the mutation rate at the modifier locus from 10−4 to 10−5 has little effect on the results—not shown).
] ∼5 × 10−5 when h = 0.5 and σ = 0.5 (under free recombination and other parameters as in Figure 4, right) and ∼3 × 10−6 when σ = 1. Selection between alleles coding for different, high rates of sex is thus extremely weak, and the change in frequencies of these alleles will be dominated by random drift (this is confirmed by the fact that the rate of sex fluctuates widely over the course of a simulation, as shown in Appendix SF). Drift at the modifier locus thus prevents the average rate of sex from reaching 1 (reducing the mutation rate at the modifier locus from 10−4 to 10−5 has little effect on the results—not shown).
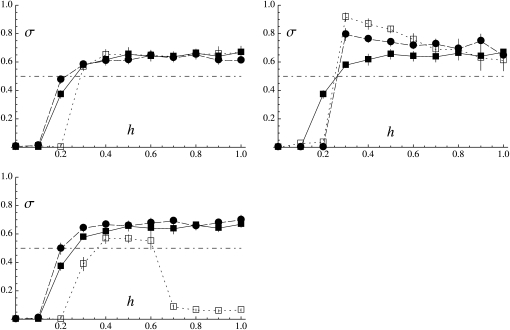
The qualitative effects of mitotic gene conversion match the predictions of the analytical model: gene conversion tends to increase sex when deleterious mutations are recessive and to decrease sex when mutations are dominant. Figure 4 shows that a rate of gene conversion of 10−4 has little effect on the results (solid circles), while a rate of 10−3 has much more of an effect (open squares). Although our analytical model (assuming δσ small) predicts an unstable equilibrium when γ > 0 and h <  (dashed-dotted curve in Figure 3), it is not clear how this should affect the dynamics in the simulations, since mutation at the modifier locus may generate new alleles coding for any rate of sex. For all points shown in Figure 4 (for which the initial rate of sex was set to σinit = 1), we performed additional simulations with an initial rate of sex σinit = 0.01. This led to very similar quantitative results when U = 0.05 (corresponding to Figure 4, left) except for h = 0 and γ = 10−3, in which case σ goes to zero (not shown). In this last case mutation–selection equilibrium is not reached during the preliminary generations of the simulation, as mutations accumulate in the heterozygous state within nearly clonal lineages, generating a very strong segregation load that prevents sex from increasing. Similar results are obtained when U = 0.5 and σinit = 0.01, except that mutation accumulation during the preliminary generations occurs for all values of h between 0 and 0.3, preventing sex from increasing. When h ≥ 0.4, the rate of sex reaches similar average values as when σinit = 1 (not shown). When σinit is set to 0.05, results for h = 0.3 become similar to results obtained when σinit = 1 (while mutations accumulate during preliminary generations when h ≤ 0.2).
(dashed-dotted curve in Figure 3), it is not clear how this should affect the dynamics in the simulations, since mutation at the modifier locus may generate new alleles coding for any rate of sex. For all points shown in Figure 4 (for which the initial rate of sex was set to σinit = 1), we performed additional simulations with an initial rate of sex σinit = 0.01. This led to very similar quantitative results when U = 0.05 (corresponding to Figure 4, left) except for h = 0 and γ = 10−3, in which case σ goes to zero (not shown). In this last case mutation–selection equilibrium is not reached during the preliminary generations of the simulation, as mutations accumulate in the heterozygous state within nearly clonal lineages, generating a very strong segregation load that prevents sex from increasing. Similar results are obtained when U = 0.5 and σinit = 0.01, except that mutation accumulation during the preliminary generations occurs for all values of h between 0 and 0.3, preventing sex from increasing. When h ≥ 0.4, the rate of sex reaches similar average values as when σinit = 1 (not shown). When σinit is set to 0.05, results for h = 0.3 become similar to results obtained when σinit = 1 (while mutations accumulate during preliminary generations when h ≤ 0.2).
Results presented in Figure 4 (and in the next figures) assume additivity at the modifier locus. Incorporating dominance effects between modifier alleles in a very general way is difficult in the framework of our simulation model, because the dominance relationships between all segregating alleles need to be specified. To have an idea of how dominance at the modifier locus may affect our results, we modified our simulation program so that each modifier allele i codes for a rate of sex σi and has a “dominance coefficient” θi, which is sampled from a uniform distribution between 0 and 1 for each new allele. The probability that an individual reproduces sexually is then given by (θ1σ1 + θ2σ2)/(θ1 + θ2), where σ1, θ1 and σ2, θ2 refer to the two modifier alleles of the individual. We ran this modified program for the parameter values corresponding to the solid squares in Figure 4 (γ = 0, U = 0.05, and U = 0.5); however, the results obtained from the two programs were almost undistinguishable (results not shown). Still, it is possible that dominance at the modifier locus would have more effect if it was modeled differently (in particular, our modified program still implies some form of average additivity).
Figure 5 shows the effect of the rate of mitotic crossing over χ on the average rate of sex, when U = 0.5. One can see that χ = 10−3 has less effect than γ = 10−3 (in particular in the case of recessive mutations). Indeed, mitotic crossing over leads to LOH at loci located between the crossover and the distal part of the chromosome only: therefore, the average rate of LOH per locus and per asexual generation is lower for χ = 10−3 than for γ = 10−3.
Figure 5.—
The same as Figure 4 for U = 0.5 and for different rates of mitotic crossing over: solid squares, solid lines, χ = 0; solid circles, dashed lines, χ = 10−3; open squares, dotted lines, χ = 10−2.
Effects of N, L, s:
Figure 6 shows the effect of varying population size N, genome map length L, and the strength of selection against deleterious mutations s, when γ = χ = 0. Changing N from 104 to 5 × 104 has only little effect on the average rate of sex when h ≥ 0.3 (Figure 6, top left). This may be due to the fact that increasing N has two opposite effects: it decreases the strength of indirect selection acting on the modifier (that favors high rates of sex when h ≥ 0.3), but it also decreases the effect of drift at the modifier locus (that tends to bring the rate of sex closer to 0.5), and the two effects may cancel each other. When h < 0.3, decreasing N increases the range of values of h for which the population evolves toward asexuality. This effect may be due to the fact that when a modifier allele coding for a low rate of sex reaches high frequency (either by selection or by drift), deleterious mutations can accumulate in the heterozygous state (in particular when h is low), which prevents the rate of sex from increasing back (as it generates a strong segregation load). This effect should be stronger for smaller population sizes (because mutation accumulation occurs faster). Effects of map length L are shown in Figure 6, top right. For intermediate values of h, decreasing map length L tends to increase the rate of sex. This is predicted by the two-locus model, as selection on the modifier through its effect on allele frequency (term in DMA + DM,A) becomes stronger when linkage is tighter, while recombination has less effect on selection through effect on genotype frequency (term in DMA,A); note that the three-locus model also predicts more selection for sex with tighter linkage (Appendix SD). When h is low, however, low recombination increases the speed of mutation accumulation, which tends to trap the population in the asexual state (as discussed above): for h = 0.2, the population evolves toward asexuality when L = 0.1 and L = 1, while L = 10 allows sex to be maintained (results under free recombination are very similar to L = 10, not shown). Note that for L = 0.1 and h ≥ 0.2, deleterious mutations fix in the population, at relatively high rates for high values of h (see additional results in Appendix SF). Finally, Figure 6 shows that increasing s leads to higher rates of sex, which is expected since the relative effect of selection through effect on allele frequencies increases with s (Equations 7–9). Furthermore, low values of s facilitate the accumulation of mutations in the heterozygous state when h is low, which again may trap the population in the asexual state. Finally, Figure 6 shows that the population evolves toward low sex when s is low and h is high (dotted line in Figure 6, bottom). This effect is not expected from the two-locus model, but can be explained in terms of interactions between pairs of selected loci (three-locus model): indeed, we have seen that sex tends to break correlations in homozygosity among selected loci (which disfavors sex whenever h ≠  ) and that this effect should predominate over other effects of interactions between loci when s is sufficiently small (see Appendix SD).
) and that this effect should predominate over other effects of interactions between loci when s is sufficiently small (see Appendix SD).
Figure 6.—
Average rate of sex observed in multilocus simulations, as a function of the dominance coefficient of deleterious mutations (h), in the absence of gene conversion or mitotic recombination (γ = χ = 0). Top left, different values of population size N: dotted line, N = 10,000; solid line, N = 20,000; dashed line, N = 50,000. Top right, different values of genome map length L: solid line, L = 10; dashed line, L = 1; dotted line, L = 0.1. Bottom: different values of the strength of selection against deleterious alleles s: dotted line, s = 0.01; solid line, s = 0.05; dashed line, s = 0.1. Other parameter values are U = 0.5, c = 1, N = 20,000 (top right and bottom), L = 10 (top left and bottom), and s = 0.05 (top). Note that when s = 0.01 (bottom, dotted line), deleterious mutations fix in the population at a high rate for h = 0.7–1 (see Appendix SF).
Epistasis:
Interactions between selected loci may also have important effects on selection for sex in the presence of epistasis. Appendix SG shows simulation results incorporating epistasis, assuming epistasis is the same among all pairs of loci and neglecting higher-order epistasis (i.e., epistatic effects between more than two loci). These results indicate that negative additive-by-additive epistasis favors sex (even when large in absolute value), while negative additive-by-dominance and dominance-by-dominance epistasis tends to disfavor sex. These results are discussed more at length in Appendix SG.
Costly sex:
The previous results assumed that sex had no intrinsic cost. Figure 7 presents the average rate of sex as a function of the cost of sex c (recall that c = 1 means no cost, while a twofold cost corresponds to c = 2), for a genomic mutation rate U = 1. In Figure 7, left, mutant alleles at the modifier locus may code for any rate of sex between 0 and 1 (as in previous results). In the case of additive deleterious alleles (h = 0.5), σ decreases sharply as c becomes >1, but then decreases slowly as c increases to 2. When the average rate of sex is <0.2, however (that is, when c ≥ ∼1.2), deleterious mutations accumulate in the population: the numbers of fixed mutations after 2 × 106 generations are ∼130, 2700, 9000, and 57,000 for c = 1.2, 1.3, 1.5, and 2, respectively (Appendix SF provides more detailed results), and mutational meltdown may thus lead to the extinction of the population (changing population size from N = 20,000 to N = 50,000 leads to similar results, as shown in Appendix SF). When deleterious alleles are recessive (h < 0.5), σ is similar to the value obtained for h = 0.5 when c is not too high, but for high costs of sex the population becomes fully asexual. As discussed previously, this is probably due to the fact that when a mutation coding for no or very little sex happens to reach a high frequency (for example, because it occurred on a good genetic background), mutations start accumulating in the heterozygous state, leading to an irreversible process (sex cannot increase again because the segregation load is too strong). Note that it is possible that asexual mutants would eventually invade at lower values of c, if the simulation could run for a larger number of generations. Figure 7, right, shows the average frequency of fully sexual individuals (σ = 1), when fully asexuals (σ = 0) occur at rate 10−4 per generation (back mutations also occurring at rate 10−4). Patterns are similar, except that when h < 0.5 asexual mutants invade at lower values of c (which may simply be due to the fact that asexual mutants appear more rapidly in the population than in the previous case). Additional results for U = 0.5, γ = 0, and γ = 10−3 are presented in Appendix SF, showing that mitotic gene conversion has little effect on these results. Introducing negative additive-by-additive epistasis increases the mean rate of sex for low to intermediate values of c (see Appendix SF); it also prevents the accumulation of deleterious alleles, allowing sex to be maintained at intermediate levels when mutations are recessive and the cost of sex is high (Figure F3, bottom right, in Appendix SF).
Figure 7.—
Average rate of sex observed in multilocus simulations, as a function of the cost of sex (c) and for different values of the dominance coefficient of deleterious mutations (h): solid squares, solid lines, h = 0.5; solid circles, dashed lines, h = 0.4; open squares, dotted lines, h = 0.3; open circles, dashed-dotted line, h = 0.2 (left panel only). Left, mutant alleles at the modifier locus can take any value between 0 and 1; right, competition between fully sexuals (σ = 1) and fully asexuals (σ = 0). Other parameter values: U = 1, γ = χ = 0, and other parameters as in Figures 4 and 5. Error bars are smaller than the size of symbols.
DISCUSSION
Two-locus model:
Deleterious mutations have been repeatedly presented as a potentially important factor favoring sex and recombination, either due to deterministic interactions among mutations (synergistic epistasis, e.g., Kondrashov 1988) or due to stochastic effects (e.g., Keightley and Otto 2006); however, many of these earlier models focused on the case of haploid organisms and did not investigate what should be the evolutionarily stable rate of sex in the population (in particular when sex is costly). In this article, we have explored the effects of deleterious mutations on the direction and strength of selection acting on a modifier gene affecting the rate of sexual (vs. asexual) reproduction, in a finite diploid population. Some of these effects stem from the fact that sex tends to bring the population closer to HW equilibrium at each selected locus (segregation). Otto (2003) has shown that in an infinite, randomly mating population, dominance generates departures from HW equilibrium that may favor sex when deleterious mutations are weakly recessive. Finite population size also generates departures from HW equilibrium (excess of heterozygotes), and we have shown that this effect favors sex when deleterious mutations are dominant or weakly recessive. It is important to stress that this stochastic effect is not the intralocus equivalent of the Hill–Robertson effect that generates negative linkage disequilibrium between loci, as the Hill–Robertson effect requires the interaction between selection and drift and tends to be smaller in magnitude than departures from HW equilibrium generated by drift alone. Because the effect of finite population size is proportional to the genetic variance at each selected locus, it may dominate over the deterministic departure from HW equilibrium generated by selection, which is proportional to the square of genetic variance. In particular, our expression for 〈DA,A〉 at quasi-equilibrium (Equation 2) shows that the stochastic effect of finite population size should dominate over the deterministic effect of selection whenever 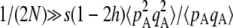 . In the deterministic limit and when h > 0, 〈p
. In the deterministic limit and when h > 0, 〈p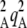 〉/〈pAqA〉 ≈ u/(hs), and the last condition thus becomes independent of s. With finite N, numerical integration over Wright's distribution shows that s(1 – 2h)〈p
〉/〈pAqA〉 ≈ u/(hs), and the last condition thus becomes independent of s. With finite N, numerical integration over Wright's distribution shows that s(1 – 2h)〈p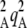 〉/〈pAqA〉 is also unaffected by s over a wide range of values of s (results not shown): therefore, increasing s will not increase the relative effect of the deterministic term over the stochastic term. We measured deleterious allele frequencies at segregating loci in our multilocus simulations for N = 20,000, U = 0.5, s = 0.05, and h = 0.2, 0.3, and 0.4 and found that 〈pA〉 ≈ 3.6 × 10−4, 2.7 × 10−4, and 2.2 × 10−4, while 〈p
〉/〈pAqA〉 is also unaffected by s over a wide range of values of s (results not shown): therefore, increasing s will not increase the relative effect of the deterministic term over the stochastic term. We measured deleterious allele frequencies at segregating loci in our multilocus simulations for N = 20,000, U = 0.5, s = 0.05, and h = 0.2, 0.3, and 0.4 and found that 〈pA〉 ≈ 3.6 × 10−4, 2.7 × 10−4, and 2.2 × 10−4, while 〈p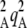 〉/〈pAqA〉 ≈ 1.4 × 10−3, 9.3 × 10−4, and 7.2 × 10−4 for h = 0.2, 0.3, and 0.4 (respectively). From this (and from Equation 2), one finds that the deterministic and stochastic terms are of similar orders of magnitude (for these parameter values), the deterministic term being slightly stronger than the stochastic term for h = 0.2, while it is weaker for h = 0.3 and 0.4. Note, however, that other associations than DA,A generate selection for sex in finite populations (such as the variance in DMA, see Equation B2 in Appendix SB).
〉/〈pAqA〉 ≈ 1.4 × 10−3, 9.3 × 10−4, and 7.2 × 10−4 for h = 0.2, 0.3, and 0.4 (respectively). From this (and from Equation 2), one finds that the deterministic and stochastic terms are of similar orders of magnitude (for these parameter values), the deterministic term being slightly stronger than the stochastic term for h = 0.2, while it is weaker for h = 0.3 and 0.4. Note, however, that other associations than DA,A generate selection for sex in finite populations (such as the variance in DMA, see Equation B2 in Appendix SB).
Heterozygote excess:
This work raises the question of the occurrence of heterozygote excess within populations. Equation 2 indicates that DA,A should be only very slightly negative in fully sexual, randomly mating populations, while it may by more strongly negative when sex becomes rare. Negative FIS values (indicating local excess of heterozygotes) have indeed been measured in some partly or fully clonal populations (e.g., Prugnolle et al. 2005; Guillemin et al. 2008). Many other studies have reported positive FIS values, often interpreted as “inbreeding”. However, positive FIS may be generated by different processes, with different consequences of the evolution of sex modifiers. Self-fertilization (or mating within families before dispersal) will generate excess of homozygotes, favoring sex when deleterious mutations are recessive (Otto 2003; Agrawal 2009) because sex tends to mask these mutations. Positive FIS may also result from population substructure into smaller panmictic units (the Wahlund effect). In this last case, heterozygote excess may occur at the level of these units (in particular in facultative sexuals), generating a selective force on sex similar to the one described in this article (assuming that competition occurs at least partly at the scale of the panmictic units). The effects of population structure on selection for sex in diploids will be explored further in a future article.
Interactions between selected loci:
Indirect selection on a sex modifier locus is also affected by associations involving the modifier and several selected loci. In particular, finite population size tends to generate correlations in homozygosity that are broken down by sex: in the case of two selected loci, sex tends to decrease the frequency of double homozygotes (hom–hom) and double heterozygotes (het–het) at these loci and to increase the frequency of homozygotes at one locus and heterozygotes at the other (hom–het). In the absence of epistasis, the average fitness of hom–het genotypes is lower than the average fitness of hom–hom and het–het genotypes whenever h ≠ 0.5 (Figure 4 in Roze 2009), selecting against sex through the term s2(1 − 2h)2〈DMAB,AB〉t in Equation 11. In particular in the case of partially recessive deleterious alleles, finite population size tends to generate associative overdominance between chromosomes carrying deleterious mutations at different loci. In the same way as overdominance at a single locus selects against sex (due to segregation load), associative overdominance also disfavors sex because sex generates lower fitness hom–het mixtures from parents heterozygous at many loci (we thank Sally Otto for pointing out this analogy). The effect of such associations involving two or more selected loci may become important when deleterious alleles segregate at many loci (high U). It becomes also particularly important when sex occurs very rarely and deleterious mutations accumulate in the population. As was found before (Charlesworth et al. 1993a,b; Charlesworth and Charlesworth 1997), we observed in our simulations that when h is sufficiently low, deleterious mutations accumulate in the population without reaching fixation: different types of strongly mutated chromosomes are then maintained in the population by associative overdominance, which strongly selects against sex. This generates an irreversible process, for when an allele coding for no sex (or very little sex) reaches high frequency, the population starts to accumulate recessive deleterious alleles in the heterozygous state, preventing sex from increasing back (this accumulation occurs faster when s and h and N and L are low and when U is high). This is particularly problematic when sex has a strong direct cost, in which case a mutation coding for low sex may quickly reach high frequency if it occurs on a genetic background carrying only few mutations. Indeed, our multilocus simulations show that when h < 0.4, the rate of sex always goes to zero when the cost of sex is sufficiently high. Estimates of average dominance coefficients of deleterious alleles vary widely, ranging from 0.1 to 0.4 in mutation-accumulation studies (e.g., Houle et al. 1997; García-Dorado and Caballero 2000; Vassilieva et al. 2000; García-Dorado et al. 2004; Halligan and Keightley 2009), while fitness assays of spontaneous mutations in yeast indicate an average h of ∼0.2 (Szafraniec et al. 2003). Taken together, these results suggest that h is likely to be <0.4 on average.
Other types of interactions among selected loci favor sex, however, and may be stronger than the effect of breaking correlations in homozygosity, in particular when h > ∼0.2–0.3, selection is not too weak, and/or rates of sex and recombination are small. Among these interactions are negative linkage disequilibria generated by the Hill–Robertson effect (Hill and Robertson 1966; Barton and Otto 2005; Keightley and Otto 2006), favoring increased recombination. However, our quasi-equilibrium results indicate that selection for sex is also driven by many other associations between pairs of selected loci (also generated by selection and drift), the linkage disequilibrium 〈DAB〉 being only a minor component of selection for sex (see Figures D2 and D3 in Appendix SD). Similar results were obtained in a previous model on the evolution of recombination modifiers in diploid, spatially structured populations (Roze 2009), the major difference being that associations 〈DMA,A〉, 〈DMB,B〉 are much stronger and play a more important role in the evolution of sex modifiers than in the evolution of recombination modifiers.
Previous multilocus simulation models on the evolution of sex in finite, haploid populations found that selection for sex (measured by the probability of fixation of a modifier increasing sex or recombination relative to the fixation probability of a neutral mutation) increases with population size (Keightley and Otto 2006; Gordo and Campos 2008). Here, we found that increasing population size may increase the average rate of sex when deleterious mutations are partially recessive (because increasing population size slows the buildup of associative overdominance that disfavors sex), but not when mutations are additive (compare, for example, Figure 7, left, and Figure F3, bottom left, in Appendix SF). Hence, increasing population size may have different effects on relative fixation probabilities of sex modifiers and on the evolutionarily stable rate of sex (note that the diffusion approximation for the relative fixation probability is 2sMNe for 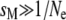 , which may increase as N increases, even if sM decreases).
, which may increase as N increases, even if sM decreases).
Effects of loss of heterozygosity:
We have also explored the effects of loss of heterozygosity due to mitotic gene conversion and/or mitotic recombination and found that it tends to favor sex when deleterious mutations are recessive (because sex tends to mask mutations that have been made homozygous by mitotic gene conversion/recombination). However, our results indicate that without a cost of sex (c = 1), this effect is important only for rates of mitotic gene conversion of the order ≥10−3 and rates of mitotic crossing over of the order ≥10−2 (Figures 4 and 5). These values are higher than most available estimates on rates of loss of heterozygosity (Tischfield 1997; Shao et al. 1999; Holt et al. 1999; Omilian et al. 2006; Mandegar and Otto 2007; Carr and Gottschling 2008), suggesting that the consequence of such events on the evolution of sex in the presence of deleterious mutations may be limited. Furthermore, we found that mitotic gene conversion does not affect much our results when sex is costly (see Appendix SF). Nevertheless, it would be interesting to obtain more data about rates of mitotic recombination, as only few estimates are available (in particular one could imagine that mitotic recombination could be more frequent in more stressful environments, if DNA damage occurs more frequently). Finally, effects of LOH on selection for sex are very similar to the effects of self-fertilization (described in Otto 2003; Agrawal 2009) and should become negligible in partly selfing populations (as rates of LOH are typically much lower than selfing rates).
Conclusion:
Taken together, our results cast doubt on the hypothesis that deleterious mutations could allow the maintenance of high rates of sex in the face of strong costs (in diploids). Although the idea that the twofold cost of sex can be paid if U ≥ 1 is often encountered in the literature, it is not always remembered that this result assumes synergistic epistasis among mutations (Kondrashov 1988), while the data available do not show any clear trend toward synergism among mutations (e.g., Elena and Lenski 1997; Rice 2002). Our simulation results for U = 1 and c = 2 indicate that a low rate of sex can be maintained when deleterious alleles are additive, while sex is not maintained when deleterious alleles are partially recessive (Figure 7, Appendix SD). Note, however, that deleterious mutations may select for higher rates of sex when they also affect the mating success of males, in species in which sexual selection is sufficiently strong (Hadany and Beker 2007). Furthermore, deleterious mutations can act in combination with other factors such as host–parasite interactions (Peters and Lively 1999; Otto and Nuismer 2004; Gandon and Otto 2007; Salathé et al. 2008), local adaptation (Pylkov et al. 1998; Lenormand and Otto 2000; Agrawal 2009), or adaptive evolution (Otto and Barton 2001). Testing to which extent a combination of these factors can favor high rates of costly sex would thus be interesting.
Finally, data about the occurrence and fitness effects of mutations leading to asexuality are badly needed: indeed, it may well be that in many cases, asexuals do not benefit from the theoretical twofold advantage over sexuals, due to pleiotropic effects of the mutation leading to loss of sex. In mammals, for example, asexual females may not be able to produce viable offspring due to the genomic imprinting system, and similar constraints may operate in other groups. In the species in which purely asexual forms coexist with sexuals, determining the relative fitnesses of sexuals and asexuals (and disentangling direct effects from effects of the genetic background) represents a promising way of evaluating current theories on the evolution of sex.
Acknowledgments
We thank Aneil Agrawal, Sally Otto, François Rousset, and two anonymous reviewers for very helpful comments and the genomics and computing service of Roscoff's Biological Station for computing time. This work has been supported by an Accueil de Compétences en Bretagne fellowship from Région Bretagne (project CycleVie) and by a research mobility grant from the Centre National de la Recherche Scientifique to D.R.
Supporting information is available online at http://www.genetics.org/cgi/content/full/genetics.109.108258/DC1.
References
- Agrawal, A. F., 2006. Evolution of sex: Why do organisms shuffle their genotypes? Curr. Biol. 16 R696–R704. [DOI] [PubMed] [Google Scholar]
- Agrawal, A. F., 2009. Spatial heterogeneity and the evolution of sex in diploids. Am. Nat. 174 S54–S70. [DOI] [PubMed] [Google Scholar]
- Agrawal, A. F., and S. P. Otto, 2006. Host-parasite coevolution and selection on sex through the effects of segregation. Am. Nat. 168 617–629. [DOI] [PubMed] [Google Scholar]
- Aylon, Y., and M. Kupiec, 2004. DSB repair: the yeast paradigm. DNA Repair 3 797–815. [DOI] [PubMed] [Google Scholar]
- Balloux, F., L. Lehmann and T. de Meuûs, 2003. The population genetics of clonal and partially clonal diploids. Genetics 164 1635–1644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barton, N. H., 1995. A general model for the evolution of recombination. Genet. Res. 65 123–144. [DOI] [PubMed] [Google Scholar]
- Barton, N. H., and B. Charlesworth, 1998. Why sex and recombination? Science 281 1986–1990. [PubMed] [Google Scholar]
- Barton, N. H., and S. P. Otto, 2005. Evolution of recombination due to random drift. Genetics 169 2353–2370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barton, N. H., and M. Turelli, 1991. Natural and sexual selection on many loci. Genetics 127 229–255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernstein, H., H. C. Byerly, F. A. Hopf and R. E. Michod, 1985. Genetic damage, mutation, and the evolution of sex. Science 229 1277–1281. [DOI] [PubMed] [Google Scholar]
- Bernstein, H., F. A. Hopf and R. E. Michod, 1988. Is meiotic recombination an adaptation for repairing DNA, producing genetic variation, or both? pp. 139–160 in The Evolution of Sex: An Examination of Current Ideas, edited by R. E. Michod and B. R. Levin. Sinauer Associates, Sunderland, MA.
- Bürger, R., 2000. The Mathematical Theory of Selection, Recombination, and Mutation. Wiley, Chichester, UK.
- Carr, L. L., and D. E. Gottschling, 2008. Does age influence loss of heterozygosity? Exp. Gerontol. 43 123–129. [DOI] [PubMed] [Google Scholar]
- Chamnanpunt, J., W. Shan and B. M. Tyler, 2001. High frequency mitotic gene conversion in genetic hybrids of the oomycete Phytophthora sojae. Proc. Natl. Acad. Sci. USA 98 14530–14535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth, B., 1990. Mutation-selection balance and the evolutionary advantage of sex and recombination. Genet. Res. 55 199–221. [DOI] [PubMed] [Google Scholar]
- Charlesworth, B., 1993. Directional selection and the evolution of sex and recombination. Genet. Res. 61 205–224. [DOI] [PubMed] [Google Scholar]
- Charlesworth, B., and D. Charlesworth, 1997. Rapid fixation of deleterious alleles can be caused by Muller's ratchet. Genet. Res. 70 63–73. [DOI] [PubMed] [Google Scholar]
- Charlesworth, D., M. T. Morgan and B. Charlesworth, 1993. a Mutation accumulation in finite outbreeding and inbreeding populations. Genet. Res. 61 39–56. [Google Scholar]
- Charlesworth, D., M. T. Morgan and B. Charlesworth, 1993. b Mutation accumulation in finite populations. J. Hered. 84 321–325. [Google Scholar]
- Chen, J.-M., D. N. Cooper, N. Chuzhanova, C. Férec and G. P. Patrinos, 2007. Gene conversion: mechanisms, evolution and human disease. Nat. Rev. Genet. 8 762–775. [DOI] [PubMed] [Google Scholar]
- Elena, S. F., and R. E. Lenski, 1997. Test of synergistic interactions among deleterious mutations in bacteria. Nature 390 395–397. [DOI] [PubMed] [Google Scholar]
- Felsenstein, J., and S. Yokohama, 1976. The evolutionary advantage of recombination. II. Individual selection for recombination. Genetics 83 845–859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gandon, S., and S. P. Otto, 2007. The evolution of sex and recombination in response to abiotic or coevolutionary fluctuations in epistasis. Genetics 175 1835–1863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- García-Dorado, A., and A. Caballero, 2000. On the average coefficient of dominance of deleterious spontaneous mutations. Genetics 155 1991–2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- García-Dorado, A., C. López-Fanjul and A. Caballero, 2004. Rates and effects of deleterious mutations and their evolutionary consequences, pp. 20–32 in Evolution of Molecules and Ecosystems, edited by A. Moya and E. Font. Oxford University Press, Oxford.
- Gordo, I., and P. R. A. Campos, 2008. Sex and deleterious mutations. Genetics 179 621–626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guillemin, M.-L., S. Faugeron, C. Destombe, F. Viard, J. A. Correa et al., 2008. Genetic variation in wild and cultivated populations of the haploid-diploid red alga Gracilaria chilensis: how farming practices favor asexual reproduction and heterozygosity. Evolution 62 1500–1519. [DOI] [PubMed] [Google Scholar]
- Gupta, P. K., A. Sahota, S. A. Boyadjiev, S. Bye, S. Shao et al., 1997. High frequency in vivo loss of heterozygosity is primarily a consequence of mitotic recombination. Cancer Res. 57 1188–1193. [PubMed] [Google Scholar]
- Haag, C. R., and D. Roze, 2007. Genetic load in sexual and asexual diploids: segregation, dominance and genetic drift. Genetics 176 1663–1678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hadany, L., and T. Beker, 2007. Sexual selection and the evolution of obligatory sex. BMC Evol. Biol. 7 245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagstrom, S. A., and T. P. Dryja, 1999. Mitotic recombination map of 13cen-13q14 derived from an investigation of loss of heterozygosity in retinoblastomas. Proc. Natl. Acad. Sci. USA 96 2952–2957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halligan, D. L., and P. D. Keightley, 2009. Spontaneous mutation accumulation studies in evolutionary genetics. Ann. Rev. Ecol. Evol. Syst. 40 151–172. [Google Scholar]
- Hastings, W. K., 1970. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 57 97–109. [Google Scholar]
- Helleday, T., 2003. Pathways for mitotic homologous recombination in mammalian cells. Mutat. Res. 532 103–115. [DOI] [PubMed] [Google Scholar]
- Hill, W. G., and A. Robertson, 1966. The effect of linkage on limits to artificial selection. Genet. Res. 8 269–294. [PubMed] [Google Scholar]
- Holt, D., M. Dreimanis, M. Pfeiffer, F. Firgaira, A. Morley et al., 1999. Interindividual variation in mitotic recombination. Am. J. Hum. Genet. 65 1423–1427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Houle, D., K. A. Hughes, S. Assimacopoulos and B. Charlesworth, 1997. The effect of spontaneous mutation on quantitative traits. II. Dominance of mutations with effects on life-history traits. Genet. Res. 70 27–34. [DOI] [PubMed] [Google Scholar]
- Iles, M. M., K. Walters and C. Cannings, 2003. Recombination can evolve in large finite populations given selection on sufficient loci. Genetics 165 2249–2258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ira, G., D. Satory and J. E. Haber, 2006. Conservative inheritance of newly synthesized DNA in double-strand-break-induced gene conversion. Mol. Cell. Biol. 26 9424–9429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson, R. D., and M. Jasin, 2001. Double-strand-break-induced homologous recombination in mammalian cells. Biochem. Soc. Trans. 29 196–201. [DOI] [PubMed] [Google Scholar]
- Judd, S. R., and T. D. Petes, 1988. Physical lengths of meiotic and mitotic gene conversion tracts in Saccharomyces cerevisiae. Genetics 118 401–410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keeney, S., and M. J. Neale, 2006. Initiation of meiotic recombination by formation of DNA double-strand breaks: mechanisms and regulation. Biochem. Soc. Trans. 34 523–525. [DOI] [PubMed] [Google Scholar]
- Keeney, S., C. N. Giroux and N. Kleckner, 1997. Meiosis-specific double-strand breaks are catalyzed by Spo11, a member of a widely conserved protein family. Cell 88 375–384. [DOI] [PubMed] [Google Scholar]
- Keightley, P. D., and S. P. Otto, 2006. Interference among deleterious mutations favours sex and recombination in finite populations. Nature 443 89–92. [DOI] [PubMed] [Google Scholar]
- Kirkpatrick, M., and C. D. Jenkins, 1989. Genetic segregation and the maintenance of sexual reproduction. Nature 339 300–301. [DOI] [PubMed] [Google Scholar]
- Kirkpatrick, M., T. Johnson and N. H. Barton, 2002. General models of multilocus evolution. Genetics 161 1727–1750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kondrashov, A. S., 1988. Deleterious mutations and the evolution of sexual reproduction. Nature 336 435–440. [DOI] [PubMed] [Google Scholar]
- Lenormand, T., and S. P. Otto, 2000. The evolution of recombination in a heterogeneous environment. Genetics 156 423–438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lettier, G., Q. Feng, A. Antùnez de Mayolo, N. Erdeniz, R. J. D. Reid et al., 2006. The role of DNA double-strand breaks in spontaneous homologous recombination in S. cerevisiae. PLoS Genet. 2 1773–1786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang, F., M. Han, P. J. Romanienko and M. Jasin, 1998. Homology-directed repair is a major double-strand break repair pathway in mammalian cells. Proc. Natl. Acad. Sci. USA 95 5172–5177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mandegar, M. A., and S. P. Otto, 2007. Mitotic recombination counteracts the benefits of genetic segregation. Proc. R. Soc. Lond. B Biol. Sci. 274 1301–1307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin, G., S. P. Otto and T. Lenormand, 2006. Selection for recombination in structured populations. Genetics 172 593–609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maynard Smith, J., 1988. The evolution of recombination, pp. 106–125 in The Evolution of Sex: An Examination of Current Ideas, edited by R. E. Michod and B. R. Levin. Sinauer Associates, Sunderland, MA.
- Nagylaki, T., 1993. The evolution of multilocus systems under weak selection. Genetics 134 627–647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Omilian, A. R., M. E. A. Cristescu, J. L. Dudycha and M. Lynch, 2006. Ameiotic recombination in asexual lineages of Daphnia. Proc. Natl. Acad. Sci. USA 103 18638–18643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otto, S. P., 2003. The advantages of segregation and the evolution of sex. Genetics 164 1099–1118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otto, S. P., 2009. The evolutionary enigma of sex. Am. Nat. 174 S1–S14. [DOI] [PubMed] [Google Scholar]
- Otto, S. P., and N. H. Barton, 1997. The evolution of recombination: removing the limits to natural selection. Genetics 147 879–906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otto, S. P., and N. H. Barton, 2001. Selection for recombination in small populations. Evolution 55 1921–1931. [DOI] [PubMed] [Google Scholar]
- Otto, S. P., and M. W. Feldman, 1997. Deleterious mutations, variable epistatic interactions, and the evolution of recombination. Theor. Popul. Biol. 51 134–147. [DOI] [PubMed] [Google Scholar]
- Otto, S. P., and S. L. Nuismer, 2004. Species interactions and the evolution of sex. Science 304 1018–1020. [DOI] [PubMed] [Google Scholar]
- Pâques, F., and J. E. Haber, 1999. Multiple pathways of recombination induced by double-strand breaks in Saccharomyces cerevisiae. Microbiol. Mol. Biol. Rev. 63 349–404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peters, A. D., and C. M. Lively, 1999. The red queen and fluctuating epistasis: a population genetic analysis of antagonistic coevolution. Am. Nat. 154 393–405. [DOI] [PubMed] [Google Scholar]
- Prado, F., F. Cortés-Ledesma, P. Huertas and A. Aguilera, 2003. Mitotic recombination in Saccharomyces cerevisiae. Curr. Genet. 42 185–198. [DOI] [PubMed] [Google Scholar]
- Prugnolle, F., D. Roze, A. Théron and T. de Meeûs, 2005. F-statistics under alternation of sexual and asexual reproduction: a model and data from schistosomes (Platyhelminth parasites). Mol. Ecol. 14 1355–1365. [DOI] [PubMed] [Google Scholar]
- Pylkov, K. V., L. A. Zhivotovsky and M. W. Feldman, 1998. Migration versus mutation in the evolution of recombination under multilocus selection. Genet. Res. 71 247–256. [DOI] [PubMed] [Google Scholar]
- Rice, W. R., 2002. Experimental tests of the adaptive significance of sexual recombination. Nat. Rev. Genet. 3 241–251. [DOI] [PubMed] [Google Scholar]
- Richardson, C., M. E. Moynahan and M. Jasin, 1998. Double-strand break repair by interchromosomal recombination: suppression of chromosomal translocations. Genes Dev. 12 3831–3842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roze, D., 2009. Diploidy, population structure and the evolution of recombination. Am. Nat. 174 S79–S94. [DOI] [PubMed] [Google Scholar]
- Roze, D., and N. H. Barton, 2006. The Hill-Robertson effect and the evolution of recombination. Genetics 173 1793–1811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roze, D., and T. Lenormand, 2005. Self-fertilization and the evolution of recombination. Genetics 170 841–857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salathé, M., R. Salathé, P. Schmid-Hempel and S. Bonhoeffer, 2006. Mutation accumulation in space and the maintenance of sexual reproduction. Ecol. Lett. 9 941–946. [DOI] [PubMed] [Google Scholar]
- Salathé, M., R. D. Kouyos, R. R. Regoes and S. Bonhoeffer, 2008. Rapid parasite adaptation drives selection for high recombination rates. Evolution 62 295–300. [DOI] [PubMed] [Google Scholar]
- Shao, C., L. Deng, O. Henegaru, L. Liang, N. Raikwar et al., 1999. Mitotic recombination produces the majority of recessive fibroblast variants in heterozygous mice. Proc. Natl. Acad. Sci. USA 96 9230–9235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sieber, O. M., K. Heinimann, P. Gorman, H. Lamlum, M. Crabtree et al., 2002. Analysis of chromosomal instability in human colorectal adenomas with two mutational hits at APC. Proc. Natl. Acad. Sci. USA 99 16910–16915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szafraniec, K., D. M. Wloch, P. Sliwa, R. H. Borts and R. Korona, 2003. Small fitness effects and weak genetic interactions between deleterious mutations in heterozygous loci of the yeast Saccharomyces cerevisiae. Genet. Res. 82 19–31. [DOI] [PubMed] [Google Scholar]
- Tischfield, J. A., 1997. Loss of heterozygosity or: how I learned to stop worrying and love mitotic recombination. Am. J. Hum. Genet. 61 995–999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uyenoyama, M. K., and B. O. Bengtsson, 1989. On the origin of meiotic reproduction: a genetic modifier model. Genetics 123 873–885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vassilieva, L. L., A. M. Hook and M. Lynch, 2000. The fitness effect of spontaneous mutations in Caenorhabditis elegans. Evolution 54 1234–1246. [DOI] [PubMed] [Google Scholar]
- Virgin, J. B., J. P. Bailey, F. Hasta, J. Neville, A. Cole et al., 2001. Crossing over is rarely associated with intragenic mitotic recombination in Schizosaccharomyces pombe. Genetics 157 63–77. [DOI] [PMC free article] [PubMed] [Google Scholar]