The Role of Advantageous Mutations in Enhancing the Evolution of a Recombination Modifier

Abstract

Although the evolution of recombination is still a major problem in evolutionary genetics, recent theoretical studies have shown that recombination can evolve by breaking down interference (“Hill–Robertson effects”) among multiple loci. This leads to selection on a recombination modifier in a population subject to recurrent deleterious mutation. Here, we use computer simulations to investigate the evolution of a recombination modifier under three different scenarios of recurrent mutation in a finite population: (1) mutations are deleterious only, (2) mutations are advantageous only, and (3) there is a mixture of deleterious and advantageous mutations. We also investigate how linkage disequilibrium, the strength of selection acting on a modifier, and effective population size change under the different scenarios. We observe that adding even a small number of advantageous mutations increases the fixation rate of modifiers that increase recombination, especially if the effects of deleterious mutations are weak. However, the strength of selection on a modifier is less than the summed strengths had there been deleterious mutations only and advantageous mutations only.

SEX and recombination between genomes are ubiquitous in nature, yet explaining their evolution has not proved to be easy (see recent reviews by Hadany and Comeron 2008 and Otto 2009). Recombination leads to the breakup of beneficial gene combinations (Barton and Charlesworth 1998), implying that offspring may suffer a recombination load (Charlesworth and Charlesworth 1975). Extra costs are incurred if sexual reproduction is also considered, such as the famous “twofold cost” (Maynard Smith 1978); sexual offspring need two parents whereas asexuals need one, so the latter can outgrow and outcompete sexuals.

Considering all of the associated costs, it has proved difficult to explain why recombination and sex are so common among eukaryotes. One hypothesis is that recombination breaks down “Hill–Robertson effects” in asexuals (Hill and Robertson 1966), which otherwise impede the response to selection. Hill–Robertson effects are the manifestation of many phenomena (discussed further in Charlesworth et al. 2009), including hitchhiking (Maynard Smith and Haigh 1974), background selection (Charlesworth et al. 1993), and the accumulation of deleterious mutations by Muller's ratchet (Felsenstein 1974; Muller 1964). Interference generates negative linkage disequilibrium (i.e., the accumulation of good alleles on bad genetic backgrounds), which reduces genetic variation in fitness compared to a population without this linkage disequilibrium (Barton 2009). Interference also reduces the effective population size, N_e (Robertson 1961; Comeron et al. 2008), because offspring from the same, fittest, lineages tend to be favored. Recombination can increase the genetic variance in overall fitness, which can improve the response to selection (Fisher 1930; Maynard Smith 1988). If a modifier for increased recombination facilitates the production of fitter offspring in this way, then it has an indirect selective advantage and increases in frequency by virtue of being associated with fitter genotypes, in line with Weismann's classic theory on the evolution of sex and recombination (Weismann 1887; Burt 2000).

Research into the Hill–Robertson effect has increased in recent years, with the development of analytical frameworks to study effects of drift at multiple loci. By extending earlier models that focused on selection alone (Barton 1995; Otto and Feldman 1997), recent work has assessed how linkage disequilibrium, created by genetic drift and interference with selection, drives the evolution of a recombination modifier (Barton and Otto 2005). Indirect selection on a modifier also arises because recombination increases the probability that beneficial mutations establish within a population, and the strength of this selection has been modeled using multitype branching processes (Otto and Barton 1997; Roze and Barton 2006).

Simultaneously, the ability to simulate large numbers of linked loci has increased, making it possible to evaluate the importance of the Hill–Robertson effect with selection acting across a genome. Simulations have demonstrated how breaking down interference can offer substantial selection on a modifier of recombination. Otto and Barton (2001), for example, showed that if a recombination modifier acts on loci experiencing directional selection, the effects of drift (which creates interference between loci) account for more selection on recombination than the effects of epistasis, in both 3-locus and 11-locus simulations. With only 3 loci, however, a modifier was not favored in populations of N > 10,000 chromosomes without epistasis. Subsequently, Iles et al. (2003) demonstrated that as the number of loci under directional selection increases, strong selection for recombination occurs in even larger populations, including the largest population size considered (100,000 haploid individuals). Furthermore, with population structure, breaking down Hill–Robertson effects remains important for modifier evolution even in infinitely large populations, with finite deme size (Martin et al. 2006). Similarly, Keightley and Otto (2006) showed that a recombination modifier is strongly favored in a population subject to recurrent deleterious mutation. The effects of drift again overwhelmed epistasis, and the dramatic reduction in the effective population size at a neutral site, N_e, in asexual populations highlighted how Hill–Robertson effects impede natural selection (e.g., reductions from N = 50,000 to N_e ≈ 100, if selection acting against deleterious mutants equaled 0.01 and there was complete linkage between loci). Selection on a sex modifier was also sufficiently strong that it could overcome a twofold cost, but only if sex was initially rare and the modifier led to modest increases in the frequency of sex.

These advantages of recombination have been supported by experiments demonstrating that recombining populations are more responsive to selection. A study by Malmberg (1977) found that allowing the bacteriophage T4 to exchange segments of its genome improved its rate of adaptation. More recent studies provide evidence that recombination increases the realized selection strength and fixation rate of new mutants in Drosophila melanogaster (Rice and Chippindale 2001); regions of the genome lacking in recombination in Drosophila show signs that selection has been impeded, whereas regions that have normal levels of recombination appear to adapt more quickly (Presgraves 2005; Betancourt et al. 2009; Charlesworth et al. 2009); sex overcomes clonal interference in Chlamydomonas reinhardtii, which then accelerates adaptation (Colegrave 2002); sex in stressed environments of yeast increases population variance in fitness and the response to selection (Goddard et al. 2005); genetic drift induced by population bottlenecks in the RNA bacteriophage Φ6 hampers the response to selection to a greater extent in asexuals then sexuals (Poon and Chao 2004); recombining populations of Escherichia coli are better able to break down interference between a known beneficial allele and other sites under selection, thereby increasing the rate of fixation of the fitter allele (Cooper 2007); and Caenorhabditis elegans evolves outcrossing if a population is subject to an increased mutation rate or the presence of a pathogen, indicating that sex improves the response to adaptation (Morran et al. 2009).

Recently, a “pluralist” framework was proposed (West et al. 1999), arguing that multiple mechanisms work together to facilitate the widespread evolution of genetic recombination. A recent example investigating this was undertaken by Oliveira et al. (2008), which aimed to gauge what degree of selection strengths acting on deleterious mutants drove the evolution of recombination via the process of background selection or through Muller's ratchet.

Here, we use computer simulations to extend the work of Keightley and Otto (2006) by considering both deleterious and advantageous mutations arising throughout the genome, in the spirit of a more pluralist approach to the Hill–Robertson effect. Whereas Keightley and Otto (2006) demonstrated that genetic recombination is selectively favored if multiple linked loci within the genome are subject to recurrent deleterious mutation, Iles et al. (2003) demonstrated that similar advantages to a modifier occur if multiple linked loci are subject to recurrent advantageous mutations. This motivates the question: In genomes subject to both deleterious and advantageous mutations, is recombination favored more compared to a population subject to only one type of mutation and, if so, by how much? Specifically, we investigate whether the benefits of a recombination modifier in the presence of deleterious and advantageous mutations are additive. That is, if the modifier has selection advantage s_Md if just recurrent deleterious mutations occur at rate U_d, and advantage s_Ma if just advantageous mutations occur at rate U_a, then with both types of mutation occurring at a total rate of U_d + U_a, additivity implies a selective advantage of the modifier equal to s_Md + s_Ma. This is a reasonable null hypothesis to start with, and it allows us to test for the presence of interference between different types of mutation.

At sites under selection, the extent to which nucleotide substitutions are driven by positive selection or occur despite negative selection has been the topic of long debate. The proportion of advantageous mutations is likely to depend strongly on the match between the species and its current environment (for a recent review see Eyre-Walker 2006). Comparing the chimpanzee and human genomes suggests that hominids have experienced little adaptive evolution at the molecular level (Chimpanzee Sequencing and Analysis Consortium 2005; Zhang and Li 2005) [although low rates of adaptive molecular evolution inferred in these species could be a consequence of population bottlenecks, which would downwardly bias estimates (Eyre-Walker and Keightley 2009)]. On the other hand, Bierne and Eyre-Walker (2004) inferred that ∼45% of amino acid substitutions in Drosophila are a consequence of adaptive evolution. This equates to one substitution in the genome every 45 years (∼450 generations) (Smith and Eyre-Walker 2002), although these estimates are subject to discussion (Sella et al. 2009). Here, we use rates of positive mutation based on these data to determine the role that adaptive mutations might play in the evolution of genetic recombination, especially when there are background deleterious mutations as well.

METHODS

Simulation of a recombination modifier:

The simulations start with a population of N mutant-free haploid chromosomes, each consisting of 100 equally spaced linked loci subject to recurrent mutation. A new generation is created by selection, recombination (if present), and mutation to produce N offspring.

Three scenarios are investigated: mutants are exclusively deleterious (as in Keightley and Otto 2006); mutants are exclusively advantageous (similar to Iles et al. 2003, although they considered standing variation only); or a proportion x = k/s_a of mutants are advantageous and 1 − x are deleterious, for k a numerical constant and s_a the selection acting on an advantageous mutant. The function x = k/s_a reflects the assumption that strongly advantageous mutants are less likely to appear than weakly selected ones (Andolfatto 2007; Jensen et al. 2008). The number of mutants is chosen from a Poisson distribution with mean U, except for the case where all spontaneous mutations are advantageous. Specifically, we assume that advantageous mutations are always a small proportion, x, of all mutations that occur. Thus, when only advantageous mutations are present, they occur at a rate Ux (this is equivalent to setting s_d = 0 in the case with both advantageous and deleterious mutants). If both advantageous and deleterious mutations are present, the overall mutation rate is not quite the sum of mutation rates from the separate scenarios; the overall mutation rate is U whereas the summed rate if mutants are deleterious only and advantageous only equals U + Ux = (1 + x)U. However, x is assumed to be small (it is always <3%) and simulations with a total deleterious and advantageous mutation rate of (1 + x)U give indistinguishable estimates of s_M, the selection strength on the modifier, compared to simulations with overall mutation rate U (results not shown).

In all scenarios, each site is equally likely to acquire a new mutation. Fitness effects of loci are multiplicative, with advantageous mutants having fixed fitness effects s_a and deleterious mutants have fitness effects of s_d. Thus with y advantageous mutants and z deleterious mutants, the fitness of a haploid individual equals (1 + s_a)^y (1 − s_d)^z. Fixed fitness effects are used to speed up simulations. Epistasis between mutations on the log-fitness scale is assumed to be absent, so that any increase in fixation rate of modifier mutations can be attributed to Hill–Robertson effects. Every 500 generations, the number of mutants is normalized; the number present in a single chromosome is reduced by the minimum number of advantageous or deleterious mutants that any haploid individual possesses so that the smallest number present in a single chromosome equals zero.

Except where noted, the population initially lacks genetic crossing over. To produce the next generation, a parent is chosen with replacement, with probability proportional to its fitness. This is then cloned and a number of mutants sampled from a Poisson distribution are added to produce an offspring. This is repeated N times until the population is replenished. A burn-in of 5N such generations is run to allow the population variance to approach a steady state. The state of the burn-in population is then saved, and a recombination modifier is introduced at a randomly selected position on a randomly selected chromosome. The processes of selection, recombination, and mutation are then repeated, except that two haploid parents are mated to allow crossovers to occur. The modifier increases the (Poisson) mean number of crossover events per chromosome during reproduction from L = 0 to L = 0.1 if it is present as a homozygote (and half that if it is heterozygous). The new modifier allele is then tracked until it is fixed or lost from the population. The process of introducing a single modifier mutation is repeated 5N times for each saved burn-in population and the total number of fixations is divided by 5N to obtain the fixation probability u. The statistic used to determine the selective advantage of the modifier is u/u*, where u* = 1/N, the fixation probability of a neutral mutation (Kimura 1983). The above constituted one “run” to produce a single statistic. Each run is executed 100 times from separate burn-ins to produce a distribution of fixation probabilities.

Parameter values used:

The per-chromosome mutation rate (if mutants are solely deleterious or deleterious and advantageous) is set to either U = 0.1 or U = 0.5, which is in the range of estimated deleterious mutation rates per chromosome in Drosophila (Halligan and Keightley 2006; Haag-Liautard et al. 2007; Keightley et al. 2009). These values should also be similar to the joint deleterious and advantageous mutation rates, since selected mutants are believed to be mainly deleterious (Crow 1970). x, the proportion of mutants that are advantageous, is set to k/s_a with k = 0.00023. This value of k is chosen so that there was, on average, one substitution every 450 generations (a rate inferred for the Drosophila genome by Bierne and Eyre-Walker 2004), in simulations that we conducted with a small population (N = 100), a low mutation rate (U = 0.1), with medium-strength advantageous and deleterious mutations both present (s_a = s_d = 0.025), and complete linkage between loci. This value of k is then used in all simulations investigated; however, this will lead to higher rates of substitution occurring in simulations with large population sizes or mutation rates.

Values of s_a are set to 0.01, 0.025, or 0.05. We wanted to ensure that Ns_a ≥ 1 for all N ≥ 100, so that the fate of mutations is not determined by the action of drift alone, even if Hill–Robertson effects are absent (Kimura 1983). These values are therefore somewhat higher then those obtained from analysis of amino acid substitution data from Drosophila, although there is some overlap (see reviews by Sella et al. 2009 and Wright and Andolfatto 2008).The appearance of strong adaptive mutations is best representative of advantageous mutants occurring at nonsynonymous sites, where the substitution rate and selection strength are highest (Andolfatto 2005).

We investigated a wide range of s_d values, from 0 to 0.05. Again precise values of s_d are hard to obtain from observations; smaller values of s_d investigated match up with estimates obtained from Loewe and Charlesworth (2006); however, García-Dorado et al. (1999) found a mean s_d of ∼0.2. This high value may have resulted from simplifications used in the Bateman–Mukai inference method (Lynch and Walsh 1988). One should be aware though that due to the strongly leptokurtic distributions of s_d found empirically, there is a great deal of variance around such estimates and many s_d values would be lower than those used in our simulations.

Measuring linkage disequilibrium for an asexual and recombining population:

The log fitness associated with a chromosome is additive in these simulations, so standard models of the expression of phenotypic quantitative traits can be used to measure differences in variance (Bulmer 1976, 1980; Keightley and Hill 1987). To measure linkage disequilibrium in an asexual population, the frequency of each individual mutant is tracked. A “garbage collection” routine is executed every 10 generations to clear memory; mutants that have become either fixed or lost are removed from the population, and a note is kept of how many new mutant alleles have fixed. There is a burn-in of 5N generations, after which the mean linkage disequilibrium is measured over 5N generations: linkage disequilibrium (LD) = V_A − V_g for genetic variance V_A and genic variance V_g of the log fitness (Keightley and Hill 1987). LD is the contribution to the genic variance of log fitness due to multilocus linkage disequilibrium (Bulmer 1980) and can be computed as above using the following terms for V_A and V_g,

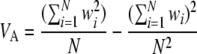(1)

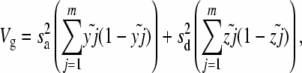(2)

where w_i is the log fitness of the ith chromosome in the population, given by s_ay_i − s_dz_i (for y_i, z_i, the advantageous and deleterious mutants, respectively, in genome i ∈ N). 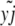, 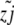are the number of genomes that a particular mutant appears in, divided by the total population size; that is, they are the frequencies of a segregating advantageous or deleterious mutant at locus j (with m segregating loci overall). Each locus has no more then two alleles segregating at any one time in this simulation.

For a population with recombination, a new mutant has a map position attributed to it drawn from a uniform [0, 1] distribution. During reproduction, the position of a crossover is drawn from the same distribution. If one crossover is chosen, allelic states are exchanged at sites where map position exceeds the recombination distance. If two crossovers occur, the states of loci are swapped where the mutant map position lies between the two crossover points. More than two crossovers are unlikely (the probability of more than two occurring is 0.00015, with L = 0.1); therefore only up to two exchanges are considered.

Measuring the strength of selection on a modifier:

To measure selection on a modifier, a modifier allele is introduced at a frequency of 50% into a population after a burn-in. Introducing the modifier at an intermediate frequency prevents its immediate loss (or fixation), which would otherwise bias our long-term estimate of selection by forcing it to equal zero for all generations following its premature loss (or fixation). After its introduction, a modifier is tracked for 200 generations or until it is fixed or lost. At each generation following its introduction the change in modifier frequency ΔM is noted, and selection on the modifier is estimated using the weak-selection equation s_M = ΔM/(p_Mq_M) (Barton 1995). The value of s_M at the 200th generation is taken as the overall strength of selection acting on the modifier. This is repeated for 5N modifiers per burn-in, so a distribution of average selection strengths is developed. This is repeated for 100 burn-ins.

Measuring N_e for asexual populations:

To estimate N_e, a neutral, linked locus is inserted into the genome at a random position (i.e., the possibility of it being telomeric or centromeric is allowed). This locus affects a quantitative trait, which has an initial effect of zero. After a burn-in, the effect of this locus is changed in each individual by adding Gaussian noise each generation with a mean of zero and variance V equal to one. It can be shown that the equilibrium variance should be VN_e for such a neutral trait (Lynch and Hill 1986). The simulation is left to run with Gaussian-distributed mutations occurring every generation at the neutral locus for a further 5N generations to reach equilibrium, at which point the variance (and N_e) is measured. Average N_e values from independent burn-ins are calculated to form an overall distribution.

RESULTS

Effects of advantageous mutations on a recombination modifier:

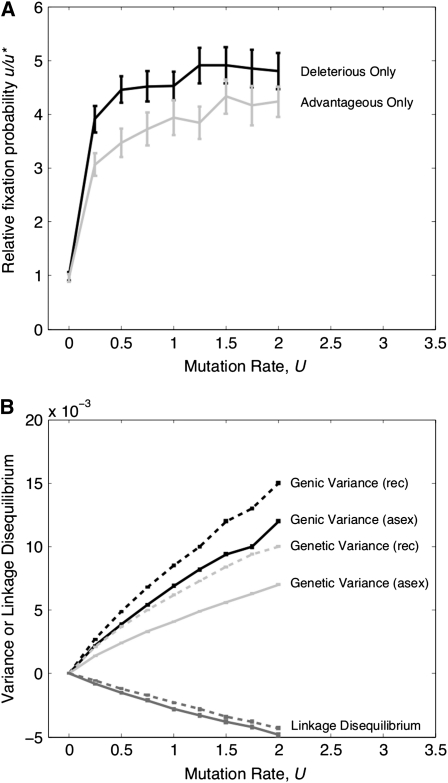
We first investigate the dynamics of a recombination modifier in the presence of different types of mutations (deleterious only, advantageous only, and both deleterious and advantageous). As observed by Keightley and Otto (2006), we found that the relative fixation probability of a modifier (u/u*) rises as N increases for all cases investigated. Also, u/u* > 1 for all simulations, indicating that a recombination modifier is always favored. Full results for all scenarios investigated are provided in supporting information, File S1.

Although advantageous mutants arise in our simulations at a low frequency (the proportion of advantageous mutants is x = k/s_a, so for s_a = 0.01 only 2.3% of mutations are advantageous), their occurrence still causes a high fixation rate of the modifier, even in the absence of deleterious mutations. For example, with an advantageous mutation rate of Ux = 0.0115 and s_a = 0.01, the relative fixation probability u/u* = 3.58 for N = 1000, which is only slightly lower than that observed with deleterious mutations only and U = 0.5. The extent to which beneficial mutations select for recombination is even greater in larger populations (for example, u/u* = 47.4 for N = 10,000), which is greater than the corresponding value for the deleterious mutations case and U = 0.5. By increasing s_a to 0.05 but holding constant the net effect of mutations by decreasing the beneficial mutation rate to Ux = 0.0023 (as x = k/s_a), recombination is even more favorable (e.g., u/u* = 81.9 for N = 10,000). So in the absence of deleterious mutations, recombination offers substantial benefits in aiding the fixation of recurrent advantageous mutants across multiple loci, especially in large populations.

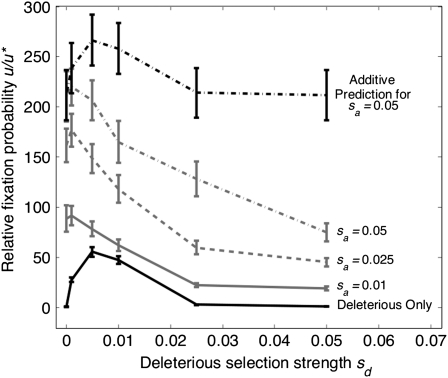
Figure 1 compares relative rates of recombination modifier fixation for cases with both advantageous and deleterious mutations present (for N = 25,000 and U = 0.1). We observe that the presence of advantageous mutations alongside deleterious mutations leads to a higher fixation probability of a recombination modifier than if mutations are solely deleterious. The highest u/u* of 220 occurs for the case of weakest selection against deleterious mutations, i.e., s_d ≈ 1/N, and strong selection in favor of advantageous mutants, i.e., s_a = 0.05. For stronger s_d, increased purifying selection acting against deleterious mutants leads to the loss of a larger fraction of advantageous mutations, reducing the extent to which they can contribute to Hill–Robertson interference (Charlesworth 1994; Peck 1994). Even if there are no advantageous mutations, strong purifying selection means that individuals carry few deleterious mutations in their genome; thus a recombination modifier behaves as more nearly neutral (e.g., u/u* = 1.32 with N = 25,000, s_d = 0.05, and U = 0.1, no advantageous mutation).

Figure 1.—

Relative fixation probability of a recombination modifier u/u* for N = 25,000 as a function of the strength of selection acting against deleterious mutants. Mutations are just deleterious or a mixture of deleterious and advantageous with strength s_a = 0.01, s_a = 0.025, or s_a = 0.05. These are compared to the expected u/u* if both deleterious mutants and advantageous mutants (s_a = 0.05) are present and u/u* is the sum of their independent fixation probabilities (with advantageous mutants only present, u/u* ∼210 with s_a = 0.05). The chromosomal mutation rate in all cases is U = 0.1. Bars are 95% confidence intervals here and throughout the article.

Such fixation probabilities may depend on the number of linked loci present (Iles et al. 2003). Consistent with this, we observe that the fixation probability rises as we increase the number of linked loci from 10 to 50 (Figure S1). However, it appears that fixation probabilities reach a plateau as the number of linked loci approaches 100, indicating that our simulations capture the maximum impact of Hill–Robertson in reducing the efficacy of selection, at least in the population sizes simulated.

With a combination of weak deleterious mutations and strong advantageous mutations, recombination offers a dual advantage, predominantly through the more efficient purging of deleterious mutants [stopping Muller's ratchet (Muller 1964; Felsenstein 1974) and reducing the mutation load (Keightley and Otto 2006)] but also by aiding the fixation of rare advantageous mutants [“Fisher–Muller” hypothesis (Fisher 1930; Muller 1932)]. The increase in modifier fixation with higher s_a is likely to arise because strongly favored mutants are likely to carry along with them many deleterious mutations in the absence of recombination (Peck 1994; Hadany and Feldman 2005) and recombination can free these advantageous mutations from their deleterious backgrounds. In line with this reasoning, Table 1 shows that for N = 1000 and U = 0.5, recombination aids the fixation of advantageous mutants and decreases the fixation rate of deleterious mutants in all cases simulated.

TABLE 1.

Number of fixed mutants

	Strength of deleterious mutations sd
Case	0.01	0.025	0.05
Only deleterious mutations
Asexual population	1260 (7.07)	823 (4.16)	471 (3.09)
Recombining population	644 (5.99)	314 (3.57)	107 (1.71)
Only advantageous mutations
Asexual population	195 (2.17)	161 (1.77)	159 (1.43)
Recombining population	378 (2.86)	362 (2.08)	371 (1.95)
Both deleterious and advantageous mutations
No. of deleterious fixed, asexual	1430 (8.88)	861 (5.09)	476 (3.14)
No. of deleterious fixed, recombining	985 (8.10)	393 (3.63)	125 (2.20)
No. of advantageous fixed, asexual	114 (1.91)	64.6 (1.54)	41.8 (1.27)
No. of advantageous fixed, recombining	269 (1.92)	149 (2.43)	90.1 (1.60)

The average number of mutants that fix over 5N generations for N = 1000 and U = 0.5 is given to three significant values. Cases considered are those where mutations are solely deleterious, advantageous only, or both deleterious and advantageous. Fixations are measured for an asexual population or a population with a constant rate of recombination. Note that if advantageous and deleterious mutants are present, the strength relates to s_d, with s_a = 0.05. Values in parentheses are 95% confidence intervals here and throughout the article. When measuring the number of mutants fixed with recombination, the population recombines throughout the burn-in.

Selection and fixation probabilities of a modifier:

We next asked whether the benefits of the modifier brought about by purging deleterious mutants and fixing advantageous mutants are additive; recall that this means that if the modifier has selection advantage s_Md if just deleterious mutations occurs at rate U_d, and advantage s_Ma if just advantageous mutations occurs at rate U_a, then if both types of mutations occur at a total rate of U_d + U_a the selective advantage is expected to equal s_Md + s_Ma. This is tested by comparing the selection coefficients at the 200th generation after the modifier is introduced for N = 1000, U = 0.5. Selection on the modifier is measured for three deleterious mutation strengths (s_d = 0.01, 0.025, and 0.05), where mutations are solely deleterious at rate U and again where both deleterious and advantageous mutations occur (with s_a = 0.05, U = 0.5). We also investigate the case where mutations are advantageous only (see points with s_d = 0; s_a = 0.05), which occurs at the reduced rate Ux = 0.0115.

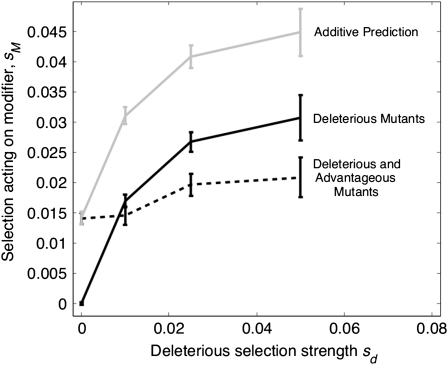
Results of this test are outlined in Figure 2. As with u/u*, if the number of linked loci under selection is increased, s_M values appear to reach a plateau as the number of loci approaches 100 (Figure S2). Whereas the addition of advantageous mutations enhances fixation of the modifier, the observed values of s_Mb (modifier strength when mutations are both advantageous and deleterious) fall short of the additive values, s_Md + s_Ma; in fact s_Mb < s_Md for all s_d > 0.01. s_Mb can exceed s_Md if the modifier is introduced at a low frequency (<10%) and s_d ≤ 0.1 (Figure S3); however, s_Mb still falls short of the additive prediction. These selection coefficients lie in contrast to the relevant fixation probabilities, u/u*, as these values increase if advantageous and deleterious mutants are present, compared to the deleterious only case. However, these fixation probabilities also act in a subadditive manner (see also File S1 and Figure 1). This decrease in s_M if advantageous and deleterious mutants are both present seems to verify the hypothesis that extra interference is present if two types of mutations are present together; breaking this down offers an increase. Selection on the modifier also increases with N (Figure S4), consistent with the hypothesis that a recombination modifier is more strongly selected for in larger populations.

Figure 2.—

Selective advantage of a modifier, s_M, inferred for cases where mutations are deleterious only and where mutations are deleterious and advantageous. This is compared to the “additive” prediction for the deleterious and advantageous case (s_M ≈ 0.013 if mutations are solely advantageous, which is the result for the deleterious and advantageous mutant case if s_d = 0). N = 1000, U = 0.5, s_a = 0.05 if present.

Interestingly, increasing s_d increases selection on the modifier, s_M, with or without advantageous mutations, whereas the fixation probability of the modifier u/u* decreases with s_d ≥ 0.01 in all simulations (Figure 1). The explanation of this paradoxical result is connected with changes in the effective population sizes N_e and how Hill–Robertson interference affects fixation of the modifier. The fixation probability of a new mutant is determined by its selection strength s and the effective population size N_e according to u = (1 − exp(−2sN_e/N))/(1 − exp(−2sN_e)) (Kimura 1983). By reducing N_e, Hill–Robertson effects can reduce the fixation probability of a new mutation (the recombination modifier in this case), even if it is more strongly favored (Table 2). With respect to a modifier, having more strongly selected deleterious mutations has a more dramatic impact on reducing N_e than increasing s_M, with the net result that the modifier is less likely to fix.

TABLE 2.

Estimates of sM and Ne

sd	Modifier sM	Ne	Pred. u/u*	Observed u/u*
Deleterious mutants only case
0.01	0.0170 (0.0010)	117.88 (8.41)	4.073	4.518
0.025	0.0268 (0.0016)	73.08 (4.36)	3.989	4.000
0.05	0.0308 (0.0034)	55.14 (2.95)	3.508	3.660
Deleterious and advantageous mutants case
0.01	0.0146 (0.0015)	97.62 (5.26)	3.021	5.206
0.025	0.0197 (0.0018)	72.48 (3.80)	3.026	4.456
0.05	0.0209 (0.0033)	52.29 (2.60)	2.460	3.900

s_M and N_e are measured for different scenarios investigated (N = 1000, U = 0.5, s_M plotted in Figure 2), along with predicted fixation rates based on these values using Kimura's formula (“Pred.”). These are compared to the fixation rate of the modifier u/u* obtained from simulations.

Whereas Kimura's formula offers accurate estimates of u/u* if mutations are deleterious, it underestimates fixation probabilities if advantageous mutants are present as well. It appears that selective sweeps alter N_e as mutations rise in frequency, by reducing fitness variance at linked sites (Maynard Smith and Haigh 1974), violating the assumption that N_e is constant at steady state. This result also suggests that the presence of Hill–Robertson effects can increase the fixation probability of a modifier, relative to that expected at a single locus. This could be due to recombination increasing fitness variance as a modifier rises in frequency (see below), increasing N_e from the value in an asexual population as interference is broken down.

Testing the effectiveness of the diffusion approximation in predicting modifier fixation rates:

The previous stochastic simulations are limited in the sense that they can be run only for population sizes that are small, compared to some of the large effective population sizes found in nature. To predict outcomes for larger N, we now investigate diffusion approximations. These predict that the behavior of a new mutant is left unchanged if N_eμ, N_es, and N_er are constant and small (note that we refer to μ, the per site mutation rate, as opposed to U, the per chromosome mutation rate; μ = U/100 and r is the recombination fraction between individual loci). The diffusion approximation should also hold if N_er is large and N_eμ and N_es are kept small but we do not focus on that situation here. A thorough overview of such work can be found in Ewens (2004) with an example provided by Gordo and Charlesworth (2000). However, the diffusion approximation may not hold for our simulation, since N_e changes with different mutation rates and increases with higher rates of recombination.

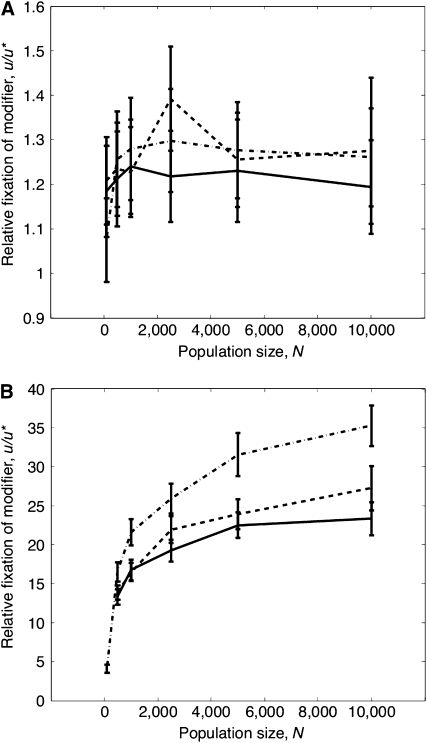
We decided to calculate u/u* for Nμ = 1, Ns = 5, and NL = 5 for all cases of mutation (deleterious only, advantageous only, and both deleterious and advantageous), to determine whether fixation is constant as a function of N. These results are plotted in Figure 3a: the graph shows that u/u* becomes approximately constant as a function of N, albeit at low values (∼1.25). This suggests that diffusion approximations might be useful as a guide to predict modifier behavior for larger N than is possible to simulate directly. However, as Figure 3b shows, u/u* increases nonlinearly with N if simulations are run for large Nμ = 10, NL = 1000, and Ns = 100. These parameter values are chosen so that U = 0.1, L = 0.1, and s = 0.01 if N = 10,000. The nonlinear estimates of u/u* obtained imply that we cannot extrapolate simulation results unless N is much larger if rates of mutation, recombination, and strength of selection are of these magnitudes (i.e., comparable to parameters observed for Drosophila). The observation that selection on the modifier is not invariant when Nμ, NL, and Ns are held constant but large could be either due to a breakdown in the diffusion approximations or due to changes in N_e caused by recombination reducing Hill–Robertson interference.

Figure 3.—

(a) u/u* as a function of N for fixed Nμ, Ns, and NL, which are of O(1) (μ is the per site mutation rate, μ = U/100) if mutations are deleterious (solid line), advantageous (dotted-dashed line) or deleterious and advantageous (dashed line). (b) u/u* as a function of N with Nμ, Ns, and NL fixed but they are no longer O(1).

Effects of variance and linkage disequilibrium on modifier selection:

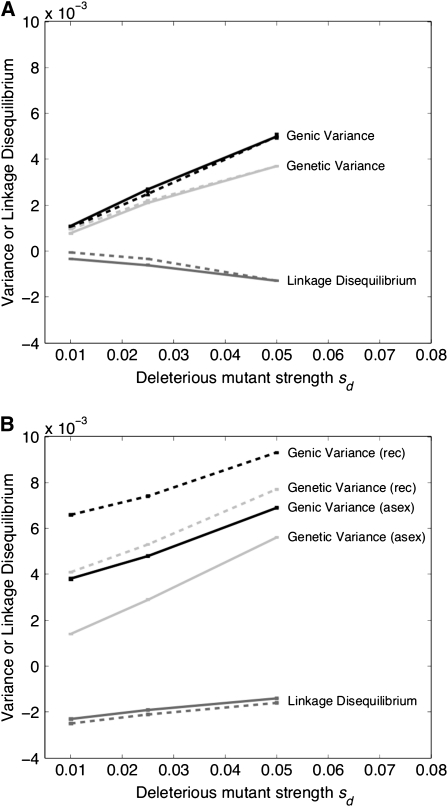
In this section, we investigate how linkage disequilibrium changes with recombination and whether these values relate to u/u*. Figure 4 compares the genic variance, genetic variance, and variance due to linkage disequilibrium in asexual and recombining populations for two mutational cases (deleterious only and deleterious and advantageous) for N = 5000 and U = 0.1. In both cases plotted, the genic and genetic variance is unchanged or it increases in the presence of recombination. With deleterious mutations only, the genetic variance is , the interference-free value of expected variance. If both advantageous and deleterious mutants segregate, the variance increases more substantially with recombination compared to the deleterious only case. By Fisher's fundamental theorem of natural selection, this increase in genetic variance should hasten the response to selection and improve the population mean fitness (Fisher 1930; Price 1972). Recombination is selected for through association with this rise in fitness.

Figure 4.—

Genic variance, genetic variance, and linkage disequilibrium for an asexual (solid lines) and a recombining (dashed lines) population. (a) The deleterious only case; (b) the advantageous and deleterious mutations case (with s_a = 0.05). N = 5000, U = 0.1.

In Figure 4, a and b, the magnitude of linkage disequilibrium is only slightly different in a recombining population. For s_d = 0.01–0.025, where modifier fixation is greatest, the magnitude of linkage disequilibrium increases by ∼10-fold if advantageous mutants are present alongside deleterious mutants, compared to the deleterious only case. This signifies a large amount of extra interference being created with the presence of advantageous mutations. However, there is not a one-to-one correspondence between increases in linkage disequilibrium and increases in u/u*. For example, with s_d = 0.05, u/u* is 11-fold higher in the presence of both advantageous and deleterious mutants than in the case with only deleterious mutants, despite there being little difference in the linkage disequilibrium present.

A possible explanation for this mismatch between the observed level of linkage disequilibrium and the fate of a modifier of recombination is that as recombination breaks down linkage disequilibrium, more advantageous alleles are rescued from poor genetic backgrounds, which increases their chance of establishment and creates extra interference. Due to this, the better predictor for the increase in modifier fixation rate is the increase in genic variance V_g within a population (Barton and Otto 2005). For example, with s_d = 0.01 genic variance increases by 0.0028 in a recombining population compared to an asexual population. If s_d = 0.05, the increase is only by a value of 0.0024. However, the corresponding fixation probability u/u* drops from 29.85 if s_d = 0.01 to 14.52 with s_d = 0.05. So although the difference in genic variance between an asexual and a recombining population decreases with stronger selection acting against deleterious mutants, the drop is not large enough to predict the steep decline in fixation probability associated with these parameter values.

Does the advantage of recombination continue to rise with U?

Interestingly, the relative fixation probability of a modifier does not rise linearly with the mutation rate (Figure 5a). This result holds even if the number of linked loci under selection is reduced (Figure S5a). This is unexpected, as one might assume that the fixation probability of a recombination modifier increases with higher U, since more mutants are produced that create extra interference between sites. One reason for this behavior is that as the mutation rate increases, the extent of Hill–Robertson interference also increases, reducing N_e and the spread of a modifier. Thus, even though selection on the modifier, s_M, rises with U (see Table 3 for the deleterious only case), the two effects cancel, leaving the fixation rate of the modifier relatively constant as U increases. s_M values are approximately equal to those shown if there are fewer linked loci under selection (Figure S5b).

Figure 5.—

(a) u/u* as a function of U if mutation is deleterious only and if mutation is advantageous only at rate Ux. N = 1000, s_d = s_a = 0.01. (b) Genic variance, genetic variance, and linkage disequilibrium as a function of U where mutations are deleterious only, for the same parameters. Populations are asexual (solid lines) or recombining (dashed lines).

TABLE 3.

Estimates of sM and Ne based on values at a neutral locus and predicted/observed u/u* values as a function of U

U	Modifier sM	Ne	Predicted u/u*	Observed u/u*
0.25	0.0119 (0.00067)	145.79 (4.51)	3.575	3.91
0.50	0.0172 (0.00097)	114.78 (3.28)	4.018	4.46
0.75	0.0213 (0.0010)	103.54 (3.11)	4.455	4.52
1.00	0.0220 (0.0013)	94.83 (2.77)	4.229	4.53
1.25	0.0230 (0.0016)	88.05 (2.61)	4.114	4.91
1.50	0.0240 (0.0017)	83.23 (2.34)	4.062	4.91
1.75	0.0250 (0.0017)	78.77 (2.03)	4.009	4.85
2.00	0.0254 (0.0018)	75.48 (2.12)	3.912	4.80

N = 1000, s_d = 0.01.

This argument is supported by investigating the underlying genetic and genic variances (Figure 5b). As U increases, the rise in the magnitude of genic variance with recombination becomes larger, indicating greater selection for the modifier. However, the magnitude of linkage disequilibrium also increases due to the presence of more segregating polymorphisms, which will drive down the effective population size. Thus, while one might expect Hill–Robertson effects to select for recombination in direct proportion to the mutation rate, genetic interference is, to a large extent, self-limiting, and we see a strong diminishing returns relationship that tapers off once chromosomewide mutation rates reach ∼U = 1.

DISCUSSION

In this article we show that for mutation rates and mean selection strengths that are representative of what is known in Drosophila, the presence of advantageous mutations can lead to substantial selection on a modifier for recombination. As Figure 1 demonstrates, the highest advantages occur if s_d is low and s_a is high. Hence the low rate of adaptive amino acid substitutions observed in Drosophila is capable of aiding the evolution of recombination and can help to account for its widespread occurrence.

That said, the addition of advantageous mutations alongside deleterious mutations increases the fixation of a modifier in a subadditive fashion (File S1 and Figure 1). This demonstrates that whereas there can be a pluralist advantage on recombination in fixing beneficial alleles as well as purging deleterious mutants, the benefit gained from aiding selective sweeps is not as great as we might have expected if assuming that the modifier acts on deleterious mutants and advantageous mutants independently. This arises due to extra interference being created by deleterious mutants causing the loss of beneficial mutants, as highlighted in Table 1.

This study also offers insight into how to best measure the rate of evolution of a recombination modifier in the presence of Hill–Robertson interference. Figure 2 shows that a recombination modifier can be strongly selected for if introduced at 50% frequency; however, due to the high levels of Hill–Robertson interference present (Table 2), it has a fixation rate that is only slightly higher than that of a neutral mutant (u/u* = 1.32). This suggests that measuring the strength of selection acting on a strong modifier can be misleading, since it does not take into account how Hill–Robertson interference impedes the spread of a beneficial mutant. This interference is broken down as a modifier increases in frequency in an initially asexual population, increasing N_e over time. However, if there was already some recombination present in the population, or if the modifier is weak, then N_e would not appreciably change, so s_M might offer accurate insight into the fate of a recombination modifier in these cases.

We also demonstrate that whereas it is theoretically possible to extrapolate fixation values of the modifier for larger N from fixation rates for small N using diffusion models, these assumptions will hold best if the values Ns, Nμ, and Nr are of O(1), which predict small rates of modifier fixation. Using larger N and parameter values, diffusion approximations break down, and thus we have to resort to full simulation.

By examining the genic and genetic variance in the simulations (Figure 4), we observe that negative linkage disequilibrium is created, which is indicative of Hill–Robertson interference (Hill and Robertson 1966). Recombination increases genetic variance in fitness within a population, in line with existing theory on the evolution of a recombination modifier in the presence of drift (Barton and Otto 2005). These results, however, highlight an important point that even though linkage disequilibrium is indicative of interference, the magnitude of it does not determine the change in frequency of a modifier (Barton 1995; Barton and Otto 2005). This is exemplified if s_d = 0.05, where linkage disequilibrium values are similar in the presence and absence of beneficial mutants, yet modifiers of recombination are more strongly favored in the latter case. This is because a particular level of genomewide linkage disequilibrium (measured by V_A − V_g) can arise when there are many segregating deleterious mutations (in which case, advantageous mutations are unlikely to fix) or when there are few segregating deleterious mutations and more advantageous mutations are able to establish.

Overall, this study demonstrates how beneficial mutations provide strong selection for a recombination modifier. However, there are a few caveats associated with the parameters used in this study, which should be investigated further to determine the full extent of the evolution of a recombination modifier.

Values of s_a used in these simulations are higher than those inferred for amino acid substitutions in Drosophila, to prevent drift overwhelming mutations for small population sizes that we investigate. Using smaller values of s_a will certainly reduce the fixation probability of the modifier, at least for the population sizes investigated in these simulations.

Dominance in diploid deleterious mutations is also not considered here. Roze (2009) showed how, if deleterious mutants are highly recessive, recombination is selected against, because breaking apart multilocus heterozygosity incurs fitness disadvantages, especially if selection on the mutations is weak. Future work should investigate how the presence of advantageous mutations affects this result, although such a study is likely to strongly rely on the dominance of beneficial mutations, which is only poorly known.

The strength of selection on adaptive mutations also depends on the organism under observation and the state of its environment. Relative fitness differences in Drosophila can be reduced if their populations are dense or if there is a lack of available food (Kondrashov and Houle 1994). On the other hand, in bacteria and viruses, advantageous mutants with larger fitness effects have been observed in stressed environments [on the order of s = 5 (Barrett et al. 2006) or even s = 12 (Bull et al (2000)]. Bearing all this in mind, the effects on a modifier over a larger range of selection parameters should be investigated.

These results also offer predictions as to when recombination can evolve. If an organism moves to a new environment to which it is maladapted, our model predicts that higher rates of recombination are more likely to arise in this new environment. Furthermore, if background deleterious mutations are frequent, recombination has an extra advantage in aiding purifying selection and is even more likely to evolve than in the presence of beneficial mutations alone. Such a scenario was discussed by Hadany and Feldman (2005) and could explain why recombination is more likely to occur in new, stressed environments (Abdullah and Borts 2001; Grishkan et al. 2003).

Finally, we did not investigate whether the advantages to a recombination modifier in the presence of advantageous mutants transfer over to a sex modifier. This requires an adjusted model to account for the costs of sex (Maynard Smith 1978) and to ensure that excessive inbreeding is avoided (if rare sexuals can mate only with other sexuals). This is a well-known problem with regard to the evolution of sex (see, for example, Peck 1993) and we will investigate this in a future research article.