Skip to main content
PMC home page
Cognitive Neurodynamics logoLink to Cognitive Neurodynamics
. 2010 Apr 27;4(2):119–131. doi: 10.1007/s11571-010-9111-3

Electrophysiological correlates of listening effort: neurodynamical modeling and measurement

Daniel J Strauss 1,4,✉, Farah I Corona-Strauss 1,4, Carlos Trenado 1, Corinna Bernarding 1, Wolfgang Reith 2, Matthias Latzel 3, Matthias Froehlich 3
PMCID: PMC2866367  PMID: 21629585

Abstract

An increased listing effort represents a major problem in humans with hearing impairment. Neurodiagnostic methods for an objective listening effort estimation might support hearing instrument fitting procedures. However the cognitive neurodynamics of listening effort is far from being understood and its neural correlates have not been identified yet. In this paper we analyze the cognitive neurodynamics of listening effort by using methods of forward neurophysical modeling and time-scale electroencephalographic neurodiagnostics. In particular, we present a forward neurophysical model for auditory late responses (ALRs) as large-scale listening effort correlates. Here endogenously driven top–down projections related to listening effort are mapped to corticothalamic feedback pathways which were analyzed for the selective attention neurodynamics before. We show that this model represents well the time-scale phase stability analysis of experimental electroencephalographic data from auditory discrimination paradigms. It is concluded that the proposed neurophysical and neuropsychological framework is appropriate for the analysis of listening effort and might help to develop objective electroencephalographic methods for its estimation in future.

Keywords: Listening effort, Modeling, Auditory evoked potentials, Wavelets, Gabor frames, Phase synchronization, Single sweeps

Introduction

An increased listening effort represents a major problem in patients with hearing impairment (Hicks and Tharpe 2002; Pichora-Fuller and Singh 2006). In the area of auditory habilitation and rehabilitation, digital signal processing has revolutionized the hearing aid technology during the last decade. Modern digital hearing aids offer vast fitting capabilities, allowing an high degree of adjustment to the needs of the individual patient, see Edwards (2007) for a survey. The utilization of this adjustment capabilities to reduce the listening effort in the individual patient is a major concern in hearing aid fitting. However, especially in non-cooperative patients, fitting procedures which preferably require a minimum cooperation of the patient are still missing and the objective estimation of the listening effort based on auditory processing correlates is an unsolved problem (Pichora-Fuller and Singh 2006; Edwards 2007).

Rather isolated past research mainly deals with double stimulation paradigms using finite resources/capacity cognitive models (Downs 1982; Rakerd et al. 1996). Here the patients have to solve a primary task related to speech discrimination and a secondary task involving their (motor) reaction time to another secondary visual stimulus, see Downs (1982), Rakerd et al. (1996) and Larsby et al. (2005) for a more recent review. However these paradigms require an increased patient cooperation, they are influenced by many non-listening effort related factors, and are a priori based on a crossmodal design, moving the focus away from the auditory modality.

Recent research pointed out the importance of non-audiological variables for hearing aid fitting, in particular, for modern and flexible digital devices, see Kricos (2000) and Pichora-Fuller and Singh (2006). Edwards (2007) identified the potential of advances in hearing science and cognition for radical innovations in future hearing aid technologies. Pichora-Fuller and Singh (2006) highlighted the importance of neuroscience research related to attention and cognitive effort estimation for hearing aid fitting and audiologic rehabilitation. Very recently, Shinn-Cunningham and Best (2008) reviewed the role of selective attention in normal and hearing impaired listeners. In particular, these authors discussed how hearing impairment may degrade selective attention.

In this paper, we present a systems neuroscience approach to the problem of listening effort. In particular, we develop a neuropsychological and neurophysical framework and propose a scheme for the objective listening effort estimation by electrophysiological methods. The model predictions are verified by measured experimental data using auditory late responses (ALRs).

This paper is organized as follows: in section “Methods” we describe the used techniques, starting with a probabilistic auditory scene analysis (ASA) framework for listening effort in section “A probabilistic auditory scene analysis framework”. The developed ASA framework is coupled in section “Corticofugal modulation and auditory late responses” with ALRs as large-scale correlates of a listening effort driven endogenous modulation. In this section we also sketch the mathematical model which is employed for the computational simulation of ALRs. In section “Subjects and experimental paradigms” we present our paradigms, measurement setups, and subjects used in our experiments. Section “Forward and inverse phase stability analysis” introduces the applied ALR analysis techniques. In order to make the paper accessible to wide audience, it skips many mathematical details in section “Methods” which focuses more on a systems level explanation. However, for the sake of technical correctness and consistency, elaborated neurobiological mappings, technicalities, and mathematical details are provided in the “Appendix”. In section “Results” the computational and experimental results are presented and in detailed discussed in section “Discussion”. Section “Conclusion” finally summarizes our conclusions of the presented study.

Methods

For the sake of a better reading and flow of the paper, we just present the fundamental equations in this section. Technicalities and necessary reviews are summarized in the “Appendix”.

A probabilistic auditory scene analysis framework

Listening Effort: Kiessling et al. (2003) described hearing as a passive function that provides access to the auditory world via the perception of sound, primarily useful to describe impairment by audiometry methods whereas listening was defined as the process of hearing with intention and attention which requires the expenditure of cognitive demands or cognitive effort. Let us now discuss listening from a bidirectional bottom–up/top–down auditory processing point of view.

Auditory Scene Analysis: Several computational theories have been developed to augment the bottom–up sensory processing with top–down feedback mechanisms, e.g., see Grossberg (1976), Mumford (1992), Ullman (1995), Friston (2005) and references therein. Employing schema based information stored in memory and driven by, e.g., expectation, experience, and emotions, these models generate predictions on higher processing areas which are projected to lower processing areas to influence the bottom–up information flow (Grossberg 1976).

Let us focus on top–down projections in the auditory modality. According to Bregman’s ASA (Bregman 1990), the processing of exogeneous information reaching conscious states involves an analytical and a synthetical stage: the perceptual stimuli are decomposed into discrete sensory elements in the analytical stage; the sensory elements that are likely to have arisen from the same acoustical source are recombined into a perceptual stream in a process called auditory grouping (synthetical stage). In auditory grouping, we can differentiate between exogenous (primitive) and endogenous (schema-driven) grouping. Exogenous grouping is a purely data-driven process. Endogenous grouping utilizes the top–down projections mentioned before.

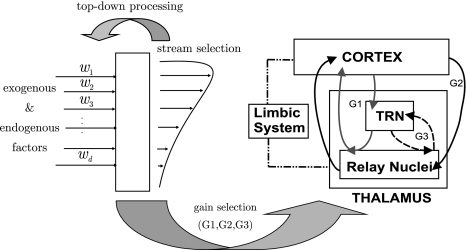
Exogeneous and automatic processing is considered to be not under conscious control, fast, parallel, and fairly effortless. On the other hand, endogenous and controlled processing is considered to be serial, slow, of limited capacity, and effortful (Kahneman 1973). Accordingly, a sketch of a probabilistic model of auditory stream selection that we developed in Trenado et al. (2009) is shown in Fig. 1 (left). The d-dimensional vector w = (w1, w2, …, wd) denotes abstract weights of the segregated streams according to their assigned probability of getting selected (highest to lowest). The selection probability depends on exogeneous (e.g., physical stimulus attributes) and endogenous factors. As listening is defined as an auditory process with intention and attention, we assume that it represents an effortful endogenous modulation of w in this scheme. Several of such effortful tasks are reviewed in Shinn-Cunningham and Best (2008), for instance, perceptual filling such as auditory induction and phonemic restoration. Also the use of memory in serial stream scanning [see Shinn-Cunningham and Best (2008) and references therein] belongs to these tasks.

Fig. 1.

Fig. 1

Open in a new tab

Simplified probabilistic model of the auditory stream selection

A common complaint of the hearing impaired is that listening in noisy situations is an exhausting experience, and a hearing impaired person is far more tired after some time in such a setting than someone with normal hearing (Edwards 2007). In noisy situations, there are many competing auditory streams. It could be argued that a distorted auditory system is of course less effective in automatic ASA processes, especially, exogeneous processes and needs more endogenous modulation and effort, e.g., expectations driven by the semantic context of a stream which would be in agreement to the findings of Edwards (2007), Pichora-Fuller and Singh (2006), and Shinn-Cunningham and Best (2008). In particular, Shinn-Cunningham and Best (2008) highlighted that the ability to selectively attend depends on the ability to analyze the acoustic scene and form perceptual auditory objects properly. Thus a degraded internal representation, e.g., a missing fine structure, would result automatically in an increased effort as the automatic stream formation is degraded due to the missing auditory atoms.

Corticofugal modulation and auditory late responses

Attention Correlates in ALRs: The N1 (also called N100) component of ALRs is influenced by exogenous and endogenous factors and is frequently used in experimental paradigms related to auditory attention, e.g., Hillyard et al. (1973), Näätänen et al. (1978), Näätänen (1979), and Janata (2001). This wave is assumed to reflect selective attention to basic stimulus characteristics, initial selection for later pattern recognition, and intentional discrimination processing. Its amplitude is enhanced (becomes more negative) by increased attention to the stimuli (Hillyard et al. 1973). The strict separation of endogenous active (or voluntary) attention and exogeneous passive (or involuntary) attention components is controversy discussed in literature. A major issue is whether the N1 component is directly modulated by attention as suggested first by Hillyard et al. (1973) or whether there are reflections of an early processing negativity in the typical N1 window and the N1 wave itself is not influenced by attention (Näätänen et al. 1978). In the first case, an endogenous top–down component is directly reflected in the N1 wave whereas in the latter case an endogenous processing negativity component is superimposed to exogenous event related potential components. The processing negativity was considered as an reflection of the orientation to an auditory stream and its primitive analysis (Näätänen 1979).

Recently we have analyzed large-scale correlates of attention by an instantaneous phase stability measure of ALR single sweeps (Strauss et al. 2005, 2008a; Low et al. 2007) and shown how these correlates are related to endogenous and effortful corticofugal modulations using large-scale ALR simulations by means of a model of corticothalamic feedback dynamics (Trenado et al. 2008). Partly, we have been able to map the obtained results to the problem of objective listening effort estimation in Strauss et al. (2008b).

Systems Neuroscience Approach: Focusing on the architecture of our model, the weights w of segregated streams are modulated by means of three corticofugal gains G1, G2, and G3 as shown in Fig. 1 (right). G1 takes positive and negative values regarding the regulatory effect in the corticofugal flux of information from the auditory cortex to the medical geniculate body through the thalamic reticular nucleus (TRN). Gain G2 takes positive values mainly emphasizing the excitatory effects on cortex and thalamus, while gain G3 represents the inhibitory effect of the TRN to the dorsal thalamus. A more detailed neurobiological mapping of these gains to the hearing pathway is given in the “Appendix A1”.

The mapping of stream probability weights wk (k = 1, …, d) in our ASA scheme, see section “A probabilistic auditory scene analysis framework”, into a specific gain interval [ai, bi] was conducted by means of a transformation of the form Gi = ai(1 − wk) + biwk (i = 1, 2, 3). The three gains correspond to the neurophysiological connectivity in the following way: The modulation of the gains G1, G2, and G3 is accomplished by means of a corticothalamic transfer function ξ that represents the activity between cortical excitatory e and inhibitory i neural populations phie,i, and subcortical incoming auditory stimuli An(·, ·), as given by

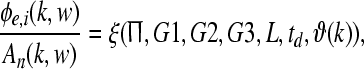graphic file with name M1.gif

where the function ξ incorporates the dendritic low-pass filtering effects L, corticofugal time delays td, amplitude modulation 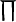Inline graphic , and a dispersion relation 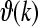Inline graphic that describes the mean field cortical pulse-wave propagation of the average response of populations of neurons (Robinson et al. 2005). Following Robinson et al. (2005), the response to an auditory stimulus An(·, ·) by considering the excitatory neural population as the main source of large-scale brain activity, is represented by 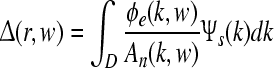Inline graphic. Here 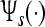Inline graphic is a function that comprises parameters related to the auditory stimulus, while the domain D represents a finite two dimensional approximation of the unfolded human cortex. ALRs as large-scale electroencephalographic responses are obtained by the inverse Fourier transform of the function 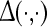Inline graphic. Based on implications of thalamic modulation as precursor for controlling attention, ALRs were simulated by varying corticothalamic loop gains and adding white gaussian noise to emulate the spontaneous activity (Raichle and Gusnard 2005). Technical details and references of this computational model are given in “Appendix A3”.

Effortful Corticofugal Modulation: Based on our numerical results in Trenado et al. (2009), this forward ALR model predicts a larger phase synchronization stability of the sweeps (see section “Subjects and experimental paradigms”) for an increased top–down endogenous modulation of the bottom–up data in the range of the N1 wave in ALRs, resulting in stable gains especially G1. This mechanism of synchronization of cortical and thalamic components needs a stable feedback control. The oscillation of the thalamocortical system must be adapted to incoming sensory events. The hub of this synchronization process is most likely the TRN. Many indications point toward this structure forming a thin veil that covers most of the dorsal thalamus and separates it from the cortex (Zikopoulos and Barbas 2006). In the searchlight hypothesis, Crick (1984) stated a key role for the TRN in attentional processes. Grossberg and Versace (2008) proposed a model incorporating functional roles for both specific and unspecific projections of the TRN, in which the inhibitory projections to the thalamic relay nuclei provide an anatomical matching of Grossberg’s adaptive resonance theory (ART). They also state a top–down on-center pathway from cortical layer 6 to the thalamic relay nuclei, supported by a TRN-mediated off-surround (Grossberg and Versace 2008) analogue to the spotlight hypothesis as indicated by some authors (Zikopoulos and Barbas 2006).

Physiologically, TRN might mediate synchronization processes due to the strong interconnection of TRN-cells by electrical synapses and additional inhibitory interneurons for inhibition normalization (Grossberg and Versace 2008), receiving also driving input from two processing stages. This gate-keeping function of the TRN depends highly on the physiological state of the TRN cells. This functional activation of the TRN is dominated by cortical top–down projections but also influenced by cholinergic and monoaminergic bottom–up projections from the brainstem, regulating the membrane potential of the TRN cells (Zikopoulos and Barbas 2007). Behavioral evidence for the important role of the TRN in corticofugal modulation is given by Wesse et al. (1999). They could demonstrate an impairment in the selection of relevant targets in an attentional orienting task after lesions in the visual sector of the TRN.

Subjects and experimental paradigms

Tone Study (TS): For the first experimental setup, subjects were student volunteers from the Saarland University and Saarland University of Applied Sciences with normal hearing. A total of 20 subjects (mean age: 27, standard deviation: 4.1; 9 female, 11 male) entered the study. ALR single sweeps were recorded using a commercially available amplifier (g.tec USBamp, Guger Technologies, Austria) and electrodes were placed at the left and right mastoid, the vertex, and the upper forehead. Electrodes impedances were below 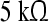Inline graphic in all measurements (filter: 1–30 Hz, sampling frequency: 512 Hz). Artifacts where removed by an amplitude threshold of 50 μV.

Two different studies with two different paradigms were used. The paradigms had a distinct degree of difficulty to solve an auditory task. This difficult tone paradigm (DP) and easy tone paradigm (EP) are explained below.

For DP we delivered 3 pure tones (1, 1.3 and 1.6 kHz) at 70 dB (SPL) of 40 ms duration each in random order to the right ear at randomized inter-stimulus interval (ISIs) of 1–2 s. Meanwhile, the left ear was presented with music which played the role as distractor. Subjects were required to pay attention to the stimulus and detect the target tone which was the 1.3 kHz stimulation.

For EP we delivered just 2 pure tones (0.5, 1.3 kHz) at 70 dB (SPL) of 40 ms duration each in random order to the right ear at randomized inter-stimulus interval (ISIs) of 1–2 s. As before, the left ear was again presented with relaxing music. Subjects were required to pay attention to the stimulus and detect the target tone which was the 1.3 kHz stimulation.

The randomized stimulation paradigms were used to maximize the entropy of the experiment such that their solution requires an effortful task. The rational for DP and EP is that solving DP requires more effort than solving EP. The subjects had to push a button after a target tone had been recognized. The number correctly identified target tones also served as control of the cooperation of the subject (the included subjects had a correct hit rate of more than 80%). For the numerical analysis in section “Results”, we considered just ALRs that were evoked by the target tone as it had the same frequency in both paradigms.

Syllable Study (SS): For the second experimental setup, subjects were student volunteers from the Saarland University and Saarland University of Applied Sciences with normal hearing. A total of 10 subjects (mean age: 27, standard deviation: 3.23; 4 female, 6 male) entered the study. ALR single sweeps were recorded using the very same system as for TS.

Two paradigms with a distinct degree of difficulty to solve a syllable detection task were used. The difficult syllable paradigm (DSP) and easy syllable paradigm (ESP) are explained below.

  • syllables: /pa/, /da/, /ba/, considered as “difficult syllable paradigm (DSP)”

  • syllables: /pa/, /de/, /bi/, considered as “easy syllable paradigm (ESP)”

We delivered the syllables at 50 dB (SPL) to the right ear, embedded in multi-talker babble noise (SNR: +5 dB) at randomized inter-stimulus interval (ISIs) of 1–2 s and in a randomized order (as before for TS). The syllables had a duration of 200 ms (rise and fall time: 25 ms). In both paradigms DSP and ESP, the target syllable was /pa/. The subjects had to push a button after a target syllable had been recognized. The number correctly identified targets also served as control of the cooperation of the subject (the included subjects had a correct hit rate of more than 80%).

Forward and inverse phase stability analysis

In this section, we introduce the scheme for the forward and inverse analysis of the instantaneous phase of ALRs. We focus here on the core equation and refer the reader to the “Appendix A2” for a technical definition of the time-scale analysis tools employed here, namely, the continuous complex wavelet transform (CCWT) and tight Gabor frames (TGFs).

Phase Synchronization Stability: Using a phase clustering analysis on the unit circle [e.g., see Dobie and Wilson (1989), Lachaux et al. (1999), and Varela et al. (2001)], we have recently shown that the stability of the instantaneous phase can be used to efficiently monitor auditory attention in maximum entropy paradigms (Low et al. 2007).

Given the sequence 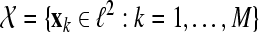Inline graphic of M ALR single sweeps, we define the phase synchronization stability by the following equation

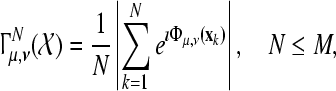graphic file with name M9.gif 1

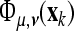where Inline graphic represents the instantaneous phase, depending on the scale parameter μ and the time parameter ν. In the case of the CCWT we obtain the wavelet phase synchronization stability (WPSS) by 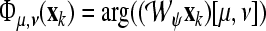Inline graphic , where Inline graphic is a discrete-time version of the wavelet operator to the wavelet ψ as defined in Eq. 2 (“Appendix A2”). 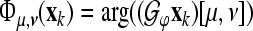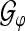For the TGFs we obtain the Gabor frame phase stability (GFPS) by Inline graphic , where Inline graphic is the tight Gabor frame analysis operator to the generating function φ as defined in Eq. 5 and “Appendix A2”.

Forward Analysis: The WPSS is well localized in time and frequency using the Heisenberg adaptivity of the wavelets, i.e., a large support in time for low frequencies with a good frequency resolution and small support (good localization) in time for high frequency components. The scale parameter can be associated with the frequency by fμ = fψ/Tμ, where T is the sampling period and fψ is the center frequency of the wavelet ψ (Abry 1997).

As for the analysis of ALRs related to N1 wave modulations by attention (Strauss et al. 2008a), we use the WPSS for the forward analysis by Eq. 1 in this study with μ = 40 which corresponds to the α/θ-border (6–9 Hz) for the chosen wavelet [the 6th derivative of the complex Gaussian function as in Strauss et al. (2008a)].

It is easy to see that the synchronization stability as evaluated by the wavelet phase stability in Eq. 1 is a value in [0, 1]. We have a perfect synchronization stability for a particular μ′ and ν′ for 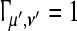Inline graphic (perfectly coherent phases) and a decreasing stability for smaller values due to phase jittering.

Phase Stability Modification: The GFPS provides a uniform decomposition of the ALR single sweep frequency band such that each modulation parameter μ can be directly associated with a frequency band in Hz (see “Appendix A2”). In contrast to the highly redundant CCWT, TGFs may provide a very efficient analysis as well synthesis of the analyzed signal using the very same function, e.g., see Søndergaard (2007) an references therein. Note that although the δ-distribution reconstruction allows also for a fast inverse CCWT (Farge 1992), it is not possible to use the same function for the inverse transform as in the case of TGFs in a computationally efficient way. However, the price that we have to pay is a fixed resolution in the time-frequency domain.

For the experiments in our study, we used a tight window generated from the Gaussian function with 128 modulations and ν = 1. Note that these values result in an overcomplete Gabor frame decomposition, see “Appendix A2”, with m = 0, 1, …, M − 1.

In order to show the effect of a stable instantaneous ALR phase in the time domain, we employ TGFs for an artificial phase stabilization/modification in the following manner: we use the analysis operator 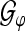Inline graphic for the analysis of ALR single sweeps. Then we introduce an artificial phase stabilization, i.e., we restrict the phase to a particular interval in order to modify the GFPS in this way. Subsequently, we use the TGF synthesis operator 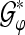Inline graphic (see “Appendix A2”) to reconstruct the phase modified ALRs. The average of the reconstructed signals provides then the phase stabilized time domain representation of the averaged ALR.

Let us describe the phase modification a bit more formally: we denote the averaged instantaneous phase for sample n of the N ALR sweeps by ξn. The phase for sample n of the analytic signal of each sweep is now adjusted by mapping it to the range [ξn, ξn + δ] where δ represents a possible (controlled) phase noise factor which we set to 0.0 for the numerical experiments in this study. In this way, we have the possibility for an inverse analysis of the phase stability effect in ALR single sweep sequences. Note that it is advantageous to use the Hilbert transform of the individual ALR sweeps instead of the ALRs itself as we can restrict our interest to positiv frequencies exclusively. The reconstructed signal is then just the real part of the synthesized complex signal, e.g., see Oppenheim and Schafer (1989) for concept of analytic signals obtained from the Hilbert transform.

Results

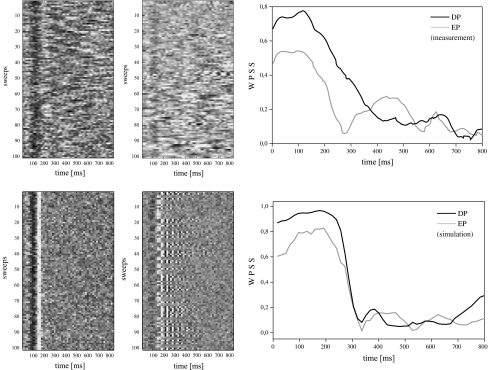
Effort & Phase Synchronization: In Fig. 2 (top, left) we have shown a time domain matrix representation of M = 100 ALR single sweeps for one subject solving DP and EP, respectively. Each row of the matrix represents one sweep. The amplitude is mapped to colors so that black corresponds to the smallest amplitude and white to the largest amplitude. The corresponding WPSS of the data sets is shown in Fig. 2 (top, right). In Fig. 2 (bottom, left) we have shown M = 100 simulated ALR sweeps in the very same way as for the measured data. The WPSS of these simulated data sets is shown in Fig. 2 (bottom, right). It can be seen that the DP data sets exhibit a more clear trace of the N1 and P2 wave than the ones in the EP condition, for both, the measured and the simulated data. In the EP data sets, the trace is more blurred. The WPSS of the DP data sets is larger than for the EP data sets, especially in the N1 and P2 wave range. Note that the WPSS is associated with larger effortful endogenous modulation according to our discussion in section “Corticofugal modulation and auditory late responses”.

Fig. 2.

Fig. 2

Open in a new tab

Left: Time domain matrix representation of ALR single sweeps for measured (top) and simulated (bottom) data obtained during DP and EP. The normalized amplitude is encoded in a grayscale so that black corresponds to the smallest and white to the largest amplitude. Right: The WPSS for the matrices at the left

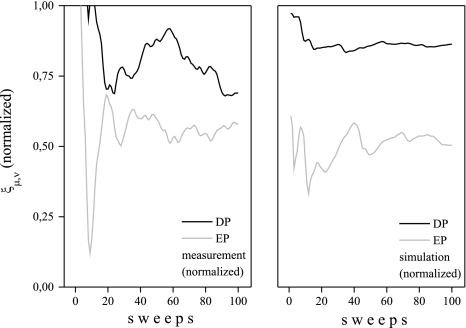
In Fig. 3 we have shown the evolution of the WPSS for an increasing number of sweeps of one subject as example. More precisely, we used Eq. 1 to obtain the (discrete) function 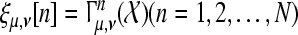Inline graphic with N = 100,  μ = 40, and ν corresponding to 110 ms, i.e., a sample from the N1 wave range.

Fig. 3.

Fig. 3

Open in a new tab

The evolution of the WPSS over the sweeps as represented by the function ξμ,ν[·] (slightly smoothed for this graph and normalized)

It is noticeable that the WPSS provides a robust discrimination of DP and EP data sets, even for a small number of sweeps for the measured and simulated data. However, in the simulated condition, the oscillatory behavior is of course different due to the highly simplified noise model.

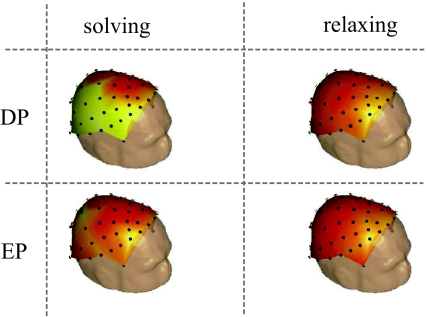
Topological Mapping: In Fig. 4 we have shown a topological mapping of the WPSS for 100 sweeps in a paradigm/condition matrix using a 64 channel recording from one subject as example. The matrix shows the WPSS for solving DP and EP and for relaxing during the DP and EP stimulation, i.e., not solving the paradigms. It is noticeable that the WPSS is much larger in temporal and parietal areas while solving the DP as compared to the solution of EP and the relaxed condition, respectively.

Fig. 4.

Fig. 4

Open in a new tab

Topological mapping of the WPSS for 100 sweeps in a paradigm/condition matrix using a 64 channel recording. The rows represent the WPSS while stimulating with DP and EP. The columns represent the WPSS while solving the paradigm and a relaxing condition. Normalized scale for WPSS: black/dark red (0) to white/light yellow (1)

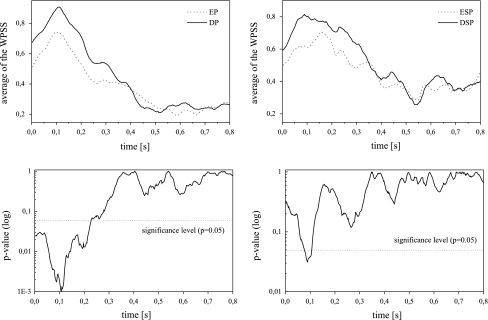
Difficult/Easy Discrimination: Figure 5 (top, left) shows the grand average (averaged over all the subjects) of the ipsilateral WPSS in Eq. 1 for a sequence of N = 100 sweeps per subject and paradigm, respectively. It is noticeable that the WPSS is much larger for the DP than for the EP, especially in the expected interval (see sections “Corticofugal modulation and auditory late responses” and “Subjects and experimental paradigms”). In Fig. 5 (bottom, left) we have shown the results for the time resolved (one-way) ANOVA (over the subjects to evaluate the significance of the grand average in the plot above). It is noticeable that in the interval of interest (see section “Corticofugal modulation and auditory late responses”) of the N1 and P2 wave in ALRs, we have significant differences between the EP and DP condition. A similar result is obtained for the syllable analysis, i.e., ESP vs. DSP, see Fig. 5 (top, right) and Fig. 5 (bottom, right). This shows that the increased effort to solve the more difficult paradigm is reflected in an increased WPSS of ALR sequences. We refer to Vidal et al. (2005) for a detailed discussion of the morphological time domain difference between tone and syllable evoked potentials.

Fig. 5.

Fig. 5

Open in a new tab

Top: Grand average of the WPSS (over all the subjects) for the different paradigms. Bottom: The results for the time resolved ANOVA (left: TS, i.e., EP vs. DP; right: SS, i.e., ESP vs. DSP)

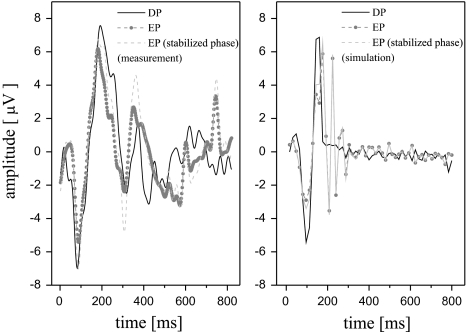
Artificial Phase Modification: In Fig. 6 we have shown the results of an experiment using the phase modification and synthesis approach described in section “Forward and inverse phase stability analysis”. In particular, we have shown the averaged time domain waveform (using N = 100 sweeps) for a DP and EP data set. The EP data set was phase stabilized at the α/θ-border and synthesized. The α/θ-border corresponds here approximately to scale 40 in the WPSS experiments before. It is noticeable that the average of the ALR single sweep set Inline graphic in the EP condition with this small band phase correction shows a large correlation to the DP data set in the N1 and P2 wave range.

Fig. 6.

Fig. 6

Open in a new tab

The averaged time domain ALRs for the DP and EP as well as EP with an artificial phase stabilization for measured (in one subject as example, left) and simulated (right) data

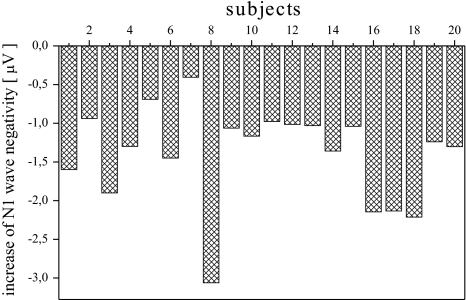
In Fig. 7 the increase of the N1 wave negativity after the phase stabilization for all the subjects (mean increase of the negativity: −1.4047 μV; standard deviation: 0.6208 μV). It is noticeable that the phase stabilization results in a larger N1 negativity for all the subjects and thus has a crucial influence on the N1 amplitude for the experimental data.

Fig. 7.

Fig. 7

Open in a new tab

The increase of the N1 negativity after the artificial phase stabilization in the EP data for all the subjects

Discussion

Neurodynamics and Listening Effort. Although there is no doubt on the importance of non-audiological variables for hearing rehabilitation (Pichora-Fuller and Singh 2006; Edwards 2007; Kricos 2000), research related to the cognitive neuroscience of listening effort is still in its infancy. Moreover, objective electrophysiological procedures for the listening effort estimation are not available up to now.

Using systems neuroscience, we tried to develop a first neuropsychological and neurophysical framework of listening effort and its objective estimation by electroencephalographic methods. In particular, we mapped a recently proposed model of corticothalamic feedback dynamics for neural correlates of auditory selective attention (Trenado et al. 2009) to the problem of listening effort in an ASA framework. With a phase synchronization stability measure that we have recently proposed to assess the endogenous modulation due to auditory attention by single sweeps of ALRs (Trenado et al. 2009; Low et al. 2007), the experimental results confirmed the model prediction. More precisely, an increased and effortful endogenous modulation results in larger phase synchronization of ALR single sweeps in the N1 and P2 wave range. By means of this measure, we found significant differences in the WPSS in the interval of interest of experimental data sets obtained during a two different multiple (pure) tone paradigms (DP and EP) which required a graduated effort for their solution. The experimental results resembled the simulated data.

Pichora-Fuller and Singh (2006) highlighted the importance of neuroscience research related to attention and cognitive effort estimation for hearing aid fitting and audiologic rehabilitation. Very recently, Shinn-Cunningham and Best (2008) reviewed the role of selective attention in normal and hearing impaired listeners using ASA arguments that follow (Bregman 1990). In particular, these authors discussed how hearing impairment may degrade selective attention. The discussion of these authors is in line with the presented probabilistic ASA stream selection framework to define the corticothalamic gain parameters G1, G2, and G3 in the sense that endogenous modulation has to complement a degraded automatic exogenous stream formation, see section “A probabilistic auditory scene analysis framework”. Thus the presented results also reinforce the ASA discussions of Shinn-Cunningham and Best (2008).

ERPs are on one hand considered as the time-locked, stimulus-locked, and synchronized activity of a group of neurons that adds to the background electroencephalographic activity. On the other hand, the evoked responses are regarded as a reorganization of the ongoing EEG. According to this view, ERP can be generated by a selective and time-locked enhancement of a particular frequency band or at least in part by a phase resetting of ongoing frequencies, see Sauseng et al. (2007) and references therein. A comprehensive review on ERP genesis was given in Sauseng et al. (2007) where evidence for both models (evoked and phase reset models) was presented. The question of the ERP generation has not yet been convincingly answered although some evidence showed that the mixture of both mechanisms is most probable.

In Fig. 6 we have shown that an artificial phase reset significantly changes the time domain morphology of the waveform—interestingly in way, such that a phase corrected (the the α/θ–border) EP data resembles DP data. For the simulated data based on a neurophysical model which is not based on the phase reset of ongoing oscillation this could not be shown in the presented example. However, solving this issue is beyond the scope of this paper.

Other ALR Components: The presented study focuses on “early” ALRs components (N100 and P200 wave) and corticothalamic interactions. Later ALR components, e.g., the P300 [see Polich (2007) and references therein], the N400 or P600 wave (Kotz et al. 2005) might also form a substrate for the analysis of listening effort related variables, the latter two especially for the analysis of semantic integration. However, these components depend on a variety, partly very individual factors (Polich 2007; Kotz et al. 2005) which have to be considered in the design of experimental paradigms. A first analysis of “later” ALR components with respect to listening effort in streaming experiments can be found in Corona-Strauss et al. (2010).

For a possible model integration of such later components, the presented model has to be complemented by other computational models which focus on corticocortical projects, e.g., see Husain et al. (2004), Husain et al. (2005). Beside later cortical integration, the inclusion of recent experimental evidence of (very) early corticofugal modulation of subthalamic processing units (Suga et al. 2002) in the presented model is also an interesting direction of further research from a theoretical point of view. Such effects can also be represented in an implicit way by dynamically modulating the input to the presented model.

Limitations and Future Work: From an applied and clinical point of view, the used experimental paradigms are of course not designed for hearing rehabilitation procedures. They are rather designed to maximize the required effort and to minimize secondary factors due to stimulus variations, e.g., different background noise and physical stimulus characteristics. Indeed, the analyzed ALRs in our study where evoked by the very same stimulus in the DP and EP condition. Thus keeping this secondary effects as small as possible was a constraint for this first inverse experimental and forward computational study.

However, we showed that the experimental data resembles the model predictions and that ALRs might provide access to listening effort related variables in electrophysiological data. The design of paradigms that are appropriate for auditory rehabilitation using this framework is a major objective of our further research.

Conclusions

We have introduced a systems neuroscience approach to the problem of listening effort. By coupling a probabilistic model of auditory stream selection with a neurophysical framework for the simulation of auditory late potentials depending on listening effort driven endogenous modulations, we showed that listening effort correlates can be assessed by the instantaneous phase stability of auditory late potential sequences. Our experimental results verified the model predictions.

It is concluded that the proposed neurophysical and neuropsychological framework forms a first step to analyze the cognitive neurodynamics of listening effort correlates. It might help to develop objective electroencephalographic methods for its estimation in future.

Appendix

A1: Map of the gain parameters to the hearing path

The corticothalamic feedback dynamics in our model is represented by three different gains which we map to the hearing path in the following.

Gain G1: The auditory cortex projects indirectly to thalamic reticular nucleus (TRN) by means of axon-collaterals of corticothalamic projections. Additionally the TRN receives inhibitory input from dorsal thalamic nuclei. Thus, the TRN provides an inhibitory influence on the specific thalamus cores, namely the medial geniculate body (MGB) in the case of auditory evoked potentials. The target of TRN projections are the ventral and the medial subnuclei of MGB. The ventral subnucleus (VMGB) is specific for auditory processing, while the medial subnucleus (MMGB) receives also information from non-auditory pathways. The VMGB projects to anterior auditory field (AAF), the posterior auditory field (PAF) and the primary (A1) auditory cortex, the MMGB projects to the ipsilateral parts of the primary (A1), and the secondary (A2) auditory cortex, and to the ipsilateral posterior PAF and the anterior AAF auditory fields.

Gain G2: The auditory cortex projects directly to all the subnuclei of MGB, namely VMGB, MMGB, and the dorsal geniculate body (DMGB), which also gets informational input from earlier stages of the auditory pathway. Back projection to the cortex occurs as described above plus efferent projections from the dorsal subnucleus (DMGB) to the auditory cortex.

Gain G3: As described above the auditory cortex projects indirectly to the TRN by means of axon-collaterals of corticothalamic projections. The TRN has no efferent fibres projecting towards the auditory cortex, but is part of a thalamocortical feedback loop. The TRN receives additional input by axon-collaterals of thalamocortical projections. Due to its inhibitory influence on specific thalamus cores (i.e. MGB) the TRN can directly regulate information flow from thalamus to cortical areas.

A2: Wavelet and gabor frame phase synchronization

Wavelet Phase Synchronization Stability: We follow our definition of the WPSS as in Strauss et al. (2008a). Let 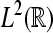Inline graphic denote the Hilbert space of all square integrable functions, i.e., 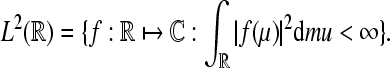Inline graphic Let further ψa,b(·) = |a|−1/2ψ((· − b)/a) where 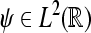Inline graphic is the wavelet with 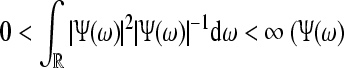Inline graphic is the Fourier transform of the wavelet), and 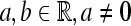Inline graphic. The wavelet transform

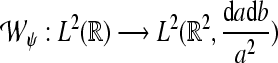graphic file with name M25.gif 2

of a signal 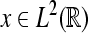Inline graphic with respect to the wavelet ψ is given by the inner L2-product 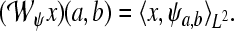Inline graphic In the following, we restrict our interest to discrete time systems and signals such that all signals are represented by sequences. For the sake of a handy notation, we denote the index of the individual sequence elements as argument in square brackets. Let 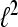Inline graphic denote the Hilbert space of all square summable sequences, i.e., 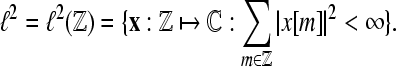Inline graphic To compute the WPSS for such sequences in 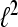Inline graphic rather than continuous time signals in 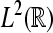Inline graphic, we used the discretization scheme of Misiti et al. (2000).

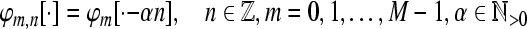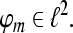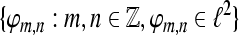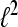Tight Gabor Frames: We restrict our interest in the following further to time-invariant systems of the form Inline graphic where Inline graphic A set Inline graphic is called a frame for Inline graphic if

graphic file with name M36.gif 3

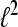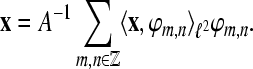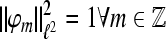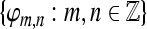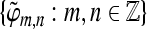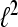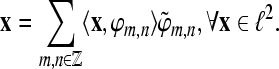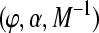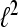For A = B the frame is called a tight frame for Inline graphic and we have the expansion Inline graphic If Inline graphic and A = 1 we obtain orthonormal expansions and for A > 1 the expansion becomes overcomplete and A reflects its redundancy. Two frames Inline graphic and Inline graphic for the Hilbert space Inline graphic are called dual frames if Inline graphic A Gabor system Inline graphic for Inline graphic is defined as

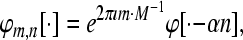graphic file with name M46.gif 4

i.e, the system represents a family of sequences which are generated by one particular sequence due to modulation and translation. A Gabor system that is also a frame for 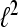Inline graphic is called a Gabor Frame for 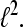Inline graphic For αM−1 > 1 the system is undersampled and cannot be a basis or a frame for 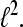Inline graphic For αM−1 = 1 we have the critically sampled case and, if the Gabor system represents a frame, it is also a basis. For α M−1 < 1 we have the oversampled case and the Gabor system cannot be a basis but a frame.

Tight Gabor frames have been constructed in Søndergaard (2007), Strohmer (1999). For a tight Gabor frame 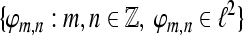Inline graphic and an index set 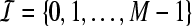Inline graphic , we define the analysis operator by

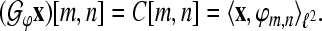graphic file with name M52.gif 5

We define synthesis operator with respect to the tight Gabor frame by

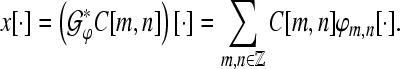graphic file with name M53.gif 6

The described Gabor decompositions can also efficiently be implemented by oversampled uniform band discrete Fourier transform filter banks as shown in Bölcskei et al. (1998).

A3: Mathematical model of corticothalamic feedback

What follows is based on the large-scale evoked potential theory proposed in Robinson et al. (1997, 2005) and Rennie et al. (2002) adapted to our discussion in sections “A probabilistic auditory scene analysis framework” and “Corticofugal modulation and auditory late responses”.

According to Freeman (1991), within a neuron the relationship between the rate of incoming pulses from excitatory or inhibitory neurons Qae or Qai and their corresponding soma potentials Ve or Vi, can be obtained by an impulse response equation of the form,

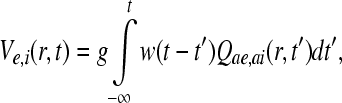graphic file with name M54.gif 7

where w(u) is a causal weight function with a characteristic width that satisfies

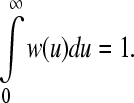graphic file with name M55.gif

As stated in Robinson et al. (1997), a suitable choice for w(u) is given by

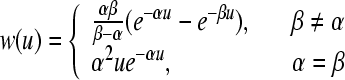graphic file with name M56.gif 8

for u > 0, where α and β represent the rise and decay times of the cell-body potential produced by an impulse at a dendritic synapse. By combining Eqs. 7 and 8 for the case β ≠ α, the mean field soma potential Va (a = e, i excitatory and inhibitory), representing the synaptic inputs from various types of afferent neurons that are summed after being filtered and smeared out in time as a result of receptor dynamics and passage trough the dendritic tree, is governed by the following equation

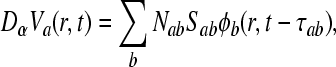graphic file with name M57.gif 9

where

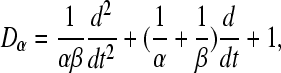graphic file with name M58.gif 10

Nab is the average number of synapses from neurons of type b = e, i, s on neurons of type a = e, i, where s stands for subcortical, Sab represents the magnitude of postsynaptic potentials, ϕb represents fields of incoming pulses and τab are synaptic time delays.

In accordance to Rennie et al. (2002), the mean firing rate Qa related to cell-body potential Va is given by a sigmoidal-type function

graphic file with name M59.gif 11

where θa is the mean firing threshold of neurons of type a, σa is the standard deviation of this threshold in the neural population, and Qmax is the maximum attainable firing rate.

An assumption that reflects the large-scale effect of neural populations is that each part of the corticothalamic system produces a field ϕa of pulses, which travels at a velocity va through axons with a characteristic range ra. Approximately such pulses propagate according to the damped-wave equation

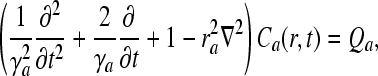graphic file with name M60.gif 12

where γa = va/ra. The simulation of auditory evoked cortical streams S is achieved by using a thalamic stimulus An(k, w) of angular frequency w and wave vector k, which for convenience is chosen to be a unit Gaussian in time and space (centered at t0s and r0s with standard deviations ts and rs), together with a function Cl(k, w) which refers to an excitatory cortical activity of a short-range neural population with local connectivity, to define a corticothalamic transfer function

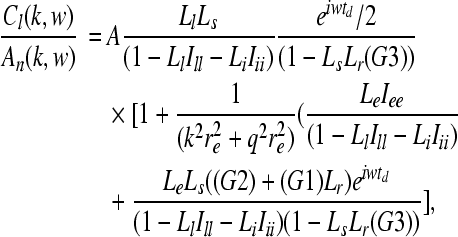graphic file with name M61.gif

in which td represents the time delay between thalamus and cortex, A represents an amplitude scaling factor, G1, G2, and G3 are the relevant corticofugal and intrathalamic gains, Lz represents a dendritic transfer function that exerts a low pass filtering effect as given by

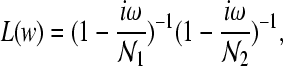graphic file with name M62.gif 13

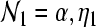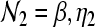where Inline graphic and Inline graphic, and Ixy stands for secundary gain factors. The indices for the parameters x, y, z = e, i, l, s, n, r denote e excitatory, i inhibitory, l excitatory cortical neurons with local axons, s excitatory thalamic neurons in specific and secondary relay nuclei, n excitatory afferents to thalamus, and r inhibitory thalamic reticular neurons. The response to the thalamic stimulus is given by

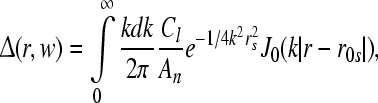graphic file with name M65.gif 14

and the desired evoked potential streams can be obtained by using

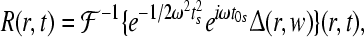graphic file with name M66.gif 15

here J0 denotes the bessel function of first kind, and 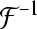Inline graphic denotes the inverse Fourier transform, see Rennie et al. (2002) for more details.

References

  1. Abry P (1997) Ondelettes et turbulence. Multirésolutions, algorithmes de décomposition, invariance d’échelles. Diderot Editeur, Paris
  2. Bregman AS. Auditory scene analysis. Cambridge: MIT Press; 1990. [Google Scholar]
  3. Bölcskei H, Hlawatsch F, Feichtinger HG. Frame-theoretic analysis of oversampled filter banks. IEEE Trans Signal Process. 1998;46:3256–3268. doi: 10.1109/78.735301. [DOI] [Google Scholar]
  4. Crick F. Function of the thalamic reticular nucleus: the searchlight hypothesis. Proc Natl Acad Sci USA. 1984;81:4586–4590. doi: 10.1073/pnas.81.14.4586. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Corona-Strauss FI, Bernarding C, Latzel M, Strauss DJ (2010) Auditory streaming and listening effort: an event related potential study (submitted) [DOI] [PubMed]
  6. Downs DW. Effects of hearing aid use on speech discrimination and listening effort. J Speech Hear Disord. 1982;47:189–193. doi: 10.1044/jshd.4702.189. [DOI] [PubMed] [Google Scholar]
  7. Dobie RA, Wilson MJ. Analysis of auditory evoked potentials by magnitude-squared coherence. Ear Hearing. 1989;10:2–13. doi: 10.1097/00003446-198902000-00002. [DOI] [PubMed] [Google Scholar]
  8. Edwards E. The future of hearing aid technology. Trends Amplif. 2007;11:31–45. doi: 10.1177/1084713806298004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Farge M. Wavelet transforms and their applications to turbulence. Annu Rev Fluid Mech. 1992;24:395–457. doi: 10.1146/annurev.fl.24.010192.002143. [DOI] [Google Scholar]
  10. Freeman WJ. Induce rhythms of the brain. Basel: Birkhauser; 1991. [Google Scholar]
  11. Friston K. A theory of cortical responses. Philos Trans R Soc Lond B Biol Sci. 2005;360:815–836. doi: 10.1098/rstb.2005.1622. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Grossberg S. Adaptive pattern classification and universal recoding: I. Parallel development and coding in neural feature detectors. Biol Cybern. 1976;23:121–134. doi: 10.1007/BF00344744. [DOI] [PubMed] [Google Scholar]
  13. Grossberg S, Versace M. Spikes, synchrony and attentive learning by laminar thalamocortical circuits. Brain Res. 2008;1218:278–312. doi: 10.1016/j.brainres.2008.04.024. [DOI] [PubMed] [Google Scholar]
  14. Hicks CB, Tharpe AM. Listening effort and fatigue in school-age children with and without hearing loss. J Speech Lang Hear Res. 2002;45:573–584. doi: 10.1044/1092-4388(2002/046). [DOI] [PubMed] [Google Scholar]
  15. Hillyard SA, Hink RF, Schwent VL, Picton TW. Electrical signs of selective attention in the human brain. Science. 1973;182:177–180. doi: 10.1126/science.182.4108.177. [DOI] [PubMed] [Google Scholar]
  16. Husain FT, Tagamets MA, Fromm SJ, Braun AR, Horwitz B. Relating neuronal dynamics for auditory object processing to neuroimaging activity: a computational modeling and an fMRI study. Neuroimage. 2004;21(4):1701–1720. doi: 10.1016/j.neuroimage.2003.11.012. [DOI] [PubMed] [Google Scholar]
  17. Husain FT, Lozito TP, Ulloa A, Horwitz B. Investigating the neural basis of the auditory continuity illusion. J Cogn Neurosci. 2005;17(8):1275–1292. doi: 10.1162/0898929055002472. [DOI] [PubMed] [Google Scholar]
  18. Janata P. Brain electrical activity evoked by mental formation of auditory expectations and images. Brain Topogr. 2001;13:169–193. doi: 10.1023/A:1007803102254. [DOI] [PubMed] [Google Scholar]
  19. Kahneman D. Attention and effort. Englewood Cliffs: Prentice Hall; 1973. [Google Scholar]
  20. Kricos PB. The the influence of nonaudiological variables on audiological rehabilitation outcomes. Ear Hear. 2000;21:7S–14S. doi: 10.1097/00003446-200008001-00003. [DOI] [PubMed] [Google Scholar]
  21. Kotz SA, Cramon DY, Friederici AD. On the role of phonological short-term memory in sentence processing: Erp single case evidence on modality-specific effects. Cogn Neuropsychol. 2005;22:931–958. doi: 10.1080/02643290442000400. [DOI] [PubMed] [Google Scholar]
  22. Kiessling J, Pichora-Fuller MK, Gatehouse S, Stephens D, Arlinger S, Chisolm T, Davis AC, Erber NP, Hickson L, Holmes A, Rosenhall U, Wedel H. Candidature for and delivery of audiological services: special needs of older people. Int J Audiol. 2003;42(Suppl 2):2S92–101. [PubMed] [Google Scholar]
  23. Lachaux J-P, Rodriguez E, Martinerie J, Varela FJ. Measuring the phase synchrony in brain signals. Hum Brain Mapp. 1999;8:194–208. doi: 10.1002/(SICI)1097-0193(1999)8:4&#x0003c;194::AID-HBM4&#x0003e;3.0.CO;2-C. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Larsby B, Hällgren M, Lyxell B, Arlinger S. Cognitive performance and perceived effort in speech processing tasks: effects of different noise backgrounds in normal-hearing and hearing-impaired subjects. Int J Audiol. 2005;44:131–143. doi: 10.1080/14992020500057244. [DOI] [PubMed] [Google Scholar]
  25. Low YF, Corona-Strauss FI, Adam P, Strauss DJ (2007) Extraction of auditory attention correlates in single sweeps of cortical potentials by maximum entropy paradigms and its application. In: Proceedings of the 3rd international IEEE EMBS conference on neural engineering, Kohala Coast, pp 469–472
  26. Mumford D. On the computational architecture of the neocortex II. The role of the cortico-cortical loops. Biol Cybern. 1992;65:241–251. doi: 10.1007/BF00198477. [DOI] [PubMed] [Google Scholar]
  27. Misiti M, Misiti Y, Oppenheim G, Poggi J-M. MATLAB-Wavelet Toolbox, Version 2.0. Natick, MA: The Mathworks Inc.; 2000. [Google Scholar]
  28. Näätänen R. Early seelctive attention effects on the evoked potential: a critical review and reinterpretation. Biol Pychol. 1979;8:81–136. doi: 10.1016/0301-0511(79)90053-X. [DOI] [PubMed] [Google Scholar]
  29. Näätänen R, Gaillard AWK, Mäntysalo S. Early selective auditory attention effect on evoked responses reinterpreted. Acta Psychol. 1978;42:313–329. doi: 10.1016/0001-6918(78)90006-9. [DOI] [PubMed] [Google Scholar]
  30. Oppenheim AV, Schafer RW. Discrete-time signal processing. Englewood Cliffs: Prentice Hall; 1989. [Google Scholar]
  31. Polich J. Updating P300: an integrative theory of P3a and P3b. Clin Neurophysiol. 2007;118:2128–2148. doi: 10.1016/j.clinph.2007.04.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Pichora-Fuller MK, Singh G. Effects of age on auditory and cognitive processing: implications for hearing aid fitting and audiologic rehabilitation. Trends Amplif. 2006;10:29–59. doi: 10.1177/108471380601000103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Raichle ME, Gusnard DA. Intrinsic brain activity set the stage for expression of motivated behavior. J Comp Neurol. 2005;493:167–176. doi: 10.1002/cne.20752. [DOI] [PubMed] [Google Scholar]
  34. Rakerd B, Seitz PF, Whearty M. Assessing the cognitive demands of speech listening for people with hearing losses. Ear Hear. 1996;17:97–106. doi: 10.1097/00003446-199604000-00002. [DOI] [PubMed] [Google Scholar]
  35. Rennie CJ, Robinson PA, Wright JJ. Unified neurophysiological model of eeg spectra and evoked potentials. Biol Cybern. 2002;86:457–471. doi: 10.1007/s00422-002-0310-9. [DOI] [PubMed] [Google Scholar]
  36. Robinson PA, Rennie CJ, Rowe DL, O’Connor SC, Gordon E. Multiscale brain modelling. Philos Trans R Soc Lond B. 2005;360:1043–1050. doi: 10.1098/rstb.2005.1638. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Robinson PA, Rennie CJ, Wright JJ. Propagation and stability of waves of electrical activity in the cerebral cortex. Phys Rev E. 1997;56:826–840. doi: 10.1103/PhysRevE.56.826. [DOI] [Google Scholar]
  38. Søndergaard PL. Gabor frames by sampling and periodization. Adv Comput Math. 2007;27:355–373. doi: 10.1007/s10444-005-9003-y. [DOI] [Google Scholar]
  39. Shinn-Cunningham BG, Best V. Selective attention in normal and impaired hearing. Trends Amplif. 2008;12:283–299. doi: 10.1177/1084713808325306. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Sauseng P, Klimesch W, Gruber WR, Hanslmayr S, Freunberger R, Doppelmayr M. Are event-related potential components generated by phase resetting of brain oscillations? A critical discussion. Neuroscience. 2007;146:1435–1444. doi: 10.1016/j.neuroscience.2007.03.014. [DOI] [PubMed] [Google Scholar]
  41. Strauss DJ, Delb W, D’Amelio R, Falkai P (2005) Neural synchronization stability in the tinnitus decompensation. In: Proceedings of the 2rd international IEEE EMBS conference on veural engineering, Arlington, pp 186–189
  42. Strauss DJ, Delb W, D’Amelio R, Low YF, Falkai P. Objective quantification of the tinnitus decompensation by synchronization measures of auditory evoked single sweeps. IEEE Trans Neural Syst Rehabil Eng. 2008;16:74–81. doi: 10.1109/TNSRE.2007.911086. [DOI] [PubMed] [Google Scholar]
  43. Strauss DJ, Corona-Strauss FI, Froehlich M (2008b) Objective estimation of the listening effort: towards a neuropsychological and neurophysical model. In: Conference proceedings of the IEEE engineering in medicine and biology society, vol 1, pp 1777–1780 [DOI] [PubMed]
  44. Strohmer S (1999) Rates of convergence for the approximation of dual shift-invariant systems in l2(z). J Appl Fourier Anal Appl 5:599–615
  45. Suga N, Xiao Z, Ma X, Ji W. Plasticity and corticofugal modulation for hearing in adult animals. Neuron. 2002;36:9–18. doi: 10.1016/S0896-6273(02)00933-9. [DOI] [PubMed] [Google Scholar]
  46. Trenado C, Haab L, Strauss DJ. Multiscale modeling of auditory attention: forward modeling of large-scale neural correlates in evoked potentials. IEEE Trans Neural Syst Rehabil Eng. 2008;17:46–52. doi: 10.1109/TNSRE.2008.2010469. [DOI] [PubMed] [Google Scholar]
  47. Trenado C, Haab L, Strauss DJ. Corticothalamic feedback dynamics for neural correlates of auditory selective attention. IEEE Trans Neural Syst Rehabil Eng. 2009;17:46–52. doi: 10.1109/TNSRE.2008.2010469. [DOI] [PubMed] [Google Scholar]
  48. Ullman S. Links sequence seeking and counter streams: a computational model for bidirectional information flow in the visual cortex. Cereb Cortex. 1995;5:1–11. doi: 10.1093/cercor/5.1.1. [DOI] [PubMed] [Google Scholar]
  49. Varela F, Lachaux JP, Rodriguez E, Martinerie J. The brainweb: phase synchronization and large-scale integration. Nat Rev Neurosci. 2001;2:229–239. doi: 10.1038/35067550. [DOI] [PubMed] [Google Scholar]
  50. Vidal J, Bonnet-Brilhaut F, Roux S, Bruneau N. Auditory evoked potentials to tones and syllables in adults: evidence of specific influence on N250 wave. Neurosci Lett. 2005;378:145–149. doi: 10.1016/j.neulet.2004.12.022. [DOI] [PubMed] [Google Scholar]
  51. Wesse GD, Phillips JM, Brown VJ. Attentional orienting is impaired by unilateral lesions of the thalamic reticular nucleus in the rat. J Neurosci. 1999;19:10135–10139. doi: 10.1523/JNEUROSCI.19-22-10135.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Zikopoulos B, Barbas H. Prefrontal projections to the thalamic reticular nucleus form a unique circuit for attentional mechanisms. J Neurosci. 2006;26:7348–7361. doi: 10.1523/JNEUROSCI.5511-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Zikopoulos B, Barbas H. Circuits formultisensory integration and attentional modulation trough the prefrontal cortex and the thalamic reticular nucleus in primates. Rev Neurosci. 2007;18:417–438. doi: 10.1515/revneuro.2007.18.6.417. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Cognitive Neurodynamics are provided here courtesy of Springer Science+Business Media B.V.

RESOURCES