Divisive normalization in olfactory population codes

Abstract

In many regions of the visual system, the activity of a neuron is normalized by the activity of other neurons in the same region. Here we show that a similar normalization occurs during olfactory processing in the Drosophila antennal lobe. We exploit the orderly anatomy of this circuit to independently manipulate feedforward and lateral input to second-order projection neurons (PNs). Lateral inhibition increases the level of feedforward input needed to drive PNs to saturation, and this normalization scales with the total activity of the olfactory receptor neuron (ORN) population. Increasing total ORN activity also makes PN responses more transient. Strikingly, a model with just two variables (feedforward and total ORN activity) accurately predicts PN odor responses. Finally, we show that discrimination by a linear decoder is facilitated by two complementary transformations: the saturating transformation intrinsic to each processing channel boosts weak signals, while normalization helps equalize responses to different stimuli.

Sensory neurons are selective for specific stimulus features. For example, a neuron in primary visual cortex may be sensitive to both the spatial location and the orientation of a stimulus. Similarly, the preferred stimulus of an olfactory neuron is defined by the molecular features of the odors that are effective at driving that neuron. Stimuli with nonpreferred features often have an inhibitory effect on a sensory neuron. The earliest illustrations of this principle came from studies of neurons in the Limulus eye (Hartline et al., 1952) and vertebrate retina (Barlow, 1953; Kuffler, 1953). These neurons respond best to light at a particular spatial location, and responses to light at the best position can be suppressed by simultaneously illuminating other locations. This concept was later extended to features other than spatial location. For example, it was observed that in primary visual cortex, a neuron's response to a grating with a preferred orientation can be suppressed by superimposing a nonpreferred orientation (Morrone et al., 1982).

The idea linking these findings is that a neuron's response to a preferred stimulus feature is inhibited by adding nonpreferred stimulus features. This phenomenon can be understood as a form of “gain control”, defined as a negative feedback loop which keeps the output of a system within a given range. It has been proposed that this type of gain control in the visual system works by performing a divisive normalization of neural activity (Heeger, 1992). According to the divisive normalization model, the response of a neuron to a complex stimulus is not the sum of its responses to each stimulus feature alone. Rather, the response is divided by a factor related to the total “stimulus energy”, which increases with stimulus intensity and complexity. For this reason, the response of a neuron to a complex stimulus is closer to an average of its responses to each feature.

A fundamental question is how gain control alters the response of a neuron to its preferred stimuli. A neuron's response to preferred stimuli is generally nonlinear, with intense preferred stimuli driving the neuron to saturation. It is important to define whether gain control scales the input to this function (thus making it more difficult to reach saturation), or the output of this function (diminishing the strength of the saturated response). Both forms of gain control seem to occur in visual processing and attentional control (Albrecht and Geisler, 1991; Cavanaugh et al., 2002; Williford and Maunsell, 2006; Reynolds and Heeger, 2009). Another important question is what cellular and circuit mechanisms form the substrate of this process. At least in some classic examples of gain control in visual processing, there is a clear role for lateral inhibition (Kuffler, 1953; Hartline et al., 1956).

One reason why these questions have been difficult to resolve is the complexity of the underlying circuits. Ideally, one would like to selectively manipulate feedforward excitation and lateral inhibition to the neuron one is recording from. From this perspective, the Drosophila antennal lobe is a useful preparation because of its compartmental organization (Figure 1A). All the olfactory receptor neurons (ORNs) that express the same odorant receptor project to the same glomerulus in the brain, where they make excitatory synapses with projection neurons (PNs). Each PN receives ORN input from one glomerulus and lateral inputs from other glomeruli (Bargmann, 2006). A PN's odor responses are disinhibited by silencing input to other glomeruli (Olsen and Wilson, 2008; Asahina et al., 2009), implying that lateral interactions are mainly inhibitory. This could explain the observation that a PN's response to an odor can be inhibited by adding a second odor that is ineffective at driving that PN when presented alone (Deisig et al., 2006; Silbering and Galizia, 2007). Similar mixture suppression effects occur in the vertebrate olfactory bulb (Kang and Caprio, 1995; Giraudet et al., 2002; Tabor et al., 2004).

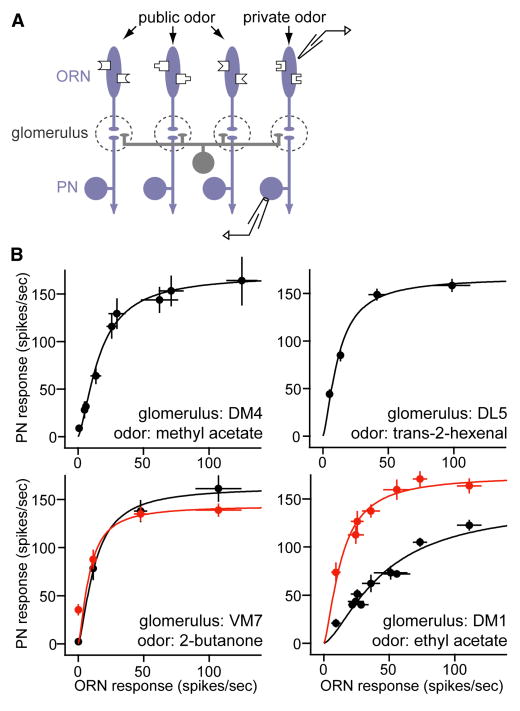
Figure 1. A generalized intra-glomerular transformation.

A. Experimental design. Varying the concentration of a private odor stimulus activates one ORN type to varying degrees. Recordings are performed from both these ORNs and their cognate PNs. In this figure, we use only private odors. In the experiments that follow, we will blend in a public odor that activates other ORNs (but not the cognate ORNs of the PNs we are recording from). This allows us to manipulate direct and lateral input independently.

B. Intra-glomerular input-output functions for four glomeruli. Within a graph, each point is a different concentration of the same private odor. GABA receptor antagonists (5 μM picrotoxin +10 μM CGP54626) increase the gain in DM1 but not VM7 (red). All values are means of 6 -12 recordings, ± SEM. Curves are best fits to Equation (1). Concentrations are: methyl acetate 0, 10^-11, 10^-10, 10^-9, 3×l0^-8, 7×l0^-8, 10^-7, 10^-6, 10^-5; trans-2-hexenal 10^-9, 10^-8, 10^-7, 5×l0^-7; 2-butanone 10^-7, 10^-6, 10^-5, 10^-4; ethyl acetate 0, 10^-14, 10^-13, 10^-12, 10^-11, 10^-9, 10^-8, 10^-7, 10^-6.

The aims of this study are to understand how lateral inhibition alters the response of a PN to its presynaptic ORNs, and how this type of gain control affects PN population codes for odors. Previous studies have used odor stimuli that activate multiple ORN types, thereby driving both direct and lateral input to a PN. Instead, we here begin with “private” stimuli, defined as stimuli that activate only one ORN type (Figure 1A). By mixing private stimuli with varying concentrations of “public” stimuli (defined as stimuli that selectively activate a population of other glomeruli), we measure how increasing activity in other glomeruli suppresses the response of a PN to its presynaptic ORNs.

Results

A uniform intra-glomerular transformation

Based on a previous study (Hallem and Carlson, 2006), we identified four likely private odors and their cognate ORN types (Supplemental Table 1). We sampled randomly from many ORNs of other types in order to confirm that these odors do not activate non-cognate ORNs (Figure S1). Moreover, where mutations were available in the cognate odorant receptors for these odors, we verified that they virtually abolish the response of the ORN population (Figure S1).

For each of the four associated glomeruli, we recorded the responses of both ORNs and PNs to a range of concentrations of their private odor. Responses were quantified as spike rates over the 500-msec stimulus period. We found that the input-output relationships for three of these glomeruli were very similar (Figure 1B). In all these cases, weak ORN inputs were selectively boosted and strong inputs saturated. In the fourth glomerulus, the relationship between PN and ORN responses was shallower, but when GABA receptor antagonists were added, this relationship reverted to the typical steeper shape. The antagonists had no effect on a more typical glomerulus (Figure 1B).

These results suggest that all glomeruli perform a similar transformation on their inputs, although in some cases this transformation is modified by GABAergic inhibition. We can formalize this by fitting all these input-output relationships with the same equation:

$$PN=R_{\text{max}}\left(\frac{{\mathit{\text{ORN}}}^{1.5}}{{\mathit{\text{ORN}}}^{1.5}+{\sigma }^{1.5}}\right)$$ (1)

where PN is the response of an individual PN to a private odor stimulus, and ORN is the response of an individual presynaptic ORN to the same stimulus. R_max is a fitted constant representing the maximum odor-evoked response, and σ is a fitted constant representing the level of ORN input that drives a half-maximum response. R_max and σ are essentially the same for all glomeruli (except that without GABA receptor antagonists σ is larger for the fourth glomerulus we examined). The saturating form of this function reflects the combined effects of short-term depression at ORN-PN synapses and the relative refractory period of PNs (Kazama and Wilson, 2008). In Equation (1), the input terms are raised to an exponent of 1.5 because this produced the best fit; a similar equation describes the contrast response functions of visual neurons, and there too an exponent >1 is generally required (Albrecht and Hamilton, 1982; Heeger, 1992; Reynolds and Heeger, 2009; see Discussion).

Lateral interactions are inhibitory

We next asked how activity in other glomeruli affects a PN's response to its cognate ORNs. Here we focused on two glomeruli, VM7 and DL5. In order to manipulate input to other glomeruli independently from input to these glomeruli, we used a “public” odor that activates many ORN types but not these ORNs (Figure 1A). We verified that this odor (pentyl acetate) does not activate either VM7 or DL5 ORNs (at dilutions up to 10^-3, see Figure S2). Thus varying the concentration of pentyl acetate allows us to vary total ORN activity, as measured by field potential recordings in the antenna (Figure 2A).

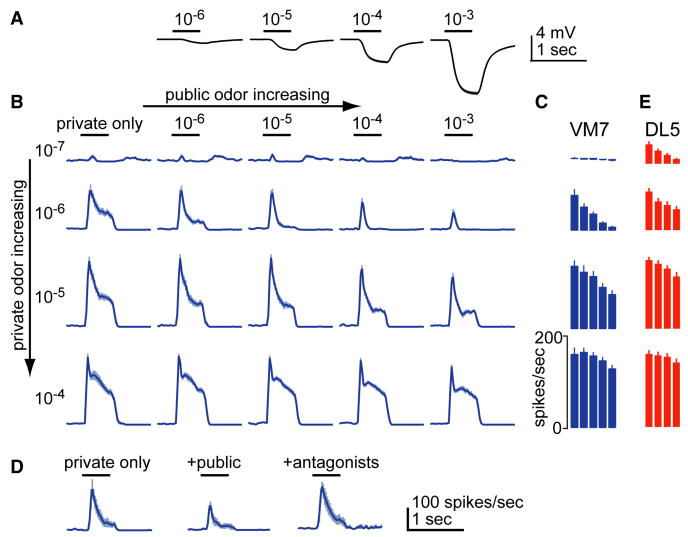
Figure 2. Increased activity in the ORN population inhibits PN responses to direct ORN input.

A. Antennal LFP shows that increasing the concentration of the public odor (pentyl acetate) increases total ORN activity. Black bars are odor stimulus period. Each trace is a mean of 9-19 recordings, ± SEM.

B. Peri-stimulus time histograms (PSTHs) for VM7 PNs, each averaged across 10-11 recordings, ± SEM. Each column is a different concentration of pentyl acetate, each row a different concentration of 2-butanone. See D for scale bars.

C. Average spike rate during 500 msec of odor presentation, ± SEM. Matrix of bars is analogous to the matrix of PSTHs in B.

D. GABA receptor antagonists block the suppressive effect of pentyl acetate (10^-3) on the response of VM7 PNs to a private odor (2-butanone 10^-6; n=5, ± SEM). Picrotoxin (5 μM) and CGP54626 (10 μM) were applied together to block both GABA-A and GABA-B receptors (Olsen and Wilson, 2008). With antagonists, the response to the blend is significantly different from the response in control saline, and not significantly different from the response to the private odor alone (p<0.05 and p=0.18, paired t-tests).

E. Same as D but for DL5 PNs. The same concentrations of pentyl acetate were used as the public odor (except 10^-6, which was omitted). The private odor was trans-2-hexenal. Each bar is a mean of 9-19 recordings, ± SEM.

We mixed pentyl acetate with 2-butanone (the private odor for VM7 ORNs) at various concentrations, generating 20 stimuli in total which we then tested on VM7 PNs. We found that pentyl acetate inhibited the responses of VM7 PNs to 2-butanone, with higher concentrations producing more inhibition (Figure 2B,C). The effect of pentyl acetate was blocked by GABA receptor antagonists (Figure 2D), as expected.

Similar results were obtained for a second glomerulus, DL5. Here we mixed pentyl acetate with trans-2-hexenal, the private odor for DL5 ORNs (Figure 2E). The magnitude of inhibition was consistently smaller for DL5 than for VM7, implying that glomeruli differ in their sensitivity to lateral inhibition.

Lateral inhibition normalizes input

We next asked whether lateral inhibition scales the horizontal or vertical axis of the input-output function (Figure 3A,B). We term horizontal scaling “input gain control”. We can express this by adding a suppression factor s to the denominator of the hyperbolic ratio function:

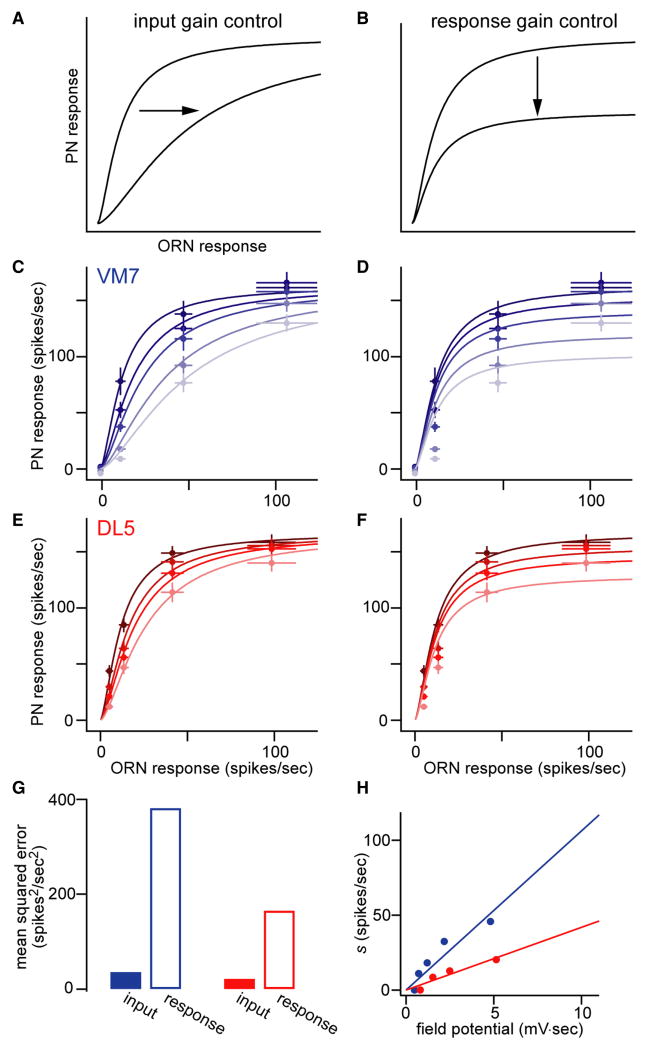
Figure 3. Input gain control describes how lateral inhibition changes the input-output function.

A. Schematic of input gain control.

B. Schematic of response gain control.

C. VM7 PN firing rates are plotted as a function of VM7 ORN firing rates. Each shade is a different pentyl acetate concentration, with ligher shades for higher concentrations. Within each curve each point is a different concentration of the private odor. Fits are to Equation (2), with R_max and σ as fixed constants, and s as a free parameter. Same PN data as Figure 2C; ORN responses are means of 5-10 recordings.

D. Same data as in B, but fits to Equation (3).

E. Same as C, but for DL5. Same PN data as Figure 2E; ORN responses are means of 5-8 recordings.

F. Same as D, but for DL5.

G. The input gain model produces better fits than the response gain model.

H. Values of the suppression factor s obtained from the fitted curves in C and E, plotted against the LFP response corresponding to each curve. A linear fit produced good predictions for novel odors (see Figure 4 and Figure S4) whereas sublinear (e.g., exponential) fits did not.

$$PN=R_{\text{max}}\left(\frac{{\mathit{\text{ORN}}}^{1.5}}{{\mathit{\text{ORN}}}^{1.5}+s^{1.5}+{\sigma }^{1.5}}\right)$$ (2)

We term vertical scaling “response gain control” (Figure 3B), and we can express this by scaling R_max:

$$PN=\left(\frac{1}{s^{1.5}+1}\right)\cdot R_{\text{max}}\left(\frac{{\mathit{\text{ORN}}}^{1.5}}{{\mathit{\text{ORN}}}^{1.5}+{\sigma }^{1.5}}\right)$$ (3)

We fit both these models to the data in Figure 2, fixing R_max and σ at the values we obtained from the curves in Figure 1B, and letting s be a fitted variable which varies with the concentration of pentyl acetate.

We found that for both VM7 and DL5, the input gain model generated better fits than the response gain model (Figure 3C-G). This reflects the fact that responses to dilute private odor were suppressed more powerfully in proportional terms than responses to concentrated private odor. The input gain model was also better than two subtractive models (see Supplemental Experimental Procedures). Thus, the effects of lateral inhibition are best described as input gain control.

Lateral inhibition scales with total ORN activity

How does the level of inhibition in a given glomerulus depend on the pattern of activity in the ORN population? It is possible that each glomerulus might receive strong inhibitory input from just a few glomeruli. However, many individual GABAergic local neurons in the antennal lobe innervate most glomeruli (Das et al., 2008; Lai et al., 2008), suggesting that they pool excitation from most ORN types and inhibit each glomerulus by a factor that depends on the total activity of this ORN population. If this were true, then our data should reveal a clear relationship between s and total ORN activity, assuming all glomeruli contribute equally to the pool.

To test this prediction, we asked how s depends on total ORN activity. We obtained s using Equation (2) for each concentration of pentyl acetate, again with R_max and σ held constant at the values obtained from the curves in Figure 1B. For each concentration of pentyl acetate, we obtained an estimate of total ORN activity by measuring the antennal local field potential (LFP, Figure 2A) because this scales linearly with ORN activity (Figure S3). We found that the relationship between s and LFP was linear for both VM7 and DL5 (Figure 3H). Thus,

$$s=m\cdot \mathit{\text{LFP}}$$ (4)

where the slope m represents the sensitivity of each glomerulus to lateral inhibition. (Note that m is larger for VM7 than for DL5, Figure 3H.) The linear relationship between s and LFP implies these glomeruli are normalized by an amount that simply scales with total ORN activity.

If lateral inhibition in each glomerulus scales with total ORN activity, then the contribution of any single glomerulus to the inhibitory signal should be weak. We therefore asked whether stimulating one glomerulus can produce substantial lateral inhibition. We used private odors to drive robust activity (∼100 spikes/sec) in a single ORN type but not in VM7 ORNs. The ORN types activated by these odors were DM4, DL5, and DM1, and the three private stimuli were the highest concentrations of their cognate private odors in Figure 1. Mixing each private odor with 2-butanone produced only weak suppression of the VM7 PN response to 2-butanone (results not shown). This result is consistent with a model whereby inter-glomerular inhibitory connections are weak, and thus input to multiple glomeruli is required to evoke measurable lateral inhibition.

Predicting PN responses to novel odors

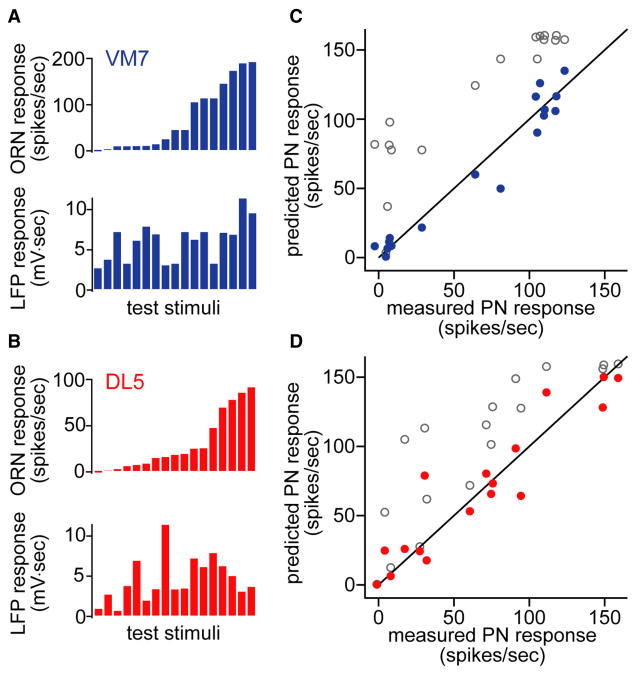
These findings imply that we should be able to predict the odor-evoked firing rate of these PNs based on only two variables: the firing rate of their presynaptic ORNs, and the firing rate of the total ORN population. To examine the quality of these predictions, we measured the responses of VM7 ORNs to a set of test odors that were not used to construct our model. As a proxy for total ORN activity, we measured the antennal LFP for each test odor (Figure 4A,B). Next, we used these measurements to predict the odor responses of VM7 PNs on the basis of Equations (2) and (4), using the value of m that represents the sensitivity of VM7 to lateral inhibition. Strikingly, predicted and measured PN firing rates were in excellent agreement, with the input gain model accounting for 95% of the variance in the data (Figure 4C). We repeated this procedure for glomerulus DL5, here using the value of m derived for DL5. Again, the input gain model made very good predictions, accounting for 87% of the variance in the data (Figure 4D). The success of these predictions provides further support for the conclusion that the suppression factor s varies linearly with the LFP (Figure S4). As expected, the response gain control model did not accurately predict PN responses (results not shown).

Figure 4. The input gain control model accurately predicts PN responses.

A. For each stimulus used to test the VM7 model, VM7 ORN responses (mean of 5-10 recordings) and antennal LFP responses (mean of 6 recordings) are shown. We selected test stimuli to span a wide distribution of ORN and LFP responses.

B. Same as A, but for DL5 test stimuli.

C. Predicted versus measured responses for VM7 PNs (r² = 0.95). Each point is a different test stimulus. Filled symbols are predictions of the input gain model (Equation (2)). Open symbols are predictions of the model without inhibition (Equation (1)). Each measured PN response is a mean of 6-12 recordings, except one where n=3.

D. Same as C, but for DL5 (r² = 0.88). Each measured PN response is a mean of 10 recordings.

Gain control reformats population codes

What are the consequences of these transformations for the way odors are encoded at the population level? To address this, we first examined the statistical properties of ORN population codes. We then used our model to simulate PN population codes and ask how their properties are altered as compared to ORNs. Ultimately, we are interested in how these transformations affect odor discrimination.

As the input to our model, we used ORN odor responses measured by reference (Hallem and Carlson, 2006), comprising 176 olfactory stimuli and 24 ORN types. This data set displays a strong statistical regularity: stimuli that evoke a robust response in a given ORN type also tend to evoke robust responses in many ORN types (Figure 5A₁). This can be quantified by principal components analysis on the odor response vectors, which shows that the first principal component (PC) accounts for fully 49% of the variance in the data. This PC is essentially a proxy for stimulus intensity (Figure S5). Another way to quantify this is to perform pairwise comparisons between ORN types, which shows that pairwise correlations are high (Figure 5B₁). These correlations have an important corollary: because some stimuli elicit weak responses in many ORN types and others elicit robust responses in many ORN types, stimuli produce widely varying levels of total activity. We quantified this by computing the magnitude of the population response evoked by each stimulus, defined as the norm of the population response vector. This distribution is broad (Figure 5C₁), meaning that total odor-evoked activity varies over a wide range. In short, all these analyses show that the responses of ORNs are not statistically independent.

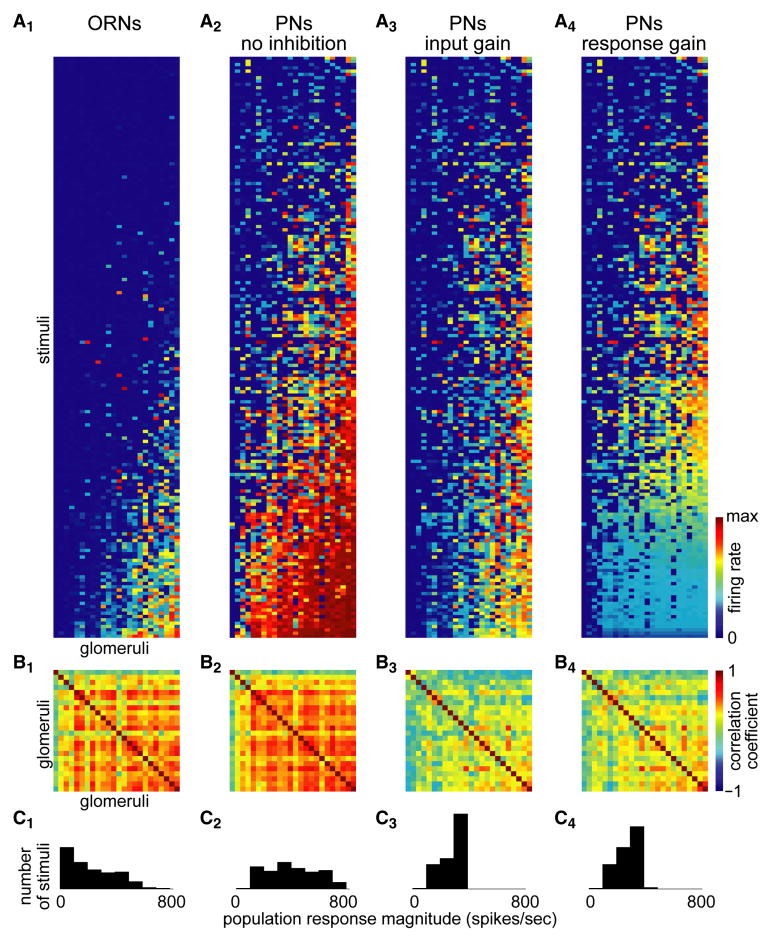
Figure 5. Modeling PN population codes for odors.

A. ORN data from Hallem and Carlson (2006). (A₁). Stimuli (176 in total) are sorted top to bottom by the number of spikes in the ORN. Glomeruli (24 in total) are sorted left to right. PNs were simulated using the intra-glomerular transformation alone (A₂), or the input gain control model (A₃), or the response gain control model (A₄). The color scale differs for ORN and PN matrices: maximum is 290 spikes/sec for ORNs and 165 for PNs.

B. Cross-correlation values for each pairwise comparison between glomeruli. Mean correlation coefficients for each panel are 0.35, 0.41, 0.09, and 0.15.

C. Histograms show the distribution of population response magnitudes (defined as the Euclidean distance of the response from the origin of 24-dimensional glomerular space). Each histogram contains 176 values, one for each stimulus.

To model PNs without inhibition, we simulated the intra-glomerular transformation by applying Equation (1) to the ORN matrix. This transformation boosts the smallest responses, while pushing the largest responses toward saturation (Figure 5A₂). After this transformation, correlations among glomeruli are largely unchanged (Figure 5B₂), and the distribution of population response magnitudes remains broad (Figure 5C₂). Thus, this transformation has little effect on statistical dependencies between glomeruli.

Next, we added lateral inhibition using the input gain control model. This requires us to know the total level of ORN activity evoked by each odor. Instead of taking LFP measurements for all these odors, we instead obtained an expression for s as a function of ORN firing rates. We measured LFP responses to a subset of the stimuli in the ORN data set, and we fit a line to the relationship between these LFP responses and the total number of ORN spikes evoked by each odor (Figure S3). The fitted line is given by:

$$\mathit{\text{LFP}}=\left(\sum _{i=1}^{24}{r}_i\right)/190\text{mV}\cdot {\text{sec}}^2/\text{spikes}$$ (5)

where r_i is the firing rate of the ith ORN type. Combining Equations (5) and (4) we obtain:

$$s=m\cdot \left(\sum _{i=1}^{24}{r}_i\right)/190\text{mV}\cdot {\text{sec}}^2/\text{spikes}$$ (6)

The constant m in Equation (6) was obtained from the fit to VM7 data with the input gain model (Figure 3H). By combining Equations (2) and (6), we were able to simulate the ORN-PN transformation according to the input gain model (Figure 5A₃). This transformation counteracts the tendency for intense stimuli to recruit strong responses across the PN population, and for this reason it decorrelates glomeruli (Figure 5B₃). It also decreases the magnitudes of the strongest population responses while leaving the weaker responses relatively unaffected, and as a result population response magnitudes are now more equal (Figure 5C₃).

To simulate response gain control (Figure 5A₄), we combined Equations (3) and (6), and we obtained the constant m in Equation (6) by fitting this equation to VM7 data (results not shown). Like input gain control, this transformation decorrelates glomeruli (Figure 5B₄) and tends to equalize population response magnitudes (Figure 5C₄). But whereas input gain makes it more difficult for PN responses to saturate, response gain control does nothing to prevent saturation. This means that intense stimuli evoke similar weak levels of activity in many PN types.

Finally, as a control, we shuffled the odor labels on each ORN response vector before computing s. In this case, inhibition does not decorrelate glomeruli or equalize population response magnitudes (results not shown). The key point is that gain control only produces decorrelation and equalization of responses if inhibition grows with increasing input to the circuit.

Input gain control promotes selective discrimination

Next, we examined how these transformations affect odor discrimination on the basis of PN population responses. PNs make excitatory synapses with third-order neurons called Kenyon cells (KCs), which are thought to integrate input from different glomeruli. Many KCs are selective for a particular stimulus, and KCs tend to respond in a binary fashion, firing either zero spikes or just a few spikes (Stopfer et al., 2003; Wang et al., 2004; Turner et al., 2007). This motivated us to ask how antennal lobe transformations would affect the ability of a binary classifier to respond selectively to a single stimulus.

We simulated a set of 176 binary linear classifiers (perceptrons), one for each stimulus. The input to each perceptron was a weighted sum of all glomerular responses, and the perceptron responded if the sum exceeds its threshold. Input weights were constrained to be non-negative, but they were adjusted for each perceptron so that it responded as selectively as possible to one stimulus. For each of the four response matrices (Figure 5A) we created a set of perceptrons with weights appropriate to that matrix. Training and test stimuli were created by adding noise to each response matrix, where the parameters of the noise were drawn from PN data (Figure S6). Each set of perceptrons was evaluated on the basis of its ability to correctly classify these noisy test stimuli. Thresholds were adjusted so that the fraction of false positives equaled false negatives.

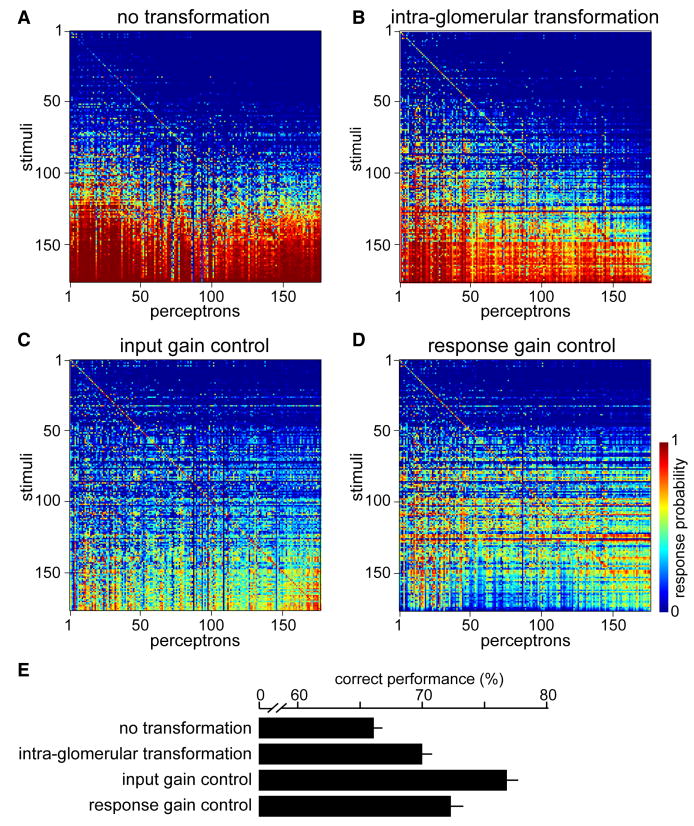
First, we examined the case where PN responses are identical to ORN responses (i.e., no transformation, using the matrix in Figure 5A₁). Perceptrons trained and tested on these responses performed relatively poorly (Figure 6A). Specifically, strong stimuli generated a high rate of false positives. This is because strong stimuli generate strong responses in many glomeruli, and thus tend to drive the weighted sum in all perceptrons above threshold.

Figure 6. Input gain control promotes odor discrimination.

A-D. Confusion matrices show the performance of 176 perceptrons, each trained to respond to a single stimulus. Each row is a different stimulus and each column is a different perceptron. Stimuli are arranged top-to-bottom in order of increasing total number of ORN spikes. Perceptron 1 targets odor 1, perceptron 2 targets odor 2, etc. Values along the diagonal indicate the probability of a correct hit, and values off the diagonal indicate the probability of a false positive; see color scale in D. Perfect performance would be represented by red squares on the diagonal and blue off-diagonal.

E. Mean performance for each set of perceptrons, averaged across 500 independent networks, ± SD. Correct performance = percent hits correct = percent misses correct (see Experimental Procedures).

Next, we examined the effect of the intra-glomerular transformation, without lateral inhibition. Perceptrons trained and tested on this matrix performed better (Figure 6B). This is because the intra-glomerular transformation selectively boosts PN responses to weak ORN inputs. This makes it easier to find weights that yield a selective response to weak stimuli. However, every perceptron still tended to respond inappropriately to many strong off-target stimuli.

Input gain control largely solves this problem (Figure 6C). This is because this model normalizes PN responses by the total level of ORN input, and so strong stimuli no longer elicit so many false positives. By comparison, the response gain control model performs more poorly (Figure 6D). Like input gain control, this model has the virtue of normalizing responses to strong stimuli. However, this model compresses the PN dynamic range when the total level of ORN input is strong, and so strong stimuli elicit weak responses in all glomeruli. This makes it difficult to find a threshold that maximizes correct hits while also minimizing false positives.

Input gain control promotes intensity invariance

Next, we asked perceptrons to respond selectively to an odor across a range of concentrations. This task is inspired by the experimental finding that some KCs respond selectively to a particular odor regardless of its concentration (Stopfer et al., 2003; Wang et al., 2004). Because we had available data on 19 odors at each of three concentrations, we trained 19 perceptrons on this task, one for each odor.

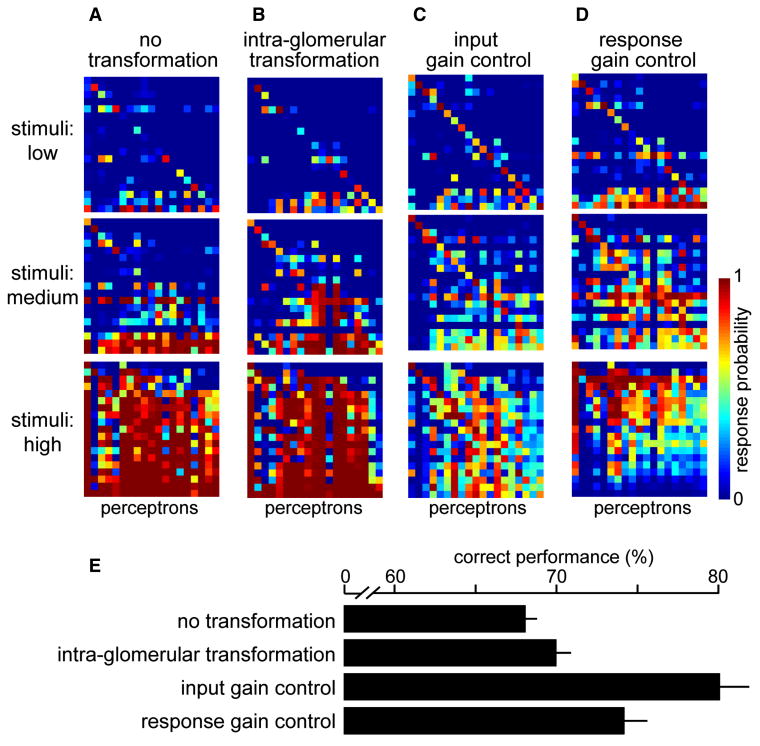
Again, we first examined the case where PN responses are identical to ORN responses (no transformation). These perceptrons did relatively poorly (Figure 7A) because low concentrations evoke such weak responses that they are not easily classified with high concentrations. The intra-glomerular transformation improves performance (Figure 7B) because it selectively boosts weak responses, and so brings low and high concentrations closer together. Input gain control creates the best performance (Figure 7C) because it normalizes for intensity, and this makes responses to different concentrations more similar. Response gain control also normalizes for intensity, but it performs more poorly than input gain control (Figure 7D). Because high concentrations elicit intense lateral inhibition which suppresses all PN responses uniformly, these strong stimuli elicit small population responses, and it becomes difficult to maximize correct hits while minimizing false positives.

Figure 7. Input gain control promotes concentration-invariant discrimination.

A-D. Confusion matrices show the performance of 19 perceptrons trained to respond to a chemical stimulus regardless of concentration. Perceptron 1 is trained to target odor 1 at low, medium, and high concentrations; perceptron 2 is trained to target odor 2 at low, medium, and high concentrations, etc.

E. Mean performance for each set of perceptrons, averaged across 500 independent networks, ± SD.

Increasing total activity makes responses more transient

For simplicity, we have thus far quantified neural activity as mean firing rates over the stimulus period. However, PN responses do not remain constant over the stimulus period. In order to investigate how lateral inhibition shapes these dynamics, we compared the time course of PN responses to different levels of private and public input. We found that, as a general rule, mixing in a public odor tended to make PN responses to private input more transient (Figure 8A,B).

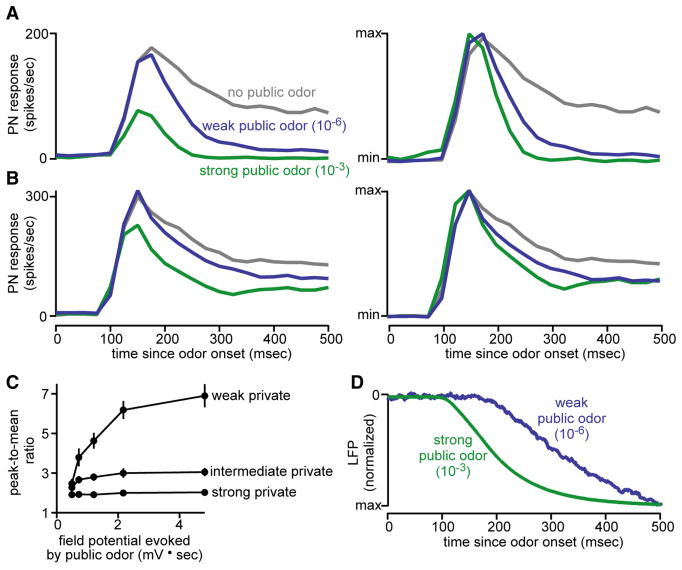
Figure 8. Increasing total activity makes PN responses more transient.

A. Mixing in a public odor modulates the dynamics of PN responses to weak private input (2-butanone 10^-6). The highest concentration of the public odor has the largest effect. PSTHs are averages of 10-11 recordings, reproduced from Figure 2B.

B. The same public odor has smaller effects on PN dynamics when the private odor is strong (10^-5).

C. Overall, increasing total ORN activity makes PN responses more transient. Transience is quantified as the ratio of peak firing rate to the mean firing rate. Each curve represents a different concentration of 2-butanone (10^-6, 10^-5, 10^-4), and each point within a curve is a different concentration of pentyl acetate (0, 10^-6, 10^-5, 10^-4, 10^-3). The dynamics of responses to the lowest concentration of 2-butanone (10^-7) were not analyzed because these responses are close to zero.

D. A strong public odor elicits a faster field potential response than a weak odor (averages of 19 and 9 LFP recordings, respectively, normalized to the same amplitude).

We quantified transience as the ratio of the peak firing rate to the mean firing rate (Figure 8C). As the public odor concentration increased, the peak-to-mean ratio systematically increased. This is probably because a strong public stimulus recruits ORNs faster. Consistent with this idea, higher public odor concentrations produce a faster increase in the antennal LFP (Figure 8D). Faster recruitment of the ORN population should recruit faster lateral inhibition, and thus more transient PN responses.

However, the effect of the public odor on PN dynamics was only large when the private odor concentration was low (Figure 8A-C). This suggests that increasing total ORN activity only makes PN responses more transient when direct input is weak. This would be consistent with an input gain control model, because in this model the effect of lateral inhibition is strongest when PNs are far from saturation. Thus, input gain can account for why lateral inhibition affects the dynamics of some PN responses more than others.

Discussion

Normalization models in olfaction and vision

As originally formulated in the visual system, the normalization model of gain control includes two conceptually separate steps: a saturating function and a normalization step (Heeger, 1992). The first step—the saturating function—is often fit by a hyperbolic ratio function (Naka and Rushton, 1966; Albrecht and Hamilton, 1982):

$$R\left(c\right)=R_{\text{max}}\left(\frac{c^n}{c^n+{\sigma }^n}\right)$$ (7)

where the variable c is the contrast of the visual stimulus, σ is a constant, and n is a constant exponent (generally empirically determined to be >1). Here we show that a similar function (Equation (1)) describes the transformation that occurs within each glomerular channel.

The second step—normalization—has been modeled in the visual system as an increase in the contrast needed to drive a neuron to half-maximum firing rate:

$$R(c)=R_{\text{max}}\left(\frac{c^n}{c^n+s^n+{\sigma }^n}\right)$$ (8)

where the suppression factor s depends on stimulus contrast and can be rather nonselective for other stimulus features, presumably reflecting summed input from neurons with diverse stimulus preferences (Heeger, 1992). Versions of this model describe neural activity in several visual cortical areas (Carandini et al., 1997; Cavanaugh et al., 2002; Zoccolan et al., 2005), and this model has also been extended to describe the effects of attention (Lee and Maunsell, 2009; Reynolds and Heeger, 2009). There are differences between the models in these studies; for example, s can be either nonselective or selective. Generally an exponent >1 is required to fit the data (Albrecht and Hamilton, 1982; Heeger, 1992; Carandini and Heeger, 1994; Reynolds and Heeger, 2009), although the mechanisms underlying this are uncertain. Nevertheless, the essential concept captured by this equation is simple: the activity of each neuron is normalized by activity in a larger pool of neurons.

Here we show that a similar function (Equation (2)) describes gain control in the Drosophila antennal lobe. By independently manipulating direct and lateral input to a PN, we show that the saturating transformation is intrinsic to each glomerular channel, whereas the normalization step is due to lateral inhibition. Thus, at least in this circuit, these two transformations are not just conceptually distinct but also mechanistically distinct.

Population codes for odors

Our results show that both the intra- and inter-glomerular transformations promote odor discrimination by a linear decoder. First, the intra-glomerular transformation selectively boosts weak ORN inputs. Because responses to weak stimuli are preferentially amplified, it becomes easier to find a combination of glomerular weights that produces a selective response to one of these stimuli. A recent theoretical study pointed out that this type of transformation should promote linear separation (Luo et al., 2008), and our results reinforce that conclusion.

Second, the normalization step decreases the steepness of the intra-glomerular transformation by a factor proportional to total input. As a result, activity in different glomeruli is decorrelated. This agrees with theoretical studies showing that normalization makes the responses of different neurons more statistically independent (Schwartz and Simoncelli, 2001). Another precedent for our results is a recent theoretical study pointing out that global lateral inhibition should decorrelate the odor selectivity of different glomeruli (Cleland and Sethupathy, 2006), although that study postulated a different type of intra-glomerular transformation than the function we describe here. Importantly, we show that this type of normalization makes it easier for a linear decoder to respond selectively to a particular stimulus. This is because stimuli of different intensities now evoke population responses with a more similar magnitude.

It is useful to consider both of these steps—boosting and normalization—in terms of efficient coding. The efficient coding hypothesis has two parts: (1) each neuron should use its dynamic range uniformly, and (2) responses of different neurons should be independent (Simoncelli, 2003). Most ORN responses are weak, so ORNs do not use their dynamic range uniformly. By selectively boosting weak inputs, the intra-glomerular transformation creates PN responses that use the available dynamic range more uniformly (Bhandawat et al., 2007). Meanwhile, most ORNs are also correlated with each other. By creating competitive interactions between neurons in different glomeruli, normalization decorrelates their responses. (Note the distinction between decorrelating neurons and decorrelating representations: global lateral inhibition does the former but not the latter, see Figure S7.)

A previous study reported that PN responses are not substantially more decorrelated than ORN responses (Bhandawat et al., 2007). Two considerations reconcile our findings with that study. First, we show here that although lateral inhibition tends to decorrelate PN odor responses, the intra-glomerular transformation tends to correlate them. Thus the net effect of both transformations is less decorrelating than lateral inhibition alone. Second, the previous study used stimuli spanning a narrow range of intensities. By contrast, the stimuli in our simulations here span a wide range, which leads to a larger decorrelation.

Toward concentration-invariant odor representations

Functional imaging studies in the olfactory bulb have shown that different concentrations of the same odor elicit different levels of activity in the bulb, but these spatial maps are similar after signals are normalized to the same amplitude (Johnson and Leon, 2000; Wachowiak et al., 2002; Cleland et al., 2007). For this reason, lateral inhibition has been proposed as a basis for concentration-invariant odor representation in the olfactory bulb (Johnson and Leon, 2000; Wachowiak et al., 2002; Cleland et al., 2007) and the antennal lobe (Sachse and Galizia, 2003; Asahina et al., 2009). Here, we provide evidence for this computation at the level of ORN input to Drosophila antennal lobe glomeruli.

Drosophila can discriminate between different concentrations of the same odor (Borst, 1983). If lateral inhibition tends to normalize for intensity, how is this possible? One potential explanation is that normalization is incomplete: the most intense stimuli in our simulation evoke responses that are substantially larger than the weakest responses. Incomplete normalization may be a useful way to preserve information about stimulus intensity while promoting a more efficient representation.

Glomerulus-specific sensitivity to inhibition

Our results show that glomeruli differ in their sensitivity to lateral inhibition. This appears as differing values of the factor m that expresses how steeply lateral inhibition depends on total ORN activity. Although we examined only two glomeruli in detail, our analysis of a published data set comprising seven additional glomeruli (Bhandawat et al., 2007) suggests that the values of m for VM7 and DL5 fall within the typical range. Another finding from this study is that one of the four glomeruli we examined (DM1) is modulated by inhibition arising from odor-evoked intra-glomerular GABA release and/or tonic inter-glomerular GABA release. This appears as a higher value of the semisaturation constant σ for this glomerulus.

This heterogeneity does not affect our overall conclusions about the consequences of gain control. If instead of using the value of m for VM7 as the default we randomly assign to each glomerulus a value of m intermediate between the values for VM7 and DL5, then the overall effects of inhibition are weaker but qualitatively unchanged. Similarly, the results of our simulations are qualitatively unchanged if we randomly assign a high value of σ to a subset of glomeruli (data not shown).

Given this, it is worth asking why heterogeneity might be useful. We speculate that some glomeruli might be specialized in their sensitivity to GABAergic inhibition because they respond preferentially to an odor with special behavioral relevance or unusual natural statistics. Mechanistically, the explanation for heterogeneity might lie in glomerulus-specific levels of GABA receptor expression (Root et al., 2008).

Circuit mechanisms: connectivity between glomeruli

It is generally thought that specific connectivity between glomeruli is important for olfactory processing (Laurent, 2002; Lledo et al., 2005). Here we show that specific connectivity is not required to account for PN odor responses: good fits to data can be obtained by assuming all-too-all connectivity and uniform connectivity weights. We found that sparser connectivity can also generate good fits (Figure S8) because the responses of different ORN types are correlated with each other, and so pooling input from only a subset of glomeruli produces an effect similar to pooling total input. However, most individual Drosophila antennal lobe local neurons innervate the majority of glomeruli (Das et al., 2008; Lai et al., 2008), and this implies a comparatively dense pattern of inter-glomerular connections.

In the mammalian olfactory bulb, one local interneuron cannot connect all glomeruli. However, dense nonspecific connectivity could be implemented on a local scale. Nearby glomeruli in the bulb are almost as diverse in their odor selectivity as distant glomeruli (Soucy et al., 2009). Thus, the summed responses of local glomeruli might produce an inhibitory signal similar to the sum of all glomeruli. Alternatively, if mammalian ORN types are not as correlated in their odor selectivity as Drosophila ORN types are, then optimal connectivity might be sparse and specific (Fantana et al., 2008).

It should be noted that excitatory lateral connections co-exist in this circuit with inhibitory ones (Olsen et al., 2007; Root et al., 2007; Shang et al., 2007). In this study, we found that the net effect of lateral input was always inhibitory. However, this does not imply that lateral excitatory connections make no contribution—only that they do not dominate.

Cellular mechanisms: pre- versus postsynaptic inhibition

Lateral inhibition in the adult Drosophila antennal lobe has a mainly presynaptic locus (Olsen and Wilson, 2008; Root et al., 2008). This raises the question of why it might be useful to implement inhibition pre-rather than postsynaptically. Our results suggest a novel answer. We show that lateral inhibition in this circuit produces input gain control rather than response gain control, and input gain control has some attractive properties. It is easy to see why presynaptic inhibition might produce input gain control: any inhibitory process that acts prior to the nonlinearity in the input-output function will tend to make it more difficult to reach saturation but will not change the level at which output saturates. The major nonlinearities in the intra-glomerular transformation are short-term synaptic depression and the postsynaptic refractory period (Kazama and Wilson, 2008), whereas presynaptic inhibition is thought to modulate an earlier step, i.e. presynaptic calcium influx. In other circuits the mechanisms of normalization may be different, and may not involve GABAergic inhibition (Carandini et al., 2002; Freeman et al., 2002).

Dynamics of gain control

We found that increasing total ORN activity (by increasing the public odor concentration) made PN responses more transient. This result has parallels in other sensory modalities, where increasing stimulus intensity generally decreases neuronal integration times. For example, in the retina, increasing the luminance of a visual stimulus produces more transient responses in ganglion cells (Shapley et al., 1972; Enroth-Cugell and Shapley, 1973). In visual cortex, increasing the contrast of a periodic visual stimulus advances the phase of neural responses (Dean and Tolhurst, 1986). Similarly, increasing sound intensity narrows the integration time of auditory cortical neurons (Nagel and Doupe, 2006). These changes create an adaptive tradeoff that should maximize information transmission over a range of stimulus intensities (Atick, 1992). Long integration times should allow neurons to overcome the effects of noise when stimulus intensities are low, whereas short integration times should maximize temporal resolution of stimulus fluctuations when stimulus intensities are high. Our findings extend this principle to olfactory processing.

Adaptive changes in integration time have been recognized as a natural extension of normalization models. For example, if normalization is implemented by an increase in postsynaptic inhibitory conductances, then the resulting decrease in the postsynaptic membrane time constant would shorten the integration time (Carandini and Heeger, 1994; Carandini et al., 1997). However, in the Drosophila antennal lobe, lateral inhibition is largely presynaptic (Olsen and Wilson, 2008), so this mechanism is unlikely to apply. Instead, our results suggest an alternate mechanism: shorter integration times are likely due to increasingly rapid recruitment of lateral inhibition by increasingly intense afferent activity.

Limitations of the model

First, our model is based on measurements from only a few glomeruli. In pilot experiments we explored other candidates, but we could not find private odors for these glomeruli. This reflects the constraint that the private odor must be selective even at concentrations high enough to approach R_max.

Second, we have not modeled the dynamics of neural activity. Because the input data set for our model consists of ORN firing rates averaged over a 500-msec time period (Hallem and Carlson, 2006), our model is not able to consider finer timescales. ORN responses are themselves dynamical, and these dynamics depend on both the odor and the ORN (Hallem and Carlson, 2006). PN response dynamics are also characteristically faster than ORN response dynamics (Bhandawat et al., 2007). Modeling these dynamics will require a more systematic understanding of these processes.

Finally, the usefulness of any transformation will depend on the decoder and the task. Our model decoders are inspired by the properties of real higher-order olfactory neurons. However, some aspects of our model decoders are unrealistic—for example, each pools input from all glomeruli. Unraveling the actual connectivity of the higher-order olfactory circuit should help us better constrain our models. Also, the tasks we set our decoders are probably easy compared to natural olfaction, which is complicated by turbulence and background odors. Understanding how these factors affect olfactory encoding should help us gain insight into the tasks this circuit has evolved to perform.

Experimental Procedures

Fly Stocks

Fly stocks were kindly provided as follows: NP5221-Gal4, NP3062-Gal4, NP3481-Gal4 (Kei Ito and Liqun Luo); Or92a-Gal4 (Leslie Vosshall); UAS-DTl/CyO (Leslie Stevens). The following were obtained from the Bloomington Stock Center: UAS-CD8GFP_I, UAS-CD8GFP_II, UAS-CD8GFP_III, Or42b^EY14886 (see Figure S1), Or42a^f04305 (see Figure S1).

Electrophysiological Recordings

The total number of observations in this study comprises 1299 ORN measurements, 225 LFP measurements, and 591 PN measurements (total n summed across all experiments). Each measurement represents the mean of 4 consecutive trials with the same stimulus. ORN spikes were recorded extracellularly from sensilla on the surface of the maxillary palp or antenna. The antennal LFP was recorded with an electrode in the body of the antennal funiculus. Whole-cell patch-clamp recordings were made from PN somata in current-clamp mode. Recordings were targeted to specific PNs by labeling them with GFP. See Supplemental Experimental Procedures for details.

Olfactory Stimuli

See Supplemental Experimental Procedures for details.

Data Analysis

Quantifying neural responses

Each cell was tested with multiple stimuli, typically with 4 trials per stimulus spaced 40-60 sec apart. The response magnitude for each cell/stimulus combination was quantified as the trial-averaged number of spikes during the 500-msec odor stimulus period, minus the trial-averaged baseline spike rate during the preceding 500 msec. To generate a peri-stimulus-time histogram, we counted the number of spikes in 50-msec bins that overlapped by 25 msec. LFP recordings were quantified as the integral during the 500-msec odor stimulus period, minus the integral during the 500 msec preceding the stimulus. All these response measures were first averaged across trials within an experiment, and then reported as mean ± SEM across experiments.

Fitting input-output functions

The input-output functions in Figure 1 were determined by fitting the private odor responses for each glomerulus to Equation (1). R_max and σ were free parameters. R_max = 170, 167, 163, and 144, and σ = 16.3, 11.8, 12.4, and 44.8, for glomeruli DM4, DL5, VM7, and DM1, respectively. Equation (1) fits these data better than the logarithmic function used in previous studies (Bhandawat et al., 2007; Olsen and Wilson, 2008).

In Figure 3, each input-output function within a panel corresponds to a different concentration of pentyl acetate. Here we used Equation (2) for the input gain model and Equation (3) for the response gain model. The parameters R_max and σ were derived separately for VM7 and DL5 from the fits in Figure 1 and were held constant across all concentrations of pentyl acetate. Thus, the only free variable in these fits was s. In Equations (1) – (3) the input variables (ORN, σ, s) are raised to an exponent (1.5). We use this exponent because it provides the best fit to our data. We determined this by fitting the data in Figure 3 with different exponents between 1 and 2 in increments of 0.1. The mean squared error had a minimum for an exponent of 1.5 and 1.6 for glomeruli DL5 and VM7, respectively. Choosing an exponent of 1.5 for VM7 produced only a slight decrease in fit quality and allowed a constant exponent to be used for all equations.

Predicting PN odor responses based on the LFP

In Figure 4, PN responses to novel stimuli were predicted from Equation (2) on the basis of two variables, the presynaptic ORN response to that stimulus (ORN) and the value of s corresponding to that stimulus. Values of s were derived from the LFP response to each stimulus according to Equation (4). The relationship between s and the LFP was obtained from the linear fit in Figure 3H (m = 10.63 for VM7 and 4.19 for DL5). Each LFP value in Figure 3H is the sum of the LFP response to one pentyl acetate concentration (Figure 2A, different for each curve) and the LFP response to the private stimulus alone (the same for each curve). Summation is reasonable because public and private odors do not activate the same ORNs, and because the LFP scales linearly with summed ORN firing rates (Figure S3). To fit a curve, we needed to represent the contribution of the private stimuli to the summed LFP with a single value, but in reality each curve was constructed with a range of the private odor concentrations, all of which elicit slightly different small LFP responses (Figure S1); for simplicity, we averaged the LFP measured for all these concentrations to estimate the contribution of private stimuli to the LFP.

Modeling

Simulating PN responses

In Figures 5-7 we used the data from Hallem and Carlson (2006) to stimulate PN population codes. Because this data set includes only 24 of the 50 ORN types, we simulated only 24 glomeruli. Unless otherwise noted, we used the following parameters for all glomeruli: R_max = 165 spikes/sec and σ = 12 spikes/sec. To simulate the PN matrix without inhibition, we used Equation (1). The input gain PN matrix was simulated using Equations (2) and (6). The constant m in Equation (6) was set to 10.63 for all glomeruli. The response gain PN response matrix was simulated using Equations (3) and (6) (m = 0.164). For all simulated PN responses, if the presynaptic ORN odor response was a negative number (a suppression of basal firing rate), then the PN response was set to zero. Population response magnitude (Figure 5C) was quantified for each stimulus as the norm of the response vector in 24-dimensional ORN or PN space:

$$\Vert r\Vert =\sqrt{\sum _{i=1}^{24}{r}_i^2}$$ (9)

where r_i is the firing rate of the ith ORN type or PN type.

Decoding simulated PN responses with a linear classifier

Each perceptron receives input from all 24 glomeruli. The perceptron classifies stimuli by computing a weighted sum on its inputs and responding if this sum crosses a threshold, c. Its response is binary:

$$\begin{array}{c}\mathit{\text{response}}=1\mathit{\text{if}},c\le w_i{r}_i+w_{i+1}{r}_{i+1}+\cdots +w_{24}{r}_{24}\hfill \\ \mathit{\text{response}}=0\mathit{\text{if}},c>w_i{r}_i+w_{i+1}{r}_{i+1}+\cdots +w_{24}{r}_{24}\hfill \end{array}$$ (10)

where r_i is the response of the ith glomerulus and w_i is the weight of that glomerulus. The weights for each perceptron were derived using the normalized perceptron learning rule:

$$w_i^{\mathit{\text{new}}}=w_i^{\mathit{\text{old}}}+\epsilon \cdot \frac{p_i}{\Vert \mathbf{\text{p}}\Vert }$$

where ‖p‖ is the norm of the training input vector, p_i is the input from ith glomerulus to the perceptron, and ε is the difference between the perceptron's output and target value. Additionally, we constrained the sign of the weights to be non-negative. If the updated weight took a negative value this weight was reverted to its previous non-negative value before presenting the next training input. The threshold c was constrained to be the same for all perceptrons within the same set, and was adjusted during training so that the false hits rate was equal to the rate of false misses.

For each set of perceptrons, we generated 100 noisy training matrices by picking the appropriate matrix in Figure 5A and adding Gaussian noise to each entry (Figure S6). Noise was drawn independently for each entry in every training matrix. Weights were adjusted for 100 iterations of the learning rule, by which time weights had converged. We tested performance by presenting the set of perceptrons with 50 noisy test matrices, generated in the same way as for the training matrices. Results in Figures 6 and 7 are shown as the mean for 500 independent networks (i.e., 100 training iterations, followed by 50 tests, this repeated 500 times).

We trained and tested perceptrons separately for two classification tasks. For the first task we generated four sets of 176 perceptrons, each designed to respond selectively to one out of the 176 stimuli. For the second task we generated four sets of 19 perceptrons, each designed to respond to the same odor across 3 different concentrations (19 × 3 = 57 stimuli). These 57 stimuli are only a subset of the 176 stimuli because Hallem & Carlson (2006) tested most odors at only one concentration. The low and medium concentrations of each odor represent 100-fold and 10,000-fold dilutions of the high concentration.

Alternative models of gain control and odor discrimination

See Supplemental Experimental Procedures.