Improvements in Ability to Detect Undiagnosed Diabetes by Using Information on Family History Among Adults in the United States

Abstract

Family history is an independent risk factor for diabetes, but it is not clear how much adding family history to other known risk factors would improve detection of undiagnosed diabetes in a population. Using the National Health and Nutrition Examination Survey for 1999−2004, the authors compared logistic regression models with established risk factors (model 1) with a model (model 2) that also included familial risk of diabetes (average, moderate, and high). Adjusted odds ratios for undiagnosed diabetes, using average familial risk as referent, were 1.7 (95% confidence interval (CI): 1.2, 2.5) and 3.8 (95% CI: 2.2, 6.3) for those with moderate and high familial risk, respectively. Model 2 was superior to model 1 in detecting undiagnosed diabetes, as reflected by several significant improvements, including weighted C statistics of 0.826 versus 0.842 (bootstrap P = 0.001) and integrated discrimination improvement of 0.012 (95% CI: 0.004, 0.030). With a risk threshold of 7.3% (sensitivity of 40% based on model 1), adding family history would identify an additional 620,000 (95% CI: 221,100, 1,020,000) cases without a significant change in false-positive fraction. Study findings suggest that adding family history of diabetes can provide significant improvements in detecting undiagnosed diabetes in the US population. Further research is needed to validate the authors’ findings.

Family history is a consistent risk factor for many chronic diseases of public health significance (1) and, in the past few years, it has increasingly been discussed as a tool for preventing common diseases and for promoting health (2–4). In 2005, the US Surgeon General launched a public health campaign to enhance the public's awareness of the importance of family history (http://www.hhs.gov/familyhistory/), and the Centers for Disease Control and Prevention (CDC) has initiated a public health research initiative on this topic. The CDC's initiative is focused primarily on several common chronic diseases, including diabetes, stroke, heart disease, and cancers (http://www.cdc.gov/genomics/famhistory/index.htm). Yet, in spite of the increased interest in family history as a public health tool, the clinical validity and utility of this readily obtained risk factor have not been systematically evaluated.

In the present study, we assessed the improvements in detecting undiagnosed diabetes among US adults that might be obtained by using information on family history. Among an estimated 24 million individuals with diabetes in the United States in 2007 (based on fasting plasma glucose), 28% (6.6 million) were undiagnosed (5). One of the rationales for asking undiagnosed people about their family history is that a number of diabetes risk models/tools have included family history of diabetes as a risk factor, with an estimated relative risk 2–6 times that of people without family history (6–15). Furthermore, other studies suggest that family history might be an effective screening tool for identifying both diabetes and undiagnosed diabetes (1, 3, 14, 16–18). Even so, none of these studies has formally evaluated the improvements in detecting undiagnosed diabetes by using family history. This is important in part because both empirical and theoretical analyses have suggested that a significant and independent risk factor for a disease does not necessarily increase the ability of detecting the disease or to enhance the discrimination ability between people with and without disease (19).

Receiver-operating characteristic (ROC) curves and the associated C statistics are commonly used to summarize the diagnostic accuracy of risk models and to assess the improvements made to such models that are gained from adding other risk factors (20). Some studies, however, have criticized ROC curves for lacking the ability to display the risk in a particular population and to assess the reclassification of individuals into different risk groups (e.g., higher risk, lower risk) (19, 21). Recently, researchers have developed several alternative methods to assess the improvements made by a new marker or risk factor in risk models (22–25). Predictiveness curves, for example, display the distribution of risk in the population and also assess the classification ability of additional risk factors (24). Alternatively, the net reclassification improvement and integrated discrimination improvement integrate sensitivity, specificity, and the information from reclassification tables to assess improvements in risk models that include new risk factors (23). A third method involves net benefit curves, which might help to determine whether it would be cost-effective to include an additional risk factor in the risk model (25). We applied both conventional and recently developed methods to assess the improvements made from using family history to detect cases of undiagnosed diabetes among adults. Our source of data was the National Health and Nutrition Examination Survey (NHANES) for 1999–2004.

MATERIALS AND METHODS

NHANES is a series of stratified, multistage probability surveys designed to obtain information on the health and nutritional status of the civilian, noninstitutionalized US population. From 1999, NHANES data have been collected continuously, with every 2 years serving as 1 analytical cycle. The data are collected by the National Center for Health Statistics, CDC, via household interviews and physical examinations and are intended to provide estimates that are representative of the US population. Detailed information is available elsewhere (http://www.cdc.gov/nchs/nhanes.htm). The present study included 3 cycles (1999–2000, 2001–2002, and 2003–2004) of samples of adults aged ≥20 years who were examined in the morning after overnight fasting (between 8 and 23 hours) and did not have diagnosed diabetes. When analyzing combined data sets, we found that the sampling weights must be recalculated to produce unbiased estimates, because weights for the 1999–2000 cycle were based on population data prior to the 2000 US Census, and weights for the other cycles were based on the 2000 US Census. Detailed NHANES analytic and reporting guidelines that provide algorithms to recalculate the sampling weights can be found at the following website: (http://www.cdc.gov/NCHS/data/nhanes/nhanes_03_04/nhanes_analytic_guidelines_dec_2005.pdf).

Undiagnosed diabetes and family history of diabetes

We excluded pregnant women and persons with diagnosed diabetes, with unknown diabetes status, and with missing values for some of the covariates. Participants with a fasting plasma glucose level of ≥126 mg/dL (7.0 mmol/L) who reported no previous diagnosis of diabetes were defined as cases of undiagnosed diabetes (26).

We classified all participants into 3 mutually exclusive groups of familial risk on the basis of their family history of diabetes among first- and second-degree relatives: 1) high (at least 2 first-degree relatives or 1 first-degree and at least 2 second-degree relatives from the same lineage); 2) moderate (just 1 first-degree and 1 second-degree relative with diabetes, or only 1 first-degree relative with diabetes, or at least 2 second-degree relatives with diabetes from the same maternal or paternal line); or 3) average (no family history of diabetes or, at most, 1 second-degree relative with diabetes) (15). We use the term “family history of diabetes” to mean all 3 groups (high, moderate, and average). Limited information on family history of diabetes in NHANES 1999–2004 does not allow further detailed analysis.

Risk models

We used logistic regression models to calculate the predicted risk for undiagnosed diabetes. To select the appropriate models, we started with the list of those risk factors suggested by the American Diabetes Association that were available in NHANES 1999–2004 (27); these risk factors included age, race/ethnicity (non-Hispanic white, non-Hispanic black, Mexican American, others), body mass index, physical activity (inactive, irregularly active, regularly active), hypertension (≥140/90 mm Hg or on therapy for hypertension), a high density lipoprotein cholesterol level of ≤35 mg/dL (0.90 mmol/L) and/or a triglyceride level of ≥250 mg/dL (2.82 mmol/L), history of cardiovascular disease, and family history of diabetes. We used the backwards selection approach, including all suggested risk factors in the multiple logistic regression models with α = 0.10 to select the final models (28, 29). These final models included age, gender, body mass index, hypertension, low high-density lipoprotein cholesterol and/or elevated triglycerides, and family history of diabetes. We found no evidence of multicollinearity among the selected risk factors (30). We tested interactions between family history and other risk factors by including the product terms in the risk models based on the Satterthwaite-adjusted F test. There is no evidence of significant interaction. We also included age as a nonlinear term, the logarithm of high density lipoprotein cholesterol as a continuous variable, and the interaction between body mass index and high density lipoprotein cholesterol in the model. The full model does not offer significant improvements over the main effect models (results not shown). For simplicity, we used the main effects models. Similar sets of risk factors have been used and validated by other studies using the NHANES data (15, 31, 32). For assessments of the improvements in detecting undiagnosed diabetes by using family history of diabetes, we calculated 2 risk models: one that had the selected risk factors excluding family history of diabetes (model 1) and the other with the selected risk factors plus family history of diabetes (model 2, nested model).

Statistical analysis

The adjusted and weighted prevalence and odds ratios and 95% confidence intervals for undiagnosed diabetes were obtained by logistic regression models by using the predicted margins by the 3 categories of family history of diabetes (33). The prevalence and odds ratios were adjusted by the risk factors selected for the final model. We estimated the mean and standard error for continuous variables, proportions for categorical variables, and their 95% confidence intervals by levels of family history of diabetes. We tested for significant differences in the mean and prevalence across levels of family history of diabetes based on Satterthwaite-adjusted F statistics and on the χ² test, respectively. All tests were 2 tailed at the α = 0.05 level of significance.

Assessment of risk models and improvements from using family history in detection of undiagnosed diabetes

For the global measure of models’ fit, we used the Akaike Information Criterion (AIC) estimated from the logistic regression models; a difference in AIC between 2 models of >2 was interpreted as a significant improvement for the model with the smaller AIC (34). For models’ calibration, we calculated Hosmer-Lemeshow goodness-of-fit statistics on the basis of deciles of risk (29). For the discrimination abilities of family history of diabetes, we constructed the weighted ROC curves and calculated the C statistics (35). To test for the significance of differences between AIC values, between weighted ROC curves, and between C statistics of different risk models, we used the rescaling bootstrap method of Cheng et al. (36) and Rao et al. (37) that takes into account the complex survey design by changing the sampling weights for each resample. We generated 1,000 rescaled bootstrap weights, calculated the distribution for the 2.5 and 97.5 percentiles, and reported these values as the 95% confidence intervals of the differences between different risk models (38).

The predictiveness curve described earlier is an integrated plot of predicted risks from logistic regression models formed by the percentiles of risk in the population (24). From the predictiveness curves, one could read off the predicted probability of an event for any corresponding true-positive fraction (sensitivity) or false-positive fraction (1 − specificity). We constructed the weighted predictiveness curves. For the summary measure of weighted predictiveness curves, we calculated the proportion-explained variations (R²) for each risk model and used the rescaling bootstrap method to make the inference about significant differences between the different R² variations (37). The difference between R² variations is equivalent to the integrated discrimination improvement index proposed by Pencina et al. (23) and Pepe et al. (39) that measures the ability of the additional risk factor to increase the predicted probability among those who had the event and to decrease the predicted probability among those who were event free (23).

For risk prediction, it is important to examine if the model with the additional risk factor can more accurately stratify individuals into higher or lower risk categories (risk reclassification) (21). Some recently developed risk reclassification measures require use of recognized risk thresholds (22, 23), but at present no researchers or clinicians have proposed any risk classification schemes (risk thresholds) for clinical use in identifying higher- or lower-risk patients for diabetes. Nor have they proposed follow-up tests such as glucose testing for people at higher or lower risk to identify those who really have diabetes. Accordingly, we used logistic regression model 1 to determine the predicted probability of events that corresponded approximately to 20%, 40%, 60%, and 80% of undiagnosed diabetes (dichotomous cutpoints at quintiles of sensitivity) and used these probability thresholds to identify the true-positive fraction and false-positive fraction from the predictiveness curves. We also calculated the net reclassification improvement index, positive predictive values, and negative predictive values for each dichotomous risk threshold for model 1 and model 2, respectively. The net reclassification improvement index is a special case of integrated discrimination improvement with the recognized risk thresholds (23). We used the rescaled bootstrap method with 1,000 samples to estimate the 95% confidence intervals of integrated discrimination improvement and net reclassification improvement (39).

To help to determine whether including a risk factor in a risk model might be cost-effective, we used decision curve analysis (25). Briefly, decision curve analysis estimates the net benefit of a model by taking the difference between the number of true positives and the number of false positives weighted by the odds of the selected threshold probability of risk for a range of threshold probabilities (25, 40). The net benefit of a model compared with the reference net benefit or compared with another model might be interpreted as the net increase in the proportion of cases identified. The reference was calculated by assuming that all people were tested for the events, and testing no one was set to a net benefit of zero. For any given threshold probability cutpoint, the risk models with the higher net benefit are the preferred model (41). We calculated and plotted the weighted net benefit curves for the reference model (testing all), model 1, and model 2, respectively. We used the quintile cutpoints of the predicted probabilities to compare the net benefits curves of model 1 and model 2 and calculated the differences in the net benefit between the 2 models for the each cutpoint and 95% confidence interval of difference between the 2 models using the rescaled bootstrap method. Unless otherwise specified, data were analyzed by using SAS, version 9.2, software (SAS Institute, Inc., Cary, North Carolina) and SUDAAN, release 9.0, software (Research Triangle Institute, Research Triangle Park, North Carolina) to account for the complex sampling design of NHANES 1999–2004 (42).

RESULTS

NHANES 1999–2004 surveyed 5,551 adults aged ≥20 years without diagnosed diabetes who were asked for a blood sample after fasting overnight. The 498 persons excluded included 324 pregnant women, 1 person with unknown diabetes status, and 173 people with missing covariates. Of the final sample (n = 5,053), 73.6% were non-Hispanic white; 10.5%, non-Hispanic black; 7.2%, Mexican American; and 8.8%, other race/ethnicity.

The prevalence of undiagnosed diabetes, adjusted odds ratios, and characteristics of the people by level of familial risk of diabetes are summarized in Table 1. The prevalence increased significantly with level of familial risk from 2.2% (95% confidence interval (CI): 1.7, 2.6) to 7.2% (95% CI: 4.2, 10.1) (P = 0.001). The adjusted odds ratio increased from 1.7 (95% CI: 1.2, 2.5) to 3.8 (95% CI: 2.2, 6.3) for moderate and high familial risk, respectively. Familial risk of diabetes was significantly associated with all the selected covariates except for physical activity.

Table 1.

Characteristics of Participants by Family History of Diabetes, National Health and Nutrition Examination Survey, 1999–2004

Characteristic	Sample, no.	Familial Risk of Diabetes						P Valuea
		Average (n = 3,526)	95% CI	Moderate (n = 1,150)	95% CI	High (n = 377)	95% CI
Prevalence of undiagnosed diabetes, %	200	2.2	1.7, 2.6	3.6	2.5, 4.7	7.2	4.2, 10.1	0.001
Adjusted odds ratiob		1.0		1.7	1.2, 2.5	3.8	2.2, 6.3	<0.001
Mean age, years (SE)	5,053	44.7 (0.43)		46.5 (0.75)		47.3 (0.87)		0.002
Gender, %
Male	2,556	49.9	48.5, 51.4	48.5	45.3, 51.8	41.6	35.0, 48.5
Female	2,497	50.1	48.6, 51.5	51.5	48.2, 54.7	58.4	51.5, 65.0	0.046
Race/ethnicity, %
Non-Hispanic white	2,682	74.8	71.2, 78.1	72.6	67.6, 77.0	63.5	55.3, 70.9
Non-Hispanic black	907	9.8	7.9, 12.0	11.1	8.6, 14.2	16.3	11.9, 21.8
Mexican American	1,131	6.6	5.2, 8.3	8.4	5.9, 11.7	10.3	7.3, 14.4
Other (including other Hispanic)	333	8.9	6.6, 11.9	8.0	5.4, 11.5	9.9	6.0, 15.9	<0.001
Body mass index category, %
<18.5 kg/m2	71	2.1	1.6, 2.9	1.0	0.5, 2.1	1.0	0.3, 3.2
18.5–24.9 kg/m2	1,628	37.4	35.1, 39.8	27.7	24.2, 31.5	26.9	21.2, 33.6
25–29.9 kg/m2	1,843	34.7	32.3, 37.2	35.9	32.4, 39.5	35.1	27.7, 43.2
≥30 kg/m2	1,511	25.8	23.7, 27.9	35.4	32.4, 38.5	37.0	30.5, 44.0	<0.001
Physical activity (n = 4,889), %
Inactive	2,023	33.4	31.0, 35.8	36.2	32.8, 39.7	39.5	33.7, 45.7
Irregularly active	1,649	38.5	36.5, 40.6	36.3	32.0, 40.9	36.8	30.5, 43.5
Regularly active	1,240	28.1	25.8, 30.5	27.5	23.6, 31.8	23.7	18.6, 29.7	0.136
Hypertension, %
Yes	2,010	31.2	29.2, 33.4	38.0	34.8, 41.3	40.0	33.9, 46.3
No	3,043	68.8	66.6, 70.8	62.0	58.7, 65.2	60.0	53.7, 66.1	<0.001
Lipid, %
HDL-C of ≤35 mg/dL or triglycerides of ≥250 mg/dL	851	15.4	14.0, 16.9	20.8	17.6, 24.5	21.2	15.7, 27.9
Other	4,202	84.6	83.1, 86.0	79.2	75.5, 82.4	78.8	72.1, 84.3	0.011
History of heart disease, %
Yes	371	4.9	4.1, 5.7	5.9	4.4, 7.9	10.5	7.2, 15.0
No	4,654	95.1	94.3, 95.9	94.1	92.1, 95.6	89.5	85.0, 92.8	0.005
Overall	5,053	71.9	69.9, 73.7	21.8	20.0, 23.8	6.3	5.5, 7.2	<0.001

Abbreviations: CI, confidence interval; HDL-C, high density lipoprotein cholesterol; SE, standard error.

^aFor prevalence and odds ratios of undiagnosed diabetes, P values were for the trend across the categories of family history of diabetes based on the Satterthwaite-adjusted F test; for categorical variables, P values were based on the χ² test; all tests were 2 tailed.

^bAdjusted for age, gender, body mass index, hypertension, a HDL-C level of ≤35 mg/dL (0.90 mmol/L) and/or a triglyceride level of ≥250 mg/dL, and family history of diabetes.

Assessing improvements in the detection of undiagnosed diabetes by using family history

Table 2 includes several statistical measures of overall fit, discrimination ability, and reclassification of risk for models 1 and 2. Compared with model 1, model 2 represented significant improvements in 3 statistical measures in detecting undiagnosed diabetes: a lower AIC, a significant improvement in the weighted C statistic, and a significant improvement in reclassification as measured by integrated discrimination improvement. Models 1 and 2 demonstrated similar levels of calibration (goodness-of-fit tests), suggesting the adequate fit of both models.

Table 2.

Comparison of 2 Models’ Fit, Discrimination Ability, and Risk Reclassification, National Health and Nutrition Examination Survey, 1999–2004

Statistical Measures of Undiagnosed Diabetes	Models		Difference (Model 1 − Model 2)	95% CIa
	Without Family History (Model 1)b	With Family History (Model 2)c
AICd	590	579	10.9	1.4, 24.3
Goodness-of-fit teste	12.6 (0.126)	7.0 (0.534)
Weighted C statistics	0.826	0.842	0.016	0.005, 0.031
R2/IDI	0.055	0.067	0.012f	0.004, 0.030

Abbreviations: AIC, Akaike Information Criterion; CI, confidence interval; IDI, integrated discrimination improvement.

^aThe 2.5 and 97.5 percentile distributions of 1,000 rescaled bootstrap samples of the differences between the different risk models.

^bModel 1 was adjusted for age, gender, body mass index, hypertension, and a high density lipoprotein cholesterol level of ≤35 mg/dL (0.90 mmol/L) and/or a triglyceride level of ≥250 mg/dL.

^cModel 2 included, in addition to the risk factors in model 1, family history of diabetes.

^dThe means and differences of AIC were generated from 1,000 rescaled bootstrap samples for the different risk models.

^eHosmer-Lemeshow goodness-of-fit test; the numbers are χ², with P values in parentheses.

^fThe difference between the R² of the 2 risk models equals the IDI.

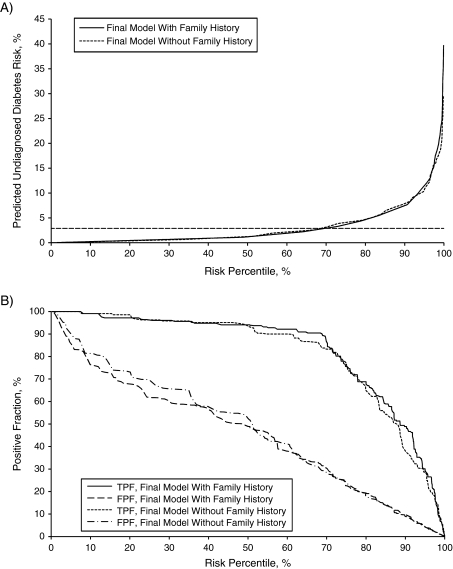
Figure 1A plots the weighted predictiveness curves, and Figure 1B shows the weighted true-positive fraction and false-positive fraction by risk percentiles in the population. These graphs show that using family history of diabetes, in addition to the selected risk factors, reclassified the people with undiagnosed diabetes to the higher predicted risk and the diabetes-free people to the lower predicted risk. Appendix Table 1 presents a detailed analysis of the selected risk thresholds. In a comparison of model 2 with model 1, for a higher risk threshold (e.g., at 7.3%, or approximately the 89th percentile of risk distribution in the population) (Figure 1), the weighted true-positive fraction (Appendix Table 1) increased from 40.0% (95% CI: 29.4, 51.5) in model 1 to 49.4% (95% CI: 37.9, 60.9) in model 2. The weighted positive predictive value rose from 11.0% (95% CI: 8.5, 14.4) to 14.2% (95% CI: 10.9, 18.2), and the net reclassification improvement in model 2 was 10.1% (95% CI: 1.0, 18.1; P = 0.009). The weighted false-positive fraction and the negative predictive value remained largely unchanged at this risk threshold. At this level of risk, model 2 would identify approximately 620,000 (95% CI: 221,100, 1,020,000) more cases of undiagnosed diabetes in the population than would model 1 (2.64 million vs. 3.26 million). As the risk thresholds lowered, model 2 was associated with a decreased false-positive fraction and little change in negative predictive value compared with model 1. However, these changes were not significant enough to have a significant improvement in risk reclassification indicated by net reclassification improvement.

Figure 1.

Weighted predictiveness curves (A) and true-positive fraction (TPF) and false-positive fraction (FPF, 1 − specificity) (B) for model with selected risk factors (model 1) and model with selected risk factors plus family history of diabetes (model 2), National Health and Nutrition Examination Survey, 1999–2004. The horizontal dashed line in A indicates the prevalence of undiagnosed diabetes in the population (2.9%).

Decision curves analysis

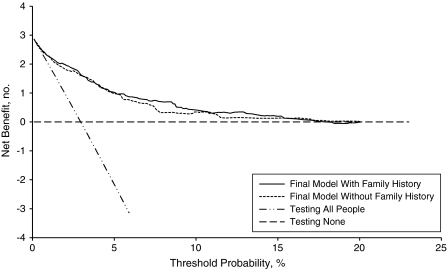
Figure 2 presents the weighted net benefit curves derived for testing all people versus testing strategies based on model 1 and model 2. Model 2 appeared to offer greater net benefit across most risk thresholds, especially from the predicted risk of around 5% to 15%. Both of the model-based net benefits were higher than testing all (the reference testing strategy). Appendix Table 2 presents the detailed analysis of net benefits for 4 selected risk thresholds. Comparing model 2 with model 1, for example, at a 7.3% risk threshold (40% sensitivity based on model 1), the difference of net benefit equals 0.32 per 100 people (95% CI: 0.06, 0.58), indicating that 3 extra cases of undiagnosed diabetes would be detected per 1,000 subjects based on model 2. The differences in net benefits between the 2 models diminished at either higher or lower risk thresholds, especially at the lower risk thresholds.

Figure 2.

Weighted decision curves for models predicting undiagnosed diabetes using models with family history of diabetes (solid line) and without this history (small dashed line), National Health and Nutrition Examination Survey, 1999–2004. The dash-dot-dot-dash line indicates the net benefit of testing all people, and the horizontal dashed line indicates testing none of the people. The y axis indicates the number of true cases identified per 100 people.

DISCUSSION

This study confirms that family history of diabetes is an independent risk factor for undiagnosed diabetes, a finding that is consistent with those of many other studies (6–15, 43). Recent National Institutes of Health state-of-the-science statements on family history recognized the important role of family history in the practice of medicine, motivation of positive lifestyle changes, and influence of clinical interventions (44). Our study assessed the improvements in detecting undiagnosed diabetes that would come from including family history in risk assessment and population screening. Our findings suggest that using a risk model with family history of diabetes offers significant improvements over a model with common risk factors in detecting undiagnosed diabetes, especially among populations at higher risk. For example, by using a risk threshold of 7.3% (the median predicted risk = 1.3% in the population), approximately 11% of the population had a predicted risk ≥7.3% based on model 1. With model 2 we had a net reclassification improvement of 10.1% (95% CI: 1.0, 18.1; P = 0.009) that was mainly due to the increase in true-positive fraction from 40.0% (95% CI: 29.4, 51.5) in model 1 to 49.4% (95% CI: 37.9, 60.9) in model 2, a 24% increase in the number of undiagnosed diabetes cases identified. In other words, using model 2 at a risk threshold of 7.3%, one would identify approximately 3.26 million cases instead of 2.64 million cases of undiagnosed diabetes of an estimated 6.6 million total cases without an increase in false-positive fraction.

Some researchers have argued that the statistical measures of risk models for performance in prediction and reclassification have limited value for evaluation of the clinical utility of the additional risk factor/marker because they do not consider cost-effectiveness (25, 41, 45). However, the traditional cost-effectiveness analysis of diagnostic tests has involved collecting additional data on alternative treatments that could involve substantial cost and sometimes might be difficult to collect (46, 47). The decision curve analysis, which does not require collecting additional data on cost and effectiveness, offers a simple approach to examining the clinical consequences of alternative testing strategies and to comparing the different risk models in terms of net benefits over a range of predicted probabilities for an event (25). The focus of the net benefit curves is not on any particular point estimate, but rather on the entire range of threshold probabilities in a way that one net benefit curve is greater or lesser than the other alternatives (25, 48). Our findings indicate that the net benefit curves derived from model 2 (versus model 1) were greater over nearly the whole range of risk thresholds, especially from 5% to 15% predicted risks, indicating the net benefit of detecting extra cases of undiagnosed diabetes based on model 2. Given the fact that little cost might be involved in collecting information on family history of diabetes, the evaluation of added value of using family history should mainly focus on the magnitude of the benefit rather than on cost-effectiveness.

The limitations to our study include, first, that NHANES is a cross-sectional survey, and it cannot be used to predict the risk of developing diabetes. Accordingly, we focused our analysis on the improvements in detecting undiagnosed diabetes that might be realized by incorporating family history of diabetes in a model. Second, NHANES 1999–2004 measured fasting glucose but did not assess glucose tolerance, and thus it might have underestimated the prevalence of diabetes. However, the American Diabetes Association has recommended that, for epidemiologic studies and estimates of diabetes prevalence, a fasting plasma glucose level of ≥126 mg/dL (7.0 mmol/L) should be used (49). Third, diabetes was self-reported in NHANES 1999–2004, and reporting bias by different groups might exist. Studies indicated that the proportion of undiagnosed diabetes was higher in men, Mexican Americans, and the uninsured compared with women, non-Hispanic whites, and the insured, suggesting some reporting bias of diagnosed diabetes (50). The prevalence of undiagnosed diabetes might be overrepresented in certain groups in NHANES 1999–2004. Fourth, the family risk of diabetes was significantly related to sex and race/ethnicity (31, 51, 52). Women tend to have a better knowledge of the presence of the disease among their relatives, and the large families, for example, non-Hispanic blacks and Mexican Americans compared with non-Hispanic whites, are likely to have a greater possibility of relatives with diabetes than the smaller families, especially among populations where the disease prevalence is high. To examine the possible effect of sex, ethnicity, or racial differences in the familial risk of diabetes on the detection of undiagnosed diabetes, we conducted stratified analysis by sex and race/ethnicity; the results suggested that the improvements in detecting undiagnosed diabetes by using family history of diabetes are consistent across sex and race/ethnicity strata (Appendix Table 3). Fifth, there are no generally recognized risk thresholds for undiagnosed diabetes; we arbitrarily used the quintile cutpoints of predicted risk that included 20%, 40% 60%, or 80% of undiagnosed diabetes cases based on risk model 1. Some statistical measures of how well a model performs in prediction, such as net reclassification improvement, might be sensitive to the risk thresholds used (23). Sixth, using the same data to fit a risk model and to assess its performance could lead to overfitting. We conducted 5-fold cross-validation and obtained an average weighted area under curve = 0.84 for the final model with family history, and external validation using the NHANES III (1988–1994) data set obtained a weighted area under curve = 0.89, indicating adequate performance of our risk models.

The major strengths of our study include the availability of fasting glucose measurements from a nationally representative sample of the US adult population and the large number of potential risk factors for undiagnosed diabetes to investigate.

Our findings suggest that family history of diabetes provides significant improvements in the detection of additional cases of undiagnosed diabetes, especially among people with higher predicted risk. It also provides greater net benefits than a risk model without family history when applied to the US population. Unlike other biomarkers, for example, prostate-specific antigen for prostate cancer or C-reactive protein for cardiovascular diseases, or genetic testing, obtaining information on family history of diabetes costs little, and no adverse effect is associated with the process. With increased awareness and education, family history could be a useful part of a public health tool designed for the detection and control of diabetes in populations.

Glossary

Abbreviations

AIC

Akaike Information Criterion

CDC

Centers for Disease Control and Prevention

CI

confidence interval

NHANES

National Health and Nutrition Examination Survey

ROC

receiver-operating characteristic

Appendix.

Appendix Table 1.

Weighted True-Positive Fraction, False-Positive Fraction, Positive Predictive Value, Negative Predictive Value, and Net Reclassification Index of Undiagnosed Diabetes Using Risk Models With and Without Family History of Diabetes, National Health and Nutrition Examination Survey, 1999–2004

Predicted Probability of Events, %	Undiagnosed Diabetes										No. of Cases of Undiagnosed Diabetes Identified in Population (× 100,000)	No. of People ≥ Predicted Probability in Population (× 100,000)
	True-Positive Fraction	95% CI	False-Positive Fraction	95% CI	Positive Predictive Value	95% CI	Negative Predictive Value	95% CI	Net Reclassification Index, %	95% CI
	Model Without Family History (Model 1)a
12.0	20.0	13.8, 29.6	3.3	2.9, 3.9	15.8	10.7, 22.6	97.6	97.1, 98.0			13.2	56.9
7.3	40.0	29.4, 51.5	9.7	9.0, 10.5	11.0	8.5, 14.4	98.1	97.4, 98.5			26.4	170.9
5.4	60.0	50.8, 69.5	15.7	14.5, 16.9	10.5	8.6, 12.7	98.6	98.1, 99.0			39.6	268.7
3.6	80.0	71.5, 86.8	26.1	24.5, 27.9	8.5	7.3, 9.9	99.2	98.7, 99.5			52.8	448.3
	Model with Family History (Model 2)b
12.0	27.2	19.1, 37.1	3.7	3.1, 4.4	18.3	13.1, 25.0	97.8	97.2, 98.2	6.3	0.6, 12.1c	17.9	63.1
7.3	49.4	37.9, 60.9	9.1	8.2, 10.0	14.2	10.9, 18.2	98.4	97.8, 98.8	10.1	1.0, 18.1c	32.6	159.4
5.4	60.0	48.2, 70.4	14.4	13.4, 15.5	11.2	9.0, 13.9	98.7	98.0, 99.0	0.7	−7.1, 7.6c	39.6	246.8
3.6	75.2	66.8, 82.1	23.5	22.0, 25.0	8.9	7.5, 10.5	99.0	98.6, 99.3	−2.3	−9.3, 3.8c	49.6	403.5

Abbreviation: CI, confidence interval.

^aModel 1 included age, gender, body mass index, hypertension, and a high density lipoprotein cholesterol level of ≤35 mg/dL (0.90 mmol/L) and/or a triglyceride level of ≥250 mg/dL.

^bModel 2 included, in addition to model 1 risk factors, family history of diabetes.

^cThe 95% confidence intervals of the net reclassification index were estimated by using 1,000 rescaled bootstrap samples for the complex surveys.

Appendix Table 2.

Weighted Net Benefit and Differences in Net Benefit for Testing All People for Undiagnosed Diabetes or According to Risk Models With or Without Family History Using Selected Thresholds of Predicted Probabilities of Undiagnosed Diabetes, National Health and Nutrition Examination Survey, 1999–2004

Predicted Probability of Events, %	True-Positive Fraction, %	95% CI	Models	Net Benefit, %	95% CIa	Differences Between Testing All vs. Model 1 and Model 1 vs. Model 2	95% CIa
12.0	20.0	13.8, 29.6	Testing allb	−10.30	−10.86, 9.85
			Model 1c	0.16	−0.09, 0.39	10.5	9.99, 11.00
			Model 2d	0.32	0.03, 0.58	0.16	0.03, 0.33
7.3	40.0	29.4, 51.5	Testing allb	−4.70	−5.23, 4.27
			Model 1c	0.44	0.10, 0.74	5.14	4.61, 5.65
			Model 2d	0.76	0.37, 1.13	0.32	0.06, 0.58
5.4	60.0	50.8, 69.5	Testing allb	−2.61	−3.13, 2.19
			Model 1c	0.91	0.52, 1.21	3.52	3.11, 3.90
			Model 2d	0.96	0.55, 1.33	0.05	−0.12, 0.32
3.6	80.0	71.5, 86.8	Testing allb	−0.69	−1.2, 0.28
			Model 1c	1.41	1.00, 1.74	2.10	1.82, 2.37
			Model 2d	1.36	0.92, 1.68	−0.03	−0.23, 0.14

Abbreviation: CI, confidence interval.

^aNinety-five percent confidence intervals of the difference in net benefit between testing all versus model 1 and model 1 versus model 2 were estimated by using 1,000 rescaled bootstrap samples for complex surveys.

^bAssuming that all people were tested for fasting glucose concentrations for diagnosis of diabetes.

^cModel 1 included age, gender, body mass index, hypertension, and a high density lipoprotein cholesterol level of ≤35 mg/dL (0.90 mmol/L) and/or a triglyceride level of ≥250 mg/dL.

^dModel 2 included, in addition to the risk factors of model 1, family history of diabetes.

Appendix Table 3.

Comparison of Models’ Fit, Discrimination Ability, Risk Stratification, and Risk Reclassification Between Models With and Without Family History of Diabetes for Detecting Undiagnosed Diabetes Stratified by Sex and Race/Ethnicity, National Health and Nutrition Examination Survey, 1999–2004

Statistical Measures	Models		Differences (Model 1 − Model 2)	95% CIa
	Without Family History (Model 1)b	With Family History (Model 2)c
Male
AICd	357.4	356.3	1.1	−3.6, 9.9
Goodness-of-fit teste	7.4 (0.289)	3.5 (0.743)
Weighted C statistics	0.837	0.848	0.011	0.001, 0.024
R2/IDI	0.0677	0.0734	0.006	−0.001, 0.031f
Female
AICd	247.3	239.2	8.1	−0.5, 18.9
Goodness-of-fit teste	5.1 (0.280)	2.0 (0.732)
Weighted C statistics	0.820	0.847	0.027	0.005, 0.054
R2/IDI	0.049	0.073	0.024	0.006, 0.065f
Non-Hispanic white
AICd	319.6	316.4	3.2	−2.6, 11.4
Goodness-of-fit teste	4.2 (0.124)	3.1 (0.213)
Weighted C statistics	0.848	0.863	0.015	0.003, 0.031
R2/IDI	0.063	0.073	0.010	0.001, 0.039f
Non-Hispanic black
AICd	131.9	128.3	3.6	−3.2, 15.5
Goodness-of-fit teste	3.2 (0.788)	6.3 (0.392)
Weighted C statistics	0.831	0.856	0.025	−0.006, 0.061
R2/IDI	0.072	0.113	0.041	0.010, 0.125f
Mexican American
AICd	125.7	118.5	7.3	−3.3, 22.2
Goodness-of-fit teste	3.1 (0.381)	4.6 (0.203)
Weighted C statistics	0.854	0.896	0.042	−0.003, 0.085
R2/IDI	0.064	0.125	0.061	0.010, 0.191f

Abbreviations: AIC, Akaike Information Criterion; CI, confidence interval; IDI, integrated discrimination improvement.

^aThe 2.5 and 97.5 percentile distributions of 1,000 rescaled bootstrap samples of the differences between the different risk models.

^bModel 1 was adjusted for age, gender, body mass index, hypertension, and a high density lipoprotein cholesterol level of ≤35 mg/dL (0.90 mmol/L) and/or a triglyceride level of ≥250 mg/dL.

^cModel 2 included, in addition to the risk factors in model 1, family history of diabetes.

^dThe means and differences of AIC were generated from 1,000 rescaled bootstrap samples for the different risk models.

^eHosmer-Lemeshow goodness-of-fit test; the numbers are χ², with P values in parentheses.

^fThe difference between the R² of the 2 risk models equals the IDI.