Middle-Ear Pressure Gain and Cochlear Partition Differential Pressure in Chinchilla

Abstract

An important step to describe the effects of inner-ear impedance and pathologies on middle- and inner-ear mechanics is to quantify middle- and inner-ear function in the normal ear. We present middle-ear pressure gain G_MEP and trans-cochlear-partition differential sound pressure ΔP_CP in chinchilla from 100 Hz to 30 kHz derived from measurements of intracochlear sound pressures in scala vestibuli P_SV and scala tympani P_ST and ear-canal sound pressure near the tympanic membrane P_TM. These measurements span the chinchilla's auditory range. G_MEP had constant magnitude of about 20 dB between 300 Hz and 20 kHz and phase that implies a 40-μs delay, values with some similarities to previous measurements in chinchilla and other species. ΔP_CP was similar to G_MEP below about 10 kHz and lower in magnitude at higher frequencies, decreasing to 0 dB at 20 kHz. The high-frequency rolloff correlates with the audiogram and supports the idea that middle-ear transmission limits high-frequency hearing, providing a stronger link between inner-ear macromechanics and hearing. We estimate the cochlear partition impedance Z_CP from these and previous data. The chinchilla may be a useful animal model for exploring the effects of nonacoustic inner-ear stimulation such as “bone conduction” on cochlear mechanics.

1. Introduction

The study of middle-ear and inner-ear mechanics explores the mechanisms by which sound pressure in the ear canal is converted to a stimulus for the sensory cells of the cochlea. With an understanding of these mechanisms comes an ability to describe the effects of middle-ear and inner-ear pathologies on hearing, to develop more reliable methods to diagnose pathologies, and to evaluate the mechanisms by which those pathologies affect hearing.

Middle-ear and inner-ear pathologies affect hearing by modifying the effective input to the cochlea. It has been proposed (e.g., Dallos, 1970) that the effective cochlear input is the differential sound pressure across the cochlear partition: the difference between scala vestibuli sound pressure P_SV and scala tympani sound pressure P_ST. (P_SV, P_ST, and all other quantities shown in bold face are complex variables with magnitude and phase that are functions of frequency f.) This differential sound pressure P_SV – P_ST induces motion of the cochlear partition that stimulates the sensory cells of the organ of Corti and leads to hearing perception. Comparisons of differential sound pressure to measures of organ of Corti sensory cell activity (cochlear potential CP – Nedzelnisky, 1980; Dancer and Franke, 1980) and analysis of hearing in patients in whom the ossicular chain is missing (Peake et al., 1992) provide support for this assertion.

In the past, researchers have used measurements at more peripheral points, such as tympanic membrane (TM) admittance, umbo or stapes velocity, and/or models of middle-ear and cochlear function based on anatomy and material properties to estimate the effective cochlear input, establish the relationship between cochlear input and ear-canal sound pressure or auditory threshold, and gauge the effects of middle-ear pathologies or reconstructions on cochlear function and hearing. Measuring sound pressures inside the cochlea has two primary advantages over more peripheral measurements: (1) These sound pressures within the cochlear scalae are the pressures actually applied to the cochlea, so complications such as which of the multiple modes of stapes motion produce effective cochlear input are moot; and (2) since sound pressure is a scalar quantity, the sound pressure at a given location inside the cochlea (unlike stapes velocity) is independent of the measurement direction.

In this paper we present new measurements of P_SV and P_ST in chinchilla using miniature fiber-optic pressure sensors (Olson, 1998; Slama, 2008; Slama et al., 2009, in press). These measurements are used with measurements of ear-canal sound pressure near the tympanic membrane P_TM to compute the middle-ear pressure gain G_MEP and the normalized differential trans-cochlear-partition pressure ΔP_CP:

$${\mathbf{G}}_{\mathbf{MEP}}={\mathbf{P}}_{\mathbf{SV}}∕{\mathbf{P}}_{\mathbf{TM}};\mathrm{and}$$ (1a)

$$\Delta {\mathbf{P}}_{\mathbf{CP}}=({\mathbf{P}}_{\mathbf{SV}}-{\mathbf{P}}_{\mathbf{ST}})∕{\mathbf{P}}_{\mathbf{TM}}={\mathbf{G}}_{\mathbf{MEP}}-{\mathbf{P}}_{\mathbf{STn}},$$ (1b)

where P_STn = P_ST/P_TM. ΔP_CP represents the effective input to the cochlear partition for a given sound pressure in the ear canal, as mentioned above. We use G_MEP and ΔP_CP to compute the input impedance of the cochlear partition Z_CP from previous measurements of the cochlear input impedance (Slama, 2008; Slama et al., in press).

The middle-ear pressure gain is one part of the description of the transformation of sound from the ear canal to the cochlea by the middle ear (the ratio of stapes velocity to P_TM is the other, e.g., Shera and Zweig, 1992). These new measurements of P_SV and P_ST, though somewhat preliminary, extend recent measurements of G_MEP in chinchilla in our laboratory (Slama, 2008; Slama et al., 2009) to higher frequencies, add to a small but growing database of cochlear sound pressure transfer functions in normal ears in various species, and therefore represent a step toward a more complete understanding of middle-ear sound transmission.

2. Methods

2.1 Preparation

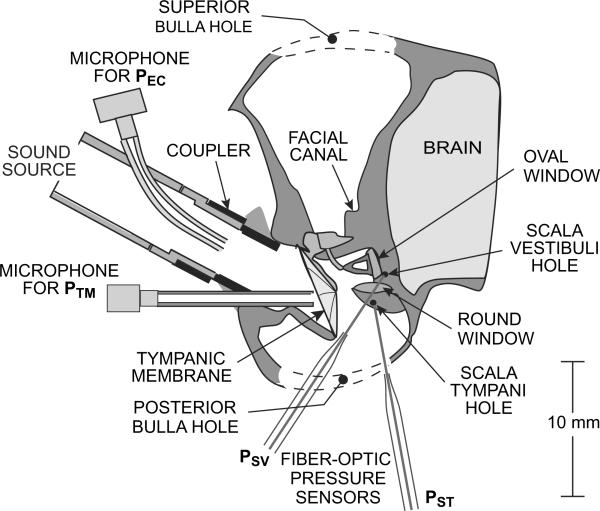
These experiments were performed in accordance with guidelines published by the U.S. Public Health Service and were approved by the Massachusetts Eye & Ear Infirmary Institutional Animal Care and Use Committee. Five ears in four chinchillas were used in this study. (Several other ears were used in preliminary experiments or had various mishaps.) Animals remained alive throughout the experiment. Most of the preparation has been described in detail previously (Songer and Rosowski, 2006). Briefly, each animal was anesthetized with Nembutal (50 mg/kg) and Ketamine (40 mg/kg) and tracheotomized, the external ear was removed (usually the left), skin and soft tissue were removed from the skull around the bony external ear canal, and openings were made in the bulla wall superior and posterior to the ear canal. Lidocaine (1%) was sometimes used as a topical anesthetic in sensitive areas. Through the superior opening, the tendon of the tensor tympani muscle and the tympanic branch of the facial nerve (which innervates the stapedius muscle) were cut to prevent random contractions of these muscles during the experiment from affecting results (see Rosowski et al., 2006).

A short brass tube was glued to the skull around the bony ear canal to allow a sound source to be coupled repeatably to the ear. A stainless steel sleeve was glued under the brass coupler to allow a probe tube microphone tip to measure sound pressure P_TM within 1–1.5 mm of the umbo within the tympanic membrane (TM) – see Figure 1. A thin web of bone that obscures the view of the stapes and the oval-window (OW) and round-window (RW) niches was carefully chipped away to provide access to the bone of the vestibule just posterior to the oval window and to the surface of the cochlear capsule inferior and posterior to the round window. A small hole was drilled through the vestibular wall with a fine pick to allow a pressure sensor to measure sound pressure within scala vestibuli P_SV. The desired hole size was between 150 and 200 μm diameter, slightly larger than the sensor tip (145 μm diameter), but in two of the ears the hole size was closer to 400 μm dia., and in two ears the bone between the hole and the OW cracked. (The cracked bone was not displaced.) The effect of the crack is discussed later.

Figure 1.

Diagram of a chinchilla left ear showing the preparation and the placement of microphones and fiber-optic pressure sensors. An earphone (not shown) was connected to the sound source. Sound pressure in the ear canal was measured by probe-tube microphones near the source (P_EC) and near the umbo within the TM (P_TM). Sound pressure in the cochlear scalae was measured by pressure sensors inserted through small holes into scala vestibuli (P_SV) and scala tympani (P_ST).

After P_SV measurements, a similar small hole was made in the cochlear capsule approximately 1 mm inferior to the RW (near the apical extent of the “hook” region) with a 0.006” (150 μm) pivot drill. The more exposed location on the cochlear capsule allowed the drill to be brought perpendicular to the surface of the cochlear capsule and allowed visibility of the tip. With this drill, a hole could be made through the hard bone of the cochlear capsule into scala tympani for P_ST measurements fairly quickly, and hole size could be controlled closely. The tight quarters and poor visibility in the OW niche and the non-perpendicularity of the vestibular wall relative to the access direction precluded using the drill for the scala vestibuli hole.

2.2 Stimuli, responses, and equipment

Stimuli were synthesized by computer and/or played by a computer-controlled signal generator (Hewlett-Packard 33120A). Stimulus levels were set by programmable attenuators (Tucker-Davis PA-5) and a reconstruction filter with programmable gain (Krohn-Hite 3901). A power amplifier (Crest 1001A) was used to drive a low-impedance earphone (Radio Shack 40-1377) to generate sound in the ear canal or a shaker for pressure sensor calibration. Two types of sound stimuli were used: A broadband chirp with uniform component magnitude from 49 Hz to 49 kHz, or a sequence of tones. Two sequences were used: 98 Hz – 49 kHz at 6 pts/octave (as permitted by a 49-Hz frequency spacing) and 14 – 49 kHz at 12 pts/octave. Chirps allowed overview measurements to be made quickly, provided sufficient frequency resolution to guide P_SV and P_ST phase unwrapping at high frequencies, and were useful for checking that measurements were stable. Tone sequences had better signal-to-noise ratio and allowed higher stimulus levels to be used at high frequencies if necessary.

Three types of responses were measured: (1) sound pressure (air) near the TM (P_TM), also in the ear canal near the acoustic source (P_EC) as a check; (2) sound pressure (liquid) in scala vestibuli (P_SV) and in scala tympani (P_ST); and (3) cochlear potential (CP) near the RW. Ear canal sound pressure was measured with small microphones (P_EC: Knowles EK-3027; P_TM: Knowles FG23652) attached to thin probe tubes. Scalae sound pressures were measured with fiber-optic pressure sensors (Olson, 1998) inserted 150–500 μm into the scalae holes described above. CP was measured with a ball electrode on the cochlear capsule ~1 mm inferior to the RW. Responses were amplified (air sound pressure and CP: Grass P5; scalae sound pressure: custom differential amplifiers), digitized at 226 kHz by a data acquisition board (National Instruments 4451), and saved on a computer. Two response channels could be saved at a time.

2.3 Microphone and sensor calibration

Microphones were calibrated against a 1/4” reference microphone (Larson-Davis 2530) at low frequencies and against a 1/8” reference microphone (G.R.A.S. 40DP) at high frequencies (e.g., Ravicz et al., 2007), using a broadband chirp stimulus. Microphones were calibrated at the beginning and end of each experiment.

The calibration of the pressure sensors includes two components: the frequency response and the sensitivity. For these sensors, the frequency response is nearly constant: the magnitude and phase of the ratio of output voltage v_sens(f) to sound pressure P₀(f) decrease smoothly and only slightly (2–10 dB and 0.1 cycle) between 100 Hz and 50 kHz (see also Olson, 1998), and this frequency shape remains constant until the sensor fails. In contrast, the sensitivity (typical |v_sens / P₀| across frequency) can be quite variable, and this variability in sensitivity affects all frequencies equally (Olson, 1998). We therefore used two methods to calibrate the sensors: in air, which gave a more accurate frequency response but a variable estimate of sensitivity (and some sensors were insensitive in air); and in water, which gave a more reliable estimate of sensitivity in vivo and was quicker and easier to perform during experiments but was less accurate at high frequencies.

For air calibration, the tip of the pressure sensor was positioned within 1 mm of the 1/8” reference microphone (see Ravicz et al., 2007), and sensor output was measured in response to a tone sequence or broadband chirp. For water calibration, the sensor tip was submerged 1 mm deep into a small vial attached to a shaker head and accelerometer (Brüel+Kjær 4290 – see Olson, 1998). Acceleration of the vial in response to a tone stimulus generated a sound pressure in the vial (e.g., Schloss and Strasberg, 1962). Water calibrations were generally more repeatable than air calibrations, especially at low frequencies; but water calibrations were sometimes spuriously high at high frequencies (due to a low signal-to-noise ratio, sensitivity to bubbles in the vial, and/or uncertainty in high-frequency acceleration due to a shaker resonance not far above the highest frequency measured). We used water calibrations at frequencies where they were not affected by the factors above and (for some ears) used smoothed air calibrations at high frequencies.

Some investigators in our laboratory (Slama, 2008; Slama et al., in press) have the monitored sensor DC output voltage (which depends on the amount of light reflected from the sensor diaphragm) as an indicator that the sensor sensitivity in vivo is the same as during calibration. We did not use stable DC as a criterion.

2.4 Experimental procedure

Experiments proceeded as follows: After the ear canal coupler was placed and after holes were made into the middle ear but before the bone web near the facial nerve was removed, CP and ear canal sound pressures P_EC and P_TM were measured at several stimulus levels with chirp stimuli. CP was measured again after the bone web was removed and once again after the scala vestibuli hole was drilled. The CP showed a compressive nonlinearity with stimulus level and decreased less than 20 dB after these manipulations, which confirmed that the ossicular chain was intact and the cochlea was healthy.¹

After calibration, a pressure sensor was inserted 150–500 μm deep into the scala vestibuli hole. P_SV was measured at several stimulus levels with chirps and with tone sequences. P_TM was measured simultaneously, including at lower stimulus levels to preclude distortion from driving the microphones too hard. Following these first P_SV measurements, the pressure sensor was withdrawn and recalibrated; then it was reinserted into scala vestibuli for another measurement series and withdrawn again for another calibration. At this point the hole was drilled into scala tympani, and another pressure sensor was calibrated and inserted 150–300 μm deep into this hole (but still far from the organ of Corti). P_ST was measured simultaneously with P_TM as described above or simultaneously with P_SV. In some ears, P_SV measurements were repeated at different insertion depths. Sensor outputs were within 2–3 dB of maximal for insertion depths of at least 150 μm. At least two measurement series were performed, and both sensors were removed and recalibrated after each series. P_SV and P_ST measurements generally varied by less than 2–3 dB between series.

At this point, the ossicular chain was disrupted, and P_SV, P_ST, and P_TM were measured as described above. Following these measurements, the experiment was terminated by an overdose of anesthesia and all sensors and microphones were recalibrated. For all data shown in this paper, sensor calibrations were constant within 2 dB throughout the measurements.

3. Results

To allow comparisons with other measurements taken at different stimulus levels or in different ears, all P_SV and P_ST data presented here are normalized by P_TM. The ratio of P_SV to P_TM is the middle-ear pressure gain G_MEP. Normalized P_ST is denoted as P_STn. In all figures, data have been omitted at frequencies above 25–30 kHz where the accuracy of P_TM measurements was suspect.

3.1 Middle-ear pressure gain

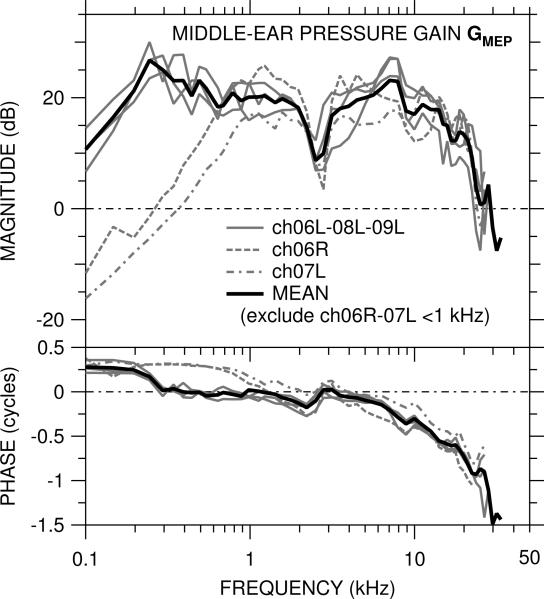
The middle-ear pressure gain G_MEP was measured in five ears and is shown in Figure 2. The measurement location was at the very base of the cochlea, which presumably corresponds to a best frequency of 22 kHz (by the cochlear map of Eldridge et al., 1981). In the two ears in which the bone near the oval window was cracked (ch06R, ch07L), G_MEP is different than in the other three ears below 1 kHz (described further below), but above 1 kHz G_MEP is similar among all ears.

Figure 2.

Middle-ear pressure gain G_MEP = P_SV / P_TM in five ears. Top: magnitude |G_MEP| in dB; bottom: phase ∠G_MEP in cycles. In two ears (ch06R, ch07L) the bone near the OW was cracked while the scala vestibuli hole was drilled. G_MEP in those ears (dashed, dot-dashed lines) is included in the logarithmic mean (solid black line) only at 1 kHz and above.

At the lowest frequencies measured (100–250 Hz) |G_MEP| increased with frequency and ∠G_MEP is near +0.25 cycles in the three ears with no OW crack (solid gray lines), which is consistent with the stiffness dominance of the middle ear at these low frequencies (e.g., Rosowski et al., 2006). A small mass component to inner-ear dynamics could also contribute to this low-frequency increase. Above a magnitude peak at 250 Hz (1 kHz in the OW-cracked ears), |G_MEP| was generally +15 to +27 dB in all ears up to ~20 kHz and ∠G_MEP was near 0 to about 8 kHz. There was a dip in |G_MEP| and a ripple in ∠G_MEP near 2.5 kHz, consistent with a resonance between the bulla holes and the air in the middle ear (Rosowski et al., 2006). Except for this dip, |G_MEP| was generally flat with frequency between the frequency where ∠G_MEP < 0.25 cycles (0.25–1 kHz) and 15–20 kHz. This |G_MEP| flatness and ∠G_MEP near 0 are consistent with the cochlea being a resistance-dominated system over a large frequency range.

The gradual accumulation of ∠G_MEP to about 1 cycle at 25 kHz indicates a delay of about 40 μsec. This delay is consistent with that computed from the phase of the P_TM-to-stapes velocity middle-ear transfer function measured by Songer and Rosowski (2006) and suggests that the delay is caused mostly by the middle ear.

In the two ears with the OW crack, the |G_MEP| peak and ∠G_MEP transition seen in the normal ears at about 250 Hz occurred at about 1 kHz, and |G_MEP| decreased rapidly as frequency decreased below 1 kHz. ∠G_MEP was near +0.25 cycles from the lowest frequency measured to about 1 kHz. The differences in G_MEP between these two ears and the rest are consistent with a mass in parallel with the cochlear resistance whose impedance is considerably less than the cochlear resistance at low frequencies. If this view is valid, then the effect of the crack near the OW is to relieve cochlear sound pressure at low frequencies and cause the middle-ear output to bypass the cochlea.

|G_MEP| remained in the +10 to +25 dB range up to approximately 20 kHz in all ears. Above 20–25 kHz |G_MEP| dropped precipitously to < 0 dB in all ears, and ∠G_MEP diverged among ears. P_SV measurements were generally 20–40 dB above the noise floor over most of the frequency range and at least 10 dB above the noise floor to about 40 kHz.

The logarithmic mean of G_MEP in all ears was computed and is shown as the solid black line. Data from the two ears with the OW crack were omitted from calculations of the mean at frequencies below 1 kHz.

3.2 Normalized scala tympani sound pressure

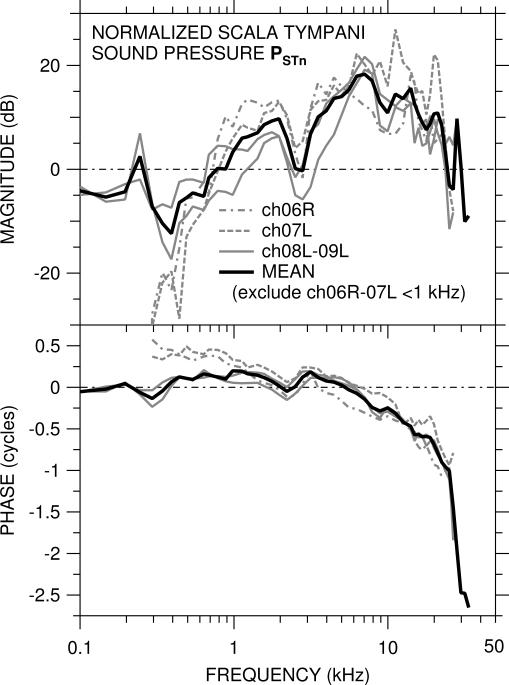
Scala tympani sound pressure P_STn (normalized by P_TM) was measured in four of the five ears above and is shown in Figure 3. The best frequency corresponding to the measurement location (~1 mm from the RW) was, we believe, approximately 10–12 kHz (see Eldridge et al., 1981). As for G_MEP (described above), P_STn was different in the two ears with the OW crack (ch06R, ch07L - dashed gray lines) than in the other two ears (solid gray lines) below 1 kHz but was similar among all ears above 1 kHz. As above, the logarithmic mean of P_STn below 1 kHz in the two ears with no OW crack and in all ears at higher frequencies is shown by the solid black line.

Figure 3.

Scala tympani sound pressure P_STn = P_ST / P_TM in four ears. Top: magnitude in dB; bottom: phase in cycles. In the two ears (ch06R, ch07L) in which the bone near the OW was cracked, P_STn (dashed, dot-dashed lines) is included in the logarithmic mean (solid black line) only at 1 kHz and above, and data are omitted below 300 Hz where |P_STn| was at the noise floor.

In the two ears with no OW crack, |P_STn| was approximately −5 dB at frequencies below 500 Hz, and ∠P_STn was approximately 0 up to 5 kHz. In the two ears with the OW crack, |P_STn| was much lower (approximately −20 dB) at frequencies below 500 Hz, and ∠P_STn decreased gradually from nearly +0.5 cycles to 0 at 5 kHz. In these ears, |P_STn| is at the noise floor below 300 Hz. In all ears |P_STn| increased to about +20 dB near 8 kHz and then decreased to about +10 dB at 20 kHz. ∠P_STn accumulated as frequency increased above 5 kHz, to about −0.7 cycles by 20 kHz, which corresponds to a delay of about 35 μsec. P_STn shows a magnitude dip and phase ripple near 2.5 kHz similar to that seen in G_MEP in these ears (see previous section). Above 20–25 kHz |P_STn| dropped rapidly and ∠P_STn accumulated rapidly.

4. Discussion

4.1 Ratio of P_ST to P_SV and comparison to a simple cochlear model

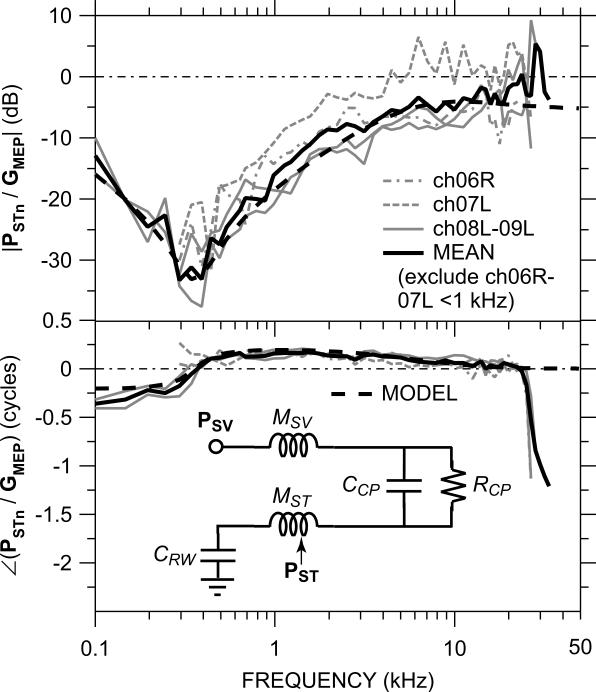
Figure 4 shows the ratio of P_STn to G_MEP in each of the four ears of Figure 3. For measurements made with equal TM sound pressure, this ratio is equivalent to the ratio of P_ST to P_SV (e.g., for P_ST and P_SV measured simultaneously.) It is notable that |P_STn/G_MEP| was similar in all ears, even those with an OW crack (dashed gray lines), which indicates that the OW crack affected P_ST and P_SV equally and implies that the mechanical properties of the cochlear partition, which presumably influences the ratio of P_ST to P_SV, were not altered by the OW crack.

Figure 4.

The ratio of P_STn to G_MEP (equivalent to P_ST / P_SV for the same P_TM) in each of the four ears in which both P_SV and P_ST were measured. Top: magnitude in dB; bottom: phase in cycles. In the two ears in which the bone near the OW was cracked (ch06R, ch07L – dashed, dot-dashed gray lines), data are omitted below 300 Hz and included in the logarithmic mean (solid black line) only at 1 kHz and above. Inset in bottom panel: Simple lumped-element circuit model of cochlear macromechanics to predict P_ST / P_SV (dashed black line).

At low frequencies, |P_STn/G_MEP| was very small, consistend with |G_MEP| ⪢ |P_STn| as described above. |P_STn/G_MEP| increased with frequency and leveled off above about 5 kHz. The mean |P_STn/G_MEP| was about −6 dB between 5 and 20 kHz, which implies that |P_STn| ≈ |G_MEP| / 2.

Near 20 kHz, |P_STn| approached |G_MEP| (the mean |P_STn/G_MEP| approached 0 dB), and at higher frequencies |P_STn/G_MEP| was between −10 and 0 dB. ∠(P_STn/G_MEP) decreased slowly from about +0.2 cycles at 500 Hz to 0 at 20–25 kHz. This relationship between P_STn and G_MEP implies that the structure(s) that influences the relative values of P_ST and P_SV gradually decreases in importance as frequency increases. If this structure is the cochlear partition, this result implies that cochlear partition impedance influences P_ST at low frequencies but not at high. Above 25 kHz ∠(P_STn/G_MEP) decreased by one cycle.

The relationship between G_MEP and P_STn is consistent with a simple model of cochlear sound pressure (adapted and expanded from Olson, 2001) shown as an inset to Fig. 4 and described in more detail in the Appendix. Because P_SV and P_ST were measured at slightly different cochlear locations (P_SV at the base, and P_ST about 2 mm from the base; see Sec. 3.2), the scala fluid mass terms M_SV and M_ST include the mass of the fluid between the P_SV measurement location or the round window and the P_ST measurement locations. M_ST also includes the mass of the fluid between the P_ST sensor tip and the cochlear partition (see Olson, 2001). Because in our preparation the RW was kept intact, our model also includes a round window compliance C_RW (important at low frequencies).

The model prediction of P_ST/P_SV (black dashed line) is a good match to both the magnitude and phase of the mean P_STn/G_MEP across nearly the entire frequency range of measurement, which implies that the model probably provides a reasonable description of the relative sound pressures within the actual cochlea. The model suggests that:

(a) The impedance of the cochlear partition is the primary determinant of the ratio of P_ST to P_SV at frequencies below about 5 kHz. At higher frequencies, the mass of the SV fluid between the OW and the P_ST measurement location influences P_ST/P_SV.

(b) The impedance of the cochlear partition is determined primarily by the cochlear resistance below 20 kHz.

(c) At very low frequencies (below 300 Hz) the stiffness of the RW membrane influences P_ST/P_SV.

4.2 Differential trans-cochlear-partition pressure

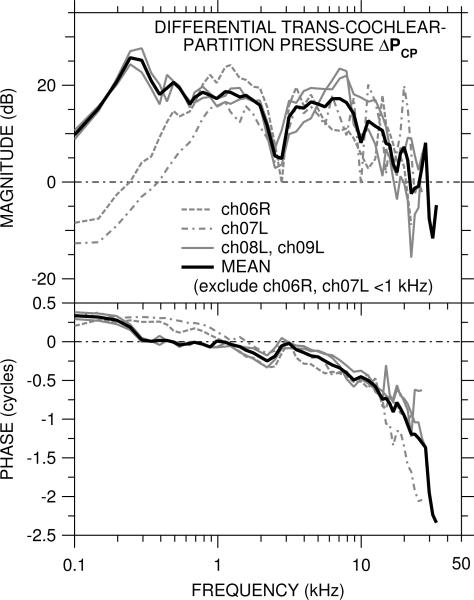
The differential sound pressure across the cochlea partition ΔP_CP computed from P_STn and G_MEP by Eq. 1b is shown for each of the four ears in Figure 5. ΔP_CP had many of the same features as G_MEP, which is not surprising given that |G_MEP| > |P_STn| over most of the frequency range of measurements. At frequencies above a few kHz, |Δp_CP| < |G_MEP|, because P_STn (which is subtracted from G_MEP) had the same phase and nearly the samemagnitude as G_MEP (see Fig. 4). At 20 kHz |ΔP_CP| ≈ 0 dB and ∠ΔP_CP accumulated >1 cycle. Above 25 kHz |ΔP_CP| decreased rapidly and ∠ΔP_CP accumulated an additional cycle.

Figure 5.

Differential trans-cochlear-partition pressure ΔP_CP = G_MEP−P_STn in each of the four ears in which both P_SV and P_ST were measured. Top: magnitude in dB; bottom: phase in cycles. In the two ears (ch06R, ch07L) in which the bone near the OW was cracked, ΔP_CP (dashed, dot-dashed lines) is included in the logarithmic mean (solid black line) only at 1 kHz and above.

4.3 Effects of experimental inner-ear modifications on G_MEP, P_STn, and ΔP_CP

All of our cochlear measurements involve inner-ear modifications, because holes must be made into the cochlear scalae to place the sensors. Preliminary data from such modifications suggest that their effects are small and limited in frequency range.

4.3.1 Effects of scala vestibuli hole

We did our best to keep the scala vestibuli and scala tympani holes as small as possible – just large enough for the sensor tip – but we were not always successful in early experiments. In those ears in which we cracked the bone around the OW (ch06R, ch07L), the low-frequency magnitude reduction and phase increase in G_MEP and P_STn (Figs. 2 and 3) are consistent with the low impedance of a large hole shunting the large cochlear resistance. The similarity in effects (Fig. 4) suggests that at low frequencies P_ST is determined primarily by P_SV and the properties of the cochlear partition rather than by input by any other path. Because ΔP_CP is determined primarily by G_MEP at low frequencies (Figs. 4 and 5), the effect of the scala vestibuli hole on ΔP_CP was similar to its effect on G_MEP.

We did not attempt to seal the sensor in the scala vestibuli hole, but Slama (2008, Slama et al., in press) showed in one ear that sealing the sensor hole increased |G_MEP| by as much as 10 dB and reduced ∠G_MEP toward zero below 200 Hz, with only small effects at higher frequencies. Neither we nor Slama (2008) observed any consistent relationship between scala vestibuli hole size and low-frequency G_MEP. We made no P_ST measurements before making the scala vestibuli hole, but P_ST was similar whether the scala vestibuli hole was filled by a sensor or left open.

Because the cracked OW bone had no consistent effect on G_MEP and P_STn at high frequencies (Figs. 2 and 3), we believe that the scala vestibuli hole had no significant effect on high-frequency ΔP_CP.

4.3.2 Effects of scala tympani hole

Opening a hole into scala tympani had a smaller and contrary effect on G_MEP than the scala vestibuli hole: a small (2–3 dB) increase in |G_MEP| and ~0.1-cycle decrease in ∠G_MEP below 1 kHz (data not shown). We had good success in keeping the scala tympani hole small, so that the sensor tip filled it. When the sensor was inserted into the scala tympani hole, G_MEP was similar to its value before scala tympani was opened.

4.4 Effects of experimental middle-ear modifications on _GMEP, P_STn, and ΔP_CP

We measured G_MEP, P_STn, and ΔP_CP in two ears (ch07L, ch08L) after disrupting the ossicular chain (interrupting the incudostapedial joint, subluxing the stapes, and/or breaking the incus long process) to estimate the importance of sound energy delivered through the RW and the cochlear capsule on intracochlear sound pressures. We found that, with the ossicular chain disrupted, (a) |G_MEP| and |P_STn| never exceeded 0 dB (pressure gain was always <1) across the frequency range, except for a narrow band around 15 kHz. Both |G_MEP| and |P_STn| were substantially less than 0 dB (−20 to −30 dB) at frequencies above 3 kHz except as noted above. (b) ∠G_MEP decreased by 0.25 – 0.5 cycle between 500 Hz and about 10 kHz, though ∠P_STn did not change. ∠G_MEP and ∠P_STn accumulated faster above 15 kHz than in the undisrupted state. (c) |P_STn| was substantially greater than |G_MEP| above 4 kHz, so ΔP_CP ≈ G_MEP below 1 kHz and ΔP_CP ≈ P_STn above 4 kHz. (d) |G_MEP| and ΔP_CP were reduced substantially at nearly all frequencies, which demonstrates that the ossicular chain is the primarily route of sound conduction to the cochlea at frequencies up to at least 30 kHz, a range that spans the chinchilla's range of hearing (Slama, 2008; Slama et al., in press).

4.5 Comparison of _GMEP with other studies

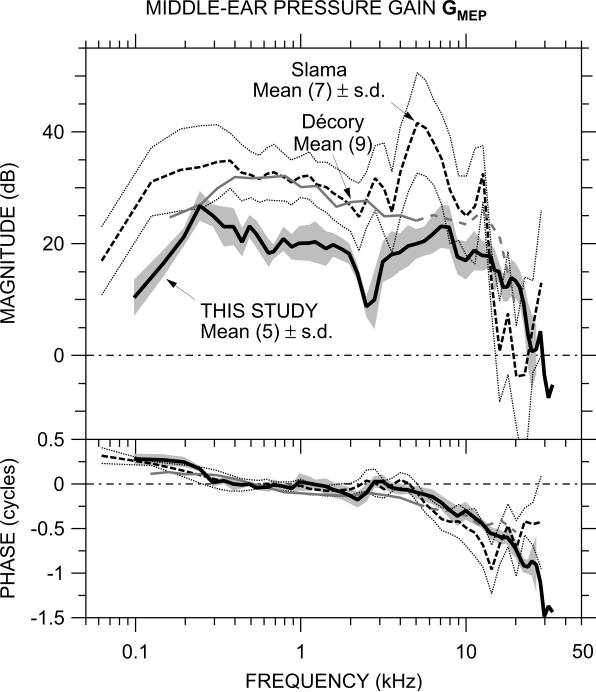
Middle-ear pressure gain in chinchilla has been measured in two other studies of which we are aware: by Slama (2008; Slama et al., 2009, in press), using the same technique in the same laboratory as this study, also using a fiber-optic pressure sensor; and by Décory (1989; Décory et al., 1990) using a piezoelectric hydrophone with a narrow probe tube inserted into a scala vestibuli hole of diameter similar to ours (but a different location – see below). G_MEP in these other studies is compared with our mean results in Figure 6.

Figure 6.

Comparison of the mean G_MEP in this study (N=5, thick black line) to the mean G_MEP from other studies in chinchilla: Slama (2008, Slama et al. 2009; N=7, dashed line) and Décory (1989, Décory et al., 1990; N=9, thin gray line). The shaded area shows ± 1 standard deviation (s.d.) of the logarithmic mean in this study; the thin dotted lines show ± 1 s.d. of the logarithmic mean of the Slama et al. study. Décory data are dashed above 5 kHz (see text).

G_MEP from all studies is fairly similar between 300 Hz and 5 kHz: all show |G_MEP| fairly flat with frequency and ∠G_MEP accumulating slowly. In all three studies, |G_MEP| decreased at lower frequencies and ∠G_MEP increased to about +0.25 cycles. The lower frequency of the flat |G_MEP| plateau varied among the studies: highest in Décory, lowest in Slama. As mentioned in Section 4.3 above, sealing the scala vestibuli hole moved this frequency down while a crack near the OW moved this frequency up, so hole sealing is a likely source of low-frequency G_MEP differences.

Another argument in support of a connection between the lower |G_MEP| plateau frequency and the sealing of the scala vestibuli hole is provided by comparing two measures of CP frequency dependence, magnitude across frequency (Drescher and Eldredge, 1974) and thresholds as a function of frequency (Dallos, 1970), with |G_MEP|. It has been established (Dancer and Franke, 1980, in guinea pig) that CP varies with |ΔP_CP|, and at low frequencies |ΔP_CP| and |G_MEP| are nearly identical (compare Figs. 2, 4, and 5), so the spectral shape of CP should be a good descriptor of the frequency dependence of |G_MEP| in the undisturbed inner ear. Both of these CP measurements show CP amplitude remaining nearly constant with frequency down to 100 Hz (the Dallos (1970) CP shows a decrease below 100 Hz), which implies that in the undisturbed inner ear the |G_MEP| plateau should extend to lower frequencies than this and previous studies have shown.

In the middle frequency range where G_MEP is approximately constant, |G_MEP| is generally about 10 dB lower in this study than in the others over this frequency range. The reason for this difference in |G_MEP| between this study and Slama's is not clear, especially since both were conducted in the same laboratory with the same type of sensor. One potential reason is a systematic error in pressure sensor sensitivity in some sensors that caused the sensitivity in vivo to be lower than in the room-temperature calibration vial. This potential source of error affects only the basic sensitivity of the sensor, not its frequency response (see Sec. 2.3).

At high frequencies, G_MEP from the various studies diverges. |G_MEP| decreases more rapidly and ∠G_MEP is flatter above 12 kHz in the Décory study (Décory, 1989; Décory et al., 1990) than in this one. Décory et al. (1990) consider sensor location as a possible source of error: in that study, the P_SV sensor was located about 5.5 mm from the OW, which is near the best place for a 5-kHz signal, and they suggest that P_SV at higher frequencies (shown dashed) could be affected by sound pressure from a cochlear traveling wave. In the Slama study (Slama, 2008; Slama et al., 2009, in press), |G_MEP| is considerably higher near 5 kHz and lower above 12 kHz than in this study, and ∠G_MEP accumulates more rapidly to 15 kHz and then reverses. The location of the TM sound pressure microphone was further from the TM in the Slama study than in this one, and the G_MEP differences above 12 kHz mentioned above are consistent with differences in sound pressure between the microphone location and the TM due to standing waves in the ear canal (see e.g., Dong and Olson, 2006; Ravicz et al., 2007).

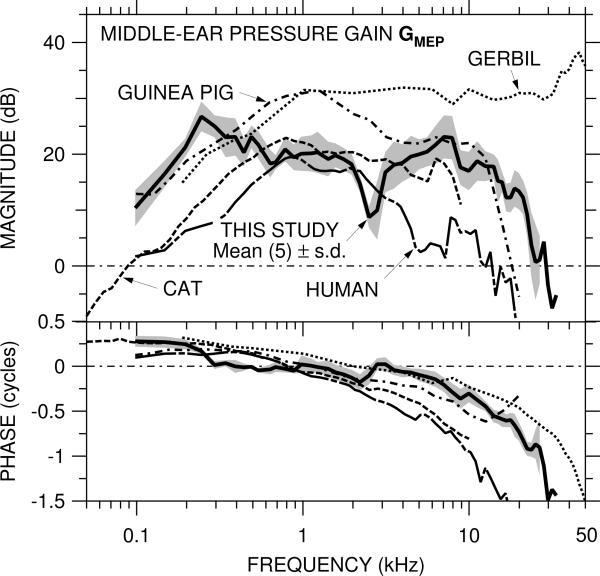
Our measurements of G_MEP exhibit several similarities to G_MEP in other mammalian species but also some differences. Figure 7 compares our mean G_MEP to G_MEP in gerbil (Olson, 2001; fiber-optic pressure sensor), guinea pig (Décory et al., 1990; hydrophone and probe tube), cat (Nedzelnitsky, 1980; hydrophone and probe tube), and human temporal bones (Nakajima et al., 2009; fiber-optic pressure sensor). In all species shown, |G_MEP| shows a plateau (where |G_MEP| is approximately constant over a wide frequency range), and ∠G_MEP is >0 at low frequencies and accumulates as frequency increases. Our chinchilla |G_MEP| is higher below 300 Hz than in the other species and higher above 12 kHz than in other species except gerbil, consistent with the relative stapes velocity transfer functions among these species (Rosowski, 1994). Another difference is that ∠G_MEP in chinchilla goes to 0 more abruptly and at a lower frequency (300 Hz) than ∠G_MEP in the other species (700 Hz – 2 kHz).

Figure 7.

Comparison of the mean G_MEP in this study (N=5; thick solid line) to the mean G_MEP from other studies in other species: gerbil (N=14; Olson, 2001; dotted line), guinea pig (N=11; Décory et al., 1990; dot-dashed line), cat (N=25; Nedzelnitsky, 1980; dashed line) and human (temporal bones: N=6; Nakajima et al., 2009; long dot-dashed line). The shaded area shows ± 1 s.d. of the logarithmic mean in this study.

Above the upper plateau frequency, |G_MEP| decreases rapidly with frequency to 0 dB or below in all species measured (except for gerbil²). This upper plateau frequency marks the upper frequency limit of effective middle-ear transmission and so could be expected to set the upper limit of hearing ability (e.g., Rosowski, 1991). If so, extending |G_MEP| measurements in gerbil (which has a higher upper frequency hearing limit than the other species listed here) to higher frequencies may show an upper plateau frequency as well.

As noted by Puria et al. (1997), the maximum |G_MEP| (near 1 kHz) in several mammalian species is generally 6 dB or so below the “anatomical transformer ratio” computed as the product of the “ossicular lever ratio” (length of the manubrium of the malleus to incus long process) and the “area ratio” (area of TM to stapes footplate). Our |G_MEP| is generally about 10 dB below the chinchilla transformer ratio of 35 dB computed from a lever ratio of 6 dB (Fleischer, 1973) and an area ratio of 29 dB (Vrettakos et al., 1988). This result that |G_MEP| is less than the transformer ratio is reasonable: (a) the flexibility observed in the ossicular chain of several mammals can reduce middle-ear transmission at low and medium frequencies (e.g., Guinan and Peake, 1965; Nakajima et al., 2005), and (b) the very compliant chinchilla TM (e.g., Rosowski et al., 2006) does not move as a unit at frequencies above a few hundred Hz (Rosowski et al., 2009), so the effective TM area that influences middle-ear transmission may be smaller than the anatomical area.

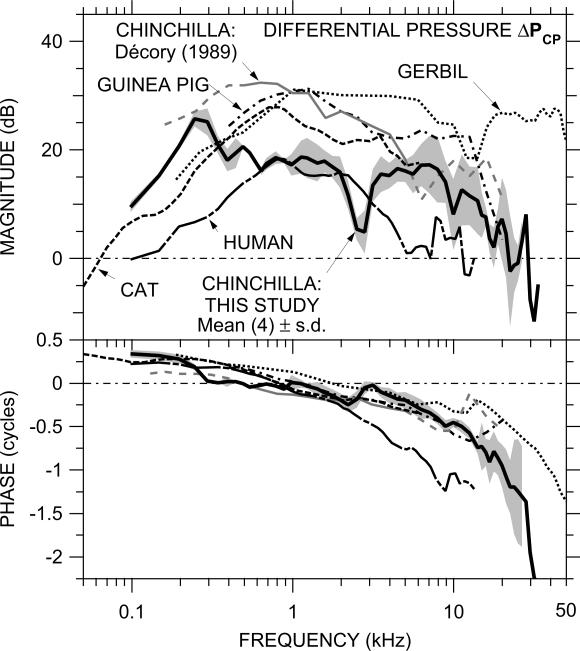
4.6 Comparison of ΔP_CP with other studies

The relationship of ΔP_CP among species in which ΔP_CP data from simultaneous measurements have been published is shown in Figure 8: chinchilla (this study), cat (Nedzelnitsky, 1980), and human (Nakajima et al., 2009). Also included in Fig. 8 are ΔP_CP estimates computed from P_SV and P_ST that were measured in the same study but not necessarily in the same individuals: gerbil (Olson, 2001) and chinchilla and guinea pig (Décory et al., 1990). (The Décory chinchilla data are shown dashed below 0.5 kHz where they are estimated from G_MEP and above 5 kHz as discussed in Sec. 4.5.) The relationship between ΔP_CP among these species is generally similar to the relationship of G_MEP (see Fig. 7): |ΔP_CP| is approximately constant across a wide frequency range, and our chinchilla |ΔP_CP| is generally lower than |ΔP_CP| in other species between 300 Hz and 20 kHz (except human) and generally higher at low and high frequencies. Our chinchilla |ΔP_CP| and |ΔP_CP| in human show a high-frequency rolloff and are less than 0 dB at high frequencies (21 kHz or 10 kHz respectively); |ΔP_CP| in other species remains above 0 dB at the highest frequencies that P_ST was measured (58 kHz for gerbil, 20 kHz for Décory chinchilla and guinea pig, 6 kHz for cat). ∠ΔP_CP in all species shows a phase accumulation characteristic of a delay, but ∠ΔP_CP accumulates much more rapidly in human than in the other species.

Figure 8.

Comparison of the mean ΔP_CP in this study (N=4; thick solid line) to published ΔP_CP in cat (median, N=6; Nedzelnitsky, 1980; dashed line) and human (temporal bones: N=6, Nakajima et al., 2009; long dot-dashed line) and ΔP_CP computed from G_MEP and P_STn in gerbil (N=14; Olson, 2001; dotted line), chinchilla (N=4; Décory et al., 1990; gray line solid or dashed <500 Hz and >5 kHz, see text), and guinea pig (Décory et al., 1990, N=5; dot-dashed line). The shaded area shows ± 1 s.d. of the logarithmic mean in this study.

Similarly, the relationship between ΔP_CP and G_MEP (see Fig. 7) is generally similar among these species. |ΔP_CP| is nearly identical to |G_MEP| at low and middle frequencies and lower than |G_MEP| by only a few dB at high frequencies. ∠ΔP_CP is similar to ∠G_MEP at low frequencies but has a greater accumulation above a few kHz. In general, except for slightly greater phase accumulation at high frequencies, G_MEP is a good approximation of ΔP_CP in all species measured.

As mentioned above, |ΔP_CP| in two species (chinchilla and human) has been shown to be bandpass with a high-frequency as well as a low-frequency limit. In these species, |ΔP_CP| decreases to 0 dB (no middle-ear pressure gain) at a frequency near the upper audiometric limit. This result supports the idea that the frequency limits of hearing are strongly influenced by the limits of middle-ear function. It remains to be seen whether higher-frequency ΔP_CP data in other species will also support this idea.

4.7 Input impedance of the cochlear partition

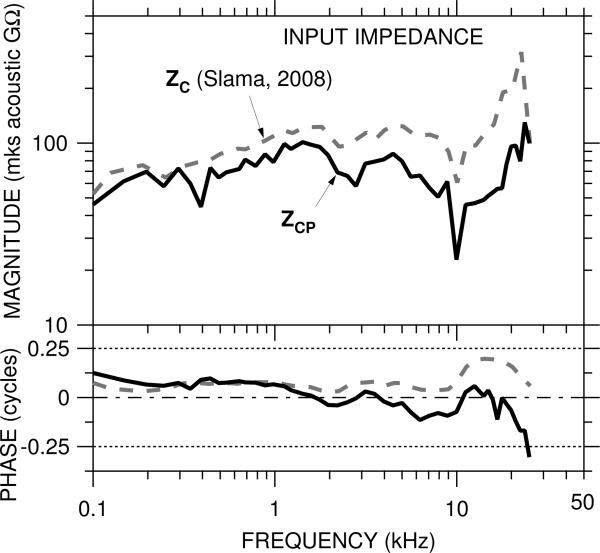
The cochlear input impedance Z_C, the ratio of P_SV to stapes volume velocity, is a measure of power absorption in the cochlea. We use our calculations of the trans-cochlear-partition differential pressure and previous measurements of Z_C to estimate the input impedance of the cochlear partition Z_CP, which can provide an indication of the power absorbed by the cochlear partition itself. Z_CP is different from the local (pointwise) cochlear partition impedance (see C_CP in the model in Fig. 4 and the Appendix); on the contrary, Z_CP is the distributed cochlear partition impedance (the integral of the local cochlear partition impedance and the mass of the scalae fluids at all points along the length of the cochlea) seen from the OW.3

The model of Figure 4 suggests that Z_CP is the primary determinant of ΔP_CP, at least at frequencies below about 10 kHz; therefore, Z_CP can be computed from Z_C by considering Z_C to be the series combination of Z_CP and the impedance of other cochlear structures (including the round window). In this case, Z_CP and ZC form a pressure divider, where P_SV−P_ST is the pressure drop across Z_CP and P_SV is the pressure drop across Z_C. Z_CP is computed from Z_C by multiplying Z_C by the ratio of ΔP_CP to G_MEP:

$${\mathbf{Z}}_{\mathbf{CP}}={\mathbf{Z}}_{\mathbf{C}}\cdot \Delta {\mathbf{P}}_{\mathbf{CP}}∕{\mathbf{G}}_{\mathbf{MEP}}.$$ (2)

An estimate of Z_CP computed from our G_MEP, our ΔP_CP, and the Z_C presented by Slama et al. (Slama, 2008; Slama et al., in press, calculated from simultaneous measurements of P_SV and stapes velocity V_S and previously-published estimates of stapes footplate area) is shown in Figure 9. Z_CP is more resistive than Z_C, as is shown by the flatter |Z_CP| with frequency and the ∠Z_CP closer to zero above 1 kHz. At low frequencies Z_CP is very similar to Z_C, as in this frequency range |P_STn| ⪡ |G_MEP| (Fig. 4) and ΔP_CP ≈ G_MEP. At high frequencies ΔP_CP ≠ G_MEP, and there is a more substantial difference between Z_CP and Z_C. Above 20 kHz |Z_CP| increases somewhat; ∠Z_CP decreases dramatically to less than −0.25 cycles, which implies that energy is introduced into the system. This could be real, as the location of the scala tympani sensor (12-kHz place) is not far from the 20-kHz place. Alternatively, P_SV or P_ST at the measurement location could be significantly different from P_SV or P_ST at the cochlear base (e.g., Olson, 2001) or transverse stapes motion (e.g., Decraemer et al., 2007 in gerbil) could have influenced V_S measurements. Despite this possible shortcoming, this estimate of Z_CP provides important empirical data for cochlear modeling.

Figure 9.

Estimate of the overall impedance of the cochlear partition Z_CP (solid line), computed from Z_C (Slama, 2008, dashed line) and the ratio of ΔP_CP to G_MEP.

5. Summary and Conclusions

(1) Middle-ear pressure gain G_MEP has approximately constant magnitude (~20 dB) over a wide frequency range (0.3 to 20 kHz) and includes a delay of about 40 μsec, comparable to the delay between stapes velocity and ear canal sound pressure. |G_MEP| decreases rapidly with frequency to 0 dB (unity gain) at 20 kHz.

(2) The trans-cochlear-partition sound pressure ΔP_CP, which represents the effective input to the cochlea, is governed by G_MEP below 5 kHz but is influenced by scala tympani pressure P_STn at higher frequencies.

(3) The magnitude of ΔP_CP is also approximately constant between 300 Hz and 20 kHz and decreases sharply at higher frequencies. The frequency of the sharp decrease is similar to the high-frequency limit of the chinchilla audiogram.

(4) The input impedance of the cochlear partition Z_CP, which is an indicator of power absorption by the cochlear partition, is resistive from 300 Hz to about 20 kHz.

The work described here extends the applicability of the chinchilla as a model for studying not only the effects of middle- and inner-ear pathologies on middle- and inner-ear mechanics but also nonacoustic stimulation of the inner ear. ΔP_CP provides an assay of cochlear response to “bone conduction” stimuli (delivered through a vibrator attached to the skull) to study the mechanisms of sound transmission to the physiologically active cochlea through the intact head. This more direct measure of cochlea response is useful for testing hypotheses of the relative importance of different bone conduction modes (e.g., Khanna et al., 1976; Stenfelt and Goode, 2005) in normal ears and in ears with inner-ear pathology such as superior semicircular canal dehiscence syndrome (SCD syndrome – Songer, 2006). These measurements also add to the knowledge of chinchilla middle-ear mechanics and, in concert with previous measurements of other middle-ear properties, provide a more complete view of middle-ear function in this species. More complete knowledge of the entire auditory periphery makes the chinchilla preparation a more useful model for exploring middle- and inner-ear function.

Abbreviations

C_CP

model local compliance of cochlear partition

CP

cochlear potential

C_RW

model local compliance of round window

f

frequency

G_MEP

middle-ear pressure gain

M_ST

model mass of scala tympani fluid

M_SV

model mass of scala vestibuli fluid

OW

oval window

ΔP_CP

normalized differential trans-cochlear-partition pressure

P_EC

sound pressure in the ear canal relatively far from the tympanic membrane

P_ST

scala tympani sound pressure

P_STn

scala tympani sound pressure normalized by sound pressure near the tympanic membrane

P_SV

scala vestibuli sound pressure

P_TM

sound pressure in the ear canal near the tympanic membrane

P₀

sound pressure in calibration setup

R_CP

model cumulative resistance of cochlear partition

RW

round window

TM

tympanic membrane

V_S

velocity of a point on the stapes

v_sens

pressure sensor output voltage

Z_C

cochlear input impedance

Z_CP

input impedance of the cochlear partition as seen from the vestibule

Appendix: Formulation of a lumped-element cochlear model

The model of cochlear macromechanics presented in Fig. 4 is based approximately on a lumped-element model presented in Fig. 4 of Olson (2001). Unlike in Olson (2001), P_SV and P_ST were measured at different distances from the cochlear base and the round window was left intact for P_ST measurements, so the intervening fluid and the RW must be taken into account. The acoustic mass terms include not only the mass of the cochlear fluid between the sensor tip and the cochlear partition but also the mass of SV fluid between the stapes footplate and the P_ST measurement location and the mass of ST fluid between the P_ST measurement location and the RW. M_SV = acoustic mass of SV fluid (perilymph and endolymph) between the apical edge of the stapes footplate and the location of P_ST measurements; C_CP = local compliance of cochlear partition; R_CP = characteristic (transmission-line) resistance of the cochlea apical to the P_ST measurement location. We neglect the helicotrema; including a helicotrema impedance as described in Dallos, 1970 (computed from Dallos's value for chinchilla helicotrema radius) does not match low-frequency P_ST / P_SV estimates. M_ST = acoustic mass of ST perilymph; the arrow indicates that some of this ST mass can be between the P_ST sensor tip and the cochlear partition. In fact, we obtained the best model fit by putting all of the ST mass between the P_ST sensor and the RW. C_RW = round window compliance. Element values are based on previously-published physiological and anatomical measurements and adjusted slightly (and a resistance R_RW, not shown in Fig. 4, added in series with C_RW) to match the data of Fig. 4. The radiation impedance from the round window Z_RAD is negligible and so is not included in Fig. 4. Element values and their sources and derivations are listed in Table A1.

Table A1.

Element values and sources for lumped-element model of Figure 4.

Symbol	Element	Source or derivation	Value	Units
MSV	SV mass	ρ lSV / SSV Beranek, 1986, Eq. 5.42		kg / m4
ρ	Fluid density	Assumed equal to water	1000	kg / m3
lSV	Distance from stapes to PST meas. location		1.7	mm
SSV	SV cross-section area	Dallos, 1970, Fig. 10; adjusted to fit data	1.0	mm2
CCP	Local CP compliance	wbm lbm / kCP Olson, 2001	4 × 10−16	m3 / Pa
wbm	Basilar membrane width	Dallos, 1970, Fig. 10; adjusted per Ruggero et al., 1990	0.13	mm
lbm	Effective basilar membrane length	Olson, 2001; adjusted to fit data	0.3	mm
kCP	Local CP mechanical stiffness	Ruggero et al., 1997; de La Rochefoucauld and Olson, 2007	0.7	Pa / nm
RCP	Cochlear resistance	Computed from Slama, 2008	9 × 1010	mks Ω
MST	ST mass	ρ lST / SST Beranek, 1986, Eq. 5.42		kg / m4
lST	Distance from PST meas. location to RW		1.0	mm
SST	ST cross-section area	Estimated from SSV per Ruggero et al., 1990; adjusted to fit data	0.5	mm2
CRW	RW compliance	Lynch et al., 1982 (for cat)	1 × 10−13	m3 / Pa
RRW	RW resistance	To fit data 300–400 Hz	2 × 109	mks Ω
ZRAD	Radiation impedance of RW	Beranek, 1986, Table 5.1 for a = 0.34 mm	< 106	mks Ω