Skip to main content
PMC home page
Cell Stress & Chaperones logoLink to Cell Stress & Chaperones
. 2009 May 20;15(1):13–23. doi: 10.1007/s12192-009-0118-9

Experimental testing of a mathematical model relevant to the extrinsic pathway of apoptosis

Vincenza Pace 1, Dina Bellizzi 1,✉, Francesca Giordano 1, Maria Luisa Panno 1, Giovanna De Benedictis 1
PMCID: PMC2866975  PMID: 19455405

Abstract

Apoptosis is a programmed cell death process, whose complexity led researchers to build mathematical models that could help to identify its crucial steps. In previous works, we theoretically analyzed and numerically simulated a model that describes a pathway from an external stimulus to caspase-3 activation. Here, the results of experiments performed on populations of synchronized cells treated with the inducer Apo2L/TRAIL are reported and are compared with model predictions. In particular, we have compared in vitro and in silico results relevant to the time evolutions of caspase-3 and caspase-8 activities, as well as of the dead cells fractions. In addition, the effect of the BAR gene silencing was evaluated. Caspase-3 activation and cell death is faster in silenced than in nonsilenced cells, thus confirming previous simulation results. Interestingly, Apo2L/TRAIL treatment in itself reduces the BAR gene expression. The qualitative agreement between model predictions and cell cultures behavior suggests that the model captures the essential features of the biological process and could be a tool in further studies of caspases activation. In this manuscript, we report the results of in vitro experiments aimed at revealing the dynamics of caspase activation in a cell population. A qualitative agreement between these results and a mathematical model describing a pathway from an external stimulus to caspase-3 activation was obtained, thus showing that the model captures the essential features of the biological process and may be a reliable tool in further studies of caspase activation.

Electronic supplementary material

The online version of this article (doi:10.1007/s12192-009-0118-9) contains supplementary material, which is available to authorized users.

Keywords: Apoptosis, Mathematical model, Caspase-3 activation, Caspase-8 activation, BAR regulation

Introduction

Apoptosis is a genetically encoded cell death program that differs from necrosis or accidental cell death by morphological and biochemical features (Degterev and Yuan 2008; Krysko et al. 2008). It is induced by extrinsic and intrinsic signals that activate intracellular signaling pathways where caspases play a pivotal role. Caspases are a family of conserved cystine proteases that cleave target proteins at specific aspartate residues. Caspases are classified as initiators (caspases-8, -9, and -10), which are activated in response to apoptotic signals, and executioners (caspases-3, -6, and -7), which are activated by initiators through proteolitic cleavage (Salvesen and Riedl 2008). Caspases are regulated by endogenous inhibitors such as the family of inhibitor of apoptosis proteins (IAPs) and the bifunctional apoptosis regulator (BAR) (Zhang et al. 2000; Dubrez-Daloz et al. 2008). Apoptosis plays a pivotal role both in fetal development and in adult organisms, where it contributes to the maintenance of normal cellular homeostasis and efficiency of the immune system (Opferman and Korsmeyer 2003; Marsden and Strasser 2003). Many evidences suggest that defects in the mechanisms of apoptosis are involved in several multifactorial diseases (Hague and Paraskeva 2004).

Because of the complexity of the apoptotic pathways, in recent years, mathematical modeling has been used to understand different aspects of these pathways and to lay down guidelines to design experimental studies (Fussenegger et al. 2000; Bentele et al. 2004; Eissing et al. 2004; Eissing et al. 2005; Stucki and Simon 2005; Bagci et al. 2006; Legewie et al. 2006; Rehm et al. 2006). The models proposed so far consist of systems of ordinary differential equations that describe the time evolution of the concentrations of the chemical species regarded as relevant for the apoptotic process: caspases, regulator proteins, and molecular complexes. These models have been studied essentially from two points of view: (a) qualitative analysis of equilibrium states and of their stability properties and (b) quantitative simulation of the time evolution of the relevant chemicals in response to a model input representative of the external or internal stimulus that triggers the apoptotic cascade.

Recently, Carotenuto et al. (2007a, b) carried out an in-depth analysis of a dynamical model of caspase activation in response to a stimulus applied to the cell membrane (extrinsic pathway). The model was originally proposed by Eissing et al. (2004), and in Carotenuto et al. (2007b), it was extended to keep into account the action of a persistent stimulus. The model describes:

  • Production and decay of procaspase-8 (C8) and of procaspase-3 (C3), and of inhibitors IAP and BAR

  • Transformation of C8 into the active form C8* by an external stimulus acting through the cell membrane

  • Activation of C3 to active caspase-3 (C3*) by C8* and positive feedback of C3* on C8 to enhance production of C8*

  • Inactivation of C8* by BAR through reversible formation of the complex C8*÷BAR

  • Inactivation of C3* by IAP through reversible formation of the complex C3*÷IAP

The model consisted of eight first-order nonlinear differential equations, whose state variables were the single-cell concentrations of procaspases 3 and 8, of respective active caspases, of inhibitors IAP and BAR, and of the inactivating complexes. Each of the model responses, computed by solving the equations with appropriate initial conditions and external forcing, can be regarded as representative of the life history of a cell, subjected to an apoptotic stimulus. One peculiar feature of the unforced model is the presence of an equilibrium state, characterized by the absence of active caspases, both free and in complexes: such equilibrium can be regarded as representative of a cell in “normal” conditions, and was called the “life” equilibrium. In Carotenuto et al. (2007a, b), an exhaustive theoretical characterization of the model equilibrium states, of the respective stability properties, and of typical bifurcation paths was provided. Moreover, the results of a huge amount of numerical simulations were reported, giving a complete picture of the possible time evolutions of active caspases-3 and -8, for different values of the kinetic parameters and of the external stimulus. The main feature of the responses to a constant input was that the variables representing active caspase-3 and caspase-8 concentrations remain almost constant at low values for a time interval whose length depends mainly on the input level; then, they show an abrupt increase to a peak value, which depends on the model parameters and not on the input level. In Carotenuto et al. (2007b), the effect of changing the production rate of regulator proteins IAP and BAR was also analyzed. The most interesting result was that a reduction of this rate essentially affects the delay between the application of the stimulus and the peak of active caspase-3 concentration, and not the peak intensity. Further information on the model and on the results of Carotenuto et al. (2007b) is in the Supplementary Material (Supplement 1).

Starting from the in silico results, we designed and carried out in vitro experiments on populations of suitably chosen cells, treated with an external factor known to elicit the extrinsic apoptotic pathway. In particular, we measured the time evolution of the activity of caspases-3 and -8, and we assayed the fraction of dead cells as an indicator of the apoptotic state.

The objective of the study was to compare the characteristic features of the experimental responses to those obtained by the model simulations.

The experiments were repeated on cells where the BAR gene was silenced, thus depressing the level of the BAR protein. The purpose was to verify if the effect of a reduced production rate of BAR, as predicted by the model simulation, could be experimentally confirmed.

We anticipate that a good qualitative agreement has been found between the results obtained by model simulations and those obtained from the experimental system. This agreement shows that the mathematical model captures the essential features of the biological process and could be a reliable tool in further studies of caspase activation.

Materials and methods

Cell culture

143B.TK− osteosarcoma cells were grown in Dulbecco's modified Eagle medium (DMEM, Invitrogen) containing 25 mM glucose and 1 mM sodium pyruvate, supplemented with 10% fetal bovine serum (Invitrogen) and 0.1 mM gentamycin (Invitrogen). The cells were cultured in a water-humidified incubator at 37°C in 5% CO2/95% air.

Set up of the experimental conditions: cell synchronization; Apo2L/TRAIL concentration assay; BAR gene silencing

Cell synchronization In complete DMEM, 1 × 106 cells were cultured into 100 mm plates for 12 h. Then, the medium was replaced with medium without serum, and the cells were cultured in this condition for 36 h. Cells were stained with propidium iodide, and the percentage of cells in each cell cycle phase was estimated by flow cytometry with fluorescence activated cell sorter (FACS) analysis.

Apo2L/TRAIL concentration assay After 36 h of serum deprivation, the synchronized cells were trypsinized and 3 × 105 cells were seeded in 60-mm well plates containing complete medium and allowed to adhere to the plate overnight. Then, the cells were treated with different concentrations (50, 100, 250, 500, 1,000 ng/ml) of recombinant Apo2L/TRAIL protein (Chemicon International) for 12 h. By measuring caspase-3 activity as described in the relevant paragraph (caspase-3 and caspase-8 activity assays), we chose an Apo2L/TRAIL concentration of 1,000 ng/ml as the most appropriate.

BAR gene silencing The cells were synchronized for 36 h as described above. After synchronization, we trypsinized and collected adherent cells only, thus removing the floating cells completely. The cells were newly plateled so that the following experiments were carried out on a “new” cell population. Then, the Fast-Forward Protocol (Qiagen) was used to obtain BAR gene silencing by BAR siRNA transfection. Next, 2.5 × 105 cells were seeded in six-well plates containing complete medium. Three concentrations (1, 5, and 10 nM) of BAR siRNA (HP Validated siRNA, Qiagen) were added to 3 µl of HiPerFect Reagent (Qiagen), and the mix was incubated at room temperature for 10 min. Cells were treated with the silencing mixture and incubated at 37°C for 24, 48, and 72 h. Untrasfected cells and cells transfected with scrambled siRNA sequence were also used as controls. Then, total RNA was extracted from cells with RNeasy kit (Qiagen) and the RNA concentration was measured in each sample by biophotometer (Bio-Rad) at 260/280 nm absorbance ratio. The reverse transcriptase polymerase chain reaction (RT-PCR) reactions were carried out by using the ImPromII Reverse Transcription System kit (Promega). A mix including 500 ng of total RNA and 500 ng of oligo-dT primer was preheated at 70°C for 5 min. The RT reaction was carried out in 40 µl final volume containing 1× RT buffer, 3 mM MgCl2, 125 µM of each deoxynucleotide triphosphate (dNTP), 20 U RNase inhibitor, and 5 U RT. The mix was incubated at 25°C for 5 min, then at 37°C for 60 min, and finally at 95°C for 10 min to inactivate the RT. Both the BAR gene and an endogenous control gene (GAPDH) that is not expected to vary among samples were amplified in each sample.

The primers used for BAR and GAPDH PCR amplification were the following:

  • BAR forward primer 5′-TCTGCCGTCACTGCCTTGGCT-3′

  • Reverse primer 5′-ACACGTTCTAGCTCCATGAG-3′

  • GAPDH forward primer 5′-GACAACTTTGGTATCGTGGA-3′

  • Reverse primer 5′-ACACGTTCTAGCTCCATGAG-3′

The PCR mixture (25 µl) contained 1 µl of cDNA, 1× buffer, 1.25 mM of each dNTP, 3.5 mM MgCl2, 0.4 μM of each primer, and 10 U DNA polymerase (EuroTaq). The PCR profile consisted of a predenaturation step at 92°C for 1 min, followed by 30 cycles at 92°C for 1 min, 62°C for 1 min, and 72°C for 1 min. The final step was an incubation at 70°C for 10 min. The PCR products were analyzed on 2% agarose gel and stained with ethidium bromide. In each sample, fluorescence intensity of the BAR product was calculated by densitometric analyses (Kodak Electrophoresis Documentation and Analysis System 290, EDAS 290) and then normalized to fluorescence intensity of the GAPDH product.

Caspase-3 and caspase-8 activity assays

Caspase-3 and caspase-8 activities were assayed by using the Caspase-3 Detection Kit (FITC-DEVD-FMK, Calbiochem) and the Caspase-8 Detection Kit (Red-IETD-FMK, Calbiochem), respectively. The assays were carried out on cells stimulated by Apo2L/TRAIL, and synchronized only, or synchronized and treated with BAR siRNA.

Caspase-3 and caspase-8 activity assays in Apo2L/TRAIL-treated cells For time intervals of different lengths, 3 × 105 synchronized cells were incubated with 1,000 ng/ml of Apo2L/TRAIL at 37°C. Synchronized but untreated cells were used as control. Then, 1 μl of FITC-DEVD-FMK (FITC-conjugated caspase-3 inhibitor) or Red-IETD-FMK (Red-labeled caspase-8 inhibitor) was added to 300 μl of cell sample. Then, the cells were incubated at 37°C for 45 min and centrifuged at 3,000 rpm for 5 min. Supernatant was removed and the cell pellet was resuspended in 500 μl of the kit wash buffer and centrifuged again. This step was repeated again one time. Finally, the cells were resuspended in 300 μl of wash buffer and analyzed by flow cytometry with FACS analysis. Then, 1 × 104 cells were acquired in list mode and analyzed with Cell Quest software. Caspase-3 and caspase-8 activities were defined as the ratio of the number of cells treated with Apo2L/TRAIL positive to FITC-DEVD-FMK (caspase-3) or positive to Red-IETD-FMK (caspase-8) to the number of untreated cells positive to FITC-DEVD-FMK or to Red-IETD-FMK.

Caspase-3 activity assay in BAR siRNA-silenced cells and treated with Apo2L/TRAIL After 36 h synchronization, the medium was removed from plates, the cells were trypsinized, and adherent cells were collected. Next, 2.5 × 105 cells were seeded in six-well plates containing complete medium. The procedure of BAR siRNA transfection was carried out for 72 h as described above (BAR gene silencing). In the last 6 h of transfection, cells were incubated at 37°C with 1,000 ng/ml of Apo2L/TRAIL. Then, caspase 3 activity was measured as described above. Caspase-3 activity was defined in both silenced and nonsilenced conditions as percentage of cells treated with Apo2L/TRAIL positive to FITC-DEVD-FMK.

Cell mortality assays

Cell mortality was assayed by Trypan Blue exclusion assay. After 36 h synchronization, floating and adherent cells were collected and 200 µl of cellular suspension was added to an equal volume of 0.4% Trypan Blue solution (Sigma). Cells were counted at 6–28 h after synchronization on a hemocytometer with an inverted light microscope using a 20× magnification.

Trypan Blue assay was used also to check mortality in cells treated either with Apo2L/TRAIL or with BAR siRNA and Apo2L/TRAIL. In both cases, after 36 h of synchronization, the medium was removed from plates, the cells were trypsinized, and adherent cells were collected, removing the floating cells completely. The cells were seeded in 60-mm well plates containing complete medium and allowed to adhere to the plate overnight. Then, the cells were treated with Apo2L/TRAIL or transfected with BAR siRNA and treated with Apo2L/TRAIL as described in previous paragraphs. Floating and adherent cells were collected and 200 µl of cellular suspension was added to an equal volume of 0.4% Trypan Blue solution (Sigma). Cells were counted on a hemocytometer with an inverted light microscope using 20× magnification.

Hallmarks of apoptosis

To assess apoptosis, we used Annexin V assay (Van England et al. 1998) and internucleosomal DNA fragmentation assay (Bortner et al. 1995). As for the first test, 5 × 105 synchronized cells were treated with 1,000 ng/ml of Apo2L/TRAIL, as described above, and incubated at 37°C for time intervals of different length. Cells were washed in phosphate-buffered saline (PBS) and resuspended in the kit binding buffer. Five microliters of FITC-conjugated Annexin V (Bender MedSystems) was added to 195 μl of cell suspension, and the samples were incubated at room temperature for 10 min. Then, the cells were washed in PBS and resuspended in 190 μl of binding buffer. Ten microliters of propidium bromide was added to the samples and the fluorescence was measured by flow cytometry. Next, 1 × 104 cells per sample were acquired in list mode and analyzed with Cell Quest software. As for DNA fragmentation assay, 1 × 106 Apo2L/TRAIL treated and untreated cells were trypsinized and centrifuged at 3,000 rpm for 5 min. The pellet was resuspended in 400 µl of lysis buffer [10 mM Tris–HCl pH 8, 20 mM ethylenediaminetetraacetic acid (EDTA), 0.2% Triton-X100] and incubated on ice for 20 min. After centrifugation at 12,000 rpm for 20 min, an equal volume of phenol/chloroform was added to the supernatant. Then, after a new 12,000-rpm centrifugation for 5 min, an equal volume of chloroform was added to the supernatant and centrifuged again. The supernatant was collected and stored at −20°C overnight after adding 0.1 vol of 3 mM sodium acetate pH 5.2 and 2 vol of ethanol. DNA precipitated was pelleted by centrifugation at 12,000 rpm for 20 min, rinsed with 70% ethanol, and resuspended in a buffer containing 100 mg/ml RNase A. After incubation at 37°C for 2 h, DNA samples were loaded on 1.5% agarose gel, electrophoresed in Tris/acetate/EDTA buffer and stained with ethidium bromide.

Simulation of the collective behavior of a cell population

The mathematical model here considered was analyzed theoretically and numerically in the papers by Carotenuto et al. (2007a, b). The assumptions at the basis of the model, the equations, the nominal parameter values, a summary of the theoretical results, and of the outcomes of the numerical simulations are reported in Supplement 1 (Electronic Supplementary Material). In the present paper, we use that model to simulate the collective behavior of a population of cells. As a model with given parameters can be regarded as representative of a single cell, a set of models, each of which is characterized by a different parameter vector, represents a population of cells whose collective behavior was simulated by computing the individual responses and averaging them over the ensemble of time histories. Specifically, a set of N parameter vectors was generated in such a way that the corresponding models are bistable, with the same “life” equilibrium state. For each parameter vector, say the k-th in the set, the model equations (Eqs. S1–S8, Supplement 1) were numerically solved by the MATLAB function ode15s, starting from the same initial condition and with the same external input q(t), acting on the interval [0, Ti]. In this way, the time evolution of the variables [C8*] = x2 and [C3*] = x6, representative of the concentration of active caspase-8 and caspase-3 in the k-th cell of the population of size N, was obtained. Denote by x6[k](t), k = 1,…, N these time functions: the model prediction of the measure of active caspase-3 concentration in the population subjected to a stimulus of duration Ti was computed by taking the average 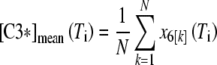Inline graphic. The same procedure was used for [C8*]. To simulate a mortality curve for the population, we assumed that the event: x6[k] exceeds some threshold value, say cD, from time tD[k] onward is representative of the activation of caspase-3 to a level that causes the death of the k-th cell. Then, for each T, the number of models for which tD[k] ≤ T, say NA(T), represents the number of cells in the population that entered the final phase of apoptosis in a time interval less than or equal to T. Obviously, the ratio 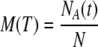Inline graphic represents the fraction of cells dead in the time interval [0, T].

Results

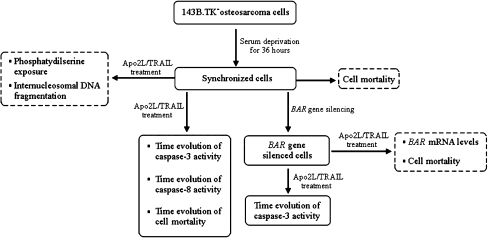
Figure 1 outlines the in vitro experiments we carried out. As we see, some experiments were realized to set up the experimental conditions (panels with dashed borders), others to compare in silico and in vitro results (panels with solid borders). All the experiments were carried out on synchronized cells in order to ensure that the apoptotic stimulus was applied to cells in the same phase of their cycle. To this purpose, we checked four synchronization protocols (serum deprivation for 24 or 36 h, Aphidicolin 5.9 μM for 16 h, Aphidicolin 5.9 μM for 16 h, plus serum deprivation for 48 h. Data not shown). The best pattern of synchronization was obtained by serum deprivation for 36 h: 82.2% of the cells were in G0/G1 phase; 9.5% in S phase, and 8.3% in G2/M phase. To make sure that a sufficient bulk of cells survived the synchronization treatment, we measured the fraction of dead cells at different times after serum deprivation. The fraction of dead cells (Trypan Blue exclusion assay) remained at about 30% in the first 12 h. Only after 24 h did the fraction of dead cells increase up to about 60% (Fig. S1 in Supplement 2, Supplementary Material). Therefore, all the following experiments were carried out on cells synchronized by 36 h serum deprivation. When further cell treatments longer than 12 h were required, dead cells were removed after synchronization as described in the “Materials and methods” (“BAR gene silencing”).

Fig. 1.

Fig. 1

Open in a new tab

Flow chart of the experimental procedure. Panels with dashed borders: experiments realized to set up the in vitro experimental conditions; panels with solid borders: experiments realized to compare in vitro results with in silico results

Since cells were undergoing heavy manipulations, we needed to verify that, in our system, we were looking at an apoptotic response. For this purpose, we used Annexin V and internucleosomal DNA fragmentation assays, which check initial and final steps of the apoptotic process, respectively.

The Annexin V assay was performed both on untreated cells and on cells treated with Apo2L/TRAIL for time intervals of increasing length. Figure S2 in Supplement 2, Supplementary Material, shows the fraction of cells positive to Annexin V as a function of the time of treatment. We see that, after the first 60 min, the fraction of Annexin V positive cells is higher in treated (red line) than in untreated (blue line) cells.

Also, the internucleosomal DNA fragmentation assay was performed both on untreated cells and on cells treated with Apo2L/TRAIL for time intervals of increasing length. Figure S3 in Supplement 2, Supplementary Material, shows the fragmentation pattern of untreated and treated cells at the specified times. The internucleosomal fragmentation is observed in cells treated with Apo2L/TRAIL for 240 and 360 min. A small level of fragmentation is also present in untreated cells, likely a noise due to synchronization.

Comparison between in vitro and in silico results: time evolution of caspase-3 and caspase-8 activities

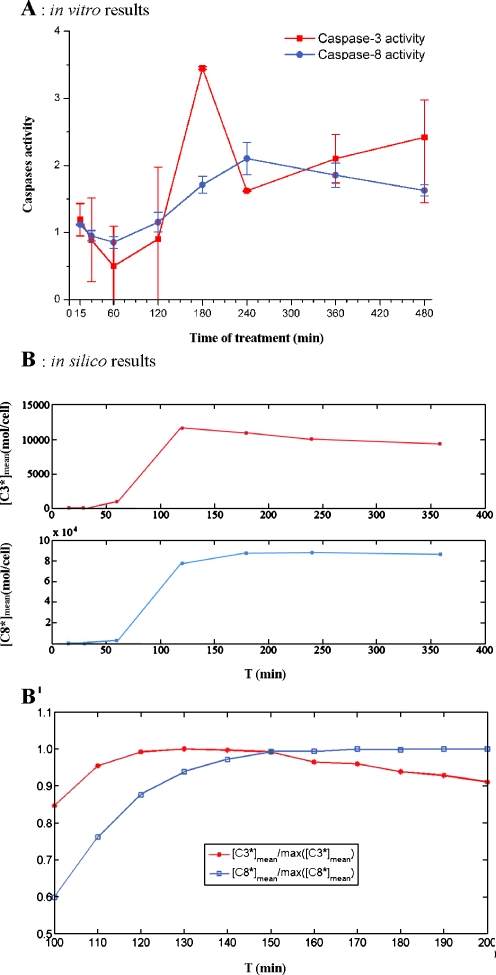
To obtain the time response of a population of cells subjected to an apoptotic stimulus, we carried out experiments in which the activities of caspase-3 and -8 were measured at successive times on the same initial cell population. Nine time intervals of increasing length were considered as shown in Fig. 2A. The two curves can be regarded as representative of the time evolution of active caspase-3 and -8 concentrations, respectively, in a population of stimulated cells. Caspase-3 activity remains nearly constant for the first 120 min of treatment. Then, a fast increase occurs between 120 and 180 min, when caspase-3 activity reaches the maximum value. Also, caspase-8 activity remains nearly constant for the first 120 min of treatment; then it increases, reaching the maximum value at 240 min. Figure 2B shows the result of model simulations that mimic the in vitro experiment. Simulations are performed as described in “Materials and methods” (“Simulation of the collective behavior of a cell population”). The qualitative agreement between the model predictions and the measured caspases activities is apparent: in both instances, we have a delay between the application of the stimulus and the onset of caspase activation. Moreover, the increase of active caspase-3 concentration precedes that of caspase-8 in both in silico and in vitro experiments, as can be better seen in Fig. 2B′.

Fig. 2.

Fig. 2

Open in a new tab

Caspase-3 and caspase-8 activation: comparison between in vitro A and in silico B results. A Caspase-3 (red line) and caspase-8 (blue line) activities were evaluated as the ratio of the number of cells treated with Apo2L/TRAIL positive to FITC-DEVD-FMK (caspase-3) or Red-DEVD-FMK (caspase-8) to the number of untreated cells positive to FITC-DEVD-FMK or Red- DEVD-FMK (see “Materials and methods”). On the Y axis, the ratios measured at the end of the time intervals of treatment (15, 30, 60, 120, 180, 240, 360, and 480 min) are reported. The values are the average of three independent experiments. Bars: one standard deviation. B Seven sets of models were generated with the procedure described in the paper by Carotenuto et al. (2007b), section 2.2.4. Each set consists of 5,000 bistable models with random parameters selected in a suitable box of the parameter space; for all models of the i-th set, the responses to a persistent stimulus of intensity q = 400 mol/cell/min and of duration Ti = 15, 30, 60, 120, 180, 240, and 360 min, respectively, were simulated. In each group, the averages [C3*]mean(Ti), [C8*]mean(Ti) of the final values of the variables that represent caspase-3 and -8 concentrations were computed and are reported in the graph on the Y axis, as a function of the stimulus duration T. A finer representation of the model response around the peaks of [C3*]mean, [C8*]mean is given in B′, which shows the ratios 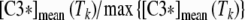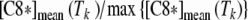Inline graphic, Inline graphic for Tk = 100, 110,…, 190, 200 min

Comparison between in vitro and in silico results: time evolution of cell mortality

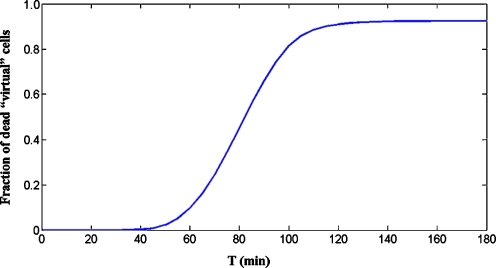
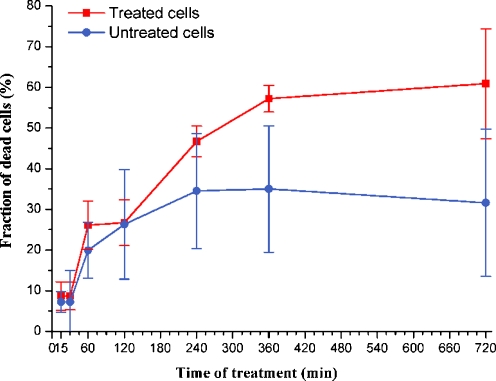
The mathematical model can be used to predict the qualitative shape of the curve relating the fraction of dead cells in the population to the time of treatment. Figure 3 shows in silico results obtained by simulations carried out according to the procedure described in “Materials and methods” (“Simulation of the collective behavior of a cell population”). The fraction of dead “virtual” cells at time T is the fraction of models for which the concentration of active caspase-3, [C3*], computed by numerically solving the model equations, has exceeded a given threshold in the interval [0,T]. The main feature of the curve is the delay between the application of the stimulus and the appearance of a significant fraction of dead “virtual” cells. As for in vitro results, Fig. 4 shows the fraction of dead cells in untreated cells and in cells treated with Apo2L/TRAIL for different intervals of time. For time intervals up to 120 min, cell mortality is almost the same in both treated and untreated cells. Then, the mortality of treated cells increases up to a value of 57% at 360 min, whereas the fraction of dead cells in the untreated population does not exceed 34% for all time intervals. The qualitative agreement between in silico and in vitro results is clear.

Fig. 3.

Fig. 3

Open in a new tab

Model prediction of the dependence of cell mortality on the time of treatment. The cell population is represented by a set Σ (“virtual” population) consisting of 75,000 models characterized by randomly generated parameter vectors (“virtual” cells), belonging to the same box used for Fig. 2B. For all models in set Σ, the active caspase-3 time responses (x6[k](t) (k = 1,2,…,75,000)) to a persistent stimulus of intensity q = 400 mol/cell/min and of duration Ti = 10, 20,…,180 min were computed. Then, the times tD[k] for which x6[k](t) reaches the threshold x6[k](t) = 5,000 mol/cell were determined. Finally, the number of models for which tD[k] ≤ Ti, say NA(Ti), was computed for all Ti, and the ratios are reported in the figure

Fig. 4.

Fig. 4

Open in a new tab

Fraction of dead cells after Apo2L/TRAIL treatment. Y axis reports the ratio: number of dead cells/total number of cells, in percentage. X axis reports the time of Apo2L/TRAIL treatment. The values represent the average of three independent experiments. Bars: one standard deviation

BAR gene silencing

Since the model takes into account the production rate of BAR, we decided to check the model by acting on the level of BAR gene expression. Before measuring the response in terms of caspase-3 activity in BAR-silenced cells, the silencing protocol was set up (see “Materials and methods”). For this purpose, we transfected the cells at different experimental conditions (siRNA concentrations and transfection times) and measured the BAR mRNA levels by semiquantitative RT-PCRs. The best result (Fig. S4 in Supplement 2, Supplementary Material) was obtained at 72 h with 5 nM BAR siRNA: in these conditions, a reduction of about 80% of the BAR mRNA level was achieved. Therefore, all the subsequent experiments were carried out at these experimental conditions.

The effects of Apo2L/TRAIL on the BAR gene expression were tested in both nonsilenced and BAR-silenced cells. Treatments with Apo2L/TRAIL of different time lengths were applied, and BAR mRNA levels were evaluated by RT-PCR at the end of the treatment intervals. Figure S5 (Supplement 2, Supplementary Material) shows the levels of BAR mRNA, normalized to GAPDH mRNA levels, as a function of the time of treatment with Apo2L/TRAIL in nonsilenced cells (panel A) and in silenced cells (panel B). In panel A, we see that the BAR mRNA levels decrease slowly up to 180 min of treatment, where the reduction is about 50%. After 240 min of treatment, the level of BAR mRNA becomes negligible. This result suggests an inhibitor role of the inductor Apo2L/TRAIL on the regulation of the expression of the BAR gene. To our knowledge, such an effect has not been reported till now. As for panel B (BAR-silenced cells), we see that the BAR silencing produces a decrease (more than 60%) of the level of BAR mRNA in cells not treated with Apo2L/TRAIL (time of treatment = 0). This level remains constant for the first 60 min of treatment and decreases by increasing the stimulation time.

We also evaluated if there are differences in cell mortality between nonsilenced and BAR-silenced cells exposed to Apo2L/TRAIL for different times. Figure S6 (Supplement 2, Supplementary Material) shows that the fraction of dead cells is the same in both nonsilenced and silenced cells in the first 30 min; a relevant increase of this fraction (from 37% to 75%) is observed in silenced cells between 60 and 240 min of treatment; then the fraction of dead cells reaches 85% after 360 min. In nonsilenced cells, an increase from 23% to 53% occurs between 60 and 240 min of treatment, resulting in nearly 62% after 360 min. This result is in line with a proapoptotic effect sustained by the BAR gene silencing.

Time evolution of caspase-3 activity in BAR-silenced cells

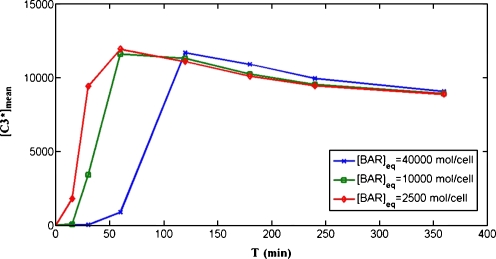
In silico results The effect of changing the production rate of the inhibitor protein BAR, represented in the model by the parameter k−12, was numerically evaluated in Carotenuto et al. (2007b). It was shown that a reduction of this rate shortens the delay between the application of the stimulus and the peak of active caspase-3 concentration, and does not noticeably affect the peak intensity. This result is not unexpected: if the production rate of BAR is reduced, a smaller amount is available to bind the active caspase-8 and form the inactive complex C8*÷BAR. This is equivalent to an increase of the intensity of the stimulus, which, in all simulations, has been recognized to decrease the delay of the peak of [C3*]. The collective behavior of a cell population in which the production of BAR is reduced was simulated by the same procedure used to obtain Fig. 2B. The same sets of models was used for the simulations, except for reducing the value of k−12 to 1/4 (line with squares) and to 1/16 (line with circles) of the value used to simulate the unperturbed population (line with stars). The perturbed models show reduced values of the BAR concentration at equilibrium: [BAR]eq = 10,000 mol/cell and [BAR]eq = 2,500 mol/cell, respectively, with respect to the unperturbed model for which [BAR]eq = 40,000 mol/cell. Figure 5 shows the plot of the average [C3*]mean in perturbed and unperturbed models as a function of the time length of the stimulus. It is clear that, also at the population level, a reduction of the production rate of BAR causes a faster response of active caspase-3 concentration to the external stimulus.

Fig. 5.

Fig. 5

Open in a new tab

Model prediction of the effect of reducing the production rate of BAR. The line with stars is the same as the line representing [C3*]mean in Fig. 2B: it is obtained using models characterized by production rates of BAR (parameter k−12) for which, at equilibrium, we have [BAR]eq = 40,000 mol/cell. The line with squares represents the averages [C3*]mean(Ti) (Ti = 15, 30, 60, 120, 180, 240, and 360 min) computed by simulating the same models as in Fig. 2B, except for the parameter k−12, which is reduced to 1/4 of the original value, thus reducing the equilibrium value to [BAR]eq = 10,000 mol/cell. The line with circles represents the averages [C3*]mean(Ti) computed by simulating the same models as in Fig. 2B, except for the parameter k−12, which is reduced to 1/16 of the original value, thus reducing the equilibrium value to [BAR]eq = 2,500 mol/cell

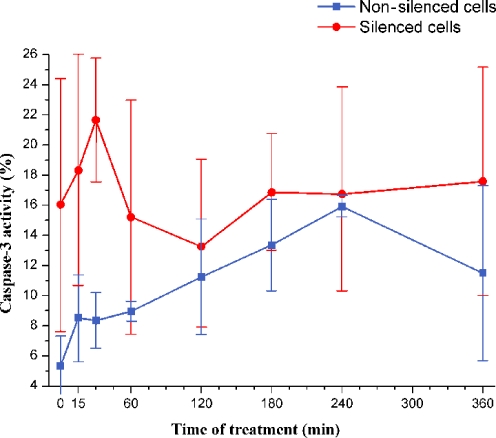
In vitro results The activity of caspase-3 was measured both in nonsilenced and in BAR-silenced cells, both incubated for 72 h in the absence/presence of BAR siRNA. In both groups of cells, the stimulation with Apo2L/TRAIL began at defined time points before the end of the 72 h of the silencing, when measurements were taken. Figure 6 shows the caspase-3 activity in nonsilenced and in BAR-silenced cells, expressed as the percentage of FITC-DEVD-FMK-positive cells (see “Materials and methods”), as a function of the time of treatment with Apo2L/TRAIL. In nonsilenced cells, a peak of caspase-3 activity occurred at 240 min of treatment. In silenced cells, the caspase-3 activity level has a clear maximum at 30 min of treatment. Although the standard deviations of measurements are high, it is clear that the peak of caspase-3 activity occurs earlier in silenced than in nonsilenced cells (see also Table S3 in Supplement 3, Supplementary Material). From these experiments, we may conclude that the activation of caspase-3 requires a shorter interval of stimulation when BAR is silenced, in agreement with the in silico results reported above.

Fig. 6.

Fig. 6

Open in a new tab

Caspase-3 activity in nonsilenced and in BAR-silenced cells. Y axis reports the caspase-3 activity in nonsilenced and in silenced cells evaluated as the percentage of cells treated with Apo2L/TRAIL positive to FITC-DEVD-FMK. On the X axis, the time of Apo2L/TRAIL treatment is reported. The values represent the average of three independent experiments. Bars: one standard deviation. Note that, in order to make clear the comparison between silenced and nonsilenced cells, the definition of caspase-3 activity is different from that used in Fig. 2 (see “Materials and methods”). Time of treatment = 0 means that cells were not treated with Apo2L/TRAIL

Discussion

“A cell, an organ, or organism, understood as a ‘system’, is a network of components whose relationships and properties are largely determined by their function in the whole. The functionality is observed as the behavior of the system. The first and probably most important lesson of systems theory is that we can only understand the behavior of a system if we systematically perturb it and record its response.” This sentence from a recent paper entitled “Defining Systems Biology: an Engineering Perspective” (Wolkenhauer 2007) well captures the approach behind the present work. Regarding the integrative study of biological systems and the way they respond to external perturbations as the essence of systems biology is not a new idea (Auffray et al. 2003). Such an approach leads to hypotheses formalized in mathematical models: on the one hand, these models are built from the results of studies about functional genomics, protein–protein interactions, signaling, and metabolic pathways. On the other hand, since a system approach is characterized by input/output descriptions relating stimuli (inputs) to responses (outputs), “the most important role of the modeler in systems biology is to support the design of stimulus/response experiments” (Wolkenhauer 2007).

In this work, the paradigm outlined above has been applied to apoptosis, a very important physiological process normally occurring in cells and whose malfunction has been related to severe pathologies such as cancer and neurodegenerative diseases.

The aim of this work was to compare in silico results with in vitro results obtained on a population of cells perturbed by an appropriate proapoptotic stimulus. The experiments were designed according to guidelines in part provided by the analysis of a model originally proposed by Eissing et al. (2004) and then studied in-depth by Carotenuto et al. (2007a, b). This model considers only the extrinsic pathway, which leads to the production of active caspase-3 starting from the binding of suitable ligands to receptors on the exterior of the cell membrane: although simple enough to allow an analytical study and a large number of numerical simulations, the model incorporates three phenomena probably critical in the evolution of the apoptotic process: (1) activation of caspase-8 by the external stimulus, (2) activation of caspase-3 by active caspase-8, and (3) activation of caspase-8 by active caspase-3 in a positive-feedback loop. An agreement between the experimentally measured responses and those predicted by simulation of the model equations would validate the assumptions that are at the basis of the model. We remark that only qualitative comparisons can be made. Indeed, the experimental procedures impose severe limitations that make an in vitro experiment very different from a conceptually identical experiment performed in silico: (a) the cells are subjected to continuous changes due to the normal cell cycle; (b) the cells are continuously subjected to random external perturbations that the experimenter cannot control; and (c) in all the experiments, the measurements that correspond to treatments of different time lengths are carried out on different subgroups of cells, although derived from the same initial population. Moreover, the model takes into account only the reactions that are regarded as the most relevant in the pathway; it does not consider all the other processes that occur in the cells and that are “disturbances” from the model point of view. In particular, the model does not consider the cell cycle or the events that lead to cell death after caspase-3 activation and assumes that, in normal conditions, no cell in the population undergoes apoptosis. The experiments were set up in order to reduce as far as possible the above sources of uncertainty and lack of homogeneity. This was the case of the synchronization procedure by which 82% of the cells are set in G0/G1 phase. The synchronization treatment by serum deprivation induces apoptosis by itself in a fraction of cells, chiefly via mitochondrial signaling pathways (Bialik et al. 1999; Pillich et al. 2005). However, the vital state of population as a whole is not seriously impaired because the fraction of vital cells remains around 70% for the first 12 h after the synchronization treatment (see Fig. S1).

Apoptosis was elicited by treating the synchronized osteosarcoma cells with an appropriate concentration of Apo2L/TRAIL. Although osteosarcoma cells are less sensitive to TRAIL than other cancer cells (Takeda et al. 2007), we chose these cells in view of a future research aimed at studying apoptosis in rho0 cells, that is cells deprived of active mitochondria (King and Attardi 1996).

Both Fig. 2 and Figs. 3 and 4 evidence a good agreement between in silico and in vitro results. In particular, as to the relationship between caspase-3 and caspase-8 activation, the experimental results confirm the model prediction that, as a consequence of the positive feedback of active caspase-3 on caspase-8, the peak of active caspase-3 concentration occurs earlier than the peak of active caspase-8 concentration (Fig. 2). What is more, both in vitro (Fig. 2A) and in silico (Fig. 2B) curves show an initial phase where active caspase concentrations are nearly independent of treatment time (120 min in vitro). The same shape is shown by the curves relevant to cell mortality obtained by in vitro experiments: for the first 120 min the fraction of dead cells in treated samples is not different from the fraction of dead cells in untreated samples (Fig. 4); the mortality in treated cells systematically exceeds that in nontreated cells only after 120 min. This behavior qualitatively agrees with the trend of “mortality” that the model predicts in a population of virtual cells (Fig. 3): the fraction of virtual cells that undergo the transition to virtual apoptosis is very low for an initial time interval, then increases to reach a value that remains constant for the subsequent time. On the whole, we have verified a good qualitative agreement between the results of the dynamical simulation of active caspases-3 and -8 concentrations (in silico) and the results of the stimulus–response experiments (in vitro).

Also, the response of the BAR gene-silenced cells confirmed the model predictions (Carotenuto et al. 2007b and Fig. 5). In the model, the dynamical simulations in which the production rate of BAR is reduced show that the time evolution of active caspase-3 is influenced by this parameter, in the sense of a faster response to the stimulus. The same faster response was observed in vitro when the rate of BAR production was reduced by BAR gene silencing: the peak of caspase 3 activity occurs at 30 min in silenced cells and at 240 min in nonsilenced cells (Fig. 6). It is worth noting that the caspase activation is accelerated in both intrinsic and extrinsic apoptosis pathways in cells deficient of X-linked-inhibitor-of-apoptosis protein, an effective intracellular inhibitor of apoptosis (O'Connor et al. 2008).

Also, the experimental determination of the fraction of dead cells confirms the proapoptotic role by BAR silencing (Fig. S6 in Supplement 2, Supplementary Material): after 30 min of Apo2L/TRAIL treatment, the fraction of dead cells in silenced cells (red line) overcomes that in nonsilenced cells (blue line)

Interestingly, in setting up the experimental protocol of BAR gene silencing, we observed that the treatment with Apo2L/TRAIL by itself causes a progressive reduction of BAR mRNA (Fig. S5, panel A, in Supplement 2, Supplementary Material). This finding is new and was not kept into account in the model.

In short, the analysis of the effects produced by BAR gene silencing also showed a good agreement between in silico and in vitro results. In addition, a new interaction (the decrease of BAR expression caused by the treatment with Apo2L/TRAIL) has been discovered.

In conclusion, the consistent qualitative agreement between the time evolutions predicted by the model and the behavior of the cell cultures indicates that the model actually captures the essential features of the biological process and could be a reliable tool in further studies of caspases activation.

Electronic supplementary materials

Below is the link to the electronic supplementary material.

ESM 1 (675.5KB, doc)

(DOC 675 kb)

Acknowledgments

The work was supported by the EU project “European Challenge for Healthy Ageing” (No. QLRT-2001-00128, Call Identifier QOL-2001-3; to GDB) and by Fondo Sociale Europeo (Ph.D. course in Molecular Biopathology, University of Calabria, Italy).

Abbreviations

Apo2L/TRAIL

Apoptosis-inducing ligand 2/Tumor necrosis factor-related apoptosis-inducing ligand

siRNA

Small interfering RNA

RT-PCR

Reverse transcriptase polymerase chain reaction

FACS

Fluorescence activated cell sorter

Footnotes

Vincenza Pace and Dina Bellizzi contributed equally to this work.

References

  1. Auffray C, Imbeaud S, Roux-Rouquié M, Hood L. From functional genomics to system biology: concepts and practices. CR Biol. 2003;326:879–892. doi: 10.1016/j.crvi.2003.09.033. [DOI] [PubMed] [Google Scholar]
  2. Bagci EZ, Vodovotz Y, Billiar TR, Ermentrout GB, Bahar I. Bistability in apoptosis: roles of Bax, bcl-2 and mitochondrial permeability transition pores. Biophys J. 2006;90:1546–1559. doi: 10.1529/biophysj.105.068122. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bentele M, Lavrik I, Ulrich M, Stosser S, Heermann DH, Kalthoff H, Krammer PH, Eils R. Mathematical modelling reveals threshold mechanism in CD95-induced apoptosis. J Cell Biol. 2004;166:839–851. doi: 10.1083/jcb.200404158. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bialik S, Cryns VL, Drincic A, Miyata S, Wollowick AL, Srinivasan A, Kitsis RN. The mitochondrial apoptotic pathway is activated by serum and glucose deprivation in cardiac myocytes. Circ Res. 1999;85:403–414. doi: 10.1161/01.res.85.5.403. [DOI] [PubMed] [Google Scholar]
  5. Bortner CD, Oldenburg NB, Cidlowski JA. The role of DNA fragmentation in apoptosis. Trends Cell Biol. 1995;5:21–26. doi: 10.1016/S0962-8924(00)88932-1. [DOI] [PubMed] [Google Scholar]
  6. Carotenuto L, Pace V, Bellizzi D, Benedictis G. Equilibrium, stability and dynamical response in a model of the extrinsic apoptosis pathway. J Biol Syst. 2007;15:261–285. doi: 10.1142/S0218339007002192. [DOI] [Google Scholar]
  7. Carotenuto L, Pace V, Bellizzi D, De Benedictis G (2007b) Dynamical Analysis of the Programmed Cell Death Pathway. In: Tzafestas S (ed) Proceedings of the European Control Conference 2007 (ECC'07), Kos, 2–5 July 2007, pp 3747–3754. http://biologia.unical.it/genetica/Carotenuto_et_al.pdf
  8. Degterev A, Yuan J. Expansion and evolution of cell death programmes. Nat Rev Mol Cell Biol. 2008;9:378–390. doi: 10.1038/nrm2393. [DOI] [PubMed] [Google Scholar]
  9. Dubrez-Daloz L, Dupoux A, Cartier J. IAPs: more than just inhibitors of apoptosis proteins. Cell Cycle. 2008;7:1036–1046. doi: 10.4161/cc.7.8.5783. [DOI] [PubMed] [Google Scholar]
  10. Eissing T, Conzelmann H, Gilles ED, Allgower F, Bullinger E, Scheurich P. Bistability analyses of a caspase activation model for receptor-induced apoptosis. J Biol Chem. 2004;279:36892–36897. doi: 10.1074/jbc.M404893200. [DOI] [PubMed] [Google Scholar]
  11. Eissing T, Allgower F, Bullinger E. Robustness properties of apoptosis models with respect to parameter variations and intrinsic noise. Syst Biol. 2005;12:221–228. doi: 10.1049/ip-syb:20050046. [DOI] [PubMed] [Google Scholar]
  12. Fussenegger M, Bailey JE, Varner JA. Mathematical model of caspase function in apoptosis. Nat Biotechnol. 2000;18:768–774. doi: 10.1038/81208. [DOI] [PubMed] [Google Scholar]
  13. Hague A, Paraskeva C. Apoptosis and disease: a matter of cell fate. Cell Death Differ. 2004;11:1366–1372. doi: 10.1038/sj.cdd.4401497. [DOI] [PubMed] [Google Scholar]
  14. King MP, Attardi G. Isolation of human cell lines lacking mitochondrial DNA. Methods Enzymol. 1996;264:304–313. doi: 10.1016/S0076-6879(96)64029-4. [DOI] [PubMed] [Google Scholar]
  15. Krysko DV, Vanden Berghe T, D'Herde K, Vandenabeele P. Apoptosis and necrosis: detection, discrimination and phagocytosis. Methods. 2008;44:205–221. doi: 10.1016/j.ymeth.2007.12.001. [DOI] [PubMed] [Google Scholar]
  16. Legewie S, Bluthgen N, Herzel H. Mathematical modelling identifies inhibitors of apoptosis as mediators of positive feedback and bistability. PLos Comput Biol. 2006;2:1061–1073. doi: 10.1371/journal.pcbi.0020120. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Marsden VS, Strasser A. Control of apoptosis in the immune system: Bcl-2, BH3-Only proteins and more. Annu Rev Immunol. 2003;21:71–105. doi: 10.1146/annurev.immunol.21.120601.141029. [DOI] [PubMed] [Google Scholar]
  18. Opferman JY, Korsmeyer SJ. Apoptosis in the development and maintenance of the immune system. Nat Immunol. 2003;4:410–415. doi: 10.1038/ni0503-410. [DOI] [PubMed] [Google Scholar]
  19. Pillich RT, Scarsella G, Risuleo G. Reduction of apoptosis through the mitochondrial pathway by the administration of acetyl-l-carnitine to mouse fibroblasts in culture. Exp Cell Res. 2005;306:1–8. doi: 10.1016/j.yexcr.2005.01.019. [DOI] [PubMed] [Google Scholar]
  20. O'Connor CL, Anguissola S, Huber HJ, Dussmann H, Prehn JH, Rehm M. Intracellular signaling dynamics during apoptosis execution in the presence or absence of X-linked-inhibitor-of-apoptosis-protein. Biochim Biophys Acta. 2008;1783:1903–1913. doi: 10.1016/j.bbamcr.2008.05.025. [DOI] [PubMed] [Google Scholar]
  21. Rehm M, Huber HJ, Dussmann H, Prehn JHM. Systems analysis of effector caspase activation and its control by X-linked inhibitor of apoptosis protein. EMBO J. 2006;25:4338. doi: 10.1038/sj.emboj.7601295. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Salvesen GS, Riedl SJ. Caspase mechanisms. Adv Exp Med Biol. 2008;615:13–23. doi: 10.1007/978-1-4020-6554-5_2. [DOI] [PubMed] [Google Scholar]
  23. Stucki JW, Simon HU. Mathematical modelling of the regulation of caspase-3 activation and degradation. J Theor Biol. 2005;23:123–131. doi: 10.1016/j.jtbi.2004.11.011. [DOI] [PubMed] [Google Scholar]
  24. Takeda S, Iwai A, Nakashima M, et al. LKB1 is crucial for TRAIL-mediated apoptosis induction in osteosarcoma. Anticancer Res. 2007;27:761–768. [PubMed] [Google Scholar]
  25. England M, Nieland LJW, Ramaekers FCS, Schutte B, Reutelingsperger CP. Annexin V-Affinity Assay: A review on an apoptosis detection system based on phosphatydilserine exposure. Cytometry. 1998;31:1. doi: 10.1002/(SICI)1097-0320(19980101)31:1<1::AID-CYTO1>3.0.CO;2-R. [DOI] [PubMed] [Google Scholar]
  26. Wolkenhauer O. Defining systems biology: an engineering perspective. IET Syst Biol. 2007;1:204–206. doi: 10.1049/iet-syb:20079017. [DOI] [PubMed] [Google Scholar]
  27. Zhang H, Xu Q, Krajewski S, Krajewska M, Xie Z, Fuess S, Kitada S, Pawlowski K, Godzik A, Reed JC. BAR: An apoptosis regulator at the intersection of caspases and Bcl-2 family proteins. Proc Natl Acad Sci U S A. 2000;97:2597–2602. doi: 10.1073/pnas.97.6.2597. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Below is the link to the electronic supplementary material.

ESM 1 (675.5KB, doc)

(DOC 675 kb)

Articles from Cell Stress & Chaperones are provided here courtesy of Elsevier

RESOURCES