Self-association of Zn-insulin at neutral pH: investigation by concentration gradient static and dynamic light scattering

Abstract

Equilibrium self-association of Zn-insulin at pH 7.0 was characterized over the range 0.3 – 5 mg/mL by simultaneous measurement of static and dynamic light scattering. Analysis of static light scattering yielded a concentration-dependent weight-average molecular weight, and analysis of dynamic light scattering yielded a concentration-dependent intensity-average diffusion coefficient. The concentration dependence of both quantities may be accounted for to within experimental precision by a simple model, according to which the basic structural unit of Zn-insulin at concentrations exceeding 0.3 mg/mL is a hexamer H. With increasing total protein concentration, hexameric protomers may self-associate in accordance with an isodesmic scheme in which a protomer may add to any prexisting oligomer H_n to form H_n+1 with an invariant stepwise equilibrium association constant.

Introduction

It is generally accepted that the tendency of insulin to self-associate in solution is strongly enhanced in the presence of zinc ion [1], which is normally present at a concentration of ca 0.2 mM in human serum [2]. In particular, under conditions where zinc-free insulin exists in monomeric form, insulin in the presence of zinc is thought to exist primarily as a hexamer binding two moles of zinc per mole of hexamer [1]. The concentration-dependent self-association of bovine Zn-insulin at pH 7.0 was previously studied by Milthorpe et al [3] via sedimentation equilibrium over the concentration range 0.03 – 0.6 mg/ml, who reported that over this concentration range the sedimentation equilibrium could be accounted for by an equilibrium between monomer and hexamer. Their data suggested the possibility of additional self-association at higher concentrations but that possibility was not explored further. In the present work we employ measurements of static and dynamic light scattering to extend the characterization of Zn-insulin self-association to an order of magnitude higher concentration.

The recently developed technique of concentration gradient – static light scattering (CG-SLS) has been shown to provide accurate information of high resolution about equilibrium self-and hetero-association in a variety of experimental systems [4–7]. In the present work we have simultaneously measured the concentration dependence of dynamic as well as static light scattering to provide two independent but complementary measures of the average state of association of insulin at equilibrium in solutions of the same pH and ionic strength as those studied by Milthorpe et al [3]. The investigation is carried out on protein solutions that have been carefully prepared as described by previous investigators in order to provide a valid comparison with earlier work, and to extend that work.

Materials and Methods

Solutions of Zn-Insulin were prepared as described by Ahamad et al [8]. Bovine pancreatic insulin (Sigma, Lot # 019K17762, Zn 0.5%), was freshly prepared by dissolving it in 0.025 M HCl (pH 1.8) solution. The solution was buffered by adding HEPES buffer (1 M stock solution; Meditech Inc) to 50 mM; pH was adjusted to 7.4 by adding NaOH [8]. Insulin concentration in stock solutions was measured spectrophotometrically by measuring the absorbance at 276 nm [9]. Solutions so prepared were then characterized via size exclusion chromatography on a Superdex 200 column (Pharmacia) coupled to a miniDAWN light scattering photometer and an Optilab differential refractometer (Wyatt). Prior to measurement of concentration gradient light scattering, insulin solutions were freshly prepared, filtered using 0.1 µm Anotop syringe filters (Whatman), degassed via centrifugation, and used for measurement within 3–8 hours.

Step gradients of concentration of insulin solution ranging from 0 to 5 g/L or from 0 to 2.5 g/L in 10% increments were automatically created using the Calypso system (Wyatt), and at each concentration step, static light scattering at multiple angles and dynamic light scattering at 108° were measured simultaneously, using a DAWN-EOS light scattering photometer equipped with a QELS accessory (Wyatt). Concentration changes were concurrently measured via differential refractive index in an Optilab rEX differential refractometer (Wyatt), the flow cell of which was configured in parallel with that of the light scattering photometer, as described in [4]. Data were simultaneously collected from the DAWN-EOS, QELS accessory, and Optilab rEX using ASTRA 4.9 (Wyatt), and exported for further analysis with user-written scripts and functions in MATLAB (Mathworks, Natick MA). All gradient experiments were performed in duplicate at 25°C as previously described [4–6].

Static light scattering data were subsequently processed as described previously [4, 5] to yield tables of the scattering intensity, expressed as the ratio of the Rayleigh ratio to the optical constant (R/K_opt), as a function of scattering angle and the total protein concentration. Results of a typical SLS gradient experiment are plotted in Figure 1. In the absence of detectable angular dependence of R/K_opt, the data obtained at all angles in a single experiment were combined into a single data set for subsequent modeling using various models for equilibrium self-association of Zn-insulin in solution. At each total protein concentration, the dynamic light scattering data, expressed as the dependence of the second-order autocorrelation function on delay time τ, could be fit to within experimental precision by a single decaying exponential expression [10]:

$$\mathit{\text{ACF}}(\tau )={\mathit{\text{ACF}}}_{\infty }+{\mathit{\text{ACF}}}_0\text{exp}(-2D_{\mathit{\text{app}}}{q}^2\tau )$$ (1)

where ACF₀ and ACF_∞ respectively denote the values of ACF in the short and long time limits. q denotes the scattering vector, which at a scattering angle of θ is given by

$$q=\frac{4\pi n_0}{{\lambda }_0}\text{sin}\left(\frac{\theta }{2}\right)$$ (2)

where n₀ denotes the refractive index of solvent and λ₀ denotes the wavelength of incident light. D_app denotes an intensity-weighted or z-average translational diffusion coefficient of the scattering species, which may vary with total protein concentration when the protein is undergoing equilibrium self-association [10]. Normalized autocorrelation functions obtained at three protein concentrations are plotted together with the respective best fits of equation (1) in Figure 2.

Figure 1.

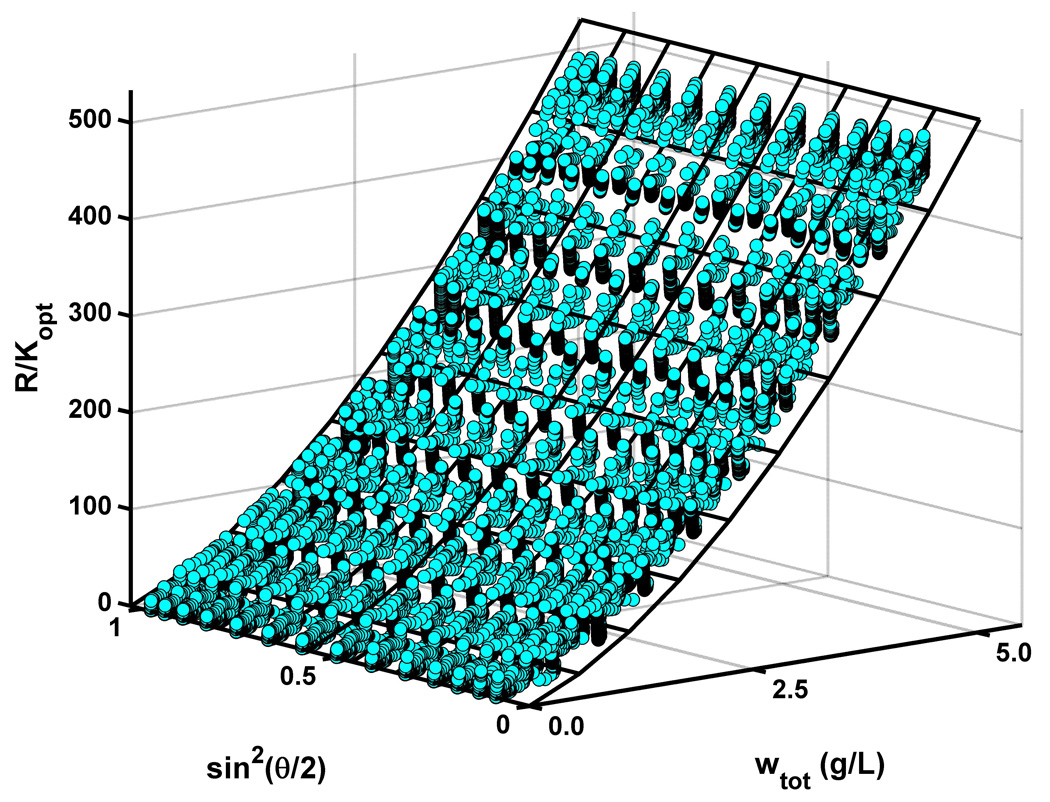
Scattering intensity in units of R/K_opt plotted as a function of the w/v concentration of Zn-insulin and scattering angle θ, prior to removal of statistical outliers and combination of data obtained at all angles for each protein concentration.

Figure 2.

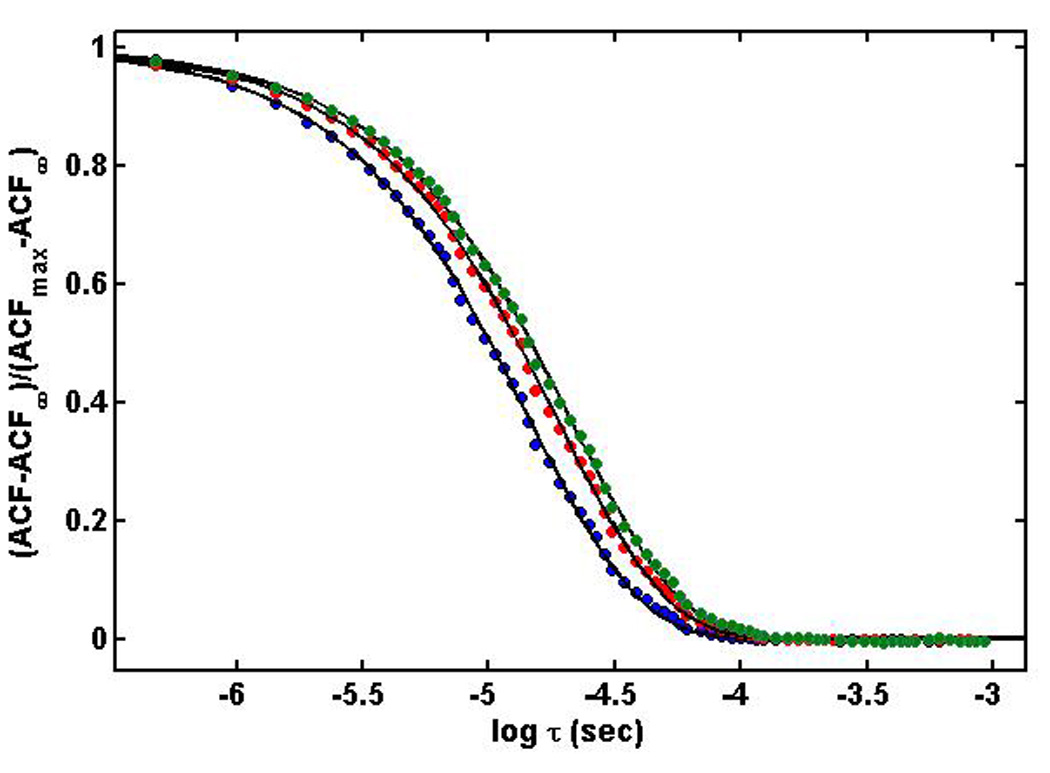
Normalized autocorrelation functions measured for the following insulin concentrations: 4.99 g/l (green), 2.52 g/l (red), and 0.48 g/l (blue), plotted together with curves calculated according to the best fit of equation (1) to the respective data set.

Analysis of concentration-dependent static and dynamic light scattering data

In dilute solution, the scaled Rayleigh ratio of solution containing a single scattering component (in the present case, insulin) is given by [11]

$$\frac{R}{K_{\mathit{\text{opt}}}}={\displaystyle \sum M_i{w}_i=M_W{w}_{\mathit{\text{tot}}}}$$ (2)

where M_i and w_i respectively denote the molecular weight and weight/volume concentration of each oligomeric state of insulin, w_tot the total weight/volume concentration, and M_W the weight average molecular weight, given by

$$M_W=\frac{{\displaystyle \sum _i{w}_i{M}_i}}{{\displaystyle \sum _i{w}_i}}=\frac{{\displaystyle \sum _i{c}_i{M}_i^2}}{{\displaystyle \sum _i{c}_i{M}_i}}$$ (3)

where c_i denotes the molar concentration of the ith species.

When the autocorrelation function obtained from dynamic light scattering measurement may be well-described by equation (1), the concentration-dependent value of D_app may be taken to be equal to the intensity-weighted average (z-average) of the translational diffusion coefficients of all species contributing significantly to the observed scattering [12, 13]:

$$D_{\mathit{\text{app}}}=D_Z=\frac{{\displaystyle \sum _i{w}_i{M}_i{D}_i}}{{\displaystyle \sum _i{w}_i{M}_i}}=\frac{{\displaystyle \sum _i{c}_i{M}_i^2{D}_i}}{{\displaystyle \sum _i{c}_i{M}_i^2}}$$ (4)

Calculation of the concentration dependence of static and dynamic light scattering according to the isodesmic indefinite self-association model

We recently found that the simplest model for indefinite self-association, namely the isodesmic model, was able to describe the concentration dependence of static light scattering of zinc-free insulin solutions at pH values between 3 and 8 with high precision (submitted for publication). We thus attempted to use the same model to account for the concentration dependence of both the static and dynamic light scattering of zinc-insulin solutions at neutral pH. In the isodesmic model for self-association, it is assumed that the oligomer size may increase indefinitely, and that the equilibrium constant for addition of a protomer to another protomer or oligomer of any size is independent of oligomer size, that is,

$$K_a=\frac{c_i}{c_{i-1}{c}_1}$$ (5)

is independent of the value of i. The conservation of mass is given by

$$c_{\mathit{\text{tot}}}=\frac{w_{\mathit{\text{tot}}}}{M_1}={\displaystyle \sum _{i=1}^{\infty }i{c}_i=\frac{c_1}{{(1-K_a{c}_1)}^2}}$$ (6)

Given values of w_tot, M₁, and K_a, equation (6) may be solved analytically for the equilibrium value of c₁, and then equation (5) utilized iteratively to obtain the equilibrium concentrations of all oligomeric species. The normalized scattering intensity is then given by

$$\frac{R}{K_{\mathit{\text{opt}}}}={\displaystyle \sum _{i=1}^{\infty }{c}_i{M}_i^2=\frac{M_1^2}{K_a}\frac{(z+z^2)}{{(1-z)}^3}}$$ (7)

where z ≡ K_ac₁. The concentration dependence of M_w may then be obtained by dividing R/K_opt by w_tot (equation 2).

In order to calculate the value of D_app, the value of each D_i must be specified. As shown in the appendix, to a good approximation the translational diffusion coefficients of a broad variety of globular (but not extended) proteins vary with M^−1/3. We shall thus assume that the diffusion coefficients of the various oligomers of insulin – provided that they do not deviate too highly from a quasispherical conformation – similarly vary with M, from which it follows that

$$D_i=D_1{i}^{-1/3}$$ (8)

Given values of w_tot, M₁, and K_a one may calculate c_i as described above. With one additional parameter, the value of D₁, the value of D_app may be calculated using the following combination of equations (4) and (8):

$$D_{\mathit{\text{app}}}=D_1\frac{{\displaystyle \sum _i{i}^{5/3}{c}_i}}{{\displaystyle \sum _i{i}^2{c}_i}}$$ (9)

Preliminary calculations established that at the highest protein concentration utilized in the present study, the sums indicated in equation (9) converged for i < 10.

Results

Size exclusion chromatography – static light scattering

200 µl each of two Zn-insulin samples (2 and 4 mg/ml) were injected. The elution profile of 90° scattering at 690 nm is plotted in Figure 3. The major peak accounts for almost 99% of total eluted protein. The average molecular weight calculated from the ratio of scattering to concentration at the peak maximum, was 33.4 (± 3) × 10³, corresponding to a hexamer of 5400 MW subunits, in agreement with results reported earlier obtained from samples under similar conditions [8, 14].

Figure 3.

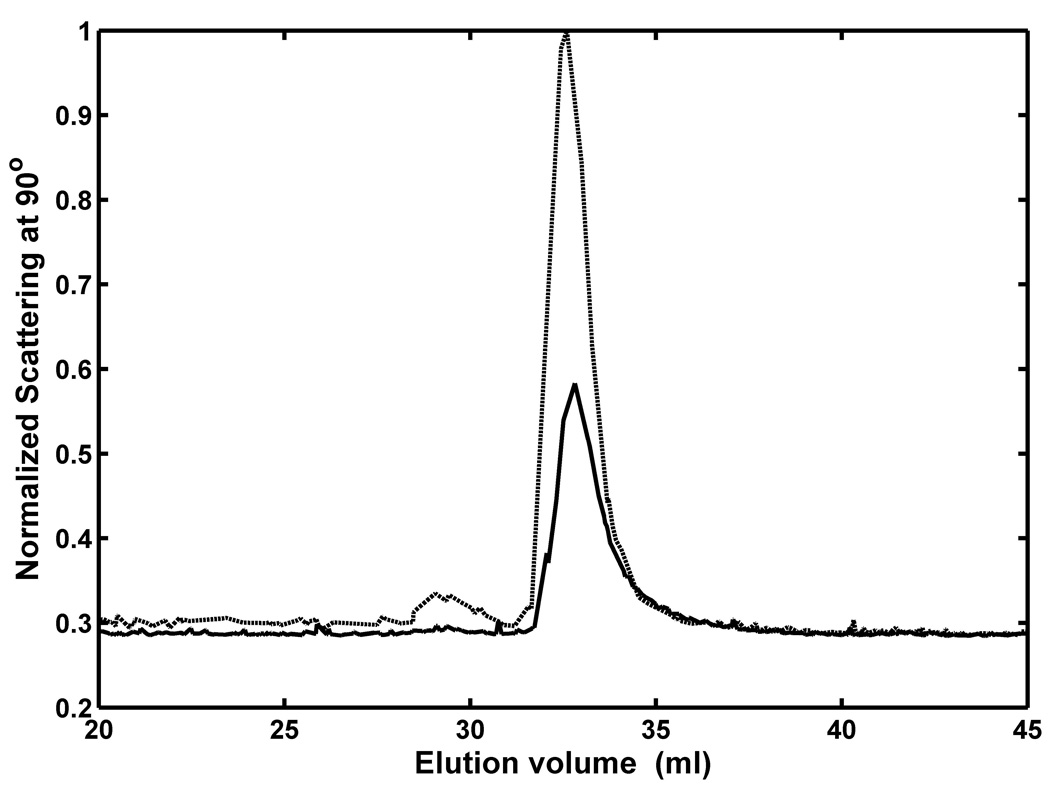
Chromatographic elution patterns obtained following injection of insulin solutions of 4 mg/ml (dashed) and 2 mg/ml concentration (solid), as monitored by intensity of 90° scattering.

Concentration dependence of static light scattering

The dependence of R/K_opt upon total w/v insulin concentration at concentrations up to 5 g/L, measured at 14 scattering angles, is plotted in Figure 4. Also plotted is the best fit of the isodesmic indefinite self-association model, calculated from equations (6) and (7) with M₁ = 32.0 (± 3.7) × 10³ and log₁₀ K_a (M⁻¹) = 4.2 ± 0.2, where the indicated uncertainty corresponds to ± 2 standard errors of estimate. It is evident that this model describes the data to well within the uncertainty of measurement. The simplest explanation for the concentration dependence of static light scattering is that the basic structural unit of insulin under the conditions of this experiment (at concentrations exceeding ca 0.3 mg/ml) is the hexamer, which may self-associate in accordance with an isodesmic scheme.

Figure 4.

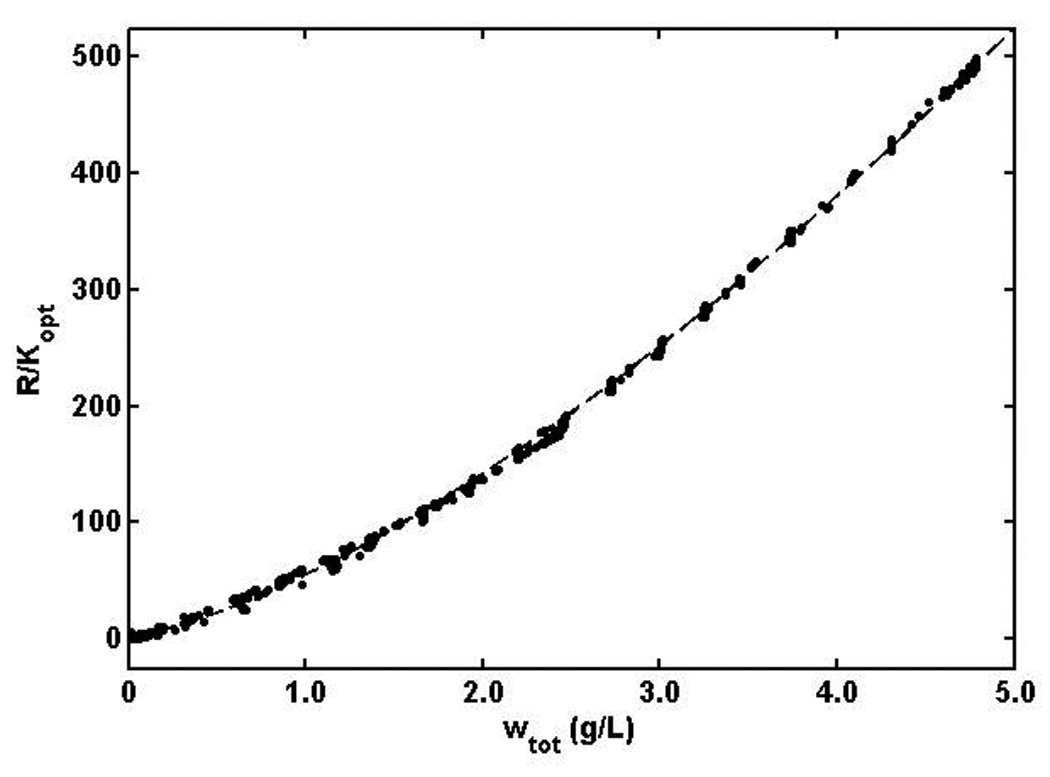
Scattering intensity in units of R/K_opt plotted as a function of the concentration of Zn-insulin. Dotted curve is best fit of isodesmic equilibrium association model, calculated using equation (7) with best-fit values of M₁ and log K_a given in the text.

Concentration dependence of dynamic light scattering

The measured dependence of D_app upon total w/v insulin concentration at concentrations up to 5 g/L is plotted in Figure 5. Also plotted is the best fit of the indefinite isodesmic self-association model incorporating the additional assumption embodied in equation (8), as calculated from equations (5), (6), and (9) with M₁ = 32.0 × 10³ (constrained), log₁₀ K_a (M⁻¹) = 4.05 ± 0.5, and D₁ = 8.5 ± 1.2 × 10⁻⁷ cm²/sec. It is shown in the appendix that the best-fit value of D₁ obtained here agrees closely with that expected from a quasispherical molecule of molar mass ca 32 × 10³ g. This demonstrates that the results of the present analysis of the concentration dependence of the apparent diffusion coefficient obtained from dynamic light scattering measurements are self-consistent, as well as entirely consistent with the results of the analysis of the concentration dependence of static light scattering intensity.

Figure 5.

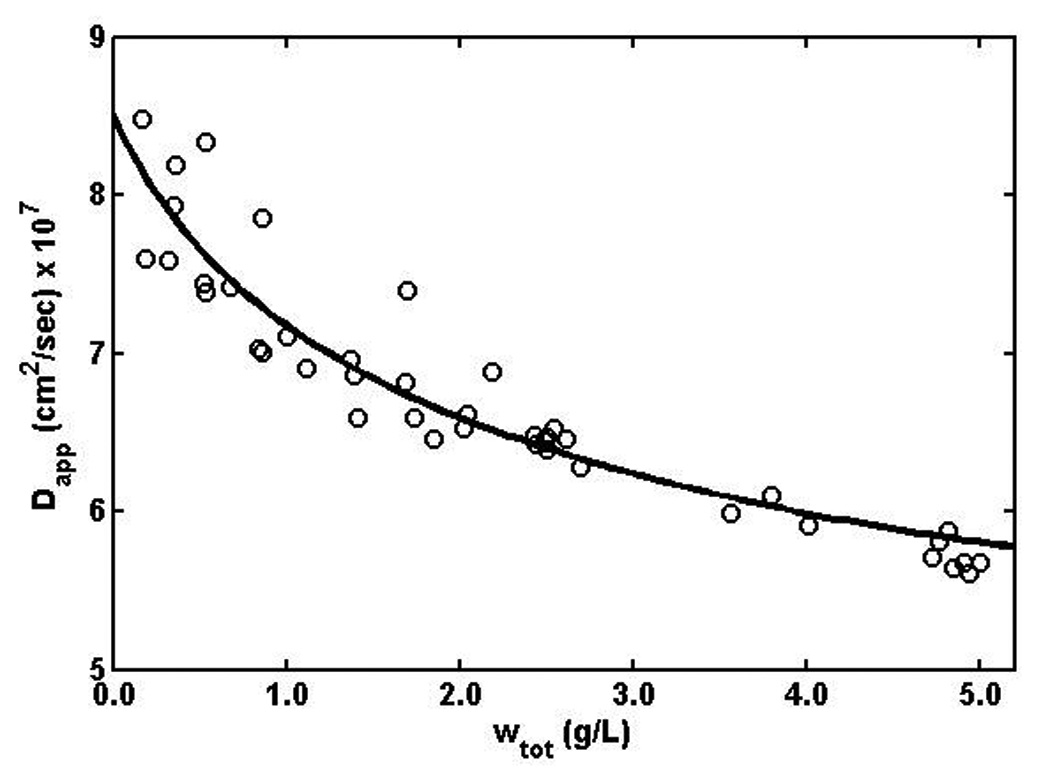
D_app plotted as a function of the concentration of Zn-insulin. Solid curve is the best fit of the isodesmic equilibrium association model, calculated using equations (5), (6), (8), and (9), with the best-fit values of M₁, log K_a, and D1 given in the text.

Discussion

The present work has shown that over the concentration range 0.3 – 5 mg/ml, the concentration dependence of both static and dynamic light scattering of bovine Zn-insulin at neutral pH may be quantitatively accounted for by a simple isodesmic equilibrium self-association scheme, with the hexamer of insulin acting as protomer for self-association. The only prior quantitative study of the self-association of insulin in the presence of a comparable concentration of zinc was carried out via measurement of sedimentation equilibrium over the concentration range 0.03 – 0.6 mg/ml by Milthorpe et al [3]. They interpreted their results as indicating the presence of a zinc-driven concerted transition between monomer that does not bind zinc and a hexamer that binds 2 moles of zinc. In Figure 6 we plot the mass fraction of monomer and various oligomers as calculated by Milthorpe et al (blue curves) and by ourselves (black curves) according to the respective equilibrium association schemes as a function of concentration over the range of concentrations studied, and extrapolated to limiting low concentration (dotted curves). From comparison of results of the two studies the following consensus picture of insulin self-association in the presence of zinc emerges. At total protein concentrations below around 0.06 – .07 mg/mL, insulin exists primarily as an equilibrium mixture of monomer M and hexamer H. As total protein concentration increases above this limit, hexamer begins to self-associate in accordance with an isodesmic scheme, leading to increasing abundances of oligomers of H.

Figure 6.

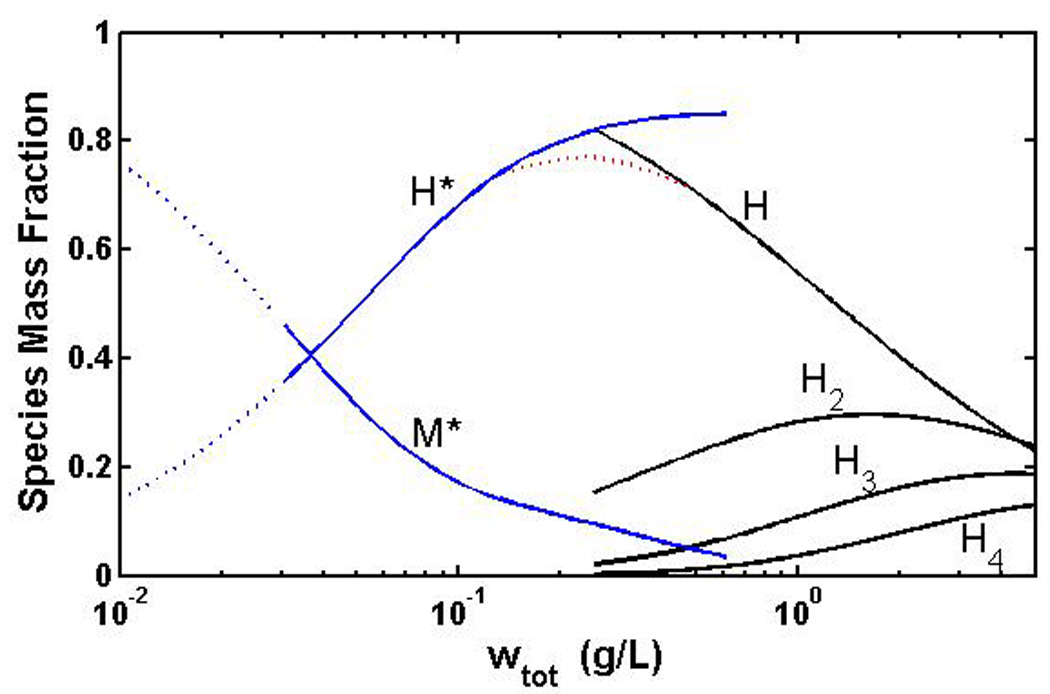
Semilog plot of the mass fraction of major association states, calculated according to the equilibrium scheme of Milthorpe et al [3] (blue curves) and the present work (black curves) plotted against insulin concentration. M* and H* represent the relative abundances of monomer and hexamer according to Milthorpe et al, and H, H₂, H₃, and H₄ represent the relative abundances of hexamer and the dimer, trimer, and tetramer of hexamers calculated according to the best-fit isodesmic association model. Solid lines are plotted over the range of experimental measurement. Dotted blue lines represent extrapolation to lower concentration, and the dotted red line represents a hypothetical “patch” between the highest concentration results of Milthorpe et al and the lowest concentration results obtained in the present work.

In addition to providing new information about insulin self-association in the presence of zinc, the work presented here demonstrates for the first time that concurrent measurement of the concentration dependence of static and dynamic light scattering of proteins provides complementary information about concentration-dependent protein associations that can be utilized to demonstrate self-consistency and validate proposed schemes for association equilibria.

Abbreviations

CG-SLS

composition gradient-static light scattering

Appendix: Empirical relation between molar mass and diffusion coefficient of globular proteins and virus particles

The values of D_20,w reported for a variety of proteins and virus particles over a broad range of molar masses are collected in Table 21-1 of Tanford [15]. To this list were added values of D_20,w obtained for bovine pancreatic trypsin inhibitor, chymotrypsin, and soybean trypsin inhibitor as measured via dynamic light scattering in our laboratory (B. Monterroso and A.P. Minton, manuscript in preparation). When values obtained for markedly aspherical proteins and viruses (fibrinogen, myosin, and tobacco mosaic virus) are deleted, the remaining data are plotted as ln D_20,w vs ln M in Figure 7. These data are well fit by the following linear equation:

$$\text{ln}(D_{\mathit{20},w}\times {10}^7)=A_{\mathit{0}}-A_{\mathit{1}}\text{ln}M$$ (A1)

with A₀ = 5.6748 and A₁ = 0.343 ± 0.02, where the indicated uncertainty represents one standard error of estimate. This is equivalent to the relation D_20,w = 2.91 × 10⁻⁵ / M^0.343, where the exponent of M agrees to within experimental uncertainty with the value 1/3 predicted for a spherical particle by the Stokes-Einstein relation.

Figure 7.

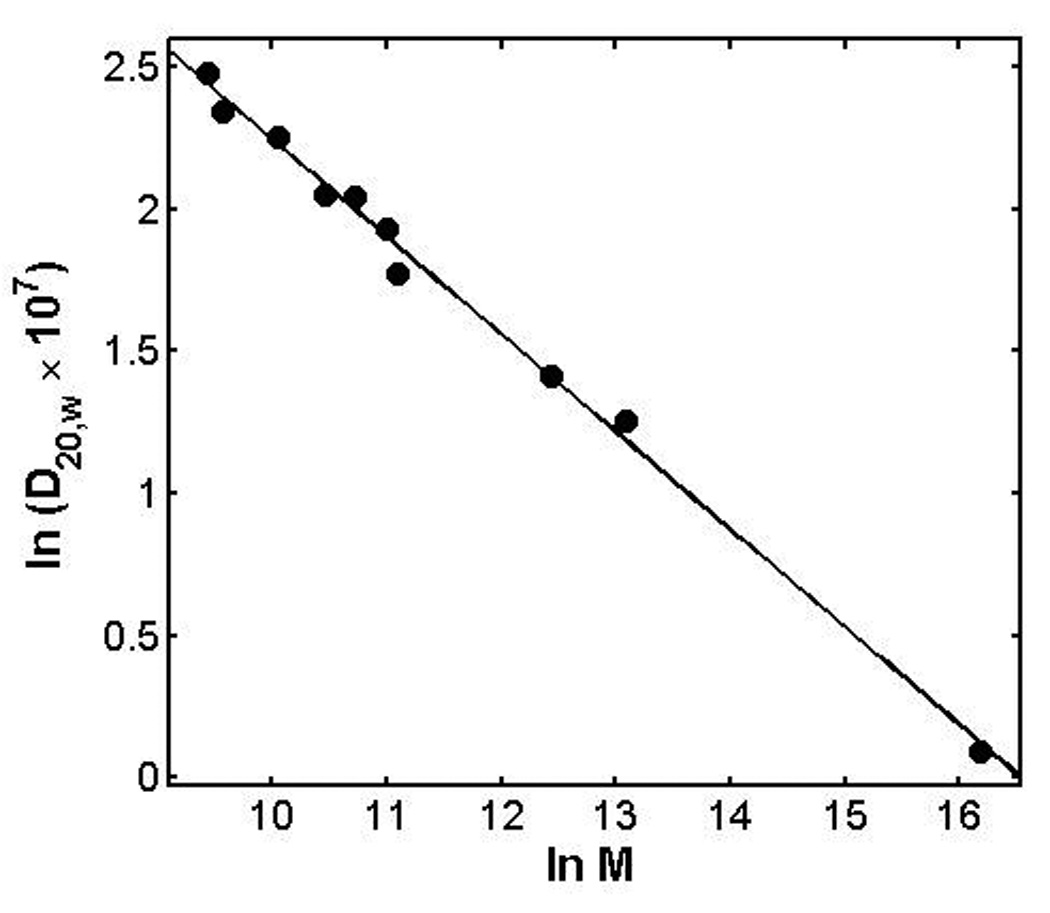
As reported in the text, the best-fit of the isodesmic association scheme to the concentration dependence of D_app yields a best-fit value of the diffusion coefficient of protomer equal to 8.5 × 10⁻⁷ cm²/sec, equivalent to a D_20,w of 8.35 × 10⁻⁷. According to the empirical relation given above, this value of D_20,w corresponds to a species of molar mass ca 31,500, i.e., a hexamer of insulin.