Abstract
DNA•RNA hybrid duplexes are biologically important molecules and are shown to have potential therapeutic properties. To investigate the relationship between structures, energetics, solvation and RNase H activity of hybrid duplexes in comparison with pure DNA and RNA duplexes, a molecular dynamics study using the CHARMM27 force field was undertaken. The structural properties of all the four nucleic acids are in very good agreement with the experimental data. The backbone dihedral angles and the puckering of the (deoxy)ribose indicate that the purine rich strands retain their A/B like properties but the pyrimidine rich DNA strand undergoes A-B conformational transitions. The minor groove widths of the hybrid structures are narrower than in the RNA duplex a requirement for RNase H binding. In addition, sampling of noncanonical phosphodiester backbone dihedrals by the DNA strands, differential solvation properties and helical properties, most notably rise, are suggested to contribute to hybrids being RNase H substrates. Differential RNase H activity towards hybrids containing purine vs. pyrimidine rich RNA strands is suggested to be due to sampling of values of the phosphodiester backbone dihedrals in the DNA strands. Notably, the present results indicate that hybrids have decreased flexibility as compared to RNA, in contrast to previous reports.
Keywords: RNase H binding, CHARMM force field, A-B transition, molecular dynamics simulation, helical properties
Introduction
DNA•RNA hybrids are heterogeneous nucleic acid duplexes containing a DNA strand and a RNA strand, which are formed as key intermediates in various biological processes including DNA transcription and replication.1–3 They also play a major role in the synthesis of retroviral cDNA by reverse transcription. More importantly, DNA•RNA hybrids have been shown to be useful as therapeutic agents in antisense therapy.3–5 Several studies have investigated the dependence of the stability of hybrid structures on affinity, specificity and substrate tolerance.6–16 It has been shown that the stability of hybrid duplexes increases when the DNA strand is chemically modified, thereby increasing the antisense target affinity.7–16 In general, hybrid structures are thermodynamically less stable than pure RNA duplexes; however, the magnitude of the melting temperature is sequence dependent.17 Among the hybrids, purine rich RNA strands are known to form more stable hybrid duplexes than those with pyrimidine rich RNA strands.17–20
RNase H, a ribonuclease, binds to DNA•RNA duplexes independent of the sequence and cleaves the RNA strand hydrolytically to yield 5’-phosphate and 3’-hydroxy terminated products. RNase H binds to both pure RNA duplexes and hybrid structures; however, it cleaves only the RNA strand in the hybrid structures leaving the DNA strand pristine. Notably, hybrids with purine rich RNA strands are resistant to RNase H cleavage, which has been shown to be important in the reverse transcription of HIV RNA.18,21 Reasons behind why RNA duplexes are inhibitors of RNase H and hybrid structures are substrates despite their structural similarities are not completely understood.
Structures of several hybrids have been characterized using X-ray crystallography22–28 and NMR spectroscopy16,20,29–34. Both X-ray and NMR derived structures reveal that the RNA strand of a hybrid is in the A-form with all the ribose moieties present in the north conformation. The structures of the DNA strand obtained by these two methods are not in agreement with each other. X-ray crystal structures indicate that most of the deoxyribose moieties are present in the north conformation, which is typical of a canonical A-form nucleic acid duplex.22,25,26,28 In contrast, NMR experiments show that a considerable number of deoxyribose sugars exist in the south form, which is typical of B-form DNA.20,29,30,35 Recently, Yang and co-workers have reported the X-ray crystal structure of RNase H bound to a DNA•RNA hybrid in which the DNA strand adopts a conformation similar to that obtained using NMR experiments observed in solution.1,36
As discussed above, there are numerous experimental studies available on DNA•RNA hybrids, whereas theoretical studies on these molecules are scarce. Cheatham and Kollman reported a 2 ns MD study on a DNA•RNA hybrid and obtained reasonable agreement with experimental data.37 Sanghani and Lavery reported a molecular modeling study to address the conformational preferences of DNA•RNA hybrids.38. MD studies have also been performed on DNA•RNA hybrids with modified DNA strands.39,40. While these simulations are only 2 ns long or less, recently Noy et al. performed a 10 ns MD simulation on a hybrid structure and proposed that RNase H distinguishes DNA•RNA hybrid from a RNA duplex based on the differential flexibility pattern in the former.41 The RNA strand exhibits A-form structure and the DNA strand exhibits B-form structure leading to an overall mixed A-/B- type conformation. Around the same time, Nina and coworkers studied a DNA•RNA hybrid and its amide-3 backbone modified analog using melting experiments and MD simulations.12 In contrast to the other computational studies, the DNA strand in the hybrids shows predominantly A-form character. Thus, while structural and simulation studies have lead to a better understanding of the properties of DNA•RNA hybrids, there is still not a clear picture of the relationship of the properties of these molecules to their stability and biological function.
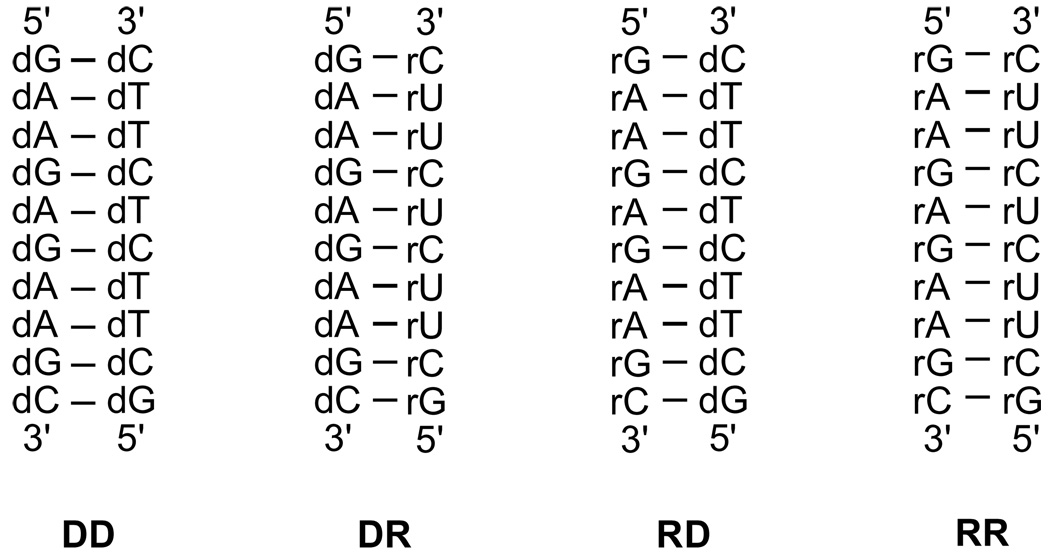
In the present study, we report results from MD simulations on a DNA (DD), two DNA•RNA hybrids (DR and RD), and a RNA duplex (RR) sharing the same sequence except that thymine is replaced by uracil in the RNA strands (Figure 1). The RNA strands in DR and RD contain 90% pyrimidine and purine bases, respectively, with only one of the terminal bases not belonging to the base class. This selection was performed to address the known thermodynamic stability ordering: RR > RD > DD > DR 19 as well as the preferential activity of RNase H towards pyrimidine rich RNA strands. Results also shed light on the intrinsic properties of hybrids versus RNA duplexes that may contribute to the former being substrates of RNase H.
Figure 1.
DNA (DD), RNA (RR) and the two hybrid (DR and RD) duplexes considered in this study.
Computational Details
Starting structures for the simulations were the published NMR structures for the respective oligonucleotides (PDB ID: 1AXP, 1DRR, 1RRD and 1RRR).20 MD simulations were performed using the CHARMM program42 employing the CHARMM27 nucleic acid force field43,44 and the modified TIP3P water model.45 The oligonucleotides were immersed in a pre-equilibrated truncated octahedron water box whose size was selected based on the condition that it extended at least 9 Å beyond the non-hydrogen atoms of the duplexes. Water molecules overlapping with the solute (solute non-hydrogen to solvent non-hydrogen distance of 1.6 Å or less) were deleted and sodium ions were added to make the system electrically neutral. For all the minimizations and MD simulations, periodic boundary conditions were employed using the CRYSTAL46 module implemented in the CHARMM program. Having a mass-weighted harmonic restraint of 5.0 kcal/mol/Å on the non-hydrogen atoms of the duplexes, the systems were subjected to 500-step adopted basis Newton-Raphson (ABNR) minimizations. This was followed by a 20 ps MD simulation in the NPT ensemble and a 100 ps simulation in the NVT ensemble with the same harmonic restraints to equilibrate the solvent molecules around the nucleic acid duplexes. The electrostatic interactions were treated via the particle mesh Ewald method47,48 in all the calculations. Lennard-Jones interactions were truncated at 12 Å with a force switch smoothing function49 from 10 to 12 Å and the non-bond atom lists were updated heuristically. MD simulations were carried out at 283 K, the temperature used in the NMR experiments.19 The structures from the equilibration steps were subjected to 500 step ABNR minimization without any restraints and used as starting structures for the production simulations. Production runs were carried out for 10 ns in the NPT ensemble with the Leapfrog integrator employing an integration time step of 2 fs. No restraints were used in the production simulation while the SHAKE algorithm was used to constrain all covalent bonds involving hydrogen atoms.50 The NPT ensemble was achieved using Hoover chains51 for temperature control with a thermal piston mass of 1000 kcal/mol/ps2 and for pressure control of 1 atm the Langevin piston method52 was used with a piston mass of 600 amu and the piston collision frequency set to 0. Helical parameters and groove widths were evaluated using the CURVES program53 and all other analyses were done using CHARMM. For all the analyses the trajectories from the final 9 ns of the MD simulations were used on coordinates saved every 2 ps. For calculation of root mean square (RMS) deviations with respect to canonical A- and B- like structures, models were generated using Sybyl 6.2 (Tripos, Inc.). Base pair and stacking interaction energies reported here were computed using the ‘INTEr’ command in CHARMM by selecting only the bases. The hydration numbers are the number of water molecules in the first solvation shell defined by those water molecules with an interatomic distance of 3.5 Å between the oxygen and any non-hydrogen atom of the oligonucleotide.
Results and Discussion
The nucleic acid duplexes considered in the present study are shown in Figure 1. DD and RR are pure DNA and RNA duplexes, respectively, and DR and RD are hybrid structures each with one DNA and one RNA strand. All the four nucleic acids share the same sequence except that the thymines of the DNA strands are replaced by uracils in the RNA strands. While the first strand in the molecules consists of nine purine bases and a pyrimidine base, the second strand is composed of nine pyrimidine bases and a purine base. The sequence of these duplexes not only allow the comparative study of hybrids with respect to the pure DNA and RNA structures, but also enable us to investigate the dependence of the purine-pyrimidine composition on the structure of the individual hybrid structures as well as their interaction with RNase H. Towards this goal, various structural and energetic factors were computed and are presented in the following sections.
Structural and dynamic characteristics
The RMS deviations of the systems were calculated with respect to the experimental NMR and X-ray crystal structures (where available), and the canonical A- and B- form structures; the results are given in Table 1. The overall RMS deviations of all the systems with respect to the experimental structures are about 2 Å or less indicating excellent agreement. For DD, 6 NMR structures were reported and for the others, 10 structures were reported,20 with a maximum RMS deviation between the individual NMR structures of around 1.3 Å, a value that is comparable to the calculated RMS values in Table 1. It is quite encouraging that the CHARMM27 all atom nucleic acid force field originally parameterized based on the canonical nucleic acids yields results that are in good agreement with experimental structures for the DNA•RNA hybrids. Though the RMS deviation of RD with respect to the X-ray crystal structure22 is only 1.6 Å, it is higher compared to the RMS deviations with respect to the NMR structure (1.3 Å). This is consistent with the previous observation that MD simulations of the hybrid duplexes in solution yield NMR like structures.41 To understand the contributions from the backbone and bases of the duplexes to the overall deviations, the RMS deviations of the same have been calculated (Table 1). The movement of the phosphodiester backbones of all the systems is more than that of the bases as reflected in the higher deviations for the backbone atoms. As expected, DD has a lower RMS deviation compared to the ideal B-form conformation than the A-form. Similarly, RR has a low difference with respect to the ideal A-form geometry. Interestingly, the RMS differences of both DR and RD with respect to the ideal A-form geometry are 1.9 Å indicating A- like structure for both. However, the deviations with respect to an idealized B-form structure are lower (3.6 and 3.4 Å for DR and RD, respectively) than that of RR (4.9 Å) indicating mixed A-/B- like geometries for the hybrid duplexes. To better understand the equilibrium between the A and B forms in the hybrids, additional analysis of various local structural aspects of the oligonucleotides was undertaken (see below).
Table 1.
Average root mean square deviations (RMSD) for the central eight nucleotides (a), the backbone (b) and the bases (c) of the duplexes compared to the NMR, X-Ray, canonical A-form and B-form structures over the last 9 ns of the simulation.
| NMR | X-Ray | A-form | B-form | |
|---|---|---|---|---|
| (a) Overall | ||||
| DD | 1.49 ± 0.01 | - | 3.67 ± 0.05 | 1.76 ± 0.05 |
| DR | 1.85 ± 0.04 | - | 1.90 ± 0.03 | 3.63 ± 0.05 |
| RD | 1.30 ± 0.02 | 1.58 ± 0.04 | 1.91 ± 0.05 | 3.38 ± 0.05 |
| RR | 2.08 ± 0.12 | - | 2.03 ± 0.16 | 4.87 ± 0.10 |
| (b) Backbone | ||||
| DD | 1.76 ± 0.01 | - | 4.36 ± 0.06 | 2.16 ± 0.05 |
| DR | 2.14 ± 0.05 | - | 2.21 ± 0.03 | 4.32 ± 0.06 |
| RD | 1.55 ± 0.03 | 1.75 ± 0.04 | 2.26 ± 0.06 | 4.02 ± 0.06 |
| RR | 2.35 ± 0.14 | - | 2.25 ± 0.18 | 5.68 ± 0.13 |
| (c) Bases | ||||
| DD | 1.06 ± 0.02 | - | 2.59 ± 0.04 | 1.08 ± 0.04 |
| DR | 1.29 ± 0.03 | - | 1.30 ± 0.03 | 2.48 ± 0.04 |
| RD | 0.87 ± 0.01 | 1.26 ± 0.03 | 1.32 ± 0.05 | 2.36 ± 0.04 |
| RR | 1.58 ± 0.10 | - | 1.58 ± 0.11 | 3.49 ± 0.07 |
Errors represent the standard error of the mean that was calculated from the block averages of 1 ns windows.
RMS fluctuations around the average structures over the final 9ns of the simulations were computed for the individual strands and for the full duplexes (Table 2). There is a clear trend showing the DD and RR duplexes to have the smallest and largest fluctuations, respectively. The higher fluctuations of the RR duplex is consistent with experimental studies indicating sub-millisecond base opening events in RNA that are not occurring in DNA based on NMR imino proton exchange experiments54 and shown to occur in simulations of RNA duplexes using CHARMM.55 Furthermore, surveys of crystal structures show the B-factors of RNA to be systematically larger than in DNA for structures over a similar range of R factors.55,56 Concerning the hybrids, their flexibility is intermediate to that of DD and RR, with the DR hybrid showing more flexibility than the RD with the differences occurring primarily in strand I. Using 2-aminopurine as a probe, O’Niel and Barton observed increased fluorescence intensities and reduced polarization in hybrid duplexes compared to DNA indicating that the bases of the hybrids sample a larger conformational space compared to DNA.57 This observation is consistent with the present results that the bases in the hybrids exhibit higher RMS fluctuations than the pure DNA duplex (Table 2). Thus, there is increased flexibility upon going from DNA to the hybrids and to RNA, with the effect being significantly damped in the hybrid duplex when the composition of the RNA strand is dominated by purine bases. Notably, the RD hybrid is more stable based on Tm data19 than the DR hybrid, which may be associated with the decreased fluctuations of the former.
Table 2.
RMS fluctuations (Å) of non-hydrogen atoms of strand I, strand II and the full duplexes. RMS fluctuations calculated following alignment of the structures from the trajectories with respect to the reference NMR structure.
| DD | DR | RD | RR | |
|---|---|---|---|---|
| Strand I | 0.80 | 1.09 | 0.81 | 1.37 |
| Strand I – backbone | 0.95 | 1.31 | 0.91 | 1.45 |
| Strand I – base | 0.64 | 0.86 | 0.68 | 1.27 |
| Strand II | 0.82 | 0.99 | 0.94 | 1.49 |
| Strand II – backbone | 0.95 | 1.07 | 1.07 | 1.53 |
| Strand II – base | 0.65 | 0.87 | 0.77 | 1.44 |
| Strand I & II | 0.81 | 1.04 | 0.87 | 1.43 |
| Strand I & II – backbone | 0.95 | 1.19 | 0.99 | 1.49 |
| Strand I & II – base | 0.65 | 0.86 | 0.73 | 1.36 |
The higher flexibility of RR compared to the DNA duplex and the hybrids are in contrast to the results obtained by Noy et al.41 As in the study by Noy et al.41 intramolecular entropies were calculated based on Schlitter58 and Andricioaei-Karplus59 methodologies to further investigate the relative flexibility of the species studied. The resulting trends in the flexibility patterns computed (Figure S1 in supporting information) are consistent with the fluctuation results. Thus, the present work indicates RNA and DNA•RNA hybrids to have greater local flexibility than DNA, consistent with crystallographic, NMR and fluorescence experiments. The contrast of the present results with those of Noy et al appear to be associated with the use of the AMBER force field60,61 in that study versus the CHARMM27 force field in the present work. Further studies are required to investigate this force field difference in greater detail.
Base pairing
Base pairing and stacking are crucial for the structure and stability of nucleic acid duplexes. Base pairing was investigated by analysis of Watson-Crick base pair distances and the interaction energy between the two bases of any given base pair, and stacking was studied via the calculation of inter and intra strand base-base interaction energies (see below). Probability distributions of the N1-N3 distances of the central eight Watson-Crick (WC) base pairs are provided in the supporting information (Figure S2). All the histograms exhibit a sharp peak at around 3 Å corresponding to the base paired states. However, an additional relatively smaller peak is observed especially for the GC pairs of RR at around 5.5 Å corresponding to partially base opened states. Previous MD simulations have shown this behavior to be consistent with experiment and suggested that local opening events observed in RNA contribute to their conformational heterogeneity.55 The base pair interaction energies were calculated for the central eight base pairs (Table 3). The base pair interaction energies of GC, AT and AU are approximately −22, −7 and −9.5 kcal/mol respectively in DD, DR and RD, and are in good agreement with the corresponding interaction energies of the optimized base dimers.43 Local base opening events observed via the base pair distances are also seen in the reduced base pairing interaction energies of the GC base pairs in RR and its larger fluctuations are demonstrated by the standard errors; as previously suggested55 the CHARMM force field may overestimate the opening of GC pairs in RNA. The average interaction energies over all base pairs are also given; interestingly those energies are inversely correlated with the observed thermodynamic stability of the duplexes,19 such that the most thermodynamically stable duplex, RR, has the least favorable average base pair interaction energy.
Table 3.
Base pair interactions obtained for the central 8 base pairs of the duplexes averaged over the final 9 ns. The errors given are the standard error of the mean calculated from the averages of 1 ns windows.
| Base Pair | DD | DR | RD | RR |
|---|---|---|---|---|
| A2-T9 | −7.1 ± 0.0 | −9.4 ± 0.0 | −6.9 ± 0.0 | −6.8 ± 0.9 |
| A3–A8 | −7.1 ± 0.0 | −9.6 ± 0.0 | −7.1 ± 0.0 | −9.6 ± 0.0 |
| G4-C7 | −22.0 ± 0.0 | −21.3 ± 0.1 | −21.6 ± 0.0 | −14.0 ± 2.0 |
| A5-T6 | −7.3 ± 0.0 | −9.4 ± 0.1 | −7.3 ± 0.0 | −9.5 ± 0.0 |
| G6-C5 | −21.8 ± 0.0 | −21.5 ± 0.1 | −21.6 ± 0.0 | −16.9 ± 1.7 |
| A7-T4 | −7.1 ± 0.0 | −9.5 ± 0.0 | −7.0 ± 0.0 | −9.5 ± 0.1 |
| A8-T3 | −7.2 ± 0.0 | −9.5 ± 0.0 | −7.1 ± 0.0 | −9.6 ± 0.0 |
| G9-C2 | −22.1 ± 0.0 | −22.2 ± 0.2 | −21.5 ± 0.0 | −19.5 ± 0.9 |
| Average | −12.7 | −14.0 | −12.5 | −11.9 |
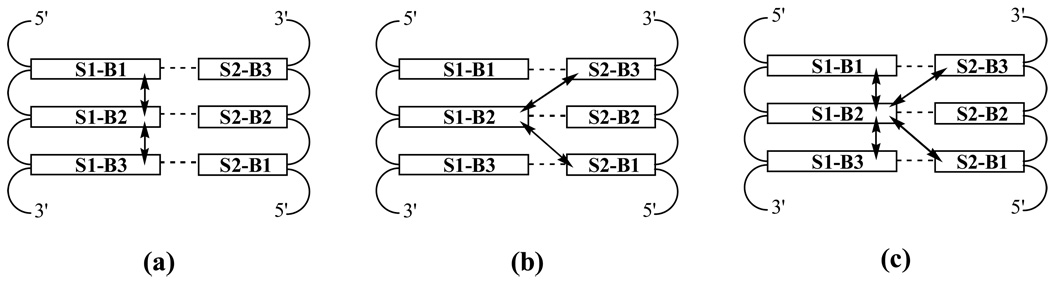
Stacking interactions
Intra strand, inter strand and overall base stacking interaction energies are given in Table 4. For individual base interaction energies and error analysis see Table S1 in the supporting information. Intrastrand stacking interaction of a given base is the interaction energy of the base with the adjacent bases (i.e. stacking partners) on both the 5’ and 3’ side on the same strand. Similarly, interstrand interaction is the interaction energy between a given base and the stacking partners of its WC base pair partner on the complementary strand. Overall stacking interaction includes the stacking partners on both strands (Figure 2). In all the cases, the intrastrand interaction energies in the purine rich strand are considerably more favorable as compared to the pyrimidine rich strand. This is consistent with the known fact that the stacking interactions between purines are more favorable compared to purine-pyrimindine interactions or interactions between two pyrimidines.62 The interaction energies are more favorable in DD compared to the hybrid structures and RR has the least favorable intrastrand interaction energies. As explained above, the reduced favorable interaction energies in RR is related to the local base opening events. As expected the interstrand interactions are much less compared to the intrastrand interactions. Clearly, the stacking interaction energies show no correlation with stability, though the least favorable stacking occurs in RNA, the most thermodynamically stable of the duplexes studied.
Table 4.
Intra, inter and total stacking interactionsa in kcal/mol averaged over the final 9 ns of the simulations.
| DD | DR | RD | RR | |
|---|---|---|---|---|
| Intra strand | ||||
| Strand I | −20.6 | −17.7 | −17.6 | −15.0 |
| Strand II | −8.1 | −6.2 | −7.1 | −4.4 |
| Strand I & II | −28.7 | −23.9 | −24.7 | −19.4 |
| Inter strand | ||||
| Strand I | −0.3 | −3.4 | −3.7 | −2.6 |
| Strand II | −0.2 | −3.4 | −4.1 | −2.9 |
| Strand I & II | −0.5 | −6.8 | −7.8 | −5.5 |
| Overall stacking | ||||
| Strand I | −20.9 | −21.1 | −21.3 | −17.6 |
| Strand II | −8.3 | −9.5 | −11.2 | −7.2 |
| Strand I & II | −29.2 | −30.6 | −32.5 | −24.8 |
Given values are calculated as the average of the interaction energies of the six central bases in each case. For the individual interaction energies and error analysis please see Table S1 in supplementary material.
Figure 2.
Schematic representation of the protocol used for the calculation of intrastrand (a), interstrand (b), and overall (c) stacking interactions of a given base (e.g. S1-B2 in the present example). (a) Interaction energy of S1-B2 with S1-B1 and S1-B3 is the intrastrand interaction energy; (b) interaction energy of S1-B2 with S2-B1 and S2-B3 is the interstrand interaction energy and (c) the overall interaction energy of S1B2 is computed as the interaction between S1-B2, and S1-B1, S1-B3, S2-B1 & S2-B3.
Backbone dihedral angles
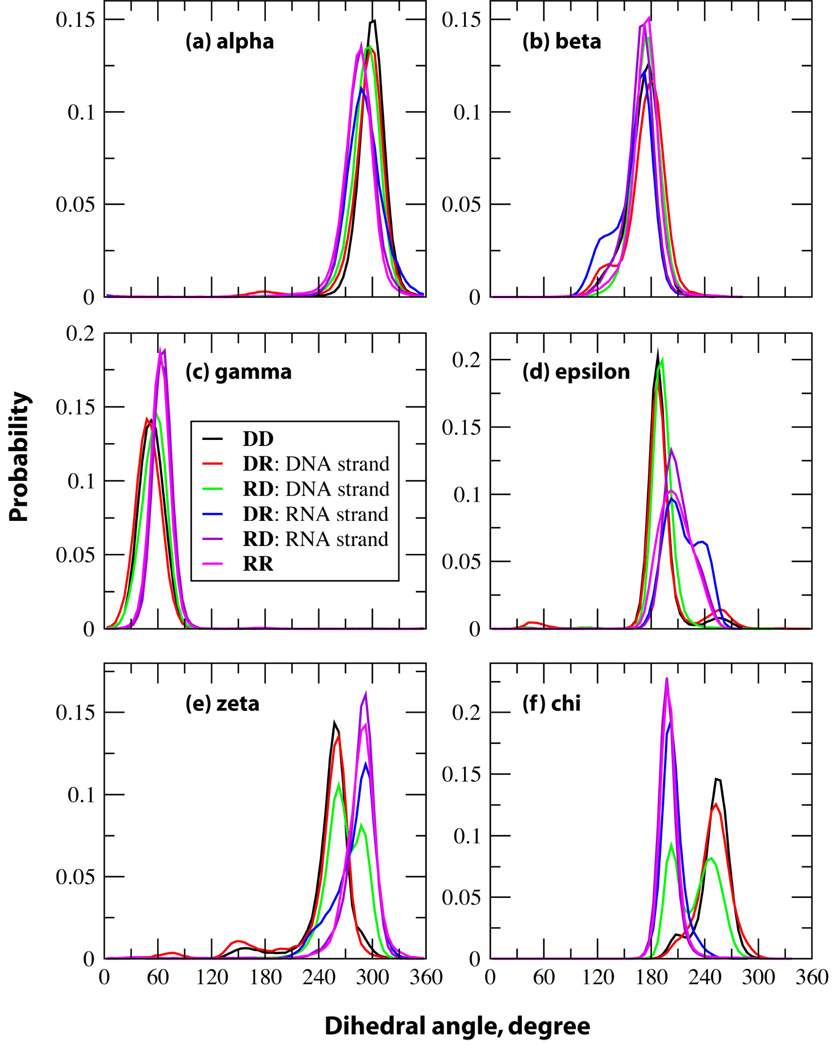
An A-form duplex can readily be differentiated from a B-form duplex via their phosphodiester backbone dihedral angles and the (deoxy)ribose puckering angles. The histograms for the α (P-O5'), β (O5'-C5'), γ (C5'-C4), ε (C3'-O3'), ζ (O3'-P) and χ (C1'-N9 for purines and C1'-N1 for pyrimidines) dihedral angles for DD and RR, and for the individual strands of the hybrid duplexes are depicted in Figure 3. The distributions calculated for these dihedral angles compare well with the dihedral angles from the experimental NMR structures (Figures S3–S6 in supporting information). No substantial differences in the α, β and γ dihedral angle distributions among the RNA and DNA strands are observed and the histograms are consistent with the previously reported crystal survey data.43 However, the probability distributions of ε, ζ and χ demonstrate interesting conformational variations in the hybrid duplexes. NMR studies have demonstrated that DNA undergoes conformational transitions between the lower energy BI and higher energy BII conformations. The ε and ζ distributions indicate short lived BII type conformations in addition to predominant BI geometry for DD and the DNA strand of DR; however, the DNA strand in RD does not sample BII type conformations in the MD simulations but exists primarily in BI and A like geometries. A-form characteristics of the DNA strand in RD are also seen in the distribution of the χ dihedral angle. The backbone of the RNA duplex and the RNA strand in RD sample only local minima exhibiting one peak for the distributions of the dihedral angles corresponding to the A-form geometry. However, the RNA strand of DR samples a larger range of conformational space shown by two distinct peaks for ε and broadening of the peak towards that observed in the DNA strands for ζ.
Figure 3.
Probability distributions of the backbone dihedral angles of the duplexes of the pure DNA and RNA structures, and those of the individual strands of the hybrid structures considered in this study. DD in black, DNA strand of DR in red, DNA strand of RD in green, RNA strand of DR in blue, RNA strand of RD in violet and RR in magenta.
North vs. south conformation of the ribose/deoxyribose rings
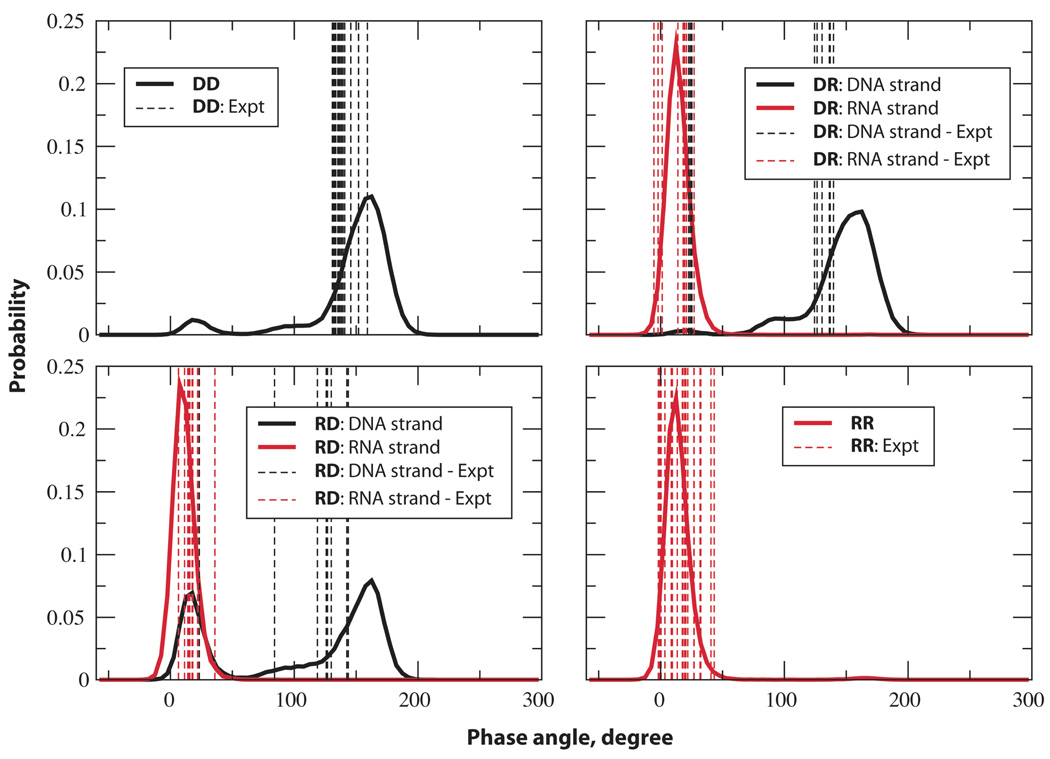
Typically, the sugar pucker is in the south and north conformations in DNA and RNA duplexes, respectively. Evaluation of phase angle along the time series for the structures considered here was done to understand the puckering of the ribose/deoxyribose rings. The histograms of the phase angle along with the experimental values are depicted in Figure 4. In general, the computed results are in very good agreement with the experimental data except for a slight shift in the DNA histograms. This may be due to the limitations in the NMR restraint data used during the structure determination, including the use of the AMBER force field61 for structure refinement. The distribution for DD is typical of B-form DNA with the south conformation corresponding to the C2'-endo (south puckering) highly populated and minor sampling of O4'-endo (east) and C3'-endo (north) conformations. Similarly, the DNA strand in DR samples primarily south puckers. The riboses in the RNA strands in the hybrids and the RNA duplex are completely in the north conformation (C3'-endo) with almost no sampling in the other regions. The probability for the phase angle in the DNA strand of RD provided a different scenario altogether. Two distinct peaks of almost similar area are observed corresponding to the north and south conformations. This further indicates that the pyrimidine rich DNA strand in RD assumes the A-form as much as it exhibits B-form characteristics. Thus, the pyrimidine rich DNA strand in RD is more stabilized in the A-form relative to the B-form as compared to duplex DNA due to the purine rich RNA complimentary strand. To understand the north-south puckering switch at the nucleotide level, the percentage of north and south puckering of each of the sugar moieties are tabulated in Table S2 in supporting information. Interestingly, the purine rich DNA strand in DR samples north-puckered sugar conformation less compared to the pyrimidine rich DNA strand in the pure DNA duplex itself. This is consistent with observations that cytosines favor A form conformations more than other bases.43 Almost all the nucleotides in the pyrimidine rich DNA strand in RD exist in both the north- and south- sugar conformation. Notable is that the central cytosine of the TCT sequence in the DNA strand seems to favor the north-pucker compared to the others.
Figure 4.
Probability distributions of the phase angles of the ribose/deoxy ribose in the pure DNA and RNA duplexes and in the individual strands of the hybrids. See each figure for color codes. Phase angles of more than 300° were offset by 360° for the convenience of presentation.
In combination the backbone dihedral and sugar pucker dihedral distributions present a consistent picture. In both hybrid structures, the pyrimidine strands display transitions between the A and B conformations and it is evident that the purine rich strand strongly influence the conformation of the overall structure of the hybrid duplexes. However, this effect is more pronounced when the purine rich strand is comprised of RNA.
A- vs. B- form in individual strands in hybrid structures
Based on the probability distributions of the backbone dihedral and phase angles as well as the RMS deviations (Table 1) it is clear that DD is in the B form, RR is in A form and the hybrids are in between, but closer to the canonical A form. It is also obvious that RD is closer to the A form than DR, because of the ability of the DNA strand to more readily adopt an A-like geometry when it is composed of pyrimidine bases. In both the structures, the RNA strands behave very much like RNA in the pure duplex except for the broadening of the peaks corresponding to ε and ζ distributions in DR. The DNA strand retains a B-like conformation when it is purine rich (DR) and adopts a mixed A-/B- form when it is pyrimidine rich and paired with a complimentary purine rich RNA strand. Therefore, in a given hybrid structure, there is a competition between the DNA and RNA strands to retain their B- and A- like conformation leading to a mixed A-/B- form duplex. While the RNA strand, to a greater extent, is successful in maintaining the A-form irrespective of the sequence, on the other hand the pyrimidine rich DNA strand is unable to retain the B-form characteristics as a whole. These results indicate the dominance of the RNA strand followed by the purine rich strand of DNA in dictating the conformational properties of the hybrid structures.
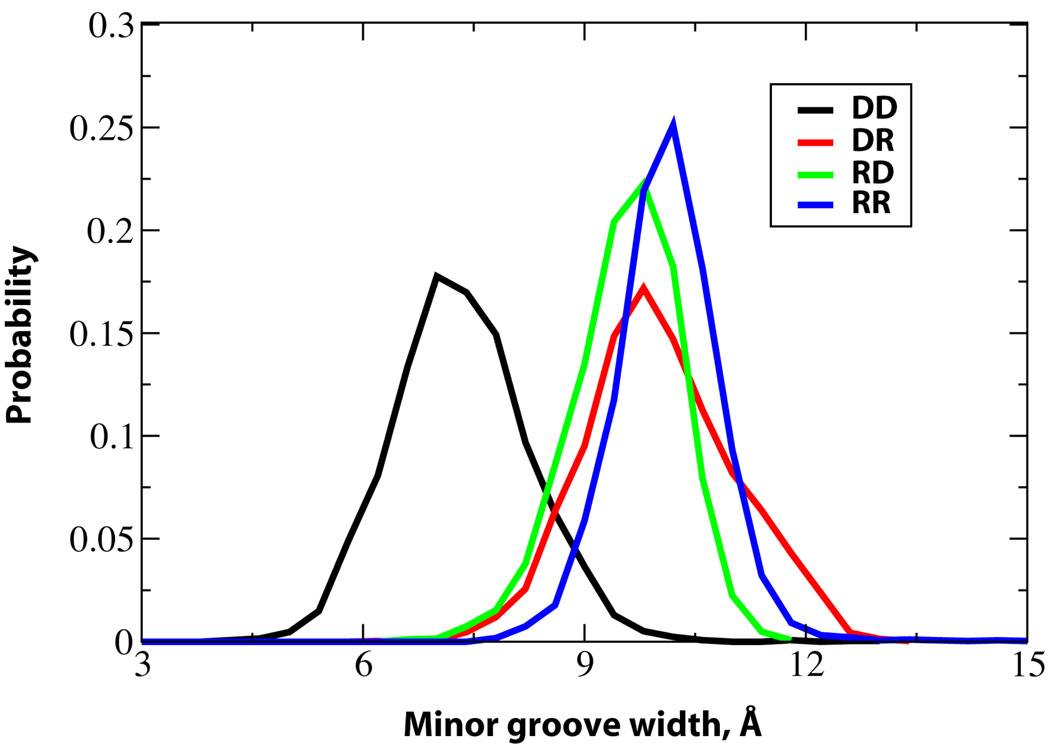
Minor groove widths
RNase H does not recognize a specific sequence in DNA•RNA hybrids in order to bind to them and cleave the RNA strand. It was proposed that it identifies hybrid structures from RNA duplexes based on the fact that DNA•RNA hybrids exhibit narrow minor grooves.1 The probability distribution of the minor groove widths calculated using the Curves program53 are shown in Figure 5. Consistent with previous studies, the minor groove widths of the hybrid structures are between that of the DNA and RNA duplexes.1,29,41,63 The minor groove width of DNA is around 2.5 Å narrower than the hybrids while in RNA it is around 0.6 Å wider than the hybrids, with significant overlap of the hybrid and RR distributions present. For both hybrid structures, the highest population is observed at a minor groove width of approximately 9.7 Å although the shape of the curves for DR and RD differ significantly. These results indicate that the difference between the minor groove widths of the hybrid structures and the RNA duplex is small suggesting that the differentiation of hybrid structures from pure RNA duplexes by RNase H is not solely based on the minor groove width.41
Figure 5.
Probability distributions of the minor groove widths of the duplexes considered in the study. Phosphorous atoms are used to define the backbone splines while calculating the minor groove widths. The distributions of DD, DR, RD and RR are given in black, red, green and blue solid lines respectively.
Helical properties
In addition to the backbone dihedral angles and the sugar puckering phase angle, helical parameters have been very valuable in defining the geometry of nucleic acid duplexes.64–66 Accordingly, the structural differences between the hybrid structures and the pure DNA and RNA duplexes were further investigated via calculation of the local inter base pair helical parameters such as shift, slide, rise, tilt, roll and twist (Table 5). The translational movements of the base pair along the helical axis, towards the grooves, and towards the backbone of the nucleic acid are defined by the shift, slide and rise parameters, respectively. These displacement parameters obtained for DD and RR are in good agreement with the values calculated for canonical B and A forms of the same sequence, respectively. Slide is the translational parameter evaluating the displacement of the base pair perpendicular to the helical axis towards the grooves. The value for the slide parameter seems to gradually decrease with the increase in the A form character indicating the movement of the bases towards the minor groove. Distance between the two planes formed by adjacent base pairs is given by the rise parameter. Near quantitative agreement of the computed rise values of DD and RR are obtained in comparison to the corresponding values for the canonical B and A forms. Interestingly, the hybrid structures have a higher rise by about 0.2–0.3 Å compared to the pure duplexes (The average rise values for the hybrid in the experimental structure complexed to RNase H is 3.44 Å; and for DD, DR, RD and RR the NMR experimental values are 3.0, 3.1, 3.2 and 3.0 Å respectively). In spite of the larger rise values in the hybrid structures, the stacking interaction energies are significantly more favorable than in RNA duplex. Base opening events occurring in the RNA are suggested to be responsible for the less favorable stacking interactions, which is also observed in the reduced twist values and increased base pair distances (see above) in RR. The deviations of the tilt and twist values of RR compared to that of the A-form geometry are also traced to the base opening events occurring in the RNA duplex. The helical parameters, mainly slide, rise, roll and twist, are unique in the hybrid forms compared to the pure nucleic acid duplexes. Hence, in addition to the intermediate minor groove widths observed for the hybrid structures, the hybrid structures are differentiated from DD and RR by a higher rise and intermediate slide, roll and twist parameters. Given that a large rise value is observed in the present calculations as well as in the crystal structure of the complex, it is suggested that rise plays an important role in the interaction of hybrids with RNase H.
Table 5.
Average values of select local helical parameters, slide, rise, roll, twist, shift and tilt. Distances are in Å and angles are in degrees.
| Parameter | DD | DR | RD | RR | B-form | A-form |
|---|---|---|---|---|---|---|
| Shift | −0.17 | −0.36 | 0.12 | 0.00 | 0.00 | 0.00 |
| Slide | −0.39 | −1.02 | −1.66 | −1.99 | −0.75 | −2.06 |
| Rise | 3.39 | 3.64 | 3.51 | 3.36 | 3.33 | 3.42 |
| Tilt | −1.60 | −3.55 | 1.63 | −1.64 | 0.01 | 0.02 |
| Roll | 4.98 | 9.45 | 6.66 | 10.73 | −3.65 | 10.78 |
| Twist | 35.4 | 30.2 | 30.7 | 26.6 | 35.9 | 30.9 |
Solvation of the nucleic acids
Solvation of nucleic acids contributes substantially to their structure and energetics.67 To understand the solvation patterns around the hybrid duplexes in comparison to the pure DNA and RNA structures, the solvent accessible surface areas (SASA), hydration numbers and the solvent-oligonucleotide interaction energies were calculated (Table 6). Radial distribution functions were also computed for the duplexes and they are very similar for all the duplexes (Figure S7). The SASA and hydration numbers are consistent with one another and reveal that the RNA is the most solvated followed by the hybrid structures and the DNA duplex is the least hydrated. The ordering is consistent with the presence of the 2'-hydroxy groups in the RNA strands. Notable is the significantly more favorable overall solvation of RR versus the hybrids were a difference of approximately −240 kcal/mol is calculated whereas upon going from the hybrids to DD the difference is approximately 45 kcal/mol. These results indicate that the desolvation penalty upon RNase H binding will be less for the RNA strand in the hybrids versus that in RNA duplexes, suggesting that desolvation effects may contribute to the inability of RR to act as substrate of RNase H.
Table 6.
Solvent accessible surface areas (SASA), hydration numbers and solvation energies of the nucleic acid duplexes, the backbone and the bases averaged over the final 9 ns of the simulation.
| DD | DR | RD | RR | |
|---|---|---|---|---|
| SASA | ||||
| Strand I&II | 2929.8 ± 2.2 | 2929.6 ± 2.7 | 2931.6 ± 4.7 | 2978.8 ± 11.8 |
| Strand I&II – backbone | 2402.1 ± 0.8 | 2427.1 ± 1.4 | 2408.6 ± 1.6 | 2414.6 ± 4.5 |
| Strand I&II – base | 527.7 ± 2.0 | 502.5 ± 2.6 | 523.1 ± 4.0 | 564.1 ± 12.6 |
| Major groove | 172.5 ± 1.1 | 234.1 ± 1.8 | 223.9 ± 2.2 | 306.3 ± 9.8 |
| Minor groove | 101.3 ± 1.6 | 136.9 ± 1.8 | 106.8 ± 0.8 | 132.2 ± 3.1 |
| Hydration number | ||||
| Strand I&II | 171.0 ± 0.2 | 179.7 ± 0.2 | 175.8 ± 0.4 | 187.8 ± 0.7 |
| Strand I&II – backbone | 142.3 ± 0.1 | 146.3 ± 0.1 | 144.6 ± 0.2 | 150.3 ± 0.2 |
| Strand I&II – base | 49.3 ± 0.1 | 52.6 ± 0.2 | 49.6 ± 0.3 | 57.8 ± 0.9 |
| Major groove | 19.9 ± 0.1 | 22.2 ± 0.1 | 23.0 ± 0.1 | 28.6 ± 0.7 |
| Minor groove | 19.4 ± 0.1 | 20.1 ± 0.1 | 18.2 ± 0.1 | 20.3 ± 0.3 |
| Solvation energy | ||||
| Strand I&II | −3930.5 ± 5.6 | −3973.8 ± 6.5 | −3977.0 ± 5.6 | −4220.4 ± 24.7 |
| Strand I&II – backbone | −3643.5 ± 4.6 | −3775.2 ± 7.5 | −3840.8 ± 5.4 | −4051.9 ± 14.6 |
| Strand I&II – base | −287.0 ± 5.7 | −198.6 ± 4.5 | −136.1 ± 6.6 | −168.5 ± 11.8 |
Analysis of the solvation parameters of the backbones and the bases indicate that the change in the solvation in the structures includes contributions from solvation of both regions. The major grooves of the duplexes are consistently more solvated than the corresponding minor grooves based on the SASA and hydration numbers. Of note are the SASA and hydration numbers of the minor grooves of the hybrids indicating that DR is more solvated than RD. The X-ray crystal structure of RNase H bound to a DNA•RNA hybrid shows that the minor groove and the backbone of both strands in the duplex bind directly to the protein, with no direct interaction between RNase H and the major groove of the duplex.1 While the more favorable solvation of the minor groove of DR would increase the desolvation penalty for RNase H-hybrid complex formation, it may also indicate the potential for the DR minor groove to interact more favorably with RNase H, contributing to it being a better substrate for the protein than RD. Supporting this notion is that the overall solvation energies of the two hybrids are nearly identical.
RNase H activity and stability of the hybrids
Experimental studies have shown that RNase H binds to hybrid duplexes and cleaves only the RNA strand. Notably, hybrids in which the RNA strand is purine rich are known to be resistant to RNase H hydrolysis. In addition, some RNA duplexes bind to RNase H, but the enzyme degrades neither of the strands of the RNA. The inability of the enzyme to bind DNA duplexes is easily understood based on vast structural differences between the B-form geometry adopted by DNA and the A-form conformation. In addition, DNA lacks the 2'-hydroxyl group which plays a key role in substrate recognition.1,14 However, the differentiation of hybrid duplexes from the RNA structures to selectively degrade the RNA strand only in the hybrid structures by RNase H is not well understood. Various factors were proposed that could possibly be influencing the selectivity of hybrid structures versus the pure RNA duplexes. These include narrower minor groove width 20,29 and increased flexibility of the hybrid14,41. The present results are consistent with a contribution from a narrower minor groove; however, the hybrids show decreased flexibility compared to the RNA duplex, arguing against that phenomenon.
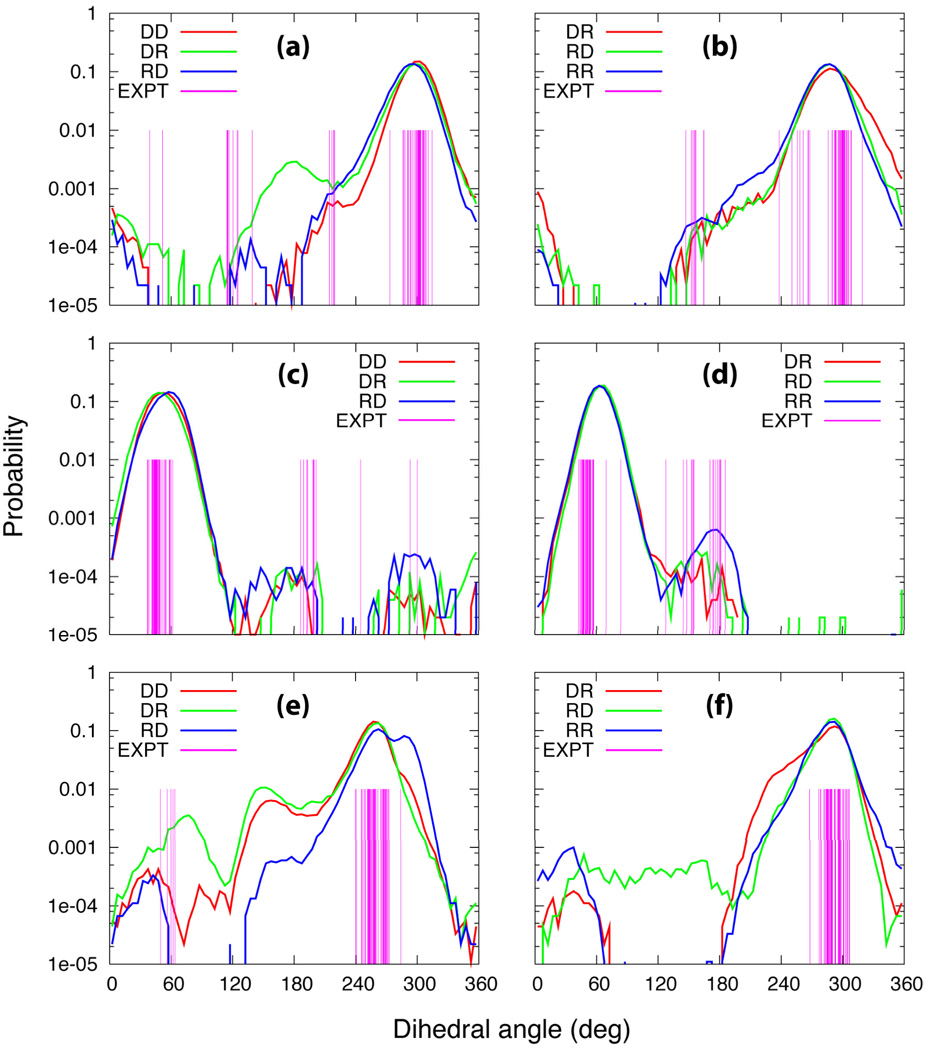
Analysis of the experimental structure of the RNase H-substrate complex indicates that one of backbone phosphate moieties of the DNA strand occupies the sulfate ion binding site found in the apoprotein.68 Binding of the DNA strand into this site resulted in a still narrower minor groove width and the distortion of the backbone phosphodiester dihedral angles. The largest distortions occur with the α, γ and ζ dihedral angles of the backbone vicinal to the sulfate binding site, which deviate by about 180° from their canonical values.1 The probability distributions of the α, γ and ζ backbone dihedral angles along with the dihedral angles of the hybrid structures bound to RNase H from the X-ray crystal structure data are depicted in Figure 6. For α in the vicinity of the sulfate binding site of RNase H in the crystal structure it deviates from its typical value of ~300° by more than 150° (Figure 6a). Both the hybrid DNA strands sample conformations corresponding to these distorted forms even in the absence of the protein. Interestingly, sampling of this range of α by DR is found to be more than that of RD, which could contribute to the hybrids with purine rich RNA strands being more resistant towards RNase H activity. Similarly, with γ, conformations not typically sampled by this dihedral are present in the hybrid-RNase H crystal structure (Figure 6c and 6d). These regions, including that >240° are sampled by the hybrid DNA strands (Figure 6c). For γ in the RNA strands (Figure 6d) sampling of non-typical γ values is observed in the crystal structures, with this region being sampled to a reasonable extent in RR as well as the two hybrids. In the case of ζ (Figure 6e) non-canonical conformations are observed in the vicinity of 60° in the DNA strand. Sampling of this region occurs to a small extent, with the largest amount occurring with DR, which may further favor this hybrid being a substrate for RNase H over RD. Thus, the ability of the DNA strands in the hybrid structures to sample non-canonical backbone conformations is suggested to contribute to the differentiation of hybrids from RNA by the enzyme. Interestingly, this sampling is largest in DR, potentially contributing to the hybrid with a purine rich DNA strand being favored as a substrate over that with a purine rich RNA strand. It is to be noted that the sampling of backbone conformations observed in the RNase H-substrate complex by the DNA strands in the hybrids while this is not occurring in the RNA duplex is not reflected in the RMS fluctuations and the intramolecular entropy calculations (Table 2 and Figure S1 of the supporting information). This indicates that the relationship of the flexibility to the range of conformational sampling is not direct, with multiple factors contributing to the overall flexibility of a system.
Figure 6.
Probability distributions of the α (a and b), γ (c and d), and ζ (e and f) phosphodiester dihedral angles of the duplexes. (a), (c) and (e) represent the DNA duplex and the DNA strands of the hybrids structures, and (b), (d) and (f) correspond to the RNA duplex and the RNA strands of the hybrids. The experimental values of the dihedral angles of the hybrid duplexes bound to the RNase H from the X-ray crystal data are also given for comparison (vertical lines in magenta). For the other dihedral angle plots, see Figures S8–11 in supplementary material.
The probability distributions of the remaining phosphodiester backbone dihedral angles were also compared with the dihedral angles of the x-ray crystal structures of the hybrid structures bound to the protein (Figures S8–S11, supporting information). In the crystal structures only conformations observed in canonical structures are observed with the only variation being seen with ε in the DNA strands. The distributions of the backbone dihedral angles of the both the DNA and RNA strands of both the hybrids and the pure duplex are very similar in all cases, encompassing the values of the respective dihedrals observed in the crystal structure.
Conclusions
MD simulations were performed on hybrid duplexes and pure RNA and DNA duplexes sharing the same sequence to understand the structure-energy relationships in hybrid structures and to investigate the structural determinants for RNase H binding/activity. Excellent agreement between the computational results and experimental data are obtained for the structural features. The RMS differences in reference to the experimental NMR structures are about 2 Å or less indicating good agreement and point to mixed A-/B- like structures for the hybrid duplexes. Clearly, the CHARMM27 all atom nucleic acid force field, which was originally parameterized based on data from canonical nucleic acids, performs quite satisfactorily in representing the noncanonical hybrid structures. Phosphodiester backbone dihedral angle and sugar puckering phase angle probability distributions indicate interesting A-B conformational transitions in the hybrid structures. While the purine rich DNA and RNA strands of the hybrids exhibit pure B- and A- form conformational characteristics, the pyrimidine rich DNA strand in RD samples conformations corresponding to both B- and A- like geometries almost to an equal extent. However, the pyrimidine rich RNA strand in DR exists primarily in A-form, but samples a larger conformational space compared to the purine rich RNA strand in RD and in the pure RNA duplex, RR indicating that the structure and dynamics of the hybrid structures are dictated by the RNA strands followed by the purine rich strands.
Increased conformational flexibility of hybrids versus RNA has previously been suggested to contribute to RNase H activity.14,41 In the present study, DNA was found to have the least local flexibility followed by the hybrids with RNA having the greatest local flexibility based on both RMS fluctuations and intramolecular entropy calculations (Table 2 and Figure S1). The increased flexibility of the hybrids over DNA is consistent with fluorescence measurements 57 and the increased local flexibility of RNA over DNA is consistent with NMR imino proton exchange 54 and survey data on B factors from crystal structures on RNA versus DNA.55,56 The increased flexibility of RNA over DNA is consistent with the relative base pairing and stacking energies (Tables 3 and 4), though the hybrids pairing and stacking interaction energies are similar to or greater than that of DNA, though the former is more flexible. Thus, the present results are consistent with experimental studies though in contrast to previous simulation studies. These differences indicate that the flexibility of DNA and RNA as well as of the hybrids is complex, as previously discussed56, and emphasizes that further studies are required to better understand this important property.
The two hybrid duplexes (DR and RD) exhibit minor grooves that are in between the minor groove widths of DNA and RNA structures. There exists substantial overlap between the minor groove width distribution curves of RNA and the hybrids precluding the possibility of RNase H recognizing hybrid duplexes solely based on minor groove width. The hybrid structures are also characterized by a higher rise parameter and intermediate slide, roll and twist values compared to DNA and RNA. Investigation of the available X-ray crystal structures of hybrids bound to RNase H indicate that the α, γ and ζ dihedral angles in the DNA strand vicinal to the sulfate binding site on RNase H vary by more than 100° from canonical values. Comparison of the experimental values of the dihedral angles with the probability distributions from MD simulations reveal that conformation corresponding to the distorted backbone are sampled by the DNA strands in the hybrid structures in the absence of protein. The pure RNA duplex on the other hand does not sample these conformations that may be essential for RNase H binding and catalysis. Interestingly, the probability of DR sampling the distorted backbone conformers is found to be higher than that of RD, possibly explaining the resistance of hybrid duplexes containing purine rich RNA strand towards RNase H activity. In addition, the solvation of the hybrids differs with the bases in DR being significantly more solvated than in RD, while the opposite is observed with the backbone. Such differential solvation may also contribute to the relative binding of these hybrids to RNase H. Hence, the pyrimidine-purine base composition seems to tailor the biochemical susceptibility of a hybrid structure towards RNase H activity. Overall, a combination of factors including a narrow minor groove width, increased rise, desolvation effects, and increased conformational sampling of the phosphodiester backbone of the DNA strand in the hybrids are proposed to affect the RNase H binding.
Supplementary Material
Acknowledgements
NIH (GM51501) is thanked for financial support. We acknowledge Advanced Biomedical Computing Center and the Pittsburgh Supercomputing Center for their generous allocation of computer time.
Footnotes
Supporting Information Available: Tables of stacking interaction energies and percentage of sugar puckers of the nucleotides, and figures of intermolecular entropies, probability distributions of base pair distances and phosphodiester backbone dihedral angles, and radial distribution functions. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Nowotny M, Gaidamakov SA, Crouch RJ, Yang W. Cell. 2005;121:1005–1016. doi: 10.1016/j.cell.2005.04.024. [DOI] [PubMed] [Google Scholar]
- 2.Rich a. J Biol Chem. 2006;281:7693–7696. doi: 10.1074/JBC.X600003200. [DOI] [PubMed] [Google Scholar]
- 3.Zamaratski E, Pradeepkumar PI, Chattopadhyaya J. J Biochem Bioph Meth. 2001;48:189–208. doi: 10.1016/s0165-022x(01)00149-x. [DOI] [PubMed] [Google Scholar]
- 4.Aboul-Fadl T. Curr Med Chem. 2005;12:2193–2214. doi: 10.2174/0929867054864859. [DOI] [PubMed] [Google Scholar]
- 5.Crooke ST. Annu Rev Med. 2004;55:61–95. doi: 10.1146/annurev.med.55.091902.104408. [DOI] [PubMed] [Google Scholar]
- 6.Juan ECM, Kondo J, Kurihara T, Ito T, Ueno Y, Matsuda A, Takenaka A. Nucleic Acids Res. 2007;35:1969–1977. doi: 10.1093/nar/gkl821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hashem GM, Pham LH, Vaughan MR, Gray DM. Biochemistry-Us. 1998;37:61–72. doi: 10.1021/bi9713557. [DOI] [PubMed] [Google Scholar]
- 8.Kanaori K, Tamura Y, Wada T, Nishi M, Kanehara H, Morii T, Tajima K, Makino K. Biochemistry-Us. 1999;38:16058–16066. doi: 10.1021/bi9909344. [DOI] [PubMed] [Google Scholar]
- 9.Amirkhanov NV, Chattopadhyaya J. J Chem Soc Perk T 2. 2002:271–281. [Google Scholar]
- 10.Freier SM, Altmann KH. Nucleic Acids Res. 1997;25:4429–4443. doi: 10.1093/nar/25.22.4429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Nielsen KE, Rasmussen J, Kumar R, Wengel J, Jacobsen JP, Petersen M. Bioconjugate Chem. 2004;15:449–457. doi: 10.1021/bc034145h. [DOI] [PubMed] [Google Scholar]
- 12.Nina M, Fonne-Pfister R, Beaudegnies R, Chekatt H, Jung PMJ, Murphy-Kessabi F, De Mesmaeker A, Wendeborn S. J Am Chem Soc. 2005;127:6027–6038. doi: 10.1021/ja0486566. [DOI] [PubMed] [Google Scholar]
- 13.Petersen M, Bondensgaard K, Wengel J, Jacobsen JP. J Am Chem Soc. 2002;124:5974–5982. doi: 10.1021/ja012288d. [DOI] [PubMed] [Google Scholar]
- 14.Tonelli M, Ulyanov NB, Billeci TM, Karwowski B, Guga P, Stec WJ, James TL. Biophys J. 2003;85:2525–2538. doi: 10.1016/s0006-3495(03)74675-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Venkiteswaran S, Vijayanathan V, Shirahata A, Thomas T, Thomas TJ. Biochemistry-Us. 2005;44:303–312. doi: 10.1021/bi0485272. [DOI] [PubMed] [Google Scholar]
- 16.Znosko BM, Barnes TW, Krugh TR, Turner DH. J Am Chem Soc. 2003;125:6090–6097. doi: 10.1021/ja021285d. [DOI] [PubMed] [Google Scholar]
- 17.Lesnik Ea, Freier SM. Biochemistry-Us. 1995;34:10807–10815. doi: 10.1021/bi00034a013. [DOI] [PubMed] [Google Scholar]
- 18.Sarafianos SG, Das K, Tantillo C, Clark AD, Ding J, Whitcomb JM, Boyer PL, Hughes SH, Arnold E. Embo J. 2001;20:1449–1461. doi: 10.1093/emboj/20.6.1449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gyi JI, Conn GL, Lane AN, Brown Tb. Biochemistry-Us. 1996;35:12538–12548. doi: 10.1021/bi960948z. [DOI] [PubMed] [Google Scholar]
- 20.Gyi JI, Lane AN, Conn GL, Brown T. Biochemistry-Us. 1998;37:73–80. doi: 10.1021/bi9719713. [DOI] [PubMed] [Google Scholar]
- 21.Huang HF, Chopra R, Verdine GL, Harrison SC. Science. 1998;282:1669–1675. doi: 10.1126/science.282.5394.1669. [DOI] [PubMed] [Google Scholar]
- 22.Conn GL, Brown T, Leonard GA. Nucleic Acids Res. 1999;27:555–561. doi: 10.1093/nar/27.2.555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Han GW. Acta Crystallogr D. 2001;57:213–218. doi: 10.1107/s0907444900017595. [DOI] [PubMed] [Google Scholar]
- 24.Han GW, Kopka ML, Langs D, Sawaya MR, Dickerson RE. P Natl Acad Sci USA. 2003;100:9214–9219. doi: 10.1073/pnas.1533326100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Horton NC, Finzel BC. J Mol Biol. 1996;264:521–533. doi: 10.1006/jmbi.1996.0658. [DOI] [PubMed] [Google Scholar]
- 26.Kopka ML, Lavelle L, Han GW, Ng HL, Dickerson RE. J Mol Biol. 2003;334:653–665. doi: 10.1016/j.jmb.2003.09.057. [DOI] [PubMed] [Google Scholar]
- 27.Sudarsanakumar C, Xiong Y, Sundaralingam M. J Mol Biol. 2000;299:103–112. doi: 10.1006/jmbi.2000.3730. [DOI] [PubMed] [Google Scholar]
- 28.Xiong Y, Sundaralingam M. Nucleic Acids Res. 2000;28:2171–2176. doi: 10.1093/nar/28.10.2171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Fedoroff OY, Salazar M, Reid BR. J Mol Biol. 1993;233:509–523. doi: 10.1006/jmbi.1993.1528. [DOI] [PubMed] [Google Scholar]
- 30.Hantz E, Larue V, Ladam P, Le Moyec L, Gouyette C, Dinh TH. Int J Biol Macromol. 2001;28:273–284. doi: 10.1016/s0141-8130(01)00123-4. [DOI] [PubMed] [Google Scholar]
- 31.Fedoroff OY, Ge Y, Reid BR. J Mol Biol. 1997;269:225–239. doi: 10.1006/jmbi.1997.1024. [DOI] [PubMed] [Google Scholar]
- 32.Gotfredsen CH, Schultze P, Feigon J. J Am Chem Soc. 1998;120:4281–4289. [Google Scholar]
- 33.Gonzalez C, Stec W, Reynolds Ma, James TL. Biochemistry-Us. 1995;34:4969–4982. doi: 10.1021/bi00015a008. [DOI] [PubMed] [Google Scholar]
- 34.Bachelin M, Hessler G, Kurz G, Hacia JG, Dervan PB, Kessler H. Nat Struct Biol. 1998;5:271–276. doi: 10.1038/nsb0498-271. [DOI] [PubMed] [Google Scholar]
- 35.Salazar M, Fedoroff OY, Miller JM, Ribeiro NS, Reid BR. Biochemistry-Us. 1993;32:4207–4215. doi: 10.1021/bi00067a007. [DOI] [PubMed] [Google Scholar]
- 36.Nowotny M, Yang W. Embo J. 2006;25:1924–1933. doi: 10.1038/sj.emboj.7601076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Cheatham TE, Kollman Pa. J Am Chem Soc. 1997;119:4805–4825. [Google Scholar]
- 38.Sanghani SR, Lavery R. Nucleic Acids Res. 1994;22:1444–1449. doi: 10.1093/nar/22.8.1444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Gyi JI, Gao DQ, Conn GL, Trent JO, Brown T, Lane AN. Nucleic Acids Res. 2003;31:2683–2693. doi: 10.1093/nar/gkg356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Venkateswarlu D, Lind KE, Mohan V, Manoharan M, Ferguson DM. Nucleic Acids Res. 1999;27:2189–2195. doi: 10.1093/nar/27.10.2189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Noy A, Perez A, Marquez M, Luque FJ, Orozco M. J Am Chem Soc. 2005;127:4910–4920. doi: 10.1021/ja043293v. [DOI] [PubMed] [Google Scholar]
- 42.Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. J. Comput. Chem. 1983;4:187–217. [Google Scholar]
- 43.Foloppe N, MacKerell AD., Jr J. Comp. Chem. 2000;21:86–104. [Google Scholar]
- 44.MacKerell AD, Jr, Banavali NK. J. Comp. Chem. 2000;21:105–120. [Google Scholar]
- 45.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Journal of Chemical Physics. 1983;79:926–935. [Google Scholar]
- 46.Field MJ, Karplus M. CRYSTAL: Program for Crystal Calculations in CHARMM. Cambridge, MA: Harvard University; 1992. [Google Scholar]
- 47.Darden T, Perera L, Li LP, Pedersen L. Struct Fold Des. 1999;7:R55–R60. doi: 10.1016/s0969-2126(99)80033-1. [DOI] [PubMed] [Google Scholar]
- 48.Essmann U, Perera L, Berkowitz ML, Darden TA, Lee H, Pedersen LG. J Chem Phys. 1995;103:8577–8593. [Google Scholar]
- 49.Steinbach PJ, Brooks BR. J. Comp. Chem. 1994;15:667–683. [Google Scholar]
- 50.Ryckaert J-P, Ciccotti G, Berendsen HJC. J. Comp. Physics. 1977;23:327–341. [Google Scholar]
- 51.Hoover WG. Phy. Rev. 1985;A 31:1695–1697. doi: 10.1103/physreva.31.1695. [DOI] [PubMed] [Google Scholar]
- 52.Feller SE, Zhang Y, Pastor RW, Brooks RW. J. Chem. Phys. Phys. 1995;103:4613–4621. [Google Scholar]
- 53.Stofer E, Lavery R. Biopolymers. 1994;34:337–346. doi: 10.1002/bip.360340305. [DOI] [PubMed] [Google Scholar]
- 54.Snoussi K, Leroy JL. Biochemistry-Us. 2001;40:8898–8904. doi: 10.1021/bi010385d. [DOI] [PubMed] [Google Scholar]
- 55.Pan YP, MacKerell AD. Nucleic Acids Res. 2003;31:7131–7140. doi: 10.1093/nar/gkg941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Perez A, Noy A, Lankas F, Luque FJ, Orozco M. Nucleic Acids Res. 2004;32:6144–6151. doi: 10.1093/nar/gkh954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.O'neill Ma, Barton JK. J Am Chem Soc. 2002;124:13053–13066. doi: 10.1021/ja0208198. [DOI] [PubMed] [Google Scholar]
- 58.Schlitter J. Chem Phys Lett. 1993;215:617–621. [Google Scholar]
- 59.Andricioaei I, Karplus M. Journal of Chemical Physics. 2001;115:6289–6292. [Google Scholar]
- 60.Cheatham TE, Cieplak P, Kollman PA. J Biomol Struct Dyn. 1999;16:845–862. doi: 10.1080/07391102.1999.10508297. [DOI] [PubMed] [Google Scholar]
- 61.Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman Pa. J Am Chem Soc. 1995;117:5179–5197. [Google Scholar]
- 62.Sponer J, Leszczynski J, Hobza P. Biopolymers. 2001;61:3–31. doi: 10.1002/1097-0282(2001)61:1<3::AID-BIP10048>3.0.CO;2-4. [DOI] [PubMed] [Google Scholar]
- 63.Lee HJ, Diavatis T, Tennakoon S, Yu PL, Gao XL. Bba-Gene Struct Expr. 2007;1769:20–28. doi: 10.1016/j.bbaexp.2006.11.004. [DOI] [PubMed] [Google Scholar]
- 64.Lavery R, Zakrzewska K, editors. Base and base pair morphologies, helical parameters, and definitions. New York: Oxford University Press; 1999. pp. 39–76. [Google Scholar]
- 65.Lavery R, Sklenar H. J Biomol Struct Dyn. 1989;6:655–667. doi: 10.1080/07391102.1989.10507728. [DOI] [PubMed] [Google Scholar]
- 66.Lavery R, Sklenar H. J Biomol Struct Dyn. 1988;6:63–91. doi: 10.1080/07391102.1988.10506483. [DOI] [PubMed] [Google Scholar]
- 67.Saenger W. Principles of nucleic acid structure. New York: Springer-Verlag; 1984. [Google Scholar]
- 68.Yang W, Hendrickson Wa, Crouch RJ, Satow Y. Science. 1990;249:1398–1405. doi: 10.1126/science.2169648. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.