Abstract
We examine how the motivational sequence that leads to childbearing predicts fertility outcomes across reproductive careers. Using a motivational traits-desires-intentions theoretical framework, we test a structural equation model using prospective male and female data from the National Longitudinal Survey of Youth. Specifically, we take motivational data collected during the 1979–1982 period, when the youths were in their teens and early twenties, to predict the timing of the next child born after 1982 and the total number of children born by 2002. Separate models were estimated for males and females but with equality constraints imposed unless relaxing these constraints improved the overall model fit. The results indicate substantial explanatory power of fertility motivations for both short-term and long-term fertility outcomes. They also reveal the effects of both gender role attitude and educational intentions on these outcomes. Although some sex differences in model pathways occurred, the primary hypothesized pathways were essentially the same across the sexes. Two validity substudies support the soundness of the results. A third substudy comparing the male and female models across the sample split on the basis of previous childbearing revealed a number of pattern differences within the four sex-by-previous childbearing groups. Several of the more robust of these pattern differences offer interesting insights and support the validity and usefulness of our theoretical framework.
A question of longstanding interest to human fertility researchers is whether fertility motivations actually predict fertility outcomes. Do women/men/couples actually fulfill their desires for children in the course of their reproductive careers? Are their desires better achieved with respect to the timing of births or with respect to the number of children? And how do these two aspects of family planning–timing and number of children- affect each other? In this paper we develop a model linking the motivational antecedents to childbearing to fertility outcomes and then test that model empirically using a prospective design and data from a U.S. probability sample.
We construct our model on the premise that there are two developmental phases during the life course affecting the motivations that promote childbearing in humans. During the first phase, biologically-based, often hereditary characteristics of the individual interact during growth and development with that individual’s childhood and adolescent social environments (Belsky 2000; Miller 1992), leading to the formation of a motivational substrate for childbearing (Miller and Pasta 2002). This process culminates at about the time that the individual’s body becomes physiologically capable of reproduction. The second phase begins in the adolescent and early adult periods and extends across the life course until the end of the individual’s reproductive career. During this phase, established childbearing motivations find expression in conscious desires and intentions, in behavior, and ultimately in the occurrence of fertility events. The latter, in turn, have a feedback effect on the underlying motivational substrate and the forms of its conscious expression (Miller and Pasta 1995a).
It is this second phase of development with which the current paper is concerned. We use our theoretical framework to model how the conscious manifestations of childbearing motivation predict two critical features in the development of young adults’ reproductive careers, namely the timing of the first or next child born and the total number of children ultimately born. We test this model with data from the National Longitudinal Survey of Youth (NLSY).
THEORETICAL BACKGROUND
Reproductive motivation may be said to have two major components, one that drives mate selection and sexual behavior and one that drives the protection and nurturance of the resulting progeny (Foster 2000; Potts 1997). It is the motivational mechanisms that subserve this second component, what Miller and Rodgers (2001) have called nurturant schemas, that play a central role in driving those behaviors that, beginning in adolescence and early adulthood, lead to the bearing and rearing of children.
Nurturant schemas are enduring dispositions to have feelings about and be motivated by babies and children. These trait-like schemas provide the underlying motive force for human childbearing, but in order to fully understand and predict childbearing decisions it is necessary to look beyond them and account for both the conscious factors that lead to behavior and the behavior itself. For this, we turn to a Traits-Desires-Intentions-Behavior (TDIB) theoretical framework (Miller, 1994). The ideas underlying this framework are fairly simple. There is a three-step motivational sequence, in which those schema-based traits that dispose the individual toward or away from bearing and caring for children are activated into conscious desires for or against having a child. These desires are, in turn, transformed by a decision-making process into intentions to have or not to have a child. This motivational sequence then leads to the implementation of the individual’s intentions through various behaviors, which in turn lead to the achievement/avoidance of conception and subsequent fertility outcomes.
Several elements of this TDIB framework have been present in the fertility research literature for a number of decades, the most common being child number desires and intentions. Demographers use variables that reflect numbers of children intended, expected, desired, and considered ideal. Based on the 1965 National Fertility Study in the United States, Ryder and Westoff (1971) showed that responses to the intended and expected number of children were “virtually indistinguishable” and that the pattern of answers to questions about intended, desired, and ideal parity in relation to current parity showed a “well ordered sequence” from ideals to desires to intentions to current behavior. In spite of these findings, considerable evidence indicates that these measures can be poor or unreliable predictors of actual fertility (Morgan 1982; Trent 1980; Westoff and Ryder 1977). Morgan (2001) has pointed out that that the predictive validity of measures such as completed parity intentions is handicapped by their change over time, making their usefulness depend on the time period over which they are projected. This observation highlights the potential importance of a second element of the TDIB framework, namely child-timing desires and intentions. This element has undergone separate study (Rindfuss, Morgan, and Swicegood 1988; Miller and Pasta, 1994).
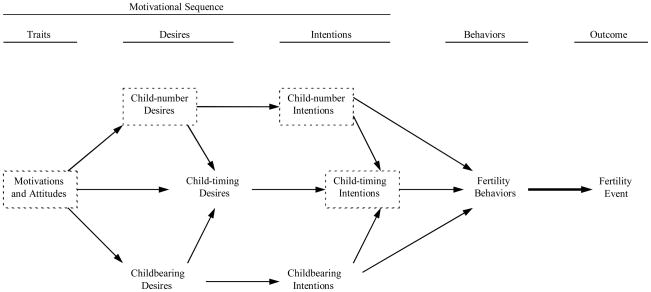
Our theoretical framework incorporates both the child-number and child-timing elements, as well as a third element based on childbearing desires and intentions. This framework is schematized in Figure 1, which is slightly modified from Miller (1994). On the left side, we show two types of traits that are relevant to fertility, motivational traits and attitudinal traits. Both are psychological dispositions that are strongly laden with the affective forces that motivate behavior. A good example of motivational traits would be positive and negative childbearing motivations of the type measured by Miller’s (1995) Childbearing Questionnaire. A good example of attitudinal traits would be traditional and modern sex role orientations as measured by Scanzoni (1975).
Figure 1.
An expansion of the TDIB model to show the interactions of two types of traits, three types of desires, and three types of intentions in their effect on fertility behavior. Dashed boxes indicate those components of the motivational sequence available in the NLSY data that will be used in testing the theoretical framework
Continuing to the right, desires have been divided into three types, corresponding to the three major issues that childbearing poses to the individual: whether to have a (another) child, how many (more) to have, and how soon to have the (next) child. The parentheses in the previous sentence help distinguish how these three questions may be framed either before or after childbearing has begun. These three issues are, of course, not independent of each other. As Figure 1 indicates and as Miller and Pasta (1994) suggested, childbearing desires are causally antecedent to child timing desires (the more you want a child, the sooner you want it), and so are child number desires (the more children you want, the sooner you want to start having them). Childbearing and child number desires share considerable common variance, represented within the context of a model like that shown in Figure 1 as a correlation.
Continuing again to the right, intentions have been divided according to the same three issues and are causally related to each other in the same way. This completes the three-step motivational sequence and leads to conception-oriented behavior, of which there are two primary types. Contraceptive behavior is oriented to the prevention of conception and itself has several different subforms that derive from the separate acts of choosing and using a contraceptive method (Miller and Pasta 1996). Proceptive behavior is oriented to the achievement of conception (Miller 1986). In a longitudinal study, Miller and Pasta (1995b) have shown that all three of the types of intentions identified above played a role in predicting proceptive behavior. Of course, sexual behavior is implicit in both of these conception-oriented behaviors but operates to a large extent on the basis of a separate motivational mechanism based on mating schemas (Miller and Rodgers 2001). Finally, on the far right Figure 1 represents the effect that the two conception-oriented behaviors, and to a much lesser extent sexual behavior (Miller, 1986), have on the occurrence (or not, in the case of contraception) of fertility events.
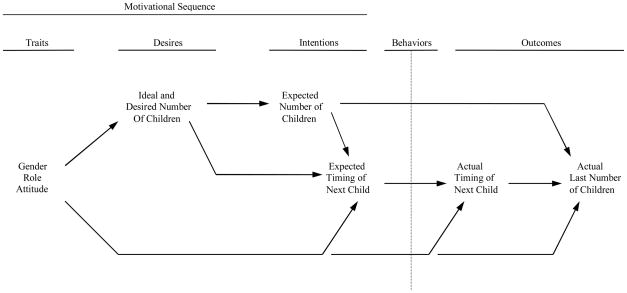
In existing data sets used for secondary analysis, not all of the Figure 1 constructs are likely to have been measured. Nonetheless, the NLSY has an extensive number of fertility-related questions that allow the testing of a subset of constructs from our overall framework. In Figure 1 we have highlighted with dashed boxes those components of the motivational sequence leading to fertility that can be measured using variables from the NLSY and incorporated in the model tested in this paper. Figure 2 represents this model with key constructs renamed to correspond to the actual variables used during NLSY data collection.
Figure 2.
The hypothesized fertility structural equation model that was fitted to the NLSY data. Fertility traits, desires, and intentions were measured during 1979 to 1982. Fertility behaviors (indicated by the vertical dotted line) were not measured but were assumed to occur subsequent to 1982, resulting in fertility outcomes. Two fertility outcomes were measured beginning in 1983 and ending in 2002.
Figure 2 contains additional modifications of the framework in Figure 1. First, gender role attitude is the trait predictor in the motivational sequence because no good measures of childbearing motivation are available in the data. However, a good measure of gender role attitude provides the opportunity to use a closely related motivational trait that has not been adequately explored in the prediction of fertility outcomes. Research has shown that embedded within the gender role attitude construct are both motivations for childbearing and motivations for female education, work, and other aspects of a modern lifestyle. For example, Scanzoni (1975) showed that for wives aged 18–29, sex role modernity (as opposed to traditionalism) predicted lower birth intentions, lower parity, and higher effectiveness of contraceptive use, and was also positively associated with greater education and predicted greater work force participation and higher income. Miller (1981) found that a traditional role attitude was strongly associated with both positive and negative childbearing motivations in women (r = 0.59 and −0.46, respectively). Overall, these findings suggest that in a multivariate context, especially one that includes a modern life-style variable such as motivation for education as a predictor (see below), the residual predictive effects of a gender role attitude variable may well reflect childbearing and childrearing motivations.
Second, because we were limited to those desires and intentions actually measured in the NLSY, ideal/desired number of children and gender role attitude are both directly connected to the expected timing of the next child. These two connections are expected to capture much of the explanatory power presumed to be passing through the two desires and one intentions variable that are unmeasured in the data.
Third, we have not included explicit behavioral variables in the model. A few questions about both contraceptive and proceptive behavior were asked in the NLSY, but none was well suited for use in this kind modeling. Further, in order to predict across the twenty year period covered by this study, many different types of behavior were relevant and the model would have become unmanageably complex. For these reasons, we assumed that the fertility outcomes reflect a complex of behaviors over time, indicating the on-going occurrence of these behaviors in Figure 2 with a vertical dotted line placed between the antecedent motivational sequence and the consequent fertility outcomes.
Various social science theorists have conceptualized fertility decision-making as a one-stage process (Becker 1960; Willis 1973), a two-stage process (Fawcett, Albores, and Arnold 1972; Namboodiri 1974), or a multistage process (Bulatao 1981). In considering most modern, developed societies, we are inclined to conceptualize fertility decision-making as occurring one birth at a time, a process that has been called conditional (McClelland 1983), successive (Fawcett 1983), or sequential (Namboodiri 1983) decision-making. This means that the framework represented in Figure 2 could be applied to any single birth, whether it was the first, second, third, etc. In this study, we are interested in examining how late adolescent/early adult fertility motivations predicted across entire reproductive careers. Therefore, in developing the theoretical framework shown in Figure 2, we have selected two fertility outcomes that are central to the definition of a fertility career, the timing of the next birth and the final number of children born. We expect the timing of the next birth to predict the final number born (the sooner you have a child, the more children you are likely to have). We also expect number intentions to predict the final number actually born and timing intentions to predict the actual timing of the next child. By confining our sample to those NLSY participants who are without children (i.e., those who have zero parity) at the beginning of the study, the two fertility outcome variables in the model span their entire fertility careers. Then, by including participants who have already had one or more children, we add to the model elements of the participants’ fertility careers that occur following the birth of the first, second, etc., child. Comparing these two models informs an across-fertility career, developmental perspective.
To this point we have focused exclusively on reproductive motivations. However, there are other motivations that can affect childbearing and further inform our modeling. An important such source is education, which derives from the behavioral domain that Miller and Rodgers (2001) call exploration/mastery. Education has a complex, multi-pathway effect on fertility that is predominantly, but not exclusively, negative (Cochrane 1979; Kohler and Rodgers 2003; Johnson and Rodgers, 2006). We model the motivation for education using a trait-like measure of educational intentions, which we expect will be negatively related to the childbearing motivational sequence and to fertility outcomes. Because we believe gender role attitude to be positively related to fertility outcomes but negatively associated with educational intentions, especially in women, we anticipate that the educational intentions and gender role attitude variables will to some extent reduce each other’s explanatory power.
One final feature of our theoretical approach requires discussion. It has been traditional in field of fertility research, and in survey research in particular, to assume that fertility falls primarily within the woman’s sphere of influence and that it is the women’s motivations that are the primary determinants of childbearing. For example, although the National Survey of Family Growth began in 1973, data from men have only begun to be collected during cycle 6 starting in 2002 (Groves et al., 2005). In contrast to the traditional approach, studies of couples have shown men to have an essentially equal role in both contraceptive (Miller and Pasta, 1996) and proceptive (Miller and Pasta, 1995b) decisions. Therefore we will make a simplifying assumption that the motivational determinants of fertility outcomes across reproductive careers are equivalent for males and females and then, in testing our theoretical framework, we will allow the data to show for what variables and to what extent relaxing that assumption will improve predictive success.
METHODS
Design
The data used to test our theoretical framework were collected during the NLSY, which was conducted under the auspices of the U. S. Department of Labor (Center for Human Resources Research, 2003). Beginning in 1979, a national probability sample of young men and women was surveyed annually through 1994 and thereafter biennially, with the most recent data available at the time of these analyses collected in 2002. As described in the caption for Figure 2, we used data bearing on the motivational sequence leading to childbearing that were collected during the 1979–1982 period to predict our two fertility outcome variables as measured beginning after 1982 and continuing through 2002. This allowed us to study the link between fertility motivation and fertility outcomes in the context of a prospective design.
Participants
The original NLSY79 1979 participants consisted of a sample of 6,111 youths representative of the U.S. as a whole, an oversample of 5,295 minority and economically disadvantaged youths, and a military sample of 1,280 youths, for a total of 12,686 youths. However, because some members of the economically disadvantaged and military samples were dropped from the survey after 1990 and 1985 respectively, the sample size from which we could actually draw our participants was 5,022 for males and 4,942 for females. Attrition during the 23 years of data collection reduced the number of participants for whom data were available for the entire 1979–2002 period to 3,683 for males and 3,883 for females (retention rates of 73.3% and 78.6% respectively). In order to test whether the model generated with these two samples was affected by this amount of attrition, we applied the final model to the data available through 1990 only. The size of these samples, which had a retention rate of 89.9% and still included the economically disadvantaged youths, was 5,241 for males and 5,401 for females.
The male and female youths who participated in the NLSY were born in 1957 through 1964, were ages 14 through 21 when the sampling occurred on December 31, 1978, and were ages 37 through 45 when surveyed in 2002. Thus childbearing for this cohort is almost complete and problems with selection bias caused by fertility timing differences across educational and SES strata are substantially resolved. Additional selected background characteristics of the study participants are shown in Table 1. Because it is obvious that many of these variables are strongly affected by even a few years change in age, we report their values as of 1982 (except for race/ethnicity) when the motivational sequence in our model ends and the fertility outcomes begin. Two continuous variables not included in the table are age in 1982 with a mean (s.d.) of 20.5 (2.3) and total net family income in 1982 with a mean (s.d.) of $21,902 ($17,155).
Table 1.
Frequency Counts for Selected Background Variables, Separately by Sex.
| Variable |
Males (n=3,683) |
Females (n=3,883) |
||
|---|---|---|---|---|
| Category |
Frequency |
Column % |
Frequency |
Column % |
| Race/Ethnicity, 1979 | ||||
| Hispanic | 676 | 18.4 | 721 | 18.6 |
| Non-Hispanic black | 1,126 | 30.6 | 1,192 | 30.7 |
| Non-Hispanic, non-black | 1,881 | 51.1 | 1,970 | 50.7 |
| Religious Affiliation, 1982 | ||||
| Protestant | 1,969 | 53.6 | 2,186 | 56.5 |
| Roman Catholic | 1,168 | 31.8 | 1,249 | 32.3 |
| Other | 86 | 2.3 | 100 | 2.6 |
| None | 448 | 12.2 | 334 | 8.6 |
| Highest grade completed, 1982 | ||||
| 8th grade or less | 183 | 5.0 | 163 | 4.2 |
| 9th–11th grade | 1,277 | 34.8 | 1,133 | 29.3 |
| 12th grade | 1,385 | 37.7 | 1,511 | 39.1 |
| 1 or 2 years of college | 547 | 14.9 | 741 | 19.2 |
| 3 or 4 years of college | 252 | 6.9 | 305 | 7.9 |
| Graduate school | 29 | 0.8 | 16 | 0.4 |
| Employment status, 1982 | ||||
| Employed | 2,167 | 58.8 | 2,030 | 52.3 |
| Unemployed | 571 | 15.5 | 526 | 13.6 |
| Out of labor force | 683 | 18.5 | 1,303 | 33.6 |
| Armed services | 262 | 7.1 | 24 | 0.6 |
| Marital status, 1982 | ||||
| Never married | 3,035 | 82.4 | 2,639 | 68.0 |
| Married | 560 | 15.2 | 1,003 | 25.8 |
| Separated, divorced, or widowed | 87 | 2.4 | 240 | 6.2 |
| Number of children ever born, 1982 | ||||
| 0 | 3,097 | 84.1 | 2,600 | 67.0 |
| 1 | 416 | 11.3 | 781 | 20.1 |
| 2 | 135 | 3.7 | 376 | 9.7 |
| 3+ | 34 | 1.0 | 126 | 3.3 |
Note. The number of missing cases in a variable column ranges from 0 to 14.
Measures
Ten fertility variables were used in estimating the model in Figure 2. All were based on single questions asked in the annual or biennial survey interviews about the participant’s ideal number of children, how many children the participant wanted altogether, how many children the participant expected to have, when the participant expected to have the first/next child, whether the participant had given birth to a child since the previous interview, and how many total children the participant had born.
An interval scale variable was used to measure the two gender role attitude variables from 1979 and 1982. Each of these was based on five of the eight attitudinal statements read to the participants, which they were asked to rate on a four point scale from strongly agree to strongly disagree. The five statements, which were strongly intercorrelated, included “A woman’s place is in the home, not the office or shop”, “A wife with a family has no time for outside employment”, “Employment of wives leads to more juvenile delinquency”, “It is much better if the man is the achiever outside the home and the woman takes care of the home and family”, and “Women are much happier if they stay home and take care of children”. Responses were combined additively for each year. Cronbach’s coefficient alpha for males/females was .75/.76 in 1979 and .81/.81 in 1982.
Three additional variables from the education domain were also used in the model estimation. Each of these was based on the same question asked in 1979, 1981, and 1982 about the highest grade the participant thought he/she would actually complete. For more complete information regarding the fertility, gender role, and education questions and question sequencing, see Chapter 3 in the NLS Handbook (Center for Human Resources Research, 2003).
Table 2 provides descriptive statistics, separately by sex, for all thirteen of the above variables, as well as two reciprocal forms of the timing variables. A suffix indicates the year in which each variable was measured. For the variables with a 2002 suffix, that date should be interpreted as an “as of” date, given that a very small proportion of participants will have a first/next child and a larger last number of children after 2002, the most recent year of data collection. Two variables, the expected and the actual timing of the next child, were coded as years and fractions of years. For example, those who reported that they expected their next child in one year and three months were coded 1.25. Using this coding convention, the higher the score the later the child was intended or actually born. However, in order to normalize these two variables and to reduce outlier effects, each score was transformed using a reciprocal transformation. Because these reciprocal variables were the ones actually used in the analyses and reported in the results section, that coding convention was reversed, i.e., the higher the score the sooner the child was intended or actually born. As a consequence, all predictions between the fertility variables in the model were expected to be positive. In contrast, all predictions between educational intentions and the fertility variables were expected to be negative. For comparison purposes, we report both the original timing variables and their reciprocal versions in the table.
Table 2.
Means and Standard Deviations, Minimum (Min) and Maximum (Max) Values, and Numbers of Missing Cases (Mis) of All Variables Used in the Structural Equation Modelinga, Separately by Sex.
| Variable |
Males (n=3,683) |
Females (n=3,883) |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| M |
SD |
Min |
Max |
Mis |
M |
SD |
Min |
Max |
Mis |
|
| Gender role attitude, 1979 | 2.36 | 0.54 | 1.00 | 4.00 | 7 | 2.09 | 0.56 | 1.00 | 4.00 | 4 |
| Gender role attitude, 1982 | 2.21 | 0.54 | 1.00 | 4.00 | 1 | 1.97 | 0.55 | 1.00 | 4.00 | 2 |
| Ideal number of children, 1979 | 3.01 | 1.33 | 0 | 10 | 15 | 2.95 | 1.29 | 0 | 10 | 10 |
| Desired number of children, 1979 | 2.58 | 1.41 | 0 | 10 | 38 | 2.49 | 1.48 | 0 | 10 | 16 |
| Ideal number of children, 1982 | 2.72 | 1.11 | 0 | 10 | 21 | 2.65 | 1.07 | 0 | 10 | 46 |
| Desired number of children, 1982 | 2.49 | 1.32 | 0 | 10 | 31 | 2.36 | 1.28 | 0 | 10 | 15 |
| Expected number of children, 1982 | 2.42 | 1.24 | 0 | 10 | 23 | 2.33 | 1.23 | 0 | 10 | 16 |
| Expected timing of next child, 1982 | 6.21 | 5.61 | 0.08 | 20 | 167 | 6.91 | 6.69 | 0.08 | 20 | 180 |
| Reciprocal, exp. timing of next child, 1982 | 0.47 | 1.17 | 0.05 | 12 | 167 | 0.55 | 1.41 | 0.05 | 12 | 180 |
| Actual timing of next child, 2002 | 11.45 | 9.18 | 0.00 | 25 | 0 | 10.33 | 9.34 | 0.00 | 25 | 0 |
| Reciprocal, actual timing of next child, 2002 | 0.23 | 0.29 | 0 | 1.00 | 0 | 0.29 | 0.33 | 0 | 1.00 | 0 |
| Actual last number of children, 2002 | 1.83 | 1.46 | 0 | 10 | 0 | 2.05 | 1.42 | 0 | 11 | 0 |
| Expected years of education, 1979 | 13.78 | 2.39 | 3 | 18 | 32 | 13.78 | 2.32 | 1 | 18 | 30 |
| Expected years of education, 1981 | 13.77 | 2.41 | 1 | 18 | 56 | 13.86 | 2.29 | 3 | 18 | 55 |
| Expected years of education, 1982 | 13.84 | 2.40 | 3 | 18 | 9 | 13.92 | 2.31 | 3 | 18 | 13 |
Although not used in the modeling, the non-reciprocal form of the expected and actual timing variables are included in the table for purposes of comparison with the inverse form.
We adopted special coding conventions for certain variables in order to avoid outlier effects. For the four ideal and desired number of children variables, we set variable values greater than 10 to 10. For the expected timing of the next child variable, we set responses greater than “20 years from now” to 20. We adopted additional coding conventions in order to keep participants in the sample when their responses were categorically different from the continuous variable but we felt their position on the continuum could reasonably be approximated. Thus for the expected timing of the next child variable, we set all those who expected no (more) children and the few who were unable to say what their expectations were to 20, indicating the most extreme expectation score possible within our coding scheme. We kept those who were pregnant at the time of the 1982 interview in the sample and coded how soon they expected to give birth. For example, the minimum of 0.08 for the expected timing variable in Table 2 represents participants who expected to give birth in one month. For the actual timing of next child variable, we arbitrarily set all those who had not yet had a first/next child in 2002 to 25 and for the reciprocal of that variable, we arbitrarily set those same participants to 0 (i.e., a rounded version of the reciprocal of 25).
Data Analysis
We estimated the hypothesized model shown in Figure 2, using the latent variable and the linear structural equation capabilities of LISREL (Joreskog and Sorbom, 1996). We analyzed separate covariance matrices for males and females. Because of the proportionally small number of missing cases (see Table 2), missing data were handled by analyzing covariance matrices calculated using the pair-wise missing option. We assumed the null hypothesis of no sex differences in both the measurement and the structural models. Therefore, we constrained parameter estimates to be equal across the two sex subsamples, relaxing those constraints when it significantly improved overall model fit, beginning with those having the largest modification indices and progressing downward. Once no further statistically significant improvement in fit could be accomplished by removing constraints, we dropped pathways with non-significant coefficients and added new pathways where modification indices suggested doing so would significantly improve model fit. In the Appendix we present the separate correlation matrices for males and females of all variables used in the LISREL modeling. In order to maximize the number of cases, these correlations are also calculated using the pair-wise missing option.
APPENDIX.
Intercorrelations between the thirteen variables used in the LISREL modeling, with females above and males below the diagonal.
| Variable | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. Gender role attitude, 1979 | .50 | −.28 | −.27 | −.27 | .10 | .05 | .07 | .04 | .05 | .03 | .06 | .06 | |
| 2. Gender role attitude, 1982 | .50 | −.28 | −.30 | −.30 | .09 | .03 | .10 | .05 | .04 | .04 | .08 | .08 | |
| 3. Expected years of education, 1979 | −.33 | −.33 | .70 | .70 | −.09 | .03 | −.06 | .02 | .04 | −.05 | −.13 | −.04 | |
| 4. Expected years of education, 1981 | −.30 | −.33 | .70 | .79 | −.06 | .04 | −.04 | .06 | .07 | −.08 | −.14 | −.05 | |
| 5. Expected years of education, 1982 | −.30 | −.32 | .67 | .77 | −.06 | .03 | −.04 | .06 | .07 | −.06 | −.14 | −.06 | |
| 6. Ideal number of children, 1979 | .07 | .05 | .02 | .01 | −.01 | .57 | .38 | .31 | .30 | .02 | .04 | .06 | |
| 7. Desired number of children, 1979 | .03 | .03 | .07 | .07 | .06 | .54 | .31 | .36 | .35 | .04 | .04 | .08 | |
| 8. Ideal number of children, 1982 | .09 | .12 | −.01 | −.01 | −.01 | .41 | .35 | .61 | .57 | .07 | .05 | .09 | |
| 9. Desired number of children, 1982 | .06 | .09 | .03 | .03 | .04 | .31 | .47 | .62 | .83 | .10 | .10 | .15 | |
| 10. Expected number of children, 1982 | .07 | .10 | −.01 | −.00 | .01 | .27 | .40 | .55 | .82 | .10 | .10 | .17 | |
| 11. Reciprocal, exp. timing of next child, 1982 | .03 | .05 | −.08 | −.10 | −.11 | .02 | .02 | .02 | .07 | .08 | .39 | .14 | |
| 12. Reciprocal, act. timing of next child, 2002 | .10 | .13 | −.15 | −.17 | −.20 | .08 | .03 | .07 | .08 | .09 | .42 | .52 | |
| 13. Actual number of children, 2002 | .16 | .18 | −.19 | −.20 | −.22 | .09 | .10 | .15 | .21 | .25 | .14 | .48 |
Measurement model
An important consideration in testing our SEM was to reduce measurement error wherever possible through the use of latent variables. Because the important variables of ideal and desired number of children were measured only twice, in 1979 and 1982, and because analyses indicated that all four were well intercorrelated, we created a single latent variable to represent child-number desires, using these four indicators.
In parallel with this, we created a second latent variable using the 1979 and 1982 measures of gender role attitudes. Efforts to create similar across-year latent variables for child-number expectations and child-timing expectations were less successful. The reason for this was that expectations were less stable over the three year interval and appeared to be particularly affected by changes in marital status and by childbearing (see Rodgers and Doughty, 2000, for empirical analysis and discussion of the stability of these NLSY fertility expectation indicators). As a result of this relative instability, the inclusion of the two across-year latent expectations variables induced a large number of within-year correlations between the four latent variable indicators and added strain to the overall model. For these reasons we decided not to include latent expectations variables in the model but rather to base these two variables on single indicators from 1982.
Finally, we included a latent variable that represented education motivation. We based it on expected years of education as measured in 1979, 1981, and 1982. Unlike the fertility expectations variables, it was more stable across that time period.
Structural Model
The connections hypothesized for the fertility motivational sequence were measured in the 1979–1982 period and predicted the two fertility outcomes, which were measured beginning in 1983 and continuing until 2002. Because we did not wish to model the relationships between the trait of gender role attitude and the trait of expected years of education, these two latent variables were treated as exogenous (ksi variables in LISREL) and allowed to freely correlate with each other and to predict the remaining variables (eta variables in LISREL).
Testing Variants of the Base Model
We conducted three validity substudies, one on the effects of sample attrition and two that tested developmental issues, by applying the base model derived as described above to data from different subsamples. First, we examined whether loss to follow-up may have appreciably affected our findings by applying the base model to data from the considerably larger sample available ten years earlier, in 1990. Second, we tested whether the eight year age spread in the base sample was large enough to obscure some important developmental differences by splitting that sample into two parts, one composed of respondents 18 years of age or older in 1979 and one composed of those younger than age 18, and testing the base model on data from both the older and younger subsamples, applying the same across-sex constraints in each case. Third, given that one-sixth of the males and one-third of the females reported having given birth to a child by 1982, we split the sample into a no childbearing subsample and a previous childbearing subsample and tested the base model on data from both subsamples, again applying across-sex constraints in each case.
RESULTS
With 110 degrees of freedom, the chi-square of the base model was 353.08, the root mean square error of approximation (RMSEA) was 0.024, and the p-value for a test of close fit (RMSEA < 0.05) was 1.00. These fit indicators indicate a good fit to the data. Most of the poor fitting parts of the model occurred between latent variable indicators that were not in the same latent variables and, largely, between indicators that were measured in the same year. These findings indicate both a small within-indicators measurement effect and somewhat larger within-years measurement effect that were not completely accounted for in the overall model.
The Measurement Model
Table 3 presents the parameter estimates and t-values for all indictors in each of the overall model’s three latent variables. For all three latent variables, male and female equality constraints remained in place, with the exception of the desired number of children in 1979. That indicator had a significantly larger parameter estimate among females, suggesting they placed a slightly greater emphasis than males on desires relative to ideals for the 1979 year. In general, for the ideal/desired number of children latent variable, the 1982 desired number of children indicator contributed the most weight and the 1979 ideal number of children indicator contributed the least, suggesting a change across years that would be expected with a construct that has state-like as well as trait-like features. For the gender role attitude latent variable, the 1982 indicator contributed only slightly greater weight than the 1979 indicator. For the expected education latent variable, both the 1982 and 1981 contributed only slightly greater weight than the 1979 indicator. Although there is a slight change across years for these two latent variables, it is minimal and is consistent with constructs that have primarily trait-like features.
Table 3.
The LISREL Measurement Model, Showing Unstandardized Parameter Estimates (P.E.) and T-Values for all Indicators of Latent Variables, Separately by Sex
| Latent Variable |
Males |
Females |
||
|---|---|---|---|---|
| Indicator |
P.E. |
T-Value |
P.E. |
T-Value |
| Ideal/desired number of children | ||||
| Desired number of children, 1982 | 1.00 | 1.00 | ||
| Ideal number of children, 1982 | 0.57 | 61.24 | 0.57 | 61.24 |
| Desired number of children, 1979 | 0.45 | 24.38 | 0.58 | 30.72 |
| Ideal number of children, 1979 | 0.35 | 26.47 | 0.35 | 26.47 |
| Gender role attitude | ||||
| Gender role attitude, 1982 | 1.00 | 1.00 | ||
| Gender role attitude, 1979 | 0.92 | 29.88 | 0.92 | 29.88 |
| Expected Education | ||||
| Highest grade expected, 1982 | 1.00 | 1.00 | ||
| Highest grade expected, 1981 | 1.01 | 93.58 | 1.01 | 93.58 |
| Highest grade expected, 1979 | 0.89 | 81.07 | 0.89 | 81.07 |
The Structural Model
Table 4 presents the parameter estimates and t-values for all the variables predicting each outcome variable, starting with an equation for the final outcome variable in the LISREL beta matrix, namely the actual last number of children, and moving backward and ending with an equation for the initial outcome variable in the beta matrix, ideal/desired number of children. The R2 is also given for each of the five prediction equations. The strongest two predictors for the first equation and the strongest single predictors for the next three equations (as judged by the t-values) are the ones hypothesized in Figure 2. The hypothesized prediction of the expected timing of the next child by the ideal/desired number of children is not observed (although see the no childbearing/previous childbearing substudies discussed below). Further, several hypothesized predictions of gender role attitude are not observed and the predictions of expected education are not consistently negative, as hypothesized. We discuss these observations further below. There are one or two instances in each equation, except for the last one, where sex differences occur, including opposite signs for the prediction of the actual last number of children by expected education. The R2 of three of the equations are substantial but the R2s for predicting the expected timing of the next child and the ideal/desired number of children are small.
Table 4.
The LISREL Structural Equation Model, Showing Unstandardized Parameter Estimates (P.E.) and T-Values for All Prediction Pathways and R2s for Outcome Variables, Separately by Sex. Bold numbers indicate the primary hypothesized pathway of the model.
| Outcome Variable |
Males |
Females |
||||
|---|---|---|---|---|---|---|
| Predictor Variable |
P.E. |
T-Value |
R2 |
P.E. |
T-Value |
R2 |
| Actual last number of children | 0.29 | 0.31 | ||||
| Actual timing of next child | 2.69 | 37.01 | 2.04 | 32.45 | ||
| Expected timing of next child | − 0.10 | − 8.62 | − 0.10 | − 8.62 | ||
| Expected number of children | 0.14 | 8.62 | 0.24 | 15.52 | ||
| Gender role attitude | 0.24 | 4.66 | 0.24 | 4.66 | ||
| Expected education | 0.03 | 2.44 | − 0.08 | − 7.05 | ||
| Actual timing of next child | 0.17 | 0.21 | ||||
| Expected timing of next child | 0.09 | 36.91 | 0.09 | 36.91 | ||
| Ideal/desired number of children | 0.02 | 5.84 | 0.02 | 5.84 | ||
| Gender role attitude | 0.06 | 3.84 | ||||
| Expected education | − 0.02 | − 10.68 | − 0.02 | − 10.68 | ||
| Expected timing of next child | 0.02 | 0.02 | ||||
| Expected number of children | 0.10 | 8.18 | 0.10 | 8.18 | ||
| Expected education | − 0.05 | − 4.90 | − 0.08 | − 6.88 | ||
| Expected number of children | 0.84 | 0.80 | ||||
| Ideal/desired number of children | 0.95 | 18.51 | 0.95 | 18.51 | ||
| Expected education | − 0.02 | − 3.82 | ||||
| Ideal/desired number of children | 0.02 | 0.02 | ||||
| Gender role attitude | 0.48 | 8.73 | 0.48 | 8.73 | ||
| Expected education | 0.08 | 8.21 | 0.08 | 8.21 | ||
If we focus first on the fertility sub-model (everything except expected education and its connections) shown in Table 4, we can observe two predictions in addition to the stronger, hypothesized ones. First, ideal/desired number of children has a direct effect on the actual timing of the next child. The effect is equal across the sexes and is positive, as expected, meaning that the more children the respondent desires, the sooner he/she actually has them. Second, the expected timing of the next child has a direct effect, equal for the sexes, on the actual last number of children. Surprisingly, the effect is negative, meaning that the sooner the respondents expect a child, the fewer they actually have. We can also observe several hypothesized effects of gender role attitude that are absent. These include its effects on expected number of children, expected timing of next child, and for males actual timing of next child. Preliminary analyses of only the fertility domain variables (results not shown) indicated that gender role attitude did predict those three variables in that submodel–with the exception of expected number of children for males–indicating that it was the presence of the expected education variable in the base model that eliminated those connections.
Expanding our focus to include education reveals several patterns that match predictions, along with some unexpected findings. As can be seen, expected education exactly replaces the three absent effects of gender role attitude, indicating an important covariance between it and gender role attitude with expected education dominating in those three predictions. Although these three predictions have the hypothesized negative sign, its predictions of ideal/desired number of children and–for males- actual last number of children are positive. Additional findings discussed below shed some light on this pattern.
Variants of the Base Model
Attrition Substudy
In 1990 NLSY data from 5,241 males and 5,401 females were available for examining whether sample attrition affected our final model. These numbers also include 664 male and 819 female economically disadvantaged participants who were dropped after the 1990 survey. We tested the base model on data from this larger sample. There were almost no changes in the model. No existing connections became non-significant, most actually having slightly increased t-values. R2s remained virtually the same. The only change suggested by modification indices was removal of the equality constraint from the connection between expected timing of the next child and actual timing of the next child, allowing the male connection to become more positive. These findings suggest that attrition bias is at most relatively minor in this study.
Age-split Substudy
We next split the 2002 sample into two age-based subsamples: males (n = 1,896) and females (n = 1,926) under 18 years of age in 1979 and males (n = 1,787) and females (n = 1,957) 18 years of age and above. We then tested the base model on data from each of those two samples separately, with the usual across-sex equality constraints applied in both cases. The R2s were closely similar across the two models and only minor changes occurred in the pattern of connections. Specifically, two existing connections became non-significant: 1. expected education predicting actual last number of children in males 18 and over; and 2. expected education predicting expected number of children in females under 18. Additionally, there were two modification indices that indicated significant additions: 1. ideal/desired number of children positively predicting actual final number of children in younger females; and 2. expected education positively predicting expected number of children in younger males.
No Childbearing/Previous Childbearing Substudy
Finally, we split the 2002 sample into two childbearing-based subsamples: males (n = 3,056) and females (n = 2,593) who had not borne a child as of 1982 (the year defining the boundary in our study between motivations and outcomes) and males (n = 627) and females (n = 1,290) who had borne a child. We tested the base model on data from each of the two subsamples separately, applying across-sex equality constraints in each case. The results of these analyses revealed that for both models, some connections became non-significant, some connections needed to be added on the basis of high modification indices, and several coefficients reversed signs while remaining significant. The number of changes, which often differed across the sexes, required several additional fitting steps and the generation of a new model for both the no childbearing and the previous childbearing subsamples. However, the resulting structural equation models for males and females in both subsamples are very similar to those for males and females in the base model where there are comparable connections and the large R2s for the two behavioral outcome variables are also quite similar. With 110 degrees of freedom, the chi-square of the no childbearing model was 351.49, the RMSEA = 0.028, and the p-value for a test of close fit (RMSEA < 0.05) was 1.00. With 114 degrees of freedom, the chi-square of the previous childbearing model was 236.36, the RMSEA = 0.026, and the p-value for a test of close fit (RMSEA < 0.05) was 1.00. In both cases, results indicate a good fit to the data.
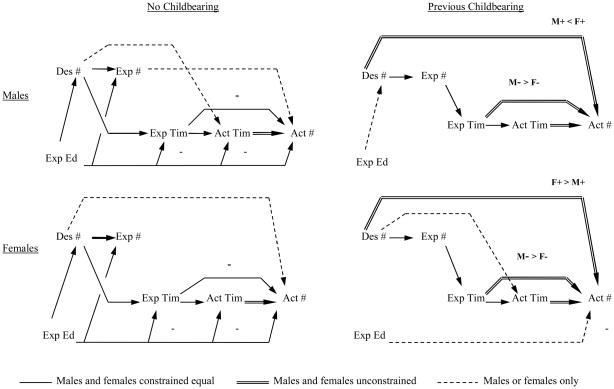
The modified base models for both subsamples are depicted graphically in Figure 3, which shows the no childbearing model for both sexes on the left and the previous childbearing model for both sexes on the right. We focus our description on changes from the full sample base model and because there were no changes in the predictions of the gender role variable, we have omitted that variable from the figure in order to improve the graphic’s clarity. In the no childbearing fertility submodel, for both sexes the prediction of the expected timing of the next child (Exp Tim) by the expected number of children (Exp #) was dropped and the prediction of the expected timing variable by ideal/desired number of children (Des #) was added, with an estimated coefficient (p-value) of 0.09 (7.83) in both sexes. Note that this addition represents an hypothesized connection that was not observed in the base model. For females only, the predictions of actual last number of children (Act #) by expected number of children and of actual timing of first child (Act Tim) by ideal/desired number of children were both dropped and a prediction of actual last number of children by ideal/desired number of children was added, with an estimated coefficient (p-value) of 0.15 (8.39). In the previous childbearing fertility submodel, for both sexes the prediction of the actual last number of children by the expected number of children was dropped and the prediction of the actual last number of children by the ideal/desired number of children was added, with an estimated coefficient (p-value) of 0.25 (4.70) in males and 0.48 (16.55) in females. For males only, the prediction of the actual timing of the next child by ideal/desired number of children was dropped. In addition, the negative relationship between expected timing of the next child and the actual number of children became significantly weaker among females than it was in the base model.
Figure 3.
Four LISREL structural equation models, two constrained across males and females in the no childbearing subsample (left column) and two constrained across males and females in the previous childbearing subsample (right column). The predictions of the gender role variable are unchanged from the base model and are omitted for the sake of clarity.
Finally, we consider the extent to which educational expectations (Exp Ed) changed in their predictions within the two subsample models. In the no childbearing subsample, the prediction of the expected number of children by expected education changed from negative for females only to positive and constrained equal across the sexes, with an estimated coefficient (p-value) of 0.02 (3.94). In addition, in females expected education changed signs relative to the base model to positively predict the actual last number of children with an estimated coefficient (p-value) of 0.04 (2.62), compared to a prediction for males of 0.07 (5.66). In the previous childbearing subsample, quite in contrast, expected education lost all predictive power, with two exceptions: it remained positively predictive of ideal/desired number of children in males with an estimated coefficient (p-value) of 0.06 (2.23) and negatively predictive of actual last number of children in females, with an estimated coefficient (p-value) of −0.08 (−4.90).
DISCUSSION
The findings of this study expand upon and considerably sharpen those from earlier studies that left the predictive role of fertility motivation in doubt. Our results indicate that, contrary to the cautionary statements of some previous researchers, fertility motivations measured in the late adolescent/early adult period do predict both fertility timing outcomes measured during these youth’s reproductive careers and fertility numbers outcomes measured twenty years later. The two primary motivational forces in our theoretical framework–the desired and intended number of children and the intended timing of the first/next child–interact to successfully predict the two corresponding fertility outcomes. As the bolded parameter estimates in Table 4 show, the main motivational thrust moves from gender role attitude, our proxy for childbearing motivational traits, through the desired and intended number of children and the intended timing of the first/next child to the actual timing of that child and, ultimately, to the final number of children born.
Our findings also expand upon earlier studies with respect to the significance of gender for fertility motivation. Contrary to the traditional perspective in which fertility is assumed to fall primarily within the woman’s sphere of influence, there are essentially no differences between males and females in the strength of the primary predictive pathways emanating from the antecedent motivational sequence.
Although the amount of variance explained is small for two of the motivational sequence variables–ideal/desired number of children and expected timing of the first (next) child, this finding is not at all surprising given what we know from previous research. Miller and Pasta (1993) showed that the variables most predictive of the desired number of children were childbearing motivational traits. Separately, Miller and Pasta (1994) showed that the major predictor of the expected timing of the next child was the desired timing of the next child. Neither of these two types of variables was available in the NLSY data set.
The two main predictive pathways for the gender role attitude trait reveal that a traditional attitude is associated with a larger desired number of children during the 1979–1982 period and a larger last number of children actually achieved by 2002. We interpret the first prediction as reflecting the childbearing motivation component of the gender role attitude variable because the presence of expected education as a co-predictor partials out much of the component that is not related to childbearing. Because the latter connection operates independently of the other variables in the fertility submodel, it represents an important substantive finding, namely that the childbearing motivation component of gender role attitude variable is a stable trait that continues to operate across the twenty years of follow up independently of the initially measured desires and intentions. The predictive pathway from gender role attitude to actual timing of the next child for females only probably represents a similar but shorter term effect in the area of birth timing.
The connections observed in the base model for expected education in the presence of the gender role attitude variable are not consistently negative as we had anticipated and they reveal some potentially interesting sex differences. However, a clearer interpretation of these findings can be made when we discuss the no childbearing and the previous childbearing models.
Within the fertility submodel of our findings, there are two important non-hypothesized findings, and both constitute what may be called by-pass predictions. An assumption of the TDIB and related models is that each step in the sequence is a major predictor of the next step. However, this assumption does not mean that a variable at one step cannot by-pass the next step to predict further downstream in the sequence as well. These by-passes are important because they call attention to features of the motivational sequence under study that do not fit into the TDIB framework. In the first non-hypothesized finding, the desired number of children variable directly predicts the actual timing of the next child, above and beyond its hypothesized indirect prediction through child-number intentions and child-timing intentions. This may represent imperfect decision-making. In other words, the two intentions variables, which presumably reflect decisions made, may be less stable than the desires variables because the decisions are not well founded at this early point in the participants’ reproductive careers. The result of such instability would be that a component of the more stable desires variable ultimately expresses itself over time in a direct prediction of the timing of the next child. We will see evidence that supports this interpretation when we discuss the no-childbearing and previous childbearing models below. Alternatively, this particular by-pass prediction may reflect the fact that desires express the participant’s own wishes, whereas intentions often take into account the partner’s wishes as well (Miller, Severy, and Pasta, 2004). This means that intentions measured at an early point in time may change as a result of having a different partner at a later point. With the extended follow-up of the present study, this kind of intentional change is very likely to have occurred at least once.
The second by-pass prediction observed in the fertility submodel is the negative one between the expected timing variable and the actual last number of children. In order to understand this finding, one must keep in mind that these two variables, as hypothesized, have a strong positive connection through the intermediate actual timing variable: timing intentions are positively predictive of actual timing of the first/next child and the latter are, in turn, positively predictive of the actual last number of children. The non-hypothesized, negative coefficient may be interpreted, then, as accommodating certain types of situations that are prevalent in the sample but not compatible with the two consecutive positive connections. One of these situations would be where individuals intended in 1982 to delay having their first/next but instead had an unplanned pregnancy and a baby born relatively soon after 1982. This outcome would have left them with a relatively long period to have more children, either planned or unplanned, which in turn would have made them likely to have more children than their original timing intentions assumed. The other situation that would fit with the observed negative coefficient would be one in which individuals intended in 1982 to have a child soon but instead found that they were limited by subfecundity/infecundity, and ended up having a child much later than they had intended, if at all. This would have left them with much less time to complete their family building and this, together with their continuing subfecundity, would have made them likely to have fewer children than their original timing intentions assumed.
Both of these scenarios would tend to produce a negative relationship between the expected timing of the next child and the actual last number of children. And, of course, other situations could also produce the same negative association. Miller and Pasta (1995b) observed that in addition to intentions, unplanned childbearing, subfecundity, and marital dissolution all predicted the actual timing of the onset of proceptive behavior. Bongaarts (2001, 2002) and Morgan (Morgan 2001; Hagewen and Morgan 2005) have developed models that condition the extent to which intentions are actually realized. These authors hypothesize three factors that augment intended fertility: unwanted fertility, replacement of children who have died, and children needed to satisfy strong gender preferences. In the U.S., the first factor has by far the greatest impact. In addition, they hypothesize three factors that reduce fertility relative to intentions: subfecundity and infecundity, postponement of intended fertility, and competition between intended fertility and other energy and time-intensive activities such as employment or health care. The last two factors are very broad categories that probably include a number of distinct reasons that fertility is delayed or foregone. The work of these authors supports our interpretation that unplanned pregnancies and subfecundity/infecundity could well explain our finding of a negative coefficient connecting timing intentions and the actual last number of children and at the same time suggests other factors that may operate in a similar way.
The two variants of the base model that emerged when it was tested on the no childbearing and the previous childbearing subsamples and modified to improve fit each show interesting differences. The importance of these differences is that they give us a picture of how the flow of motivation from traits to the actual last number of children may be different once childbearing has begun, thereby enhancing our fertility career perspective. It should be kept in mind that some of these motivational differences may have been antecedent to any childbearing that did or did not occur in the two childbearing subsamples. However, the overall similarity of the two variant models and the specific patterns of their differences suggest that these differences also strongly reflect the effects of childbearing and caretaking on the respondents.
In our discussion of the four models shown in Figure 3, we will focus on three patterns of difference from the full sample base model that distinguish the two no childbearing models from the two previous childbearing models. Other patterns of difference appear to involve sex-by-previous childbearing interactions, the interpretation of which is more speculative. Discussion of these patterns can be found in a working paper, available on line (Miller, Rodgers, and Pasta, 2008). One pattern involves the two ways that child-number desires affect the expected timing of the next child; directly in both the no childbearing males and females and indirectly through child-number intentions in both the previous childbearing males and females. This pattern suggests that child-number intentions are not sufficiently well formulated in the no childbearing group to meaningfully govern child-timing intentions. We hypothesize that the arrival of a child leads youth to formulate more realistic child-number intentions that serve as a better conduit for their child-number desires.
A second pattern involves the appearance in the previous childbearing group of a differential strength between sexes of the negative connection between timing intentions and final number of children, with the connection being less important in females. Recalling our interpretation that unplanned childbearing and infecundity might account for this negative connection, we further conjecture that the first of these two factors accounts for the sex difference in the negative connection. This pattern would obtain if females who already had borne at least one child were less likely than males to have their next pregnancy be unplanned.
The third pattern involves the major differences between the no childbearing and previous childbearing groups in the way that expected education predicts variables within the fertility submodel. In the no childbearing subsample, male and female respondents with higher educational intentions both desire and expect more children, although at the same time they expect to have them later and actually do so. Once these potentially conflicting motivations are partialed out, higher educational intentions predict a greater actual last number of children, with a considerably stronger effect in males.
We interpret the positive effect of educational intentions on number desires and intentions in the no childbearing group to reflect the way that the high aspirations of youth infuse both the educational and childbearing domains with the same positive feelings. Further, we interpret the negative effect of educational intentions on the two timing variables to mean that these youth want and intend to delay childbearing until after completing their educational plans. Finally, we interpret the positive effect of educational intentions on actual last number of children as reflecting a type of wealth effect, one in which the earning power that results from higher educational achievement leads to more children once the delaying effect of greater education on child timing has been partialed out. Hakim (2003) has argued that lifestyle preferences determine women’s employment pattern and fertility over the life course. Although we have not included a measure of employment desires or intentions in these analyses, it seems that the combination of the gender role attitude and educational intentions captures a good portion of the lifestyle preference construct that is central to her argument. Perhaps the most interesting result from that perspective, and somewhat in contrast to Hakim’s emphasis on women, is that the consequences for child bearing of a traditional gender role attitude and lower educational intentions are so similar for our sample’s no childbearing males and females.
This overall pattern of findings in the no childbearing group suggests that before the youth in the study have had any children educational intentions have an effect on every step of the motivational sequence and on both of the actual timing and number outcomes. Quite in contrast, in the previous childbearing group, only two of the ten possible predictive connections (to five fertility variables by two sexes) are present. The prediction of number desires in males surely reflects the same high aspirations of youth seen in the no childbearing subsample. The relatively small negative prediction of the actual last number of children in would seem to reflect the deterrent effect of more education for women on their having a larger family size. It should be kept in mind, however, that this overall pattern in the previous childbearing group may reflect a characteristic that played a role in their starting childbearing to begin with.
There are several threats to the validity of our findings, including the 26% loss to follow-up that occurred by 2002, the eight year age range in the sample, and the inclusion in the sample of some participants with previous childbearing. We have addressed these issues through special analyses with results that were reassuring with respect to both sample attrition and the sample’s initial age range. The results for the two groups with and without previous childbearing were highly informative and add texture to the reproductive career perspective underlying this research. Although some of the interpretations that we have offered of our research findings require further study and evaluation, the overall results reported here provide substantial support for the value of the TDIB framework as a theoretical guide to the organization of the motivations that lead to childbearing and to the developmental expression of those motivations across reproductive careers.
CONCLUSIONS
We have modeled how the childbearing motivations of late adolescent and early adult youth affect their actual childbearing across a twenty year period that represents almost all of their reproductive careers. Our theoretical framework links antecedent desires and intentions for both the timing of childbearing and the number of children born to the actual timing of the next child and the final number of children born. Our findings confirm the primary hypothesized pathways from motivational traits to fertility outcomes across the reproductive careers of the study youths. Of considerable interest and importance, these primary pathways are gender neutral in that they are essentially the same for both sexes. However, our findings do reveal that the connecting pathways do vary according to whether or not the youth have already borne one or more children. We have included measures of gender role attitude and educational intentions, and our findings also show how these variables, which reflect lifestyle preferences, affect both the flow of fertility motivations and the reproductive outcomes that they drive.
Our findings underscore the importance of combining timing and number outcomes in the same framework. Demographers struggle constantly to improve their forecast of fertility trends from period fertility rates, which represent a confounding of quantum (birth number) effects with tempo (birth timing) effects (Bongaarts 2002). It seems likely that the inclusion of both child number and timing motivations, which together have helped make our model both successful and meaningful, might fruitfully be employed together in demographic modeling.
The work reported here has been motivated in part by our interest in exploring the extent to which fertility motivations have a biological basis. In spite of long-held beliefs that traits related to reproductive success tend to become fixed by evolution, with little or no genetic variation, there is now considerable evidence that the natural variation of fertility within populations is genetically influenced and that a significant proportion of that influence is related to motivational factors (Rodgers, Hughes, et al. 2001; Rodgers, Kohler, et al, 2001; Kohler et al. 2005). In a companion paper to this one (Miller, Bard, Pasta, and Rodgers 2009), we use the motivational constructs and the model of their relationships presented here to explore the biometric variation of fertility motivation, not in isolation by itself but rather in the context of predicting the actual timing and number of children born.
Footnotes
This study was supported by the National Institutes of Health Grant R01 HD43265. We greatly appreciate the comments of David E. Bard on an earlier version of this manuscript.
Contributor Information
Warren B. Miller, Email: rennie@tfri.org, Transnational Family Research Institute, Aptos, California, 95003-4626. Phone and Fax: 831-662-8440
Joseph Lee Rodgers, Department of Psychology, University of Oklahoma, Norman, OK.
David J. Pasta, DMA Corporation, Palo Alto, CA
References
- Becker GS National Bureau of Economic Research. Demographic and Economic Change in Developed Countries. Princeton: Princeton University Press; 1981. An Economic Analysis of Fertility; pp. 209–231. [Google Scholar]
- Belsky J. Conditional and Alternative Reproductive Strategies: Individual Differences in Susceptibility to Rearing Experiences. In: Rodgers JL, Rowe DC, Miller WB, editors. Genetic Influences on Human Fertility and Sexuality: Theoretical and Empirical Contributions from the Biological and Behavioral Science. Boston: Kluwer; 2000. pp. 127–146. [Google Scholar]
- Bongaarts J. Fertility and Reproductive Preferences in Post-Transitional Societies. In: Bulatao RA, Casterline JB, editors. Global Fertility Transition. New York: Population Council; 2001. pp. 260–281. [Google Scholar]
- Bongaarts J. The End of the Fertility Transition in the Developed World. Population and Development Review. 2002;28(3):419–443. [Google Scholar]
- Bulatao RA. Values and Disvalues of Children in Successive Childbearing Decisions. Demography. 1981;18:1–25. [PubMed] [Google Scholar]
- Center for Human Resources Research. NLS Handbook 2003. Columbus, OH: Center for Human Resource Research; 2003. [Google Scholar]
- Cochrane SH. Fertility and Education: What Do We Really Know? Baltimore: Johns Hopkins University Press; 1979. [Google Scholar]
- Fawcett JT. Perceptions of the Value of Children: Satisfactions and Costs. In: Bulatao RA, Lee RD, editors. Determinants of Fertility in Developing Countries. Vol. 1. New York: Academic Press; 1983. pp. 429–457. [Google Scholar]
- Fawcett JT, Albores S, Arnold F. The Value of Children Among Ethnic Groups in Hawaii: Exploratory Measurements. In: Fawcett JT, editor. The Satisfactions and Costs of Children: Theories, Concepts, and Measures. Honolulu: East-West Center; 1972. pp. 234–259. [Google Scholar]
- Foster C. The Limits to Low Fertility: A Biosocial Approach. Population and Development Review. 2000;26(2):209–234. [Google Scholar]
- Groves RM, Benson G, Mosher WD, et al. Vital Health Statistics. 42. Vol. 1. Washington, DC: National Center for Health Statistics; 2005. Plan and Operation of Cycle 6 of the National Survey of Family Growth. [PubMed] [Google Scholar]
- Hagewen KJ, Morgan SP. Intended and Ideal Family Size in the United States, 1970–2002. Population and Development Review. 2005;31(3):507–527. doi: 10.1111/j.1728-4457.2005.00081.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hakim C. A New Approach to Explaining Fertility Patterns: Preference Theory. Population and Development Review. 2003;29(3):349–374. [Google Scholar]
- Johnson A, Rodgers JL. The impact on the lives of women of having children: The effects of children questionnaire. Journal of Applied Social Psychology. 2006;36(11):2685–2714. [Google Scholar]
- Joreskog KG, Sorbom D. LISREL 8: User’s Reference Guide. Chicago, IL: Scientific Software International; 1996 . [Google Scholar]
- Kohler H-P, Rodgers JL. Education, Fertility, and Heritability: Explaining a Paradox. In: Wachter KW, Bulatao RA, editors. Offspring: Human Fertility Behavior in Biodemographic Perspective. Washington: National Academies Press; 2003. pp. 46–90. [PubMed] [Google Scholar]
- Kohler HP, Rodgers JL, Miller WB, Skytthe A, Christensen K. Bio-Social Determinants of Fertility. International Journal of Andrology. 2005;29:46–53. doi: 10.1111/j.1365-2605.2005.00606.x. [DOI] [PubMed] [Google Scholar]
- McClelland GH. Family Size Desires as Measures of Demand. In: Bulatao RA, Lee RD, editors. Determinants of Fertility in Developing Countries. Vol. 1. New York: Academic Press; 1983. pp. 288–343. [Google Scholar]
- Miller WB. The Psychology of Reproduction. Washington: National Technical Information Service; 1981. [Google Scholar]
- Miller WB. Proception: Important Fertility Behavior. Demography. 1986;23:579–594. [PubMed] [Google Scholar]
- Miller WB. Personality Traits and Developmental Experiences as Antecedents of Childbearing Motivation. Demography. 1992;29:265–285. [PubMed] [Google Scholar]
- Miller WB. Childbearing Motivations, Desires, and Intentions: A Theoretical Framework. Genetic, Social, and General Psychological Monographs. 1994;120:223–258. [PubMed] [Google Scholar]
- Miller WB. Childbearing Motivation and Its Measurement. Journal of Biosocial Science. 1995;27:473–485. doi: 10.1017/s0021932000023087. [DOI] [PubMed] [Google Scholar]
- Miller WB, Bard DE, Pasta DJ, Rodgers JL. Biodemographic Modeling of the Links between Fertility motivation and fertility Outcomes in the NLSY79. Submitted for publication. 2009 doi: 10.1353/dem.0.0107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller WB, Pasta DJ. Motivational and Nonmotivational Determinants of Child-Number Desires. Population and Environment. 1993;15:113–138. [Google Scholar]
- Miller WB, Pasta DJ. The Psychology of Child Timing: A Measurement Instrument and a Model. Journal of Applied Social Psychology. 1994;24:221–250. [Google Scholar]
- Miller WB, Pasta DJ. How Does Childbearing Affect Fertility Motivations and Desires? Social Biology. 1995a;42:185–198. doi: 10.1080/19485565.1995.9988900. [DOI] [PubMed] [Google Scholar]
- Miller WB, Pasta DJ. Behavioral Intentions: Which Ones Predict Fertility Behavior in Married Couples? Journal of Applied Social Psychology. 1995b;25:530–555. [Google Scholar]
- Miller WB, Pasta DJ. The Relative Influence of Husbands and Wives on the Choice and Use of Oral Contraception, a Diaphragm, and Condoms. Journal of Applied Social Psychology. 1996;26:1749–1774. [Google Scholar]
- Miller WB, Pasta DJ. The Motivational Substrate of Unintended and Unwanted Pregnancy. Journal of Applied Biobehavioral Research. 2002;7:1–29. [Google Scholar]
- Miller WB, Rodgers JL. The Ontogeny of Human Bonding Systems: Evolutionary Origins, Neural Bases, and Psychological Manifestations. Boston: Kluwer; 2001. [Google Scholar]
- Miller WB, Rodgers JL, Pasta DJ. Modeling the links between fertility motivations and fertility outcomes: A prospective analysis of NLSY data. 2008 www.tfri.org.
- Miller WB, Severy LJ, Pasta DJ. A Framework for Modeling Fertility Motivation in the Dyad. Population Studies. 2004;58:193–205. doi: 10.1080/0032472042000213712. [DOI] [PubMed] [Google Scholar]
- Morgan SP. Parity-Specific Fertility Intentions and Uncertainty: The United States, 1970–1976. Demography. 1982;19:315–334. [PubMed] [Google Scholar]
- Morgan SP. Should Fertility Intentions Inform Fertility Forecasts? In: Spencer GK, editor. Proceedings of US Census Bureau Conference: The Direction of Fertility in the United States. Washington: U.S. Census Bureau; 2001. pp. 153–178. [Google Scholar]
- Namboodiri NK. Which Couples at Given Parities Expect to Have Additional Births? An Exercise in Discriminant Analysis. Demography. 1974;11:45–56. [PubMed] [Google Scholar]
- Namboodiri NK. Sequential Fertility Decision-Making and the Life Course. In: Bulatao RA, Lee RD, editors. Determinants of Fertility in Developing Countries. Vol. 2. New York: Academic Press; 1983. pp. 444–472. [Google Scholar]
- Potts M. Sex and the Birth Rate: Human Biology, Demographic Change, and Access to Fertility Regulation Methods. Population and Development Review. 1997;23:1–39. [Google Scholar]
- Rindfuss RR, Morgan SP, Swicegood G. First Births in America: Changes in the Timing of Parenthood. Berkeley: University of California Press; 1988. [DOI] [PubMed] [Google Scholar]
- Rodgers JL, Doughty D. Genetic and Environmental Influences on Fertility Expectations and Outcomes Using NLSY Kinship Data. In: Rodgers JL, Rowe DC, Miller WB, editors. Genetic Influences on Human Fertility and Sexuality: Theoretical and Empirical Contributions from the Biological and Behavioral Sciences. Boston: Kluwer; 2000. pp. 85–106. [Google Scholar]
- Rodgers JL, Hughes K, Kohler HP, Christensen K, Doughty D, Rowe D, Miller WB. Genetic Influence Helps Explain Variation in Fertility Outcomes: A Review of the Recent Behavioral and Molecular Genetic Literature. Current Directions in Psychological Science. 2001;10:184–188. [Google Scholar]
- Rodgers JL, Kohler HP, Kyvik K, Christensen K. Behavior genetic modeling of human fertility: Findings from a contemporary Danish twin study. Demography. 2001;38:29–42. doi: 10.1353/dem.2001.0009. [DOI] [PubMed] [Google Scholar]
- Ryder NB, Westoff CF. Reproduction in the United States 1965. Princeton: Princeton University Press; 1971. [Google Scholar]
- Scanzoni JH. Sex Roles, Life Styles, and Childbearing. New York: The Free Press; 1975. [Google Scholar]
- Trent RB. Evidence Bearing on the Construct Validity of “Ideal Family Size”. Population and Environment. 1980;3:309–327. [Google Scholar]
- Westoff CF, Ryder NB. The Predictive Validity of Reproductive Intentions. Demography. 1977;14:431–453. [PubMed] [Google Scholar]
- Willis RJ. A New Approach to the Economic Theory of Fertility Behavior. Journal of Political Economics. 1973;81:514–569. [Google Scholar]