Significant blood resistance to nitric oxide transfer in the lung

Abstract

Lung diffusing capacity for nitric oxide (Dl_NO) is used to measure alveolar membrane conductance (Dm_NO), but disagreement remains as to whether Dm_NO = Dl_NO, and whether blood conductance (θ_NO) = ∞. Our previous in vitro and in vivo studies suggested that θ_NO < ∞. We now show in a membrane oxygenator model perfused with whole blood that addition of a cell-free bovine hemoglobin (Hb) glutamer-200 solution increased diffusing capacity of the circuit (D) for NO (Dno) by 39%, D for carbon monoxide (Dco) by 24%, and the ratio of Dno to Dco by 12% (all P < 0.001). In three anesthetized dogs, Dl_NO and Dl_CO were measured by a rebreathing technique before and after three successive equal volume-exchange transfusions with bovine Hb glutamer-200 (10 ml/kg each, total exchange 30 ml/kg). At baseline, Dl_NO/Dl_CO = 4.5. After exchange transfusion, Dl_NO rose 57 ± 16% (mean ± SD, P = 0.02) and Dl_NO/Dl_CO = 7.1, whereas Dl_CO remained unchanged. Thus, in vitro and in vivo data directly demonstrate a finite θ_NO. We conclude that the erythrocyte and/or its immediate environment imposes considerable resistance to alveolar-capillary NO uptake. Dl_NO is sensitive to dynamic hematological factors and is not a pure index of conductance of the alveolar tissue membrane. With successive exchange transfusion, the estimated in vivo θ_NO [5.1 ml NO·(ml blood·min·Torr)⁻¹] approached 4.5 ml NO·(ml blood·min·Torr)⁻¹, which was derived from in vitro measurements by Carlsen and Comroe (J Gen Physiol 42: 83–107, 1958). Therefore, we suggest use of θ_NO = 4.5 ml NO·(min·Torr·ml blood)⁻¹ for calculation of Dm_NO and pulmonary capillary blood volume from Dl_NO and Dl_CO.

nitric oxide (NO), in combination with carbon monoxide (CO), has been used to measure gas transfer in the lung since the 1980s (5, 11, 30, 31). Similar to CO, NO combines with high affinity to hemoglobin (Hb), but, in contrast to CO, the rate of combination is ∼250 times faster (5, 12), so that the lung diffusing capacity for NO (Dl_NO) is a measure of diffusive gas conductance independent of chemical reaction. Lung transfer of a gas that combines with Hb can be described by the equation of Roughton and Forster (25), which was originally applied to CO

$$\frac{1}{{\text{D}}_{\text{L}}}=\frac{1}{{\text{D}}_{\text{M}}}+\frac{1}{\mathrm{\Theta }{\text{V}}_{\text{C}}}$$ (1)

where Dl is conductance across the lung and Dm is alveolar membrane conductance [ml gas·(min·Torr)⁻¹], θ is the rate of combination of gas (ligand) with erythrocyte [ml gas·(ml blood·min·Torr)⁻¹], and Vc is the pulmonary capillary blood volume (in ml). The left-hand term (1/Dl) represents the overall resistance to lung gas transfer, and the right-hand terms represent the resistance of the membrane (1/Dm) and the resistance of pulmonary capillary blood (1/θVc). The equation for 1/θ contains a term for diffusion resistance (a) and a term for chemical reaction resistance (b); both terms are hematocrit-dependent. Roughton and Forster exploited this and calculated Dm and Vc by measuring Dl at several Po₂ levels and applying known values for θ_CO derived from in vitro measurements using a rapid-reaction apparatus (25, 26). On the basis of their experiments in healthy adult men, resistance of the membrane was approximately equal to resistance of blood. Guenard et al. (11) assumed that since the reaction of NO with Hb is effectively infinite, θ_NO must be infinite; therefore, Dl_NO = Dm_NO ≈ 2 Dm_CO, since the ratio of diffusion of NO to diffusion of CO is directly proportional to the ratio of their respective solubility coefficients (α) and inversely proportional to the ratio of the square root of their molecular weights (MW)

$$\frac{{\text{DL}}_{\text{NO}}}{{\text{DM}}_{\text{CO}}}=\frac{{\text{DM}}_{\text{NO}}}{{\text{DM}}_{\text{CO}}}=\frac{{\alpha }_{\text{NO}}\sqrt{{\text{MW}}_{\text{CO}}}}{{\alpha }_{\text{CO}}\sqrt{{\text{MW}}_{\text{NO}}}}\approx 2$$ (2)

Implicit in their assumption is that resistance of the erythrocyte membrane, its interior, and the immediately surrounding plasma is negligible. With this assumption, Eq. 1 can be solved from simultaneous measurements of Dl_CO and Dl_NO in a single maneuver and with a known value of θ_CO. The values for Dm and Vc obtained in this way were close to those obtained via Dl_CO measured at two levels of Po₂ (24, 30). Combined Dl_NO-Dl_CO measurement offered a rapid way of obtaining Dm and Vc in a variety of clinical situations, obviating the need for multiple Dl_CO measurements.

However, disagreement soon arose as to whether Dl_NO = Dm_NO (1, 4). The in vitro maximum rate constant of NO binding is 500–1,000 times faster with free Hb solution (2 × 10⁵ M⁻¹·s⁻¹) than with red blood cells (12, 33), suggesting the presence of intrinsic transmembrane or intracellular properties of the erythrocyte that limit NO uptake. In 1958, using a rapid-reaction apparatus, Carlsen and Comroe (6) measured in vitro NO reaction with human erythrocytes and found a second-order rate constant for erythrocytes (j′c) of 167 mM⁻¹·s⁻¹, from which θ_NO = 4.5 ml NO·(min·Torr·ml blood)⁻¹ at Hb = 14.6 g/dl can be derived (3, 4), i.e., substantially less than infinity. To address this issue, we used a membrane oxygenator model primed with horse blood to measure in vitro NO transfer (Dno) and eliminated red cell resistance by water-induced hemolysis (2). In this model, hemolysis was accompanied by a rise in Dno, suggesting that red cell resistance to NO transfer was finite, i.e., Dno < Dm_NO. Water-induced hemolysis is impracticable in laboratory animals or isolated lung preparations, inasmuch as it disrupts the endothelium and epithelium, immediately altering in vivo Dm. However, a cell-free heme-based blood substitute (bovine Hb glutamer-200) is approved for canine clinical use (13, 14). In this study, we first progressively added bovine Hb glutamer-200 in the membrane oxygenator and examined its effect on Dno, comparing it with in situ hemolysis and with hemolyzed red blood cells. Then we progressively replaced whole blood in anesthetized dogs with bovine Hb glutamer-200 and examined the effect on Dl_NO. We reasoned that if resistance of the blood to NO were significant, in vitro Dno and in vivo Dl_NO would increase progressively as erythrocytes are “bypassed” by replacement with cell-free Hb.

METHODS

In Vitro Experiments

Membrane oxygenator circuit.

Our circuit is described in detail elsewhere (2, 9). Briefly, two membrane oxygenators (Cobe Duo CML, Cobe Cardiovascular, Arvada, CO) were connected in series to form a continuous circuit perfused with 1–1.5 liters of horse blood (TCS Biosciences, Buckingham, UK) with hematocrit of 40–50% depending on batch and flowing at 2.5 l/min and 37°C. One oxygenator received a gas flow of 2.5 liters of a mixture of 22% O₂, 0.02% CO, 5 parts per million (ppm) NO, and the remainder N₂; the second oxygenator scrubbed the oxygenated blood with 8.3% CO₂ in N₂. In this way, near-physiological levels of O₂, CO₂, and pH were maintained over several hours in a steady state without apparent hemolysis (9).

Diffusing capacity measurements.

Dno and Dco were measured from the difference in gas concentrations leaving and entering the first oxygenator as follows (2)

$${\text{D}}_{\text{NO}}=\text{gas}\hspace{0.17em}\text{flow}\hspace{0.17em}\text{rate}·\frac{273}{\left(273+\text{Temp}\right)\left[{\text{P}}_{\text{B}}-\left({\text{P}}_{{\text{H}}_{\text{2}}\text{O}}·\text{RH}\right)\right]}·\text{ln}\left(\frac{{\text{NO}}_{\text{in}}}{{\text{NO}}_{\text{out}}}\right)$$ (3)

where Temp is ambient temperature (°C), Pb is barometric pressure (Torr), Ph₂o is saturated water vapor pressure (Torr), RH is relative humidity, and NO_in and NO_out are NO concentrations at the inlet and outlet ports. For CO, the calculations were identical, except CO_in and CO_out were substituted for N_in and N_out.

Addition of blood substitute.

Bovine Hb glutamer-200, a cell-free heme-based blood substitute licensed for canine clinical use (Oxyglobin, Dechra, Overland Park, KS), was added in 25-ml aliquots at 5-min intervals to a total of 250 ml via the oxygenator blood-sampling port, and Dno and Dco were measured after each addition.

Addition of free Hb.

For preparation of Hb, the cells were allowed to separate in a 1-liter bag of horse blood overnight; then the plasma was expressed by a separating clamp. Tap water was added to a total volume of 1 liter to achieve complete hemolysis.

Comparison with hemolysis.

Oxyglobin was added to a total of 250 ml in 25-ml aliquots, and hemolysis was induced by addition of 100-ml aliquots to a total of 700 ml and a potassium concentration >9.5 mmol/l.

Statistical analysis.

Dno was entered as a dependent variable in ANOVA (SPSS version 17.0, SPSS, Chicago, IL). Solution added (Hb or Oxyglobin) was entered as an independent variable, and volume added was entered as a covariate.

Animal Experiments

The Institutional Animal Care and Use Committee at the University of Texas Southwestern Medical Center approved all protocols and procedures. Three purpose-bred adult male foxhounds [28.3 ± 1.0 kg body wt (mean ± SD)] were studied. Circulating blood, plasma, and red cell volumes were determined by the Evans blue dye-dilution method (22) on a separate day before the main study while the animal was awake and at rest.

Anesthesia and catheterization.

The animal was fasted overnight and premedicated with acepromazine (0.2 mg/kg) and glycopyrrolate (0.01 ml/kg) by subcutaneous injection. A peripheral intravenous catheter was inserted. Anesthesia was induced with intravenous propofol and maintained by an infusion of ketamine and diazepam titrated to effect. Additional boluses of propofol (0.3–0.5 mg/kg iv) were administered as needed to maintain deep anesthesia and minimize fluid load. A urinary catheter was placed to monitor fluid balance. The animal was intubated with a cuffed endotracheal tube, placed supine, and mechanically ventilated (model 607, Harvard Apparatus, Millis, MA) at a tidal volume (10–12 ml/kg) and rate (18–24 breaths/min) sufficient to suppress spontaneous ventilation. Transcutaneous O₂ saturation and heart rate were monitored continuously. One external jugular vein was catheterized with an 8.5-French introducer and one femoral artery with a 5-French catheter. Through the jugular introducer, a pulmonary artery catheter was placed, and its position was verified by pressure tracing. The catheters were flushed with heparinized saline and sutured to skin. A balloon-tipped polyethylene catheter was positioned in the distal one-third of the esophagus, and the balloon was inflated with 0.5–1.0 ml of air for measurement of esophageal pressure.

Blood analyses.

Arterial and mixed venous blood samples (3 ml) were drawn, at baseline and on completion of rebreathing maneuvers following each exchange transfusion, for measurement of Hb concentration, conventional blood gases, and O₂ saturation by blood analyzers (models ABL720 and OSM3, Radiometer America, Westlake, OH). The instruments were calibrated for dog blood. Hematocrit was determined using a microcapillary centrifuge.

Pressure-volume curves.

Static pressure-volume curves were measured at the beginning and end of the experiment by stepwise increments and then decrements (15, 30, 45, and 60 ml/kg) of inflation volume delivered using a calibrated syringe from end-expiratory lung volume. Transpulmonary pressure was calculated as the difference between mouth and esophageal pressures. Paired measurements at each volume were averaged.

Rebreathing measurements.

Rebreathing was measured as described elsewhere (19). Briefly, a known volume (45 ml/kg) of test gas mixture containing 0.3% CO, 0.3% methane, 0.8% acetylene, and 40–55 ppm NO in balance of 21% or 99% O₂ was delivered from end-expiratory lung volume via a calibrated syringe and mixed with resident gas in the lung by rebreathing maneuvers for 20 s. Gas concentrations were measured at the end of the endotracheal tube. Concentrations of methane, acetylene, and CO were measured using rapid-response infrared analyzers (Act II S, Sensors, Saline, MI). NO concentration was measured by chemiluminescence (model NOA 280, GE Analytical Instruments, Boulder, CO). Duplicate measurements at each inspired O₂ fraction were averaged. On completion of these procedures, a separate rebreathing maneuver (20 s) was performed while the animal breathed 100% O₂ followed by slow (over 7 s) exhalation, during which alveolar NO concentration was measured. In addition, CO backpressure was measured.

Exchange transfusion.

After baseline measurements, 10 ml/kg of blood was removed via the femoral artery catheter into a collection bag containing citrate-phosphate-dextrose-adenine (CPDA-1, Fenwal, Lake Zurich, IL) and replaced with an equal volume of Oxyglobin solution warmed in a water bath to 37°C and infused via the central venous port. The exchange transfusion took ∼1 h. Then arterial and venous blood analyses and rebreathing measurements were repeated. The exchange transfusion-and-measurement procedure was performed twice more for a total exchange volume of 30 ml/kg. The removed blood was refrigerated.

Recovery.

The catheters were removed, and pressure was applied until bleeding stopped. On the next day, a venous blood sample was collected for measurement of hematocrit and Hb concentration, and a portion (10 ml/kg) of the removed blood was warmed to body temperature and reinfused into the dog via a peripheral vein with use of a blood filter (Baxter, Deerfield, IL). This procedure was performed twice more on consecutive days until all the removed blood had been reinfused.

Data analysis.

Lung volumes were calculated from methane dilution. Pulmonary blood flow was calculated from the logarithmic disappearance of acetylene relative to methane, corrected for the intercept of CO disappearance. Dl_CO and Dl_NO were calculated from end-tidal logarithmic disappearance of CO and NO, respectively, relative to methane (27, 30). Gas exchange septal (tissue + blood) volume was calculated from the extrapolated intercept of the acetylene disappearance curve (28). Dm_CO and Vc were estimated by three methods, each with the assumption of different values of θ_CO or θ_NO (Table 1): 1) by the Roughton-Forster (RF) method (Eq. 1) from DL_CO measured at two alveolar Po₂ (Pa_O2) levels and the θ_CO value given by Holland (18) for canine whole blood incorporating a temperature correction for 39°C and made at pH 7.4 using a stopped-flow apparatus (17), calculated from the mean Pa_O2 during rebreathing and Hb concentration ([Hb])

$$\frac{1}{{\theta }_{\infty }}=\left(0.929+0.00517·{\text{P}}_{{\text{AO}}_{\text{2}}}\right)·\frac{14.6}{\left[\text{Hb}\right]}$$ (4)

2) from simultaneously measured Dl_NO and Dl_CO (NO-CO method) (5, 11) with the assumption that θ_NO = ∞ (Dl_NO = Dm_NO) and an empirical Dl_NO-to-Dm_CO ratio = 2.34 measured in 69 dogs cumulatively studied in our laboratory (unpublished observation), and 3) by the NO-CO method as described above, but with the assumption of a finite θ_NO = 4.5 ml NO·(ml blood·min·Torr)⁻¹ derived from the j′c of Carlsen and Comroe (6) and Dm_CO = Dm_NO/2. Equation 1 was solved for CO and NO in turn using Mathematica software (Wolfram Research, Champaign, IL). This approach gives a solution identical to that previously published (3). These data were expressed as means ± SD and compared before and after exchange transfusion by repeated-measures ANOVA. P < 0.05 was considered significant.

Table 1.

A summary of methods and assumed values for estimating Dm_CO and Vc

Method	1/θCO	DmCO	1/θNO
1) Roughton-Forster (RF)	(0.93 + 0.0052 alveolar Po2) · (14.6/Hb)	Calculated using θCO at 2 alveolar Po2 levels	Not used
2) NO-CO	(0.93 + 0.0052 alveolar Po2) · (14.6/Hb)	= DlNO/2.34	0
3) NO-CO	(0.93 + 0.0052 alveolar Po2) · (14.6/Hb)	= DlNO/2	0.222

Vc, pulmonary capillary blood volume; θ, rate at which gas [carbon monoxide (CO) or nitric oxide (NO)] combines with erythrocytes; Dm_CO, alveolar membrane conductance of CO.

RESULTS

In Vitro Experiments

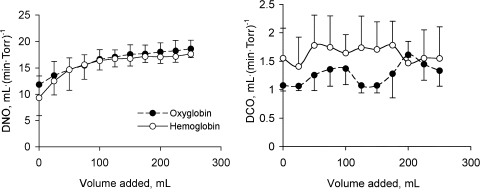
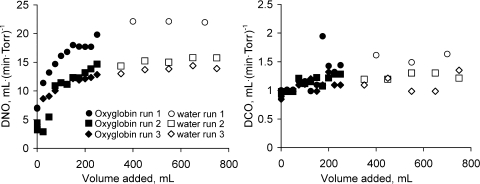
Addition of Oxyglobin to our oxygenator circuit increased Dno from 13.4 ± 0.115 to 18.6 ± 1.659 (SD) ml·(min·Torr)⁻¹ (n = 3, P < 0.001), while Dco increased from 1.075 ± 0.05 to 1.33 ± 0.139 ml·(min·Torr)⁻¹ (n = 3, P = 0.006; Fig. 1). The increase in Dno after addition of Oxyglobin was not significantly different (P = 0.44) from that after addition of hemolyzed free Hb, whereas the mean Dco was significantly greater with Oxyglobin than with free Hb (P = 0.001). No significant further increase in Dno or Dco was observed after hemolysis was induced in the oxygenator circuit (Fig. 2). A highly significant between-run effect was observed for Dno (P < 0.001) and Dco (P = 0.002).

Fig. 1.

In vitro diffusing capacity for nitric oxide (Dno) and carbon monoxide (Dco) measured in the membrane oxygenator model after successive addition of free Hb or bovine Hb glutamer-200 (Oxyglobin) solution. Values are means ± SD of 3 replicate runs.

Fig. 2.

In vitro Dno and Dco measured in the membrane oxygenator model with successive addition of bovine Hb glutamer-200 (Oxyglobin) solution followed by water hemolysis. Individual runs are shown.

In Vivo Experiments

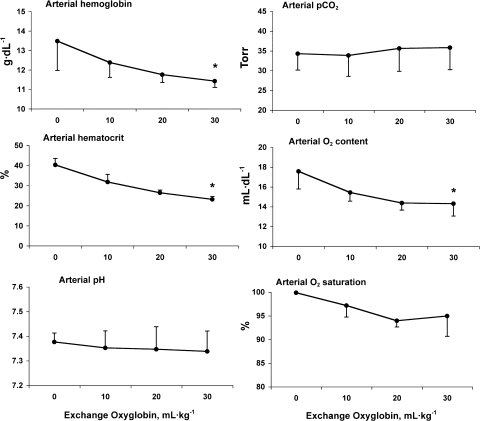
Baseline hematological parameters measured during wakefulness at rest were normal in all three animals [hematocrit = 0.45 ± 0.02, plasma volume = 74.5 ± 6.3 ml/kg, red cell volume = 60.0 ± 6.6 ml/kg, and total blood volume = 134.6 ± 11.5 ml/kg (mean ± SD)]. All animals recovered from exchange transfusion without adverse effects, except for temporary darkening of the mucous membrane and the urine. From baseline to postexchange, pressure-volume curves and systemic and pulmonary arterial blood pressures were unaltered (data not shown). Hematological data and arterial blood gases are shown in Fig. 3. Dl_CO was not corrected for reduction in Hb, since the anticipated alteration was <10%.

Fig. 3.

Blood parameters before and after successive in vivo exchange transfusion with Oxyglobin solution. Values are means ± SD. *P < 0.05 vs. baseline.

As expected, exchange transfusion reduced arterial hematocrit from 40.3 ± 3.3% to 23.2 ± 1.4%. There were also absolute declines in postexchange Hb concentration from 13.5 ± 1.5 to 11.4 ± 0.3 g/dl and in arterial O₂ saturation from 100 ± 0% to 95 ± 4% (P < 0.05) without significant changes in arterial Pco₂ or pH.

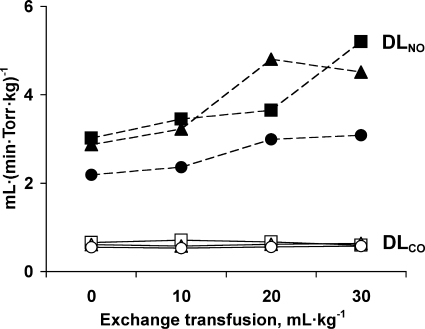
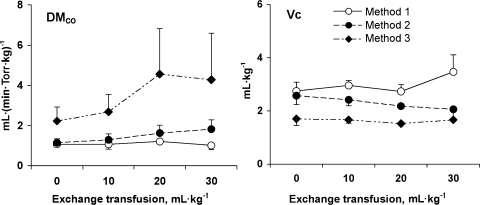
Rebreathing data obtained during 21% O₂ breathing are summarized in Table 2 and Fig. 4. Compared with baseline, Dl_NO increased 59% after exchange transfusion (P = 0.021), while mean Pa_O2, lung volumes, and Dl_CO did not change. With use of Eq. 4 and the assumption that θ_NO = ∞, estimates of Dm_CO by the RF or NO-CO method (methods 1 and 2, respectively, in Table 1) were similar at baseline. As a result of a rising Dl_NO with each exchange transfusion, Dm_CO estimated by method 2 progressively increased, whereas the corresponding Dm_CO estimated by method 1 did not change (Fig. 5, left). In a reciprocal relationship, Vc estimated by method 2 progressively declined with exchange transfusion compared with the corresponding Vc estimated by method 1 (Fig. 5, right).

Table 2.

In vivo data

	Exchange Transfusion, ml/kg
	0	10	20	30	P
Hb, g/dl	13.5 ± 1.5	12.4 ± 0.8	11.8 ± 0.4	11.4 ± 0.3	*
Hematocrit, %	40.3 ± 3.3	31.8 ± 3.8	26.5 ± 1.3	23.2 ± 1.4	*
Mean alveolar Po2, Torr	141 ± 3	141 ± 6	137 ± 7	135 ± 2
Heart rate, beats/min	119 ± 5	107 ± 11	100 ± 22	106 ± 10
Pulmonary blood flow, ml · (min · kg)−1	121 ± 5	114 ± 20	119 ± 18	109 ± 10
End-expiratory lung volume, ml/kg	32 ± 5	32 ± 5	31 ± 5	31 ± 8
End-inspiratory lung volume, ml/kg	84 ± 5	84 ± 4	83 ± 5	83 ± 8
Septal tissue volume, ml/kg	5.10 ± 2.15	4.88 ± 1.84	3.80 ± 1.45	4.30 ± 1.92
DlCO, ml · (min · Torr · kg)−1	0.61 ± 0.05	0.61 ± 0.10	0.61 ± 0.06	0.60 ± 0.03
DlNO, ml · (min · Torr · kg)−1	2.69 ± 0.44	3.01 ± 0.57	3.81 ± 0.92	4.27 ± 1.08	*
	Method 1 (RF)
DmCO, ml · (min · Torr · kg)−1	1.08 ± 0.11	1.07 ± 0.23	1.21 ± 0.10	1.01 ± 0.21
Vc, ml/kg	2.75 ± 0.33	2.96 ± 0.19	2.73 ± 0.26	3.47 ± 0.64	*
	Method 2 (NO-CO, θNO = ∞)
DmCO, ml · (min · Torr · kg)−1	1.15 ± 0.19	1.29 ± 0.29	1.63 ± 0.39	1.82 ± 0.46	*†
Vc, ml/kg	2.57 ± 0.33	2.42 ± 0.22	2.18 ± 0.05	2.06 ± 0.35	*†
	Method 3 (NO-CO, θNO = 4.5)
DmCO, ml · (min · Torr · kg)−1	2.23 ± 0.70	2.68 ± 0.86	4.55 ± 2.28	4.28 ± 2.31	†
Vc, ml/kg	1.70 ± 0.25	1.66 ± 0.12	1.52 ± 0.06	1.66 ± 0.03	†

Values are means ± SD. RF, Roughton-Forster method using θ_CO from Eq. 4. NO-CO method assumes Dl_NO/Dm_CO = 2.34 and θ_NO = ∞ or θ_NO = 4.5. Repeated-measures ANOVA and post hoc Fisher's protected least significant difference:

^*P < 0.05 vs. exchange transfusion;

^†P < 0.05 vs. method 1.

Fig. 4.

In vivo lung diffusing capacity for NO (Dl_NO) in individual animals (closed symbols, dashed lines) rose significantly after successive exchange transfusion with Oxyglobin solution compared with baseline (P < 0.05 by repeated-measures ANOVA), while DL_CO in each animal (open symbols, solid lines) remained unchanged.

Fig. 5.

Membrane diffusing capacity for CO (Dm_CO) and pulmonary capillary blood volume (Vc) estimated by the Roughton-Forster method (method 1), the NO-CO method with the assumption that specific transfer conductance of blood per milliliter for NO (θ_NO) = ∞ (method 2), and the NO-CO method with the assumption that θ_NO = 4.5 ml NO·(ml blood·min·Torr)⁻¹. Values are means ± SD. Estimates by all 3 methods were significantly different from one another by repeated-measures ANOVA (all P < 0.05).

Dm_CO and Vc calculated using different values of θ_NO and θ_CO are given in Table 2, and their comparisons are shown in Table 3. At baseline, methods 1 and 2 (NO-CO assuming θ_NO = ∞) yielded similar estimates of Dm_CO and Vc. Method 3 [NO-CO assuming θ_NO = 4.5 ml NO·(ml blood·min·Torr)⁻¹] approximately doubled the estimated Dm_CO and halved the estimated Vc compared with method 2. With successive exchange transfusions, estimates of Dm_CO and Vc by method 1 remained relatively stable until 30 ml/kg of blood had been exchanged. In contrast, method 2 yielded progressively increasing values of Dm_CO and declining values of Vc with each exchange transfusion. Method 3 also yielded increasing values of Dm_CO with exchange transfusion, while the estimates of Vc were more stable.

Table 3.

Comparison of methods

	Exchange Transfusion, ml/kg
	0	10	20	30
DlNO/DlCO	4.44 ± 0.40	4.94 ± 0.54	6.22 ± 1.38	7.07 ± 1.68*‡
	NO-CO method using different θNO (method 3/method 2)
DmCO θNO4.5/θNO∞	1.90 ± 0.33	2.04 ± 0.31	2.68 ± 0.71	2.53 ± 0.75
Vc θNO4.5/θNO∞	0.66 ± 0.03	0.69 ± 0.03	0.72 ± 0.04	0.74 ± 0.02*†

Values are means ± SD. Repeated-measures ANOVA and post hoc Fisher's protected least significant difference:

^*P < 0.05 vs. 0 ml/kg;

^†P < 0.05 vs. 20 ml/kg;

^‡P < 0.05 vs. 10 ml/kg.

Using the in vivo data (Table 2) and applying Eq. 1 to NO and CO individually (rearranged in Eq. 5), we may estimate the likely range of θ_NO values

$${\theta }_{\text{NO}}={\theta }_{\text{CO}}\times \left(1/{\text{DL}}_{\text{CO}}-1/{\text{DM}}_{\text{CO}}\right)/\left(1/{\text{DL}}_{\text{NO}}-1/{\text{DM}}_{\text{NO}}\right)$$ (5)

At baseline, Dl_CO = 0.61 and Dl_NO = 2.69 ml·(min·Torr)⁻¹. Since Dm_CO = 0.5 Dm_NO, 1/Dm_CO = 2/Dm_NO. θ_CO was calculated at 141 Torr arterial Po₂ (Table 2) = 0.6 ml CO·(ml blood·min·Torr)⁻¹. With the assumption that with each successive exchange transfusion the measured Dl_NO (line 10, Table 2) more closely approximates true conductance of the tissue membrane (Dl_NO → Dm_NO), in vivo θ_NO values were as follows: 0.6 × (1/0.61 − 2/3.01)/(1/2.69 − 2/3.01) = 14.8, 0.6 × (1/0.61 − 2/3.81)/(1/2.69 − 2/3.81) = 6.1, and 0.6 × (1/0.61 − 2/4.27)/(1/2.69 − 2/4.27) = 5.1 ml NO·(ml blood·min·Torr)⁻¹ after 10, 20, and 30 ml/kg exchange, respectively; i.e., with each exchange, the in vivo θ_NO declined in a nonlinear fashion toward the in vitro value of 4.5 ml NO·(ml blood·min·Torr)⁻¹ (4).

DISCUSSION

Summary of Findings

In vitro and in vivo replacement of whole blood with hemolyzed blood and a cell-free Hb solution (Oxyglobin) caused Dl_NO to increase progressively, suggesting that Dm_NO exceeds Dl_NO. The final value achieved using Oxyglobin in vitro is identical to that after hemolysis. The cell-free Hb solution penetrates the plasma surrounding the erythrocytes and between the erythrocytes and the endothelial layer; it reduces blood resistance by “bypassing” the erythrocyte membrane and interior and increases the effective surface area of tissue membrane available for gas exchange by allowing all perfused tissue surfaces to directly contact Hb. On the basis of our data, it is almost certain that θ_NO in vitro and in vivo is substantially less than infinity; the true in vivo θ_NO is probably close to the in vitro estimate of 4.5 ml NO·(ml blood·min·Torr)⁻¹ given the results from Eq. 5. The only (and unlikely) alternative explanation would be the presence of a periendothelial plasma layer that offered the sole blood resistance to NO transfer. Estimates of Dm_CO and Vc obtained by the combined NO-CO methods (methods 2 and 3) are highly sensitive to the addition of cell-free Hb, while estimates obtained by the RF method (method 1) are relatively insensitive, because the former use Dl_NO in their calculation. Dl_NO increases with exchange transfusion.

Critique of Methods

Although the in vitro post-Oxyglobin, post-hemolyzed blood, and post-Oxyglobin posthemolysis values of Dno are similar, they are appreciably lower than those reported in our previous work (2). The marked between-run variation observed on the same day with blood from a single horse shows that the variation is between oxygenators.

Oxyglobin does not cause hemolysis (14), and repeated administration over 1 yr caused no adverse physiological effects in dogs (13). The Hb content of Oxyglobin (13 g/dl) is similar to that of baseline canine blood under anesthesia (13.5 g/dl). After equal volume exchanges of blood with the Hb solution, arterial Hb concentration progressively declined to 11.4 g/dl, likely because of the known plasma-expanding effect of Oxyglobin. We followed the clinical slow-infusion protocol (10 mg/kg over 1 h) up to the recommended maximum (30 mg/kg total) to minimize, but not eliminate, the effect. Hemodilution would have reduced Dl_CO more than Dl_NO, because the blood resistance to CO transfer is greater than that to NO transfer.

A small decrease in Dl_CO due to hemodilution could have offset a small expected increase in Dl_CO because of reduced erythrocyte diffusion resistance with Oxyglobin, thereby explaining why in vitro Dco increased with exchange transfusion but in vivo Dl_CO did not. In the oxygenator, Dco increased more with blood replacement by Oxyglobin than with blood replacement by lysed blood; given the predominant reaction dependence of Dco, this likely reflects a slower reaction rate of CO with free Hb in lysed blood than with Oxyglobin. We have no in vitro data for the reaction kinetics of CO or NO with Oxyglobin. Using the oxygenator, we observed a considerably higher Dno-to-Dco ratio than was observed in vivo (Dl_NO-to-Dl_CO ratio); the difference has been discussed previously (2) and attributed to the design of the multipore membrane, where gas directly contacts a thin boundary layer of blood, resulting in a higher Dm-to-Vc ratio in the oxygenator than in the lung.

There was a modest reduction in arterial and mixed venous O₂ saturation with exchange transfusion, consistent with a rightward shift of the O₂ dissociation curve caused by Oxyglobin [Po₂ necessary to obtain 50% O₂ saturation of Hb (P₅₀) = 34 Torr] (8). We observed a similar rightward shift when using the oxygenator (Dunningham and Borland, unpublished observations).

Estimation of Dm and Vc by the NO-CO method requires knowledge of the Dm_NO-to-Dm_CO ratio, which theoretically is ∼2 (Eq. 2). Experimentally, we observed Dl_NO/Dm_CO = 2.42 in healthy human subjects and 2.24 in patients with pulmonary sarcoidosis (24, 30). The empirical value in dogs (2.34) is within this range. This variability in the Dl_NO-to-Dm_CO ratio per se makes little difference to method 2, which assumes Dl_NO = Dm_NO. If we assumed a ratio of 2.42, instead of 2.34, the estimated Dm_CO would be only 3.4% lower and the estimated Vc would be 3.1% higher. With the assumption that θ_NO is infinite, the empirical Dm_NO-to-Dm_CO ratio (2.24–2.42) is modestly (12–20%) higher than the theoretical value. This difference may be explained by the range of θ_CO values given in the literature, which easily causes a 20% variation in the estimated Dm_CO. Other possible explanations have been discussed previously (24). 1) The NO solubility coefficient may be higher in plasma than in water. 2) Facilitated NO diffusion may occur in plasma; NO interacts with sulfhydryl groups in plasma lipids and proteins and can be transported as S-nitrosothiols.

Relative Resistance of Tissue and Erythrocyte Membranes

From Table 2, the baseline and postexchange transfusion Dl_CO values [0.61 and 0.60 ml·(min·Torr·kg)⁻¹, respectively] may be used in conjunction with Dm_CO [1.08 and 1.01 ml·(min·Torr·kg)⁻¹, respectively] obtained by method 1 to estimate the percentage of in vivo resistance to CO uptake (1/Dl_CO) due to resistance of the tissue-plasma-erythrocyte diffusion barrier (1/Dm_CO), i.e., 100 × Dl_CO/Dm_CO. At baseline, the combined barrier resistance was (100 × 0.61/1.08) = 56% of total CO resistance. After exchange transfusion, the barrier resistance was (100 × 0.60/1.01) = 59% of total CO resistance. These values agree with previous estimates showing about equal diffusion and reaction limitation for CO uptake (20). Exchange of erythrocytes for cell-free Hb contributed little (3%) to overall CO resistance. For NO uptake, 1/Dl_{NO pre} = membrane + red cell resistance, while 1/DL_{NO post} = membrane resistance only; mean values of Dl_NO before and after exchange transfusion were 2.69 and 4.27 ml·(min·Torr·kg)⁻¹, respectively (Table 2). Thus

$$=100\times \frac{\left(\frac{1}{{\text{DL}}_{\text{NOpre}}}-\frac{1}{{\text{DL}}_{\text{NOpost}}}\right)}{\frac{1}{{\text{DL}}_{\text{NOpre}}}}=\left(1-\frac{{\text{DL}}_{\text{NOpre}}}{{\text{DL}}_{\text{NOpost}}}\right)=\left(1-\frac{2.69}{4.27}\right)\times 100=37\%$$ (6)

This value (37%) represents a lower-limit underestimation of true erythrocyte-related barrier resistance in alveolar capillaries, since only a fraction of erythrocytes was removed.

Values for θ_CO

The initial justification for the veracity of the NO-CO method (method 2) used by Guenard et al. (11) was the apparent agreement between values for Dm and Vc obtained by their method and by the traditional RF method (method 1) using the θ_CO values given by Roughton and Forster (25) as 1/θ_CO = a + b·Pa_O2 = 0.34 + 0.0061·Pa_O2. Until now, the greatest challenge to their method came from Robert E. Forster himself (10). He acknowledged that the earlier θ_CO value had been obtained at pH 7.8–8.0 and, in 1987, repeated the measurements in red blood cells from five normal individuals at pH 7.4 and 37°C obtaining a new relationship: 1/θ_CO = a + b·Pa_O2 = 1.3 + 0.0041·Pa_O2. Using the 1987 value, instead of the 1957 value, of θ_CO gives a 36% lower value for Vc and a twofold greater Dm_CO in normal adult subjects (20), an observation also made by others (35). These later values no longer agree with those obtained from the NO-CO method (method 2) with the assumption that θ_NO = ∞.

DL_NO and Hb

One way to determine whether θ_NO is infinity or less might be to examine the effect of altering Hb concentration, which might alter θ_NO, were it less than infinity, while leaving Dm and Vc unchanged. However, clinical studies involving patients with anemia have yielded conflicting results (1, 23, 32) at least partly attributed to the difficulty of selectively altering θ without altering Dm and Vc in pathological states. For example, patients with renal failure, especially those undergoing dialysis, will have permanent or temporary alteration in Dm and Vc. Because Dm is intrinsically “coupled” to Vc (20), it will vary as Vc varies (3). Furthermore, clinical alterations in Hb may not be sufficient to allow the effect of θ to be dissected out from other changes. Because the membrane oxygenator is a rigid structure, we were not only able to alter Hb without changing Vc or Dm, but we were also able to alter Hb 1,000% between 1 and 10 g/dl (2).

There is also a fundamental chemical kinetic reason why θ_NO may be less than infinity and yet independent of hematocrit. θ derives from the rate constant for the reactions of Hb and ligands. For NO, the reaction is second order: d[NO]/dt = j′[NO][HbO₂]. Roughton and Forster and colleagues extended chemical kinetic theory to red blood cells in vitro and in vivo, so that the reaction for NO becomes d[NO]/dt = j′c[NO][HbO₂], where j′c is the second-order rate constant for red blood cells (167 l·mmol⁻¹·s⁻¹), which equates to θ_NO = 4.5 ml NO·(ml blood·min·Torr)⁻¹ (4). There are good grounds for thinking that this reaction could be zero-order with respect to Hb and, therefore, just pseudo-first-order for NO. If the Hb concentration is great compared with NO concentration, then so few binding sites would be used in the reaction that altering Hb concentration would have little effect on reaction rate. Inhaling 40 ppm NO gives a plasma concentration of 2.5 × 10⁻⁹ M compared with 9 × 10⁻³ M for Hb concentration; i.e., Hb is greatly in excess. This argument assumes that the Hb is well mixed in solution. If Hb is packaged in red blood cells and there is an advancing front effect (20), then the effective Hb concentration would be much smaller. Nevertheless, pseudo-first-order kinetics could explain why some clinical studies (32) found no effect of Hb on Dl_NO.

True Values for θ_NO

An apparent inconsistency in the approach of Guenard et al. (11) (method 2) was to accept the earlier θ_CO value in the RF method (25) but reject the data of Carlsen and Comroe (6), which gave a finite value for θ_NO obtained in the same laboratory using the same continuous-flow rapid-reaction apparatus. Their approach may not be as illogical as it first appears: the values for θ_CO and θ_NO may be underestimated unpredictably by diffusion limitation in stagnant layers in the apparatus. This effect is likely to be greater for NO, since it is exclusively diffusion limited, in contrast to CO, which is equally reaction and diffusion limited. The stagnant layer effects are likely to be less in the continuous-flow than in the stopped-flow apparatus. In support of the approach of Guenard et al. (method 2), indirect estimates of θ_NO using thin layers of blood are significantly higher than that reported by Carlsen and Comroe; Heller and Schuster (16) used a value of 14 ml NO·(ml blood·min·Torr)⁻¹, which appears to have been calculated from (θ_O2 = 9.2) obtained from Heidelberger and Reeves (15) by multiplying by the ratio of water solubilities (α_NO/α_O2) and Krogh diffusion constants (k_NO/k_O2), although we obtain a higher value: 9.2 × 0.041/0.021 × 1.76 = 27.7 ml NO·(ml blood·min·Torr)⁻¹. Chakraborty et al. (7), using computer simulation to eliminate the stagnant layer effect, report θ_NO = 4.2 × 10⁶ ml NO·(ml blood·min·Torr)⁻¹! This raises the counterargument that stagnant layers could well be present in alveolar capillaries in vivo, a possibility that Hughes and Bates (20) emphasize strongly. Indeed, if, as suggested by this and our previous work (2, 4), θ_NO approximates 4–5 ml NO·(ml blood·min·Torr)⁻¹, then the thin film work (15) supports the argument that the major resistance to red cell-associated NO diffusion lies immediately adjacent to, rather than within, the cell or its membrane. This fits in neatly with recent work examining Hb and red cell effect on vasoconstriction and the effect of chemically and physically altering the red cell membrane and observing red cell NO uptake (21). These experiments point to diffusion limitation of NO in vivo by a cell-free zone along the endothelium, an unstirred layer around the red blood cell, and, finally, the red cell membrane itself (21). The respective contribution of these three barriers remains in dispute.

Taken together, our in vitro experiments favor the red cell membrane and its surrounding layer as a major source of the diffusion resistance to NO. Reducing hematocrit will proportionately increase plasma and reduce red cell surface area by approximately (hematocrit)^2/3. Although we found a statistically significant relationship between 1/Hb and 1/Dno in vitro, there was little change in Dno above Hb ∼4 g/dl. By contrast, the effect of hemolysis and bypassing the red cell membrane using Oxyglobin is striking. One way to circumvent some of these difficulties is to consider the entire diffusion barrier from air-tissue-plasma-erythrocyte to intracellular Hb as a single dynamic resistance (1/Db), measured as 1/Dno, separate from the chemical reaction rate with Hb; then the latter becomes the empirically measured gas uptake by 1 ml of free Hb solution at a given concentration (θ_Hb), i.e., 1/Dl = 1/Db + 1/(θ_Hb·Vc). This approach assumes similar chemical reaction kinetics between free extra- and intraerythrocyte Hb; this assumption may or may not be true (29) and requires further examination.

Use of Blood Substitutes

It is increasingly clear that the “encapsulation” of Hb within erythrocytes markedly slows NO scavenging by heme-binding sites, allowing NO to act as a vasodilator “downstream.” Cell-free heme-based blood substitutes accelerate removal of NO, risking local vasoconstriction and potentially limiting their application (34). This work should encourage the development of encapsulated heme-based blood substitutes, and our oxygenator circuit could be used to test the NO-scavenging properties of blood substitutes.

Implication for Clinical Use of Dl_NO

All the recent reports of Dl_NO have assumed θ_NO to be infinite and used Dl_NO as a pure and direct measure of membrane conductance, i.e., unaffected by any diffusive resistance associated with capillary erythrocytes. Our findings showed this assumption to be untrue: 1/Dl_NO is 37% erythrocyte resistance and 63% nonerythrocyte resistance. Caution is warranted when interpreting isolated Dl_NO measurements. Reconciling the different methods and θ values remains challenging. Method 1 (the RF method) yields stable estimates of Dm and Vc during exchange transfusion until 30 ml/kg of blood has been exchanged. Method 2 yields Dm and Vc that change in opposite directions with exchange transfusion. Method 3 yields relatively stable estimates of Vc, whereas Dm increases with exchange transfusion. The important point is to ensure internal consistency within a given study. On the basis of current data, when calculating Dm_NO and Vc from Dl_NO and Dl_CO, we recommend the use of θ_NO = 4.5 ml NO·(min·Torr·ml blood)⁻¹.

Red cell dependence also raises the following question: Should Dl_NO be adjusted for Hb concentration? With use of the finite θ_NO = 4.5, Dm_NO = 4.27 ml·(min·Torr·kg)⁻¹, and Vc = 1.7 ml/kg, substituting in Eq. 1 the reduction in Dl_NO is ∼0.1 ml·(min·Torr·kg)⁻¹ per (g/dl) until Hb <8 g/dl. Therefore, a Hb correction is not needed in routine clinical practice.

GRANTS

This research was supported by National Heart, Lung, and Blood Institute Grants R01 HL-040070, HL-054060, and HL-062873.

DISCLAIMER

The contents of this article are solely the responsibility of the authors and do not necessarily represent the official views of the National Heart, Lung, and Blood Institute or of the National Institutes of Health.

DISCLOSURES

No conflicts of interest are declared by the author(s).