Abstract
Regional blood flow in the lung is known to be influenced by the alveolar Pco2 and alveolar Po2. For the healthy lung, the extent to which this influence is of functional importance in limiting heterogeneity in alveolar gas composition by matching regional perfusion (q̇) to regional ventilation (v̇) remains unclear. To address this issue, the efficiency of regulation (E) was defined as the percent correction to an initial perturbation in regional alveolar gas composition generated by the pulmonary vascular response to the disturbance. This study develops the theory to calculate E from global measurements of vascular reactivity to CO2 and O2 in human volunteers. For O2, these data were available from the literature. For CO2, an experimental component of the present study used Doppler echocardiography to evaluate the magnitude of the global vascular response to hypercapnia and hypocapnia in 12 volunteers over a timescale of ∼0.5 h. The results suggest a value for E of ∼60% over a wide range of values for v̇-to-q̇ ratio (∼0.1–10) encompassing those found in normal lung. At low v̇/q̇ (<0.65), the vascular response to O2 forms the dominant mechanism; however, at higher v̇/q̇ (>0.65), the response to CO2 dominates. The values for E suggest that the pulmonary vascular responses to both CO2 and O2 play a significant role in ventilation-perfusion matching in the healthy human lung.
Keywords: carbon dioxide, oxygen, pulmonary circulation, ventilation perfusion matching
regional blood flow in the lung is known to be influenced by experimental manipulations of the alveolar Po2 (PaO2) and alveolar Pco2 (PaCO2) (4). However, it remains uncertain whether these responses play any significant role in correcting for mismatches of perfusion to ventilation arising during normal daily activities that change ventilation and/or posture as well as during pathological processes such as acute lung injury (24). In this study, our general aim was to develop the theory necessary to link global measurements of vascular reactivity to PaCO2 and PaO2 in humans with some measure of their expected influence on ventilation-perfusion matching within the healthy lung.
The particular measure that we have adopted is the efficiency (E) of feedback regulation. This measure is given by
| (1) |
where h0 is a step-function disturbance to the system in PaCO2 or PaO2. In Eq. 1, h1 represents the residual disturbance in PaCO2 or PaO2 after feedback correction. For example, in an open-loop system (where there is no feedback correction), h1 will equal h0, and so the efficiency will be 0%. On the other hand, for a closed-loop (feedback) system in which the loop gain tends toward infinity so that the error is almost completely corrected, h1 will tend toward zero, and so the efficiency will be close to 100%. The theoretical section of this paper moves from measures of vascular reactivity to PaCO2 and PaO2 in humans, to estimates of closed-loop gains from which efficiencies of regulation may be calculated.
The particular measure of pulmonary vascular reactivity to variations in PaCO2 and PaO2 that we adopted for this study is the maximum pressure gradient across the tricuspid valve during systole as assessed by Doppler ultrasound. This variable is denoted by the abbreviation ΔPmax to emphasize that it is a maximum pressure difference between two cardiac chambers. The usefulness of this measure as an index of pulmonary arterial pressure in normal humans has been well documented (1, 42); nevertheless, a difficulty remains, as global variations in PaCO2 and PaO2 influence not only vascular tone but also cardiac output (Q̇), which independently will influence both vascular tone and pulmonary arterial pressure. The theoretical approach that we have adopted accounts fully for this complication. In the case of O2, the required data are already available in the literature. In the case of CO2, additional data are required to assess the speed and magnitude of responses over the relevant timescales, and these results form an experimental component of the present study.
In the healthy lung, a regional disturbance of ventilation-to-perfusion ratio would be expected to alter regional PaCO2 and PaO2, and the efficiency of regulation in this part of the lung will vary with the absolute value of this ratio. The results from this study demonstrate how the efficiency of regulation varies with ventilation-perfusion ratio. It is important to note that the efficiency of feedback regulation E defined by Eq. 1 is distinct from the more general concept of the efficiency of gas exchange for the lung as a whole. For a lung to be efficient in gas exchange, there may be several requirements. One of these is uniformity of matching of ventilation and perfusion throughout the lung. Another is avoidance of diffusion limitation of gas transfer. In this paper, we restrict ourselves to a computation of E. Thus “good” feedback with a high efficiency is seen as feedback that restores the regional values of PaCO2 and PaO2 toward their normal values from which they have been disturbed and not necessarily toward a single uniform value for the lung as a whole.
Finally, it is important to note that this study is concerned with the contribution to ventilation-perfusion matching from vascular responses to CO2 and O2. However, previous studies have shown the potential for upper airway detection of CO2 and O2 to contribute to regional matching of ventilation to perfusion in the lung (6, 41). Thus the efficiencies arising from the pulmonary vascular responses to CO2 and O2 reported in this study should be viewed as lower bounds to the overall contributions of these gases to ventilation-perfusion matching within the healthy human lung.
METHODS
Overview
This study has two main components. The first component is the development of the theory necessary to predict the efficiency of regulation of regional PaCO2 and PaO2 from the pulmonary vascular responses to global variations in PaCO2 and PaO2. The analysis requires experimentally determined coefficients for these responses. These are available from the literature for O2, but only in part for CO2. The second main component of this study is experimental and provides the measurements of global pulmonary vascular response to hypercapnia and hypocapnia that are required to complete the analysis.
Theory for CO2
In this section, our first purpose is to estimate the steady-state, closed-loop gain (in the normal lung, under normal conditions) for the feedback loop between regional PaCO2 and regional pulmonary vascular tone (Fig. 1). This estimate enables an assessment to be made of whether the mechanism contributes significantly to the maintenance of ventilation-perfusion matching within the lung during everyday activities.
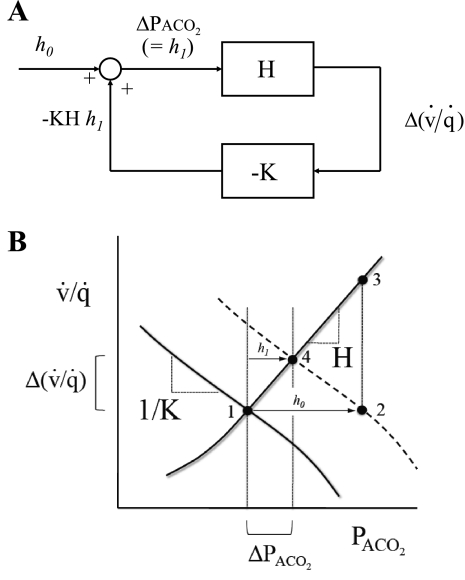
Fig. 1.
Depiction of the control system regulating the local alveolar Pco2 (PaCO2) within the lung [for alveolar Po2 (PaO2), the analysis is analogous]. A and B illustrate the derivation of Eq. 15. In A, the lines represent variables [e.g., Δ(v̇/q̇), where v̇/q̇ is ventilation-to-perfusion ratio] within the control system, the rectangular boxes depict the transforms for the change in 1 variable brought about by the change in another, and the circle represents the addition of the changes in 2 incoming variables to generate an outgoing variable. In the absence of any disturbance (i.e., h0 = 0), ΔPaCO2 and Δ(v̇/q̇) are both 0, and the control system is at point 1 (see B). A step-function finite disturbance in PaCO2 (i.e., h0 ≠ 0) is illustrated at point 2 in B. If no feedback is present (an open loop), then this disturbance would result in a disturbance of v̇/q̇ illustrated at point 3 in B. However, in the presence of feedback (a closed loop), the control system is at point 4 in B. Here, the final value for ΔPaCO2 is h1 [and the final value for Δ(v̇/q̇) is h1H]. Summation at the junction depicted by the circle in A yields the result that ΔPaCO2 (= h1) = h0 − KHh1, which is Eq. 15.
The approach taken is to consider the feedback loop as a dynamic system composed of two components (Fig. 1A). The first component of the loop is a description of the influence of the pulmonary vascular response to CO2 on the regional ventilation-to-perfusion ratio (v̇/q̇). The dynamic properties of this component remain to be well characterized, and so the time course of changes in v̇/q̇ in response to changes in regional Pco2 is not modeled here. The sensitivity (H) of this component is derived from the experimental measurements of this study together with certain other values taken from the literature. The second component of the loop is a description of the influence of changes in v̇/q̇ on regional PaCO2 and follows directly from considerations of mass balance. As for the first component, the dynamic properties of this second component are not well defined and therefore not analyzed in this study. The sensitivity of this part of the feedback loop is termed −K. The product of the two sensitivities yields the closed-loop gain: −K × H.
In Fig. 1B, point 1 represents the regional values of PaCO2 and v̇/q̇ before any disturbance has occurred. Point 2 represents a step-function disturbance h0 in PaCO2. If no feedback is present (open loop), then this disturbance would result in a disturbance of v̇/q̇ illustrated at point 3 in Fig. 1B. Point 4 represents the situation for the closed loop, in which the control system has reduced ΔPaCO2 to h1 by inducing a rise in v̇/q̇ equal to Δ(v̇/q̇).
Estimation of H for CO2: effect of changes in regional PaCO2 on v̇/q̇.
H is defined as the change in v̇/q̇ that results from a change in the regional PaCO2 when the lung continues to be perfused at constant in-flow pressure, in our case specified by the tricuspid valve maximum pressure difference (ΔPmax), which is described in Experimental Study below:
| (2) |
We now assume that a regional change in PaCO2 influences regional blood flow but not v̇. There is some evidence, outlined in discussion, that alveolar gas composition can modify the distribution of v̇ in such a manner as to make our estimate of loop gain a lower bound. Equation 2 can be expanded using the quotient rule to obtain one term equal to (1/q̇)(∂v̇/∂Pco2)ΔPmax and a second term equal to −(v̇/q̇2)(∂q̇/∂Pco2)ΔPmax According to our assumption that a regional change in PaCO2 does not affect v̇, (∂v̇/∂Pco2)ΔPmax becomes equal to zero, the second term can be expressed using a logarithm, and the above expression can be written as follows:
| (3) |
The challenge now is to relate a proportional change in regional blood flow (q̇) under the condition of constant perfusion pressure to the measured global changes in flow (Q̇) in the experiments presented in Experimental Study below (where perfusion pressure does not in general remain constant).
First, we assumed that the vasculature of the lung behaves uniformly in the sense that the proportionate change in regional blood flow in response to a regional change in PaCO2 is the same as the proportionate global change in blood flow in response to a global change in the mean PaCO2 (assuming conditions of constant perfusion pressure in each case). Assuming that PaCO2 is uniform throughout the lung, we may write (using PCO2 as an abbreviation for PaCO2 in the following equations):
| (4) |
The principal difficulty in obtaining (∂lnQ̇/∂Pco2)ΔPmax in Eq. 4 from experimental measurements in humans in vivo is that this differential contains the constraint that perfusion pressure (ΔPmax) remains constant. This is not something that can be achieved experimentally in humans. However, we show below that (∂lnQ̇/∂Pco2)ΔPmax can be written as a function of three variables that are accessible experimentally in humans: two of these are measured directly in the experimental component of this study [vide infra, δ(ΔPmax)/δPco2 and δQ̇/δPco2 of Eq. 10] and a third variable [vide infra, (∂ΔPmax/∂Q̇)Pco2 of Eq. 10] that has been obtained in a previous study. A secondary difficulty (for which we accept some approximation) is that the distribution of PaCO2 throughout the lung is not completely uniform.
We proceeded by noting that, for the lung as a whole, ΔPmax may be regarded as a function of both Q̇ and PaCO2. Consequently, an increment in ΔPmax [δ(ΔPmax)] may be considered to arise through an increase in flow at constant vascular tone and an increase in vascular tone at constant flow, as follows:
| (5) |
To obtain a general expression containing the partial derivative (∂Q̇/∂Pco2)ΔPmax in Eq. 4, we can set δ(ΔPmax) = 0 in Eq. 5 and divide through by δPco2 to obtain:
| (6) |
or
| (7) |
Combining Eqs. 2, 3, 4, and 7 yields:
| (8) |
A rearrangement of Eq. 5 yields:
| (9) |
Combining Eqs. 8 and 9 yields:
| (10) |
In Eq. 10, the term (∂ΔPmax/∂Q̇)Pco2 may be given a value of 0.6 Torr·l−1·min derived from the literature (3). The terms prefaced by δ now reflect values for the whole lung when all three variables (ΔPmax, Q̇, and Pco2) change simultaneously and may be estimated from the measurements made in Experimental Study.
Estimation of −K for CO2: effects of changes in v̇/q̇ on regional PaCO2.
Using the principles of mass balance, we may equate the CO2 exchange for the blood and gas phases for a region of the lung as follows:
| (11) |
where Cv̄CO2 is systemic mixed venous (pulmonary arterial) CO2 concentration, CecCO2 is pulmonary end-capillary CO2 concentration, and Patm is atmospheric pressure. Assuming that the dissociation curve for CO2 may be regarded as linear over the physiological range in the form (Cv̄CO2 − CecCO2) = β (Pv̄CO2 − Pco2), Eq. 11 may be written:
| (12) |
Differentiating with respect to v̇/q̇, assuming no change in Pv̄CO2, and noting that the resulting derivative equals −K (Fig. 1) yields:
| (13) |
It is important to note the significance of the assumption of no change in Pv̄CO2 in the derivation of Eq. 13. This is equivalent to assuming that the local region of the lung in which the disturbance of v̇/q̇ occurs is small enough for it not to lead to any change in the composition of systemic mixed venous (pulmonary arterial) blood. This completes the calculation of the effect on regional PaCO2 of a given change in v̇/q̇.
Overall loop gain for CO2.
The closed-loop gain (−K × H) is given by the product of the sensitivities of the two components of the loop (Eqs. 10 and 13) and may be written:
| (14) |
Significance of overall loop gain for CO2.
In the closed-loop setting, an initial disturbance in PaCO2 of magnitude h0 is attenuated by the feedback system, such that the final steady-state disturbance, h1, is given by the relationship:
| (15) |
This relationship is depicted graphically in Fig. 1B. It follows from Eq. 15 that the ratio of disturbance in regional PaCO2 between the closed and open loop situations is given by:
| (16) |
From this, it is possible to define a measure of control efficiency, E, according to Eq. 1 as:
| (17) |
For a feedback system that is completely ineffective (KH = 0), E = 0%. For a feedback system that exerts total control (KH tends to infinity), E = 100%.
Theory for O2
The calculation of closed-loop gain for hypoxic pulmonary vasoconstriction proceeds in a reasonably analogous manner to that for hypercapnic pulmonary vasoconstriction.
Estimation of H for O2: effect of changes in regional PaO2 on v̇/q̇.
The derivation of the expression for H for O2 proceeds in a completely analogous manner to that for CO2. The resulting equation (equivalent to Eq. 10) is as follows:
| (18) |
In Eq. 18, the term (∂ΔPmax/∂Q̇)Po2 may be given the same value from the literature of 0.6 Torr·l−1·min−1 (3) as has been used for CO2. However, a complication in the case for O2 is that neither δΔPmax/δPo2 nor δQ̇/δPo2 is a constant across the physiological range of interest for Po2. However, in the case of the pulmonary vascular response to Po2, it has been found that the response is reasonably linear if it is related to the saturation (S) of hemoglobin that corresponds to the Po2 values of interest (22). Severinghaus provides a convenient relationship for humans for converting values of Po2 to values for S (32): S = {[(Po23 + 150 Po2)−1 × 23,400] + 1}−1 (with Po2 in Torr). Using this relationship, we can estimate from the literature (39) a value for δ(ΔPmax)/δS of −0.461 Torr/%. We may then estimate δ(ΔPmax)/δPo2 for any particular value for Po2 using the relationship:
| (19) |
where dS/dPo2 is obtained by differentiating the expression given by Severinghaus (32).
A similar approach has been adopted for δQ̇/δPo2. From the literature (39), we estimate a value for δQ̇/δS of −0.07 l·min−1·%−1. We may then estimate δQ̇/δPo2 for any particular value for Po2 using the relationship:
| (20) |
Estimation of −K for O2: effects of changes in v̇/q̇ on regional PaO2.
Unlike the case of CO2, the equation relating the exchange of O2 in blood and gas phases has to incorporate the presence of O2 in the inspired gas and is given by (20):
| (21) |
where PiO2 is inspired Po2, Cv̄O2 is systemic mixed venous (pulmonary arterial) O2 concentration, and CecO2 is pulmonary end-capillary O2 concentration.
CecO2 is a function of regional PaO2 as follows (20):
| (22) |
where Hb is the concentration of hemoglobin in blood, c is the maximum binding capacity of hemoglobin, and α is the solubility in blood of molecular O2. Values used were Hb = 157 g/l (36), c = 1.34 × 10−3 l (stpd)/g (32), and α = 3.1 × 10−5 l (stpd)·l−1·Torr−1 (32).
Substituting for CecO2 from Eq. 22 into Eq. 21, we obtain
| (23) |
A numerical value for Cv̄O2 in this expression may be obtained using the same function that relates CecO2 to Po2 (Eq. 22) and assuming a standard value for systemic mixed venous S of 0.711 (36), which corresponds to a Po2 of 37 Torr (32). As in the handling of CO2, we are again assuming that the local region of the lung in which the disturbance of v̇/q̇ occurs is small enough for it not to lead to any change in the composition of systemic mixed venous (pulmonary arterial) blood.
Differentiating Eq. 23 with respect to Po2 and inverting both sides of the relation, we obtain
| (24) |
Overall loop gain for O2.
The closed-loop gain (−K × H) is given by the product of the sensitivities of the two components of the loop (Eqs. 18 and 24) and, noting that we may substitute for the term v̇/q̇ using Eq. 23, is given by
| (25) |
It should be noted that the closed-loop gain for O2 (Eq. 25) is given as a function of PaO2, whereas that for CO2 (Eq. 14) is given as a function of v̇/q̇. However, v̇/q̇ and PaO2 are related to each other through Eq. 23; therefore, a value for PaO2 that corresponds to any particular value for v̇/q̇ may be obtained through numerical solution of this equation.
The measure of overall efficiency of control, E, is analogous to that for CO2, as given in Eq. 17.
Theory for CO2 and O2 Combined
Assuming that, for relatively small changes, any nonlinear interaction between the combined stimuli of CO2 and O2 can be neglected, then the combined efficiency of regulation by both CO2 and O2 can be derived in an additive manner. The combined closed-loop gain, −Gtot, is given by
| (26) |
where −(KH)CO2 and −(KH)O2 are the individual closed-loop gains, respectively, for CO2 and O2.
The measure of overall control efficiency (Etot) is given by
| (27) |
Experimental Study
The experimental methods described in this section were those used to estimate values for the two following coefficients of Eq. 14: δ(ΔPmax)/δPco2 and δQ̇/δPco2. The coefficients apply to the situation in which PaCO2 is varied and both ΔPmax and Q̇ are allowed to change freely. As explained in the theory above, Eq. 14 applies to a model of the lung that is uniform with respect to alveolar gas composition. This condition is not completely fulfilled in healthy volunteers (or others); therefore, we must accept some (modest) degree of inaccuracy in our estimates arising from this approximation. The experimental study also allowed the speed of response of ΔPmax to variations in PaCO2 to be assessed to ensure that this was sufficiently rapid for effective control through CO2 to occur.
Volunteers.
Twelve healthy volunteers (6 women and 6 men, age 26.6 ± 2.9 years, means ± SD) participated in the present study. Volunteers were evaluated using Doppler echocardiography and were included in the study, provided that ultrasound images could be obtained easily. Female volunteers were asked to participate only during the first 14 days of their menstrual cycle. Informed written consent was obtained from all volunteers on each experimental day. The study was approved by the Central Oxford Research Ethics Committee and performed in accordance with the Declaration of Helsinki.
Protocols.
In the protocols described in the following paragraph, euoxic eucapnia refers to the condition in which end-tidal Po2 (PetO2) is maintained at 100 Torr and end-tidal Pco2 (PetCO2) is maintained either at, or just above (+1–2 Torr), each volunteer's normal value. Euoxic hypercapnia refers to the condition in which PetO2 is maintained at 100 Torr and PetCO2 is maintained 10 Torr above each volunteer's normal value. Euoxic hypocapnia refers to the condition in which PetO2 is maintained at 100 Torr and PetCO2 is maintained 10 Torr below each volunteer's normal value.
Each volunteer undertook three different protocols separated by at least 48 h from each other. The “hypercapnia protocol” consisted of 5 min of euoxic eucapnia, followed by 25 min of euoxic hypercapnia, followed by a further 5 min of euoxic eucapnia. The “hypocapnia protocol” consisted of 5 min of euoxic eucapnia, followed by 25 min of euoxic hypocapnia, followed by a further 5 min of euoxic eucapnia. The “control protocol” consisted of 35 min of euoxic eucapnia.
Each protocol was performed twice within 24 h (with a separation of more than 4 h). This was done so that almost continuous Doppler measurements of ΔPmax could be obtained during one repeat of the protocol and almost continuous measurements of Q̇ could be obtained during the other repeat of the protocol. Such measurements could not be obtained simultaneously. The order of the two measurements was varied; half of the volunteers always had ΔPmax measured first, and the other half had Q̇ measured first.
Control of end-tidal gases.
Volunteers lay in a semi-left lateral position and breathed through a mouthpiece while wearing a nose clip. The partial pressures of the inspired gases were adjusted breath-by-breath using an end-tidal forcing system so that the desired end-tidal values were maintained, as described previously (29). In both the hypercapnia protocol and control protocol, breathing was spontaneous. In the hypocapnia protocol, voluntary hyperventilation was used.
Voluntary hyperventilation.
Throughout the hypocapnia protocol, volunteers were asked to breathe to a predetermined tidal volume and respiratory frequency. An oscilloscope was used to help volunteers adjust their tidal volume by following a line to a specific point on the screen during inspiration. An audible signal was used to maintain regular breathing. Before the beginning of the experiment, a level of hyperventilation was identified for each volunteer that lowered the volunteer's PetCO2 to slightly more than 10 Torr below their normal value while they breathed air. This level of hyperventilation was used during the succeeding experiment. During the experiment, CO2 was added to inspired gas to produce the desired profile in PetCO2 using the end-tidal forcing technique.
Echocardiography.
Echocardiographic measurements were performed using a Hewlett Packard Sonos 5500 ultrasound machine with an S4 two-dimensional transducer (2–4 MHz). Volunteers were examined while they were in a recumbent position (lying on their left side) on a suitably modified couch. A super-VHS video recorder was used to store spectral waveforms for the entire duration of each experiment. The tapes were played back at a later time for spectral waveform analyses. For each measurement point, averages were obtained from three or more envelopes recorded at end-expiration or as close as possible to it. Using this approach, we could average measurements for ΔPmax for intervals as small as 30 s. Heart rate (HR) and a respiratory waveform were also recorded.
Tricuspid valve maximum pressure difference (ΔPmax).
In a majority of people, ultrasound can be used to detect a regurgitant jet through the tricuspid valve. We identified volunteers in whom this jet could be detected and measured the velocity (v) with which it leaves the right ventricle and enters the right atrium. On the assumption that the jet can be regarded as steady, Bernoulli's equation (Eq. 28) can be used to relate ΔPmax to v:
| (28) |
where ρ is the density of blood. We have previously shown that ΔPmax provides a sensitive index of the pulmonary vascular response to hypoxia in healthy humans while changing little with Q̇ in the absence of changes in the composition of alveolar gas (3). In accord with that study, we initially anticipated that only ∼5% of any change in ΔPmax with hypercapnia or hypocapnia would be attributable to any concurrent change in Q̇. On the basis of these findings and following earlier studies (2, 16), we take ΔPmax to be our primary measure of the speed and intensity of action of hyper/hypocapnia on pulmonary vascular smooth muscle. It is important to note, however, that the assumptions underlying Eq. 14 require only that, for the lung as a whole, ΔPmax may be regarded as a function of both Q̇ and PaCO2. The fact that ΔPmax is influenced to a more minor degree by Q̇ than by PaCO2 in healthy volunteers may be of value in some applications but is not a requirement of our study.
ΔPmax was measured using a standard technique (27). An apical four-chamber view of the heart was used to observe the tricuspid valve in two dimensions; color Doppler format was then used to detect the regurgitant jet. After alignment with the Doppler beam, continuous-wave spectral analysis at a sweep speed of 50 mm/s was used to record the velocity profile of the jet. During analysis, the maximal velocity of the jet was measured using an electronic caliper tool integrated with the echocardiography machine. Each measurement of ΔPmax was made from at least three velocity profiles taken toward the end of expiration.
Cardiac output.
An apical five-chamber view of the heart was used with Doppler mode to identify flow through the aortic valve during systole. Using pulsed-wave spectral mode at a screen sweep speed of 100 mm/s, we obtained the velocity profile of the aortic flow. Doppler sampling of the flow was taken immediately below the orifice of the aortic valve. The flow was quantified automatically using the velocity time integral, which is the mean distance through which blood travels in the outflow tract during ventricular contraction. Each measurement of velocity time integral was made from at least three velocity profiles taken toward the end of expiration.
The diameter of the aortic valve was measured from a parasternal long axis view, and the aortic valve area (A) was calculated. Stroke volume (SV) was calculated from velocity time integral × A; Q̇ was calculated from SV multiplied by HR. Measurements of Q̇, SV, and HR are presented at minute intervals.
Modeling.
Our results were quantified through the parameter values of simple models that describe the acute responses of the variables ΔPmax, SV, HR, and Q̇ to hypercapnia and hypocapnia. The parameter values for the models were obtained through a process of fitting the model to the experimental data. Each model has one parameter for the value of the variable under conditions of steady eucapnia (M), a second parameter for the sensitivity of the response (G) to hypercapnia or hypocapnia (depending on protocol), and a third parameter that gives the time constant (τ for the response). The model is given by:
| (29) |
where P is the value for PetCO2 during eucapnia, Pco2(n) is the value for PetCO2 at the nth time point, Δt is the time interval between the data points (either 0.5 min or 1 min), and y variously represents one of the four variables (ΔPmax, SV, HR, and Q̇). For each volunteer, the model was fitted to the data for each repeat of the hypercapnia and hypocapnia protocols using a program written in Matlab 6.1.
Statistical Analysis
For the measured variables, repeated-measures ANOVA (rmANOVA) was undertaken to determine whether there was an interaction between time and protocol. A separate test of rmANOVA was then performed on the data from just the control protocol to check that time did not have a significant effect in this protocol. Ordinary, univariate, ANOVA was used to assess the significance of differences between protocols for the parameter estimates for the models.
RESULTS
The first part of the results relates to our main objective, which is to present the efficiency of feedback regulation of the alveolar gases by the pulmonary vasculature. For CO2, these calculations require experimental estimates of the coefficients δ(ΔPmax)/δPco2 and δQ̇/δPco2. The detailed results from the experimental study that provide these coefficients are given in the second part of the results. As a secondary objective, these experimental results provide time constants for the speed of the pulmonary vascular response to CO2.
Estimates of Closed-Loop Gain and Efficiency of Control
The results from this part of the study are presented in Fig. 2, in which the calculated variables are shown as a function of v̇/q̇. The range of values of v̇/q̇ was chosen to be 0.1–10 to encompass those anticipated in the healthy human lung (40) and presented on a logarithmic scale.
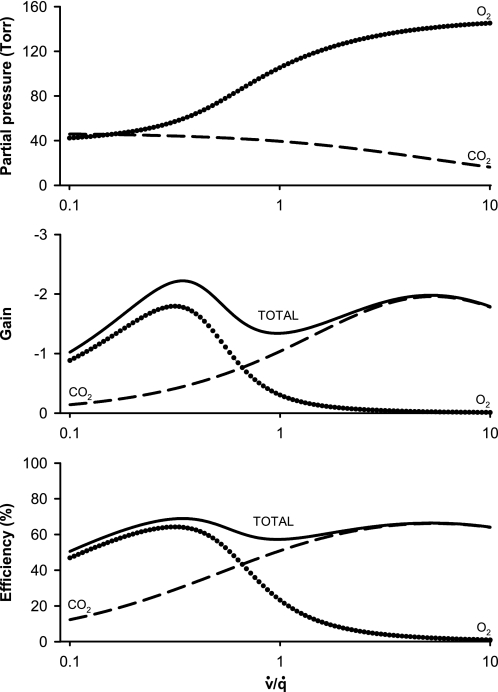
Fig. 2.
Top: PaCO2 and PaO2 as a function of regional v̇/q̇. Middle: feedback loop gains for the regulation of regional v̇/q̇ by hypercapnic and hypoxic pulmonary vasoconstriction. Bottom: efficiencies of regulation of regional v̇/q̇ by hypercapnic and hypoxic pulmonary vasoconstriction. Dashed lines, responses relating to CO2; dotted lines, responses relating to O2; solid lines, combined responses to both CO2 and O2. Note that the regulatory effect of O2 is greater than that for CO2 at low values for v̇/q̇, that the regulatory effect of CO2 is greater than that for O2 at higher values of v̇/q̇, and that the total regulatory efficiency remains relatively constant over the range of values displayed for v̇/q̇.
Figure 2, top, shows PaO2 and PaCO2 obtained from Eqs. 21 and 12, respectively. The range of values for PaO2 is from 42 to 145 Torr, whereas that for PaCO2 is from 16 to 46 Torr. Figure 2, middle, shows the steady-state closed-loop gains for O2 and CO2 and the combination of O2 and CO2 together, as calculated, respectively, from Eqs. 25, 14, and 26. Figure 2, bottom, shows the efficiency of feedback control for O2 and CO2 and the combination of O2 and CO2 together, as calculated from Eq. 17 for O2 and CO2 and from Eq. 27 for the combination of O2 and CO2.
The efficiency for combined regulation by CO2 and O2 remains fairly close to 60% across the entire range of values shown for v̇/q̇. However, the individual contributions from CO2 and O2 vary markedly with v̇/q̇. Whereas O2 has a greater regulatory effect at the lower values of v̇/q̇, CO2 has a greater effect at values of v̇/q̇ above ∼0.65. As the average value for ratio of ventilation to perfusion is ∼0.9–1.0 (40), the result suggests that the regulatory effects of CO2 may be greater than those of O2 throughout much of the lung; around the mean ratio the effects of CO2 may be twofold greater than those of O2.
Experimental Study
Gas control.
Figure 3 shows the values for inspired and end-tidal Po2 and Pco2 for all three protocols. Separate graphs are shown for the repetitions of each protocol for the different Doppler measurements (ΔPmax and Q̇), showing that nearly identical conditions were successfully achieved. In the hypercapnia protocol, a very quick transition into and out of hypercapnia was achieved with a step duration of <30 s. The transition into and out of hypocapnia in the hypocapnia protocol was slower, with a step duration of ∼2 min. During the control protocol, PetCO2 was maintained very constant, within ∼1 Torr of the normal air-breathing values. Ventilations during the initial 5-min periods of the hypercapnia, hypocapnia, and control protocols were, respectively, 12.6 (SD 2.7), 22.9 (SD 5.7), and 12.0 (SD 2.8) l/min. Mean ventilations during the 20-min periods of hypercapnia, hypocapnia, or control for the three protocols were, respectively, 35.6 (SD 9.0), 23.8 (SD 5.4), and 12.6 (SD 2.4) l/min.
Fig. 3.
Composition of respired gas during each of the 3 main protocols. Top: hypercapnia protocol consisting of a 25-min period of euoxic hypercapnia preceded and followed by a 5-min period of euoxic eucapnia. Ventilation was spontaneous throughout. Middle: hypocapnia protocol consisting of a 25-min period of euoxic hypocapnia preceded and followed by a 5-min period of euoxic eucapnia. The volunteers undertook voluntary hyperventilation throughout. Bottom: control protocol consisting of a 35-min period of euoxic eucapnia. Ventilation was spontaneous throughout. Left: values during the determination of the maximum pressure difference across the tricuspid valve (ΔPmax). Right: values during the determination of cardiac output. Results show inspired Pco2 (PiCO2; triangles), inspired Po2 (PiO2; diamonds), end-tidal Pco2 (PetCO2; circles), and end-tidal Po2 (PetO2; squares). Closed symbols indicate periods of either hypercapnia or hypocapnia; open symbols indicate periods of eucapnia. Data are means for 12 subjects; error bars are ± SE. Note that, in the hypercapnia protocol, PiCO2 is close to 40 Torr during euoxic hypercapnia, which coincidentally is very close to PetCO2 before and after this period.
Pulmonary vascular responses to hypercapnia and hypocapnia.
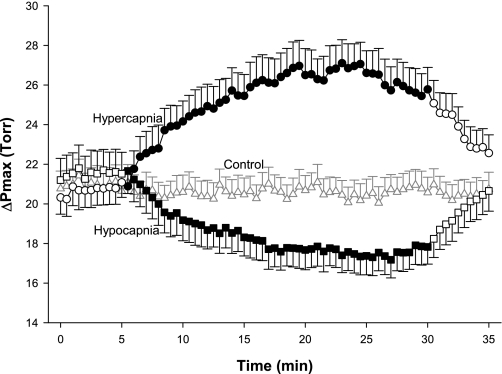
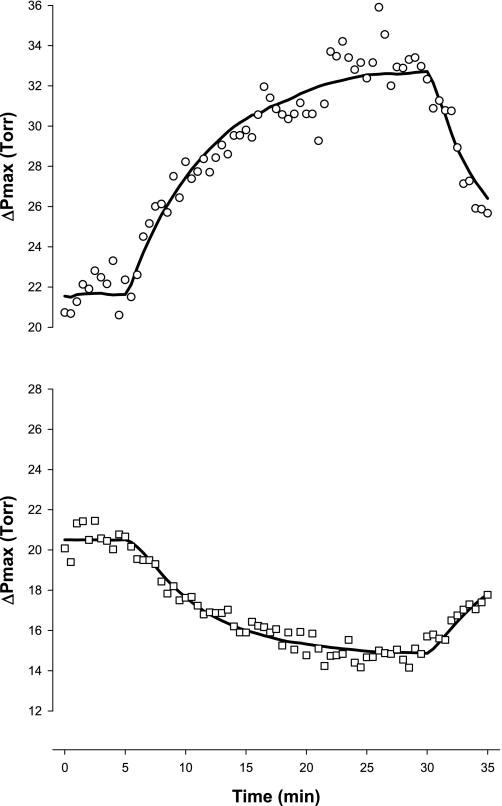
ΔPmax responses for all three protocols are shown in Fig. 4. ΔPmax increased by ∼6 Torr with hypercapnia and decreased by ∼4 Torr with hypocapnia. Both responses were significantly different from control responses (rmANOVA, P < 0.001). The effects of hypercapnia and hypocapnia were quickly reversed when euoxic eucapnia was restored. The control experiment revealed no changes in ΔPmax for the entire duration of the exposure.
Fig. 4.
Tricuspid valve maximum pressure difference (ΔPmax) during the 3 main protocols: hypercapnia (circles), hypocapnia (squares), and control (triangles). Closed symbols indicate measurements made under hypercapnic (hypercapnia protocol) or hypocapnic (hypocapnia protocol) conditions; open symbols indicate measurements made under eucapnic conditions. Data are means for 12 subjects; error bars are ± SE. ΔPmax was significantly affected by both hypercapnia and hypocapnia compared with control (P < 0.001, rmANOVA).
Q̇, SV, and HR.
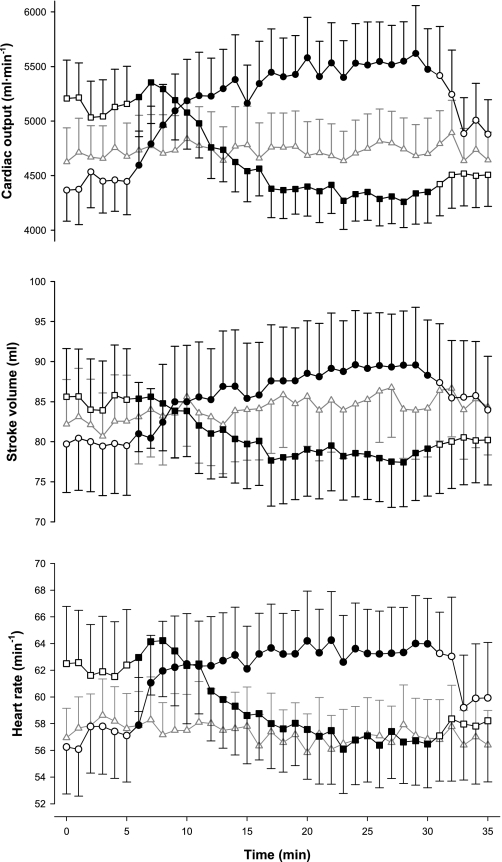
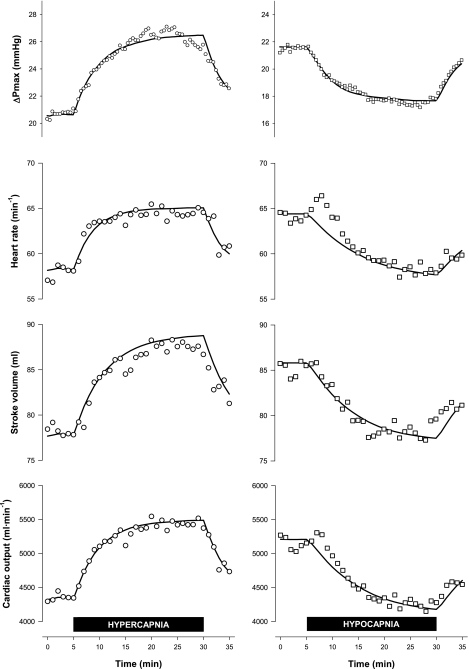
The responses of Q̇ and its components (SV and HR) are shown in Fig. 5. Baseline values for these three variables were higher in the hypocapnia protocol than in the other two protocols. In the hypocapnia protocol, ventilation was elevated throughout by volunteers who performed voluntary hyperventilation, whereas this was not the case in the other two protocols. During hypercapnia, Q̇ increased by ∼1 l/min (∼22%, rmANOVA, P < 0.001), SV increased by ∼10 ml (∼12%, rmANOVA, P < 0.04), and HR increased by ∼6 beats/min (∼11%, rmANOVA, P < 0.003) when compared with baseline. During hypocapnia, Q̇ decreased by ∼0.8 l/min (∼16%, rmANOVA, P < 0.001), SV decreased by ∼7 ml (∼8%, rmANOVA, P < 0.001), and HR decreased by ∼5 beats/min (∼8%, rmANOVA, P < 0.002) when compared with baseline.
Fig. 5.
Cardiac output (top), stroke volume (middle), and heart rate (bottom) during the 3 main protocols: hypercapnia (circles), hypocapnia (squares), and control (triangles). Closed symbols indicate measurements made under hypercapnic (hypercapnia protocol) or hypocapnic (hypocapnia protocol) conditions; open symbols indicate measurements made under eucapnic conditions. Data are means for 12 subjects; error bars are ± SE.
Model parameters: ΔPmax.
Figure 6 illustrates a typical model fit to the data for one volunteer, and Table 1 lists the parameter values obtained for each volunteer from this process. Figure 7, top, shows the extent to which the average output of the model describes the mean data. For the hypercapnia protocol, the mean sensitivity obtained was 0.76 Torr per Torr change in PetCO2; for the hypocapnia protocol, the mean sensitivity was 0.40 Torr per Torr change in PetCO2. The sensitivities from these two protocols differed significantly (P < 0.001, ANOVA). In the absence of further information from the literature concerning the degree to which the pulmonary vascular response to CO2 is curvilinear, we have adopted the assumption of linearity and used these data to give the coefficient δ(ΔPmax)/δPco2 in Eq. 14 a mean value of 0.58 Torr per Torr. For both protocols, the time constants for the response were similar (hypercapnia protocol = 4.9 min; hypocapnia protocol = 4.2 min).
Fig. 6.
Example for a single volunteer (number 1256) of the fit of the model for the response of ΔPmax in 2 protocols. Top: hypercapnia protocol. Bottom: hypocapnia protocol. Solid lines = model response; symbols = experimental data points.
Table 1.
Model parameters for responses of ΔPmax and cardiac variables to hypercapnia and hypocapnia
| ΔPmax |
HR |
SV |
Q̇ |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Subject | M, Torr | G, Torr/Torr | τ, min | M, beats/min | G, beats·min·−1·Torr−1 | τ, min | M, ml | G, ml/Torr | τ, min | M, ml/min | G, ml·min−1·Torr−1 | τ, min |
| Hypercapnia protocol | ||||||||||||
| 1229 | 22.46 | 0.90 | 4.27 | — | — | — | — | — | — | — | — | — |
| 1096 | 26.28 | 0.64 | 2.63 | 49.89 | 1.12 | 2.04 | 98.52 | 1.00 | 0.01 | 4,895 | 172.5 | 1.66 |
| 1236 | 16.54 | 0.66 | 7.90 | 52.37 | 1.26 | 4.02 | 76.67 | 3.10 | 20.07 | 4,015 | 240.1 | 8.71 |
| 1238 | 14.96 | 0.39 | 4.99 | 40.92 | 0.59 | 7.56 | 64.31 | 1.78 | 7.82 | 2,624 | 119.3 | 7.77 |
| 1156 | 19.24 | 0.76 | 6.29 | 88.35 | −0.75 | 1.66 | 60.28 | 0.59 | 0.94 | 5,304 | 7.240 | 0.02 |
| 1142 | 23.05 | 0.33 | 2.35 | 72.88 | 1.01 | 4.59 | 45.94 | 0.85 | 5.94 | 3,340 | 116.1 | 5.36 |
| 1091 | 23.06 | 0.72 | 2.74 | 51.85 | 1.22 | 5.21 | 123.74 | 1.46 | 3.85 | 6,402 | 240.5 | 4.63 |
| 1252 | 19.92 | 0.54 | 3.05 | 62.70 | 1.64 | 4.79 | — | — | — | 3,991 | 164.9 | 8.12 |
| 1198 | 18.83 | 0.80 | 6.98 | 55.30 | 0.57 | 0.55 | 63.81 | 0.69 | 1.01 | 3,534 | 76.12 | 0.69 |
| 1250 | 20.04 | 0.92 | 6.75 | 59.05 | 1.60 | 5.89 | 80.00 | 0.63 | 2.34 | 4,725 | 168.1 | 4.36 |
| 1256 | 21.55 | 1.53 | 7.22 | 46.13 | 0.72 | 2.76 | 74.17 | 2.67 | 11.12 | 3,418 | 177.7 | 6.78 |
| 1209 | 20.77 | 0.90 | 3.08 | 59.36 | 0.63 | 3.17 | 89.33 | 1.57 | 6.95 | 5,303 | 152.6 | 4.92 |
| Means ± SE | 20.56 ± 0.88 | 0.76 ± 0.09 | 4.85 ± 0.60 | 58.07 ± 3.98 | 0.87 ± 0.20 | 3.84 ± 0.62 | 77.68 ± 6.99 | 1.43 ± 0.28 | 6.01 ± 1.92 | 4,323 ± 333.4 | 148.6 ± 20.46 | 4.82 ± 0.90 |
| Hypocapnia protocol | ||||||||||||
| 1229 | 25.50 | 0.42 | 5.66 | 55.25 | −0.22 | 0.02 | 120.21 | 2.09 | 11.70 | — | — | — |
| 1096 | 27.41 | 0.35 | 3.34 | 54.42 | 1.14 | 16.73 | 109.67 | 1.41 | 12.44 | 5,964 | 186.5 | 14.28 |
| 1236 | 15.82 | 0.22 | 4.46 | — | — | — | — | — | — | — | — | — |
| 1238 | 16.33 | 0.20 | 1.41 | — | — | — | 80.94 | 0.32 | 16.03 | 5,122 | 105.7 | 25.24 |
| 1156 | 25.74 | 0.66 | 5.36 | 89.00 | 0.73 | 2.13 | 62.19 | 0.51 | 7.84 | 5,515 | 81.01 | 4.03 |
| 1142 | 20.62 | 0.40 | 3.43 | 79.91 | 0.93 | 10.59 | 51.01 | 1.02 | 15.33 | 4,070 | 119.5 | 13.04 |
| 1091 | 25.84 | 0.47 | 5.98 | 52.64 | 0.68 | 12.59 | 112.19 | 0.66 | 5.83 | 5,902 | 103.2 | 9.39 |
| 1252 | 21.44 | 0.31 | 2.72 | 71.59 | 0.97 | 16.24 | 66.52 | 0.69 | 1.97 | 4,710 | 85.58 | 5.27 |
| 1198 | 19.02 | 0.39 | 4.12 | 47.89 | −0.41 | 0.01 | 79.22 | 0.51 | 0.01 | 3,792 | −6.65 | 0.01 |
| 1250 | 19.24 | 0.37 | 4.28 | 80.52 | 1.85 | 9.81 | 82.58 | 0.78 | 6.30 | 6,632 | 199.1 | 8.47 |
| 1256 | 20.50 | 0.57 | 6.54 | 47.57 | 0.34 | 13.79 | — | — | — | 4,185 | 83.62 | 19.87 |
| 1209 | 22.05 | 0.41 | 2.72 | 65.37 | 1.35 | 15.06 | 93.78 | 0.84 | 3.55 | 6,111 | 152.2 | 8.34 |
| Means ± SE | 21.63 ± 1.10 | 0.40 ± 0.04 | 4.17 ± 0.44 | 64.42 ± 4.76 | 0.74 ± 0.22 | 9.70 ± 2.09 | 85.83 ± 7.25 | 0.88 ± 0.16 | 8.10 ± 1.76 | 5,200 ± 308.9 | 111.0 ± 18.67 | 10.79 ± 2.39 |
M, value of variable under conditions of steady eucapnia; G, sensitivity of response to alterations in end-tidal Pco2; τ, time constant for response; ΔPmax, maximum pressure difference across tricuspid valve; HR, heart rate; SV, stroke volume; Q̇, cardiac output. Parameter values for individual fits have been excluded for cases in which the models could not fit the data meaningfully.
Fig. 7.
Average of the model outputs for ΔPmax, heart rate, stroke volume, and cardiac output compared with mean data. Left: hypercapnia protocol. Right: hypocapnia protocol. Solid lines = model response; symbols = experimental data points.
Model parameters: cardiac variables.
Table 1 displays the parameter estimates for each volunteer for the fit of the models to the data for Q̇, SV, and HR. Parameter values for individual fits have been excluded from Table 1 when models could not fit the data meaningfully. Figure 7, bottom, shows the extent to which the average outputs of these models describe the mean observations. Notable differences were observed between the time courses of the cardiac variables in hypercapnia and hypocapnia. During the hypercapnia protocol, HR changed rapidly with a time constant of 3.8 min, whereas, during the hypocapnia protocol, HR changed more slowly with a time constant of 9.7 min (P < 0003, ANOVA). During the hypercapnia protocol, SV changed with a time constant of 6.0 min; during the hypocapnia protocol, it changed with a time constant of 8.1 min (P < 0.04, ANOVA). During the hypercapnia protocol, Q̇ changed with a time constant of 4.8 min, whereas, during the hypocapnia protocol, Q̇ changed with a time constant of 10.8 min.
The sensitivities of Q̇, SV, and HR to changes in PetCO2 were similar in both the hypercapnia and hypocapnia protocols. These data were used to give the coefficient δQ̇/δPco2 in Eq. 14 a mean value of 0.130 l·min−1·Torr−1.
Model parameters: order in which the measurements of ΔPmax and Q̇ were made.
To assess whether the measurements of ΔPmax and Q̇ were affected by the order in which they were made, we compared M (baseline) and G (sensitivity) for both ΔPmax and Q̇ and for both the hypercapnia and hypocapnia protocols, between the six volunteers for whom ΔPmax was measured first and the six volunteers for whom Q̇ was measured first. No significant differences were found for any of the eight comparisons. These results suggest that a wait of 4 h between a first and second exposure to 20 min of either hypercapnia or hypocapnia was sufficient to prevent the first exposure from influencing the results of the second exposure.
Sensitivity of efficiency to changes in δ(ΔPmax)/δPco2 and δQ̇/δPco2.
Equations 14 and 17 can be combined to estimate the extent to which the calculated value of E is sensitive to variability between individuals in the measured values of δ(ΔPmax)/δPco2 and δQ̇/δPco2, respectively, tabulated as G for ΔPmax and G for Q̇ in Table 1. In the midrange of v̇/q̇ close to a value of 1, where E is 50% and the gain equals −1, we find that a 10% variation up or down in δ(ΔPmax)/δPco2 results in either a 2.7% increase or 3.1% decrease, respectively, in E. Correspondingly, we find a 10% variation up or down in δQ̇/δPco2 results in either a 0.4% decrease or 0.4% increase, respectively, in E. These relatively small changes in E suggest that the values of E shown in Fig. 1 are fairly insensitive to changes in the measured coefficients in Eq. 14.
Correlation between δ(ΔPmax)/δPco2 and δQ̇/δPco2 for all volunteers.
It is of physiological interest to determine the extent to which sensitivities of ΔPmax and Q̇ to hypercapnia and hypocapnia are related to each other; does one high sensitivity within an individual imply that the second sensitivity will be high? The results suggest no significant correlation: r = 0.12 and r = −0.21 for hypercapnia and hypocapnia, respectively.
DISCUSSION
The major finding of this study is that the efficiency of regulation of local v̇/q̇ by the pulmonary responses to Pco2 and Po2 is ∼60% over the range of the v̇/q̇ values encountered in the healthy lung. The effects of O2 are dominant at values of v̇/q̇ below ∼0.65 and the effects of CO2 are dominant at values of v̇/q̇ above 0.65. Apart from providing coefficients for the CO2 component of the analysis, the experimental study also demonstrated that the dynamics of the pulmonary vascular response to CO2 were broadly comparable with those previously reported for O2.
Limitations of Theoretical Component of Study
An assumption of the theory is that only q̇, and not v̇, is affected by the local composition of alveolar gas (Eq. 3). However, there is evidence in the literature that airway gas composition can alter the distribution of v̇. Thus, for example, the presence of 5% carbon dioxide in the airways of anesthetized dogs during late inspiration reduces ventilation-perfusion heterogeneity, probably by a dilatory effect on airway smooth muscle in the conducting airways (6). In rat lungs ventilated with liquid, a direct measure of airway compliance during hypercapnia suggested bronchial and/or parenchymal relaxation (8). Correspondingly, bronchodilation of both small and large airways has been demonstrated during hypoxia in anesthetized miniature pigs by computed tomography (41). Another pertinent line of evidence suggesting that regulation of v̇ may occur in response to changes in alveolar gas is the measurable temporal variance of v̇ seen in anesthetized sheep (30), which may reflect changes in ventilation induced by changes in q̇ (31). It remains unclear to what extent these airway mechanisms contribute to ventilation perfusion matching during normal daily activities. If they do play a significant role, then the loop gains and efficiencies resulting from the effects of CO2 and O2 on perfusion that we have calculated in Fig. 2 represent approximate lower bounds for the overall effects of CO2 and O2 on ventilation perfusion matching in the lung.
A second feature of our analysis is that we infer local effects of hypercapnia and hypoxia on the pulmonary vasculature from the global effects of hypercapnia and hypoxia within the lung (Eq. 4). The evidence that both CO2 and O2 act locally as vasoactive agents within the lung comes from a number of different approaches. In their early work, Kato and Staub (15) used rapid freezing of feline lung segments from locally hypoxic lobes to demonstrate that the major site of hypoxic constriction was in small muscular pulmonary arteries of internal diameter ∼200 μm at the level of terminal respiratory bronchioles. Their results also suggested that the combination of local hypercapnia and hypoxia yielded more vigorous constriction than hypoxia alone. Micropuncture studies by Nagasaka et al. (25) in in situ but otherwise isolated cat lungs confirmed that most of the constriction in response to hypoxia was above the level of arteries of diameter 30–50 μm and ameliorated by hypocapnia. In another direct approach, Shirai et al. (35) in 1986 used an X-ray television system to visualize the changes in diameter of small feline pulmonary vessels in the range of diameter 100–600 μm in response to both hypoxia and hypercapnia. Vigorous responses to both stimuli were at their maximum in arteries of internal diameter 200–300 μm, consistent with the older observations of Kato and Staub. Significantly, vessels in a second lobe remained unchanged when alveolar gas changes were restricted to the first lobe.
Less direct approaches have been consistent with the above findings. Hakim et al. (12) used sudden arterial and venous occlusions in isolated lung lobes of dogs and demonstrated that hypoxia acts mainly on small distensible vessels rather than on larger relatively indistensible arteries. The evidence of direct action of alveolar and mixed venous blood gases on small pulmonary vessels is further supplemented by fractal temporal analysis, which suggests that one level of regulation of regional blood flow is within components of lung tissue representing ∼3% of the lung (10). Finally, studies in anesthetized dogs of how acetazolamide impairs matching of ventilation and perfusion suggested that normal vascular (and bronchial) responses to changes in alveolar Pco2 are both localized and rapid (on a timescale of ∼1 min) because of the local availability of carbonic anhydrase to speed changes in Pco2 into changes in pH (37, 38).
However, such evidence cannot exclude the possibility that global hypercapnia or hypoxia may also exert global effects on pulmonary vascular tone through either neural or endocrine pathways, although the latter would seem unlikely given the relatively modest variations in Pco2 and Po2 with which we are concerned. The pulmonary vasculature is innervated by both adrenergic and cholinergic nerves (7, 13), where the net effect of stimulation of the sympathetic system appears to be vasoconstriction and that of the cholinergic system is vasodilation (26, 28). Little is known regarding the effects of CO2 on the autonomic regulation of the pulmonary vasculature, but neither sympathetic nor complete autonomic blockade appears to modify the pulmonary vascular response to hypoxia once the confounding effects of these interventions on Q̇ have been taken into account (18, 19). We cannot exclude some error in our estimates arising from neuroendocrine mechanisms. Our analysis regarding the efficiency of regulation of local v̇/q̇ by the pulmonary responses to PaCO2 and PaO2 should therefore be regarded as speculative, pending further studies.
A third assumption within our analysis is that the local region of the lung in which the disturbance of v̇/q̇ occurs is small. Under this condition, alterations in local v̇/q̇ do not themselves give rise to changes in either ΔPmax (21) or the overall composition of systemic arterial blood. A change in this latter variable would be expected to induce changes in both ventilation and the composition of systemic mixed venous (pulmonary arterial) blood. In practice, many disturbances, such as changes in posture, may generate more widespread variations in v̇/q̇.
A fourth assumption of our analysis is that the effects of CO2 and O2 on the pulmonary vasculature are additive in nature. This assumption is used to calculate the total closed-loop gain and regulatory efficiency when the effects of both CO2 and O2 on the pulmonary circulation are combined. If the two stimuli were synergistic in their effects, then this would lead us to underestimate the magnitude of the total closed-loop gain. However, animal studies suggest that any such synergy is relatively small (4, 34).
Limitations of Experimental Component of Study
The experimental component of this study examined the effect of variations in PaCO2 on an echocardiographic index of the in-flow pressure to the pulmonary circulation. A complication of any such study is that changes in the in-flow pressure will be affected by changes in Q̇ induced by CO2 as well as by the direct effect of CO2 on the pulmonary vascular smooth muscle. For O2, the contribution of changes in Q̇ to the overall change in ΔPmax appears to be small (∼5%) in the normal lung (3). For CO2, the data in this study suggest that the contribution of changes in Q̇ to the overall change in ΔPmax is ∼10–15%. However, it is important to appreciate that the theoretical component of this study does not rely on the small size of the overall contribution of Q̇ to changes in ΔPmax. Our theory treats ΔPmax as a function of both Q̇ and alveolar gas tension.
Second, it is also possible that inflow pressure is affected independently by different levels of ventilation. Ventilation in the hypercapnia protocol was higher than in the hypocapnia protocol, and this might be related to the differences in the values of G computed for ΔPmax for these two stimuli. An indication that any such effect may be minimal comes from the data for the eucapnic 5-min period at the beginning of each of the protocols when the level of ventilations differed. During this period, the voluntary hyperventilation reported above for the hypocapnia protocol was 10.3 l/min greater than the spontaneous ventilation in the hypercapnia protocol, whereas ΔPmax was only 1.07 Torr greater in the former protocol (Table 1). Given that Q̇ in the hypocapnia protocol during this period was 877 ml/min greater than in hypercapnia protocol (Table 1), these observations are consistent with hyperventilation having a small effect on ΔPmax through an increase in Q̇, as observed elsewhere (3). By taking a mean value of G from the two protocols, we have attempted to minimize any effect of ventilation on the measurements of ΔPmax.
A third limitation to the experiment is the possibility that a rise in mixed venous Pco2 during hypercapnia and a fall in mixed venous Pco2 during hypocapnia might independently affect in-flow pressure to the lungs. If this were to occur, then the assumption underlying Eq. 5, namely, that for the lung as a whole ΔPmax may be regarded as a function of both Q̇ and PaCO2, would no longer be valid. We know of no data in humans that address this question, but a study in sheep using extracorporeal circulation separately to elevate mixed venous Pco2 and lower mixed venous Po2 while holding alveolar gas composition constant found little change in pulmonary artery pressure (33). The small changes seen were compatible with being attributable to small changes in Q̇ alone.
Physiological Significance of Calculated Efficiency
The overall efficiency for regulation of v̇/q̇ by the combined effects of CO2 and O2 on the pulmonary vasculature has been estimated in this study at ∼60%. On the one hand, an efficiency of 60%, which corresponds to a closed-loop gain of −1.5, may be considered to provide a reasonable degree of correction in response to a disturbance. On the other hand, other physiological control systems can have far higher closed-loop gains. For example, the steady-state closed-loop gain for the ventilatory system regulating arterial Pco2 is perhaps approximately −20 for an individual who is breathing air under resting conditions. The efficiency associated with this is ∼95%. One possible reason for the limited magnitude of the closed-loop gain for the control of v̇/q̇ is that higher gains could result in an excessive degree of pulmonary hypertension if conditions of global hypercapnia/hypoxia were to occur.
Our calculations are for disturbances of relatively short duration, such as might be generated, for example, by changes in posture or by the known cyclical changes in functional residual capacity with a period between 8 and 28 min (14). Longer disturbances are likely to give rise to greater efficiencies because the sensitivities of pulmonary vasoconstriction to both hypercapnia (2) and hypoxia (23, 39) increase over longer periods. Our calculations apply to healthy lungs under resting conditions, perfused with blood of a standard mixed venous composition and ventilated with air at sea level. Further investigations would be required to assess the roles of hypercapnic and hypoxic pulmonary vasoconstriction in other settings.
There are very few other studies that have tried to assess the functional significance of pulmonary vascular reactivity to CO2 and O2 for v̇/q̇ matching within the normal lung. However, one such study is that of Grant et al. (11), who wedged fine bronchial catheters in subsegmental bronchi of anesthetized coatimundi, measured changes in regional blood flow in response to changes in alveolar gas composition, and applied control theory to these measurements to predict the strength of the feedback control of perfusion provided by the vasomotor responses. In this preparation, it was found that changes in PaO2 around physiological values had larger effects than changes in PaCO2 and that the feedback responses were typically capable of reducing perturbations in regional blood flow to ∼50% of their initial value in the absence of the feedback. The latter result is very similar to the findings of the present study.
Although not within the setting of the normal lung, Brimioulle et al. (5) used stimulus response data from experiments on dogs to estimate the contribution of hypoxic pulmonary vasoconstriction to the matching of perfusion to ventilation in lung injury. Naeije and Brimioulle (24) have interpreted these calculations as suggesting that, in both chronic obstructive pulmonary disease and acute respiratory distress syndrome, hypoxic pulmonary vasoconstriction may typically increase arterial Po2 by up to 20 Torr.
Comparison of Experimental Findings With Other Results From the Literature
The literature contains relatively few data on the effects of CO2 on the pulmonary circulation compared with the immense number of publications on the effects of hypoxia. Indeed, analyses of the control of the pulmonary circulation by alveolar and mixed venous gases have typically considered only the effects of hypoxia (5, 21). The findings of the present study confirm those of earlier studies that showed a marked vasoconstrictor effect of hypercapnia on the pulmonary circulation (2, 4, 16, 17, 34). Few studies have examined the effects of hypocapnia on the pulmonary circulation. In relation to this, one influential view has been that “because of the low initial tone, attempts to vasodilate the normal pulmonary circulation are destined to be fruitless” (9). However, the present study confirms earlier findings in both sheep (34) and humans (2) that hypocapnia induces significant pulmonary vasodilatation within the lung.
A novel finding from this study is that the initial human pulmonary vascular response to CO2 has a time constant of the order of 4–5 min, which is of the same order of magnitude as the time constant of ∼2–3 min that has been reported for the initial human pulmonary vascular response to hypoxia (23, 39). This finding suggests that fairly rapid adjustments can be generated by CO2 as well as by O2 in response to activities such as changes in posture.
GRANTS
This research was supported by the Wellcome Trust and the Dunhill Medical Trust.
DISCLOSURES
No conflicts of interest are declared by the authors.
ACKNOWLEDGMENTS
We thank D. F. O'Connor for techical assistance.
REFERENCES
- 1. Allemann Y, Sartori C, Lepori M, Pierre S, Melot C, Naeije R, Scherrer U, Maggiorini M. Echocardiographic and invasive measurements of pulmonary artery pressure correlate closely at high altitude. Am J Physiol Heart Circ Physiol 279: H2013–H2016, 2000 [DOI] [PubMed] [Google Scholar]
- 2. Balanos GM, Talbot NP, Dorrington KL, Robbins PA. Human pulmonary vascular response to 4 h of hypercapnia and hypocapnia measured using Doppler echocardiography. J Appl Physiol 94: 1543–1551, 2003 [DOI] [PubMed] [Google Scholar]
- 3. Balanos GM, Talbot NP, Robbins PA, Dorrington KL. Separating the direct effect of hypoxia from the indirect effect of changes in cardiac output on the maximum pressure difference across the tricuspid valve in healthy humans. Pflügers Arch 450: 372–380, 2005 [DOI] [PubMed] [Google Scholar]
- 4. Barer GR, Howard P, Shaw JW. Stimulus-response curves for the pulmonary vascular bed to hypoxia and hypercapnia. J Physiol 211: 139–155, 1970 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Brimioulle S, LeJeune P, Naeije R. Effects of hypoxic pulmonary vasoconstriction on pulmonary gas exchange. J Appl Physiol 81: 1535–1543, 1996 [DOI] [PubMed] [Google Scholar]
- 6. Brogan TV, Robertson HT, Lamm WJ, Souders JE, Swenson ER. Carbon dioxide added late in inspiration reduces ventilation-perfusion heterogeneity without causing respiratory acidosis. J Appl Physiol 96: 1894–1898, 2004 [DOI] [PubMed] [Google Scholar]
- 7. Downing SE, Lee JC. Nervous control of the pulmonary circulation. Annu Rev Physiol 42: 199–210, 1980 [DOI] [PubMed] [Google Scholar]
- 8. Emery MJ, Eveland RL, Kim SS, Hildebrandt J, Swenson ER. CO2 relaxes parenchyma in the liquid-filled rat lung. J Appl Physiol 103: 710–716, 2007 [DOI] [PubMed] [Google Scholar]
- 9. Fishman A. The Pulmonary Circulation: Normal and Abnormal. Philadelphia, PA: University of Philadelphia Press, 1990 [Google Scholar]
- 10. Glenny RW, Polissar NL, McKinney S, Robertson HT. Temporal heterogeneity of regional pulmonary perfusion is spatially clustered. J Appl Physiol 79: 986–1001, 1995 [DOI] [PubMed] [Google Scholar]
- 11. Grant BJ, Davies EE, Jones HA, Hughes JM. Local regulation of pulmonary blood flow and ventilation-perfusion ratios in the coatimundi. J Appl Physiol 40: 216–228, 1976 [DOI] [PubMed] [Google Scholar]
- 12. Hakim TS, Michel RP, Minami H, Chang HK. Site of pulmonary hypoxic vasoconstriction studied with arterial and venous occlusion. J Appl Physiol 54: 1298–1302, 1983 [DOI] [PubMed] [Google Scholar]
- 13. Hebb C. Motor innervation of the pulmonary blood vessels of mammals. In: Pulmonary Circulation and Interstitial Space, edited by Fishman AP, Hecht HH. Chicago: University of Chicago, 1966, p. 195–222 [Google Scholar]
- 14. Hlastala MP, Wranne B, Lenfant CJ. Cyclical variations in FRC and other respiratory variables in resting man. J Appl Physiol 34: 670–676, 1973 [DOI] [PubMed] [Google Scholar]
- 15. Kato M, Staub NC. Response of small pulmonary arteries to unilobar hypoxia and hypercapnia. Circ Res 19: 426–440, 1966 [DOI] [PubMed] [Google Scholar]
- 16. Kiely DG, Cargill RI, Lipworth BJ. Effects of hypercapnia on hemodynamic, inotropic, lusitropic, and electrophysiologic indices in humans. Chest 109: 1215–1221, 1996 [DOI] [PubMed] [Google Scholar]
- 17. Kilburn KH, Asmundsson T, Britt RC, Cardon R. Effects of breathing 10 per cent carbon dioxide on the pulmonary circulation of human subjects. Circulation 39: 639–653, 1969 [DOI] [PubMed] [Google Scholar]
- 18. Liu C, Smith TG, Balanos GM, Brooks J, Crosby A, Herigstad M, Dorrington KL, Robbins PA. Lack of involvement of the autonomic nervous system in early ventilatory and pulmonary vascular acclimatization to hypoxia in humans. J Physiol 579: 215–225, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Lodato RF, Michael JR, Murray PA. Absence of neural modulation of hypoxic pulmonary vasoconstriction in conscious dogs. J Appl Physiol 65: 1481–1487, 1988 [DOI] [PubMed] [Google Scholar]
- 20. Lumb AB. Nunn's Applied Respiratory Physiology. Oxford: Butterworth Heinemann, 2000 [Google Scholar]
- 21. Marshall BE, Marshall C, Frasch F, Hanson CW. Role of hypoxic pulmonary vasoconstriction in pulmonary gas exchange and blood flow distribution. 1. Physiologic concepts. Intensive Care Med 20: 291–297, 1994 [DOI] [PubMed] [Google Scholar]
- 22. Marshall C, Marshall B. Site and sensitivity for stimulation of hypoxic pulmonary vasoconstriction. J Appl Physiol 55: 711–716, 1983 [DOI] [PubMed] [Google Scholar]
- 23. Morrell NW, Nijran KS, Biggs T, Seed WA. Magnitude and time course of acute hypoxic pulmonary vasoconstriction in man. Respir Physiol 100: 271–281, 1995 [DOI] [PubMed] [Google Scholar]
- 24. Naeije R, Brimioulle S. Physiology in medicine: importance of hypoxic pulmonary vasoconstriction in maintaining arterial oxygenation during acute respiratory failure. Crit Care 5: 67–71, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Nagasaka Y, Bhattacharya J, Nanjo S, Gropper MA, Staub NC. Micropuncture measurement of lung microvascular pressure profile during hypoxia in cats. Circ Res 54: 90–95, 1984 [DOI] [PubMed] [Google Scholar]
- 26. Nandiwada PA, Hyman AL, Kadowitz PJ. Pulmonary vasodilator responses to vagal stimulation and acetylcholine in the cat. Circ Res 53: 86–95, 1983 [DOI] [PubMed] [Google Scholar]
- 27. Peacock AJ, Challenor V, Sutherland G. Estimation of pulmonary artery pressure by Doppler echocardiography in normal subjects made hypoxic. Respir Med 84: 335–337, 1990 [DOI] [PubMed] [Google Scholar]
- 28. Porcelli RJ, Bergofsky EH. Adrenergic receptors in pulmonary vasoconstrictor responses to gaseous and humoral agents. J Appl Physiol 34: 483–488, 1973 [DOI] [PubMed] [Google Scholar]
- 29. Robbins PA, Swanson GD, Howson MG. A prediction-correction scheme for forcing alveolar gases along certain time courses. J Appl Physiol 52: 1353–1357, 1982 [DOI] [PubMed] [Google Scholar]
- 30. Robertson HT, Kreck TC, Krueger MA. The spatial and temporal heterogeneity of regional ventilation: comparison of measurements by two high-resolution methods. Respir Physiol Neurobiol 148: 85–95, 2005 [DOI] [PubMed] [Google Scholar]
- 31. Robertson HT, Neradilek B, Polissar NL, Glenny RW. Sporadic coordinated shifts of regional ventilation and perfusion in juvenile pigs with normal gas exchange. J Physiol 583: 743–752, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Severinghaus JW. Simple, accurate equations for human blood O2 dissociation computations. J Appl Physiol 46: 599–602, 1979 [DOI] [PubMed] [Google Scholar]
- 33. Shanley CJ, Shah NL, Overbeck MC, Kulkarni NB, Bartlett RH. Effect of independent changes in mixed-venous Pco2 or Po2 on cardiac output in anesthetized sheep. J Surg Res 71: 107–116, 1997 [DOI] [PubMed] [Google Scholar]
- 34. Sheehan DW, Farhi LE. Local pulmonary blood flow: control and gas exchange. Respir Physiol 94: 91–107, 1993 [DOI] [PubMed] [Google Scholar]
- 35. Shirai M, Sada K, Ninomiya I. Effects of regional alveolar hypoxia and hypercapnia on small pulmonary vessels in cats. J Appl Physiol 61: 440–448, 1986 [DOI] [PubMed] [Google Scholar]
- 36. Sun XG, Hansen JE, Stringer WW, Ting H, Wasserman K. Carbon dioxide pressure-concentration relationship in arterial and mixed venous blood during exercise. J Appl Physiol 90: 1798–1810, 2001 [DOI] [PubMed] [Google Scholar]
- 37. Swenson ER, Graham MM, Hlastala MP. Acetazolamide slows VA/Q̇ matching after changes in regional blood flow. J Appl Physiol 78: 1312–1318, 1995 [DOI] [PubMed] [Google Scholar]
- 38. Swenson ER, Robertson HT, Hlastala MP. Effects of carbonic anhydrase inhibition on ventilation-perfusion matching in the dog lung. J Clin Invest 92: 702–709, 1993 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Talbot NP, Balanos GM, Dorrington KL, Robbins PA. Two temporal components within the human pulmonary vascular response to approximately 2 h of isocapnic hypoxia. J Appl Physiol 98: 1125–1139, 2005 [DOI] [PubMed] [Google Scholar]
- 40. West JB. Ventilation/Blood Flow and Gas Exchange. Oxford: Blackwell, 1990 [Google Scholar]
- 41. Wetzel RC, Herold CJ, Zerhouni EA, Robotham JL. Hypoxic bronchodilation. J Appl Physiol 73: 1202–1206, 1992 [DOI] [PubMed] [Google Scholar]
- 42. Yock PG, Popp RL. Noninvasive estimation of right ventricular systolic pressure by Doppler ultrasound in patients with tricuspid regurgitation. Circulation 70: 657–662, 1984 [DOI] [PubMed] [Google Scholar]