Contribution of serial and parallel microperfusion to spatial variability in pulmonary inter- and intra-acinar blood flow

Abstract

This study presents a theoretical model of combined series and parallel perfusion in the human pulmonary acinus that maintains computational simplicity while capturing some important features of acinar structure. The model provides a transition between existing models of perfusion in the large pulmonary blood vessels and the pulmonary microcirculation. Arterioles and venules are represented as distinct elastic vessels that follow the branching structure of the acinar airways. These vessels are assumed to be joined at each generation by capillary sheets that cover the alveoli present at that generation, forming a “ladderlike” structure. Compared with a model structure in which capillary beds connect only the most distal blood vessels in the acinus, the model with combined serial and parallel perfusion provides greater capacity for increased blood flow in the lung via capillary recruitment when the blood pressure is elevated. Stratification of acinar perfusion emerges in the model, with red blood cell transit time significantly larger in the distal portion of the acinus compared with the proximal portion. This proximal-to-distal pattern of perfusion may act in concert with diffusional screening to optimize the potential for gas exchange.

the regional distribution of blood in the lung is determined by the interaction of multiple factors, including gravitational forces acting on the blood and the parenchymal tissue, the structural and material properties of the vascular trees, their interaction with the lung tissue, and the physical properties of the blood. Numerous mathematical models have been proposed to study the origin of isogravitational variability in perfusion and the relationship between pulmonary artery pressure and blood flow. Because of the complex structure of the pulmonary vasculature, most mathematical model analyses treat the macro- and microcirculations separately. However, some models have aimed to describe perfusion through the whole lung from right to left heart (3, 24, 28, 48, 49). These existing computational models of perfusion in the whole lung share some common properties: arteries and veins are modeled as distensible tubes, and blood flow in capillary sheets is calculated via the sheet flow theory of Fung and Sobin (11–15), where branching networks of arteries and veins are assumed to be joined at their terminal vessels by sheets of capillary vessels. That is, no existing model considers the structural detail of the transition that occurs at the level of the pulmonary acinus between large blood vessels and the microcirculation. Theoretical models of gas transport within the lung stress the importance of the branching structure of the pulmonary acinus for effective lung function (37, 42). However, modeling studies of intra-acinar perfusion have not placed the same emphasis on structure (3, 24, 28, 48, 49).

The pulmonary acinus is commonly described as perfused in parallel and ventilated in series (19, 37, 43). However, although much perfusion in the acinus occurs through parallel capillary units, the noncapillary blood vessels within the acinus follow a branching structure similar to that of the respiratory airways (25, 32). Terminal arterioles—the final noncapillary vessels—have been observed to branch from Strahler diameter-ordered arteries as high as order 8 in humans (25). Similarly, terminal veins have been observed to sprout from vessels of high Strahler order (25). Vessel resistance increases rapidly with each generation in the smallest arteries and veins. Assuming an arterial resistance that follows Poiseuille's law, resistance is proportional to vessel length divided by the fourth power of vessel radius. In human arteries with length and diameter as defined by Huang et al. (25), resistance increases by a factor of 10⁵ between order 8 and order 1 (the final precapillary arterioles). Therefore, capillary beds that sprout high up in the arterial tree will have encountered far less resistance to flow than those further down the tree. This implies a variation in blood flow through the precapillary vessels of the acinus that is not captured in previous models of pulmonary perfusion. Indeed, there is direct evidence in rats and dogs (41, 46) and indirect evidence in humans (33, 34) that there is a proximal-to-distal reduction in blood flow through the acinus, which is consistent with an increase in precapillary vessel resistance through the acinus. The intra-acinar distribution of blood may be important in “diffusional screening,” which has been proposed as a phenomenon that influences the efficiency with which the acinus exchanges respiratory gases (37, 42). As oxygen (O₂) traverses distally through the acinar airways during inspiration, its partial pressure on the air side of the gas exchange surface decreases as O₂ crosses to the blood. This could in theory result in a significant concentration gradient that influences the total gas exchange; however, diffusional screening will also be dependent on the distribution of transit times of blood in the alveoli.

Here we build upon the seminal works of West (44, 45) and Fung (11–15) to present a model of perfusion within a human pulmonary acinus that takes into account some key structural properties of acinar blood vessels. We show that the presence of a hierarchical structure of these blood vessels within the acinus results in regional variation in blood flow that may be important in the optimality of gas exchange.

METHODS

Geometric Representation

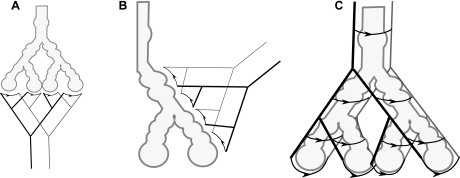
The airways and air spaces in the acinus branch in an irregular dichotomy with an average of nine generations (range 6–12; Ref. 19). Intra-acinar arterioles and venules branch along and between the alveolated airways and have numerous small (precapillary) vessels arising from their walls that lead to the capillary units that cover the alveolar septae (23, 32). Capillaries, on the other hand, have no apparent regular branching structure and are often considered to form a “sheet” structure (12). The acinar airways have previously been represented as an idealized symmetrically branching structure (19, 37), or equivalently as a single path. A model of the acinar circulation with the same structure is shown in Fig. 1A, with symmetrically branching arterioles leading to capillary sheets at the distal alveolar sacs. Here we adopt a description of the acinar blood vessels that distinguishes between small noncapillary and capillary vessels. Arterioles and venules are represented as distinct elastic vessels that follow the branching structure of the acinar airways. These vessels are assumed to be joined at each generation by capillary sheets that cover the alveoli present at that generation, forming a “ladderlike” structure. Nine acinar blood vessel generations are considered, following the idealized symmetric acinar airway structure given in Ref. 19. A visualization of this acinar vascular geometry is shown in Fig. 1C. Geometries used in previous models of acinar oxygen transport, as described by Sapoval et al. (37) are shown for comparison (Fig. 1, A and B). The study of Sapoval et al. considered air side function only, but the blood vessels shown in these images reflect the structure of perfusion models with all capillary beds occurring at the same level within the arterial tree (19, 37).

Fig. 1.

A and B: an acinar unit perfused only at the alveolar sacs (A) and an acinar unit perfused at each generation but with capillary units assumed to be identical (B). C: a visualization of the acinar geometry used here to model perfusion in the acinus. Capillary units are marked with arrows in the direction of blood flow to allow clear distinction from larger noncapillary vessels. The acinar configurations shown in A and B represent those depicted in Fig. 1 of Ref. 37.

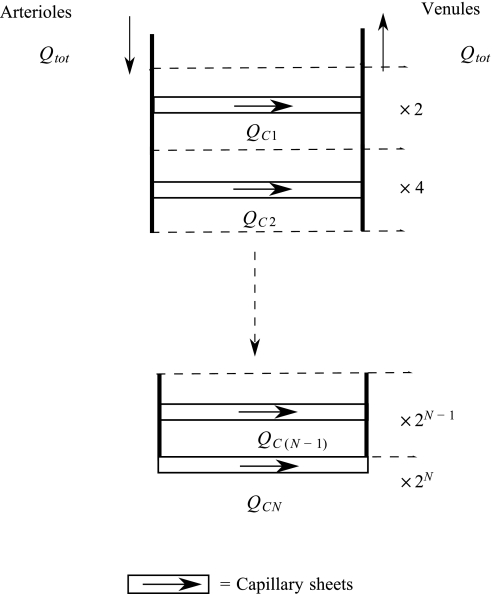
Following the approach of Fung et al. (11–15), capillary beds are modeled as sheets that are the diameter of a capillary apart and supported by “posts” of septal tissue. Capillary beds can arise from all arterioles that accompany the acinar airways, and can take several different structures. They may arise directly from the side of vessels, after short precapillary vessels, or they may form capillary loops terminating an arteriole (23, 32). The blood pressure entering and leaving a capillary sheet at the midpoint of each arteriole and venule generation is assumed to be a good approximation to the average pressures into and out of pre- and postcapillary vessels arising from this generation. A capillary sheet then joins the midpoint of each arteriolar branch to its corresponding venule branch. This results in a ladderlike structure as shown in Fig. 2, with perfusion occurring both in parallel and in series. Each sheet represents the capillary bed over multiple alveoli (with ∼10–15 alveoli per sheet) and may have several feeding precapillary vessels; the small precapillary vessels that do not follow the branching structure of the larger arterioles and venules and have diameters approaching those of the capillary vessels are incorporated into the sheet for modeling purposes.

Fig. 2.

A symmetric branching arteriole/venule structure with N symmetric branches, joined by capillary sheets at each generation. Arrows show the direction of blood flow. Dashed lines represent a bifurcation in the arterioles and venules and so a doubling in the number of arterioles, venules, and capillary sheets. Q_tot, total blood flow into system; Q_C, flow through capillary sheet.

Flow across each arteriole, venule, and capillary segment satisfies

$$\Delta {\text{P}}_{\text{S}}={\text{Q}}_{\text{S}}{\text{R}}_{\text{S}}$$ (1)

where ΔP_S is the pressure drop, Q_S is the flow, and R_S is the resistance across each individual vessel segment S. Resistance across each segment depends on the classification (arteriole, venule, or capillary) of the vessel in question.

Resistance in arteriole and venule segments.

Resistance in each arteriole and venule segment is described with Poiseuille's equation. In generation j the resistance in each segment of arteriole (R_Aj) or venule (R_Vj) is then

$$R_{xj}=\frac{8{\mu }_{xj}{L}_{xj}}{\pi r_{xj}^4}$$ (2)

with x = A, V representing arterioles and venules respectively. Here L_xj represents the length, r_xj the radius, and μ_xj the apparent viscosity of blood in a vessel segment in generation j.

Arterioles and venules are elastic, and thus vessel segment radii are a function of transmural pressure, P_tm; in the acinus the vessel transmural pressure is approximately the difference between blood (P_b) and alveolar (P_alv) pressure (11). The relationship between radius and transmural pressure has been shown to be approximately linear in small pulmonary blood vessels, for P_tm less than some upper bound (21, 47), P_U. Thus vessel radius is modeled as a piecewise linear function

$$r_{xj}=\{\begin{array}{cc}0,& {\text{P}}_{\text{tm}}<0,\\ r_{xj}^{\prime }\left(1+{\alpha }_{xj}{\text{P}}_{\text{tm}}\right),& 0\le {\text{P}}_{\text{tm}}<{\text{P}}_{\text{U}},\\ r_{xj}\left(1+{\alpha }_{xj}{\text{P}}_{\text{U}}\right)& {\text{P}}_{\text{tm}}\ge {\text{P}}_{\text{U}},\end{array}$$ (3)

where r_xj′ is the unstrained (P_tm = 0) radius of the vessel and α_xj is an elasticity constant. It has been shown that in pulmonary vessels α_xj may be considered as independent of vessel diameter and species (9, 28, 35).

The apparent viscosity μ_xj of blood in small vessels is dependent on factors such as hematocrit and vessel size (11, 26). Here we follow Fung (p. 379, Ref. 11) and assume that μ_xj varies linearly with generation from 4.0 × 10⁻³ to 1.92 × 10⁻³ Pa·s in the largest to smallest acinar vessels, respectively.

The unstrained radius r_xj′ and length L_xj of a vessel segment depend on its position within the acinus. Krenz and Dawson (28) observed that morphometric data on vessel lengths and diameters across species fit reasonably well to

$$N_{xj}=a_{1X}{\left(2r_{xj}^{\prime }\right)}^{-{\beta }_{1X}},\hspace{0.17em}{L}_{xj}=a_{2X}{\left(2r_{xj}^{\prime }\right)}^{-{\beta }_{2X}}$$ (4)

where a_1x, a_2x, β_1x, and β_2x are constants fitted to morphometric data and N_xj is the number of vessels in generation (or order) j. Here, the constants a_1x, a_2x, β_1x, and β_2x were obtained for humans by regression analysis, assuming a symmetric vascular tree and using combined morphometric data from human studies (23, 25, 38).

Resistance in capillaries.

In the capillaries resistance is described with the sheet flow model of Fung and Sobin (11–15). In the sheet flow model, pressure and velocity are averaged in the x-y plane of the capillary sheet and the mean blood flow rate (Q̄) per unit width of the pulmonary alveolar sheet is

$$\overline{Q}=\frac{1}{{\mu }_{c}f}{H}^3\nabla \left({\text{P}}_{\text{tm}}\right)$$

where μ_C is apparent viscosity of blood in the capillaries, f is a numerical factor that depends on the sheet characteristics, and H is the local mean capillary sheet thickness (12). Alveolar pressure is held constant at atmospheric pressure (0 Pa) in this work, consistent with zero airflow.

Flow through the alveolar sheet is calculated by integrating the mean flow along each streamline through the sheet

$$\text{Q}\hspace{0.17em}\text{=}\hspace{0.17em}\frac{\text{S}A}{{\mu }_{c}f{l}_c^2}{\displaystyle \int H^3\frac{{\text{dP}}_{\text{tm}}}{\text{ds}}\text{ds}}$$ (5)

where A is the area of the capillary sheet, S is the vascular space-tissue ratio (the proportion of the sheet that is comprised of capillaries), and l_C is the average path length from a single arteriole to a single venule (12). Resistance across the capillary sheet is equal to the flow through the capillary sheet divided by the pressure drop across the sheet. Mean blood transit times (TT) through capillary sheets can also be calculated with the theory of Fung and Sobin (12) by dividing the mean path length from arteriole to venule (l_C) by the mean flow velocity in the capillary sheet. This results in the formula

$$\text{TT}=\frac{{\mu }_{c}f{l}_c^2}{{\displaystyle \int H^2\frac{{\text{dP}}_{\text{tm}}}{\text{ds}}\text{ds}}}$$ (6)

Mean transit times give an indication of the rate at which blood passes through a capillary sheet. However, it should be noted that the mean value of a transit time distribution does not give a complete picture of the distribution of blood flow within the capillary bed.

The thickness of the capillary sheet H is approximately linearly dependent on P_tm up to some threshold value (13) and so is represented by a piecewise linear function in the same manner as arteriole and venule radius

$$H=\{\begin{array}{cc}0,& {\text{P}}_{\text{tm}}<0,\\ H\prime \left(1+{\alpha }_c{\text{P}}_{\text{tm}}\right),& 0\le {\text{P}}_{\text{tm}}<{\text{P}}_{\text{CU}},\\ H_{\max }\hspace{0.17em}=\hspace{0.17em}H\prime \left(1+{\alpha }_c{\text{P}}_{\text{CU}}\right)& {\text{P}}_{\text{tm}}\ge {\text{P}}_{\text{CU}},\end{array}$$ (7)

where H′ is the unstrained height of the capillary sheet, α_c is an elasticity constant for the sheet, and P_CU is an upper bound for pressure beyond which sheet height is approximately constant. Calculations for blood flow and transit time through the capillary sheet depend on the value of P_tm at both the arterial and venous sides of the capillary sheet, respectively. Explicit calculations are given in the appendix.

The total alveolar surface area (146 m²) and capillary surface area (126 m²) in a human lung have been estimated from morphometric measurements by Gehr et al. (16). The ratio of capillary surface area to alveolar surface area gives a value for S of 0.86. Gehr's measurements were made at full inflation [so at approximately total lung capacity (TLC)]. The total alveolar surface area represents the surface available for gas exchange. Because capillary sheets have two surfaces in contact with the alveolar air, the total physical capillary sheet area in the lung is 73 m². An estimate for the total number of acini in a human lung is 2¹⁵; therefore individual sheet surface area at TLC, A_TLC, is estimated to be

$$A_{\text{TLC}}\hspace{0.17em}=\hspace{0.17em}\frac{73}{2^{15}{\displaystyle \sum _{i=1}^{i=9}{2}^i}}{\text{m}}^2$$

This assumes that the alveolar sheets connecting each arteriole and venule have equal surface area.

Estimates for sheet surface area must be scaled to estimate perfusion distribution in the acinus when alveoli are not fully expanded. The transpulmonary pressure-volume (P-V) relationship for whole lungs has a characteristic sigmoidal shape (40). Mercer et al. (31) have shown that P-V curves in individual rat alveoli have a similar form. We assume a simple P-V relationship that describes P-V well for volumes >50%.

$$\text{V}\left({\text{P}}_{\text{tp}}\right)={\text{V}}_{\text{TLC}}-\left({\text{V}}_{\text{TLC}}-{\text{V}}_{\text{ref}}\right)e^{-{\text{CP}}_{\text{tp}}}$$ (8)

where V_TLC is lung volume at TLC (100% volume), V_ref is a reference lung volume that corresponds to zero transpulmonary pressure (P_tp), and C is a constant reflecting the lung compliance. A representative reference volume for a human lung may reasonably be considered to be 20% of the volume at TLC (29). The parameter C is assigned a value of 0.1 cmH₂O⁻¹ (2), and P_tp depends on the position of the acinus within the lung. An estimate for the surface area of a capillary sheet for a given transpulmonary pressure is then

$$A=A_{\text{TLC}}{\left(\frac{\text{V}}{{\text{V}}_{\text{TLC}}}\right)}^{2/3}=A_{\text{TLC}}{\left(1-0.8e^{-{\text{CP}}_{\text{tp}}}\right)}^{2/3}$$

We similarly scale the parameter l_C, the average path length from arteriole to venule, using

$$l_c=l_{\text{TLC}}{\left(\frac{\text{V}}{{\text{V}}_{\text{TLC}}}\right)}^{2/3}$$

where l_TLC is the average path length at TLC.

Zone 2 flow.

In West's zone 2, there is a possibility of some parts of the alveolar sheet being collapsed. This occurs when venous blood pressures are less than alveolar pressures. Flow is maintained through the corner vessels [the vessels where 3 septa meet between adjacent alveoli (6)] or by arterial pressure being sufficiently high to maintain a “waterfall effect.” This effect occurs when arterial side pressure is sufficient to maintain flow through the capillary bed independent of the downstream venous side pressures. Because the sheet flow model is an averaged model, it is unable to give a detailed description of flow in zone 2. However, Fung and Yen (15) constructed a theory to account for a reduction of capillary flow due to collapsed vessels under zone 2 conditions. The maximum possible flow through the sheets is given by traditional sheet flow theory, with P_tm set to zero at the venous side of the sheet. This maximum flow, however, is unlikely to be obtained because of sheet collapse. The flow rates (and transit times) under these conditions are then scaled by

$$1-F+\text{Fexp}\left[-\frac{{\left({\text{P}}_{\text{bv}}-{\text{P}}_{\text{alv}}\right)}^2}{2{\sigma }^2}\right]$$

where F is the maximum possible proportion of the sheet that can be collapsed, P_bV is the blood pressure at the venous side of the sheet, and σ is a constant that affects the extent of capillary sheet collapse with decreasing venous blood pressure (15). These parameters are not established in the literature for the human lung, and so values measured in the cat lung (11) are used in the present study.

Conservation of flow.

Flow must be conserved through the acinar blood vessels. We define Q_tot to be the total flow into the system from the blood vessels that accompany the transitional bronchioles. All flow through the system must pass through a capillary sheet, and thus

$${\text{Q}}_{\text{tot}}={\displaystyle \sum _{j=1}^9{2}^j{\text{Q}}_{\text{C}j}}$$ (9)

where Q_Cj is flow through a capillary sheet attached to an arteriole of generation j.

Model Solution

The nonlinear equations relating pressure, flow, and resistance in each vessel segment (Eq. 1), along with continuity of flow (Eq. 9), can be solved if two boundary conditions are prescribed. These boundary conditions can be any two of blood pressure into the acinus (P_in), blood pressure at the venous exit of the acinus (P_out), or total blood flow through the acinus (Q_tot). The model equations were solved by calculating resistance for an initial pressure distribution, solving the governing equations assuming the calculated resistance, and updating iteratively until convergence was achieved. Because the system of equations solved at each iteration was linear, the converged solution was unique for any given initial pressure distribution. The final converged solution was insensitive to choices of this pressure distribution, implying a unique solution.

Acinar model: gravitationally dependent perfusion heterogeneities.

Gravitationally dependent perfusion heterogeneities were investigated assuming a linear increase in intrapleural pressure (P_pl) down the lung of 24.52 Pa (0.25 cmH₂O)/cm lung height, a linear increase in (arterial and venous) blood pressure of 98.06 Pa (1 cmH₂O)/cm lung height, (6) and a pressure drop across the acinus of 784.48 Pa (8 cmH₂O). The gravitational reference height used was 14 cm (midlung). The value of P_pl was set at −416.76 Pa (−4.25 cmH₂O) at the reference height to represent a lung at approximately functional residual capacity (FRC).

Full circuit models.

To illustrate the significance of capillary connections throughout the generations of acinar blood vessels, a simple model of perfusion in a whole human lung was constructed. The lung was assumed to consist of 25 symmetric generations of arteries and veins; extra-acinar vessels were represented by the first 16 generations and intra-acinar vessels by the final 9 generations. Resistance in extra-acinar blood vessels was described with Poiseuille's equation (Eq. 2), with vessel radius and length defined by Eqs. 3 and 4. The apparent viscosity of blood in these vessels was assumed constant and equal to that in the largest acinar vessels (4.0 × 10⁻³ Pa·s). Two models for perfusion in the nine acinar generations are considered: circuit model A consists of nine symmetric blood vessel generations connected by a capillary bed only at the final generation; circuit model B is the ladder-type model as described above, with capillary connections at each acinar generation. The total area of the capillary bed was held constant between models. The pressure at the inlet to the arteries was assumed to equal pulmonary arterial pressure (PAP), and the pressure at the outlet from the veins was assumed to equal left atrial pressure (LAP) (see Table 2 for pressure values).

Table 2.

Comparison of model predictions to literature values of perfusion measures

	Reference	Literature Values	Circuit Model A	Circuit Model B
PAP at rest, mmHg	18	10 (diastolic), 25 (systolic)	17–25 (input)	17–25 (input)
LAP at rest, mmHg	8, 11, 35	4.0–10	7 (input)	7 (input)
PVR, dyn · s · cm−5	36	<240	286	235
Flow through lungs at rest, l/min	11, 22, 30	4.0–6.5	2.8–5.0	3.4–6.1
% Pressure drop through arteries	1, 9, 20	20–50 (dog)	22.6	23.1
% Pressure drop through acinus			82.7	79.1–79.0

Units are converted from SI units to those commonly used in the literature. Because pulmonary arterial pressure (PAP) varies over a heartbeat, a range of values for this parameter was used for model input. Output values given correspond to the extremes of the range for input PAP. LAP, left atrial pressure; PVR, pulmonary vascular resistance.

RESULTS

Acinar Model: Gravitationally Dependent Perfusion Heterogeneities

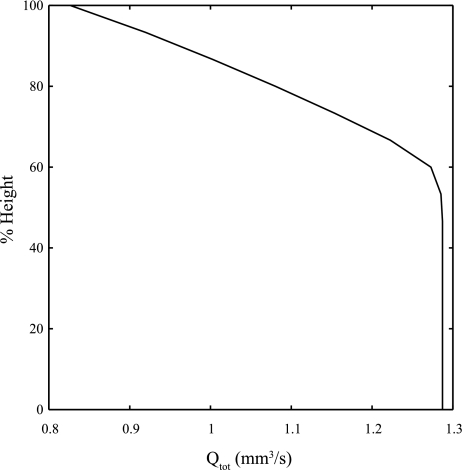
Figure 3 shows model predictions of flow per acinus (Q_tot) over a 30-cm upright lung with gravitationally dependent pressure boundary conditions. Flow increases with decreasing vertical height (along the craniocaudal axis) in the upper portion of the lung, corresponding to zones 2 and 3 of West's zonal flow model. In the lower region of the lung model where arterial and venous pressures are greater than P_CU, we assume a constant difference in pressure across the sheets and our model predicts that the capillary sheets are fully distended. This means that the model flow in this region is independent of vertical height even though it is by definition in zone 3 (or 4) of West's zonal model. This occurs because the model excludes any effect of variation in preacinar resistance pathways on either side of the acinar model.

Fig. 3.

Acinar model predictions of total flow through an acinus plotted against % vertical height in a 30-cm upright lung. A linear increase in intrapleural pressure down the lung of 24.52 Pa (0.25 cmH₂O)/cm lung height, a linear increase in (arterial and venous) blood pressure of 98.06 Pa (1 cmH₂O)/cm lung height, and a constant pressure drop across the acinus of 784.48 Pa (8 cmH₂O) are assumed.

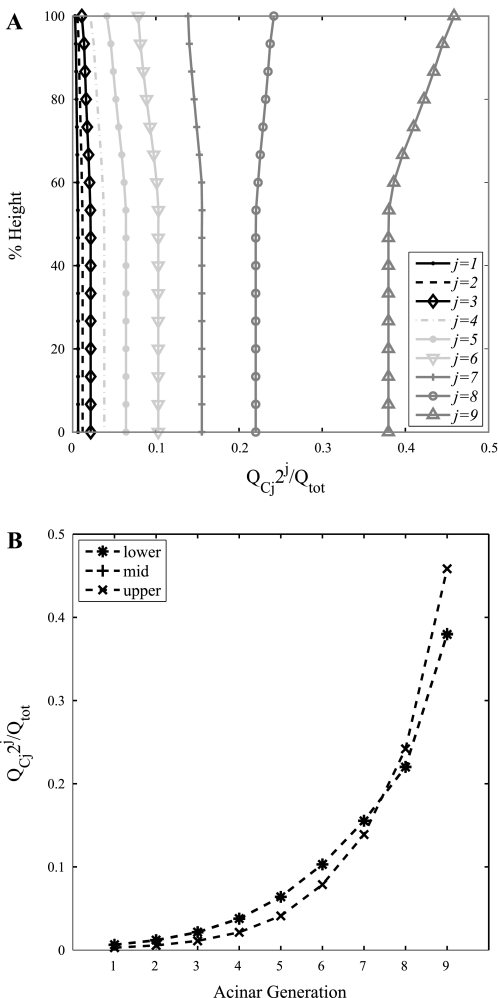
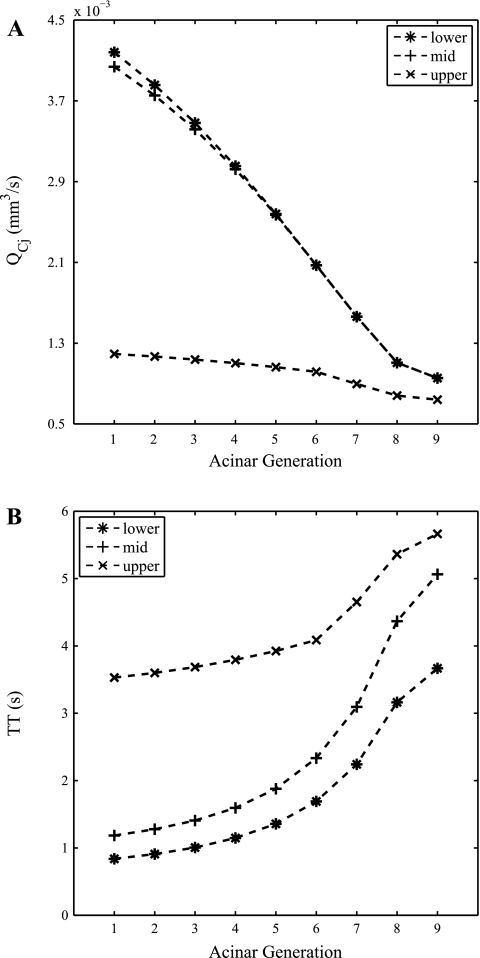
Figure 4A shows model predictions of the proportion of the total flow through an acinus that passes through capillary sheets arising from each generation of acinar arterioles. The acinar model predicts that the majority of blood flows through the distal acinar generations, which is to be expected because this is where the majority of alveoli reside. In the upper region of the lung more blood flows through the distal part of the acinus than in the lower region of the lung. To further illustrate this result, the proportion of flow passing through each acinar generation in three representative acini in the upper, middle, and lower regions (corresponding to heights of 2, 14, and 28 cm in the upright lung) are plotted in Fig. 4B. This shows that the proportions of flow through each acinar generation in the lower and midlung are indistinguishable from one another and increase distally through the acinus. Although the proportion of flow into the acinus that passes through each capillary generation increases from the proximal to the distal vessels, the rate of flow decreases through the generations. This decrease in flow rate is illustrated in Fig. 5A and is associated with an increase in mean transit time as shown in Fig. 5B.

Fig. 4.

Acinar model predictions of the proportion of the total flow into the acinus that passes through capillaries branching from each acinar generation, plotted against vertical height in a 30-cm upright lung (A) and for 3 representative acini (B) in the upper [blood pressure into (P_in; 588.36 Pa) and out of (P_out; −196.02 Pa) acinus and intrapleural pressure (P_pl; −759.97 Pa); 28-cm height], middle (P_in 1,961.2 Pa, P_out 1,176.7 Pa, P_pl −416.76 Pa; 14-cm height), and lower (P_in 3,137.9 Pa, P_out 2,353.4 Pa, P_pl −122.58 Pa; 2-cm height) regions of the lung. The majority of blood flows through the distal portion of the acinus throughout the lung, but this is more pronounced in the nondependent upper region of the lung. Q_Cj, Q_C for acinar generation j.

Fig. 5.

Acinar model predictions of flow through a capillary sheet in each acinar generation (A) and mean blood transit times (TT) through representative acini in the upper, middle, and lower regions of the lung (B). Flow profiles differ significantly between the dependent and nondependent regions of the lung.

An analysis of the sensitivity of acinar blood flow to model parameters is given in Table 1. The model is relatively insensitive to those parameters that have not been accurately determined in the human lung (C, F, and σ). The parameters that the model is most sensitive to, namely, the regression coefficients, particularly β_1A and β_1V, have been obtained from the results of detailed morphometric studies. This allows some confidence in the results of this computational study. However, accurate experimental determination of unknown parameters and those to which the model is most sensitive would of course improve its accuracy.

Table 1.

Model parameters and sensitivity analysis (% change in total flow through acinus for ±10% change in parameter value in a representative midlung acinus)

				Sensitivity in Qtot to
	Parameter	Value	Reference	10% Increase	10% Decrease
a1A	Regression constant (no units)	8.13	See text	−3.9%	+3.3%
a1V	Regression constant (no units)	7.55	See text	−6.3%	+5.8%
a2A	Regression constant (no units)	1.05	See text	+2.8%	−2.6%
a2V	Regression constant (no units)	1.23	See text	+4.8%	−4.3%
A	Area of capillary sheet, m2	See text	See text	+3.0%	−2.7%
aAj, αVj	Elasticity constant for arterioles and venules, Pa−1	1.33 × 10−6	9, 28, 35	<1%	<1%
αC	Elasticity constant of capillary sheets, m/Pa	1.30 × 10−9	11	+3.0%	−2.9%
β1A	Regression constant (no units)	2.45	See text	−22%	+14%
β1V	Regression constant (no units)	2.42	See text	−34%	+30%
β2A	Regression constant (no units)	0.75	See text	−4.4%	+4.1%
β2V	Regression constant (no units)	0.78	See text	−9.4%	+9.7%
C	Numerical constant, Pa−1	0.1	See text	<1%	<1%
f	Numerical constant (no units)	21.6	12	−3.0%	+2.7%
F	Highest proportion of sheet collapse (no units)	0.104	15	<1%a	<1%*
H′	Unstrained sheet height, m	3.5 × 10−6	11	+5.6%	−5.4%
lTLC	Average path length from arteriole to venule, m	1,186 × 10−6	48	+6.0%	−5.3%
S	Vascular space-to-tissue ratio (no units)	0.86	16	+3.0%	−2.7%
σ	Numerical constant, Pa	436 Pa = 4.45 cmH2O	15	<1%a	<1%*
Palv	Alveolar pressure, Pa	0		N/A	N/A
PU, PCU	Upper bounds for linear pressure-radius/height relations, Pa	1,471 Pa = 15 cmH2O	11	−2.9%	+2.4%
μC	Apparent capillary blood viscosity, Pa · s	1.92 × 10−3	11, 47	−3.0%	+2.7%
μAj, μVj	Apparent blood viscosity in arterioles/venules, Pa · s	4.0 × 10−3, −1.92 × 10−3	See text	+11%	−9%

Q_tot, total flow through acinus; N/A, not applicable.

^*Because the parameters F and σ are related to zone 2 conditions, which occur in the upper regions of the lung, the sensitivity analysis for these parameters was carried out in a representative acinus located in the upper lung.

Full Circuit Models

Table 2 provides comparison between the two models of perfusion in an idealized lung circuit (circuit models A and B) and with values from the literature for perfusion measures. Both models compare well with measurements from the literature; however, model A has a higher pulmonary vascular resistance (PVR).

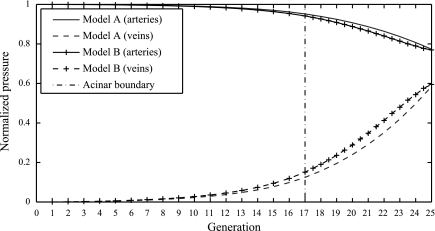
Figure 6 shows blood pressure (normalized so that PAP equals 1 and LAP equals 0) versus blood vessel generation as predicted by each model. Circuit model A, which has the same structure as previous models of the whole lung, shows a normalized pressure drop across the full arterial and venous trees that is very similar to that predicted by circuit model B, which incorporates our new acinar perfusion model. However, the difference in predictions of the nature of the pressure drop within the arterial and venous trees given by the two models is small but significant. Circuit model B predicts a smaller pressure drop across the acinus than circuit model A. The difference allows circuit model B to carry blood at a higher flow rate than model A. Table 2 shows that for a given pressure drop though the lung PVR is decreased, and so flow is increased in circuit model B compared with circuit model A. Under these conditions circuit model B represents an increase in flow of >20% of the flow predicted by circuit model A due to reduced vascular resistance.

Fig. 6.

Normalized blood pressure drop across the arteries (solid lines) and veins (dashed lines) plotted across 25 symmetric blood vessel generations with acinar blood flow described as a symmetric branching structure connected only at the final generation by capillary beds (circuit model A) and connected at each generation by capillary beds (circuit model B). Pressures are normalized so that pulmonary arterial pressure equals 1 and left atrial pressure equals 0.

Matlab (Version 7, 2007, The Mathworks) code that is capable of reproducing the results of Figs. 3–6 and Table 2 accompanies this article as Supplemental Material.¹

DISCUSSION

Previous studies of pulmonary perfusion have generally considered “large-scale” effects—such as the contribution of arterial and venous branching structure—separately from microvascular effects. We have developed a mathematical model of perfusion in the pulmonary acinus and applied this model, along with pressure boundary conditions, to simulate combined serial and parallel perfusion within the acini of the upright lung. Assuming a linear gravitational gradient in pleural and blood pressures, our model successfully predicts the trends in flow rate with lung height that are related to the structure and function of small blood vessels, that is, the presence of zone 2 where the “waterfall effect' is observed and an increase in flow with pressure as capillary beds are recruited to their maximum height. The ladderlike structure of this model allows recruitment and distension of capillary sheets nonuniformly within the acinus, which is an advance over previous models, and may be important in understanding the distribution of gas exchange within the acinus.

Inter-acinar Distributions of Perfusion: Zonal Flow

In the upper region of the lung, under the conditions modeled here, alveolar pressure is zero and the blood pressure at the venous side of the acinus is negative. When pressure on the venous side of a capillary sheet is less than alveolar pressure, some portion of the capillary sheet is collapsed and flow through that sheet depends only on the pressure at the arterial side of the sheet (see Zone 2 flow above). Although the pressure drop across the whole acinus is constant in each region of the lung considered, acini with negative venous exit pressures have collapsed areas of capillary bed. The rate of flow through proximal capillary sheets with collapsed areas is reduced compared with the rate of flow in completely open capillary sheets (such as those lower down the lung), even if the pressure drop across the sheets is the same. This reduction in flow through capillary sheets in the first generations of the acinus allows more blood to pass through to the distal generations, and so flow through the most distal capillary sheets is proportionally increased. When the arterial and venous blood pressures are increased (thereby eliminating zone 2 flow), flow distributions throughout the lung tend to those observed in the middle and lower section of the lungs in Fig. 4.

Although predictions of the rate of blood flow in the lower and middle regions of the lung are very similar (Fig. 5A), transit times in the midregion of the lung are up to 1.5 s longer than those in the lower lung (Fig. 5B). This occurs because of nonuniform alveolar inflation over the height of the lung, a result of the pleural pressure gradient in the lung and its relation to volume (Eq. 8). Midlung capillary beds are more “stretched out” than those in the lower lung, because of alveolar expansion. Therefore, blood pathway length in the midlung is increased and transit times are longer compared with the lower lung.

Physiologically, an increase in the blood flow and pressure gradient across the lung may occur as a result of exercise. In humans, the intra-acinar gradient of blood flow has been observed to be altered in some subjects during exercise (33); these subjects also showed a redistribution of blood flow to the upper regions of the lung following exercise. Increasing the pressure drop across each model acinus increases the flow through that acinus but reduces the proportion of the lung in which predicted flow is dependent on vertical height. This is consistent with the recruitment of areas of capillary beds that are collapsed in zone 2 under normal conditions but open with increased blood pressures. Under these conditions the acini in the upper region of the lung have increased potential to recruit areas of capillary bed compared with those lower down the lung.

In the lower region of the model where the sheets are fully distended the model flow is independent of vertical height. This is in contrast to the traditional description of zone 3, where flow increases with decreasing vertical height. This occurs in the model because it does not include branching asymmetry in the preacinar structure, and therefore there is no difference in the pressure differential across the acini that are modeled at different vertical locations. Capillary sheets become fully distended in our model because the transmural pressure exceeds the upper bound beyond which sheet height is approximately constant (P_CU). The value of 15 cmH₂O used here for P_CU has been cited in modeling studies as the appropriate value in the human lung (11, 49). However, in the cat lung P_CU is cited as 25 cmH₂O (11, 49), and earlier studies in humans by the same authors suggest P_CU may be as high as 32 cmH₂O (39, 47). Increasing P_CU in our model has the effect of reducing the proportion of the lung in which flow is independent of vertical height and increasing the proportion of the lung in which the traditional zone 3 is present. Zone 4 flow is not present within the isolated acinar flow model. Zone 4, the region of reduced flow in the most dependent region, is a consequence of fluid dynamics in the pre-acinar arteries (5, 27, 44) and therefore is not expected to be reproduced by a model of perfusion in the acinus.

Intra-acinar Distributions of Perfusion: Serial and Parallel Perfusion

Our model—parameterized with human data and animal data where human data were not available—showed a decrease in blood flow rate from the proximal to the distal vessels within the acinus with the ratio of flow rates at the proximal end to the distal end of the acinus of ∼4:1 in the lower and midlung and 1.5:1 in the upper lung. West et al. (46) estimated that in the secondary lobule of dogs flow differs by ∼20% between the proximal and distal vessels (a ratio of 1.2:1). In rats, estimates for this decrease in flow are higher, with an approximate ratio of flows from the apex to the base of the secondary lobule of 4:1 (41, 46). On the basis of these experimental studies Wagner et al. (41) and Read (34) suggest that the anatomic structure of the noncapillary acinar vessels is the major factor responsible for the decrease in blood flow through the acinus. This led the authors of these studies to develop a conceptual model of blood flow in the secondary lung lobule that is very similar in structure to our model geometry (see Figs. 9 and 2 of Refs. 41 and 34, respectively).

A decrease in the rate of blood flow through the acinus is of significance when considering oxygen (O₂) transport. O₂ transport in the conducting airways is primarily by advection; in the acinus the predominant transport mechanism is diffusion. Diffusion to the periphery of the acinus is accompanied by diffusion into the bloodstream. According to the theory of “diffusional screening” (37, 42), the continual movement of O₂ into the blood means that its concentration at the most distal gas exchange surface could theoretically be quite low. Our model suggests an increase in red blood cell (RBC) transit time in the distal portion of the acinus compared with the proximal portion. This reduces the potential for disparity in ventilation-to-perfusion ratios (V′/Q′) within the acinus compared with the case of a close to homogeneous blood flow throughout the acinus (34). Because an increased RBC transit time will increase the potential for O₂ uptake from inhaled air to the blood and/or CO₂ release from blood to air, the arrangement of the acinar blood vessels may act in concert with diffusional screening to optimize the potential for gas exchange. Previous representations of acinar perfusion with capillary sheets only at the terminal generation imply that gas exchange occurs only at a single location; hence such a model cannot be used to investigate this possibility.

Symmetric Lung Circuit

A validation of our model of acinar perfusion is gained through its coupling with an idealized model of perfusion in the whole lung (circuit model B) and its comparison with the classic model that neglects acinar structure (circuit model A). The pressure drop across the venous tree predicted by both models is larger than that across the arterial tree because veins are (in general) smaller than their corresponding arteries. The normalized pressure drops are largely independent of inlet and outlet pressures and are determined by the relative radii of arteries and veins. This result is in agreement with the study of Krenz and Dawson (28), who showed that in an arteriovenous network with common distensibility in each vessel the fraction of the total flow passing through each vessel segment is constant. This is the case in the arterial and venous structures considered here, although a small variation occurs because the capillary segments joining the arterial and venous trees do not distend in the same manner as the larger blood vessels. Pressure drops across pulmonary arteries down to diameters of 20–50 μm have been measured in dogs, with estimates of pulmonary arterial pressure drops ranging from 20% to 50% of the total pulmonary pressure drop (1, 9, 20). Both models considered here give an arterial pressure drop of 22.6–23.1% in humans, which corresponds well to that observed in dogs. Although circuit models A and B predict very similar normalized pressure drops across the lung, circuit model B provides additional information about differences in flow rates and transit times within the acinus that circuit model A is not able to capture.

Although there is some variation in literature estimates of normal pulmonary blood pressures and PVR, values of mean PAP of >25 mmHg and PVR of >240 dyn·s·cm⁻⁵ are considered to be clinically significant cutoff points for abnormal lung function (36). To achieve pulmonary blood flow in the normal range of 4.0–6.5 l/min (11, 22, 30, 35), model A must have inlet pressures that are close to or above what is considered to be normal for PAP. Circuit model A also predicts PVR values above the normal range. PVR as predicted by circuit model B (which incorporates our acinar model) may still be considered high but falls within a normal range. Normal pulmonary blood flow is also achievable in model B without leaving the range of normal PAP. This suggests that the structure of the acinar blood vessels is crucial to the ability of the lung to carry high volumes of blood with a relatively small driving pressure gradient. A possible reason for the PVR predicted by circuit model B being at the high end of what is considered normal is the omission of supernumerary vessels from the model described here. Supernumerary vessels (10) sprout directly from large pulmonary blood vessels to supply the nearest acinar unit. Additional perfusion via vessels such as these may provide increased flow to the acinus, even under normal lung function, hence reducing PVR. A small decrease in PVR occurs with increasing PAP; this decrease may be more significant in a nonsymmetric model geometry with geometric and gravitational influences playing a larger role.

Model Limitations

Fung's sheet flow model relies on the geometric simplification that represents flow in the pulmonary microcirculation as occurring between parallel plates supported by posts of connective tissue, rather than representing the capillary bed as a network of branching tubules (17). This geometric and mathematical simplification results in a model of averaged flow in the capillary bed, which necessarily results in some loss in the detail of flow heterogeneity in the microcirculation. However, Fung's approach is based on a thorough fluid dynamical analysis, and the model is in general agreement with experimental data for flow and resistance across the pulmonary capillary bed.

Capillary beds connecting each arteriole and venule in the acinar structure are here assumed to be identical in size. This follows Haefeli-Bleuer and Weibel (19) and puts ∼0.2% of the total capillary surface area in acinar generation 1 and 50% in generation 9. The first two or three generations of airways within the acinus are not completely alveolarized (19), and connections between arterioles and veins are certainly less frequent at high compared with low Strahler order (25). Our model may therefore slightly overestimate the proportion of blood flow that occurs through generations 1–3.

For illustrative purposes our acinar perfusion model was coupled to symmetric arterial and venous trees. The asymmetric structure of the large blood vessels and gravity have previously been shown to influence the heterogeneity of pulmonary blood flow (5). Similarly, assuming a symmetric acinar branching structure may underestimate perfusion heterogeneity in the acinus. However, these simplifications allow for a computationally straightforward perfusion model that is able to provide insight into the effects of acinar structure on perfusion across a population. An advantage of a computationally straightforward model for acinar blood flow is its potential for coupling to computationally expensive models describing perfusion in anatomically realistic large blood vessels (4, 5) or capillary beds (6). The concepts discussed in this article could be applied to anatomically realistic arteriole and venule branching structures if detailed morphometric studies of these blood vessels become available in the future.

A steady laminar blood flow is assumed in the acinus for modeling purposes. The assumption of laminar blood flow may underestimate vascular resistance, and does not account for a reduction in flow rate at vessel bifurcations. However, turbulent flow is unlikely to occur in any but the largest pulmonary blood vessels, because Reynolds numbers in the pulmonary blood vessels are generally sufficiently small. This study focuses on the distribution of flow through the acinus, and information gained from simplified flow equations is sufficient to gain important information regarding this distribution. Although some models of perfusion in the lung consider pulsatile flow (24, 48), most consider steady flow (3, 5, 28, 49), and this approach is considered to be appropriate in studies of PVR (7).

Conclusions

In conclusion, our model of acinar perfusion provides physiologically realistic output. It provides a transition between existing models of perfusion in the large pulmonary blood vessels and the pulmonary microcirculation. This transition is of importance as the small pulmonary blood vessels provide a high resistance to flow, and hence have a significant influence on the lung's capacity to carry blood. We have shown that the hierarchical structure of blood vessels within the acinar unit is able to provide the lung with an increased capacity for blood flow compared with an acinar unit with capillary beds only connecting the most distal blood vessels. In addition, we have shown that the stratification of blood flow within the acinus observed in some mammals (41, 46) can be explained by the structure of the acinar blood vessels. This model has several potential applications, both in studies of perfusion in anatomically accurate lung models as well as in studies of ventilation and perfusion matching in the acinus, because it is able to provide detailed information on acinar perfusion variability via a computationally inexpensive model. Although it is not practical for a single model to incorporate every possible factor contributing toward perfusion heterogeneity, a combination of theoretical models investigating the contribution of large vessel structure (5), supernumerary vessels (4), the structure of the acinus (the model proposed here), and capillary blood flow (6, 26) could make a significant contribution to the understanding of perfusion distribution throughout the lung.

GRANTS

This work was supported by National Heart, Lung, and Blood Institute Grant R01-HL-064368 (E. A. Hoffman, lead principal investigator). K. S. Burrowes was supported by an Engineering and Physical Sciences Research Council (EPSRC) Post-doctoral Fellowship at the Life Sciences Interface.

DISCLOSURES

No conflicts of interest are declared by the author(s).

APPENDIX

BLOOD FLOW AND TRANSIT TIMES IN CAPILLARY SHEETS

Blood flow and transit times through the alveolar sheet must be calculated in four distinct regions. Letting P_tmA and P_tmV be the difference between blood and alveolar pressure at the arterial and venous sides of the alveolar sheet, respectively, if P_tmA < 0 the sheet is collapsed. There is no flow through the sheet and RBC transit time cannot be calculated (West's zone 1).

For P_tmA ≥ 0 there are three possible flow types. The first occurs when 0 ≤ P_tmV ≤ P_tmA ≤ P_CU and Eqs. 5 and 6 give rise to

$$\text{Q}\hspace{0.17em}\text{=}\hspace{0.17em}\frac{\text{S}A}{4{\mu }_{\text{C}}f{l}_{\text{C}}^{\text{2}}{\alpha }_{\text{C}}}\left[{\left(H\prime +{\alpha }_{\text{C}}{\text{P}}_{\text{tmA}}\right)}^4-{\left(H\prime +{\alpha }_{\text{C}}{\text{P}}_{\text{tmV}}\right)}^4\right]$$ (A1)

$$\text{TT}=\frac{3{\mu }_{\text{C}}f{l}_{\text{C}}^{\text{2}}{\alpha }_{\text{C}}}{{\left(H\prime +{\alpha }_{\text{C}}{\text{P}}_{\text{tmA}}\right)}^3-{\left(H\prime +{\alpha }_{\text{C}}{\text{P}}_{\text{tmV}}\right)}^3}$$ (A2)

This is the standard definition of flow in a capillary sheet as given by Fung and Sobin (12).

When 0 ≤ P_tmV ≤ P_CU and P_tmA > P_CU, sheet height is maximal at the arterial side and less than maximal at the venous side. Flow through the sheet can be split into two regions: that where the pressure is greater than P_CU and that where pressure is less than P_CU. The integral (Eq. 5) then becomes

$$\text{Q}\hspace{0.17em}\text{=}\hspace{0.17em}\frac{\text{S}A}{4{\mu }_{\text{C}}f{l}_{\text{C}}^{\text{2}}}{\displaystyle \underset{{\text{P}}_{\text{tnV}}}{\overset{{\text{P}}_{\text{UC}}}{\int }}{\left(H\prime +{\alpha }_{\text{C}}{\text{P}}_{\text{tm}}\right)}^3{\text{dP}}_{\text{tm}}+\frac{\text{S}A{H}_{\max }^3}{4{\mu }_{\text{C}}f{l}_{\text{C}}^{\text{2}}}{\displaystyle \underset{{\text{P}}_{\text{CU}}}{\overset{{\text{P}}_{\text{tmA}}}{\int }}{\text{dP}}_{\text{tm}}}=}\hspace{0.17em}\frac{\text{S}A}{4{\mu }_{\text{C}}f{l}_{\text{C}}^{\text{2}}}\left\{H_{\max }^3\left({\text{P}}_{\text{tmA}}-{\text{P}}_{\text{CU}}\right)+\frac{1}{4{\alpha }_{\text{C}}}\left[H_{\max }^4+{\left(H\prime +{\alpha }_{\text{C}}{\text{P}}_{\text{tmV}}\right)}^4\right]\right\}$$ (A3)

Similarly, Eq. 6 becomes

$$\text{TT}=\frac{3{\mu }_{\text{C}}f{l}_{\text{C}}^{\text{2}}{\alpha }_{\text{C}}}{3{\alpha }_{\text{C}}{H}_{\max }^2\left({\text{P}}_{\text{tmA}}-{\text{P}}_{\text{CU}}\right)+H_{\max }^3-{\left(H\prime +{\alpha }_{\text{C}}{\text{P}}_{\text{tmV}}\right)}^3}$$ (A4)

Note that a sheet under these conditions would have a resistance across it given by

$$R=\frac{{\text{P}}_{\text{tmA}}-{\text{P}}_{\text{tmV}}}{\text{Q}}$$

with Q given by Eq. A3. Note that this differs from Bshouty and Younes's (3) resistance calculation under the same conditions, which is given by Equation 6 in that paper with resistance independent of arterial pressure. The flow described here is calculated directly from the governing equations for sheet flow (the direct integral of Eq. 5), and flow and resistance depend on the pressure at both the arterial and venous sides of the sheet.

Finally, when P_tmA, P_tmV >P_CU the sheet is maximally distended and Eqs. 5 and 6 become

$$\text{Q}\hspace{0.17em}\text{=}\hspace{0.17em}\frac{\text{S}A}{{\mu }_{\text{C}}{\text{fl}}_{\text{C}}^{\text{2}}}{H}_{\max }^3\left({\text{P}}_{\text{tmA}}-{\text{P}}_{\text{tmV}}\right)$$ (A5)

$$\text{TT}=\frac{{\mu }_{\text{C}}f{l}_{\text{C}}^{\text{2}}}{H_{\max }^2\left({\text{P}}_{\text{tmA}}-{\text{P}}_{\text{tmV}}\right)}$$ (A6)

Flow through the sheet is then directly proportional to the pressure drop across it. This is analogous to Darcy's law that describes flow through a porous medium through a sheet of constant height. The resistance under these conditions corresponds to that calculated by Bshouty and Younes (3).