Brief Sounds Evoke Prolonged Responses in Anesthetized Ferret Auditory Cortex

Abstract

Neurons in the auditory cortex of anesthetized animals are generally considered to generate phasic responses to simple stimuli such as tones or noise bursts. In this paper, we show that under ketamine/medetomidine anesthesia, neurons in ferret auditory cortex usually exhibit complex sustained responses. We presented 100-ms broad-band noise bursts at a range of interaural level differences (ILDs) and average binaural levels (ABLs), and used extracellular electrodes to monitor evoked activity over 700 ms poststimulus onset. We estimated the degree of randomness (noise) in the response functions of individual neurons over poststimulus time; we found that neural activity was significantly modulated by sound for up to ∼500 ms following stimulus offset. Pooling data from all neurons, we found that spiking activity carries significant information about stimulus identity over this same time period. However, information about ILD decayed much more quickly over time compared with information about ABL. In addition, ILD and ABL are coded independently by the neural population even though this is not the case at individual neurons. Though most neurons responded more strongly to ILDs corresponding to the opposite side of space, as a population, they were equally informative about both contra- and ipsilateral stimuli.

INTRODUCTION

The relative intensity of sound at the two ears (the interaural level difference, ILD) is an important cue for localizing high-frequency sounds. The firing of neurons in auditory cortex is modulated by ILD, and an intact auditory cortex is necessary for normal sound localization (Heffner and Heffner 1990; Jenkins and Merzenich 1984; Kavanagh and Kelly 1987; Malhotra et al. 2004; Smith et al. 2004). However, the ILD responses of cortical neurons are also modulated by average binaural level (ABL), and measuring tuning curves along both dimensions produces a wide variety of two-dimensional (2-D) response surfaces. Early studies focused on assigning these shapes to different classes (Irvine 1987; Phillips and Irvine 1983; Rutkowski et al. 2000; Semple and Kitzes 1993; Zhang et al. 2004). We have previously suggested that these class boundaries are largely artificial because the distribution of tuning curve shapes shows no evidence of distinct or partially overlapping response types (Campbell et al. 2006).

Here we focus on two aspects of binaural responses not explored in our previous study. First, over what time course is binaural information processed in auditory cortex? Although simple stimuli such as noise bursts can produce more than just phasic onset and offset responses (see following text), such responses have seldom been studied in detail. Second, because the firing of most neurons is influenced by both ILD and ABL (Semple and Kitzes 1993), single neurons cannot represent these parameters unambiguously. Here we ask whether this confound is resolved at the population level. To address these questions, we used extracellular electrodes to obtain binaural response functions from cortical neurons under ketamine/medetomidine anesthesia. Our stimulus set allowed us to assess the dependence of spiking on both ILD and ABL.

Neural responses recorded from the auditory cortex of anesthetized animals have a reputation for being simple and transient, whereas responses in unanesthetized cortex are generally considered to be more sustained with richer temporal profiles (Chimoto et al. 2002; Hromádka et al. 2008; Petkov et al. 2007; Qin et al. 2007; Recanzone 2000; Wang et al. 2005). There are reasons to think this distinction is an oversimplification: even with barbiturates there are striking examples of evoked spikes occurring well after stimulus offset in both ferrets (Mrsic-Flogel et al. 2005) and rats (Sally and Kelly 1988). Furthermore, work by Moshitch and colleagues (2006) shows convincingly that there is significant information about stimulus identity up to ∼300 ms (the longest duration analyzed) following stimulus offset in halothane anesthetized cats. Despite this, most research, particularly in anesthetized preparations, has focused on responses derived from the onset peak alone, ignoring any potential contribution of later components to the stimulus sensitivity of the neurons.

The main purpose of this study was to search for evidence of stimulus-modulated neural activity at long intervals (≤600 ms) following stimulus offset. Analyzing neurons individually, we found that very few exhibited onset responses alone, and some maintained stimulus-related activity for ≤500 ms following stimulus offset. Analyzing the neurons as a population using multiple discriminant analysis (MDA) revealed that information about stimulus identity also persists over this time frame. Surprisingly, we found that ABL information persisted over a much longer time period than ILD information. Finally, we used multidimensional scaling to show that ILD and ABL are coded independently at early time points.

METHODS

General

The data presented here were collected from the auditory cortex of anesthetized ferrets used for a previous study on binaural response classes (Campbell et al. 2006). Seven adult (aged ≥4 mo) pigmented ferrets (Mustela putorius) with normal middle ear function (assessed by otoscopic examination and tympanometry) were used. All experimental procedures were approved by the local ethical review committee and licensed by the UK Home Office under the Animal (Scientific Procedures) Act of 1986. At the end of each experiment, the animal was killed by anesthetic overdose. All recordings were carried out under general anesthesia by continuous infusion of ketamine (Ketaset, 5 mg·kg⁻¹·h⁻¹; Fort Dodge Animal Health, Southampton, UK) and medetomidine hydrochloride (Domitor 10 μg·kg⁻¹·h⁻¹; Pfizer, Sandwich, UK) in Hartmann's solution. For surgical details see Campbell et al. (2006).

Stimuli

Auditory stimuli were created using TDT System 3 hardware (Tucker Davis Technologies, Alachua, FL) and presented using Panasonic RP-HV297 headphones (Panasonic, Bracknell, UK). The transfer function of the earphones was canceled from the stimulus using an inverse filter. Closed-field calibration was carried out using an 1/8-in condenser microphone (Type 4138, Brüel and Kjær UK, Stevenage, UK). After calibration the Panasonic drivers produced a flat (plus or minus <5 dB) frequency response over the 0.5–25 kHz range.

Broadband (0.5–25 kHz) Gaussian noise stimuli of 100-ms duration with 5-ms raised cosine onset and offset ramps were presented to both ears with an interstimulus interval of 1,000 ms. In all cases, data acquisition was performed for 700 ms following stimulus onset. We presented ILDs at a range of ABLs by sampling randomly from a matrix of sound level combinations at the two ears (Fig. 1A). Large ILDs (>50 dB) were excluded to prevent acoustic cross-talk. In a single “stimulus run” the 80 level combinations were presented in a randomized order. For most units (239/310), we recorded 10 such runs consecutively with a new randomized presentation order on each run. In 20/310 cases there were 7 runs and in 51/310 cases there were 15 runs.

Fig. 1.

Sensitivity in interaural level difference (ILD) and average binaural level (ABL) in the ferret auditory cortex. A: the black points show the 80 sound level combinations used in this study. The gray lines are the axes along which ILD and ABL vary. B–E: responses of one unit in ferret auditory cortex to the binaural stimulus set. B: response function derived from the first peak in the pooled PSTH (13–43 ms). The unit fired most for intense contralateral sounds, as indicated by the white region in the response function. C: pooled PSTH representing the response summed across all 80 tested sound level combinations. The stimulus was presented during the first 100 ms (gray box). D: raster plot showing the pooled PSTH broken down by sound level combination. Each point represents a spike and each row of spikes represents a different stimulus presentation. In this case, each sound level combination (i.e., condition) was presented 10 times, and different conditions are segregated by the horizontal lines (during recordings the stimulus conditions were randomly interleaved not presented in blocks). The sound level combination is indicated by the numbers along the y axis, with “C” meaning contralateral sound level (dB SPL) and “I” meaning ipsilateral sound level. For clarity, only every other stimulus condition is labeled. The responses do not show evidence of adaptation and are fairly homogenous within conditions. This is highlighted by the inset plot (E), which shows 17 of the conditions in greater detail.

Electrophysiological recording

Binaural responses were obtained from a total of 310 units (79% of which were single units according to criteria described in the following text) recorded extracellularly from seven ferrets. Most units (274/310) were recorded from the middle ectosylvian gyrus (MEG), where the primary auditory cortical fields are located. The remaining 36 units were recorded from the anterior ectosylvian gyrus (AEG), which contains higher order auditory fields (Bajo et al. 2007; Bizley et al. 2005).

In four animals, we used a linear array (spanning 1–2 mm) of four tungsten-in-glass microelectrodes (∼1 MΩ). In the other three animals, we used 16-channel silicon probes (Neuronexus Technologies, Ann Arbor, Michigan), consisting of 4 prongs each with 4 active sites. This formed a 4-×-4 square matrix of active sites with an intersite separation of 0.2 mm. We did not analyze our responses as a function of depth because it was not possible to make lesions with these probes. Estimating depth was difficult because the probe substantially depressed the cortical surface when it was inserted. All electrode signals were band-pass filtered (500 Hz to 5 kHz), amplified (15,000 times) and digitized at 25 kHz. Stimulus generation and data acquisition were coordinated by Brainware (Tucker-Davis Technologies). Data sweeps were triggered by the onset of the stimulus. The latency and shapes of all events with a magnitude >2.5 SD from the mean were considered to be potential spikes and stored for off-line analysis.

Spike sorting

Off-line spike sorting was expedited by a k-means clustering algorithm. The number of clusters was chosen by assessing cluster separability based on the similarity of spike shapes between and within the candidate clusters. We used the presence of a refractory period in the autocorrelation histogram and the quality of the spike shapes to determine whether we were recording from a single unit or a small multiunit cluster. Recorded clusters containing <1% of spikes with an interspike interval of <1.5 ms were classed as single units. The remaining units were considered to be small multiunit clusters, even though these did show some evidence for a refractory period.

Statistical analysis

The raw data were exported to Matlab (The Mathworks, Natick, MA) with which all further analysis was carried out. Discriminant analysis and multidimensional scaling (see following text) were implemented using functions from Matlab's statistics toolbox.

We used MDA to predict stimulus identity based on neural population responses. A single population response is defined as a vector of n spike counts, where each count is derived by counting spikes from one neuron over a fixed time window (see results). For this analysis, n = 290 since neurons with <10 repeats were excluded. Each stimulus was repeated 10 times, producing a group of 10 population vectors. There were 80 different stimuli and so 800 response vectors in total. MDA estimates the probability with which each vector is assigned to the correct group (i.e., stimulus). The dataset has n = 290 degrees of freedom; to avoid over-fitting, we reduced dimensionality to 15 using principal components analysis (PCA). The firing of each neuron across all stimuli was z scored prior to PCA to avoid introducing bias. The first 15 principal components described 35% of the variance for response vectors calculated over the first 30 ms of the response. All analyses were based on the first 15 dimensions because this produced the best classification accuracy at most time slices. Adding more components did not improve classification accuracy because group identities were assigned using cross-validation (see following text).

Classification was performed using a “leave one out” cross-validation where each response was removed in turn; the model was then fitted to the remaining responses and used to predict the stimulus class of the missing observation. The missing observation did not contribute to the parameters of the model. We used the linear version of MDA, which produces a straight decision boundary separating each pair of groups. Response class was estimated using a centroid-based method. We generated a vector of assigned group identities and compared this to the true group identities. Using this we could calculate the proportion of correct classifications and also the magnitude of misclassifications (expressed in dB) along either the ILD or ABL axes.

We also used the mutual information (MI) to quantify the strength of the relationship between actual stimulus identity (x) and that predicted by the classifier (y). If the distributions of actual and predicted stimuli are not independent, then knowing the value of one will provide some information about the other. The stronger this relationship the more information is “common” between the two variables. It is this common information that is known as the MI

$$\text{MI}={\displaystyle \sum _x{\displaystyle \sum _{y}p\left(x,y\right){\log }_2\left(\frac{p\left(x,y\right)}{p\left(x\right)p\left(y\right)}\right)}}$$

By convention, MI is measured in bits: 1 bit = log₂(2) and is sufficient to discriminate two stimuli. A confusion matrix based on s stimuli has a maximum MI of log₂(s). MI measures tend to be positively biased (Cover and Thomas 1991), and so all values presented here were de-biased using a bootstrapping approach that estimates the MI when the classifier performs at chance. This was done by running the MDA algorithm multiple times with the stimulus labels randomized. The mean of these bootstrapped runs was subtracted from the observed MI to yield the de-biased MI. The de-biased MI will have a value of zero when the classifier performs at chance.

We used multidimensional scaling (MDS) to map the high-dimensional neural population onto 2-D space in a way that best preserves the distances between data points (Martinez and Martinez 2005). Points in the full-dimensional space were defined as a matrix of relative distances. MDS seeks a low-dimensional (i.e., 2- or 3-D) configuration of the data which conserves this distance matrix as closely as possible. Ideally, points near to one another in the full-dimensional space will also be near in the reduced space. In this respect, MDS is similar to nonlinear manifold learning techniques, such as locally linear embedding (Roweis and Saul 2000). We used Euclidean distance to measure dissimilarity, δ, in the full space. δ_ij is the dissimilarity between points i and j; larger values of δ_ij indicate greater dissimilarity (i.e., points that are further apart). The corresponding distance between points i and j in the low dimensional space is denoted d_ij, and is calculated iteratively. We seek a transform onto the low-D space such that

$$d_{ij}=f\left({\delta }_{ij}\right)$$

We used “nonmetric MDS”, meaning that f() is the rank order of the dissimilarities. The re-mapping simply seeks to preserve the rank order of the distances in the full space. As a result, location, rotation, reflection, and scale are indeterminate. The difference between d_ij and δ_ij serves as the basis for a metric known as “stress,” which evaluates the success of the transform. Stress varies between 0 and 1 according to

$$\text{stress}=\sqrt{\frac{{\displaystyle \sum _{i\ne j}{\left[f\left({\delta }_{ij}\right)-d_{ij}\right]}^2}}{{\displaystyle \sum _{i\ne j}{d}_{ij}^2}}}$$

stress = 0 would indicate a perfect transformation since this means that d_ij = δ_ij in every case. As a rule of thumb, stress values less than ∼0.2 indicate that the transformation is reasonable, and values less than ∼0.1 indicate that the transformation is good.

RESULTS

Binaural stimuli evoke multi-peaked responses

We presented ILDs at a range of ABLs by sampling randomly from a matrix of binaural sound level combinations (Fig. 1A). Visual inspection of the data suggested that of the 310 recorded units, very few exhibited only a brief onset response; the vast majority had sustained or prolonged responses of some sort. Figure 1C shows an example of such a unit with three notable peaks in the pooled poststimulus time histogram (PSTH). Figure 1B shows the binaural response function obtained by averaging spikes derived from the first peak (13–43 ms). This unit had a fairly high threshold and responded most strongly to sounds with contralateral ILDs. The timing of spikes in this unit depended greatly on the binaural stimulus configuration (raster plot, Fig. 1D). In this case, the first and last peaks of the PSTH were clearly driven by different sound level combinations (y axis, different stimuli separated by lines). Figure 1E, inset, highlights a subset of the data at sufficient resolution for responses to individual stimulus repeats to be resolved. There is no evidence of adaptation across stimulus runs (the 80 stimulus conditions were presented in a randomized order within each run; see methods). All units recorded in this study exhibited a similar lack of adaptation.

Using smoothness to quantify structure

The first goal of this study was to investigate which periods in poststimulus time exhibited significant stimulus-dependent modulation of the firing rate. Figure 2 shows how binaural responses changed as a function of poststimulus time for three different units. At each of 13 evenly spaced 30-ms time windows, binaural response functions were calculated and arranged below the PSTH as surface plots (presented in the same format as that in Fig. 1B). For example, the binaural response field labeled “t = 0 ms” in Fig. 2A was calculated from the spike rates measured at each sound level combination over the first 30 ms. The time bins contributing to each response function are highlighted in the PSTH using darker shades of gray. The darkest indicate whether the 30-ms time slice contained a response function with a significant (nonrandom) receptive field. The statistical test for this is described in the following text.

Fig. 2.

Three examples showing how binaural response properties change as a function of time. Each case shows the pooled PSTH of one unit with spike rate calculated over 5-ms bins. We extracted 13 binaural response functions along the PSTH using a series of 30-ms windows, which are highlighted as darker regions along each PSTH. The binaural response functions derived from these time slices are shown below each PSTH. The response functions are in the same format as Fig. 1B, but the gray scale of each function is normalized to the range of values for that time slice. The number above each response function indicates the window start time in milliseconds. The number below each response function is the z score indicating its smoothness, which is related to the signal-to-noise ratio of the response function (see main text for details). z scores less than −2.5 were taken to be significantly smoother than expected by chance and these are denoted in bold text. Significant time windows are highlighted on the PSTH in dark gray.

The traditional test for stimulus-driven activity compares the number of spikes in an arbitrary “response window” to a period in which the neuron is considered to be firing spontaneously. A more direct approach, carrying fewer assumptions, is to ask whether spikes from a single time window yield a response function that contains nonrandom structure. We measured the degree of randomness using ideas from the emerging field of functional statistics (Ramsay and Silverman 2002). In this case, we used the smoothness of the receptive field as a proxy for the entropy of the response function. A function composed of noise alone will have maximum entropy and yield the most “bumpy” (least smooth) response surfaces.

The rationale for using smoothness as a test of significance is straightforward. In general, if two stimuli are sufficiently similar, the evoked neural response rates will also be similar. Thus, provided that stimulus parameters are sampled at sufficiently fine intervals, neural tuning curves tend to be smooth because evoked responses to similar stimuli are correlated. When there is no stimulus-dependent activity, and stimuli are presented in a random order, then recorded spikes become independent random samples and there is no systematic relationship between the data points. Under these circumstances, adjacent points in a response function are uncorrelated, and the curve is not smooth. We can therefore look for evidence of significant stimulus effects by asking whether the observed response function is smoother than would be expected by chance. The degree of smoothness (or lack of it) that is to be expected in random response functions can easily be estimated using resampling techniques. This gives us the basis for a nonparametric test for the statistical significance of any observed response function.

For each of the 30-ms-wide time windows shown in Fig. 2, we quantified smoothness of the binaural response function by calculating the root mean square (RMS) value of its second order derivative (we used the 2nd order approximation to the Laplacian). We will refer to this smoothness measure as the “observed dRMS” of each time slice. Lower dRMS values indicate smoother surfaces with a completely flat surface having dRMS = 0. We then estimated the range of dRMS values expected to arise by chance by shuffling the mean spike rates evoked by each of the 80 stimulus conditions so that each firing rate became associated with a new, randomly chosen, binaural sound level combination. In this manner, we generated 1,000 random response fields for each time slice and calculated a dRMS value for each of these. If the observed dRMS obtained from the original response function was ≥2.5 SD smaller than the mean of the shuffled dRMS values (i.e., if the original dRMS value had a z score of ≤ −2.5), then we concluded that the observed binaural response function was smoother than expected by chance. This is strong evidence for significant stimulus-induced structure. We emphasize that the observed dRMS of each time slice was tested against a random distribution generated from that time slice alone. The z score for each response function in Fig. 2 is shown beneath it. Those response periods with dRMS smoothness z scores less than −2.5 are highlighted in dark gray on the PSTH and using bold text. Note that significant stimulus dependencies sometimes occurred well after the end of the stimulus (100 ms) and were not necessarily associated with an overt peak in the PSTH (e.g., the 308-ms window in Fig. 2C).

Although somewhat arbitrary, significance thresholds are useful for categorizing data. We chose a conservative value of 2.5 SD to maintain a low Type 1 error rate (α = 0.006). For the example units in Fig. 2, we show 13 time windows. At the chosen α level, there is a 92% chance that a unit with no driven response would also produce no false-positives in these 13 windows.

How common were long-latency responses?

Figure 3A summarizes the incidence of significant bins for all 310 units. Each row corresponds to a different unit with responses divided into 23 nonoverlapping 30-ms bins. Those bins associated with a z score value of up to −2.5 are black, and units have been arranged so that those with similar patterns of significant bins are adjacent to each other. This arrangement was generated automatically using hierarchical clustering based on the Euclidean distances between rows in Fig. 3A. There was a great deal of variety in temporal response properties across cells. Onset responses were very common with one of the first two bins coded black in almost every case. At all time points there are more significant bins than expected by chance. For a single 30-ms bin, the false alarm probability is P = 0.6% (α = 0.006), so over the 310 recorded neurons we would expect 0.006 × 310 = 1.86 false positive bins for that 30-ms time slice. Reading Fig. 3A column-wise, it is clear that there are more than two significant windows at all time periods. Using the false discovery rate (FDR) (Benjamini and Hochberg 1995; Benjamini et al. 2001) to control for multiple comparisons, we found that 283/310 neurons had at least one significant (P < = 0.01) bin during 0–120 ms, and 150/310 neurons had at least one significant bin at times >120 ms. The distribution of significant (α = 0.006) response windows is summarized in Fig. 3B. The proportion of units exhibiting a structured (significant) response function in each time bin is shown as by the shaded region. Around 50% of units exhibited offset responses, as judged by the peak near 150 ms. The cumulative proportion of significant windows over time is shown by the solid line. About 20% of significant responses occurred at latencies of >300 ms, well after the expected time window for phasic offset responses (commonly called “rebound from inhibition”).

Fig. 3.

Distribution of smoothness scores over the neural population. A: the incidence of significant bins (black rectangles) for each unit. Units are arranged so that those with similar patterns of significant bins are adjacent to each other. The response of each unit is divided into 23 nonoverlapping time slices. Those time bins with z scores < −2.5 are filled black. B: the proportion of units exhibiting a nonrandom response function at each time bin (shaded region). Solid line, the cumulative proportion of all significant response windows over time. C: box plots of the observed smoothness z scores from all 310 units at each 30-ms time bin. For example, the box plot at t = 0 ms describes data in the 0- to 30-ms time window. Circles show the median; boxes, the interquartile range; and whiskers, 2.7 SD. Open circles, values >2.7 SD, which are jittered along the abscissa to aid visualization. Dotted lines indicate z = ±2.5, the significance cutoff used in previous figures. The observed z scores at each time point either have negative medians or are skewed toward negative values, which indicate smoother response profiles.

Figure 3C demonstrates the presence of nonrandom structure at long latencies without thresholding data to an arbitrary significance criterion. The box plots show the distributions of observed smoothness z scores over all 310 units for each 30-ms time bin. More negative values indicate increased structure (lack of randomness) with the −2.5 smoothness SD threshold highlighted by dotted lines. At almost every time point, the observed z scores are skewed to negative values, indicating a tendency for response functions to be smoother than expected by chance. This further confirms that the conclusions drawn from Fig. 3, A and B, cannot be due to type I error (false positives) arising from the large number of significance tests. Receptive fields created via random draws from the Poisson distribution and tested for smoothness in the same way did not produce biased z scores using λ parameter values between 0.1 and 2 (data not shown). The skewness observed in Fig. C cannot therefore be attributed to bias in the statistical test.

How informative are long-latency responses?

The smoothness analysis implies that information about stimulus identity should persist for ∼500 ms after stimulus offset. We tested this suggestion using a classification algorithm (MDA), which attempted to predict stimulus identity based on the spiking activity of all neurons in our population (see methods). Using MDA we were able to measure classification accuracy in the ILD and ABL domains, quantifying how information about each stimulus parameter decays over time.

The MDA was run in the following way for each 30-ms time window. We created a single population response vector by counting the number of spikes produced by each neuron from a single stimulus presentation. We used the first 10 repeats of each stimulus class to produce 10 population responses per class. We repeated this procedure until there were 10 population responses for each of the 80 stimuli. For this analysis, we used 290/310 neurons because the other 20 neurons had <10 repeats. Note that because we did not record all neurons simultaneously, the vector is a simulated population response. MDA tests whether multiple presentations of the same stimulus are more similar to each other than to presentations of different stimuli. For stimuli where this is the case, the classifier will perform with 100% accuracy. In practice, noise causes responses to different stimuli to overlap and this introduces classification errors. The MDA was conducted on the first 15 principal components and was cross-validated to avoid over-fitting (for details see methods).

MDA can assign each population response to any of the 80 different stimuli; however, to visualize the results, data were collapsed into the ILD and ABL domains. In other words, we determined whether each stimulus was assigned to the correct ILD (ignoring ABL) or the correct ABL (ignoring ILD). Figure 4A, top, shows confusion matrices describing classification accuracy in the ABL domain and the bottom shows the ILD domain. In each confusion matrix, rows indicate assigned stimulus identity and columns true stimulus identity. The color of each square indicates how many times each assignment was made. Hotter colors indicate more assignments for a particular pair of actual and assigned stimulus values. The identity matrix (a diagonal of white squares against a black background) would indicate perfect classification accuracy. An unstructured confusion matrix indicates no relationship between the actual and predicted stimulus class. There is substantial information about both ILD and ABL at 0–30 and 60–90 ms. Classification errors tend to be small at these early time points and accuracy is greatest at near zero ILDs, which matches behavioral performance for free-field stimulation (Nodal et al. 2008). Interestingly, despite the fact that most high-frequency neurons in A1 are excited by contralateral sounds and inhibited by ipsilateral sounds (Irvine et al. 1996; Kelly and Sally 1988; Zhang et al. 2004), the classifier performs equally well for both positive (contralateral) and negative (ipsilateral) ILDs. Similarly, classification accuracy in ABL is surprisingly uniform across the 90 dB range of tested values. The confusion matrices show that ILD information is retained until ∼390 ms, whereas ABL retains a hint of information even at 570 ms.

Fig. 4.

Classification of ILD and ABL over time using cross-validated multiple discriminant analysis (MDA). A: confusion matrices summarizing classification accuracy in ILD and ABL (see main text) for 5 example time windows. B: classification accuracy in bits derived from sequential 30-ms time windows. Accuracy is broken down into ILD (red) and ABL (black). C: classification accuracy expressed as the mean absolute error magnitude for ILD (red) and ABL (black). Shaded error bars show 1.96 SD of the bootstrapped chance distribution (see main text).

The confusion matrices were quantified by two statistics: the mutual information (MI; Fig. 4B), and the average magnitude of the classification error, expressed in decibels (Fig. 4C). The maximum MI depends on the number of bins in the confusion matrix and is 3.5 bits for ILD and 4.2 bits for ABL (see methods). MI measures cannot be negative: even when stimulus and response are unrelated, the MI between them will be positive. We used a bootstrapping approach to calculate this bias, running the above MDA procedure 50 times for each time window with the stimulus labels randomized prior to MDA. The curves in Fig. 4B show the bias-corrected MI for ILD (red) and ABL (black). The error bars indicate ±1.96 SD for the 50 chance classification runs. Both ILD and ABL curves exhibit a peak at 150 ms, corresponding with the phasic offset response. Whereas ILD reaches chance performance at 270 ms, ABL remains above chance until ∼550 ms. Thus while both stimulus parameters are represented after stimulus offset, ABL information persists substantially longer than ILD.

The average error magnitude (Fig. 4C) behaves in a similar way to the MI with errors initially low (<10 dB) but increasing over time. Chance performance is indicated by the shaded lines which show the mean ±1.96 SD for the 50 chance runs. The higher mean error for the ILD data is due to the fact that this variable is spaced at 10 dB intervals, whereas ABL is spaced at 5 dB intervals (although both variables span a similar range). Nevertheless, ILD reaches the 1.96 SD threshold at 300 ms, whereas ABL only begins to approach 1.96 at ∼540 ms.

Are ILD and ABL coded independently?

The stimulus space contained two orthogonal dimensions, ILD and ABL, but because the firing rate of individual neurons varies along both dimensions (Campbell et al. 2006; Semple and Kitzes 1993; Zhang et al. 2004), information from single cells is ambiguous. We used multidimensional scaling (MDS; see methods for details) to determine whether this confound is resolved at the population level. MDS is a data visualization technique that measures the relationship between data points in a high-dimensional space and maps this onto a low dimensional space (typically a 2- or 3-D space) while attempting to retain the relationship between points. If successful, points near to each other in the high dimensional space will stay near each other in the low dimensional space. Here, the responses to the 80 sound level combinations exist in a 310-D space (the response of each neuron is a separate dimension in the response space), which was mapped onto a 2-D subspace to explore the distribution of ILD and ABL. We chose to map onto two dimensions because this is the dimensionality of our stimulus space. We chose to use MDS because, in contrast to PCA, this algorithm seeks to preserve distances between data points in high-dimensional space. Here “distance” is derived from the relative firing rate of the 310 neurons in our sample. Similar sound level combinations tend to evoke similar firing rates, so, if ILD and ABL are represented orthogonally by the neural population, we would expect MDS to generate a “map” that resembles Fig. 1A. Note that MDS is not provided with information regarding stimulus identity; it merely organizes the data so that similar neural population responses are placed near each other in a 2-D space.

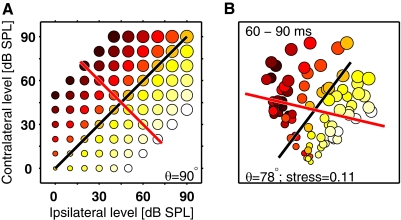
Figure 5A is a schematic of our stimulus space. If the neural population encodes both ABL and ILD effectively and independently, then we might expect the topography of the MDS mapping to reflect that of this stimulus space. The color of the circles represents ILD and the size of the circles represents ABL. The black and red lines are generated by linear regression and indicate the directions that account for the most variance in ILD (red) and ABL (black). The regression lines are orthogonal to one another since ILD and ABL are independent. Each fit is calculated by modeling one of the two variables as a function of the x and y axes, which in Fig. 5A is the sound level at the two ears. For example, the following model was fitted for the ILD line

$$\text{ILD}=ax+by+c$$

Fig. 5.

Population responses in multidimensional scaling (MDS) space. A: schematic of the stimulus space (Fig. 1A) where color represents ILD and circle diameter represents ABL. Under ideal conditions, one would expect 2-dimensional (2-D) MDS on the neural population responses (see main text) to produce a plot resembling this. The lines are generated by linear regression and indicate the directions that account for the most variance in ILD (red) and ABL (black). θ, the angle between the lines, is equal to 90° because ILD and ABL are orthogonal dimensions in stimulus space. B shows the results of an MDS projection from the 60- to 90-ms time window (part of the onset response) presented in the same format as A. The neural population data produce a map remarkably similar to the stimulus space. ILD and ABL vary in a systematic manner in neural space and the regression lines indicate that these variables are represented along largely orthogonal directions (θ = 78°). Information about these variables is therefore encoded largely independently. The MDS projection provides a good representation of the data because stress, a measure of the success of the transformation, equals 0.11 (0 is a perfect reconstructions; see methods).

For simplicity and consistency, we use this linear model for all fits described in the following text even though data at some time points are slightly curvilinear.

Figure 5B shows the results of an MDS projection from the 60- to 90-ms time window (part of the onset response) presented in the same way. There is a clear resemblance between this MDS map and the stimulus space. Note, however, that the orientation of the MDS map is arbitrary and is not constrained to match that of the stimulus space. Regression lines are fitted as in Fig. 5A except that here x and y are the two MDS dimensions. The regression models show that ILD and ABL are represented along approximately orthogonal directions: θ, the angle between the lines, is equal to 78°. The neural population therefore encodes ILD and ABL information almost independently at this time point (60–90 ms). The MDS stress value is relatively low, 0.11, indicating that this 2-D map captures much of the variance in the neural population responses (see methods).

Figure 6, A—C, shows data from a later time slice (150–180 ms) in more detail; here the angle between the regressions is again close to the orthogonal (87°). In addition to the MDS space, Fig. 6, B and C, shows how well the MDS space represents ABL and ILD, respectively. For each variable, we plot the fitted value of the stimulus parameter, predicted by the regression in MDS space, against the actual value. In each case, R² is the proportion of the variance in the neural responses to that stimulus parameter which is explained by the distribution of responses in MDS space. If R² = 1 then the MDS would be able to predict the stimulus parameter with perfect accuracy. The R² values for ABL and ILD are both high, being 0.80 and 0.79, respectively. Figure 6, D—F, shows results from the 240- to 270-ms time slice. Both ILD and ABL representations have degraded, but ABL has decreased relatively less. By 570–690 ms (Fig. 6G), the neural population retains a representation of ABL (Fig. 6H; R² = 0.53), but the ILD representation is now at chance (Fig. 6I; R² = 0.04). As a consequence, the angle of the ILD regression axis is random, and so the angular difference between the ILD and ABL lines (Fig. 6G) is meaningless.

Fig. 6.

Representation of ILD and ABL by the neural population as a function of poststimulus time. A: an MDS projection from the 150- to 180-ms time window. As in Fig. 5, ILD is represented by color and ABL by the size of the circles. The red line describes the direction in which ILD varies most and the black line the direction in which ABL varies most. The angle between these lines is 87°, indicating that the variables are represented independently. B and C: the distribution of the data around the ABL and ILD regressions, respectively. Each plot shows the predicted value of the parameter in MDS space as a function of the true value. An R² of 1 would indicate that the neural population could perfectly predict the stimulus. At this time point accuracy is high. D–F: data for the 240- to 270-ms time window. G–I: data for 570- to 600-ms window. At the longer latencies post stimulus onset, there is still a substantial quantity of ABL information (H), whereas ILD information is no longer present (I). J: variation in R² as a function of poststimulus time for ILD (red) and ABL (black). ILD information drops sharply at ∼240 ms, whereas ABL information drops off gradually over time and persists for much longer. Blue points shows the angle between the regression lines as a function of time. Time points with R² <0.3 for ILD or ABL are shown as a dashed line.

To summarize the accuracy with which ILD and ABL are encoded, Fig. 6J shows the values of R² and θ (the angle between the ILD and ABL regression lines) as a function of poststimulus time. During the first 250 ms, the responses of the recorded neurons explain a high proportion of the stimulus variance in both the ILD (red) and ABL (black) dimensions. A sharp drop in variance explained occurs after this point for the ILD curve despite the fact that the variance explained in the ABL dimension remains high and drops off much more gradually over time. θ (blue) is high for cases where it can be meaningfully measured. The dashed line indicates where either ILD or ABL had an R² of <0.3, and it is only at these times that θ values drop. High θ values at very long latencies are due to chance.

DISCUSSION

We have shown that neurons in auditory cortex exhibit complex sustained temporal patterns that persist for hundreds of milliseconds following stimulus offset. We detected the presence of statistically significant receptive fields from single neurons over long time periods following stimulus offset. A population-based classification algorithm confirmed this and revealed that, at long latencies, the population codes ABL rather than ILD. Furthermore the neural population response encodes both ILD and ABL with uniformly high accuracy over the entire stimulus range. A multidimensional scaling analysis confirmed that at early time points, ILD and ABL are represented orthogonally and that the representation of ABL persists for longer in the neural population response than that of ILD.

Previous studies of long latency activity

A recent study by Moshitch et al. (2006) recorded in cat auditory cortex and used information theoretic approaches to confirm the presence of significant long-latency activity in response to tones. Our study extends these observations by exploring the relative amounts of information conveyed about different stimulus parameters over time. The importance of long-lasting stimulus effects in audition has been illustrated by other studies (e.g., Bartlett and Wang 2005; Brosch and Schreiner 1997; Brosch et al. 1999; Calford and Semple 1995; Malone et al. 2002), which found that recent stimulus history can profoundly affect neural response properties in the auditory cortex. The duration of the events described in our study are consistent with the time course over which responses to different stimuli interact in cortex (Bartlett and Wang 2005).

Complex temporal response properties are not confined to the awake state

The activity of auditory cortical neurons tends to be reduced by general anesthetics, such as barbiturates and ketamine (Zurita et al. 1994). Tonic or sustained firing is sometimes considered a hallmark of the awake state with anesthetized preparations having more phasic responses (Qin et al. 2003; Wang et al. 2005). Nevertheless neurons with complex tonic responses have been found in ferret auditory cortex under both barbiturate (Mrsic-Flogel et al. 2005) and ketamine/medetomidine anesthesia (Bizley et al. 2005). In barbiturate-anesthetized rats, stimulus-induced oscillatory firing can persist over hundreds of milliseconds (Sally and Kelly 1988). Moreover, halothane-anesthetized cats have cortical responses reminiscent of those seen in the present study (Moshitch et al. 2006). Walker et al. (2008) found only subtle differences between cortical responses recorded in awake and ketamine/medetomidine-anesthetized ferrets. Animals were presented with natural stimuli. In the awake state, neurons gave stronger responses to sound onset and offset, but the capacity of neurons to follow rapid (∼50 Hz) fluctuations in the stimulus waveform was similar in both conditions. Ferret cortical neurons also exhibit very similar stimulus-timing dependent plasticity in both awake and anesthetized states (Dahmen et al. 2008). On the other hand, the stimulus sensitivity of cortical neurons can undergo pronounced changes in the awake state when an animal engages in a task (Fritz et al. 2005; Otazu et al. 2009) in which it has to attend to the stimulus (Fritz et al. 2007), suggesting that behavioral context is a more important factor than the absence of anesthesia per se in influencing the firing properties of these neurons.

Representing sound-source location in the auditory cortex

From the midbrain onwards, neurons in the auditory pathway tend to respond best to broad regions of space on the contralateral side of the body, which has led to the proposal that information in the left and right hemispheres might be compared with determine sound source location (reviewed in McAlpine 2005). However, this view conflicts with the finding that unilateral lesions (e.g., Heffner and Heffner 1990; Jenkins and Merzenich 1984; Kavanagh and Kelly 1987) or inactivation (Malhotra et al. 2004; Smith et al. 2004) of auditory cortex result in contralateral deficits in sound localization. The results of those behavioral studies imply that each hemisphere is concerned predominantly with the representation of the opposite side of space. A small proportion of cortical neurons are, however, tuned ipsilaterally, and it has been demonstrated that ABL-invariant opponent-channel models can be built using cortical neurons from just one hemisphere (Stecker et al. 2005).

Our own data show that it is possible to assign a response to the correct ILD irrespective of ABL without partitioning neurons into two opposing channels. Furthermore, ILD classification accuracy is equally good for ipsi- and contralateral sounds, a finding that is in broad agreement with previous studies showing that the discharge patterns of cat cortical neurons can convey information across the full range of sound azimuth (Middlebrooks et al. 1994). Although this would appear to obviate the requirement to compare information from the two hemispheres, it does not explain why unilateral cortical lesions result in contralateral localization deficits. However, maximum likelihood estimates of stimulus location suggest that the population responses of neurons in monkey auditory cortex convey more information about contralateral than ipsilateral space (Miller and Recanzone 2009). The spatial tuning of cortical neurons depends not only on ILDs but also the directional properties of the external ears (e.g., Middlebrooks and Pettigrew 1981; Schnupp et al. 2001) and interaural time differences (Malone et al. 2002) with the contribution of each spatial cue varying with the frequency tuning of the neurons. Sensitivity to localization cues other than ILDs could therefore make the responses more informative about particular regions of space. Alternatively, the contralateral deficits observed in animals with unilateral lesions of A1 could simply reflect the fact that each side of the brain is most strongly activated by sound sources on the opposite side with the elimination of activity in one hemisphere greatly reducing the transmission of information to higher areas that have a more specialized role in sound localization.

Why have long latency activity?

It is possible that long-latency activity provides information about stimulus identity that is independent of that provided by the onset peak. Evolving stimulus representations appear to de-correlate responses to similar odors over time in the zebra fish olfactory bulb (Friedrich and Laurent 2001). Calculating independence across time is not trivial for our dataset because signal to noise decreases as a function of poststimulus time. Independence will therefore always appear to increase regardless of the underlying evoked response. However, unlike the zebrafish data, our MDA-based classification algorithm does not perform better over time, arguing that progressive de-correlation is not taking place in auditory cortex. The difference in the results is probably system specific rather than species specific: a recent study of temporal coding in rat auditory cortex (Bartho et al. 2009) found that responses to different 1-s tones do not progressively decorrelate during presentation of the stimulus.

Animals often have to accumulate sensory evidence over hundreds of milliseconds when making difficult choices (Kiani et al. 2008). However, the membrane time-constant of individual neurons is orders of magnitude faster than behavioral integration times. How is activity about the upcoming choice processed over hundreds of milliseconds? Recurrent networks may provide one solution to this problem because they allow stimulus-induced activity to persist over long time periods. Sensory stimulation (Anderson et al. 2000) and thalamic activity (Rigas and Castro-Alamancos 2007) can trigger cortical “up” states, potentially providing a way of maintaining persistent activity in a stimulus-dependent fashion. The response to a particular stimulus sometimes appears to “reverberate” in a characteristic way (for example, Fig. 2B). Such behavior is an integral part of so-called liquid state machines (LSMs), which are an emerging class of computational models for neural function (Maass et al. 2002). LSMs have a number of interesting properties, one of which is the ability to deal realistically with temporal features of neural codes. Assuming the network is nonchaotic, long-term reverberations allow LSMs to access past states of the system.

In terms of the binaural cues used in the present study, it is possible that the presence of sustained cortical responses might be particularly useful for the detection of stimulus motion. However, because the time domain is important for providing a context for acoustic stimuli, persistent activity may well play a more general role in auditory processing.

GRANTS

This work was supported by the Wellcome Trust through a 4-year studentship to R.A.A. Campbell and a Principal Research Fellowship to A. J. King and Biotechnology and Biological Sciences Research Council Grant BB/D009758/1 to J.W.H. Schnupp and A. J. King.

DISCLOSURES

No conflicts of interest are declared by the authors.