Receptive Field Dynamics Underlying MST Neuronal Optic Flow Selectivity

Abstract

Optic flow informs moving observers about their heading direction. Neurons in monkey medial superior temporal (MST) cortex show heading selective responses to optic flow and planar direction selective responses to patches of local motion. We recorded MST neuronal responses to a 90 × 90° optic flow display and to a 3 × 3 array of local motion patches covering the same area. Our goal was to test the hypothesis that the optic flow responses reflect the sum of the local motion responses. The local motion responses of each neuron were modeled as mixtures of Gaussians, combining the effects of two Gaussian response functions derived using a genetic algorithm, and then used to predict that neuron's optic flow responses. Some neurons showed good correspondence between local motion models and optic flow responses, others showed substantial differences. We used the genetic algorithm to modulate the relative strength of each local motion segment's responses to accommodate interactions between segments that might modulate their relative efficacy during co-activation by global patterns of optic flow. These gain modulated models showed uniformly better fits to the optic flow responses, suggesting that coactivation of receptive field segments alters neuronal response properties. We tested this hypothesis by simultaneously presenting local motion stimuli at two different sites. These two-segment stimuli revealed that interactions between response segments have direction and location specific effects that can account for aspects of optic flow selectivity. We conclude that MST's optic flow selectivity reflects dynamic interactions between spatially distributed local planar motion response mechanisms.

INTRODUCTION

Dorsal MST (MSTd) neurons respond to the large-field patterns of optic flow (Saito et al. 1986; Tanaka and Saito 1989) encoding self-movement heading direction (Duffy and Wurtz 1991a, 1995; Lappe et al. 1996). Many MSTd neurons are responsive to planar, radial, and circular patterns in a manner that is consistent with a planar directional mechanism in the peripheral visual field although such a mechanism is not always readily apparent in responses to patches of local motion responses or to moving spots. Others show either planar and radial or planar and circular responsiveness, consistent with an eccentric planar response mechanism that is selectively activated by either radial or circular patterns that contain orthogonal motion throughout the stimulus. The most selective neurons show only planar, or radial, or circular responsiveness with yet unclear relations to planar response mechanisms (Duffy and Wurtz 1991a,b). This spectrum of response selectivities is compatible with a range of MSTd neuronal response properties in a three-dimensional (3D) pattern direction space (Graziano et al. 1994).

The view that planar motion sensitivity is the basis of optic flow analysis was undermined by evidence that human heading estimation is unaffected by concurrent pursuit eye movements that distort retinal motion patterns (Warren and Hannon 1990). These findings were interpreted as supporting computational models of optic flow analysis that avoid the distorting effects of eye rotation by deriving separate rotational and translational components from the optic flow field (Longuet-Higgins and Prazdny 1980; Prazdny 1981). A number of biologically plausible models of optic flow component decomposition have augmented these views by the consideration of the combined contributions of direction and speed tuning (Barraza and Grzywacz 2005; Dyre and Andersen 1997; Heeger 1987; Lappe and Rauschecker 1993; Perrone 1992). Emphasis on the role of planar motion sensitivity in optic flow analysis was bolstered by evidence that nonvisual signals about pursuit eye movements support heading estimation during eye rotation (Banks et al. 1996; Royden et al. 1992). Thus the influence of pursuit signals on MSTd's neuronal responses supported the notion that many of these cells might combine visual motion responses with oculomotor signals in shaping their responses to optic flow (Bradley et al. 1996; Page and Duffy 1999, 2003), although it is increasingly evident that purely visual mechanisms might also achieve such effects (Beintema and van den Berg 1998; Bremmer et al. 2010).

In the current studies, we examined the role of planar motion response mechanisms in optic flow analysis by expanding on an earlier approach (Duffy and Wurtz 1991a,b), recording responses to both large-field optic flow and local planar motion during visual fixation. We modeled MSTd's planar motion responses using mixture of Gaussians models because of their utility as an unbiased approach to describing the probability density functions of observed variables. Our experience with the highly diverse shape of MSTd neuronal planar direction response functions led us to conclude that simpler models are inadequate (Duffy and Wurtz 1991b, 1997c). We used a genetic algorithm to optimize the mixture of Gaussians models guided by response magnitude and selectivity error functions. We use these dual criteria to avoid response function biases and accrue greater resistance to local minima encountered in the fitting process (Bleeck et al. 2003; Van et al. 2008). By combining data from various stimulus paradigms, we incrementally refined our model of MSTd neuronal responses to identify factors that might shape planar motion mechanisms so that they are more specifically suited to optic flow analysis.

METHODS

Animal preparation

Rhesus monkeys were accommodated to the laboratory routine and then underwent surgery in preparation for single neuron recording. Surgical procedures were preceded by sedation with ketamine (15 mg/kg im) and Robinul (glycopyrrolate) (0.011 mg/kg im), followed by venous catheterization, endotracheal intubation, and general anesthesia using inhaled isoflurane. Continual verification of the surgical plane of anesthesia was maintained while measuring heart rate, core temperature, O₂ saturation, and end-expired CO_2.

We excised a 3 × 4 cm section of scalp, debrided the exposed calverium, and inserted 16–24 dental pins around the edge of the exposed bone to stabilize the implant. We placed bilateral scleral search coils by peri-limbotomy, tunneling the leads to connectors within the area of excised scalp (Judge et al. 1980). A head holder socket was placed over the frontal midline and bilateral recording cylinders were placed over 2 cm trephine holes above area MSTd [AP –2 mm, ML±15 mm, angle 0 (perpendicular to the stereotaxic plane)]. The dental pins, coil connectors, head holder, and recording chambers were then encased in a dental acrylic cap.

Postoperatively, the animal was returned to its home cage when it could maintain postural stability and coordinate its limb movements. Close monitoring of its behavior guided analgesia with banamine (1 mg/kg im) as judged appropriate by the veterinary staff. Daily cleaning of the excised scalp edge and of the recording chambers was maintained thereafter. All protocols were approved by the University of Rochester Committee on Animal Research and complied with U. S. Public Health Service and Society for Neuroscience policy on the care of laboratory animals.

When the animals had fully recovered from surgery, they were trained to maintain visual fixation during visual stimulus presentation as confirmed by eye position monitoring using the magnetic search coils (Robinson 1963). Trials began with a stationary, red fixation point centered at eye height directly in front of the animal. The monkeys were required to maintain fixation (±3°) throughout the trials while patterns of optic flow stimuli were presented. Successful completion of a trial was accompanied by the sounding of an auditory tone and the delivery of a liquid reward. Single neuron recording sessions were begun after the animal consistently completed >90% of the stimulus presentation trials.

Visual stimuli

After the isolation of responses from a single neuron, its receptive field characteristics were mapped using a hand-held projector presenting varying size bars and random dot patterns. We then began the automated presentation of patterned visual motion stimuli generated by a personal computer driving a television projector (Electrohome ECP4100) at 60 Hz to cover the central visual field (90 × 90°).

We first presented optic flow covering the entire stimulus area as a random sequence of 2 s stimuli. We then presented local motion stimuli in a randomly interleaved sequence of one of the nine 30 × 30° nonoverlapping segments of the display with one of the four cardinal directions of motion. Finally, we used the real-time display of the single stimulus data to select hot spots to be the focus of a series of dual local motion stimulus studies in which a selected display segment was combined with the four directions of motion at the other sites.

The optic flow stimuli simulated the self-movement scene for 16 different heading directions. The 16 directions were presented in a pseudo-random sequence until each had been presented during six to eight successful fixation trials. Each optic flow stimulus consisted of 500 white dots (0.19° at 2.61 cd/m²) on a black background (0.18 cd/m²) stimulating the central 90 × 90° of the visual field. All dots were replaced by lifetime expiration (33–1,000 ms) or by a smoothing algorithm that maintained a uniform and consistent dot density across the stimulus in all frames. Dots for these radial patterns accelerated as a sine × cosine function of their distance from the focus-of-expansion maintaining an average speed of 40°/s across the stimuli. We used the same speed in all visual motion stimuli of this study as we have previously found that it activates MST neurons optimally (Duffy and Wurtz 1997a).

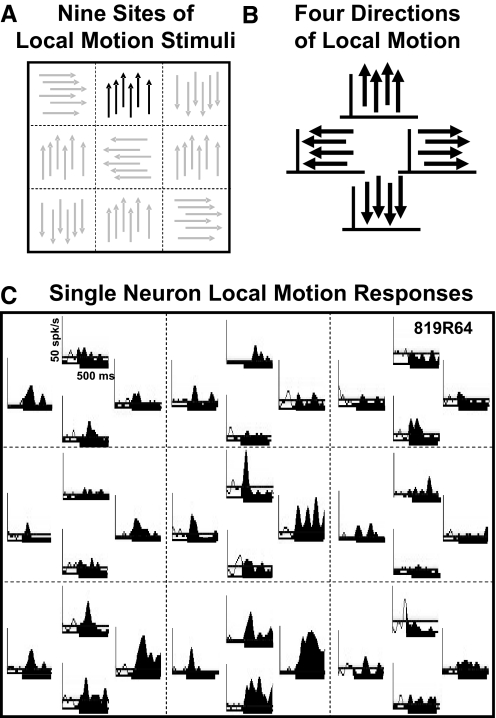
In other blocks during the recording session, the visual stimulus was subdivided into nine, nonoverlapping, 30 × 30° screen segments (Fig. 1A). Planar motion in the four cardinal directions was presented in each segment separately (Fig. 1B), accommodating the multiplicative effect of additional stimulus directions on the time required to complete each study. Each stimulus interval presented either motion in a single segment or in two independently selected segments. The preselection of locations for the paired stimulus presentations was based on the review of receptive field characteristics to identify the most responsive segments of the display area. The segment and direction of motion, and the presentation of single or paired stimulus segments, were all interleaved pseudorandomly.

Fig. 1.

Local planar motion stimuli evoke direction and location selective responses in dorsal medial superior temporal (MSTd) neurons. A: the 90 × 90° stimulus screen was divided in to 9 equal 30 × 30° stimulus segments. B: 4 directions of planar moving dot stimuli were presented in each segment with remaining segments remaining blank. C: the neuronal spike density histograms for a neuron showing the responses to planar motion in each of the corresponding screen segments (- - -) and motion direction (up, left, right, down).

Trials began with the monkey fixating a central target followed by the presentation of a random series of the nine locations and four planar motion directions shown for 500 ms each. In the data analysis, we deleted the first 10% of each stimulus period (50 ms of the 500 ms stimulus period) to diminish the impact of response transients and focus on the tonic responses of each neuron (Duffy and Wurtz 1997c).

Neural recording and data handling

In these studies, single neuron responses were recorded from two cerebral hemispheres of two rhesus monkeys. Tungsten microelectrodes (Microprobe) were passed through a trans-dural guide tube to record neuronal activity (Crist et al. 1988). A dual window discriminator digitized discharges that were stored with event markers on the REX experiment control system (Hays et al. 1982). MSTd was identified by determining that the recording sites contained neurons having large receptive fields (>20°²) that include the fixation point, with direction selective responses, preferring pattern to bar motion (Duffy and Wurtz 1991a; Komatsu and Wurtz 1988a).

When these experiments were completed, we placed electrolytic marking lesions at selected sites in the recording region. Subsequent histological analysis confirmed that our recording sites were in the anterior bank of the superior temporal sulcus, overlapping with the heavy myelinated zone that is associated with MSTd. In our preliminary data analysis, neuronal spikes were convolved with a 20 ms Gaussian to produce spike density functions that were averaged over the six to eight presentations of each visual stimulus.

Mixture of Gaussians models

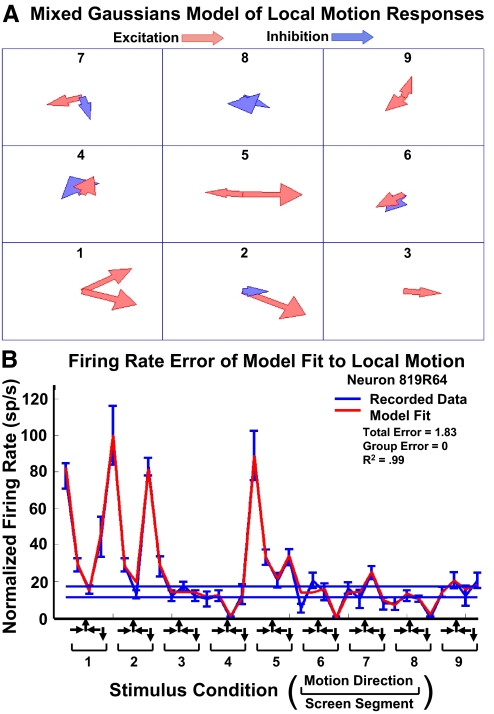
In these experiments, the visual display area was divided in to a 3 × 3 array of nine spatial segments (Fig. 1A). We developed a generative model in which the responses of each segment was modeled as a mixture of two Gaussian functions (Fig. 2A). The mixture of Gaussians was implemented to enable any combination of excitatory and inhibitory mechanisms, accommodating the shape of local motion response functions that ranged from apparently sharp unimodal to distinctly bimodal excitation or inhibition. We then simulated the presentation of optic flow stimuli to the nine segment composite model, combined as the linear sum of the individual segment responses, to predict that neuron's responses to optic flow (Fig. 2B).

Fig. 2.

Mixture of Gaussians local motion models of 9 screen segments recorded in 1 neuron. A: model used either excitatory (red) or inhibitory (blue) vectors to match the neuronal responses. Vector direction and amplitude (length of vector) indicate the tuning of each of the 2 Gaussian functions in each of the 9 segments. B: the mixture of Gaussians model created highly accurate fits (red) for the responses to the 36 local motion stimuli (blue). The 10 models generated for this neuron yielded consistently excellent fits to the local motion data: mean total error = 2.72 spike/s, mean group error = 0.03 classes, mean r² = 0.98.

Four parameters were estimated for each of the Gaussian functions in each screen segment's mixture of Gaussians model of the neuronal firing rate responses

$$G{\left(x,c,p,\mu ,\sigma \right)}_{i,j}=c_{i,j}·p_{i,j}·\exp \left[-{\left(x-{\mu }_{i,j}\right)}^2/2{\sigma }_{i,j}^2\right]$$ (1)

where x is the motion direction, c is the gain constant modulating the magnitude of the Gaussian, p is the polarity of the excitatory or inhibitory response function, μ is the mean angular direction of the segment's preferred visual motion, σ² is the variance around the preferred direction, i represents the stimulus screen segment (i = 1, 2, … , 9), and j represents the two Gaussians within each screen segment (j = 1, 2).

Thus there were eight parameters estimated for each of the nine segments. The complete local motion model of responses, with nine stimulus segments, required the estimation of 72 parameters. In consideration of the risk of over-fitting, we tested the local motion models with independent data from the same neurons, acquired using optic flow stimuli. To do so, the output of each Gaussian, relative to that neuron's baseline firing rate (during fixation without visual motion stimulation) was summed across all nine segments and then summed with the baseline firing rate to predict the firing rate response to the full-field optic flow stimuli. In later versions of these models, the relative gain of each segment was independently adjusted, matching the gain factors of the two Gaussians in each segment's model. When each of the individual Gaussian response mechanisms was assigned an independent gain, the gains were modulated independently.

Genetic algorithmic modeling

Several different approaches might be used to estimate the mixture of Gaussians parameters. In this work, we use a computational genetic algorithm. Genetic algorithms are a class of computational methods that seek to solve an optimization problem, in this case, how to optimize the fit of a mixture of Gaussians to responses to local motion data about any one of the nine stimulus segments.

The problem is formulated in terms of 1) creating a randomly generated initial population of candidate models from which a best fit model will be developed; 2) a fitness function repeatedly applied to evaluate each candidate model as to the quality of its fit to the data; 3) a selection method that implements the criteria by which the best fitting models of each successive generation will be chosen to the parental foundations of the next generation; 4) producing the next generation of the population by applying crossover and mutation methods to the parental models selected from the previous generation; and 5) selecting the final best-fit model from each trial application of the genetic algorithm.

Creating the initial population

To create the initial population of candidates, we randomly produced 1,300 individual models. Each parameter in Eq. 1 was represented by a binary string: (e.g., 10110101 00110101 00011111 …) in which each set of eight bits forms a byte that is used to represents a parameter value. The number of bytes used for each parameter depends on the upper bound of that parameter's values; the greatest number of bytes that might be required to represent that parameter. Thus each of the 1,300 individuals in the first generation had a randomly created set of bits describing a specific model by specifying each of the parameters in Eq. 1.

Evaluating each model

The genetic algorithm determined the goodness of the fit between each model's predicted responses to the local motion stimuli and the observed responses. Specifically, we sought a set of model parameters that minimized the difference between the model's firing rates and the firing rates of the neuron recording in the neurophysiological experiment. The quality of the fit of each candidate model was determined by combining two equally weighted error functions.

The first error function was the total error, the sum of the differences between a model's predicted firing rate responses and the observed averaged, normalized firing rates evoked by each of the stimuli entered in to that comparison, weighted by the firing rate standard error from the responses to each presentation of that stimulus

$$d_{\text{e}}={\displaystyle \sum _{i=1}\left|r_{m_i}-r_{n_i}\right|}/{\text{se}}_i$$ (2)

where d_e is the total error, r_m is the model's firing rate response, r_n is the neuron's firing rate response, se is the SE of the neuron's firing rate response, and i is the index value across the number of stimuli in that stimulus set (36 for local motion, 16 for optic flow).

The second error function was the sum of the differences in response classification based on a cluster analysis that included the average firing rates of all stimuli in the respective study. The cluster analysis used a k-means algorithm set to yield three clusters (k = 3) separated in Euclidean space to minimize cluster scatter. The three group cluster analysis was independently applied to the model's firing rate responses and the observed firing rate responses of the corresponding neuron. The cluster cutting yielded two types of clusters that were approximately equally represented in the sample of neurons: excitatory responses, nonresponses, and inhibitory responses and large and small excitatory responses and nonresponses.

We then summed the cluster classification differences across all of the visual motion stimuli presented in that study as

$$d_{\text{g}}={\displaystyle \sum _{i=1}\left|\text{kmc}\left(r_{{\mathrm{m}}_i},k\right)-\text{kmc}\left(r_{{\mathrm{n}}_i},k\right)\right|}$$ (3)

where d_g is the group error, r_m and r_n are as in Eq. 2 and kmc (x, k) is the k-means clustering of the xth responses, across the ith stimulus in that stimulus set.

Selecting parental models

The two fitness functions were independently used to rank each model from best to worse fit to the corresponding neuron's firing rate data, resulting in two ordered lists. The best 25 individuals from each list were chosen to be parents. Each of the 25 lowest total firing rate error individuals were then crossed over with each of the 25 lowest group classification error individuals, and each parent produced two offspring.

Evaluating each model

The four offspring from each pair of parents was generated by cleaving the bit sequence of each at a random location within a selected parameter's gene. This split that variable bit string into two pieces that were then combined: left piece from parent 1 to left piece from parent 2, left piece from parent 1 to right piece from parent 2, right piece from parent 1 to left piece from parent 2, and right piece from parent 1 to right piece of parent 2. If any of the resulting crossed-over variables contained an invalidly high number, it was set to the maximum value allowed. The resulting total offspring of 1,250 was combined with the 50 parent individuals to populate the next generation for successive application of the genetic algorithm.

To prevent convergence of the population to a local minimum, 5% of the individuals in each generation underwent a toggling of randomly selected bits from their parameter bit strings, a process that is intended to mimic the occurrence of mutations in biological evolution. We terminated the algorithm after a fixed number of generations to avoid having different numbers of generations for different neurons. The number of generations for each condition was determined by reviewing the error gradients from test runs of the algorithm. As a result, the algorithm was terminated after 75 generations for the local motion models, 50 generations for the gain modulated models, and 25 generations for the dual stimulus interaction models.

Final model selection

At the completion of the selected number of generations, the model with the smallest total error score was selected as the final model for that neuron. The modeling of the local motion responses was repeated ten times with independently selected random starting parameters to assess the impact of those parameters and minimize the risk of the final model's reflecting local minima in the error functions.

In evaluating the success of these modeling efforts, we used the final values of the total and group error functions as well as a measure that was independent of the modeling algorithm. In the latter case, we ordered the local motion responses by increasing average firing rate and compared them to the model's corresponding firing rate predictions using a linear regression model (SPSS 2007).

RESULTS

We studied the responses of 52 neurons from two hemispheres of two Rhesus monkeys using three stimulus sets presented during centered fixation: single site local planar motion, two site local planar motion, and large-field optic flow. All neurons were recorded from electrodes passing through guide tubes that yielded characteristics typical of MSTd neurons (Komatsu and Wurtz 1988a,b): large receptive fields that include the fovea, preferring pattern motion to moving bars, and showing strong direction selectivity. Subsequent histological examination of the recording sites confirmed that they were in the dorsal-anterior bank of the superior temporal sulcus in the region associated with the medial superior temporal area.

Modeling responses to local motion

We presented a randomly interleaved series of 36 local motion stimuli to each neuron. These stimuli were limited to one of nine 30 × 30° screen segments juxtaposed to cover the same 90 × 90° stimulus area of the previously presented optic flow stimuli (Fig. 1A). At each of the nine sites, we presented four different planar motion directions: left, right, up, and down (Fig. 1B). These stimuli revealed a diverse array of local motion direction selectivities across the stimulus area, typically including both excitatory and inhibitory responses to different directions of motion (Fig. 1C). This combination of responses yielded distinctly different directionality profiles in different stimulus segments.

To characterize the local motion responses, we derived separate mixture of Gaussians models of the responses evoked for each of the nine stimulus segments. This was achieved by using a genetic algorithm to simultaneously optimize the fit of the averaged responses to the four directions of local motion in each segment using free parameters of the direction (0–359°), magnitude (spike/s), and sign (excitatory or inhibitory) of the model responses for each of the two Gaussians (Fig. 2A). Ten independent models were calculated for each neuron to assess the intrinsic variability of the genetic algorithm and its dependence on its randomly assigned starting values.

We assessed the success of each model using the model's two equally weighted error functions of total firing rate error and k-means (k = 3) cluster analysis classification error. In addition, we derived a measure of the model's effectiveness that was independent of the modeling process using a linear regression of the ordered set of observed firing rate responses and the model's predicted firing rates.

The genetic algorithm achieved excellent fits to the local motion with the model's responses closely matching the local motion responses in all neurons (Fig. 2B). The 10 models for each neuron yielded comparable fits to the recorded data, reflected in the low variance of the fitting error across the 10 models: mean total error = 6.03 spike/s, mean group error = 0.17 of the three clustering groups, mean r² = 0.90.

To test the similarity of the ten models generated for each neuron, we correlated each model's prediction of the local motion responses to those derived from each of the other models of that neuron. We averaged the r²'s for all combinations of the 10 models of each neuron and then averaged across neurons to derive a net r² = 0.88 with a mean SD of the r²'s across neurons of ±.06. These results suggest that the 10 models for each neuron yield highly similar predictions of the local motion responses, implying convergence of the modeling process across multiple trials seeded with randomly selected starting conditions.

Local motion models of optic flow

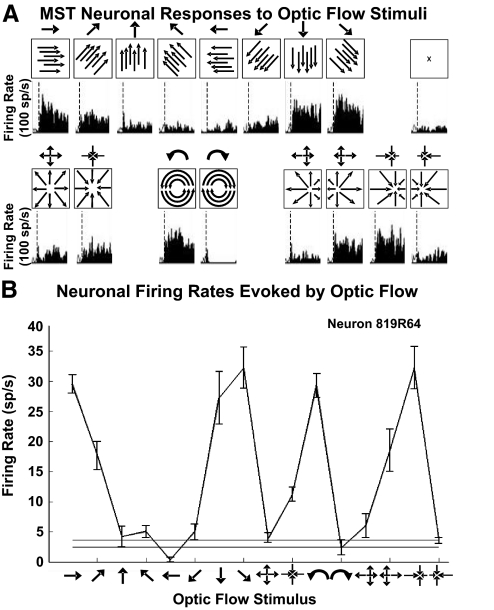
The activity of these neurons was also recorded during the presentation of large-field (90 × 90°) optic flow stimuli during centered fixation. We randomly interleaved 16 optic flow stimuli including eight directions of planar, six radial, and two circular patterns (Fig. 3A). Combinations of excitatory and inhibitory responses to planar, radial, and circular stimuli were encountered as previously described (Duffy and Wurtz 1991a). These responses were characterized by determining the mean firing rate during the 1 s stimulus interval of six to eight repetitions of each stimulus and compared with the mean firing rate during blank screen fixation trials (Fig. 3B).

Fig. 3.

Optic flow stimuli evoke heading direction selective responses in MSTd neurons. A: 16 optic flow stimuli were presented in a pseudorandom sequence with each stimulus repeated 6–8 times. Schematic plots (boxes) indicate optic flow pattern on screen along with corresponding spike density histograms. Dashed vertical line indicates the start of the trial. B: responses of an MSTd neuron to the 16 optic flow stimuli along with variance (±SE). The icons along the abscissa indicate the optic flow stimulus evoking the corresponding firing rate response.

We used the mixture of Gaussians model of the local motion responses of each neuron to predict that neuron's responses to the 16 full-field optic flow stimuli. First, for each neuron, we calculated each of the nine stimulus segments' responses to each of the 16 optic flow stimuli. This was achieved for each stimulus segment by determining the firing rate that would be expected from its mixture of Gaussians model when shown the local motion that would cover its screen segment during the presentation of each optic flow stimulus. Second, for each neuron, we summed the firing rates for each of the nine stimulus segments to predict a net response of that neuron to each of the 16 optic flow stimuli. Finally, we used the net responses of each neuron to create an optic flow response profile for that neuron and compared that profile to the observed firing rates profile obtained from that neuron's responses to the 16 optic flow stimuli.

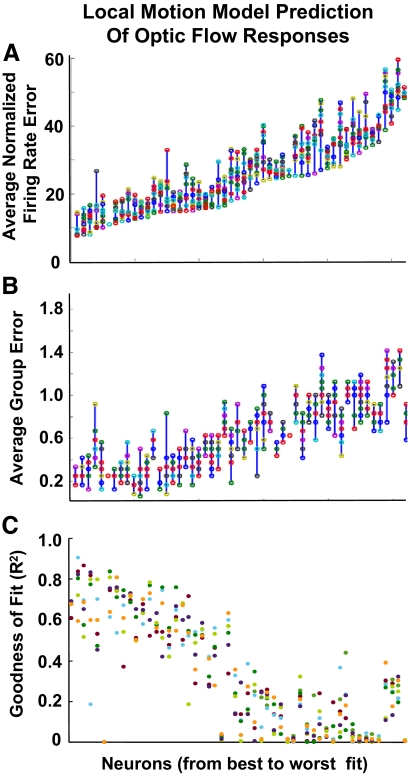
We assessed the local motion models' ability to predict the optic flow responses using the same three metrics used to assess the local motion fits: the differences in the predicted and observed normalized firing rates summed across the 16 optic flow stimuli, the sum of the differences in response classification based on a three group cluster analysis of the optic flow responses, and r²'s derived from an ordering of optic flow responses by increasing amplitude and comparing them to the corresponding predicted response amplitudes.

Three salient points emerged from our examining the local motion model's predictions of the optic flow responses using all three response metrics: first, across the sample of neurons, there is a wide range of accuracies in predicting optic flow responses (Fig. 4, A and B), although every neuron yielded at least one significant fit by the r² measures (C). The best fits are highly accurate, with little firing rate (Fig. 4A) or group classification (B) error compared with the observed responses, whereas some other neurons yielded fits that are up to five times worse by the error metrics. Second, all three fit metrics yield similar orders of model accuracy across the sample of neurons; neurons that yield the best model fits do so by all three measures. Third, in individual neurons, the 10 independent local motion models yielded similar fits to the responses. There was less variability in the quality of the fit across the ten models of any neuron than across the sample of neurons.

Fig. 4.

Local motion mixture of Gaussians model fits to responses to 16 optic flow stimuli. The neuronal responses to the optic flow stimuli were compared with the model predictions by 3 methods: normalized total errors (A), normalized group errors (B), and the r² regression fits of the model prediction to the neuronal response data (C). In all panels, the neuron number (abscissa) was maintained in the order of increasing total error to facilitate comparisons between the 3 metrics.

These findings suggest that the optic flow response selectivities of some neurons are adequately explained by the summation of simple planar motion responsiveness distributed across MSTd neuronal receptive fields. In many other neurons, optic flow responses have not been readily predicted as the sum of local planar motion responses.

Weighted local motion models of optic flow

The common failure of local motion models to predict optic flow responses prompted us to consider the hypothesis that the relative influence of various receptive field segments might be altered during their co-activation by optic flow. To assess this possibility, we used the genetic algorithm to adjust the relative influence of the nine screen segments and optimize each model's fit to that neuron's optic flow responses.

First, we randomly assigned a multiplicative gain to the mixture of Gaussians model of each of the nine screen segments without changing the other fit parameters. Then the genetic algorithm modified these nine weightings to minimize the total and group errors for each of the 10 models of each of the neurons. This approach does not alter the direction specificity of the nine segments but modifies the strength of each segment's influence on their composite prediction of optic flow responses.

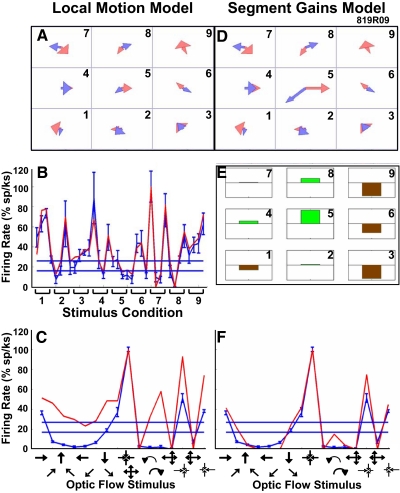
The resulting segment gain modulated models yielded a substantial improvement of the fit to optic flow for many neurons. The neuron illustrated in Fig. 5 yielded a local motion model (A) with an excellent fit to the recorded local motion data (B) but not to optic flow. In this example, the local motion model inconsistently predicted the responses to the eight directions of planar motion and the radial and circular optic flow patterns (Fig. 5C). The segment gain modulated model (Fig. 5D) showed substantial and systematic changes from the parent local motion model. These changes are shown as segmental gains that increase the influence of the middle segment and decrease the influence of the segments on the right side of the display area (Fig. 5E). When tested with optic flow stimuli, the segment gain modulated model showed a substantially better fit to the recorded optic flow responses (Fig. 5F).

Fig. 5.

The transformation of a neuron's mixture of Gaussians models by segmental gain modulation. A: mixture of Gaussians model derived from local motion responses in the 9 stimulus segments. B: corresponding fit of the local motion model to neuronal responses to the 36 planar stimuli (format as in Fig. 2). C: corresponding fit for the local motion model (red) to the 16 optic flow patterns showing a poor model fit to the neuronal responses (blue). D: mixture of Gaussians model after segmental gain modulation. E: segmental gain changes that were implemented by the model to modulate the weight of the mixture of Gaussians model in each of the 9 segments (increases, green; decreases, brown; full-scale ± 10×). F: fit of the segment gain modulated model to the 16 optic flow patterns shows a substantial improvement for all optic flow stimuli compared with that of the unmodulated local motion model shown in C.

We explored the hypothesis that interactions between local motion response mechanisms, simultaneously activated by large-field optic flow stimuli, might alter the behavior of the local motion direction selective mechanisms modeled as the 18 Gaussian filters in the nine stimulus segments. To test this hypothesis of nonadditive response interactions, we allowed the genetic algorithm to independently modify the relative weighting of the 18 Gaussians filters in the local motion models of each neuron. The resulting changes in the response gains of the 18 Gaussians can modify the composite direction selectivity of each of the nine stimulus segments as well as their relative weight, potentially altering the spatial distribution of response directionality and strength.

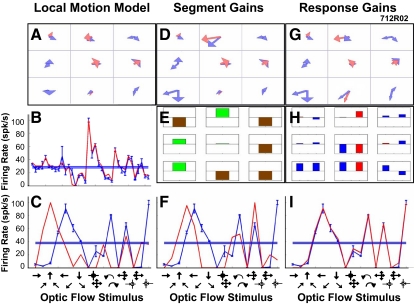
Figure 6 illustrates the mixture of Gaussians models of a single neuron derived from local motion stimuli and modified by segment and response gain modulation. This neuron showed a variety of models Gaussians across its nine stimulus segments (Fig. 6A) with an excellent fit to the local motion responses (B) but a poor fit to the optic flow responses (C). Segment gain modulation substantially changed the nine models (Fig. 6D) and resulted in lower segmental gains in the upper left segment and on the right with higher segment gains elsewhere (E) and a better fit to the optic flow responses (F). Response gain modulation substantially changed the 18 Gaussians (Fig. 6G) with lower gains in the center segment and higher gains in the lower segments (H) that resulted in an excellent fit to the optic flow responses (I).

Fig. 6.

The transformation of a neuron's mixture of Gaussians models by response gain modulation. A–F: format as in Fig. 5. G: mixture of Gaussians model after response gain modulation. H: response gain changes that were implemented by the model to modulation the weight of each of the 18 Gaussians (increases, above line; decreases, below line; excitatory Gaussians, red; inhibitory Gaussians, blue; full-scale ±10×). I: fit of the response gain model to the 16 optic flow patterns shows a substantial improvement for all optic flow stimuli compared with both the unmodulated local motion model (C) and the segment gain modulated model (F).

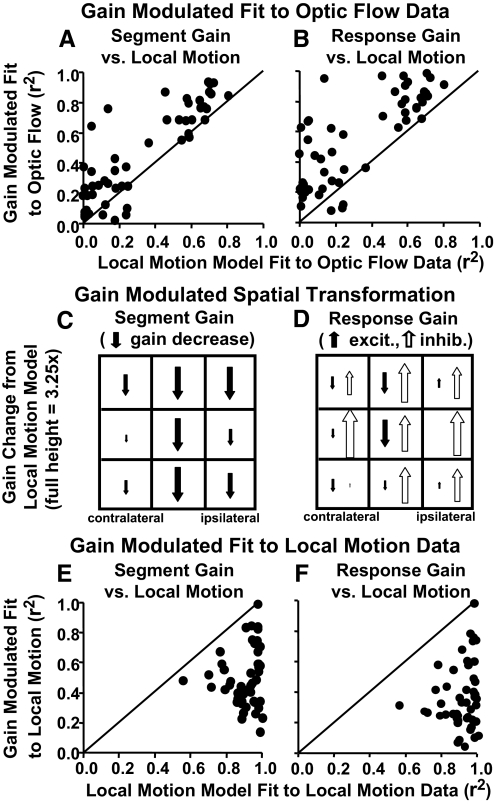
The models' predictions of the optic flow responses were compared with the actual responses from each neuron using a least squares regression fit to quantify model accuracy. This measure was used to compare the results of the original local motion models of each neuron to the results of that neuron's models after segment gain (Fig. 7A) and response gain (B) modulation. Both gain modulated models yielded substantially better fits than the local motion models as illustrated by almost all points being above the unity lines shown in those plots. The segment gain modulation resulted in a mean r² increment = 0.18 over local motion models. Response gain modulation resulted in a mean r² increment = 0.28 over local motion models. Improvements with segment gain modulation demonstrate that changing only the relative influence of the nine screen segments enhances the fits to optic flow. Greater improvements with response gain modulation imply that changes in the relative contributions of the mixture of Gaussians models yields additional benefit, still without changing the individual Gaussians' directionality derived from the local motion studies.

Fig. 7.

Comparison of fits to neuronal responses derived from the local motion models (abscissas) and the 2 approaches to the gain modulation of those models (ordinates). The r² values are from linear regression fits of each neuron's observed firing rate responses to each model's predicted responses (each data point represents 1 neuron). A and B: the r²'s for the correlation between observed and predicted responses to the 16 optic flow stimuli. Both segmental gain (A) and response gain (B) modulated models yielded better fits to the neuronal responses than did the original local motion model as indicated by the points being above the unity line. C and D: the spatial distribution of gain modulations combined across all models for the 9 stimulus segments. The size of each arrow is scaled to reflect relative gains across segments in the models yielding higher r² increments, downward arrows reflect decreased gains. The distributions for left hemisphere neurons were reversed to match the majority right hemisphere orientation. C: segmental gain modulation resulted in greater declines in the influence of vertical midline more than ipsilateral segments with little effect on contralateral segments. D: response gain modulation resulted in declines in midline excitatory Gaussians (filled arrows) with widespread increases in inhibitory Gaussians (open arrows). E and F: the r²'s for the correlation between observed and predicted responses to the 36 local motion stimuli. Both segmental gain (E) and response gain (F) modulated models yielded poorer fits to local motion neuronal responses than did the original local motion response models as indicated by the points being below the unity line.

Impact of local motion weightings

Our use of gain modulation to optimize the composite fit of local motion models to optic flow data had several other effects. Across all neurons, there was a roughly equal balance of total excitatory and inhibitory Gaussian response amplitude in the original local motion models (3.3% greater excitation) and in the segmental gain modulated models (2.1% greater excitation). In contrast, response gain modulated models showed greater net inhibitory amplitude (14.4% greater inhibition). Thus response gain modulation more closely fit the optic flow data using a preponderance of inhibitory effects.

Response gain modulation's emphasis on inhibitory mechanisms was still more evident in the spatial distribution of gain modulation effects. In general, there was a great deal of variation in the patterns of gain modulation across neurons. We identified trends across the sample by combining the segmental gain modulation data from all models of all neurons in a two-way ANOVA with main effects of horizontal and vertical segments. Using the segmental gain modulation data, this analysis yielded significant main effects of horizontal position [F(2, 2789) = 7.26, P = 0.001] but not vertical position (P = 0.31) or their interactions (P = 0.26), with post hoc tests distinguishing the midline from the contralateral side (Tukey's HSD, P < 0.05). Selecting for gain modulated models with higher r²'s, or with higher r² increments over the local models, by median split, yielded the same pattern of results but somewhat larger and more significant effects (Fig. 7C). Thus using segmental gains to fit optic flow responses resulted in an overall relative decrease in the weight of vertical midline and ipsilateral segments.

We took the same approach to the response gain modulation data, separately considering changes in the gains of excitatory and inhibitory Gaussians. The analysis of excitatory Gaussians yielded significant main effects of horizontal [F(2, 2825) = 8.14, P < 0.001] but not vertical (P = 0.35) position, and no significant interactions (P = 0.51), with post hoc tests distinguishing the ipsilateral side from the midline and contralateral side (Tukey's HSD, P < 0.05). The analysis of inhibitory Gaussians yielded significant main effects of horizontal [F(2, 2876) = 4.63, P = 0.01] and vertical [F(2, 2876) = 8.38, P < 0.001] position, and their interactions [F(4, 2876) = 5.62, P < 0.001], with post hoc tests distinguishing the ipsilateral from the contralateral sides, and distinguishing the lower segments from the middle and upper segments (Tukey's HSD, P < 0.05). Again, selecting for gain modulated models with higher r²'s, or with higher r² increments over the local models, by median split yielded the same pattern of results but somewhat larger and more significant effects (Fig. 7D). Thus using response gains to fit the optic flow responses resulted in an overall relative decrease in the midline segments.

We considered that gain modulation might have improved the fit to the local motion data and only secondarily improved the fit to the optic flow. To test this hypothesis, we used the gain modulated models to predict the responses of each of the nine stimulus segments to the local motion data. In all but one neuron, the gain modulated models showed poorer fits to the local motion data than was achieved by the original local motion models (Fig. 7, E and F). This suggests that gain modulation captures some differences between the response mechanisms activated by local motion versus optic flow.

Several points summarize the impact of segment and response gain modulation: First, both approaches improved fits to optic flow responses in all neurons, somewhat more so with response gain modulation but neither approach resulted in perfect fits in all neurons. Second, the spatial distribution of effects resulted in an overall increase in the relative weighting of the contralateral hemi-field. Third, the gain modulated model's poorer fits to the local motion data implies that some effects that are not captured in the local motion data must contribute to optic flow selectivity.

Interactions between local motion stimuli

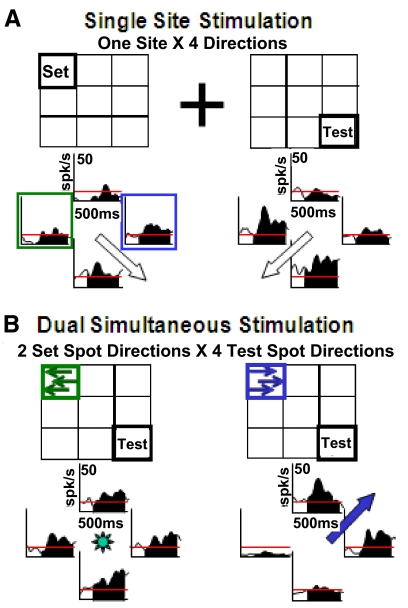
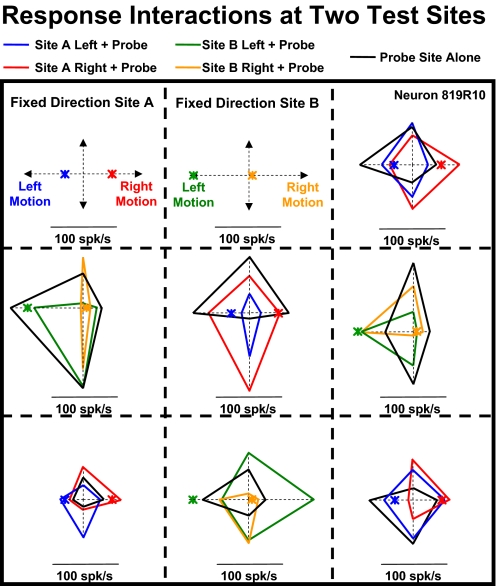
The response interactions implied by the success of the gain modulated models was assessed by presenting dual, simultaneous local motion stimuli. The four directions of local motion evoked different direction selectivities at different sites within the visual field. When two local motion stimuli were presented together they revealed a variety of direction and location specific interaction effects. These interactions are illustrated in Fig. 8. In this neuron, two nonadjacent screen segments yield substantially different net direction selectivities (Fig. 8A). When these two segments were both activated at the same time, with varying directions of motion, we saw direction specific response interactions: rightward motion in the upper left corner evoked upper and rightward response preferences from the lower right screen segment (Fig. 8B). Thus response interactions across nonadjacent screen segments can modify the direction selectivities of MSTd neurons.

Fig. 8.

An example of a 2-segment stimulation study that reveals neuronal response interactions between local motion stimuli presented at the set location or the test location. A, left: spike density histograms (SDHs) of responses to local motion at the fixed-direction location, indicating a preference for right-downward planar motion (open arrow). Right: SDHs of responses to local motion at the probe location, indicating a preference for left-downward planar motion. B: responses when local motion was presented simultaneously at both the fixed-direction and probe locations. Left: when leftward motion was presented at the fixed-direction location (green arrows), the direction preference for stimuli at the probe location (SDHs) yielded little net direction selectivity. Right: when rightward local motion was presented at the fixed-direction location (blue arrows), the direction preference for stimuli at the probe location (SDHs) yielded strong right-upward selectivity, a 180° change from the probe location's original directionality.

We recorded two-segment local motion responses across a variety of stimulus segments. Figure 9 depicts findings from a neuron in which we placed left- or rightward motion in either the upper-left (fixed direction site A) or upper-middle (fixed direction site B) segments and combined those stimuli with the four different cardinal directions of motion in the other stimulus segments. Two examples are illustrative: 1) center segment response interactions: local motion in the center segment alone showed left- and upward direction preferences with no response to downward motion (black diamond). However, when downward motion in the center segment was combined with rightward motion in upper-left segment (site A), it evoked the largest responses recorded in this neuron (red diamond). 2) Middle-left segment response interactions: local motion in the middle-left segment alone showed a moderate response to upward motion (black diamond). However, when upward motion in the middle-left segment was combined with the small responses to rightward motion in the upper-middle segment (site B), it evoked large responses (orange diamond); when upward motion in the left-middle segment was combined with the large responses to leftward motion in the upper-middle segment, it evoked small responses (green diamond).

Fig. 9.

Site and direction specificity of response interactions as revealed by simultaneous stimulation at 2 different locations. The spatial location of the 2 stimuli, and their directions of motion, interacted to produce a variety of idiosyncratic responses. Responses to motion at the fixed direction sites presented alone are shown as colored asterisks. Responses to motion at the probe sites alone are shown as black diamonds. Two-segment responses are plotted in the probe location's segment as colored diamonds with the color corresponding to that used for the fixed direction component.

This example suggests several points: first, two-segment stimulation evoked nonadditive interactions across stimulus segments. Second, those interactions are idiosyncratically direction selective. Third, these idiosyncratic direction selective interactions differ across different pairs of stimulus segments. These findings support the notion that large-field patterns of optic flow might activate response interactions that impart properties that are not evident in responses to local motion stimuli.

Comparison across the other two-segment combinations supports the impression that the directional specificity of response interactions is not homogenous across the stimulus area. Thus response interactions across stimulus segments are both highly nonadditive, within a pair of stimulus segments, and highly variable across different pairs of stimulus segments.

These findings led us to consider that response interactions across stimulus segments might account for differences between neuronal responses to optic flow and those that are predicted by the local motion models. To test this hypothesis, we used the two-segment responses to modify local motion models to account for response interactions across stimulus segments.

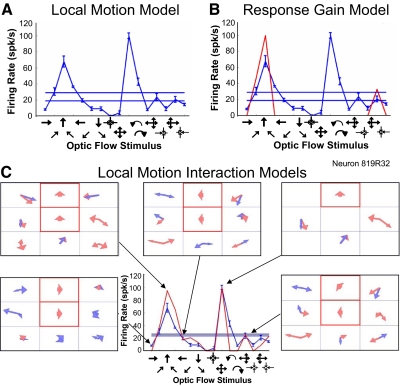
Figure 10 depicts findings from a neuron in which we used the center and upper-middle segments as set stimulus locations. Again, two examples are illustrative: 1) when leftward motion filled both test locations, the resulting combined local motion data were best fit by a model that predicted the moderate firing rate that would result from uniform leftward optic flow, an effect not captured by the single stimulus local motion models or its gain modulated variants. 2) When upward motion filled the upper-middle test locations, with the center segment remaining blank, the resulting combined local motion data were best fit by a model that predicted the high firing rate that would result from outward radial optic flow, also an effect not captured by the single stimulus local motion models or its gain modulated variants.

Fig. 10.

Example of transformation of mixture of Gaussians models by local motion interaction effects. A: the local motion model fails to predict the neuronal response to optic flow in this neuron (recorded responses, blue; predicted responses; red, which overlaps the axis to indicate predicted net firing rate of 0 for all optic flow stimuli). B: the response gain model improved the fit to several of the optic flow stimuli but failed to predict the neuronal response to many others. C: the local motion interactions model yielded much better fits to the optic flow responses (lower middle). The 5 frames show the mixture of Gaussians models used for each of the 5 optic flow patterns indicated by the black arrows. In each model, the segments outlined in red were the set sites and their red arrows were the set site directions, used to probe local motion interactions. These experiments yielded unique mixture of Gaussians models for each combination of set site directions, those set site directions specifying the optic flow stimulus to which that model might correspond best. The interactions related to optic flow responsiveness: rightward planar optic flow (lower-left frame), upward planar optic flow (upper-left frame), leftward planar optic flow (upper-middle frame), outward radial optic flow (upper-right frame), and clockwise optic flow (lower-right frame). The differences between the mixture of Gaussians models derived from local motion stimuli in the context of each set site direction provided the basis for the improved predictions of optic flow responses.

Across the sample of neurons, 74% (14/19) of the neurons with the poorest performance of their local motion models (group error >9) showed better fits with interactions models. Neurons that were well fit by their local motion models, or by the gain modulated variants of those models, less clearly benefited from the consideration of two-segment stimulus interactions. This suggests that some neurons may have more substantial interactions than others, although we cannot reject the possibility that our arbitrary selection of test locations might not have included locations with substantial interactions in all neurons. Nevertheless, these studies demonstrate that response interactions evoked by the co-activation of two stimulus segments can explain some of the observed inadequacies of local motion models' abilities to predict neuronal responses to optic flow stimuli.

DISCUSSION

Local motion mechanisms of optic flow selectivity

Neuronal optic flow selectivity may reflect the composite effects of spatially distributed planar motion sensitivities or specific sensitivity to distributed properties of optic flow fields. Early studies showed that optic flow selectivity in some MSTd neurons might reflect converging planar directional input from MT (Saito et al. 1986; Tanaka et al. 1989). Later studies found that many of these responses were maintained despite changes in the size and position of the stimuli, suggesting a role for distributed response sensitivities (Duffy and Wurtz 1991b). These findings suggest a spectrum of optic flow selectivities in MSTd. At one end are neurons with planar, circular, and radial responses that can often be explained by local planar directional mechanisms confined to a segment of the visual field, although studies of responses to local directional and moving objects do not consistently demonstrate the predicted underlying response mechanisms to the point that we should not make assumptions about the reciprocal relations between responses to different types of stimuli. At the other end are neurons with either circular or radial responses and greater position invariance and little or no underlying planar directionality (Duffy and Wurtz 1991a; Graziano et al. 1994).

We have now tested relations between local motion responses, recorded at nine segments across the central visual field, and optic flow responsiveness by developing mixture of Gaussians model of MSTd receptive field mechanisms that accommodated any combination of dual excitatory and inhibitory response mechanisms. We assessed the performance of the modeling process using the error criteria imbedded in the model (total firing rate error and response classification error), as well as an independent criterion (r²'s), all of which produced the same pattern of results (Fig. 4). We used these models to predict neuronal responsiveness to optic flow, finding substantial variation in success of this approach.

These findings reinforced our impression that the optic flow responses of some neurons reflect local planar motion mechanisms, whereas other neurons may respond to more fundamental attributes of optic flow. One such attribute is the increasing divergence of visual motion elements that define the outward radial pattern seen during forward self-movement (Koenderink and van Doorn 1975, 1981), potentially implemented by a normalization of motion properties across a segment of the visual field to derive the affine motion of elements in that segment (Beusmans 1993). Extension of a subspace algorithm led to a biologically plausible two-layered population encoding network for heading estimation that accommodates eye rotation and depth of field effects (Lappe and Rauschecker 1993). This approach led to insights about potential receptive field subunit structures, including circular arrangements promoting radial selectivity for heading estimation from optic flow (Beintema et al. 2004; Calow and Lappe 2008).

Two practical constraints of these studies must be kept in mind: first, the small magnitude of MST neuronal responses to small stimuli might limit the ability to detect receptive field subunits that could resolve apparent incompatibilities between optic flow and local motion responses. Second, the sparse sampling of the many optic flow and local motion stimuli that might be used, imposed by practical constraints on recording time, might fail to detect discontinuities in response functions that could resolve apparent incompatibilities between optic flow and local motion responses.

As an alternative to such explanations, we considered that dynamic interactions between planar motion response mechanisms might account for optic flow selectivity. This view prompted our combining computational and experimental approaches to characterize planar motion response interactions in MSTd neurons.

Gain modulation by optic flow

We used a genetic algorithm to explore the possibility that the simultaneous co-activation of different response mechanisms might alter their relative influence on neuronal responses. We randomly assigned a 0.1× to 10× multiplier to the relative amplitude of the local motion models using two approaches: first, we treated the nine stimulus segments as spatially defined response mechanisms and assigned a single weight to each segment. Second, we treated the 18 Gaussians as separate response mechanisms and assigned independent weights to each Gaussian.

Gain modulation accessed the optic flow responses to direct their improvement across successive generations (Figs. 5 and 6). As expected, the net effect is improved fits to optic flow with the response gain approach yielding larger average r² increments than the segment gain approach (Fig. 7, A and B). Both approaches yielded significant spatial distributions of gain changes reflecting the lowering of the relative influence of segments in the vertical midline and on the ipsilateral side of the visual field (Fig. 7, C and D). Thus co-activation of all nine stimulus segments by optic flow induces a spatially selective decline in responsiveness that emphasizes the influence of the contralateral hemifield and de-emphasizes the visual periphery. These effects may be viewed as a large-field version of lateral inhibition in which one part of the receptive field deactivates others.

We verified that gain modulation was not simply creating better fits to local motion data to secondarily improve fits to optic flow. When the gain modulated models were back fit the local motion responses, we found that they do not fit the local motion as well as the original local motion models (Fig. 7, E and F). Thus gain modulation incorporated aspects of optic flow responsiveness that are not available in the responses to local planar motion stimuli presented separately.

The success of local planar motion models in predicting the optic flow responses of some neurons is consistent with both neuronal template models (Perrone and Stone 1994) and nonlinear response mechanisms evoked by the global patterns of optic flow (Lappe and Rauschecker 1993). The incremental enhancement of our models with changes in the relative influence of receptive field segments supports the view that MSTd is optimized for optic flow direction selectivity (Duffy and Wurtz 1995; Lappe et al. 1996) independent of other motion parameters (Calow and Lappe 2007). This selectivity may be the result of the dynamic adjustment of weightings on the inputs to each neuron (Wang 1995), possibly through Hebbian shaping guided by heading direction feedback (Zhang et al. 1993). This optimization might use MSTd's co-activation by signals from object motion (Logan and Duffy 2006; Royden and Hildreth 1999; Zemel et al. 1998) and vestibular input (Duffy 1998; Gu et al. 2006; Page and Duffy 2003) about self-movement.

One can think of the nine mixture of Gaussians local motion models as reflecting separate inputs from neurons projecting to MSTd, potentially from adjacent area MT's planar motion selective neurons (Boussaoud et al. 1990, 1992; Felleman and Kaas 1984; Ungerleider and Desimone 1986; Zeki 1980). Co-activation of distinct inputs can result in nonadditive interactions yielding increases or decreases in neuronal firing (Doiron et al. 2001; Holt and Koch 1997). MT subpopulation projections to MSTd might form dendritic compartments to create a substrate for response interactions (Hausser and Mel 2003; Rabinowitch and Segev 2006). Dendritic compartment mediated response interactions can be expected to have gain modulation effects that can activate or inactivate the effects of an input on neuronal firing (Larkum et al. 2004, 2009). The gain modulation effects we have modeled in MSTd are consistent with effects on the partitioning of spatially separated, or synapse-spine morphologically distinct, local motion inputs from MT subunits in independently modifiable MST neuronal dendritic compartments.

Co-activation dependent directionality

We assessed interactions between local planar motion response mechanisms by simultaneously presenting two local motion stimuli in different segments of the visual field. These studies revealed substantial changes in the net directionality of co-stimulated areas compared with that seen with the isolated stimulation of either area (Figs. 8 and 9). These effects accounted for many of the differences observed between local motion models and optic flow responses in MSTd, including those that were not accounted for by adding gain modulation to the models (Fig. 10). The need to invoke several underlying mechanisms (e.g., local motion, gain modulation, and directional interactions) in different neurons undermined our ambition to create a comprehensive model of MSTd. In part, this is because of the observed diversity of mechanisms appears to reflect a nonhomogenous neuronal population requiring more substantial sampling of each type of neuron. Additionally, we are restrained by a perceived need to accommodate temporal response dynamics that might limit the comparability of sequentially tested local motion responses and simultaneously evoked large-field optic flow responses.

While such effects might be intrinsic to MST, we might speculate that MT's direction selective inputs to MST might include such conditional modifications. The two-stage orientation and coherence selectivities model of MT, reflecting sequential processing in V1 and MT, created fixed neuronal direction preferences (Adelson and Movshon 1982). However, surround effects defining nonclassical receptive fields of some MT neurons (Allman et al. 1985) with potent center-surround antagonism (Tanaka et al. 1986) highlighted the potential for winner-take-all interactions adding complexity and flexibility to MT neuronal responses (Bulthoff et al. 1989).

Integrating the idiosyncratic spatial distributions of direction and speed sensitivities of these neurons can promote the segmentation of complex scenes in to objects and surfaces (Mikami et al. 1986; Nowlan and Sejnowski 1994; Xiao et al. 1995). The rectification and normalization of these responses, possibly through divisive inhibitory response interactions, would refine population responses and favor particular response mechanisms (Simoncelli and Heeger 1998) in a manner that might be disproportionate to their spatial summation based on the spatial extent of visual stimuli (Britten and Heuer 1999).

Rather than viewing response interactions as being obligatorily and antagonistic, we note that different MT neuronal subpopulations show fundamentally different center-surround interactions with some altering response directionality, whereas others do not (Huang et al. 2008). This more complex view of MT neuronal responses is consistent with the cascade model of MT response processing that incorporates both linear and nonlinear processing in the V1 to MT transformation (Rust et al. 2006). The diversity of MT responses might provide a basis for differential processing to support optic flow selectivity (Tohyama and Fukushima 2005) in MST and ventral intraparietal cortex (VIP), two adjacent areas that share optic flow selectivity, vestibular, and oculomotor signals (Bremmer et al. 1997; Colby et al. 1993; Schaafsma and Duysens 1996; Schlack et al. 2002; Zhang et al. 2004). Extensions of this work should compare MST and VIP with considerations of nonlinear spatiotemporal response dynamics by relating optic flow, local motion, and object motion responses.

The extensive connections between MT and MSTd are paralleled by neurophysiological and functional homologies. The planar motion response properties of MT neurons range from simple direction selectivity to dynamically interacting directionalities (Albright et al. 1984; Movshon et al. 1986; Rodman and Albright 1989) that define subpopulations that respond to either the components of two superimposed directions or to their composite pattern (Bair and Movshon 2004; Kohn and Movshon 2004; Movshon and Newsome 1996) with related illusory perceptions of plaid pattern motion (Beutter et al. 1996; Welch 1989). Similarly, the planar motion response properties of MSTd neurons range from clear correspondence with optic flow selectivities to the spatio-directional dynamic relations evident in our two-stimulus interaction studies (Fig. 9) that may correspond to subpopulations with distinct responses to overlapping planar and radial motion (Duffy and Wurtz 1997c) that create illusory transformations of optic flow (Duffy and Wurtz 1993; Lappe and Duffy 1999; Lappe and Rauschecker 1995). Finally, spatial attentional effects have been recorded in areas MT and MST with local motion stimuli (Treue and Maunsell 1996) revealing simultaneous stimulation effects like those seen in this study (Treue and Maunsell 1999) and optic flow response modulation that might be linked to those mechanisms (Dubin and Duffy 2007).

The anatomical connections and functional similarities between these areas suggest a continuum of dorsal extrastriate response properties from MT to MSTl and MSTd and on to VIP and 7a in which visual motion response mechanisms are preserved across increasing spatial scale from receptive field segments in MT to visual hemi-space representations in 7a. It remains to be determined whether the phasic and tonic responses of these neurons (Duffy and Wurtz 1997b) might also distinguish these populations across the temporal dynamics of sequential activation by optic flow (Froehler and Duffy 2002; Paolini et al. 2000) or moving object stimuli (Logan and Duffy 2006).

GRANTS

This work was supported by National Eye Institute grants R01-EY-10287 and P30EY-01319.

DISCLOSURES

No conflicts of interest are declared by the authors.