Comparison of the New Perimetric GATE Strategy with Conventional Full-Threshold and SITA Standard Strategies

Abstract

Purpose

A new, fast-threshold strategy, German Adaptive Thresholding Estimation (GATE/GATE-i), is compared to the full-threshold (FT) staircase and the Swedish Interactive Thresholding Algorithm (SITA) Standard strategies. GATE-i is performed in the initial examination and GATE refers to the results in subsequent examinations.

Methods

Sixty subjects were recruited for participation in the study: 40 with manifest glaucoma, 10 with suspected glaucoma, and 10 with ocular hypertension. The subjects were evaluated by each threshold strategy on two separate sessions within 14 days in a randomized block design.

Results

SITA standard, GATE-i, and GATE thresholds were 1.2, 0.6, and 0.0 dB higher than FT. The SITA standard tended to have lower thresholds than those of FT, GATE-i, and GATE for the more positive thresholds, and also in the five seed locations. For FT, GATE-i, GATE, and SITA Standard, the standard deviations of thresholds between sessions were, respectively, 3.9, 4.5, 4.2, and 3.1 dB, test–retest reliabilities (Spearman’s rank correlations) were 0.84, 0.76, 0.79, and 0.71, test–retest agreements as measured by the 95% reference interval of differences were −7.69 to 7.69, −8.76 to 9.00, −8.40 to 8.56, and −7.01 to 7.44 dB, and examination durations were 9.0, 5.7, 4.7, and 5.6 minutes. The test duration for SITA Standard increased with increasing glaucomatous loss.

Conclusions

The GATE algorithm achieves thresholds that are similar to those of FT and SITA Standard, with comparable accuracy, test–retest reliability, but with a shorter test duration than FT.

Clinical diagnoses for the presence and state of glaucoma and other diseases affecting vision can be made from the spatial pattern of visual thresholds obtained by visual field testing. Clinical visual field testing is performed on commercial perimetric devices, and employs psychophysical techniques to obtain thresholds of differential luminance sensitivity (DLS) at multiple retinotopic locations. DLS thresholds are determined by confronting patients with stimuli of varying luminance, with each presentation constituting a “yes–no” response. Patients respond by depressing a response button to indicate a yes for seeing a spot of light, and their failure to respond is assumed to be a no for seeing the spot of light. From the pattern of responses, a threshold estimate can be obtained.¹ Theoretically, the accuracy of a threshold estimate increases with the number of questions used to obtain the estimate. In practice, however, increased test times may introduce fatigue artifacts caused by the patient’s erroneous answers, thus decreasing the quality of threshold estimates.² In an effort to decrease these potential problems and also to decrease the burden of visual field testing on patients, numerous researchers have developed newer threshold strategies that decrease the duration of an examination while retaining a similar degree of accuracy in obtained thresholds.^3–7

The need for a fast-threshold strategy becomes even more apparent when the number of stimulus locations is increased (>100 locations). Increasing the number of tested locations provides a finer spatial resolution for the disease state than conventional test grids, but also causes the examination time to exceed 15 minutes if a full-threshold strategy is applied. This introduces a greater potential for fatigue artifacts. One solution for testing many additional locations is to split the examination into two separate sessions, so that some locations are tested in the first session and the remaining locations are tested in the second session.⁸ However, this solution is not desirable for everyday use in the clinical setting.

GATE reduces the examination time per stimulus location by, among other things, taking into account the results from previous examinations. GATE is an algorithm that will be well suited for condensed grid testing: (1) thresholds can be obtained at any spatial location without relying on databases of location-specific threshold distributions, (2) the examination duration is relatively short, and (3) the accuracy of the obtained thresholds is comparable to currently used strategies.

The purpose of this study was to evaluate this new fast-threshold algorithm, GATE, and to compare its performance to the full-threshold (FT) staircase and the Swedish Interactive Thresholding Algorithm (SITA Standard) strategies.

Methods

The Centre for Ophthalmology, Institute for Ophthalmic Research, University of Tübingen, coordinated this prospective multicenter study. Data were collected from the Hamilton Glaucoma Center, University of California, San Diego; Casey Eye Institute, Oregon Health and Science University; University Eye Hospital, Freiburg; the University Eye Hospital, Mainz; and the Centre for Ophthalmology, University of Tübingen. Data from each site were anonymized and sent electronically to the coordinating center in Tübingen to be stored in a central local database for further processing and evaluation. The study was approved by all local Institutional Review Boards and adhered to the tenets of the Declaration of Helsinki.

Subjects

Sixty subjects (12 per site) older than 18 years were recruited for participation in the study. All subjects had a maximum spherical ametropia within ±8 D, maximum cylindrical ametropia within ±3 D, distant visual acuity better than 10/20, and pupils at least 3 mm in diameter. Subjects with amblyopia, strabismus, ocular motility disorders, relevant opacities of central refractive media (cornea, lens vitreous body), retinal diseases (e.g., macular degeneration, diabetic retinopathy), a history or signs of neuro-ophthalmic diseases, mental diseases (e.g., psychosis), acute infections, pregnancy, intake of miotic drugs, insufficient or inadequate perimetric quality control indices (false-positive and -negative rates of catch trials exceeding 30%, each), and suspected insufficient compliance were excluded from the study.

Each site was asked to recruit eight subjects with manifest glaucoma, two with suspected glaucoma, and two with ocular hypertension (OHT). Subjects were categorized according to the criteria of the European Glaucoma Society.⁹ Manifest glaucoma subjects had manifest visual field defects (Aulhorn stages I–III, according to the first visual field result) and unequivocal glaucomatous alterations of optic nerve head, retinal nerve fiber layer (RNFL) morphology, or both. Those with suspected glaucoma had suspect morphologic changes of the optic nerve head, the RNFL, or both and normal visual fields, or manifest visual field defects with normal optic nerve heads and RNFL. OHT subjects had untreated intraocular pressure (IOP) exceeding 21 mm Hg, with normal optic nerve heads, RNFL, and visual fields. For manifest and suspected glaucoma, if visual field defects were manifest in both eyes, one eye was chosen according to a randomization list.

Visual Fields

Subjects were evaluated in two separate sessions within 14 days. In each session, they were examined with white-on-white, full-threshold (FT), SITA Standard, GATE-initial (GATE-i), and GATE strategies on pattern 24-2 grids. The test order remained the same between sessions within an individual, but was randomized across individuals. Since GATE relies on the values obtained in GATE-i, GATE-i always preceded GATE within a session, but otherwise the test order was random across subjects. The subjects could ask for a pause in the testing at any point in the examination. FT, GATE-i, and GATE were performed on the Octopus 101 perimeter (Haag-Streit, Inc., Köniz, Switzerland), and SITA Standard was performed on the Humphrey Field Analyzer II (HFA-II) perimeter (Carl Zeiss Meditec, Inc., Dublin, CA, and Jena, Germany). The two perimetric devices are similar, except that the maximum luminance level for the HFA-II is greater (3200 cd/m² = 10,000 asb) than it is for the Octopus 101 (320 cd/m² = 1000 asb). The DLS thresholds were compared between the two instruments by converting them with the background luminance (10 cd/m² = 3.2 asb) used as the reference intensity, which was the same between both instruments. The resulting decibel scale values of the Octopus 101 are easily transformed into the original HFA II decibel scale by adding +25 dB.¹⁰

Threshold Algorithms

Table 1 gives a comparative overview of the three threshold algorithms. The FT (Tübingen) method uses a 4-2-1 staircase algorithm and obtains threshold estimates by presenting stimuli with luminances that are adaptively based on a patient’s responses.^11,12 FT, as implemented in this study, begins by testing five seed locations using a 4-2 staircase strategy (see Fig. 4A) These values are compared to the age-related, normal hill of vision. The seed location with the smallest deviation from the normal hill of vision is used to translate the values of the entire hill of vision, essentially assuming that the patient has a normal hill of vision that translates linearly at each location with a general adjustment for overall sensitivity. For the remaining locations, the initial FT stimulus tests 2 dB above the adjusted hill-of-vision. If the patient responds yes to the initial stimulus, then subsequent stimuli are 4 dB dimmer than the previous stimulus, until the first response reversal is obtained. A response reversal occurs when the response for the presented stimulus differs from the response to the previous stimulus. If at the first stimulus the patient does not respond, it is interpreted as “not seen,” and subsequent stimuli are 4 dB brighter than the previous stimulus until a response reversal occurs. If a response reversal occurs, subsequent stimuli are presented 2 dB dimmer if the stimulus was previously seen, or 2 dB brighter if it was previously not seen, until another response reversal occurs. After the second response reversal, stimuli are adjusted by 1 dB until the third response reversal occurs. The local threshold is estimated after the third response reversal occurs, applying the maximum-likelihood procedure.¹³

Table 1.

Comparison of Specific Features and Characteristics of the Four Threshold Algorithms

	FT Tübingen	SITA Standard	GATE
			GATE-i	GATE
Seed points, n (strategy)	5 (4-2 dB staircase)	5 (4-2 dB staircase)	5 (4-2 dB staircase)	None
Strategy	4-2-1 dB staircase	Modified 4-2 dB staircase	Modified 4-2 dB staircase	Modified 4-2 dB staircase
Reversals, n	3	≤3	2	2
Additional termination condition	Precocious termination in areas of deep or absolute defects: In case of a “no” response to the initial stimulus, a stimulus of maximum luminance is presented; in case of another “no” response, the testing is terminated at that location.	Determination of threshold estimate’s precision using Bayesian inference. Location specific prior probability distribution functions of both, glaucomatous and normal populations. Appears to terminate prematurely at high sensitivity levels.	Precocious termination in areas of deep or absolute defects: In case of a “no” response to the initial stimulus, a stimulus of maximum luminance is presented; in case of another “no” response, the testing is terminated at that location.	Precocious termination in areas of deep or absolute defects: In case of a “no” response to the initial stimulus, a stimulus of maximum luminance is presented; in case of another “no” response, the testing is terminated at that location.
Further reduction of questions asked	No	Eliminating catch trials for false-positive responses by instead considering response times.	No	Starting values are based on individual previously determined local thresholds from GATE-i with a randomized offset to reduce the “threshold from prior” bias.
Threshold estimation	Maximum likelihood	Maximum likelihood (The details of the post- processing procedure are proprietary and unpublished)	Maximum likelihood	Maximum likelihood
Restriction to certain cohorts/diseases	No	Designed for specific use in manifest glaucomatous damaged and normal eyes.	No	No
Consideration of previous sessions	No	No	No	Yes

Figure 4.

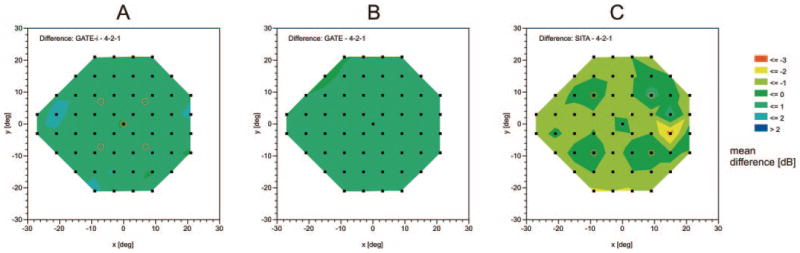
Color-coded mean difference (in decibels) in DLS thresholds between the three fast-threshold strategies with the full-threshold strategy (4-2-1) at each location in the visual field: between the (A) GATE-i, (B) GATE, or (C) SITA Standard strategy and the full-threshold strategy. (A, ○) Five seed point locations of the full threshold and the GATE-i strategies; (C, ○) four seed point locations of the SITA Standard strategy.

The implementation of the SITA Standard was similar to that of the FT in this study, except for (1) the use of seed locations, (2) the termination criteria for a staircase, (3) catch trials for false-positive and -negative responses, and (4) a postprocessing algorithm.⁵ At the beginning of an examination, SITA Standard uses a full-threshold 4-2-2 staircase strategy to evaluate the thresholds at four seed locations (Fig. 4C). This strategy is similar to the FT used in this study, except that the smallest increment of adjustment is 2 dB. The thresholds at these seed locations govern the starting luminances for the threshold staircases at adjacent locations in the visual field. SITA Standard utilizes essentially the same staircase procedure as FT, but in addition to terminating the staircase after three response reversals, the SITA Standard gives the option of terminating testing earlier at a location if the threshold’s estimate at that location reaches a certain precision. This additional termination criterion reduces the number of questions asked per examination. The SITA Standard determines the threshold estimate’s precision by using Bayesian inference. It begins with location-specific prior probability distribution functions of possible thresholds in both glaucomatous and normal populations. After each stimulus presentation, a likelihood function updates the prior probabilities based on the patient’s response. Testing terminates at either the third response reversal or at the response when one of the distributions reaches a certain width, as described by its variance, whichever comes first. The SITA Standard further reduces the number of questions asked per examination by eliminating catch trials for false-positive responses and instead determines such responses from the history of response-times within the test.¹⁴ The details of the postprocessing algorithm are proprietary and unpublished.

GATE-i and GATE are perimetric strategies with accurate threshold determination over the entire sensitivity range, that can be applied to any disease and any test point arrangement. The underlying algorithm with optimized timing of stimulus presentation is based on a modified 4-2-dB staircase strategy, allowing exceptions in areas of deep or absolute defects. The GATE-i algorithm begins by testing five pre-defined seed locations (anchor points). These values are compared to the age-corrected normal hill of vision. The seed location with the smallest, absolute deviation from the normal hill of vision is used to translate the values of the entire hill of vision. For the remaining locations, the initial GATE-i stimulus tests slightly above the adjusted hill-of-vision values, which assumes that the patient has a normal hill of vision. If the tested subject responds yes to perceiving the initial stimulus, then the stimulus is made dimmer by 4 dB until the subject responds no. The stimulus luminance level is then made 2 dB brighter, and the subject’s response is obtained. If the patient responds no to the initial stimulus, then a stimulus of maximum brightness is presented. If the patient responds no to the maximum stimulus intensity, than testing is terminated at that location. If the patient responds yes to the maximum stimulus intensity, then testing resumes at 4 dB brighter than the initial stimulus, increasing by 4 dB until a yes response occurs. At that time, a 2-dB dimmer stimulus is shown, and the patient’s response is obtained. The local DLS (i.e., the local threshold) is taken as the value between the dimmest stimulus seen and the brightest stimulus not seen.

The GATE algorithm, which is applied in subsequent sessions, is similar to that of GATE-i, except that the starting values are based on, but not identical with, the previously determined local thresholds instead of referring to age-related normal values as in GATE-i. This procedure is similar to the Octopus Master Fields.¹⁵ The starting values with GATE are slightly brighter than the previously determined local thresholds. The suprathreshold level is varied between test locations by a random offset, to avoid or at least reduce the effect of regression to the mean. Especially in regions of low sensitivity, this procedure helps to avoid multiple unidirectional steps that are fatiguing and uninformative before achieving a reversal of response.

Analyses

Bias describes the systematic difference between threshold measurements from two threshold strategies. This potential bias was illustrated by plotting the distribution of the differences of the local DLS thresholds between the different strategies against their binned mean values, depicted by the 5th and 95th percentiles and the quartiles (according to Artes et al.¹⁶).

Test-retest reliability describes the association of thresholds in repeated tests of the same subject using the same strategy. It was measured at each location by computing Spearman’s rank correlation coefficient, which is restricted to values between −1 and 1. Values near 1 are indicative of reliable results. The nonparametric Spearman’s rank correlation coefficient was desirable, as there were values at the limits of the dynamic range of the instruments in some fields. As the distribution of these rank correlation coefficients is restricted to the interval from −1 to 1, and values tended to form negatively skewed distributions, their medians rather than their means are reported. Agreement, a stricter form of reliability, takes into account the repeatability of the threshold values and not just the association of their rank values. Root-mean square (RMS) errors were calculated to compare the test–retest variability of the different strategies. Point-wise RMS errors were plotted against average sensitivity, to explore the relationship between sensitivity and test–retest variability.

Furthermore, the differences between test and retest values of local DLS were illustrated according to Artes et al.¹⁶: The baseline sensitivities were plotted with box plots against the retest sensitivities.

Accuracy of DLS thresholds, the test–retest reliability and agreement of the local thresholds, and the examination duration for the different threshold strategies were compared. Accuracy comprises precision and trueness, which are measured by variance and bias, respectively.

Variance was estimated using an analysis of variance (ANOVA) model¹⁷ and assuming the hill-of-vision model of visual sensitivity.¹⁸ Test–retest reliability was measured by Spearman’s rank correlation, and test–retest agreement was assessed with a modified Bland-Altman plot. Differences in examination durations for the different threshold strategies were estimated from an ANOVA model.

DLS thresholds were modeled by mixed-factors analysis of variance (ANOVA) with three between-subjects factors (examination type, test number, and subject [random]) and one within-subject factor (day). The ANOVA model addressed the main effects of examination type, test number, and day, as well as the interactions of examination type × day and test number × day. Main effects or interactions that failed to reach significance at the 5% level were removed from the final analysis. The mean and standard deviations of the DLS thresholds for each testing strategy were estimated from the ANOVA model of thresholds. Differences between DLS thresholds from the threshold strategies were estimated from the model.

Examination times were assumed to follow log-normal distributions, as this was close to the estimated Box-Cox transformation and seemed appropriate more often. The time distribution is skewed in the papers from Schiefer et al.⁸ and Nowomiejska et al.,¹⁹ and so ANOVA was used to model the log values of time, with factors similar to those of the ANOVA model for thresholds. From the resulting ANOVA model, the 95% confidence intervals for the ratio of geometric mean times to the geometric mean time for GATE are reported. Trends in examination durations across SITA Standard mean defect (MD) were explored by fitting splines with equal smoothness (λ = 1000) for each strategy and described by level 5% t-tests for the components of polynomial trends suggested by those splines.

Results

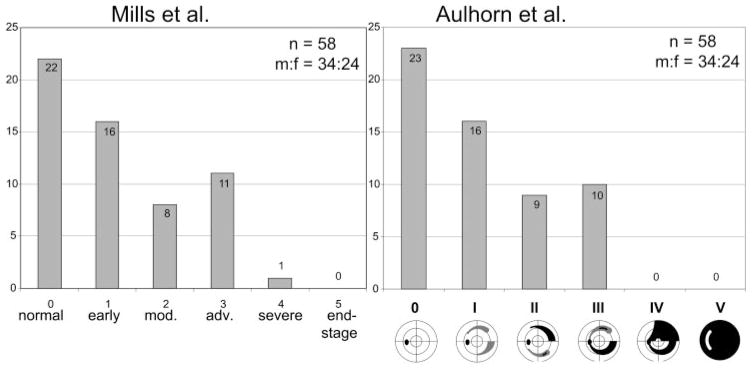
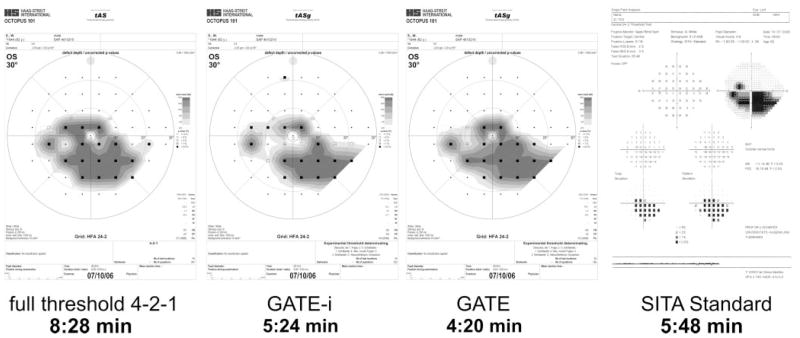
Fifty-eight subjects (24 women, 34 men) were included in the analysis. Two subjects from the manifest glaucoma subset did not meet the inclusion criteria: one was at glaucoma stage Aulhorn IV and one had a false-positive rate of 46% in SITA Standard. For detailed characterization of the subgroups according to the stage of glaucomatous visual field loss, see Figure 1. Figure 2 shows a representative example of the visual field results and examination times obtained with the FT, GATE-i, GATE, and SITA Standard strategies from a patient with manifest glaucoma and advanced glaucomatous visual field loss.

Figure 1.

Frequency distribution of glaucomatous field loss, according to the scoring system of Aulhorn et al.,²⁰ which refers to the morphologic pattern of the glaucomatous visual field defects, and to the classification system according to Mills et al.²¹ Staging was performed according to the first SITA Standard visual field results.

Figure 2.

Examination results with the four thresholding strategies: full threshold 4-2-1, GATE-i, GATE, and SITA Standard from a patient with manifest glaucoma and advanced visual field loss (Aulhorn stage III)

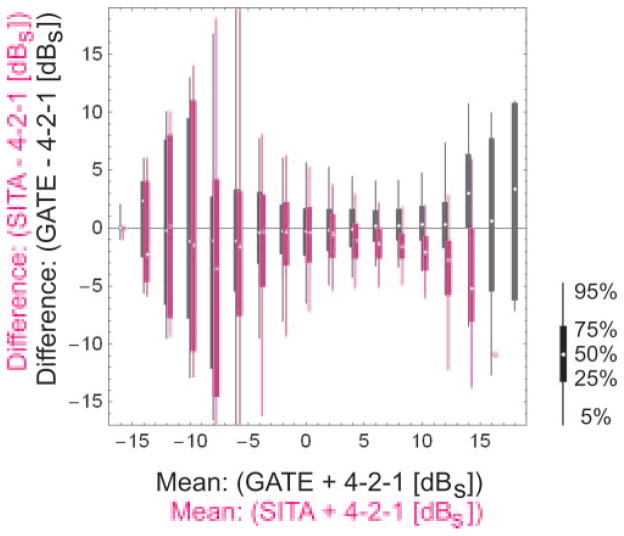
The GATE-i thresholds were 0.6 dB (95% confidence interval [CI] 0.5–0.7 dB) higher than the FT thresholds. There was no relevant difference (0.0 dB, CI: −0.1 to 0.1 dB) in thresholds between GATE and FT. SITA Standard thresholds were 1.2 dB (95% CI: 1.1–1.3 dB) lower than FT thresholds. Overall, the standard deviations of differences in thresholds for the same threshold strategy between visits dates were 3.9 dB for FT, 4.5 dB for GATE-i, 4.2 dB for GATE, and 3.1 dB for SITA Standard. Figure 3 illustrates the bias in threshold measurements between the threshold strategies in a fashion similar to that in Artes et al.¹⁶

Figure 3.

Differences between local DLS thresholds, obtained with (magenta) SITA Standard (SITA) and full-threshold (4-2-1), and with (black) GATE-i (GATE) and full threshold (4-2-1). Vertical lines: 5th and 95th percentiles; vertical bars: interquartile ranges; small dots: median values (graphic modified after Artes et al.¹⁶). All DLS values are given in standardized decibels (dB_S), referring to the background luminance level, which is identical between all perimeters (10 cd/m²), instead of referring to the regular decibel scale, which is related to the maximum stimulus luminance level, which differs from instrument to instrument. The dB_S values can be transformed into the Humphrey dB scale by adding 25.

All DLS values are given in decibels, referring to the background luminance level, which is identical between all perimeters (10 cd/m²) instead of referring to the regular decibel scale, which is related to the maximum stimulus luminance level and differs from instrument to instrument. The standardized decibel (dB_S) values can be transformed into the Humphrey dB scale by adding 25.

The bias obviously rises greatly in areas of advanced visual loss for all algorithms (i.e., for values to −5 dB_S, corresponding to values down to 20 dB on the Humphrey scale). At these levels, the bias is no longer measurable, because of a floor effect.

Figure 4 summarizes the mean differences between thresholds of FT compared with SITA Standard, GATE-i, and GATE as they occur at each stimulus location in the pattern 24-2 test grid. SITA Standard has no systematic bias near the four seed locations, which are the first locations tested in SITA Standard, but shows slight underestimation of thresholds in the remaining locations compared with FT. This spatial trend does not occur for GATE-i and GATE, when compared with FT.

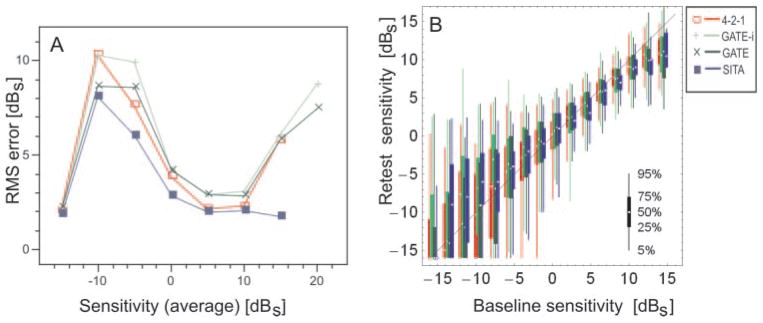
Test–retest reliability was measured by Spearman’s rank correlation coefficient, and was 0.84 for FT, 0.76 for GATE-i, 0.79 for GATE, and 0.71 for SITA Standard. Values closer to 1 are indicative of reliable threshold measurements, whereas values closer to 0 are indicative of poor correlation between measurements taken on the two sessions for a given threshold strategy. Test–retest agreement is illustrated in Figure 5 in a fashion similar to that in Artes et al.¹⁶ Whereas trueness was constant, precision decreased with increasing deficit.

Figure 5.

(A) Average point-wise RMS errors of DLS thresholds, obtained with (red) full threshold (4-2-1), (light green) GATE-i for the initial examination, (dark green) GATE for subsequent examinations, and (blue) SITA Standard (SITA) as a function of average baseline sensitivity. Note that all strategies have high error rates below −5 dB_S (20 dB on the Humphrey scale). The low rate of errors on the far left of the graph reflects a floor effect of range restriction of measurement for all instruments and strategies. The apparent low error rate for the SITA Standard on the far right may reflect the tendency of this strategy to terminate prematurely with high sensitivities, thereby artificially lowering variability. (B) Differences between test–retest values of local DLS thresholds as a function of baseline sensitivity. Vertical lines: 5th and 95th percentiles; vertical bars: interquartile ranges, respectively; small dots: median values. Graphics modified in accordance with Artes et al.¹⁶ For a description of DLS values, see Figure 3.

The median examination duration for FT was 9.0 minutes (5%–95% reference interval [RI]: 7.6–10.5), 5.7 minutes (RI: 4.8–6.5) for GATE-i, 4.7 minutes (RI: 4.1–5.2) for GATE, and 5.6 minutes (RI: 4.0–7.9) for SITA Standard. The fast-threshold strategies all demonstrated remarkably shorter durations than did FT. When SITA Standard was taken as the reference, examinations lasted 65% longer (95% CI: 59%–72% longer) with FT, 3% longer (95% CI: 1% shorter–7% longer) with GATE-i and 13% shorter (95% CI: 10%–17% shorter) with GATE.

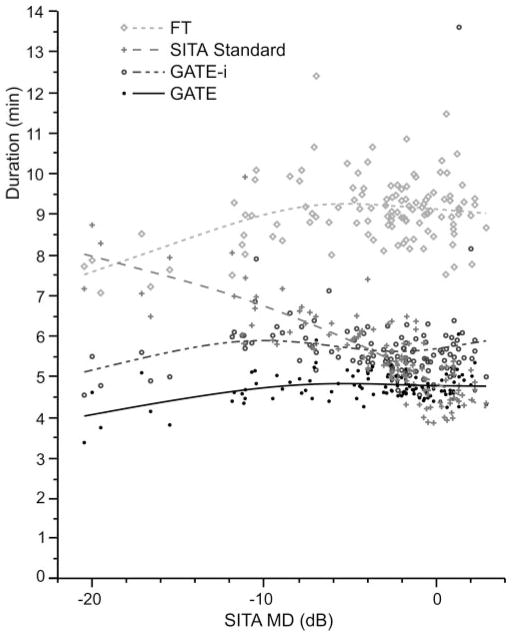
Figure 6 illustrates the differences in duration for each threshold strategy as a function of SITA MD; the trend is illustrated by using splines. Test time for SITA depends on the severity of the visual field, with fewer pronounced defects resulting in longer examination durations. GATE-i and GATE examination durations were not affected by visual field severity. For a SITA Standard MD of −20 dB, FT, GATE-i, GATE, and SITA Standard were 7.50, 4.88, 3.93, and 7.83 minutes in duration, respectively. For a SITA Standard MD of 0 dB, examination durations were 9.06, 5.56, 4.72, and 4.74 minutes, respectively.

Figure 6.

The effect of visual field severity on examination duration for FT, SITA Standard, GATE-i, and GATE. Flexible splines were fit to the data from each threshold strategy to illustrate the relationship between defect depth and examination duration.

Discussion

Although several fast-threshold strategies already exist, the creation of GATE is motivated by its potential utility in scotoma oriented perimetry (SCOPE), a novel testing strategy that adapts to an individual’s visual field history and adaptively places additional stimulus locations on the visual field. The addition of extra visual field test locations necessitates the use of fast-threshold strategies to keep examination durations manageable for the clinical staff and the patients undergoing testing. GATE is well suited for examinations that test in locations that are not part of the current, pattern 24-2 test grid. Normative values of SITA Standard, which are proprietary, are not published. Therefore, an interpolation between tested locations is not feasible. GATE does not require location-specific distributions of thresholds from normal and glaucomatous persons. Therefore, it can be applied to stimulus locations where normal or disease-specific distributions are not yet known. Also, since GATE maintains short examination durations, the addition of a moderate number of test locations will not increase the examination duration considerably.

The GATE algorithm achieved threshold estimates that were similar to those of FT and SITA Standard. When compared to FT, GATE-i thresholds were slightly greater than those of FT by an average of 0.6 dB, but this difference was not apparent in the subsequent thresholds obtained by GATE. The GATE threshold strategy did not exhibit any systematic bias in thresholds across the testable range when compared with FT (Fig. 3). When each location was considered separately, GATE-i and GATE exhibited no spatial bias in threshold compared with FT, whereas SITA Standard exhibited no bias for thresholds in the seed locations, but slightly underestimated the threshold in the remaining locations compared with FT. Retest reliability was similar for all the threshold strategies, and test–retest agreement exhibited no systematic differences across the testable range for any of the threshold strategies. Retest reliability increased remarkably in cases of advanced visual field loss for all strategies.

GATE-i and GATE achieved examination durations that were similar to those of SITA Standard. All three of these fast-threshold strategies had examination durations that were considerably shorter than those of FT. The reduction of test time with SITA Standard is reported to be approximately 50% of that of conventional full-threshold algorithms.^4,6 In this study, however, the reduction in test times with SITA Standard was not evident in persons with mild to advanced visual field loss. In these persons, examination time increased with increasing field loss and nearly equaled that of conventional “full threshold” strategy when the loss was advanced (Fig. 6). Wild et al.²² also found an increase of examination duration for SITA Standard with advancing severity.

All threshold strategies had greater test–retest variability for locations with moderate to advanced glaucomatous visual field loss compared with regions that were normal or had early visual field loss (Fig. 5). So far, no algorithm has been shown to be accurate below approximately 20 dB sensitivity in terms of reproducibility (Woodward KR, et al. IOVS 2008;49:ARVO E-Abstract 1075). GATE had greater test–retest variability within these regions of loss compared with the SITA Standard. This difference in test–retest variability may be due to GATE’s not increasing the number of questions in locations with moderate to advanced visual field loss. This result can explain, then, why SITA Standard examination durations increased with visual field severity, while GATE examination durations did not.

The difference in the number of questions asked, however, does not by itself explain why the test–retest variability was greater in FT than SITA Standard, since the maximum number of questions asked by SITA Standard is equal to the number of questions asked by FT. The reduction of examination time with SITA Standard has also been thought to reduce subject fatigue, thus enhancing retest reliability by reducing the test–retest variability. This effect could be one explanation for why SITA Standard achieved smaller test–retest variability than did FT, a finding that is supported by Aoke et al.,²³ but not found by Artes et al.¹⁶ GATE and FT had greater test–retest variabilities than SITA Standard in regions with high DLS (Fig. 5A). A reason for this may be that SITA Standard seemed to terminate threshold estimation at a certain level of (high) DLS values. This cutoff may also have contributed to the generally lower or missing threshold values of SITA Standard, compared to GATE and FT, at high DLS levels (Fig. 3).

There are obvious differences between the Humphrey and Octopus FT (Tübingen) strategies: Humphrey uses a 4-2-dB strategy with two reversals, whereas FT Tübingen applies a 4-2-1-dB strategy with three reversals. Therefore, the effects of fatigue on FT may have been more pronounced in this study, since the FT strategy that was used is potentially more exhausting than that used in other studies. Extending the threshold algorithm to adjust for local defect depth could enhance the precision in these locations.

Conclusions

In conclusion, the German Adaptive Threshold Estimation (GATE) algorithm achieves threshold estimates that are similar to FT and SITA Standard, with similar accuracy, test–retest reliability, and short test duration. In addition, GATE achieves these without the use of location-specific distributions of glaucomatous and normal populations. GATE will be suitable for scotoma-oriented perimetry (SCOPE), since it maintains short examination times while obtaining adequate threshold estimates that do not depend on databases of location-specific distributions of thresholds.