Actin filament remodeling by actin depolymerization factor/cofilin

Abstract

We investigate, using molecular dynamics, how the severing protein, actin depolymerization factor (ADF)/cofilin, modulates the structure, conformational dynamics, and mechanical properties of actin filaments. The actin and cofilactin filament bending stiffness and corresponding persistence lengths obtained from all-atom simulations are comparable to values obtained from analysis of thermal fluctuations in filament shape. Filament flexibility is strongly affected by the nucleotide-linked conformation of the actin subdomain 2 DNase-I binding loop and the filament radial mass density distribution. ADF/cofilin binding between subdomains 1 and 3 of a filament subunit triggers reorganization of subdomain 2 of the neighboring subunit such that the DNase-I binding loop (DB-loop) moves radially away from the filament. Repositioning of the neighboring subunit DB-loop significantly weakens subunit interactions along the long-pitch helix and lowers the filament bending rigidity. Lateral filament contacts between the hydrophobic loop and neighboring short-pitch helix monomers in native filaments are also compromised with cofilin binding. These works provide a molecular interpretation of biochemical solution studies documenting the disruption of filament subunit interactions and also reveal the molecular basis of actin filament allostery and its linkage to ADF/cofilin binding.

Actin is an abundant and evolutionary conserved eukaryotic cell protein that is essential for a broad range of cellular movements. Actin exists in two forms: a globular/monomeric form and a self-assembled linear filament polymer that grows and shrinks from its ends. The dynamic equilibrium between the forms is controlled by a number of factors including solution conditions and regulatory proteins (1). Actin filaments are a main structural feature of all muscle tissue (2), and controlled polymerization of branched networks of actin filaments produce force for cell motility (3). A key dynamical feature of networks of actin filaments is a continuous reorganization based on controlled polymerization and depolymerization.

The actin regulatory protein, actin depolymerization factor (ADF)/cofilin, serves a vital function in cells by severing filaments, thereby increasing the number of filament ends from which polymerization and depolymerization can occur (4). ADF/cofilin binds cooperatively to actin filaments in a 1∶1 stoichiometric ratio (5–9). The ADF/cofilin binding site on a filament subunit is believed to be near the hydrophobic binding pocket between subdomain 1 (SD1) and SD3 of actin (7, 10).

Actin filaments fully decorated with ADF/cofilin (termed cofilactin hereafter) filaments have significantly different structural properties compared with their bare actin counterparts. ADF/cofilin filaments have an altered helical twist (7), modified lateral contacts within the actin core (11), and an altered subunit tilt (12). Given the role of ADF/cofilin in filament severing, it is perhaps not surprising that ADF/cofilin binding enhances destabilizing modes within the actin filament (12).

Cofilactin filaments also have unique elastic properties. ADF/cofilin binding increases the torsional (13) and bending flexibilities (14) of actin filaments, the latter is manifested as a reduction in the persistence length. This increased flexibility has been attributed to a disruption of the contacts between two adjacent actin subunits in the helical strands of the filament—when visualized by electron microscopy, contacts between SD1 and SD2 of neighboring intrastrand subunits are compromised with cofilin binding (12, 15). This interpretation is supported by biochemical studies (16) showing that ADF/cofilin alters the average distance between the C terminus and DNase-I binding loop (DB loop) of adjacent filament subunits.

A number of key unanswered questions remain regarding the structure of cofilactin as well as the underlying molecular origin of the experimentally observed modulation of filament elasticity. Molecular simulation, specifically all-atom molecular dynamics (MD), is well-suited for investigating these questions because it permits sampling all atomic degrees of freedom in a system. MD has been valuable in providing all-atom descriptions of fundamental aspects of actin assembly, dynamics, and function. For example, classical and biased MD simulations have recently been successfully employed to investigate the role of actin polymerization in the rate of ATP hydrolysis (17), the role of nucleotide state in determining the conformational state of the DB loop (18), and how the DB loop conformation influences the elastic properties of filaments (18–20). This body of work in conjunction with a number of other MD studies of actin (19, 21–23), ADF/cofilin (24), and actin-related proteins (23, 25) demonstrate the potential of computer simulation to provide atomic information underlying the behavior of the actin cytoskeleton.

Herein we seek to address some important unanswered questions regarding cofilactin filaments, namely the structural basis of altered cofilactin filament bending mechanics and cofilin-linked filament allostery. We report previously undescribed MD simulations of various actin and cofilactin filament models—we have performed over 200 ns of simulation of cofilactin and additionally reanalyzed some of our previous studies of filamentous actin. The simulation results are used to compute the persistence length, provide an overall molecular interpretation of the experimental evidence that point to reorganization of SD2 in actin, and identify an overall mechanism for how ADF/cofilin binding alters the structure of actin filaments.

Results and Discussion

We present all-atom MD simulations of cofilactin filaments and an expanded analysis of actin filament simulations from our previous study (17). Technical details regarding the MD simulations and preparation of the initial structures are detailed in the methods section. Within the present study we systematically varied the structure of the filament [Oda et al. (26) vs. Galkin et al. (15)], the configuration of the DB loop (α-helical vs. loop), and additionally investigate the effect of ADF/cofilin binding on a native (26) actin filament. All cofilactin models tested have a single cofilin bound between SD1 and SD3 of each filament subunit (10).

Structural Properties of Cofilactin Filaments.

The cofilactin structure used for simulations was derived from electron microscopy studies by Galkin et al. (15). Cofilactin filaments have an altered twist and tilt compared to native (i.e., bare) actin filaments (7, 12). The cofilactin filament has a twist of ∼163 degrees, corresponding to a helical repeat of ∼30 nm, which is markedly shorter than native filaments with a helical repeat of ∼36 nm (13 subunits/repeat) and twist of ∼166 degrees.

The native actin filament structure was based on the recent refinement by Oda et al. (26). We additionally simulated an unmodified cofilactin filament (referred to hereafter as cofilactin-13) inspired by a recently published model (10), wherein it was suggested that such a structure may resemble an initial binding mode of cofilactin. To provide a clear set of control simulations, filaments were simulated with the DB loop in the folded and unfolded conformation.

These various models comprehensively evaluate the effects of cofilin decoration, subunit tilt, and DB loop disorder on the filament structure and dynamics. Recent studies (27, 28) that indicate actin filaments in solution exist in three equilibrium states—a canonical (e.g., Holmes or Oda-like), tilted (i.e., as in our cofilactin simulations herein) or with SD2 completely disordered. This distribution is modulated by cofilin binding (13, 27, 29). Kinetic analysis of cofilin binding has also revealed the existence of two distinct cofilactin filament states in a reversible equilibrium (29). In this work we systematically test the ability of the canonical and tilted equilibrium conformations to account for the filament mechanics. The third conformation with SD2 disordered (30, 31) could not be studied via MD simulation because atomic coordinates of the disordered SD2 region are lacking. Nonetheless, as detailed below, MD simulations of these two filament conformations yield a plausible molecular basis for enhanced cofilactin flexibility.

We first compared the overall structure and stability of native (i.e., bare) and ADF/cofilin-saturated (cofilactin) filaments during MD simulations from the equilibrium unit cell dimension (i.e., the length of one cofilactin or actin helical repeat length in our simulation), filament root mean squared deviation (RMSD), and subunit RMSD of the DB loop and C terminus, respectively (Table 1). The filament RMSD was calculated with respect to the initial structure and included only the 11 or 13 individual actin subunits for clarity of comparison between the bare and cofilactin filaments. We calculated the subunit RMSD for the DB loop by aligning a single actin subunit against the initial subunit structure (not including the atoms of the DB loop) and then calculating the displacement. Such an approach is an effective way to determine the conformational flexibility of a small region of a large protein. The same approach was used for the C terminus (defined as the final five residues of each subunit).

Table 1.

Structural properties of cofilactin and actin filaments

System	Helical Repeat Length (Å)	RMSD (Å)	RMSD DB loop (Å)	RMSD C-term (Å)	HL Contacts	RMSD HL (Å)	Filament Radius (Å)	Lp (μm)
Cofilactin (DB fold) *	308(±1.0)	8.3(±0.2)	7.3(±1.4)	2.6(±0.5)	3.5(±0.9)	2.0(±0.4)	17.8(±2.3)	3.7(±0.1)
Cofilactin (DB unfold)	303(±1)	8.0(±0.2)	9.0(±1.3)	2.3(±0.3)	4.9(±0.5)	2.1(±0.5)	17.8(±3.0)	9.0(±0.2)
Cofilactin 13	363(±2)	4.6(±0.1)	5.6(±1.2)	3.2(±0.9)	7.7(±0.2)	2.5(±0.8)	16.2(±1.7)	19.1(±0.1)
F-actin (DB fold) †	357(±3)	6.4(±0.6)	6.5(±1.0)	2.9(±0.6)	7.2(±0.3)	2.7(±0.4)	16.6(±3.4)	8.7(±0.1)
F-actin (DB unfold) †	357(±4)	5.6(±0.4)	5.1(±1.0)	2.9(±0.5)	6.6(±0.2)	2.4(±0.4)	17.0(±3.2)	17.2(±0.4)
Cofilactin (experiment) ‡	297						20.6	2.2
F-actin (experiment) §	360						16.5	9.1(±0.3)

All simulation results are for ADP-bound filaments with the conformation of the DB loop noted in the table. The equilibrium helical repeat length along the helical filament axis is compared to the experimental repeat length.

^*Values for this system are averaged over two independent MD simulations.

^†Values for ADP F-actin reproduced from simulations previously published by our group (17).

^‡Cofilactin experimental values for filament structure obtained from Galkin et al. (15) and filament L_p obtained from McCullough et al. (14)

^§Actin filament experimental values for filament structure obtained from Oda et al. (26), and persistence length obtained via averaging results from Isambert et al. (53) and McCullough et al. (14)

The impact on cofilin binding on actin’s hydrophobic loop (HL) (residues 262–274) was also evaluated. Both the RMSD of the HL (analyzed in an identical fashion as the DB loop) and also the number of cross-strand contacts between the HL and actin are reported (Table 1). The overall stability of the HL is identical for both actin and cofilactin, but the number of cross-stand contacts decreases by nearly a factor of two in the cofilactin filament, consistent with structural studies showing that cofilin weakens lateral filament contacts (11). We note for clarity that this procedure was performed on each of the 11 or 13 actin subunits within each filament to obtain maximal sample size. The enhanced conformational flexibilities of the actin DB loop and C terminus are particularly interesting given their role identified in filament structure and dynamics (32).

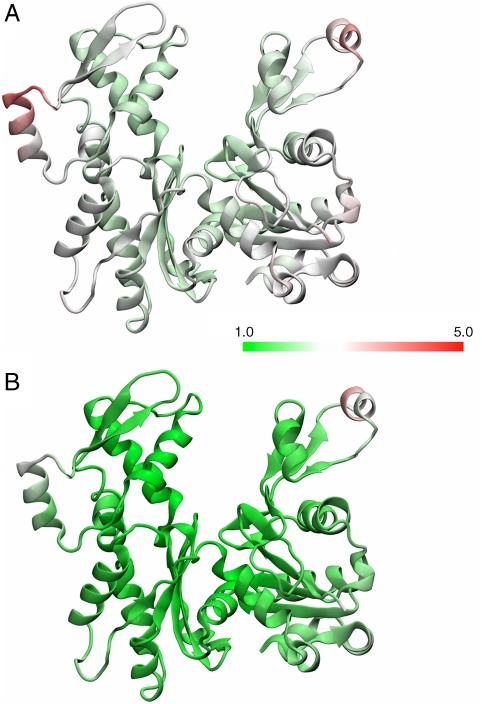
All filament equilibrium lengths determined from MD are in good agreement with their experimental counterparts (Table 1). The overall RMSD of the cofilactin filaments are significantly higher than both the bare actin filaments and the cofilactin-13 filament. In fact, cofilactin-13 was, overall, the most stable filament investigated. Additionally, the RMSD of the DB loops showed that in the cofilactin systems, the DB loop has noticeably higher flexibility. In contrast, the RMSD of the C termini of the filaments ranges from 2.3–3.2 Å, a value that is nominally similar to that observed for the entire actin protein itself (19, 22, 23). Fig. S1 shows a comparison between an initial ADF/cofilin simulation and a snapshot from the simulation as well as a comparison with bare actin. The higher flexibility of the DB loop relative to the rest of the actin subunit (Fig. 1 and SI Text) may be the source of disorder observed by electron microscopy (15, 33).

Fig. 1.

Relative flexibilities of the bare actin (A) and cofilactin (B) subunits. The protein subunits are colored according to the numeric scale that represents the mean-squared fluctuation of the residue. A value of 1 (Green) indicates that region of the protein has the minimum observed flexibility as observed in MD. Details of the calculation are given in SI Text.

We also calculated the average radius for each system, which is related to the width and helical heterogeneity of the filaments (Table 1). The filament radius at each frame of the trajectory was calculated from

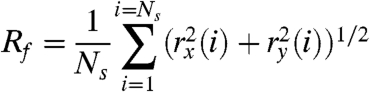[1]

where N_s refers to the number of subunits in the filament (11 or 13) and r_x/r_y refer to the x and y coordinates of the center of mass of the ith actin subunit in the filament. Eq. 1 assumes that the filament has been centered on the origin and that the z direction is aligned with the filament axis. Cofilactin filaments are wider than bare actin filaments (Table 1), but both cofilactin systems are slightly more narrow than the initial starting configuration, consistent with the observation that the equilibrium unit cell length is slightly longer than the initial configuration.

Persistence Length of Cofilactin Filaments.

The persistence lengths (L_p) of cofilactin filaments and bare actin filaments calculated from MD simulations ((17, 19); Table 1) indicate that the L_p of actin filaments depends strongly on the conformation of the DB loop of each filament subunit (17, 19, 30). In both the cofilactin and bare actin filaments a change from an unfolded loop to a folded alpha helix in the DB loop lowers the L_p approximately twofold. However, only in the remodeled cofilactin filament are the values in line with experimental measurements. The cofilactin-13 filament has a significantly higher L_p value compared to experiment, as predicted from geometric arguments (14). Given the good agreement between experiment and MD simulations in the bare actin simulations, and the present level of agreement between the cofilactin (DB folded) simulation and the reported experimental cofilactin value, we conclude that the two major determinents of the overall cofilactin filament stabiltiy and stiffness are the ADF/cofilin-induced change in the filament structure and the DB loop conformation.

As an additional test we simulated the cofilactin (DB fold) filament with bound cofilin mass density removed. While this may not represent a state extensively populated in vivo, there is increasing evidence that cofilin shifts the equilibrium of states normally populated by native actin filaments (12, 13, 15). In addition, this simulation allows us to directly eliminate cofilin contributions to filament stiffness arising from the increased geometric moment, thereby revealing the mechanical properties of the remodeled cofilactin filament. This filament has a persistence length of 1.8–2.1 μm, slightly lower than the experimental value of 2.2 μm obtained for cofilactin in solution (14).

ADF/Cofilin-Induced Actin Reorganization.

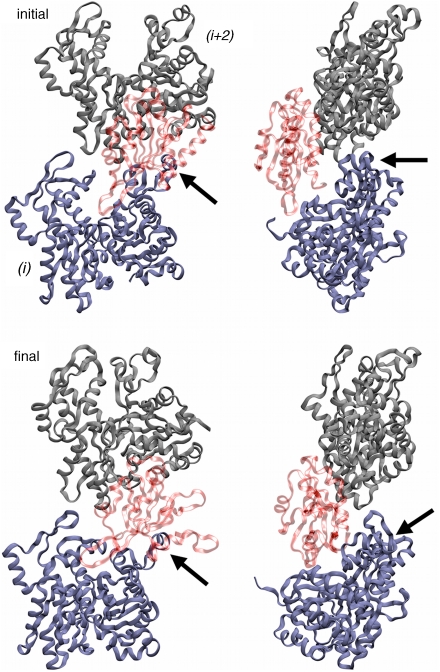
A number of recent experimental studies of cofilactin have led to the development and support of the hypothesis that ADF/cofilin binds between subdomains 1 and 3 of actin, and that the origin of the increased flexibility of cofilactin (compared with bare filamentous actin) must have its roots in a modified interaction between subdomain 2 (SD2) and subdomain 1 (SD1) of the adjacent long-pitch helix subunit (10, 13, 15, 32, 34, 35). We observed during simulation that ADF/cofilin binding does indeed result in reorganization of DB loop of subdomain 2 (SD2; Fig. 2). Additionally, the cofilin binding surface (Fig. S2) retains its initial character as well as contact between cofilin/actin of residues that were previously determined via mutagenesis experiments to be important for binding (36).

Fig. 2.

ADF/cofilin-induced remodeling of actin subdomain 2. Snapshot of a two-subunit intrastrand sequence from cofilactin filament simulations. The snapshots are of the initial and final trimer sequence and show front and side views showing the movement of subdomain 2 (noted with Arrows) away from the filament core.

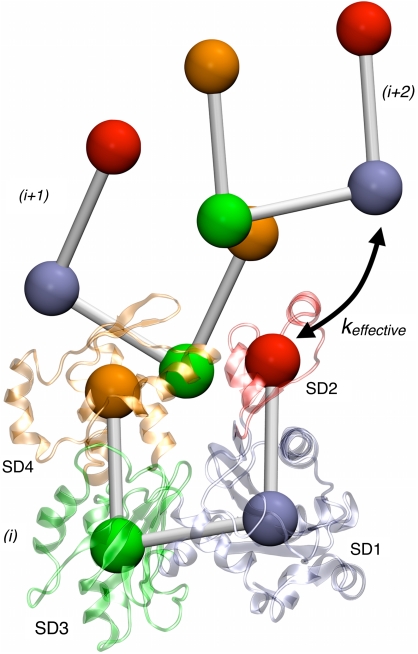
We quantified the observed reorganization of SD2 using a number of features extracted from the MD trajectory (Table 2). An effective harmonic spring constant that describes the interaction between SD2 of one actin subunit and SD1 of an adjacent intrastrand subunit (i.e., an i + 2 actin subunit in the filament), shown schematically in Fig. 3 and based on a previous (19, 25, 37) 4-site coarse-grained representation (CG) for actin, was obtained by fitting the distribution of bond distances between the COM of the two subdomains to a Gaussian probability distribution (38). We fit only a single Gaussian function to reproduce the CG bond distributions because the multiple-Gaussian technique, while clearly more accurate, sacrifices a simpler physical interpretation. The spring constants for the cofilactin systems are significantly smaller than the corresponding bare actin filament systems (Table 2), indicating that the interaction between SD2 of a filament subunit with SD1 of an intrastrand neighbor is greatly weakened by ADF/cofilin binding. This SD2—SD1 interaction has indeed been shown from CG actin filament simulations to be very important to the overall stability and stiffness of the filament (37).

Table 2.

Structural properties of cofilactin filaments related to reorganization of subdomain 2

System	keffective (kcal/mol/Å2)	Number of intrastrand SD2/SD1 contacts	Probe distance (Å)	ADF/cofilin contact ratio *
Cofilactin (DB fold) †	0.046(±0.005)	4.5(±0.3)	16.1(±2.9)	1.4(±0.2)
Cofilactin (DB unfold)	0.031(±0.001)	4.8(±0.8)	16.5(±2.0)	0.9(±0.1)
Cofilactin 13	0.060(±0.001)	8.2(±0.4)	13.2(±2.6)	1.0(±0.1)
F-actin (DB fold)	0.42(±0.05)	8.6(±0.2)	11.8(±1.5)
F-actin (DB unfold)	0.17(±0.0001)	9.1(±0.2)	13.0(±1.3)

Parameters from are actin filaments are also reported for comparison when possible. All parameters are defined in the results section.

^*Ratio of contacts between SD1—bound ADF/cofilin, and SD1—adjacent (i + 2) ADF/cofilin.

^†Values for this system are averaged over two independent MD simulations.

Fig. 3.

Effective interactions used to describe ADF/cofilin-induced increased flexibility. A three-subunit actin sequence is shown in and coarse-grained (CG) representation and atomistic (Cartoon) representation of the 1st subunit. The four subdomains labeled are: SD1 (Blue) residues 1–32, 70–144 and 338–375; SD2 (Red) residues 33–69; SD3 (Orange) residues 145–180 and 270–337; and SD4 (Green) residues 181–269. The effective harmonic spring constant is labeled in the figure.

The number of contacts between the DB loop and SD1 of adjacent intrastrand subunits, defined as being present when two C^α atoms were located within 10.0 Å of each other, is significantly reduced with ADF/cofilin binding, thereby providing a molecular-level basis for the greatly reduced effective CG spring constant. The calculated average distance between residue Q41 of the DB loop and adjacent intrastrand subunit C-terminal residue C374 has been shown in a recent spectroscopic study to correlate with the effect of ADF/cofilin binding on actin filament dynamics (32). This experimental spectroscopic probe length is also directly calculable via simulation, and the present MD simulations yield similar results to those from experiment. Note that since the C terminus of each actin subunit is relatively stable (c.f., columns four and five of Table 1), the main contributing factor to the experimentally observed variations in probe length arises from the conformational flexibility of the DB loop. It is noteworthy to see that the cofilactin-13 filament has a probe distance similar to that found in bare actin filaments.

We also investigated how ADF/cofilin binding to the actin filament changed during the course of the MD simulation. The simulation trajectories show that before the DB loop (of subunit i) moves radially away from the core of the filament, SD1 of the adjacent actin subunit (i.e., nearest longitudinal neighbor in i + 2 position) moves longitudinally away from the DB loop. Additionally we observe this happening in concert with ADF/cofilin (bound at SD1/SD3 of subunit i) increasing its contact order with SD1 of the actin subunit in the i-2 position, i.e., the bound ADF/cofilin extends far enough to make an impact not only on the neighboring (i-2) SD2, but also the neighboring (i-2) SD1. We quantified this behavior by calculating the ratio of contacts that SD1 makes with the adjacent bound ADF/cofilin (i.e., bound to the i + 2 actin monomer) to the number of contacts that SD1 makes with its own bound ADF/cofilin (Table 2). The cofilactin (DB fold) simulation shows that ADF/cofilin binding is increased to the adjacent ADF/cofilin compared to the cofilactin (DB unfold) and ADF/cofilin-13 simulations (Fig. S3) and offers a possible mechanism for how ADF/cofilin softens actin. First, ADF/cofilin binds to a filament subunit where between SD1 and 3 (10), which introduces structural reorganization (altered twist and subunit tilt) of the filament. This perturbation causes ADF/cofilin to preferentially bind SD1 and in doing so compromises stabilizing intrastrand contacts between SD2 and SD1 of neighboring, long-axis subunits. As a result, SD2 moves laterally away from the filament.

The above molecular interpretation is able to account for many biochemical observations about cofilactin dynamics, including slow association kinetics and a favorable entropic component of the binding free energy (39). Moreover, the i to i + 2 subunit cooperativity observed in the simulations explains why binding models that incorporate nearest-neighbor cooperative interactions describe well the cooperative ADF/cofilin binding to actin at both the equilibrium and kinetic level (4, 29, 39).

Conclusions

We have presented results from previously undescribed all-atom MD simulations of the cofilactin filament. By systematically varying structural features of cofilactin and additionally by comparing to results from our previous studies of the bare actin filament, we have gained important insights into cofilactin structure and dynamics. Based on the simulations results presented in the previous section, we are able to now address from a molecular perspective two key questions related to cofilactin structure and function.

What Is the Structure of Actin with Bound ADF/Cofilin?.

Given the results we have previously obtained (17, 19) for computing filament persistence lengths from all-atom MD simulations, the present calculations can be used as a means to discriminate between various cofilactin filament models. Only the cofilactin filament with a remodeled actin core [vis-à-vis the electron microscopy experiments by Galkin et al. (15)] and with a folded DB loop reproduces the experimentally observed increased filament flexibility with ADF/cofilin binding. Conformational transition of the DB loop from an unstructured coil to a folded helix lowers the filament L_p by approximately a factor of two. Additionally, compared to bare actin and cofilactin-13, the two cofilactin filaments with a reduced twist were found to have much a much higher RMSD, both in the overall unit helical repeat length as well as the DB-loop region, consistent with the commonly held notion that ADF/cofilin binding increases the overall conformational dynamics of actin. Based on these observations, we infer that the cofilactin filament with helical DB-loop is most likely (of all the structures we considered) to represent the predominant cofilactin structure in solution.

What Is the Origin of the Observed Increase in Flexibility of Cofilactin?.

Our simulations yield general agreement (vis-à-vis the computed persistence length values) with the experimental observation that ADF/cofilin increases the bending flexibility of actin filaments (14). We have identified a number of structural features that provide a molecular interpretation for a large body of experimental work performed in solution with purified actin and ADF/cofilin proteins. Consistent with many previous hypotheses derived from experimental studies (7, 11, 13–15, 35), the different quantities computed from the MD simulations consistently show that the interactions between adjacent intrastrand subunits in actin are significantly modified by ADF/cofilin. The SD2—SD1 intrastrand subunit interaction is significantly weakened with ADF/cofilin binding, the DB loop has increased flexibility (increased RMSD), and the DB loop moves radially away from the filament core (increase probe distance). Furthermore, simulations of unmodified actin filaments with bound cofilin (cofilactin-13) show a pronounced stiffening compared to both bare actin and cofilactin, as predicted from geometric arguments (i.e., increase in geometric moment) (14).

It is the remodeling of the actin filament as a consequence of ADF/cofilin binding that generates the observed softening (14). This remodeling overcomes the enhanced filament stiffness associated with an increase in mass and geometric moment (14). Because bound cofilin does not contribute to intersubunit interactions, its contribution to filament stiffness through increased geometric moment could be insensitive or completely independent of its precise orientation when bound to actin. This presumably explains why the precise orientation of bound cofilin influences the overall filament mechanical properties obtained from the simulations much less than does reorganization of actin.

Methods

The coordinates for the actin portion of the of the cofilactin filaments were based on the electron microscopy studies by Galkin et al. (15). The cofilactin-13 filament was generated using the Oda (26) model with the DB loop in a folded conformation is in the spirit of the “early binding mode” model proposed by Paavilainen et al. (10). All of the models in this work locate cofilin between SD1 and SD3 of the actin monomer according to the Paavilainen et al. binding site (10) with a single cofilin bound to each actin subunit. We additionally reanalyzed some recent simulations (17) of bare actin that were based on the Oda (26) filament model with either the DB loop in a folded or unfolded conformation. The unfolded conformation used was published by Oda et al. in PDB entry 2ZWH (26). The folded conformation was built by taking the folded DB loop from PDB entry 1J6Z (40), splicing it into the 2ZWH structure, and relaxing the structure with an energy minimization routine. The initial coordinates for all of the filaments were obtained in an identical manner to a previously published study (19) from our group. The cofilactin filament is based on bovine actin structure 2BTF (41) and ADF/cofilin structure 1HQZ (42). The filament was placed in a box of explicit TIP3P water molecules (43) with a minimum distance of 15 Å between the protein and the border of the periodic boundary conditions. The charge of the system was neutralized via random placement of counterions (KCl) using the VMD autoionize plugin (44). All filament simulations were performed with longitudinal periodicity so that the first and last subunits were simulated as though they were in contact through periodic boundary conditions (requiring the use of 11 subunits/cofilactin filament and 13 subunits/actin filament).

All MD simulations were completed using NAMD 2.6 (45). Potential energies and forces were calculates using the CHARM22/27 (46) force field, and electrostatic interactions were calculated with the particle mesh Ewald sum method (47). A 2 fs integration time step was made possible by constraining all intramolecular hydrogen bonds with the SHAKE (48). After 100 ps preequilibration period was used to bring the system to 310 K by means of velocity rescaling. Next, the simulations were continued in the isobaric-isothermal (constant NPT) ensemble (310 K, 1.01325 bar) using Langevin dynamics and the Langevin piston method via its implementation in NAMD (49, 50). The damping coefficient used for Langevin dynamics was 0.5 ps^-1 and the Langevin piston was controlled using a piston period decay of 2 ps. Each simulation was continued for at least 50 ns, or until the unit cell length had equilibrated and sufficient equilibrated sampling of the NPT ensemble was achieved. The strategy we employed was to run the NPT simulation until the box length along the filament axis stabilized (normally 30 ns), and then continued for an additional 20–40 ns “production phase.” The unit cell length was the slowest property to equilibrate. By comparison, the filament RMSD, system pressure, and total energy, equilibrated far faster. The initial cofilactin structure (15) is based on a fit of an atomic model to an EM density map and has a reported resolution of ∼20 Å. In spite of this resolution we are confident in the structures used given that we employed strict convergence criteria employed in this work, as well as the fact that we demonstrate strong sensitivity of the filament mechanics to the initial starting structure and good agreement with experimental measurements of filament mechanics.

Unless otherwise noted, results reported from MD simulations of actin are based on the last 20 ns of each trajectory, and results reported from simulations of cofilactin are based on the last 40 ns each trajectory. The cofilactin simulations were found to be much more correlated due to their higher mass and slow internal relaxation times; therefore a longer sampling period was used. Analysis of MD calculations and creation of all protein figures was performed using Visual Molecular Dynamics (44). Error estimation was performed with a standard block-averaging technique used in molecular simulation (51, 52). For average values of a property of a single actin subunit, that were derived from filament simulations, the error for that property for each subunit was estimated via block-averaging, and the subsequent 13 error estimates were averaged to obtain an overall average error estimate.