Collective dynamics underpins Rayleigh behavior in disordered polycrystalline ferroelectrics

Abstract

Nanoscale and mesoscopic disorder and associated local hysteretic responses underpin the unique properties of spin and cluster glasses, phase-separated oxides, polycrystalline ferroelectrics, and ferromagnets alike. Despite the rich history of the field, the relationship between the statistical descriptors of hysteresis behavior such as Preisach density, and micro and nanostructure has remained elusive. By using polycrystalline ferroelectric capacitors as a model system, we now report quantitative nonlinearity measurements in 0.025–1 μm³ volumes, approximately 10⁶ times smaller than previously possible. We discover that the onset of nonlinear behavior with thickness proceeds through formation and increase of areal density of micron-scale regions with large nonlinear response embedded in a more weakly nonlinear matrix. This observation indicates that large-scale collective domain wall dynamics, as opposed to motion of noninteracting walls, underpins Rayleigh behavior in disordered ferroelectrics. The measurements provide evidence for the existence and extent of the domain avalanches in ferroelectric materials, forcing us to rethink 100-year old paradigms.

Hysteretic response to external stimuli is a ubiquitous feature of disordered systems ranging from friction, capillary condensation, metal-insulator transitions, to magnetic, ferroelectric, and ferroelastic materials. Hysteresis in ferroic systems is utilized in many applications, including magnetic and ferroelectric memory technologies (1) and shape-memory and high-toughness materials (2). The traditional objects of study in the field of ferroic materials driven by information technology applications are strong-field hysteresis loops corresponding to complete switching of material between the limiting states. However, equally important are hysteretic responses in weak (subcoercive) fields, which directly underpin the enhanced properties often observed in disordered and multidomain materials (3 and 4). For ferroelectrics, enhanced electromechanical coupling and dielectric responses enabled by domain wall motion strongly influence electromechanical energy conversion in medical transducers, actuators for precise positioning, and piezoelectric and composite magnetostrictive sensors (5). At the same time, local hysteresis is the primary mechanism of energy losses and dissipation. Design of materials with high coupling coefficients and acceptable losses necessitates deciphering fundamental mechanisms behind low-field hysteresis behavior.

In disordered magnetic systems, the weak-field hysteresis has been a field of active study since the seminal 1870 work by Rayleigh (6), who described the universal parabolic law for ferromagnetic minor loops,

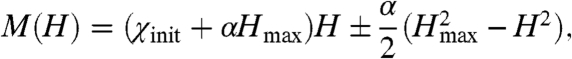[1]

where M(H) is the field-dependent magnetization, χ_init is the initial susceptibility, H_max is the maximum applied magnetic field, and α is the irreversible Rayleigh constant. The same constant defines the field-dependent susceptibility,

[2]

Eqs. 1 and 2 describe the pertinent aspects of materials response, including the low-field susceptibility, remanent magnetization, power losses (area inside the loop), and the imaginary part of susceptibility. Hence, the (phenomenological) Rayleigh constant α describes the essential link between the hysteresis and nonlinearity; microscopically, it is related to internal disorder in the material (7 and 8).

While the majority of studies have been concentrated in the field of magnetism, similar behavior was found for ferroelectric materials for polarization-field, P(E), and charge-stress, Q(X), behavior (9–11), as shown in Fig. 1. In many ferroelectric films, α is smaller than it is in bulk ceramics of the same composition, presumably due to a lower domain wall mobility. In general, lead-based ferroelectric films adhere to Rayleigh behavior up to electric fields of ∼1/3 to 1/2 of the coercive field (12). The α and ε_init values for the films in this work are slightly higher than those in (12), largely due to improved quality of the films. These observations suggest that Rayleigh-like behavior is a ubiquitous aspect of the physics of ferroic systems (13 and 14). Beyond ferroics, methods based on the Rayleigh or more general Preisach formalisms have been successfully applied for description of strongly correlated oxides (15 and 16) and spin glasses (17).

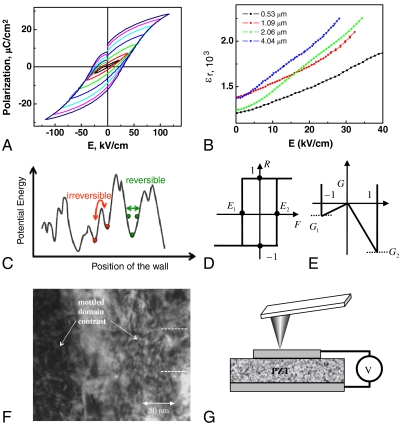
Fig. 1.

(A) A family of minor and major hysteresis loops measured using large area electrodes showing the evolution of hysteresis with the excitation window for the 1.09 μm PZT film used in this study. (B) Field dependence of the dielectric constant vs. ac field for different PZT film thicknesses. For these films, the permittivity dependence on dc bias, V_ac, and frequency are all consistent with domain wall motion being the dominant contributor to the observed nonlinearity. (C) Landscape of potential energy of a domain wall. The circles denote the positions of domain walls. Applied electric fields can cause the walls to move either reversibly within a well or irreversibly between wells, (D) In a Preisach model, hysteresis behavior of material is determined by the distribution function ρ(E₁,E₂) of the elementary hysterons, where E₁ and E₂ are lower (higher) coercive fields. This hysteresis loop corresponds to double-well free energy shown in (E). The Rayleigh limit corresponds to ρ(E₁,E₂) = const. Despite extensive studies, the relationship between the pinning potential (C) and statistical descriptions (D, E) is elusive. (F) Section from a bright field TEM micrograph of the cross-section of a 1 μm thick film, showing the domain structure. The large scale defects parallel to the substrate result from the original spin and crystallization steps. (G) Schematics of experimental set-up illustrating sample geometry and PFM measurements.

Despite the wide spread occurrence of Rayleigh or Rayleigh-like behavior in disordered (e.g., multidomain, polycrystalline, or defective) ferroics, there are numerous unanswered questions regarding the underlying mechanisms. The early work of Neel (18) and Kronmuller (19) analyzed the reversible and irreversible single domain wall dynamics in a defect-induced potential energy profile, as shown in Fig. 1C. Preisach (20) and Mayergoyz (21) provide a statistical description of the hysteresis, with Rayleigh behavior corresponding to the special case of uniform Preisach density, i.e., uniform energy distribution for the activation energies in the double-well barriers in Fig. 1D. In ferroelectrics, Arlt (22) and Bassiri-Gharb (12) review the pinning sources responsible for hysteretic responses; grain boundaries, point defect dipoles, dislocations, phase boundaries, the density of domain walls, and residual stresses are all known to decrease the mobility of the mobile interfaces (such as domain walls) responsible for nonlinearity.

Despite the available phenomenological knowledge, the most basic questions regarding the mechanism underpinning nonlinear behavior remain unanswered. Is Rayleigh behavior a property of a single interface moving either rigidly or via bowing (23), an average response of multiple noninteracting interfaces, or collective behavior emerging in a system of multiple interacting interfaces? (7) Can the individual defect centers be ascribed with individual double-well potentials, providing microstructural analogs for Preisach hysterons? How many mobile interfaces must be sampled in the measurement for Rayleigh behavior to be observed, and what is the corresponding critical length scale (e.g., coherence length (8), pinning center density, grain size, etc)? Despite the obvious importance for the physics of these systems, these answers are not known, and even the relative importance of the nature and density of pinning sites is not determined. In fact, systematic studies demonstrate that the Rayleigh nonlinearity in polycrystalline PbZr_0.52Ti_0.48O₃ (PZT) films is suppressed in films below 1 μm in thickness, although the grain size (the upper boundary on the scale of disorder) was ∼50 nm (nanometer) (24). The detailed microstructural origins of the pronounced size effect are unknown, as is the relative importance of grain size and pinning sites associated with the film interfaces. Overall, despite the ubiquity of the behavior described by Eqs. 1 and 2 and the existential importance of link between hysteretic and nonlinear behaviors, the underpinning mechanisms—both in ferroelectric and ferromagnetic materials—remain elusive.

We explore the origins of Rayleigh behavior on the 100 nm length scale using band excitation (25) piezoresponse force microscopy of capacitor structures (26). The nonlinearity mapping reveals the formation of micron-sized islands of nonlinear response in a weakly nonlinear matrix in the films of about 1 μm in thickness. The density of the islands increases with the film thickness and for thick films they form the percolative network. As will be shown here, this unexpected behavior illustrates that collective micron-scale processes, rather then single wall dynamics, underpin Rayleigh behavior in disordered ferroelectrics.

Results and Discussion

Mapping Local Nonlinearity.

As the model system, we have chosen polycrystalline ferroelectric capacitors, for which the dielectric and electromechanical properties and Rayleigh responses (including their thickness dependences) are known (24). The relatively large scale of the disorder (upper bound given by a ∼50 nm grain size) renders these materials well-suited for mesoscopic studies. High-resolution electron microscopy studies have illustrated the presence of the 20–30 nm irregular domains, as expected in compositions close to morphotropic boundary between tetragonal and rhombohedral PZT. Note that the TEM contrast highlights only non-180° walls associated with strain changes, and the presence of additional 180° walls cannot be excluded. At room temperature, the thickness of the domain walls in these ferroelectric thin films is on the order of 1 nm (27–29). To perform the local nonlinearity measurement, we use Piezoresponse Force Microscopy (PFM) of capacitor structures (30) with a band excitation (BE) signal. In BE, the excitation and detection is performed using a signal having defined amplitude and phase content in a given frequency interval (25), as compared to the single frequency used in current scanning probe microscopes (SPMs). This allows efficient use of resonance enhancement in PFM spectroscopy, avoiding artifacts due to changes in resonance frequency as a function of probe position or bias. In addition, any bias dependence of the resonance frequency allows identification of the nonlinear behavior of the tip-surface contact (e.g., softening).

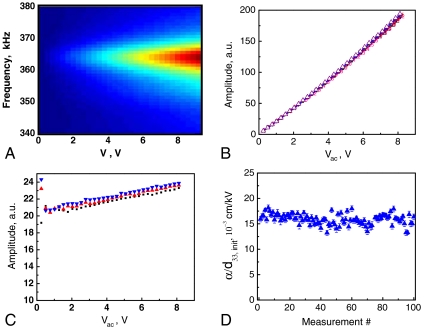
It was first essential to demonstrate that the amplitude dependence of the piezoelectric response can be measured by SPM quantitatively at a single spatial location. Shown in Fig. 2 is an example of a BE spectrum acquired at a single location on a sample surface. The map illustrates the evolution of electromechanical response as a function of frequency and the amplitude of the applied voltage, V_ac. The individual curves were analyzed to yield the amplitude at the resonance (maximal response), A_max, resonant frequency, ω_r, and the mechanical quality factor (width at the half maximum), Q, as a function of position, (x,y), and voltage, V_ac. The amplitude A_max(V_ac) is shown in Fig. 2B. The contact resonance frequency at single point is essentially independent of V_ac (changes of 100 Hz as compared to ∼5 kHz peak width). This voltage independence strongly indicates that tip-surface contact and cantilever dynamics are nearly linear, and the nonlinearity in A_max(V_ac) dependence originates from amplitude dependence of piezoelectric response of the material.

Fig. 2.

Single-point voltage spectroscopy performed at fixed tip location on a 4.04 μm thick PZT film. (A) Single-point two-dimensional spectrum of response as a function of ac bias and frequency. Bias dependence of the (B) response and (C) effective piezoelectric constant, showing several datasets. (D) The response nonlinearity measured at a single point for 100 sequential datasets.

Fig. 2B illustrates that the amplitude is a nonlinear function of the driving force, and can well be approximated as a second-order polynomial, 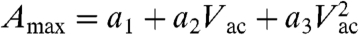with a₁ ≈ 0, (i.e., a₁ < 1% of the linear term for V_ac > 0.38 V). The ratio A_max/V_ac exhibits almost perfect linear behavior with V_ac, indicative of Rayleigh response; no threshold field for depinning was detected. Note that in this case, the amplitude is directly proportional to the sample surface displacement h, A_max = βh, where β is cantilever sensitivity. Differentiation yields the Rayleigh law as in Eq. 3.

[3]

The corresponding linear behavior is illustrated in Fig. 2C. Note that deviation from linearity is observed only for V_ac < 0.5 V, indicative of the high fidelity of Rayleigh behavior. Remarkably, the ratio of quadratic and linear terms is independent of β, i.e., the local nonlinearity is measured quantitatively. This independence on the probe and cantilever properties is highly unusual for any SPM method.

To estimate the reproducibility of these measurements and thus estimate the effect of the detection electronics (noise) and instrumental drift, the measurements were performed 100 times at the same location, as shown in Fig. 2D for the ratio of nonlinear to linear response. Note that the measurements yield α_d/d_33,init = (16 ± 1.6)10^-3 cm/kV (i.e., the response has been normalized to field, rather than voltage to facilitate comparison between films of different thickness. The relative error is ∼10% for this film thickness), and does not exhibit any systematic long-term drift. Furthermore, the measured nonlinearity is very close to the macroscopic value (as will be discussed later) despite the fact that the probed volume in SPM is almost 10⁶ times smaller, as seen in Table 1. We note that this level of precision is enabled by the use of the BE method and decoupling the material and tip junction nonlinearities, i.e., the elastic properties of the contact are controlled by the electrode, but the bias dependence of excitation force is determined by piezoelectric nonlinearity.

Table 1.

Resolution of BE-PFM measurements as a function of PZT film thickness

PZT film thickness	Estimated lateral resolution	Estimated volume sampled
	∼(aH + bL): a = 0.14, b = 0.40	(area * thickness)
0.53 μm	0.094 μm	∼0.0037 μm3
1.09 μm	0.173 μm	∼0.025 μm3
2.06 μm	0.308 μm	∼0.15 μm3
4.04 μm	0.586 μm	∼1.09 μm3

Note that this estimate of resolution was derived for vertical domain walls in the fully elastically coupled material, and provides an upper estimate for columnar films.

H - PZT thickness, L - Electrode thickness

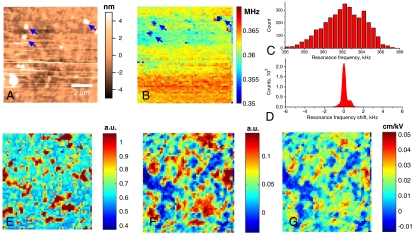
The spatially resolved nonlinearity mapping in 1.09 μm thick ferroelectric capacitor is shown in Fig. 3. The surface topography (Fig. 3A) is relatively featureless, with a roughness of several nm. A number of topographic contamination spots are clearly seen. The resonance frequency map is shown in Fig. 3B; it exhibits some line-to-line drift due to changes in the tip, and a number of spots due to resonance frequency shifts at contamination spots (marked by arrows). The significant spatial variability of resonance frequency (point-to-point dispersion of ∼10 kHz, as compared to 5 kHz peak width) obviates the use of constant-frequency resonant PFM in these measurements. Note that in comparison the single-point resonant frequency is almost voltage independent, Fig. 3D. Finally, the d_33,init, α_d, and α_d/d_33,init maps are shown in Fig. 3 E–G. The maps illustrate the presence of large-scale features (of the order of ∼0.5–1 μm), well above the grain size. Remarkably, the nonlinearity α_d/d_33,init image also illustrates the presence of the micron-sized clusters. These clusters appear to be only weakly correlated with the piezoelectric response, d_33,init, shown in Fig. 3E. The nonlinearity is large within the clusters, and is smaller in the surrounding matrix.

Fig. 3.

Nonlinearity imaging in 1.09 μm thick polycrystalline capacitors. (A) Surface topography and (B) resonance frequency map. Arrows mark the contamination spots and associated frequency shifts. Histograms of (C) position-dependent resonance frequency and (D) shift in resonance frequency as a function of bias dependence at any point (same scale). Maps (arbitrary units) of nonlinear fitting coefficients—(E) slope, a₂, (proportional to d_33,init) (F) quadratic coefficient, a₃ (proportional to α_d) and (G) ratio α_d/d_33,init.

The formation of the clusters of nonlinear response shown in Figs. 3 and 4 is highly nontrivial. First, it confirms that Rayleigh behavior can be observed in extremely small volumes, where the number of domain walls sampled is considerably (∼10⁶ times) smaller than that in global measurements. Secondly, the clusters provide a spatial distribution of regions with activated depinning (31); domain walls in regions of high nonlinearity are less strongly pinned than those in the matrix. Thirdly, the existence of clusters is proof that the dominant nonlinearity is associated with domain wall motion, and not with any intrinsic nonlinearity, as there is no reason that the intrinsic nonlinearity should be suppressed in only the matrix and not in isolated clusters (as further confirmed by the lack of strong correlation between d_33,init and nonlinearity images).

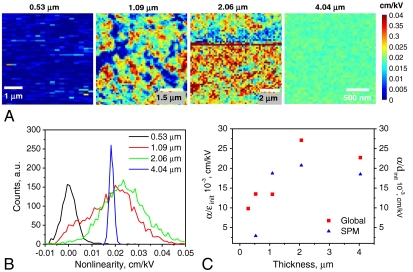
Fig. 4.

Evolution of nonlinearity with film thickness. (A) Spatial maps of nonlinearity for different film thicknesses (thicknesses shown across top). (B) Histograms of nonlinearities for different film thicknesses (the areas are not normalized). (C) Comparison of macroscopic dielectric measurements and averaged PFM piezoelectric data (no free parameters).

Nonlinearity Behavior in Thickness Series.

To obtain insight into the evolution of nonlinear responses as a function of film thickness, measurements were performed on a series of the capacitors with different thicknesses. The resulting maps are shown in Fig. 4. Note that in the 0.53 μm thick film the nonlinear response is essentially zero, i.e., the material is linear within the measurement errors. In the 1.09 and 2.06 μm films, the nonlinear regions form well-defined clusters that occupy approximately 1/3 and 4/5, respectively of the surface area embedded in a piezoelectric matrix with small nonlinearity. Finally, 4 μm film shows an almost uniform nonlinear response. The presence of sharp boundaries on the clusters and the numerical estimates in Table 1 suggest that the resolution is higher than the measured cluster sizes for the thinner films, and hence the observed behaviors cannot be interpreted as the effective change in the spatial resolution.

Shown in Fig. 4B is the evolution of the histograms of nonlinear response, illustrating the presence of bimodal distribution corresponding to clusters and matrix that can be clearly seen for 1 μm film. The comparison between averaged local nonlinearity from PFM measurements and the global nonlinearity from macroscopic dielectric measurements in Fig. 4C illustrates that average values are comparable for the range of film thicknesses studied. This agreement is remarkable, given that probing volume in PFM is ∼10⁶ times smaller then in macroscopic measurements, and the well known difficulty of quantitative SPM measurements.

A second key point to recognize here is that the similarity of the global dielectric and local piezoelectric nonlinearity measurements suggests that the same population of domain walls is contributing to both signals, as has been suggested elsewhere for dielectric and piezoelectric measurements on large area electrodes in similar films (32). No effort is made here to determine which domain walls dominate the nonlinear response; we note only that even when non-180° domain walls are strongly clamped in films (33–35), it is possible to observe Rayleigh piezoelectric behavior (36).

These observations illustrate the following scenario for the nonlinear behavior in disordered ferroelectrics. Macroscopically, films show a gradual loss of nonlinearity below 1–2 μm in thickness. Microscopically, films above 2 μm show virtually uniform nonlinear behavior (i.e., the response is averaged over the (larger) collection volume of the probe, precluding cluster identification). In the intermediate thickness range, the film breaks into clusters that have high nonlinear response ensconced in a weakly nonlinear matrix. The density of the clusters decreases with thickness and their presence was not identified in thin films. This behavior illustrates that the domain wall motion responsible for the nonlinear properties is the result of the collective behavior on the micron scale, comparable to the length scale for correlated switching in similar films (24). This model is drastically different from classical descriptions that consider motion of noninteracting domain walls in a disordered potential (11, 18, 19). Attempts to model more complex and realistic cases have been reported only recently and are still limited in scope (7).

These observed dynamics can be attributed to several possible mechanisms. First, as the film thickness increases, the sampling volume from the BE-PFM increases from ∼0.025 μm³ in the 1 μm thick film to ∼1.1 μm³ in the 4 μm thick film, as shown in Table 1. When a top electrode is utilized (so that long-range domain interactions are more readily probed) (24) the density of sites with high domain wall mobilities can be on the order of 1 per μm³ for this family of films, and thus that the response becomes homogeneous on this volume scale. This density would account for the apparent homogeneity of the measured nonlinearity in the 4 μm thick film. However, it is clear that volume alone is not a complete descriptor, because there is a clear evolution in the nonlinearity as a function of film thickness in large area (large volume) dielectric measurements. According to the theories developed for ferromagnetic materials (8), the reduction in α with decreasing thickness is likely to be due to an increase in either the concentration of defect centers or in their pinning strength, or both.

In analyzing the thickness effect of nonlinearity and cluster formation, we note that virtually all ferroelectrics illustrate a characteristic dielectric relaxation time scale of τ ∼ 1 ns, (37 and 40) attributed to domain wall vibration. The natural speed of elastic interactions is limited by the speed of sound, which is approximately 4.35 - 4.8 km/s in hard PZT ceramics (38). Hence, the characteristic interaction range affected by a moving domain wall is τc_l ∼ 4–5 μm, i.e., close to the experimentally observed cluster size (∼0.5–2 μm). A schematic illustration of this behavior is given in Fig. 5. In films (35) and ferroelectric ceramics (39), the domain configurations are governed by the system energetics, yielding a characteristic domain size. The destabilization and motion of one wall in an external field, should thus impose an effective pressure on walls within a given interaction volume, and hence increases the probability of their simultaneous displacements, leading to the domino effect (40). The characteristic length scale of this interaction is expected to be proportional to the acoustic wavelength, and in fact the latter is close both to the critical thickness for both substantial nonlinearity and observed cluster sizes. This work provides a measurement of the scale of such cascades in ferroelectrics in subswitching conditions. The results demonstrate that the correlated domain wall motion cannot be treated as though it were confined to a single grain.

Fig. 5.

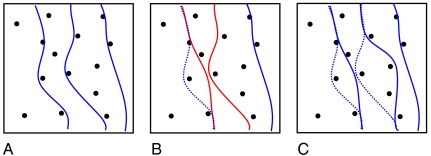
Proposed model for cooperative interactions in the film. Increase of the external field from initial state (A) leads to the destabilization of nearby walls (B) and their cooperative displacement. The lines are domain walls, the points are pinning centers. Note that the figure does not imply that the affected walls must be near neighbors; the schematic shows the evolution of the avalanche only, not the specific wall configuration.

Hence, the nonlinearity is a function of the dynamic coupling between domain walls and includes long-range cooperative interactions, reminiscent of dynamic heterogeneity in disordered materials and liquids (41) and avalanche-type dynamics observed in modeling of Ising systems or Barkhausen noise (42). Note that reminiscent behavior—transition from averaged to single-cluster mediated dynamics was also observed in metal-insulator transitions using nanopatterned devices (43 and 44). In that case as well the cross over was observed at length scales well above those expected for phase-separated nanoregion. Hence, results obtained in this study can be applicable to a much broader range of materials systems. Further work is required to understand the factors governing the volume of the film participating in each avalanche event.

Finally, we note that ferroelectric materials are ideal model systems for more complex metal-insulator transitions, ferromagnetic and ferroelastic systems, and structural glasses. In ferroelectrics, the field-induced polarization dynamics is reversible and can be readily probed on the nanoscale through electromechanical responses. In comparison, nanoscale probing of dynamic magnetic phenomena is a challenge, while dynamic processes in structural glasses and other systems are often irreversible. Beyond ferroics, the universality of weak-field hysteretic behavior can provide insight into other areas of physics, e.g., percolation phenomena and dynamics of water-gas interfaces in porous media.

Materials and Methods

Measurements were performed on a 0.53, 1.09, 2.06, and 4.04 μm thick chemical solution deposited lead zirconate titanate (PZT 52/48) polycrystalline PZT sample with sputter-deposited Pt top electrodes. The processing of the films is described elsewhere (45 and 46). The film was polycrystalline with some degree of {100} and {111} orientation. The dielectric constants were on the order of 1,000–1,400 (depending on thickness), with loss tangents of about 3%. The surface grain size was on the order of 50 nm, and the microstructure is columnar (i.e., most grains span the film thickness).

Band excitation PFM was implemented on a commercial Asylum MFP-3D system with an additional lock-in amplifier (Stanford Research Systems SRS844) and function generators (SRS DS 345). The electric field is directed through the film thickness, between top and bottom electrodes. For measurements made on electroded areas, the bottom electrode was grounded, while the tip was floating, and served as a passive strain sensor. The electrodes were connected through wire bonds to an external power source. Pt coated tips (Olympus Electrilever) were used to measure the piezoelectric response of the ferroelectric film in contact mode. A high voltage amplifier module (Asylum Research HVA220) was used to enable bias voltages greater than 10 V. A LabView-Matlab code developed in-house and synchronized with the controller through transistor - transistor logic (TTL) channel was used for generating the probing signal and for data acquisition and analysis. For bare surfaces, the bias was applied directly through the SPM probe, with the bottom electrode again held at ground. The spatial grid was adjusted depending on experimental conditions and image stability, but generally a grid size of ∼50–160 nm was used. The amplitude of V_ac was calibrated to account for the Resistance-capacitance RC-behavior of the circuit. The variation of resonance frequency was determined as the distribution of resonance frequencies averaged over voltage, 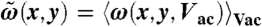. The voltage dependence of resonance frequency was determined as the distribution of .