Exotic behavior and crystal structures of calcium under pressure

Abstract

Experimental studies established that calcium undergoes several counterintuitive transitions under pressure: fcc → bcc → simple cubic → Ca-IV → Ca-V, and becomes a good superconductor in the simple cubic and higher-pressure phases. Here, using ab initio evolutionary simulations, we explore the behavior of Ca under pressure and find a number of new phases. Our structural sequence differs from the traditional picture for Ca, but is similar to that for Sr. The β-tin (I4₁/amd) structure, rather than simple cubic, is predicted to be the theoretical ground state at 0 K and 33–71 GPa. This structure can be represented as a large distortion of the simple cubic structure, just as the higher-pressure phases stable between 71 and 134 GPa. The structure of Ca-V, stable above 134 GPa, is a complex host-guest structure. According to our calculations, the predicted phases are superconductors with Tc increasing under pressure and reaching approximately 20 K at 120 GPa, in good agreement with experiment.

Calcium exhibits a nontrivial and somewhat mysterious behavior under pressure. At 19.5 GPa it transforms from the fcc to the body-centered cubic (bcc) structure, and then, at 32 GPa, to the simple cubic (sc) structure (1, 2). Such a sequence of transitions is exactly opposite to normal intuition, as it is accompanied by a decrease of coordination numbers (12 → 8 → 6) and sphere packing efficiency (0.74 → 0.68 → 0.52). Good metal at ambient conditions, fcc-Ca shows increasing electrical resistivity under pressure (3–5). Even more intriguingly, the resistivity of the fcc phase at and just below this maximum has negative temperature derivative, characteristic of the nonmetallic (semiconducting) state, consistent with a small band gap found in ab initio calculations (6) in the same pressure range. Such demetallization under pressure is counterintuitive, because at sufficiently high pressure all materials must become free-electron metals, the expected behavior is an increasing tendency to the free-electron limit under pressure (see ref. 7 for a discussion). Contrary to these expectations, strong departure from the free-electron state under pressure has also been found for sodium (8, 9) and lithium (10–12) at megabar pressures.

Ab initio calculations (13) confirmed the fcc → bcc → sc structure sequence and yielded reasonably accurate values for the transition pressures. However, the sc phase encounters problems: It cannot be explained within the Hume–Rothery approach (Fermi surface–Brillouin zone interaction) unless one assumes 4 valence electrons per atom (14), and, even more seriously, lattice dynamics calculations (15, 16) showed that it is dynamically unstable, and although this dynamical instability may be lifted by anharmonic effects (16), other structures (see below) have much lower enthalpies. This seeming contradiction with experiments that initially showed a perfect sc structure (1, 2, 17) is largely resolved by recent experimental data showing that the sc structure in reality is indeed distorted and that the observed low-temperature behavior of calcium is likely affected by metastability.

Remarkably, Ca is a superconductor above 50 GPa (18), and its Tc rapidly (and with an increasing slope) soars with pressure, reaching 25 K at 161 GPa (19)—the highest Tc value found in any element. Whereas the sc phase is already superconducting, the most intriguing high Tc values are found in the stability fields of other phases; a recent x-ray diffraction study (2) found two further phases beyond sc—Ca-IV (stable at 113–139 GPa) and Ca-V (stable above 139 GPa). First structural models, proposed in (20), gave a structure possessing the P4₃2₁2 space group and 8 atoms in the unit cell (here denoted as P4₃2₁2-8) for Ca-IV and Cmca-8 for Ca-V. The P4₃2₁2-8 structure, proposed for Ca-IV, has indeed been confirmed experimentally (21). A very recent theoretical study made a different proposition—a Pnma-4 structure for Ca-IV and the same Cmca-8 structure for Ca-V (22). However, using evolutionary global optimization techniques, for Ca-V we found (see below) a self-hosting structure, more stable than the Cmca-8 structure proposed in (20), and providing an excellent match to experimental diffraction data and observed stability field of Ca-V.

Here we predict and examine unique crystal structures and address the counterintuitive behavior of calcium under pressure—the apparent decrease of its packing efficiency, transition into the semiconducting state at moderate pressures, link between structure and superconductivity, stability of self-hosting structures under pressure, and unusually high Tc values observed for calcium. All these aspects make calcium one of the most anomalous and interesting elements in the periodic table.

Remarks on the “Simplicity” of Calcium

Before discussing the new structures predicted here, let us briefly consider two aspects of nontrivial behavior of calcium at moderate pressures (< 50–100 GPa): (i) the apparent opening of the band gap below the fcc → bcc transition (19.5 GPa), and (ii) the anomalous fcc → bcc → sc transition sequence.

With an even number (two) of valence electrons in the primitive cell, calcium could be an insulator—it is a metal only due to band overlap (or, in real-space language, due to the spatial extent of the wavefunctions being much larger than the shortest interatomic distance). Very compressible, the atomic volume of calcium shrinks by a factor of 2.4 on going from the atmospheric pressure to 50 GPa (see theoretical and experimental equations of state in ref. 6), inducing large changes in the electronic structure. Whereas in the isolated calcium atom only s- and p-orbitals are occupied (it is the last element in the periodic table without d-electrons), d-orbitals are low-energy and can be populated under pressure—indeed, theory predicts an s → d transition in calcium and all heavy alkali earth and alkali metals (6, 13, 23). Compression has a different effect on the energies of different orbitals (or bands), and generally higher-l orbitals that are unoccupied in the free atom become populated under pressure. In calcium’s group-I neighbor, potassium, d-electrons become dominant at the Fermi level already at approximately 10 GPa (e.g., ref. 23)—i.e., slightly earlier than in calcium. The s → d transition greatly affects reactivity of potassium and may enable it to alloy with Fe in the Earth’s core (24) (this is geochemically very important, as ⁴⁰K is an important source of radiogenic heat in the Earth and the only possible radioactive element in the core); similarly large changes in reactivity may also occur in calcium.

Given that the ionic radius of Ca²⁺ is 1.0 Å (which is an effective core radius) and the 4s-orbital radius is 1.69 Å, from the equation of state of calcium we deduce that the (interatomic) core-valence overlap is large at all pressures above 30 GPa, and core–core overlap becomes significant at 300 GPa. Overlaps of valence and core orbitals of one atom with core orbitals of another atom can lead to extremely interesting physical effects, such as expulsion of valence electrons into the “empty” space of the structure leading to the formation of strong nonnuclear charge maxima and possible demetallization (8, 12, 25).

The degree of localization of these electron pairs increases with pressure, which explains the observed increase of the resistivity and semiconducting behavior of fcc calcium under pressure. This is seen also in a very non-free-electron-like electronic density of states (Fig. 1), showing a small band gap (approximately 0.1 eV) at 18 GPa. The increase of the nonnuclear density maxima under pressure is correlated with a rapid increase of d-orbital occupancy n_d: projecting wavefunctions inside atom-centered spheres of 2.0 Å radius, we find n_d = 0.36 at 1 atm and n_d = 0.83 at 18 GPa (see also refs. 6, 13, 26). Across all alkali earth metals n_d > 0.92 appears to be a good phenomenological criterion for the onset of superconductivity (26).

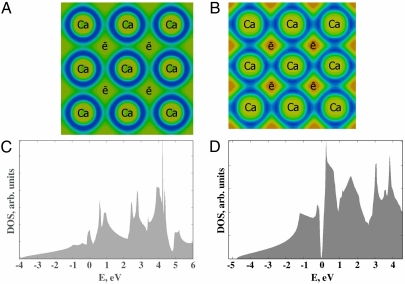
Fig. 1.

Valence ELF (including semicore 3s and 3p states) and density of states of fcc-Ca at (A, C) 1 atm and 18 GPa (B, D). ELF plots (A, B): (100) sections through positions of Ca atoms and nonnuclear electron density maxima (“e”). Minimum/maximum ELF values are 0.05/0.73 in (A) and 0.08/0.84 in (B), with contour spacing of 0.05. Note ELF peaks in the core regions and in the interstices (valence electrons expelled from the core regions); at 18 GPa interstitial valence electrons are more localized than semicore electrons. In DOS plots, energies are relative to the Fermi level; note the narrow band gap at 18 GPa.

Fig. 1 shows an unusual distribution of the valence electron localization function (ELF) (27) in fcc-Ca at 1 atm: it has maxima not only at the nuclei, but also in the octahedral voids between them (thus, ELF maxima form a NaCl-type structure). These maxima become much more pronounced on increasing pressure, and their origin can be traced to the exclusionary effect of the core electrons on the valence electrons, first predicted to occur in lithium (12, 25) and sodium (8, 9).

The fcc → bcc → sc structural sequence is less anomalous than often thought. The sphere packing efficiencies (i.e., the ratio of the volume occupied by touching atomic spheres to the total volume) of the fcc, bcc, and sc structures are 74%, 68%, and 52%, respectively. If atoms were of the same size (or bonds of the same length) in all structures, fcc would be the densest. However, in reality the bcc and sc structures are denser (at transition pressures) than fcc because of the shorter interatomic distances. Greater density of the bcc and sc structures has often been explained by the s → d electronic transition; this is not necessary and even incorrect: indeed, magnesium (not undergoing any electronic transitions) has a similar transition (hcp → bcc) at 50 GPa (28). Generally, lower-coordination structures can be denser than fcc or hcp even in the absence of electronic transitions, because lower coordination corresponds to shorter bonds. Indeed, atomic sizes and bond lengths R depend on the coordination number ν (29)

[1]

where R and R₀ are expressed in Å, R₀ is a bond-specific constant and b = 0.37 Å. Using [1], the ratio of atomic volumes in the fcc and bcc structures at 1 atm is

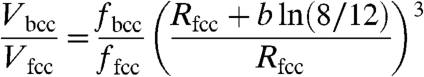[2]

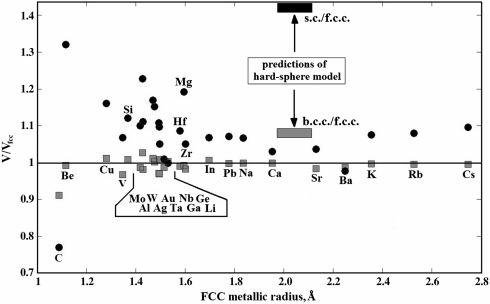
where f are the packing efficiencies, and R_fcc is the bond length in the fcc structure. This expression does indeed show that in very many cases, without any need for electronic transitions, the bcc structure can be denser than fcc or hcp at 1 atm, and more stable under pressure. Whereas the hard-sphere model fails completely (Fig. 2), model [2] is more consistent with the computed atomic volumes, but still does not give quantitative agreement (to achieve which one might need a more complicated model, including higher coordination spheres and delocalized electrons). Fig. 2 shows that in most cases bcc and fcc structures have similar densities, with bcc being slightly denser. Thus, the fcc → bcc transition is not an anomaly. On the other hand, the sc structure is usually much less dense and is denser than fcc or bcc only for a handful of elements (Li, C, Ba). Note that for calcium at 1 atm the sc structure is slightly less dense than fcc (Fig. 2) and becomes denser under pressure due to its higher compressibility.

Fig. 2.

Atomic volumes in the bcc (Gray Squares) and sc (Black Circles) phases, relative to those in the fcc structure. In the horizontal axis the elements are arranged by the metallic radius in the fcc phase. All results are based on present GGA calculations. Whereas bcc phases have similar densities to fcc (and for most elements are even slightly denser), hypothetical sc phases are usually less dense, except C, Li and Ba. It is clear that predictions of the hard-sphere model are inconsistent with ab initio calculations.

Results of Evolutionary Simulations: New Phases of Calcium

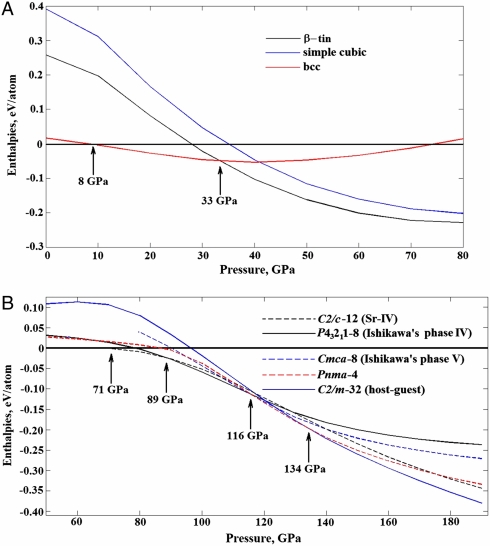
Evolutionary simulations at 20 GPa and 30 GPa found the bcc structure to be stable, in agreement with experiment (1, 2, 17). The lowest-enthalpy structure found at 40 GPa and 70 GPa is, however, not sc, but an I4₁/amd structure (β-tin type), which has recently been reported in theoretical studies (30, 31) and can be described as a strongly distorted sc structure. Fig. 3 depicts how the β-tin structure is favored against sc and becomes the theoretical ground state above 33 GPa, exactly the value of pressure at which very recent experiments found that fcc and bcc phases are no longer stable (17). Previous theoretical works (15, 16, 32) that found sc structure to be dynamically unstable due to strong nestings in its Fermi surface. At 40 GPa the I4₁/amd phase is slightly (0.9%) less dense than the sc structure, but significantly (52 meV/atom) more favorable.

Fig. 3.

(A) Enthalpies of the bcc, sc, and I4₁/amd (β-tin phase) structures (relative to fcc). (B) Enthalpies of several competitive phases (relative to the β-tin phase). A few other structures [C2/c-32 (host–guest), C2/c-24, I4/mcm-32 (host–guest)], very nearly degenerate with the ground states, are not shown for clarity.

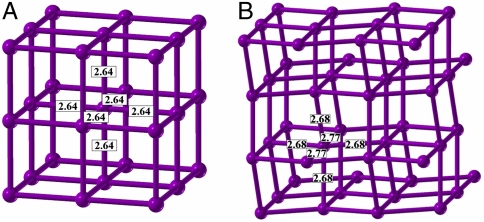
This enthalpy difference between β-tin and sc is not expected to be overcome by the zero point energy (ZPE) considering that in our calculations at 50 GPa the ZPE in the latter phase is just 5 meV/atom lower. As shown in Fig. 4, the coordination of Ca atoms is octahedral (as in the sc phase), but distorted—with 4 nearest neighbors at 2.68 Å, and 2 neighbors at 2.77 Å, suggesting a Jahn–Teller or Peierls distortion (at this pressure, Ca atoms have an electronic configuration close to s^0.5p^0.5d¹, which is expected to show the Jahn–Teller effect). This distortion opens a pseudogap, which decreases the density of states at the Fermi level and lowers the electronic kinetic energy of the preferred I4₁/amd phase over the sc. The same structure type is known for other elements—Sn, and high-pressure forms of Ge, Si. Most interestingly, it is adopted by the phase III of strontium in the pressure range 26–35 GPa (33, 34).

Fig. 4.

Structures of (A) simple cubic, (B) β-tin-type tetragonal distortion (I4₁/amd) of the simple cubic structure for Ca at 40 GPa. The I4₁/amd structure is significantly more favorable. Bond lengths are indicated.

At 71 GPa the β-tin structure distorts into a C2/c-12 (Sr-IV) structure with 12 atoms in the conventional unit cell, and this structure remains stable up to 89 GPa. C2/c-12 (Sr-IV) structure is a helical distortion of the β-tin structure with a triplication of the unit cell size. The same helical distortion of the β-tin structure was reported in Sr-IV phase (ref. 34, where the space group, however, was misdetermined as Ia, whereas a closer inspection shows it to be C2/c). Up to this point, the observed (33) sequence of phase transitions in strontium and the predicted sequence in calcium are identical: fcc → bcc → I4₁/amd → C2/c-12 (Sr-IV). The next higher-pressure phase of strontium, Sr-V, is an incommensurate host–guest structure. We do find such a structure also for calcium, but preceded by two other phases.

On increasing pressure to approximately 100 GPa, we find extremely distorted versions of the simple cubic structure. One of these is a metastable (but very competitive) Cmca-16 structure, which can be described as a frustrated structure intermediate between sc and hexagonal close-packed structures. Fig. 3 shows that in the pressure range 100–130 GPa there are several energetically extremely close structures, and the most stable structure at 89–116 GPa is the P4₃2₁2 - 8 structure proposed by Ishikawa et al. (20), this structure also can be derived from sc by a large distortion and has recently been experimentally confirmed for Ca-IV phase (25). The Pnma-4 structure is the stable phase at higher pressures, 116–134 GPa, and is the last stable structure related to sc. The structure proposed in (24) for Ca-V (also belonging to the family of sc-derived structures) is never stable at T = 0 K.

The structure we found for Ca-V is a host–guest structure, similar to Sr-V and Ba-IV (35) (Fig. 5). This result is similar to that recently reported by Arapan et al. (36), who found this structure by educated guess based on a possible analogy with Sr. Such phases for Sr and Ba are incommensurate—since incommensurate structures cannot be predicted within strictly imposed periodic boundary conditions, we can only produce their commensurate approximants. In fact, our evolutionary simulations yielded several energetically nearly degenerate and geometrically very similar structures, such as C2/m-32 (host–guest) (the most stable structure) and I4/mcm-32 (host–guest) and C2/c-32 (host–guest) structures. Specific details on these structures are available in SI Text. This near degeneracy suggests that the system is frustrated by competing interactions—a common reason behind incommensurate phases. In experiments (2), Ca-V was seen coexisting with Ca-IV above 139 GPa. This metastable coexistence implies a large energy barrier for the phase transition, likely due to large structural differences between Ca-IV and Ca-V. This is consistent with our results, whereas in (20) both proposed structures are rather similar derivatives of the sc structure. We also note that because Ca-IV is related to the sc structure, finding it with a neighborhood search method (metadynamics, starting from the sc structure, was used in ref. 20) is very efficient, whereas Ca-V would be more challenging to neighborhood algorithms and a fully global search based on evolutionary algorithms should be preferred.

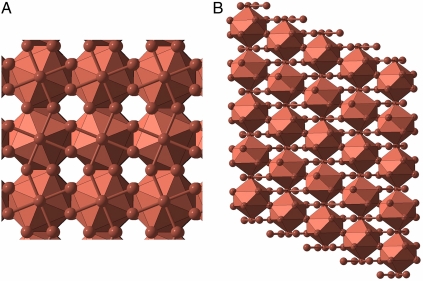
Fig. 5.

C2/m-32 (host–guest) structure at 150 GPa. 10-coordinate polyhedra (bicapped square antiprisms) are shown: (A) view along the pseudotetragonal axis, (B) side view showing packing of the polyhedra (it can also be seen that the genuine symmetry of this periodic approximant is lower than tetragonal). This structure can be described as self-hosting, the host structure makes a framework in which guest atoms occupy 10-coordinate sites. Other structures are illustrated in SI Text.

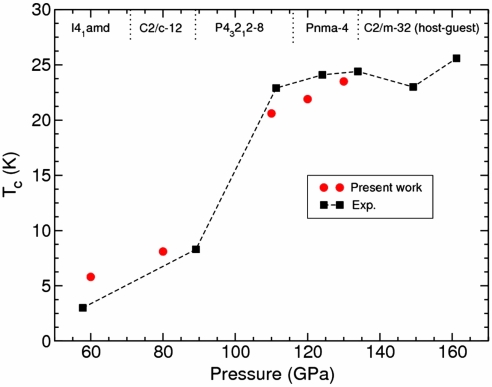
Interestingly, all distortions of the simple cubic structure (β-tin, C2/c-12 (Sr-IV), P4₃2₁2-8 and Pnma-4), predicted to be stable below 134 GPa, have a highly coupled soft mode associated to the distortion as a major contributor to the observed superconductivity (SI Text). For instance, the maximum phonon linewidth for the β-tin structure at 60 GPa corresponds to a strongly softened optical mode around the Γ-point. It is worth noting that such mode corresponds to the unstable anharmonic mode at M symmetry point (20) in the sc phase. Due to a Peierls distortion this mode is stabilized in the β-tin phase and becomes the one with largest partial contribution to the electron–phonon coupling constant λ. Additionally, Fig. 6 displays our calculated superconducting transition temperatures for these structures at 60, 80, 110, 120, and 130 GPa. The calculations closely agree with the experimental data (19) and reflect the pressure-induced enhancement of Tc, reaching 23.5 K at 130 GPa, supporting the validity of the proposed structures.

Fig. 6.

Comparison of the calculated Tc with the experimental values obtained by Yabuuchi et al. (19). The calculated Tc values show good agreement with experimental data across the whole pressure range.

Discussion

We have predicted a number of different phases of calcium, one of the most interesting and enigmatic elements in the periodic system—an element that displays nearly all of the puzzling phenomena recently discovered in the elements (high-pressure superconductivity, host-guest structures, unexpected phase transformations accompanied by electronic transitions, and a decrease of coordination numbers and packing efficiencies). The sequence of structures found here differs significantly from the traditional picture (33), but is very similar to the one known for strontium, the closest analogue of calcium. The main difference is that instead of a single sc phase we find a family of sc-derived structures, which are energetically more favorable. It was recently proposed (16, 30) that the dynamical instability of the sc structure can be overcome by anharmonic effects even at quite low temperatures. This does not automatically imply thermodynamic stability and we suggest a reconsideration of the experimental evidence for the sc structure and search for additional phases predicted here at T = 0 K.

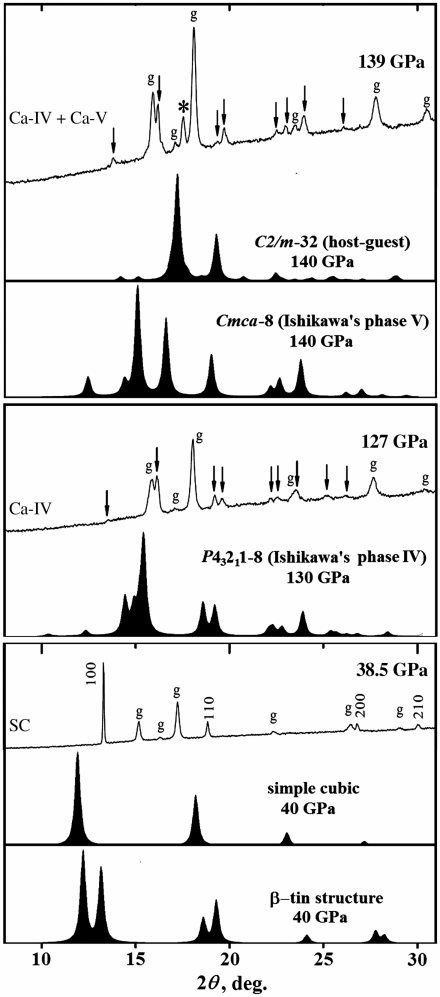
The similarity of the several structures stable at 33–134 GPa [β-tin, C2/c-12 (Sr-IV), P4₃2₁2-8, Pnma-4] with the sc structure is evident not only from their appearance, but also from their x-ray diffraction profiles (Fig. 7) that bear great similarity to the diffraction pattern of the sc structure, but have split peaks due to lower symmetries. Because some extra peaks can become invisible due to possible texturing of the samples used in experiments, the β-tin structure could explain the experimental diffraction patterns ascribed to the simple cubic structure. However, recent single crystal x-ray diffraction experiements imply that slight distortions are present in the sc structure, and that the β-tin structure may be a true ground state, not seen in low-temperature experiments due to kinetic problems. We also note that our host–guest structure provides a better explanation of experimental data for the Ca-V phase than the model proposed in (20). Our model has a single strong peak that corresponds to the extra peak found in (2), all other peaks are explained by Ca-IV.

Fig. 7.

Summary of x-ray diffraction patterns. λ = 0.6198 Å. Structures I4/mcm-32 (host–guest) and C2/c-32 (host–guest) have very similar diffraction patterns to C2/m-32 (host–guest) shown here. The absence of several reflections, predicted for the β-tin structure at 40 GPa, in the experimental diffraction pattern, might be explained by preferred orientation with a unique [101] or [111] direction. The experimental diffraction pattern at 139 GPa is explained (as proposed in ref. 2) by a mixture of phases IV and V.

As discussed above, fcc-Ca possesses a number of chemical and physical anomalies related to the strong electron localization in the interstitial space. In all the higher-pressure phases the degree of interstitial electron localization progressively decreases, and can be considered negligible for all phases beyond the β-tin phase (pressures > 71 GPa). We showed that the fcc → bcc transition is a normal phenomenon in the elements under pressure, due to the usually higher density of the bcc structure. Further transitions to the β-tin (or sc) derivative structures are more difficult to explain in simple terms. We note, however, that (i) several elements adopt such structures under pressure, (ii) the pressure of the bcc → sc-family transition corresponds to a large occupancy of the 3d-orbitals and a large core-valence interaction on neighboring atoms, and (iii) that the β-tin structure can be stabilized by the Jahn–Teller distortion enabled by the s → d electronic transition in calcium. The large number of these derivative structures and their frustrated topologies and similar enthalpies suggest the presence of competing factors—namely, bonding (which favors simple and symmetric structures) and density (the increase of which necessitates electronic transitions). Finally, at 134 GPa, an entirely different type of structures takes over—host–guest structures unrelated to the sc structure and displaying another type of geometric frustration related to the incommensurate modulation. The precise origins of such host–guest structures are still unclear: Orbital characters of both host and guest calcium atoms are very similar and the material appears to be a good metal without any strong nonnuclear density maxima. The extent of the stability of the host–guest structure is not known yet, but both from present theory and experiment (19) it appears to be very large (from 134 GPa to at least 161 GPa). Our simulations show that the hcp structure [which succeeds the host–guest one for Ba (33) on increasing pressure] is stable only above 564 GPa. At such pressures the s → d transition is completed (as in the very similar double-hcp structures of K, Rb, Cs (25), which succeed the complex incommensurate host–guest structures in these elements) and core–core (not just core–valence) overlap is significant. Complex behavior of calcium at 32–564 GPa is a consequence of (i) competition of bonding (energetic) and density factors, (ii) gradual s → d transition (related to compression and core-valence overlaps) and two effects related to it—the Jahn–Teller distortion and s-d hybridization that gives rise to directional bonding. At pressures of stability of hcp-Ca (> 564 GPa), the PV term (> 23.4 eV) far exceeds bond energies, and electronic kinetic energy is significantly greater than potential energy (this favors electronic delocalization and destruction of directional bonding and leads to a simple and symmetric hcp structure).

Methods

All calculations presented here are based on density functional theory within the generalised gradient approximation (37) and using the all-electron projector-augmented wave (PAW) method (38). Structure prediction calculations were done using an evolutionary algorithm developed by Oganov and Glass and implemented in the USPEX code (39–41), whereas lattice dynamics and superconducting properties were studied using density-functional perturbation theory (DFPT) (42) using the Quantum-ESPRESSO package (43).

Detailed evolutionary simulations were performed at 70, 100, 130, and 160 GPa with system sizes of 3, 4, 6, 8, 9, 12, and 16 atoms in the unit cell. Exploratory runs with 8 atoms/cell were also done at 20, 30, and 40 GPa, and with 16 atoms/cell at 300 and 600 GPa. Each generation contained between 10 and 40 structures (increasing with the system size), and the first generation was always produced randomly. All structures were locally optimized using the VASP code (44). In a typical evolutionary run, the lowest-enthalpy 60% of each generation were used to produce the next generation (70–80% of these were produced by heredity, and the remaining 20–30% by lattice mutation, and in addition to that the lowest-enthalpy structure survived into the next generation). Gaussian strength of lattice mutation (40) was set to 0.5–0.55. Local optimizations performed during structure search, were done with the conjugate gradients method and were stopped when the enthalpy changes became smaller than 1 meV/cell. The PAW potential used in these calculations has the (Ne) core (radius 2.3 a.u.). We used the plane wave cutoff of 350 eV, which proved to give excellent convergence of the stress tensor and energy differences. The Brillouin zone was sampled with Monkhorst–Pack meshes (45) of 2π × 0.09 Å^-1 resolution, and the Methfessel–Paxton electronic smearing scheme (46) with the electronic temperature of 0.1 eV. These settings proved to give excellent convergence for the stress tensor and energy differences between structures. Analyzing the results of evolutionary simulations, we selected a number of distinct lowest-enthalpy structures and optimized their structures as a function of pressure using VASP and very dense (2π × 0.03 Å^-1 resolution) k-points meshes.

Electron–phonon coupling calculations were performed using DFPT, with an ultrasoft pseudopotential (47) with a [Ne] core. Convergence tests showed that Monkhorst–Park k-point meshes of 16 × 16 × 16, 12 × 6 × 6, 9 × 9 × 3 and 8 × 8 × 8 for the I4₁/amd, C2/c-12 (Sr-IV), P4₃2₁2-8 and Pnma-4 structures, respectively, were adequate for Brillouin zone integrations. The transition temperatures to the superconducting states were calculated making use of the Allen–Dynes modified McMillan equation (48) where the typical value of μ^∗ = 0.1 was taken for the Coulomb pseudopotential.