Probing myosin structural conformation in vivo by second-harmonic generation microscopy

Abstract

Understanding of complex biological processes requires knowledge of molecular structures and measurement of their dynamics in vivo. The collective chemomechanical action of myosin molecules (the molecular motors) in the muscle sarcomere represents a paradigmatic example in this respect. Here, we describe a label-free imaging method sensitive to protein conformation in vivo. We employed the order-based contrast enhancement by second-harmonic generation (SHG) for the functional imaging of muscle cells. We found that SHG polarization anisotropy (SPA) measurements report on the structural state of the actomyosin motors, with significant sensitivity to the conformation of myosin. In fact, each physiological/biochemical state we probed (relaxed, rigor, isometric contraction) produced a distinct value of polarization anisotropy. Employing a full reconstruction of the contributing elementary SHG emitters in the actomyosin motor array at atomic scale, we provide a molecular interpretation of the SPA measurements in terms of myosin conformations. We applied this method to the discrimination between attached and detached myosin heads in an isometrically contracting intact fiber. Our observations indicate that isometrically contracting muscle sustains its tetanic force by steady-state commitment of 30% of myosin heads. Applying SPA and molecular structure modeling to the imaging of unstained living tissues provides the basis for a generation of imaging and diagnostic tools capable of probing molecular structures and dynamics in vivo.

The description of molecular structural dynamics occurring in a living cell and determining its biology requires a variety of techniques to encompass the spatial and temporal scales involved. In fact, crystallography provides static structures with atomic resolution, whereas complementary techniques are needed to follow structural dynamics in the cellular context. The collective chemomechanical action of myosin motors in the sarcomere, the structural unit of striated muscle, represents a classic example in this respect. Knowledge of the atomic structures of myosin (1) and actin (2), combined with information from cryo-EM (3), electron paramagnetic resonance (EPR) (4), x-ray diffraction (5), and fluorescence polarization (6) has led to a structural description of the chemomechanical energy conversion in terms of the lever-arm hypothesis of the working stroke in the myosin motor (7, 8).

Here, we describe a label-free optical imaging method for probing protein conformation in vivo. We employed second-harmonic generation (SHG) for the functional imaging of the muscle sarcomere and we demonstrated the sensitivity of this technique to the structural conformation of myosin motors in different physiological/biochemical states. SHG is a frequency-doubling nonlinear optical process taking place in hyperpolarizable materials, including some biological samples (9–11). Recently, a strong SHG signal has been detected from the myosin-based A band of unstained muscle cells and myofibrils. The signal is entirely and exclusively dependent on the presence of myosin thick filaments: Biochemical extraction of myosin abolishes SHG signal, whereas bright SHG bands are still visible at sarcomere lengths entailing no overlap between myosin and actin (12, 13). These observations opened the way for the application of label-free muscle tissue imaging in diagnostics (14).

SHG derives from a coherent sum over all contributing elementary emitters (named hyper-Rayleigh scatterers, HRSs), and is sensitive to the orientation distribution of the HRSs within the excitation volume. Such orientation distribution can be probed by measuring SHG intensity (I_SHG) at different laser polarizations, i.e., by performing SHG polarization anisotropy (SPA) measurements. The use of SPA for the measurement of structural conformation of the myosin motor relies critically on the geometrical distribution of the HRSs within the myosin molecule. In fact, this protein is composed of a static part (the light meromyosin (LMM), that lies on the backbone of the myosin filament) and a dynamic part [the heavy meromyosin (HMM), that extends from the myosin filament to attach to actin]. The latter is further divided into a globular S1 subdomain (the myosin head, which is the molecular motor responsible for coupling ATP hydrolysis and actin binding to the performance of mechanical work) and a rod-like S2 subdomain (a coiled coil joining S1 to LMM). Previous measurements on myofibrils had led to the conclusion that SHG is dominated by the static portion of myosin and it is, therefore, not sensitive to the orientation of the myosin S1 heads (13). Here, we demonstrate that SPA is responsive to physiological/biochemical states characterized by different HMM conformations and, thus, records the structural dynamics of the motor. On the general ground of the origin of SHG from peptides and proteins, studies of SHG from melittin and synthetic oligopeptides led to identify the C-N pair of the peptide bond as the HRS within proteins (15, 16). We applied this finding to the molecular interpretation of SPA from complex biological materials, such as collagen and muscle. Specifically, combining SPA measurements with simulations based on an all-atom model of the thick filament enabled us to obtain information on the molecular conformation of myosin motors in different physiological states.

The combination of sensitivity to molecular structure with the peculiar properties of SHG (optical imaging, label-free, three-dimensional micron-scale resolution in deep tissue) provides an opportunity to complement other methods in the effort to bridge the gap between atomic structure and structural dynamics of the myosin motors in the cellular context.

Results

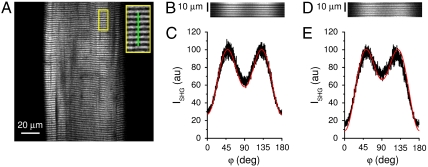
SPA measurements were performed on rabbit demembranated muscle fibers by acquiring I_SHG over a range of laser linear polarizations between 0° and 180° relative to the fiber axis. Full imaging of a fiber segment spanning several sarcomeres (Fig. 1A) requires an acquisition time of ∼1 s. Performing SPA in full imaging mode (2D scan), therefore, is not feasible for physiological studies. In fact, acquiring one full image for each polarization and sampling several polarizations (as needed for SPA) would required several seconds. The measuring time is reduced by switching from a 2D scan to a 1D linear scan performed on a selected line on the sample (Fig. 1A, Inset, green line). In the SPA measurement, the beam is scanned back and forth repeatedly along the selected line, while the laser polarization is rotating at constant angular velocity (see Materials and Methods). With this method, we were able to perform a full SPA measurement in ∼1 s. Fig. 1B shows the SPA raw data obtained on a demembranated fiber from rabbit psoas in rigor (at full overlap between thick and thin filaments; sarcomere length, SL = 2.4 μm): The intensity variation visible along the horizontal axis (i.e., determined by polarization rotation) highlights the sample polarization anisotropy and represents the basis for SPA measurements (Fig. 1C, black curve). According to SHG theory (see Materials and Methods), HRSs distributed with cylindrical symmetry (as in a muscle fiber) give rise to an intensity profile described by

[1]

where φ is the angle between the fiber axis and the laser polarization, and γ is a geometrical factor related to the average angle of HRSs with respect to the fiber axis. The red line in Fig. 1C shows the best fit of Eq. 1 to the experimental data, with γ as a free fit parameter. Repeated measurements on five different rigor fibers yield an average value of γ_rig = 0.68 ± 0.01 (mean ± SD). The same measurement performed on a demembranated relaxed fiber produced the results shown in Fig. 1 D and E. An average of five fibers yields γ_relax = 0.46 ± 0.03. The large difference between γ_rig and γ_relax (t-test: p = 0.0016) indicates that SPA is sensitive to the structural differences between these two states of the myosin motor.

Fig. 1.

SPA in demembranated fiber. (A) SHG image of a single demembranated rabbit psoas fiber in rigor (SL = 2.4 μm). The bright bands in the image correspond to sarcomeric A bands. The inset shows, at 2.5× magnification, the area highlighted in yellow. The green line corresponds to the line scanned for SPA measurement. (B) Rigor fiber line scan raw data, horizontally varying in brightness with changing polarizer angle for 1,000 successive axial 1D scans along the green line in panel A Inset. The data are represented as a kymograph of the scanned line, i.e., the I_SHG from each scan trace is displaced one pixel from the previous scan trace along the horizontal time axis, incrementing from left to right the accumulating array of repeated SHG 1D scans, each scan recording the sarcomeric cross-striation pattern of A and I bands in six axially successive sarcomeres. The temporal horizontal axis is mapped in terms of polarization rotation with the same scale as in C. (C) SPA curve in rigor. Each I_SHG data point (in black) reports the intensity integrated by summing the 100 pixel values that form the corresponding vertical line in B. The red line shows the best fit of Eq. 1 to the data, yielding, as best fit parameter, γ = 0.68. D and E are the same as B and C but measured on a relaxed fiber. The best fit parameter in E is γ = 0.36.

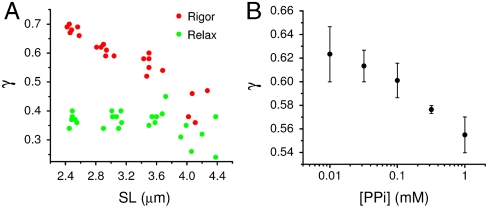
In the rigor state of vertebrate skeletal muscle, all myosin heads bind to actin (17), provided that there is full overlap between thick and thin filaments. The fraction of heads attached to actin can be modulated by changing SL and, thus, the degree of overlap between actin and myosin filaments. Due to the different conformations of attached and detached myosin molecules, γ_rig should, therefore, depend on the degree of overlap (i.e., on SL). Fig. 2A (red circles) shows the dependence of γ_rig on SL in a demembranated rabbit fiber. In the SL range between 2.4 and 3.9 μm, the fraction of cross-bridges that can attach to actin decreases linearly and so does γ_rig. In contrast, in the relaxed state all myosin molecules remain detached regardless of the SL and the γ_relax data (Fig. 2A, green circles) do not change with SL. In a fiber in rigor, the fraction of actin-attached myosin heads can also be modulated biochemically by pyrophosphate (PPi) in a concentration-dependent manner (18). Fig. 2B shows the measurement of γ_rig as a function of [PPi]: The data show that, as the fraction of attached motors diminishes (with increasing [PPi]), γ_rig decreases, in agreement with the behavior of the rigor data in Fig. 2A. These results show the sensitivity of γ to partitioning of myosin heads into a mixture of different states (in this case, attached and detached), offering the possibility of probing the structure of the myosin motor inside a living cell.

Fig. 2.

SPA sensitivity to the fraction of attached myosin cross-bridges. (A) Measured γ versus SL in a representative demembranated rabbit fiber. The data in relaxing solution and in rigor are shown by green and red circles, respectively. (B) Measured γ versus PPi concentration. Each point represents the average ± SD of three fibers.

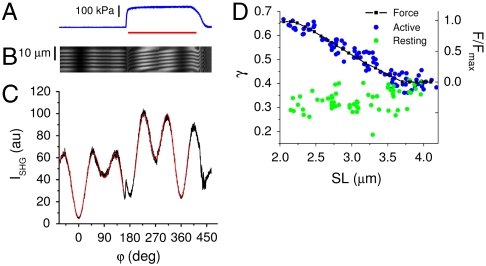
To this end, we performed measurements on single intact muscle fibers. Although rabbit psoas is the generally preferred sample for the preparation of demembranated fibers, isolation of intact fibers requires using frog muscle. We compared directly SPAs at rest and during isometric tetanic contraction at an SL of 2.0–2.2 μm, at which all myosin molecules can bind to actin (Fig. 3 A–C). Fig. 3C shows a clear difference in the SPA profiles between resting (from -70° to 155°) and active (from 200° to 385°). Repeated measurements on seven different fibers yielded a dependence of γ on the physiological state: γ_rest = 0.30 ± 0.03; γ_act = 0.64 ± 0.02. This dependence suggests that SHG is sensitive to the myosin structural changes occurring during force production. In Fig. 3C, the beginning of tetanic stimulation is associated with a discontinuity in the I_SHG trace, reflecting an overall increase of I_SHG during isometric contraction. Absolute intensity values, however, were not used for further analyses, because they are affected by the movement of the sample along the optical axis upon force production.

Fig. 3.

SPA in intact muscle fibers. A–C show force (A, blue line), line scan raw data (B, for detailed explanation see legend of Fig. 1B), and SPA curve (C, black line) measured in a single intact frog fiber at SL = 2.2 μm. The common horizontal axis is mapped in terms of polarization rotation with the scale of C. The red bar in A indicates the period of tetanic stimulation. During tetanic contraction, some sliding of the fiber segment monitored by line scan occurs, giving rise to the tilt of the sarcomere pattern in the kymograph (B). The red lines in C show the best fits of Eq. 1 to the data at rest (from -70° to 155°, yielding as best fit parameter γ = 0.35) and during contraction (from 200° to 385°, yielding as best fit parameter γ = 0.69). (D) Measurements of γ versus SL in seven intact fibers at rest (green circles) and during contraction (blue circles). The black squares and line represent the normalized isometric force (right axis) of a representative fiber.

Similar to what was observed above for rigor in regard to SL, also SPA measured in active contraction is expected to depend on the degree of filaments overlap. Fig. 3D shows the dependence of γ on SL at rest (green circles) and at the plateau of isometric contraction (blue circles). In the SL range between 2.2 and 3.6 μm, the fraction of cross-bridges that can attach to actin decreases linearly, as indicated also by the tetanic isometric force (black squares and line in Fig. 3D). The γ_act data track remarkably the force behavior, confirming that SPA is sensitive to the fraction of attached myosin heads. As such fraction goes to zero at no overlap (SL > 3.6 μm), γ_act approaches γ_rest. The γ_rest values, on the other hand, display a larger dispersion and much smaller dependence on SL, in line with what was observed for γ_relax.

A comparison of the SHG properties of the two species employed in this work (rabbit and frog) was performed by measuring SPA in rigor frog fibers. The results (Fig. S1) demonstrate a similarity in the values of γ at full overlap, as well as in the general dependence of γ on SL.

As described above, γ is related to the angular distribution of the HRSs. It has been shown that the peptide bond C-N pair provides the main charge electron transfer site (i.e., the HRS) within a polypeptide (15, 16). We developed a full calculation of the HRSs distribution within a chosen protein based on its atomic structure. This calculation allows prediction of a protein SHG signal in terms of both intensity and anisotropy (see Materials and Methods). The validity of these calculations is best tested on a simple and static protein, avoiding, in the first instance, the conformational variability of the myosin motor. Collagen is a strong SHG emitter and its SPA has been measured. From collagen atomic structure [1K6F, (19)], we computed γ_col = 1.39. This value is in excellent agreement with the average of published experimental measurements: 1.47 ± 0.10 (20–22). Next, we used this calculation to interpret the muscle fibers SPA measurements in terms of myosin conformation. The atomic structures of myosin and actin, their polymeric organization in filaments, and the overall sarcomeric ultrastructure are known. Based on these data, a model of the actin and myosin filaments with atomic resolution was constructed and the relative I_SHG contributions from actin and myosin were calculated. We found that myosin contribution is three orders of magnitude larger than that of actin, in agreement with the experimental evidence of SHG as myosin based. In light of the physical origin of the SHG signal from C-N peptide bonds, ubiquitous in all proteins, the largely different SHG intensities from the two major muscle proteins allows interesting structural conclusions. A first level of order (required for constructive interference) is achieved by organization of peptide bonds in a helical pattern; however, a second level of order is also necessary, consisting in substantial alignment of the helices themselves in the protein. The α-helices present in G actin display an orientational dispersion leading to the low SHG contribution. Myosin, on the other hand, is endowed with some extraordinarily long α-helices highly aligned in the thick filament.

The results shown in Figs. 2 and 3 demonstrate SPA sensitivity to the conformation of myosin HMM. To assess the molecular origin of this sensitivity, we compared the I_SHG from whole myosin (I_WM) and headless myosin (devoid of S1, I_HL). We found that I_WM/I_HL = 1.1. So, the contributions from LMM and S2 quantitatively dominate myosin SHG. However, the small but not negligible (10% of the total) contribution from S1 can provide SHG with fine sensitivity to the orientation of myosin motors.

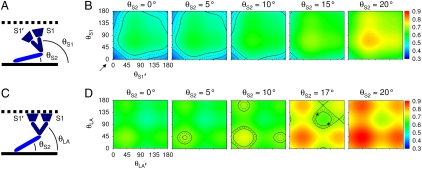
In the calculation of γ, the conformation of myosin was varied with rigid body rotations about selected hinges. For detached heads, the whole S1 was considered as a rigid body and free rotations at the S1-S2 and S2-LMM junctions allowed variations of the θ_S1 and θ_S2 angles, respectively (see Fig. 4A). Fig. 4B shows computed γ as a function of the orientation of each head (θ_S1 and θ_S1^′) of the same myosin molecule for different orientations of S2 (θ_S2) ranging from 0° to 20°; the range of θ_S2 explored in the model was limited to 20° considering geometrical constraints determined by molecular dimensions and the interfilament spacing. It can be noticed that the general features of the landscape are largely determined by θ_S1 and θ_S1^′, whereas increasing tilt of S2 away from the fiber axis has the effect of offsetting the whole landscape toward higher values of γ. Comparing the experimentally measured γ_rest in intact fibers (the value lies at the lower left corner of the first plot in Fig. 4B, as pointed by the black arrow) with the computed γ, it is apparent that only a myosin configuration with both S1 heads and S2 parallel to the fiber axis and pointing toward the Z line is compatible with our SPA result. On the other hand, γ_relax in demembranated fibers (black iso-γ curves in Fig. 4B) can be interpreted in terms of several myosin conformations, all characterized by a tendency of the myosin molecule to recline on the fiber axis. For example, if θ_S2 = 15°, the two S1 heads should be pointing toward the Z line, whereas with θ_S2 = 0°, at least one S1 head should be parallel to the fiber axis.

Fig. 4.

SPA modeling. (A) Scheme of the myosin molecule (S2 in light blue and S1 in dark blue, thick filament as black continuous line) detached from actin (black dotted line). In the scheme, the Z line is on the right side. The two S1 heads are indicated by S1 and S1′. For clarity, only the angle of one head is indicated (θ_S1). (B) Calculation of γ (surface color plot) as a function of θ_S1 and θ_S1^′ for different values of θ_S2. The value of γ_rest on the surface plot is pointed by the arrow. The black iso-γ curves (average, dashed line; one SD interval, solid lines) report the measured value of γ_rest. (C) Scheme of the myosin molecule attached to actin. The catalytic domains (dark blue trapezoids) are rigidly fixed to actin. For clarity, only the lever-arm angle of one head is indicated (θ_LA). (D) Calculation of γ as a function of θ_LA and θ_LA^′ for different values of θ_S2. The black iso-γ curves report the measured value of γ_rig. The asterisks show the geometry of rigor heads according to cryo-EM.

In the simulation of rigor state, due to the attachment of myosin to actin, the catalytic domain of S1 was fixed and only the lever-arm angles (θ_LA and θ_LA^′) were allowed to vary (Fig. 4C). Comparison of the results shown in Fig. 4D with those in Fig. 4B demonstrates that fixing the catalytic domain in the rigor configuration produces an overall increase of γ. This result is supported by the observation that γ increases in physiological or biochemical states associated with head attachment. Similar to what was observed in Fig. 4B, tilting of S2 away from the fiber axis shifts the γ landscape upward. Indeed, for θ_S2 = 0° or θ_S2 = 20° no orientation of lever arm can produce a γ value compatible with our rigor measurement. On the other hand, for θ_S2 ranging from 5° to 17°, several lever-arm orientations give rise to γ values compatible with the measured γ_rig (black iso-γ curves in Fig. 4D). In particular, for θ_S2 = 17°, the lever-arm angles measured in rigor by cryo-EM (23) produce a value of γ consistent with our measurement (see asterisks in Fig. 4D). Although the plots in Fig. 4D cover the full 0–180° surface, it should be recognized that parts of such surface are not physically allowed, due to geometrical constraints imposed by lattice spacing and double-head attachment.

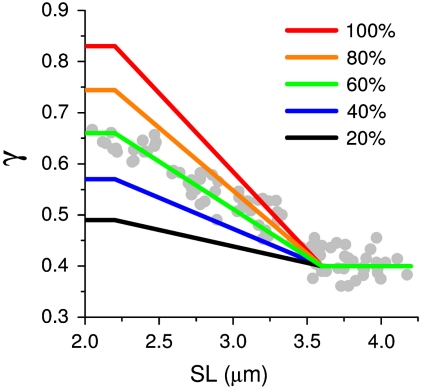
Because γ probes the average angular distribution of all HRSs in the focal volume, it is clear that a SPA measurement does not provide direct access to molecular structure. Moreover, the results shown in Fig. 4 B and D demonstrate that, for a complex molecule such as myosin, even under the simplifying assumption of few rigid body rotations, a value of γ is not uniquely coupled to a single conformation. Nonetheless, if a system is constituted of a mixture of structurally well-known states, SPA can be used to assess the fractional occupancy of these states and, possibly, measure the dynamics of interconversion between them. For example, during isometric contraction, myosin heads adopt a steady-state distribution of different conformations, including those of attached and detached molecules. SHG can probe this distribution, as demonstrated by the dependence of γ on SL (Fig. 3D) in the range from full overlap (maximal number of attached molecules attained) to nonoverlap (no molecule can attach). For the calculation of the fractional occupancy, the γ values associated to detached and attached myosin molecules must be determined. The γ for detached myosin heads is assumed 0.40, based on the measurement of γ_act at SL > 3.7 μm, where there is no overlap between myosin and actin filaments. The γ for actin-attached heads was computed based on the myosin conformation obtained by x-ray diffraction (24), producing a value of 0.83 (see Materials and Methods). Simulating a mixture of attached and detached molecules, with relative weight k and (1 - k), respectively, we found a linear relation between k and computed γ. In this relation, the value of γ_act measured at full-overlap was predicted with k = 0.60 ± 0.05. This value represents the fraction of attached myosin molecules recruited in the overlap region for force generation during isometric contraction. Fig. 5 summarizes the dependence of γ on SL computed for different values of k, displaying the quality of agreement between the measured data (gray circles) and the predicted γ trend for k = 0.60 (green line).

Fig. 5.

Fraction of attached heads during isometric contraction. The gray circles show γ_act versus SL (same as in Fig. 3D). The colored lines show the trends of γ calculated for different fractions of attached myosin molecules, as indicated.

Discussion

In this work, we demonstrated that SPA (quantified by γ) is sensitive to different physiological/biochemical states of muscle: In our measurements, γ spans in a range between 0.30 and 0.68. Low values of γ are attained in physiological states characterized by detached myosin heads (relaxed skinned fiber and intact fiber at rest), whereas high values of γ are attained upon myosin heads attachment to actin (skinned fiber in rigor and intact fiber in isometric contraction). Furthermore, we found that γ probes the proportion between attached and detached heads, as demonstrated by the dependence on SL (Figs. 2A and 3D) and by the measurable effect of PPi-induced detachment (Fig. 2B). These results are in contrast with the previous report that SHG is not sensitive to the orientation of myosin heads (13). Our modeling work shows that, even though the SHG signal is dominated by the rod portion, S1 provides a small but nonnegligible contribution (10% of the total intensity). In fact, quantitative measurements of γ with adequate signal-to-noise ratio (more than 10) reveal that SHG is sensitive to HMM changes induced by physiological and biochemical factors. Plotnikov et al. reported, for scallop myofibrils in rigor, an average HRS angle of 61.2° (13) and associated this value with the 68.6° helical pitch angle of the myosin rods (25, 26) to assert that SHG arises from the rod domains. It should be noted that the boundary values of the γ range we measured in different physiological states correspond to a variation of the average HRS angle (see Materials and Methods) from (59.7 ± 0.2)° in rigor to (68.8 ± 1.0)° at rest. In light of these results, the assimilation of angles done by Plotnikov et al. (13) is misleading. In fact, it is the 68.8° angle we measured at rest that matches remarkably well the 68.6° helical pitch angle of the myosin rod domains, indicating that, in the resting state, indeed, HMM does not bias the signal. On the other hand, the value we measured in rigor is statistically different from that due to the sole contribution of the rod domains, indicating a significant contribution of rigor HMM to the signal.

In the states characterized by detached heads, the rod domains contribution becomes more dominant. However, also in this case, we found a significant difference between γ_rest (intact fibers) and γ_relax (skinned fibers), indicating a structural diversity of detached myosin heads in these two conditions. Fig. 4B provides a possible molecular interpretation of such diversity: The resting HMMs are parallel to the fiber axis and point toward the Z line; the relaxed HMMs may adopt a variety of conformations (see Results) including the conformation indicated by Cryo-EM in phosphorylation-regulated striated muscle with the two heads projecting toward the M line (27). Also, the SPA results in rigor are well interpreted in terms of previous findings by Cryo-EM, as shown in Fig. 4D. It should be noted that all our modeling rests on the simplification that the main myosin domains behave as rigid bodies. In fact, due to the overparametrization of the full SHG model of a myosin molecule, it is obviously not possible to determine a molecular structure from SPA data; what this method allows is prediction of SPA from known atomic structures. We applied this approach to the myosin head distribution during isometric contraction, characterized by a mixture of detached and attached heads, with the aim of estimating the fraction of heads attached, which has been controversial (6, 17, 28–31). Our data indicate that the tetanic force in an isometrically contracting muscle is produced by steady-state commitment of 60% of myosin molecules. Under the condition that only one of the two heads of a myosin molecule is interacting with actin during isometric force production (24, 32), our finding of 60% of myosin molecules attached to actin agrees with evidence from single fiber mechanics that only 30% of myosin heads contribute to force and stiffness during isometric contraction (33).

With the line scan SPA measurements reported in this work, myosin conformation can be probed with a time resolution of 1 s, allowing measurements in a stationary state (such as the plateau of an isometric contraction). Direct probing of the myosin working stroke (occurring on a millisecond time scale), on the other hand, might be possible with a stroboscopic approach, such as the one used for x-ray diffraction (34). Time resolution can be further improved by restricting SPA measurements to two orthogonal angles (parallel and perpendicular to fiber axis; see Materials and Methods).

The investigation of cross-bridge structural changes associated with force production has been pursued over the last decades with several techniques, ranging from x-ray diffraction to various spectroscopic and optical approaches. The sensitivity of SPA to physiological states of the myosin motor in muscle is analogous to previous observations based on birefringence (35, 36), EPR (30, 37), fluorescence polarization (38), x-ray diffraction (39–41), and cryo-EM (42). More specifically, the variation between γ_rig and γ_relax is well interpreted in terms of motor orientation (see Fig. 4) going from perpendicular to parallel to the fiber axis, in agreement with current structural views (8). Furthermore, the dependence of γ_rig and γ_act on SL confirms the findings obtained with EPR (37), fluorescence polarization (43), and birefringence (35, 44), which demonstrated that the characteristic features of attached myosin heads are abolished at no overlap. On the other hand, each of these methods has largely different technical requirements and applicative implications. In this regard, we consider as a fundamental feature of SHG its capability of imaging unstained muscle with subsarcomeric resolution and deep tissue penetration. The latter property distinguishes SHG from other label-free techniques (for example, birefringence), enabling better perspectives in the development of tissue morphofunctional imaging (45); further advantages will be gained from the capability of probing molecular conformation in vivo as shown in this work.

Materials and Methods

Imaging.

The basic design of our SHG imaging system has been described (46). Briefly, a mode-locked Ti:sapphire laser (MIRA 900F, Coherent; 150 fs width pulses, 80 MHz repetition rate, 880 nm wavelength) was coupled into a custom-made scanning system based on a pair of galvanometric mirrors (VM500, GSI Lumonics). The laser was focused onto the specimen by a 40× objective lens (Nikon, 0.8 N.A.). A physiology objective (Nikon, 60×, 1.0 N.A.) was used for collection of the transmitted SHG signal, with 440/10 nm optical filter and photomultipliers (H7710-13, Hamamatsu) for signal detection. The necessary temporal resolution was obtained using the line-scanning mode (1,000 lines per second with 100 pixels per line and signal collection also during focal spot fly back). The line scans were oriented parallel to the fiber axis. During the line scan, the laser linear polarization (ellipticity < 0.1%) was rotated at 0.5 Hz by a polarizer, placed before the focusing objective and after a quarter-wave plate. The power after the objective lens was ∼45 mW and remained constant to within 2% over a 360° rotation of the polarizer. The length of sarcomeres under investigation was measured from the SPA kymograph (Fig. 1B). The SPA curve (Fig. 1C) was obtained by integrating the SHG signal over each vertical line of the kymograph, after subtraction of background noise.

Muscle Fiber.

Single demembranated muscle fibers were prepared from rabbit psoas as described elsewhere (47). Rigor was induced at 4 °C in rigor solution [MgCl₂ 3.22 mM, EGTA 53 mM, glutathione (GSH) 10 mM, N-[tris(hydroxymethyl)methyl]-2-aminoethanesulfonic acid (TES) 100 mM, pH 7.1]. Relaxing solution had the following composition: Na₂ATP 5.44 mM, MgCl₂ 7.70 mM, EGTA 25 mM, Na₂ creatine phosphate 19.11 mM, GSH 10 mM, TES 100 mM, pH 7.1. Measurements at different SL were performed in each fiber by setting a chosen SL in relaxing solution and, after SPA measurement in relax, inducing rigor. After relaxation, the fiber length was changed to a new SL and a new SPA measurement was performed, first in relaxing solution and then in rigor. Measurements with the ATP analog MgPPi were performed in rigor buffer varying the concentration of pyrophosphate (18). SHG measurements in demembranated fibers were performed at room temperature. Intact fibers were isolated from the tibialis anterior muscle of the frog (Rana esculenta) and mounted, by means of aluminum foil clips (48) between a strain gauge force transducer (AE801 SensoNor Horten) and a clamped hook in Ringer’s solution (NaCl 115 mM, KCl 2.5 mM, CaCl₂ 1.8 mM, phosphate buffer 3 mM, pH 7.1). SHG measurements on frog muscle fibers were performed at 10 °C. Fused tetani were elicited by trains of electric pulses of alternate polarity (40–60 Hz, duration of stimulation ≈1 s) at 4 min intervals.

SHG Polarization Anisotropy Analysis.

By combining muscle symmetry invariance under rotation around the y axis (fiber axis, in a system of coordinates with the z axis along the laser propagation direction) and the Kleinmann symmetry assumption (49), the second-order susceptibility tensor can be expressed as

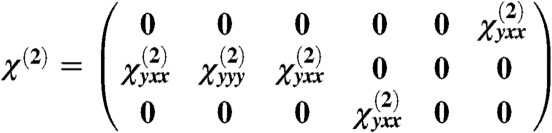[2]

The total SHG intensity (I_SHG) can be expressed as a function of the angle (φ) between the fiber axis and the laser polarization as reported in Eq. 1 with 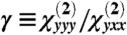. In this work, γ was obtained by fitting Eq. 1 to SPA data over a polarization range between 0° and 180°. From Eq. 1, it is also found that 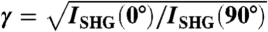, so that measurement of I_SHG at two orthogonal angles would, in principle, be sufficient. The parameter γ is related to the average orientation of HRSs and it critically depends on the characteristics of their angular distribution. As demonstrated for membrane-embedded chiral dyes (50), in the case of HRSs distributed on the surface of a cone with aperture angle α, γ = 2/(tan α)².

Modeling.

The atomic-resolution structure of full-length myosin was reconstructed using the α-helix coiled coil LMM and S2 [2FXO (26)] and the model of double-headed rigor S1 [1MVW (23)]. Based on the structure of the thick filament, full-length myosin molecules were repeated with the proper axial periodicity and helical symmetry to generate the quasi-helical 42.9-nm-long elementary unit containing nine myosin molecules. The actin filament structure was taken from ref. 51. For the calculation of χ⁽²⁾, we assumed that all C-N HRSs have the same nonlinear hyperpolarizability tensor, characterized by β_{z^′z^′z^′} as the only nonzero component in the x^′y^′z^′ molecular reference system. Then we averaged direction cosines between laboratory (xyz) and molecular (x^′y^′z^′) coordinate systems over all molecules:

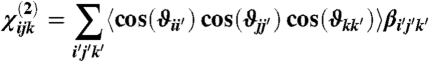[3]

In our calculations, a focal volume of ∼1 fL contained 3.27 × 10⁶ actin molecules (372 C-N HRSs per molecule) and 5.28 × 10⁵ myosin molecules (4,325 C-N HRSs per molecule). From the computed hyperpolarizability tensor, we calculated the SHG intensity as 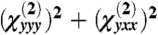and γ as 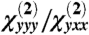. Computational modeling was performed in Matlab. To model attached and detached myosin heads, the full myosin rigor structure described above was used and three pivot points of the molecule were considered (fulcrum between the lever arm and the catalytic domain of S1 at Cys707, S1-S2 joint, and S2-LMM joint). For detached myosin molecules, the rotation of the whole myosin S1 head as a rigid body was assumed. For attached myosin molecules, the catalytic domain was considered attached to the actin filament, while interdomain rotation of the lever arm of S1 at Cys707 was allowed. In the model for isometric contraction, each attached cross-bridge has one attached head with θ_LA = 60° (see Fig. 4C) and one detached head with θ_S1 = 70° (see Fig. 4A), as indicated by previous studies of the change in the M3 reflection during rapid length changes applied to actively contracting muscle fibers (24).