Why Hofmeister effects of many salts favor protein folding but not DNA helix formation

Abstract

The majority (∼70%) of surface buried in protein folding is hydrocarbon, whereas in DNA helix formation, the majority (∼65%) of surface buried is relatively polar nitrogen and oxygen. Our previous quantification of salt exclusion from hydrocarbon (C) accessible surface area (ASA) and accumulation at amide nitrogen (N) and oxygen (O) ASA leads to a prediction of very different Hofmeister effects on processes that bury mostly polar (N, O) surface compared to the range of effects commonly observed for processes that bury mainly nonpolar (C) surface, e.g., micelle formation and protein folding. Here we quantify the effects of salts on folding of the monomeric DNA binding domain (DBD) of lac repressor (lac DBD) and on formation of an oligomeric DNA duplex. In accord with this prediction, no salt investigated has a stabilizing Hofmeister effect on DNA helix formation. Our ASA-based analyses of model compound data and estimates of the surface area buried in protein folding and DNA helix formation allow us to predict Hofmeister effects on these processes. We observe semiquantitative to quantitative agreement between these predictions and the experimental values, obtained from a novel separation of coulombic and Hofmeister effects. Possible explanations of deviations, including salt-dependent unfolded ensembles and interactions with other types of surface, are discussed.

Salts typically exert both specific (Hofmeister) and nonspecific (coulombic) effects on biomolecular processes (1–6). To manipulate and probe biopolymer processes using salts, it is extremely important to develop quantitative methods to interpret and predict these effects in terms of structure. coulombic, valence-specific effects of salt ions (due to screening of surface charges) are most significant at relatively low salt concentrations (< 0.1 M). At higher concentrations (> 0.1 M), ion-specific effects and relatively nonspecific osmotic effects (due to the lowering of water activity) become increasingly significant. In 1888, Franz Hofmeister discovered that the effectiveness of salts for protein precipitation generally followed a specific order, regardless of the protein being investigated (7). Since then, the so-called Hofmeister series of salt effects has been observed in physical properties of aqueous salt solutions (e.g., surface tension and surface potential) (8, 9), as well as salt effects on a variety of macromolecular processes (e.g., micelle formation, “salting out” nonpolar compounds, and protein folding) (10–13). The general ranking of ions, in decreasing order of effectiveness (best to worst) in driving processes where surface area is buried (e.g., folding and precipitation) or macroscopic surface is lost (transfer of water from the air–water interface to bulk), is as follows (14):

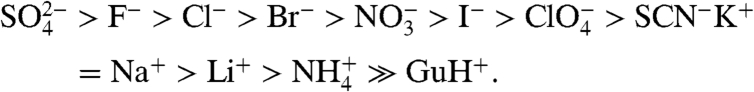Although it is generally accepted that interactions of salts with hydrocarbon surface are unfavorable and salt-specific, following the above order (1, 3, 11, 14–16), less is known about the interactions of Hofmeister salts with polar N and O surfaces, and, consequently, less is known about the origin of their effects on processes that expose or bury mostly polar surface (e.g., DNA melting).

We previously quantified Hofmeister ion exclusion from, or accumulation at, hydrocarbon (C) and amide nitrogen and oxygen (N, O) surfaces and showed how the net exclusion or accumulation of salt ions affects the solubility of model hydrocarbons, peptides, and micelles (13, 17). Our analysis of these studies (13, 17) quantified the conclusion drawn by earlier investigators (15, 18) that the interactions of Hofmeister salts with amide surface are favorable and relatively nonspecific. Thus, the observed Hofmeister ordering of salt effects on solubility of small peptides is primarily due to the ∼75% of the surface that is hydrocarbon. Unfolding of globular proteins exposes a surface similar in composition to the peptides (i.e., 65–75% hydrocarbon and 15–20% amide) (19, 20). By contrast, melting of DNA duplexes exposes a surface that is only ∼35% hydrocarbon, with the remainder being primarily polar N and O (21). These differences in the compositions of the surfaces exposed have striking implications for the prediction of Hofmeister salt effects on DNA melting. Although all salts stabilize DNA against denaturation at low salt concentration for coulombic reasons, we predict from our ASA-based analysis of model compound data that no salt will have a stabilizing noncoulombic effect on DNA duplex stability due to the dominance of polar N, O surface in the ΔASA of melting. Until now, no systematic studies of the effects of the full range of Hofmeister salts on the equilibrium constant of DNA helix formation have been performed.

Effects of neutral and destabilizing Hofmeister salts on the midpoint temperature (T_m) of thermal denaturation of DNA were determined by Hamaguchi and Geiduschek in 1962 (22); the Hofmeister series order is qualitatively observed, but no stabilizing salts were included in the study for direct comparison with our predictions. Gruenwedel and coworkers investigated the effects of “stabilizing” salts (sulfates) on DNA thermal stability (23, 24); curvature in plots of T_m as a function of log[Na₂SO₄] was observed at high salt concentration (0.3–1.6 M), but the curvature was eliminated when analyzed using Na₂SO₄ activity. To compare the effects of salts on protein unfolding and DNA melting and to test our qualitative predictions about the differences between the two systems, we have systematically investigated the noncoulombic effects of biochemically relevant salts from the Hofmeister series on equilibrium constants at ∼40 °C for two-state melting of a marginally stable globular protein [the well-characterized DNA binding domain (DBD) of lac repressor, lac DBD (25)] and a marginally stable DNA oligomer duplex.

Background on Solute m-Values and Chemical Potential Derivatives μ₂₃

Noncoulombic Hofmeister effects of salts on biopolymer processes such as folding and binding are quantified by m-values, defined as derivatives with respect to salt concentration (m₃) of the observed standard free energy change of the process 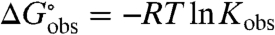, where K_obs is the observed equilibrium concentration quotient (expressed in terms of concentrations and not thermodynamic activities):

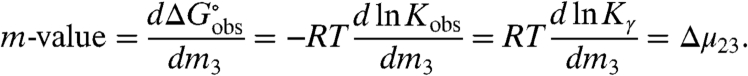[1]

In Eq. 1, K_γ is the quotient of biopolymer activity coefficients corresponding to the concentration quotient K_obs and μ₂₃ = RTd ln γ₂/dm₃^†; μ₂₃ is closely related to the preferential interaction coefficient Γ_μ3 (4, 5), which can be predicted if the ion distributions near the biopolymer are known (26, 27).

Classically, solubility measurements have been used to determine quantities analogous to μ₂₃. The observable is the derivative 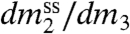, the change in solubility (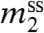, the concentration in the saturated solution) of a model compound or biopolymer as the concentration of the perturbing solute (m₃) is changed. This derivative is related to by the following approximate equation (valid at low to moderate ):

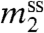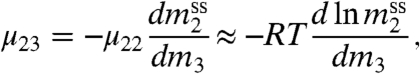[2]

where μ₂₂ = (RT/m₂)(1 + d ln γ₂/d ln m₂) can be approximated as RT/m₂ for sparingly soluble model compounds.

As a first level of interpretation of an experimental value of Δμ₂₃/RT or μ₂₃/RT (see Eqs. 1 and 2), we dissect it into additive contributions from chemically distinct, coarse-grained surface types (17, 28–31). This is analogous to the Tanford-Bolen approach, which assumes that a solute m-value for protein unfolding can be decomposed into additive contributions from the 20 side chains and the peptide backbone units exposed in unfolding. Our use of chemically distinct surface types (e.g., aliphatic and aromatic hydrocarbon, amide oxygen, and nitrogen) allows one to use fewer terms in the dissection and to obtain a more straightforward molecular interpretation of the values obtained. We propose that the contribution of each type of surface (i) to μ₂₃/RT is the product of a solute interaction potential [contribution per unit of ASA; (μ₂₃/RTASA)_i] and the ASA of that surface. The experimental value of the chemical potential derivative μ₂₃/RT is therefore represented as the sum of terms:

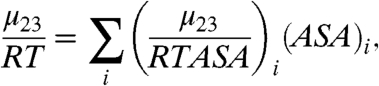[3]

where the interaction potential (μ₂₃/RTASA)_i quantifies the interaction of the salt of interest with one Ų of surface of type i on any compound or biopolymer, and (ASA)_i is the water-accessible area in Ų of surface type i on the model compound or biopolymer being analyzed. (The relevant surface for a biopolymer process with a corresponding m-value, or Δμ₂₃, is the ASA exposed or buried, or ΔASA.) The observed chemical potential derivatives μ₂₃/RT are model-independent thermodynamic quantities; the solute potentials (μ₂₃/RTASA)_i therefore provide a model-independent description of the effect of the solute per unit area of a particular type of water-accessible surface on the biomolecule or model compound.

If salt interaction potentials are known for various biopolymer surface types and ΔASA composition is available from structural data, then Eq. 3 can be used to predict the effect of any salt on any biopolymer process. We previously analyzed salt concentration and identity dependences for hydrocarbon and peptide solubility (Eq. 2) and reported salt (and salt ion) partition coefficients [K_p, where μ₂₃/RTASA ∝ (K_p - 1) quantifying exclusion or accumulation near (aliphatic and aromatic) hydrocarbon and amide surfaces] (17). Here, the solubility data analyzed in ref. 17 were globally fit for each salt to determine values of (μ₂₃/RTASA)_i (as in ref. 31), presented in Table 1.

Table 1.

Salt-surface interaction potentials from ASA-based analysis of solubility/distribution studies with model compounds

	μ23/(RTASA) × 103, (m-1 Å-2)*
Salt	Aliphatic C	Aromatic C	Amide (O,N)
Na2SO4	6.0 ± 0.1	5.9 ± 0.2	−6.8 ± 0.5
(NH4)2SO4	3.8 ± 0.1		−3.3 ± 0.3
KF	3.4 ± 0.1	2.4 ± 0.1	−4.6 ± 0.3
GuH2SO4†	2.2 ± 0.3	0.3 ± 0.5	−5.8 ± 1.0
NaCl	2.2 ± 0.1	2.0 ± 0.1	−4.2 ± 0.2
KCl	2.0 ± 0.1	1.7 ± 0.1	−4.2 ± 0.2
KBr	1.7 ± 0.1	1.2 ± 0.2	−4.1 ± 0.4
NaClO4	0.9 ± 0.1	1.1 ± 0.1	−7.0 ± 0.3
NH4Cl	0.8 ± 0.3		−1.2 ± 0.8
GuHCl	0.3 ± 0.1	−0.8 ± 0.2	−3.7 ± 0.4

^*Model compound dataset is identical to that in ref. 17. Ammonium salts were not included in ref. 17 due to scarcity of data; values here are estimates obtained from analysis of two [(NH₄)₂SO₄] or three (NH₄Cl) solubility μ₂₃/RT values and one vapor pressure osmometry μ₂₃/RT value (see Fig.  S1). Salts are assumed to be neither accumulated at, nor excluded from, small amounts of ester oxygen surface (6–13% of total ASA) on model peptides.

^†Obtained from Na₂SO₄, NaCl, and GuHCl values assuming ion additivity.

Results and Analysis

Salt Effects on lac DBD and DNA Melting.

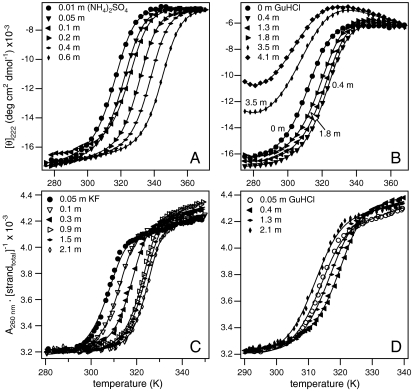
Fig. 1 shows typical unfolding/melting curves for lac DBD and a 12-bp DNA duplex; for each process the effects of salts from both “stabilizing” and “destabilizing” ends [(NH₄)₂SO₄ and KF; GuHCl] of the Hofmeister series are shown. For both processes, at low salt concentrations (≲0.5 m), increases in concentrations of all salts increase the stability of the ordered, higher charge density state (i.e., the midpoint temperature for the melting transition increases with salt concentration). Higher concentrations of GuHCl reverse this initial trend and destabilize both lac DBD and DNA (Fig. 1B and D). The effects of the “stabilizers” at high concentrations are starkly different for the two processes. As shown in Fig. 1A, over the whole range of (NH₄)₂SO₄ concentrations for which the entire transition can be observed (10–600 mmol/kg), the midpoint temperature increases monotonically with concentration. (This is also observed qualitatively at higher concentrations, where melting does not reach completion by 98 °C.) In contrast, the stabilizing effect of KF on DNA duplex formation reaches a plateau at high concentrations (Fig. 1C).

Fig. 1.

Thermal melting transitions of lac DBD and DNA oligomer at different salt concentrations. Protein unfolding data for Na₂SO₄ (A) and GuHCl (B) and 12 bp DNA melting data for KF (C) and GuHCl (D). Mean residue molar ellipticities [θ]₂₂₂ and absorbances (A₂₆₀) are plotted vs. temperature. Curves indicate global fits to the two-state melting transitions.

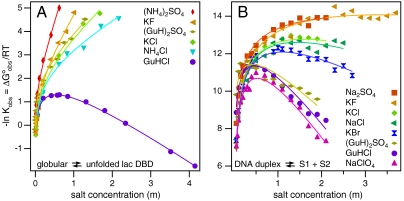
Melting equilibrium constants and standard free energy changes (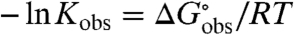) at ∼40 °C, obtained from fits of the transition curves (see Materials and Methods), are shown as a function of salt concentration in Fig. 2. Qualitatively, the protein unfolding data are consistent with a large body of T_m data as a function of salt concentration (32–36); our study is the only systematic investigation of effects of salts from the full range of the Hofmeister series on protein unfolding and DNA duplex dissociation in which isothermal equilibrium constants and 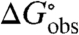as a function of concentration are obtained. For both processes, the curves exhibit two qualitatively different regions of effects of salts on thermal stability. As mentioned above, at low concentrations, all salts, whether typically considered stabilizers or destabilizers, increase the stability of the native state to similar extents as salt concentration is increased. At higher salt concentrations, Fig. 2 shows very different effects of salts from the “stabilizing” end of the Hofmeister series on protein unfolding and DNA melting. For lac DBD unfolding in all salts except GuHCl,^‡ native state stability continues to increase with salt concentration up to the highest concentrations investigated; the effectiveness of the salts as stabilizing agents differs though, manifesting in different high-concentration values of Δμ₂₃/RT (equivalent to m-value/RT). This is not observed for DNA melting in high concentrations of salts; on the contrary, the range of effects observed here includes only varying degrees of effectiveness at destabilizing the duplex. No salt is observed to stabilize the duplex at concentrations above ∼1.5 m; increasing concentrations of KF and Na₂SO₄, salts containing anions from the “stabilizing” end of the Hofmeister series, appear to have no effect on thermal stability of the duplex at these high salt concentrations.

Fig. 2.

Equilibrium constants (ln K_obs) for lac DBD unfolding and DNA oligomeric duplex melting are plotted as a function of molal salt concentration (mol/kg). Curves are fit to a three- or four-parameter equation for the separation of Hofmeister from coulombic salt effects (see Materials and Methods).

In order to quantify the Hofmeister m-values, coulombic effects must be extracted. We have fit the curves in Fig. 2 to equations containing nonlinear Poisson Boltzmann (NLPB)-predicted functional forms expected for coulombic effects of salts on protein unfolding and oligomeric duplex dissociation, respectively (see Materials and Methods for more details) along with a term that is linear in salt concentration [the slope of which is m-value/RT, or h (Eq. 7), quantifying the Hofmeister effect]. Hofmeister coefficients obtained from these fits are shown in Table 2; the functional forms used appear justified by the quality of the fits for both transitions at all concentrations of salts studied and the reasonable coulombic parameters obtained (see Materials and Methods). This dimension of the work will be discussed in a forthcoming paper.

Table 2.

Comparison of experimental Hofmeister salt m-values for protein (lac DBD) unfolding and 12-bp DNA melting (Eq. 7) with predictions from an ASA analysis of model compound data

	lac DBD unfolding m-value/RT, (m-1)		12-bp DNA duplex melting m-value/RT, (m-1)
Salt	Experimental	Predicted*	Experimental	Predicted†
Na2SO4	—	—	−0.1 ± 0.2	−0.2 ± 0.5
(NH4)2SO4	4.6 ± 0.2	5.4 ± 0.2	—	—
KF	2.3 ± 0.1	3.9 ± 0.5	−0.4 ± 0.1	−1.3 ± 0.3
(GuH)2SO4	1.5 ± 0.1	1.0 ± 0.5	−2.6 ± 0.3	−3.1 ± 0.3
KCl	1.3 ± 0.1	1.6 ± 0.2	−1.0 ± 0.1	−1.8 ± 0.2
NaCl	—	—	−1.1 ± 0.1	−1.7 ± 0.2
NH4Cl	0.8 ± 0.1	0.9 ± 0.6	—	—
KBr	—	—	−1.5 ± 0.1	−2.1 ± 0.3
GuHCl	−1.2 ± 0.1	−1.3 ± 0.3	−3.6 ± 0.2	−3.5 ± 0.4
NaClO4	—	—	−3.6 ± 0.2	−4.3 ± 0.3

^*Based on 92% of ΔASA; remaining 8% assigned zero contribution.

^†Based on 64% of ΔASA; remaining 36% assigned zero contribution.

Comparison Between Observed m-Values for lac DBD Unfolding and Predictions from Model Compound Analysis.

For lac DBD unfolding, which exposes mainly hydrocarbon surface, Hofmeister effects of salts range from very stabilizing [4.6 m^-1 for (NH₄)₂SO₄] to moderately destabilizing (-1.2 m^-1 for GuHCl). Hydrocarbon and amide N and O comprise ∼90% of the ΔASA exposed in this process, so the interaction potentials in Table 1, along with the composition of this ΔASA, can be applied to predict the high-concentration Hofmeister slope (m-value/RT = Δμ₂₃/RT = h; Eqs. 1, 3, and 7). To obtain the ΔASA for this process, a model for the unfolded state is required. In previous analyses (20, 25), we successfully used a fully extended model for the unfolded state; initial calculations using this maximum ΔASA suggested that this state was not appropriate for solutes that interact strongly (here unfavorably) with hydrocarbon surface. The recent web application ProtSA generates sequence-dependent atomic models of unfolded proteins (39, 40); tests for selected proteins indicate consistency with experimental residual dipolar couplings and small-angle x-ray scattering data (41). ProtSA was therefore used to generate an unfolded ensemble for the 51 residue lac DBD, consisting of 1,919 acceptable conformations. The average ASA is ∼6400 Å (see Materials and Methods), approximately 85% of the accessible area calculated for a completely extended chain. The 40 conformers of Protein Data Bank (42) PDB ID code 1OSL [first 51 residues of both monomers of the nonspecifically bound lac headpiece dimer (43)] were used to model the folded state. The resulting average ΔASA composition is presented in Table S1.

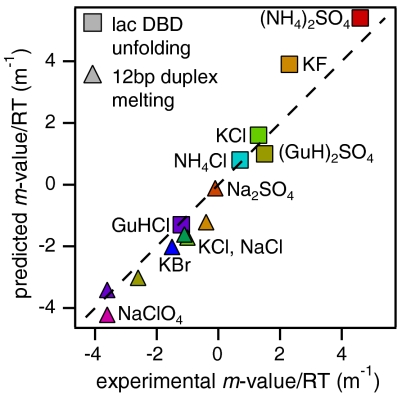
A quantitative comparison of predicted values of Δμ₂₃/RT (using the interaction coefficients in Table 1 and the ΔASA composition in Table S1) with experimental h coefficients (Eq. 7) is shown in Fig. 3 and Table 2. Over the entire range of effects (h values from -1.2 to +4.6 m^-1), good to excellent agreement is attained. For the set of six salts studied with lac DBD, a root mean square deviation of 0.8 is observed for predicted and observed values of h. The predictions for strongly perturbing salts [e.g., KF, (NH₄)₂SO₄], are the farthest from the experimentally observed values. For example, the predicted Hofmeister m-value/RT for KF (3.9 m^-1) is 70% larger than the observed value of 2.3 m^-1. Deviations at the highly excluded end of the spectrum of salts could be explained by an effect of the salt identity on the unfolded ensemble, possibly analogous to what we previously observed for the model process of micelle formation, where better agreement was observed between calculated and observed salt effects when more headgroups were assumed to be buried in excluded salt solutions (13). Here, compaction of the unfolded state in excluded salt solutions could result in the larger discrepancies observed for those salts.

Fig. 3.

Plot of predicted vs. observed Hofmeister salt Δμ₂₃/RT values for lac DBD unfolding and DNA oligomeric duplex melting. Predicted values are determined from the ΔASA compositions for the two processes (Table S1) and the interaction potentials in Table 1. Observed values of Δμ₂₃/RT are the h coefficients (Eq. 7) obtained from the global fits shown in Fig. 2. The dashed line represents equality of predicted and observed values.

Comparison Between Observed m-Values for 12 bp DNA Melting and Predictions from Model Compound Analysis.

Hofmeister coefficients for DNA duplex melting, obtained from the fits in Fig. 2, are shown in Table 2. As might be expected from the accumulation of all salts at (amide) nitrogen and oxygen surface, the values of h (Eq. 7) for DNA melting are all negative, indicating that the Hofmeister effects of all salts studied on duplex DNA are destabilizing. For example, Hofmeister effects of salts range from completely neutral (h = -0.1 m^-1 for Na₂SO₄) to modestly destabilizing (h = -1.5 m^-1 for KBr) to very destabilizing (h = -3.6 m^-1 for GuHCl and NaClO₄).

In order to use model compound data to predict effects of Hofmeister salts on DNA melting (h coefficients), a model for the partially unstacked DNA strands is necessary. No program to do this (i.e., comparable to ProtSA) is currently available. As an approximation, we assume that (i) the only surface area that is newly exposed upon melting is on the DNA bases and (ii) the amount of surface area exposed on each base is proportional to the overall extent of base unstacking in each denatured strand (see Table S1). An additional assumption arises in classification of surface area types. Unlike lac DBD unfolding, melting of the DNA duplex exposes functional groups not included in the model compound analysis (e.g., amino nitrogens and heteroatomic aromatic rings). As a first approximation, carbonyl oxygens and adjacent nitrogens are classified as “amide” (N, O), and all types of surface not in Table 1 are assigned null interaction (i.e., salts are neither accumulated nor excluded).

Shown in Fig. 3 (and in Table 2) is the comparison between the predicted values obtained as described above and the observed Hofmeister effects obtained from the fits. The predictions here are only for 64% of the surface, yet the root mean square deviations for the predicted and observed salt m-values for duplex melting (0.7) and lac DBD unfolding (0.8) are similar. Remarkably, the predictions correctly capture the difference in rank order of (GuH)₂SO₄ for DNA melting vs. protein unfolding. Whereas (GuH)₂SO₄ has long been known to be a relatively inert protein cosolute [i.e., neither a strong stabilizer nor a strong denaturant (3)], the increased amount of N and O surface exposed in DNA helix dissociation and unstacking shifts this salt toward much greater accumulation (see Table 1) and hence destabilization. Except for Na₂SO₄ and GuHCl, predicted values of Δμ₂₃/RT are consistently more negative (by 0.5–0.9 m^-1) than observed values. This suggests that the salts interact favorably (μ₂₃/RTASA = -0.7 × 10^-3) with the composite of the surface types not included in the calculation; we are testing this prediction in model compound studies.

Concluding Discussion.

Salts of ions from the extremes of the Hofmeister series are widely used at high concentrations in biochemistry (e.g., ammonium sulfate for precipitation and crystallization; guanidinium chloride or thiocyanate for denaturation), but the molecular basis of their ion-specific effects remains controversial. Hofmeister ions have often been discussed as either water structure breakers (“chaotropes”) or structure makers (“kosmotropes”), and Hofmeister effects have been attributed to the “ordering” or “disordering” of bulk water structure effected by a particular ion; however, proposals of long-range ordering (or disordering) of water in concentrated salt solutions are not supported by water activity data (44) nor by spectroscopic results (45, 46). Pioneering investigations of Nandi and Robinson and others [salt effects on solubility of model compounds (10, 11, 15, 47)], von Hippel and others [recycling chromatography on polyacrylamide columns (18, 48)], and Arakawa and Timasheff [preferential interactions of salts with native proteins (16)] have emphasized the importance of the competition between salt ions and water for interactions with molecular and macromolecular surfaces. The various effects of different ions on water structure (bulk and/or local), although potentially of interest, are not the direct origins of thermodynamic effects on biomolecular processes. Instead, nonuniform ion distributions (accumulation and exclusion) near surfaces are responsible for the thermodynamic effects of concentration of Hofmeister salts on a very wide range of aqueous processes (4, 5, 28).

The idea that direct interactions of ions (in competition with water) with nonpolar surface (e.g., air–water and molecular hydrocarbon) are the source of the Hofmeister effect has gained traction in recent years (13, 17, 49–51). Our work quantifying the accumulation or exclusion of Hofmeister ions near various biochemically relevant surfaces (13, 17, 52, 53) has allowed us to make qualitative predictions about the difference between Hofmeister effects on protein folding and DNA melting. Additionally, we have obtained isothermal m-values (i.e., h coefficients) for the effects of a wide range of Hofmeister salts on globular protein unfolding and DNA duplex melting. Results for both processes are in semiquantitative to quantitative agreement with our predictions based on the model compound analyses. The deviations observed for lac DBD could be explained by an effect of the salt identity on the unfolded ensemble, similar to what we previously observed for the model process of micelle formation (13), whereas those for DNA could indicate the existence of favorable, relatively nonspecific interactions of the salts studied with the 35% of DNA ΔASA for which we have no model compound data.

Materials and Methods

Calculation of K_obs and 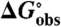from CD and UV Data.

Circular dichroism data at 222 nm (see SI Text for experimental details), characterizing the helicity of the lac DBD, were converted to mean residue ellipticity ([θ]₂₂₂, in units of deg cm² dmol^-1), and the unfolded fraction (f_U) of the population was calculated as a function of temperature:

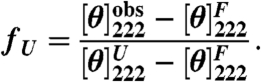[4]

Completely analogously, the DNA absorbance data at 260 nm can be used to obtain the single-stranded fraction of the population (f_ss) as a function of temperature. The use of Eq. 4 and the analogous equation containing the absorbances of the double- and single-stranded components requires the establishment of baselines denoting the native and denatured states. For lac DBD unfolding in all salts except GuHCl, linear baselines with a single linked slope and floated intercepts (due to variations in instrumental baseline) were determined by globally fitting datasets for a particular salt. A previous study of thermal unfolding of lac DBD in urea found that the upper baseline was a quadratic function of temperature (25); this behavior is not observed for the salts in the current dataset. For GuHCl, the upper baseline slope was allowed to float, due to clear differences between the different salt concentrations; i.e., as GuHCl concentration increases, the upper baseline gets steeper (cf. Fig. 1B). For DNA melting, baseline slopes and intercepts were floated.

For two-state protein unfolding (F↔U), the observed equilibrium constant for the process is simply the equilibrium concentration ratio of the unfolded and folded populations (determined by the upper and lower baselines):

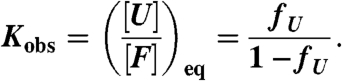[5]

For two-state DNA oligomeric duplex melting (duplex↔S1 + S2), the observed equilibrium constant for the process depends on the total strand concentration ([str]_total = [S1] + [S2] + [duplex]) but is equally easily determined using the fraction of the population in the melted (single-stranded) state:

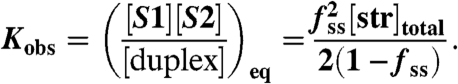[6]

To determine various thermodynamic parameters for different temperatures and solution conditions, nonlinear regression was performed using IgorPro 5.04B to fit K_obs to the constant ΔC_p van’t Hoff equation (25).

Extraction of Coulombic and Hofmeister Contributions to Observed Salt Effects on Protein Unfolding and DNA Duplex Melting.

In order to make comparisons to the predictions of Hofmeister salt effects based on the model compound analysis, long-range coulombic salt effects for both processes must be extracted. NLPB calculations at low salt concentrations indicate a linear dependence of ln K_obs on the logarithm of the salt concentration (ln m₃). Although this appears sufficient for modeling the coulombic contribution to lac DBD stability at all salt concentrations, NLPB calculations indicate that an additional quadratic dependence on ln m₃ is required for the DNA oligomer. Hofmeister effects on ln K_obs are typically observed to be linear in salt concentration (13). Assuming additivity of free energy contributions for coulombic and Hofmeister effects yields a simple equation to describe the salt dependences of ln K_obs over the full range of concentrations:

[7]

In Eq. 7, the parameter h is the Hofmeister slope (linear in m₃) at high concentrations. All other parameters describe the coulombic effects (where x = 0 for lac DBD unfolding), where the term b is an offset, equal to the fit value of ln K_obs at 1-m salt and h = 0.

For the fit to lac DBD unfolding data as a function of salt concentration (Fig. 2), the “coulombic” parameters in Eq. 7 (b and c) were linked for salts of the same valence. Uni-divalent and uni-univalent salts have similar values of c (∼0.5 and ∼0.7, similar to the NLPB results of 0.52 and 0.62) and b (∼2.4). For the four-parameter fits to the DNA melting data, the limiting slope in ln(m₃), c, was linked for all salts of the same valence. The value obtained for the uni-univalent salts (c = 1.66) is within 5% of the NLPB calculated value (1.74). For KF, KCl, NaCl, and KBr, b and x were also linked. For GuHCl and NaClO₄, these parameters were not linked to the other 1∶1 salts, and in the case of GuHCl (also GuH₂SO₄), x had to be constrained to be greater than zero. For the two uni-divalent salts, c was constrained to be within 10% of the NLPB calculated value (1.23) based on the results for the uni-univalent salts. The coefficient x varies widely depending on the structural model used for the NLPB calculations; the values obtained are reasonably consistent with those observed in the NLPB calculations (see Table S2).

Surface Area Calculations.

Water-accessible surface areas (ASA) are calculated using Surface Racer (54) with the Richards’ set of van der Waals radii (55) and a 1.4 Å probe radius for water. A unified atom model is used, wherein hydrogens are treated as part of the atom to which they are covalently bonded. Table S1 contains the results and additional details of the lac DBD and oligomeric duplex ΔASA calculations.