Abstract
The FNR (fumarate nitrate reduction) protein plays a central role in the global oxygen response of a variety of bacteria. In Escherichia coli, FNR is the master transcriptional regulator of the transition between aerobic and anaerobic growth. Regulation of FNR is achieved by cycling the molecule between three states in a process dependent on oxygen. In an effort to better understand the nature of this post-transcriptional cyclic regulatory mechanism, we formulated a kinetic model of the FNR protein and its regulation in E. coli. The values for the parameters of the model were fit to experimental data for the wild-type organism, and the model was validated by successfully predicting the behavior of fnr mutant strains characterized in the literature. We characterized the steady-state behavior of the FNR system by determining its sensitivity to changes in parameter values and its response to changes in the concentration of iron–sulfur cluster assembly proteins and the protease ClpXP. We also determined the steady-state induction characteristic that provides a direct estimate for the levels of the active form of FNR as a function of oxygen concentration. This result, in combination with reporter assays for expression of FNR target operons, gives an estimate for the equilibrium dissociation constant for the binding of active FNR to its recognition sequences in the DNA. Finally, we predicted the dynamics of the aerobic-to-anaerobic transition and determined distinct contributions to the dynamic profile of regulatory mechanisms operating at the transcriptional and post-translational levels.
Keywords: FNR, oxygen sensing, genetic regulation, compartmental analysis, biochemical systems theory
Introduction
As a facultative anaerobe, Escherichia coli regulates respiration based on the availability of electron acceptors. Molecular oxygen is the preferred acceptor, and it represses all other types of respiration and fermentation. In the absence of oxygen, nitrate becomes the favored oxidizing agent. Four global regulators, FNR, ArcA, NarL, and NarP, control the various pathways of respiration. FNR takes its name from mutants deficient in fumarate and nitrate reduction. Its role is to sense oxygen and determine whether the cell will grow aerobically or anaerobically. The regulation of this global transcription factor, which is the focus of this study, involves a cyclic network of interactions at the post-transcriptional level and autorepression at the transcriptional level.
FNR sits at the master level of respiratory regulation and fulfills its functional role as a transcription factor under oxygen-limiting conditions. As oxygen becomes limited, FNR activates hundreds of genes adapting E. coli for anaerobic growth.1,2 In an oxygen-rich setting, FNR is inactive and the default state is to grow aerobically. The total amounts of FNR protein present aerobically and anaerobically are similar.3
Active FNR is a dimeric DNA binding protein wherein each monomer contains an oxygen-labile [4Fe–4S]2+ cluster.4–6 The [4Fe–4S]2+ clusters promote dimerization. Oxygen destabilizes dimeric FNR, resulting in two [2Fe–2S]2+-containing monomers.3–7 FNR monomers return to the apoprotein state, losing their Fe–S cluster altogether, by further reaction with .4 The three states of the FNR protein are from hereon referred to as apoFNR, 2Fe–FNR, and 4Fe–FNR. These respectively denote the apoprotein, [2Fe–2S]2+, and [4Fe–4S]2+ forms of FNR.
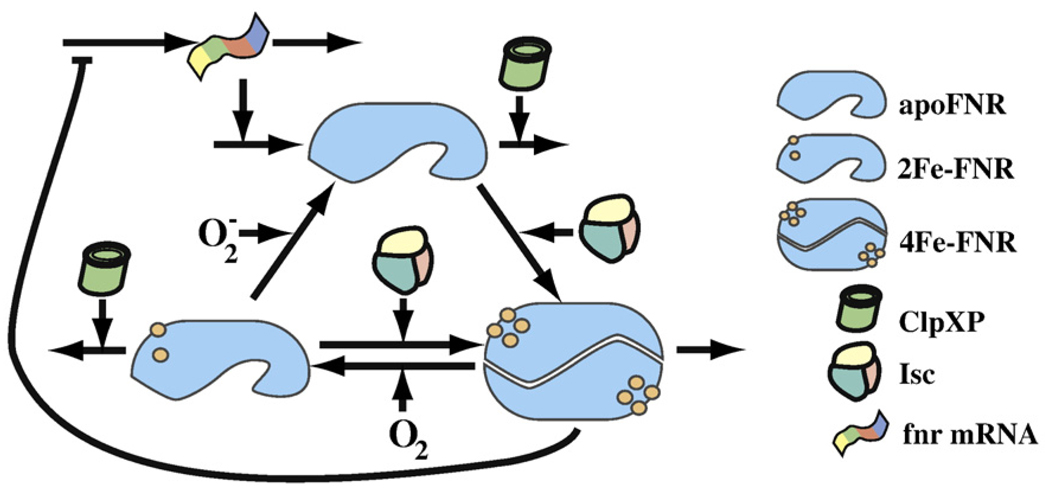
The fnr mRNA generates a steady supply of apoFNR (Fig. 1). Molecules from the apoFNR pool are either degraded via the ATP-dependent protease ClpXP or converted to 4Fe-FNR.8,9 In an oxygen-rich environment, 4Fe-FNR is rapidly converted into 2Fe-FNR, which keeps the concentration of 4Fe-FNR low and precludes unfavorable repression of aerobic genes and/or expression of anaerobic genes.3 The 2Fe-FNR returns to the apoFNR pool, but the exact rate is difficult to obtain due to problems posed by controlling levels.4 Degradation by ClpXP offers an alternative pathway exiting the 2Fe-FNR pool.8 In vitro analysis has shown similar kinetics for ClpXP-driven degradation of 2Fe-FNR or 4Fe-FNR, indicating that ClpXP degrades monomeric forms of FNR in a similar fashion.8
Fig 1.
A representation of the FNR system in E. coli. FNR regulates the shift between aerobic and anaerobic growth. Dimeric 4Fe-FNR adapts the cell to oxygen-limiting conditions. Aerobically, oxygen inactivates FNR, but the cell continues to produce and reactivate it. This results in constant cycling of FNR between its three states—apoFNR, 4Fe-FNR, and 2Fe-FNR. Aerobic cycling is tuned so that the inactive apoFNR predominates. Under anaerobic conditions, the absence of oxygen results in rapid buildup of 4Fe-FNR. The 4Fe-FNR form dimerizes to produce an active transcription factor.
The FNR system has been well studied, but many open questions remain. It is not yet known if the experimental data can be integrated into a model that explains the existing data and tests the internal consistency of studies from different laboratories. The wild-type concentrations of the inactive and active FNR species are not readily determined by current experimental methods. Experimental expression profiles of FNR target operons have been examined as oxygen levels vary, but it is not clear how well these profiles correlate with active FNR expression. To what extent is the expression of active FNR sufficient to explain the induction profiles of the operons it regulates? How do the post-translational cycling of active FNR and the transcriptional regulation of FNR shape the dynamics of the aerobic-to-anaerobic transition?
In this study, we first constructed a model and fit it to the wild-type behavior as described in the literature. Then, we validated the model by testing its ability to predict behavior not used in the development of the model or the fitting of its parameters. We predicted for the first time the wild-type concentrations of the inactive and active FNR species. We compared experimental expression profiles of three FNR target operons against model-predicted active FNR concentrations as oxygen levels vary. Finally, we characterized the steady-state and dynamic properties of the system.
Results
We formulated a model based on data available in the literature, established a set of criteria to fit the model against, located a nominal set of values in parameter space that captures the known behavior of the system, and determined confidence intervals for these nominal parameters. Having formulated a reasonable model with physiologically realistic parameter values, we went on to test the ability of the model to predict known mutant behavior (not used in the fitting of the model) and explored the model’s steady-state and dynamic behaviors. Further information and technical details are provided in Modeling Procedures.
Formulation of the model
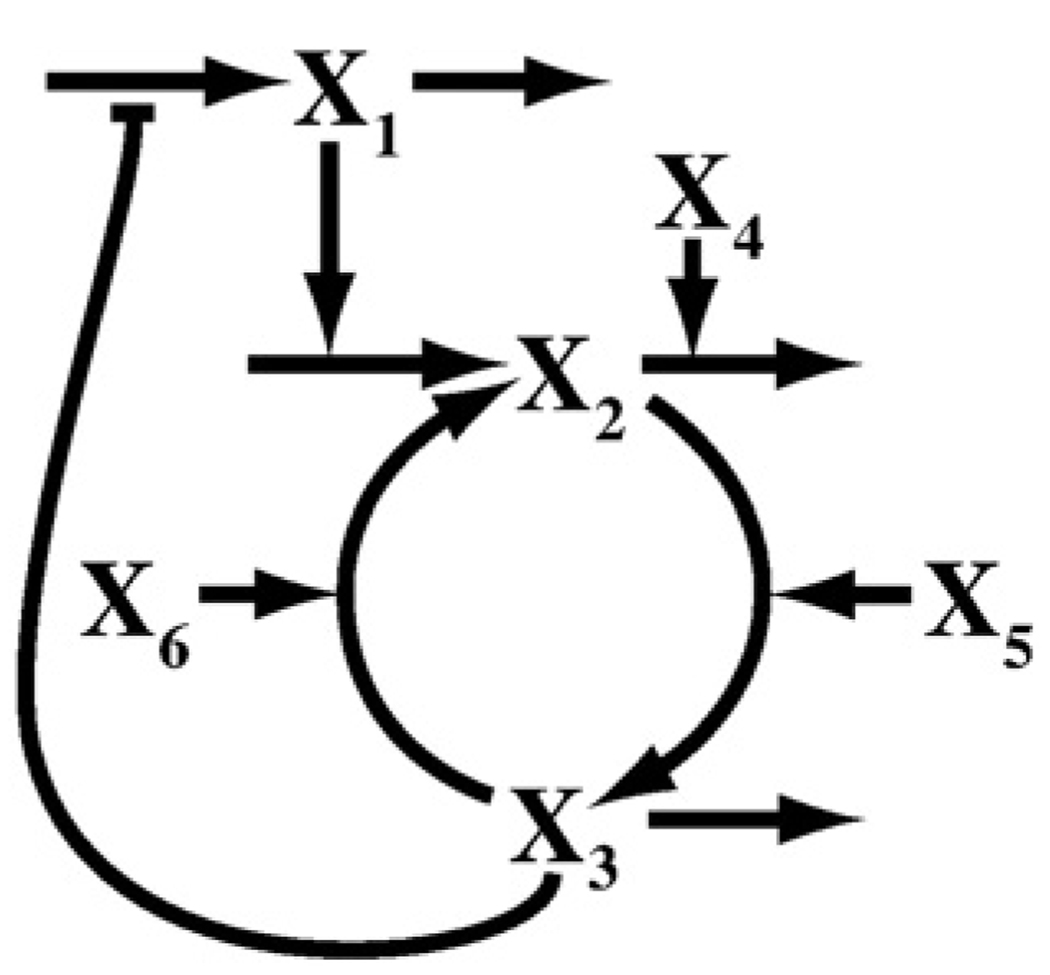
We began by constructing a mathematical model of the FNR network based on data available in the literature. After integrating the available information, we arrived at the network shown in Fig. 1, which represents the actual system. We then formulated the kinetic model shown in Fig. 2. The decision to lump the concentrations of apoFNR and 2Fe-FNR together as a single variable was done to simplify the model without significant loss of information. Both apoFNR and 2Fe-FNR are monomeric forms of FNR incapable of binding DNA, and they share similar degradation kinetics.8
Fig 2.
A diagram of the kinetic model for the FNR system. X1, fnr mRNA; X2, apoFNR and 2Fe-FNR; X3, 4Fe-FNR; X4, ClpXP protease; X5, iron–sulfur cluster assembly proteins (Isc); X6, molecular oxygen. The nucleotide and amino acid pools are assumed to be well regulated, and their nearly constant values are implicitly accounted for in the appropriate rate constants for transcription and translation. The fate of material lost from the system by degradation and/or dilution is not shown. (See the text for further details.)
The system of equations describing the network is a piecewise representation within the power-law formalism.10,11
| (1) |
| (2) |
| (3) |
Equation (1) describes the mRNA pool with a two-piece approximation. Values of X3 above the critical threshold X3c exhibit autorepression of fnr mRNA synthesis by the active 4Fe-FNR dimer. Values of X3 below X3c have a maximal rate of fnr mRNA synthesis, denoted α1,max. Equation (2) describes the apoFNR and 2Fe-FNR pool. The description includes two positive terms, synthesis of apoFNR and conversion of 4Fe-FNR into 2Fe-FNR, along with two negative terms, degradation via ClpXP and conversion to the 4Fe-FNR form. Equation (3) describes the 4Fe-FNR pool whose rate of change depends on influx from the apoFNR–2Fe-FNR pool, oxygen-dependent efflux back to the apoFNR–2Fe-FNR pool, and loss due to dilution resulting from cell growth.
Some parameters have state-specific values for the aerobic (“off”) and anaerobic (“on”) states. This is due to differences in growth rate between these two conditions that alter the dilution rate. Thus, not shown in the general set of equations [Eqs. (1)–(3)] are the following state-specific parameters: β1,off, β1,on, β21,off, β21,on, β31,off, and β31,on. There are also state-specific independent variables that represent the forces modulating the transition between the off and on states. The independent variables are X4, X5, and X6, where X6,off and X6,on represent the state-specific values. Dependent variables represent the outputs of the system; these are X1, X2, and X3. The X2 pool describes the inactive monomeric forms of FNR. Under aerobic conditions, almost all FNR molecules should be in the X2 pool. The X3 pool describes the active dimeric form of FNR. Under anaerobic conditions, most FNR’s should be in the X3 pool.
Nominal values for the parameters and independent variables
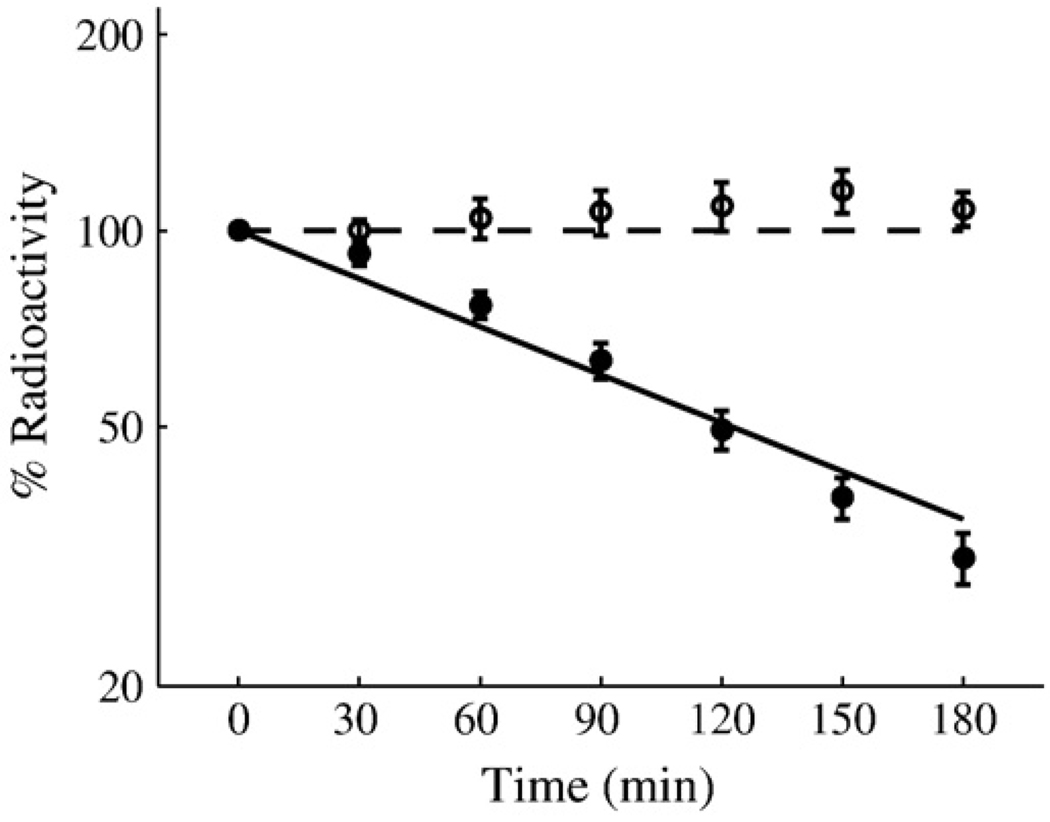
Table 1 is a list of criteria, based on data in the literature, that must be satisfied by any physiologically reasonable model of the FNR system. Using these criteria, which include two wild-type pulse-chase curves (Fig. 3), we employed a genetic algorithm to locate a nominal set of values in parameter space that captures the known behavior of the system and determined confidence intervals for these nominal parameters (Table 2).
Table 1.
Criteria used to fit the parameters of the model to experimental data and the results for each criterion when using the nominal values in Table 2
| Criteria |
||
|---|---|---|
| Description | Source | Fitted results |
| Under aerobic conditions, inactive FNR predominates (X2,off>10X3,off) |
Ref. 12 |
X2,off=4.63 µM 2X3,off=0.16 µMa |
| Under anaerobic conditions, active FNR predominates (X3,on>10X2,on) |
Refs. 5 and 12 |
X2,on=0.15 µM 2X3,on=3.48 µMa |
| Total aerobic FNR concentration is 4.8 µM | Ref. 3 | 4.79 µMa |
| Total anaerobic FNR concentration is 3.65 µM | Ref. 3 | 3.63 µMa |
| Removal of autorepression results in a 2-fold increase in total FNR under anaerobic conditions |
Ref. 13 | 2-fold |
| Reproduce the aerobic pulse-chase data | Ref. 8 | RMS of 4.43b |
| Reproduce the anaerobic pulse-chase data | Ref. 8 | RMS of 7.96b |
| Aerobic doubling time should be 60 min (β31,off/2=0.0115) |
Ref. 8 | 60.1 min |
| Anaerobic doubling time should be 90 min (β31,on/2=0.0077) |
Ref. 8 | 93.8 min |
| Critical level of active FNR should fall between 0.2 and 0.4 µM (0.2<X3c<0.4) |
Ref. 13 | X3c=0.389 µM |
| The critical level of active FNR must be greater than its aerobic steady-state concentration (X3c>X3,off) |
This study |
X3c=0.389 µM X3,off = 0.08 µM |
| Dimerization and disassociation of the FNR dimer, under aerobic conditions, should be faster than transcription of the fnr mRNA (, α22X3X6>α1,max, , β22X22X5>α1,max) |
This study | α22X3,offX6,off=25.4 min−1 µM β22X22,offX5=25.4 min−1 µM α1(X3,off)g13=0.28 min−1 µM |
| Dimerization and disassociation of the FNR dimer, under aerobic conditions, should be faster than translation of the FNR protein (α22X3X6>α21X1, β22X22X5>α21X1) |
α1,max=0.135 min−1 µM α21X1,off=0.078 min−1 µM α21X1,on=0.053 min−1 µM |
|
| Aerobic ClpXP-dependent degradation must be faster than dilution of the active FNR dimmer (β21X2X4>β31X3) |
This study | β21,offX2,offX4=0.075 min−1 µM β31,offX3,off=0.001 min−1 µM |
| Aerobic values of β21 and β31 must be larger than their anaerobic values (β21,off>β21,on, β31,off>β31,on) |
This study | β21,off/β21,on=1.3 β31,off/β31,on=1.56 |
Here, Xi,off and Xi,on refer to the off (aerobic) and on (anaerobic) steady-state values of Xi.
Expressed in terms of the molecular weight of the FNR monomer.
Root mean square.
Fig 3.
A replot of experimental data from Mettert and Kiley8 compared with the output of the model in Fig. 2. Shown are in vivo degradation rates of wild-type FNR under aerobic (filled circle) and anaerobic (open circle) conditions as measured by [35S]methionine pulse-chase radiolabeling assays followed by immunoprecipitation of FNR. Also shown are model-generated degradation rates of wild-type FNR under aerobic (continuous line) and anaerobic (broken line) conditions. Each pulse-chase data point represents the average of at least three experiments. The y-axis is total radioactivity as a percentage of the initial value at time zero. Time is in minutes.
Table 2.
Nominal values for the parameters and independent variables obtained by optimization along with confidence intervals for each value
| Parameter | Value |
|---|---|
| α1 | 0.0871±0.031 |
| α1,max | 0.135±0.045 |
| α21 | 0.484±0.1 min−1 |
| α22 | 4.09±0.31 min−1 µM−1 |
| β22 | 2.6±0.63 min−1 µM−2 |
| β1,off | 0.838±0.39 min−1 |
| β1,on | 0.613±0.26 min−1 |
| β21,off | 0.0821±0.055 min−1 µM−1 |
| β21,on | 0.0634±0.042 min−1 µM−1 |
| β31,off | 0.0231±0.0015 min−1 |
| β31,on | 0.0148±0.0005 min−1 |
| g13 | −0.464±0.023 |
| X4 | 0.196±0.22 µM |
| X5 | 0.455±0.13 µM |
| X6,off | 80 µMa |
| X6,on | 0 µMa |
| X3c | 0.389±0.024 µM |
X6,off and X6,on are selected to represent a well-oxygenated environment and a fully anaerobic environment, respectively.
These values are physiologically reasonable and in many cases are in excellent agreement with experimentally determined values as illustrated in the following two examples. In the first case, experimental evidence indicates that at saturating oxygen the pseudo-first-order rate of oxygen-dependent disassociation of the FNR dimer is 4.09 min−1 µM−1.3 This provides an upper bound on α22, as the further conversion between the 2Fe-FNR and apoFNR forms is not directly accounted for in the model. We see that at 4.09 min−1 µM−1 the nominal value of α22 is in agreement with the experiments.
The second case centers on the growth rate. Reproducing the observed doubling time is among the criteria used in the fitting process, and an interesting result reflected in the nominal parameter set is the prediction of doubling times that differ slightly from 60 min aerobically and 90 min anaerobically. As β31 represents the decay of the dimer (and twice the dilution rate of radioactivity), we expected the fitted value of β31,off/2=0.0115 min−1 to reflect the growth rate. If the exact doubling time were 60.3 min as opposed to 60 min, then 0.0115 min−1 is exactly what we would expect for the value of β31,off/2. Similarly, the expected growth rate under anaerobic conditions with a doubling time of ~90 min is µ=0.0077 min−1. The value obtained by fitting is β31,on/2=0.0074 min−1, and this is the value we would expect if the exact doubling time were 93.7 min.
Behavior of fnr mutants
Having satisfied the criteria in Table 1 and generated a set of physiologically relevant parameters, we wanted to further explore the logical implications of this model and assess whether or not our model is sufficient to explain experimental behavior characterized in the literature. We generated model predictions for the behavior of fnr mutants and checked these predictions against experimental data. These represent independent tests since data from the fnr mutants were not used in the formulation or the fitting of the model.
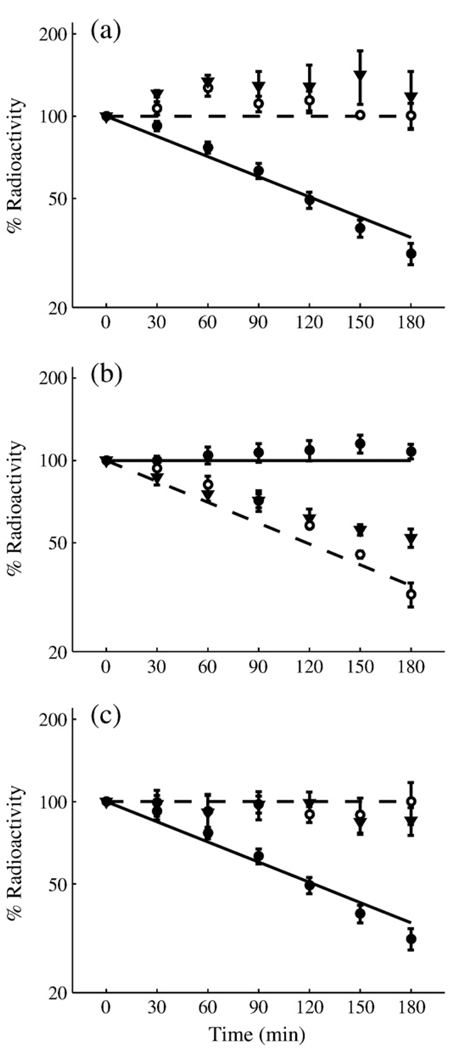
The same laboratory that generated the wild-type pulse-chase data (Fig. 3) collected similar data for three classes of fnr mutants: mutants insensitive to oxygen, mutants unable to dimerize, and mutants lacking ClpXP.8 Each of these mutations corresponds to abolishing a specific flux in our model. We eliminated the relevant flux and simulated the pulse-chase experiments to produce the curves in Fig. 4 (see Modeling Procedures for details).
Fig 4.
Mutant behavior as predicted by the FNR model (lines) and as determined experimentally by pulse-chase data (points) for FNR decay from experimentally characterized mutant strains.8 (a) Aerobic degradation of constitutive dimer (open circle, inverted filled triangle) and wild-type (filled circle) strains compared against the model-generated prediction of mutant (broken line) and wild-type (continuous line) behaviors. (b) Anaerobic degradation of constitutive monomer (open circle, inverted filled triangle) and wild-type (filled circle) strains compared against model-generated prediction of mutant (broken line) and wild-type (continuous line) behaviors. (c) Aerobic degradation of FNR in wild-type (filled circle), ClpP− (open circle), and ClpX− (inverted filled triangle) strains compared against model-generated prediction of mutant (broken line) and wild-type (continuous line) behaviors.
The similar nature of the data and model results shown in Fig. 4 arises from fundamentally different mutations causing analogous physiological changes to the FNR system. The model reproduces the results at the level of the physiology while accounting for the different processes that are affected in each mutant. Specifically, each class of mutants in Fig. 4 corresponds to the removal of one of the following processes: disassociation of dimeric FNR [constitutive dimer mutants, panel (a)], formation of dimeric FNR [constitutive monomer mutants, panel (b)], and active degradation of inactive FNR [ClpP−/ClpX− mutants, panel (c)]. The overall physiological effect of these mutants on protein degradation or stability is to make the system behave as if the environment is always aerobic (e.g., constitutive monomer mutants) or always anaerobic (e.g., constitutive dimer and ClpP−/ClpX− mutants) regardless of the presence/absence of O2. Thus, the mutants mimic certain aspects of the wild-type behavior, which is included in Fig. 4 as a control. As shown, the behavior of our model is in good agreement with the behavior of the actual system. This includes mutant behavior that was never used in the formulation of the model or the estimation of its parameters.
Steady-state response
Steady-state properties of the FNR model are characterized by the system’s amplification/attenuation of input signals (logarithmic gains14) and robustness to variation in parameters defining its structure (parameter sensitivities15). The logarithmic gains characterize the extent to which input signals (represented by changes in the steady states of independent variables) are amplified or attenuated as they are transmitted throughout the system to generate output signals (represented by changes in the steady states of the dependent variables). For example, a 1% increase in X4 results in a 1.8%±0.016% decrease in the aerobic steady state of X3 (Table 3). This analysis is valid for small signals, and it thus describes the local behavior of the system.
Table 3.
Percentage change in the aerobic and anaerobic steady states of dependent variables X1 (mRNA), X2 (inactive FNR), and X3 (active FNR) in response to percentage change in the independent variables X4 (ClpXP), X5 (Isc complex), and X6 (oxygen)
| Logarithmic gains |
||||||
|---|---|---|---|---|---|---|
| Aerobic |
Anaerobic |
|||||
| Independent variable | X1 | X2 | X3 | X1 | X2 | X3 |
| X4 | 0 | −0.91±0.0081 | −1.8±0.016 | 0.011±0.0011 | −0.012±0.0011 | −0.024±0.0021 |
| X5 | 0 | −0.045±0.004 | 0.91±0.0081 | −0.0055±0.0005 | −0.49±0.0005 | 0.012±0.0011 |
| X6 | 0 | 0.045±0.004 | −0.91±0.0081 | —a | —a | —a |
The mean and standard deviation for the logarithmic gains are computed with respect to the parameter sets that define the confidence intervals.
Logarithmic gains are not defined under anaerobic condition as X6=0.
Table 3 summarizes all of the logarithmic gains under aerobic and anaerobic conditions computed with respect to the parameter sets that define the confidence intervals in Table 2. As illustrated in Table 3, the errors in the parameter estimates do not significantly affect the logarithmic gains. Note that under aerobic conditions, X3 (active FNR) does not repress transcription of the fnr gene. Thus, X1 is independent of X4, X5, and X6 and the corresponding logarithmic gains are all zero.
The decision to turn on or off aerobic and anaerobic genes depends upon the concentration of X3. Active FNR is expected to be responsive to the oxygen level and to other system inputs to fulfill its role as an oxygen sensor. In the aerobic state, the FNR model predicts that X3 responds more sharply than X2 (inactive FNR) to changes in oxygen, iron–sulfur cluster assembly proteins (Isc), and ClpXP. This is of course desirable, because if X2 were the more responsive protein, then we would expect X2 rather than X3 to bind DNA. Interestingly, both X2 and X3 show their greatest variation in response to changes in ClpXP.
Under anaerobic conditions, all logarithmic gains (Table 3), which were nontrivial under aerobic conditions, are reduced, except for the variation in X2 resulting from changes in X5 (Isc effect on inactive FNR). This indicates that once active FNR is fully induced, the system produces a robust signal promoting anaerobic growth that is less responsive to small changes. Similar to the aerobic case, the anaerobic logarithmic gain in active FNR to changes in ClpXP is double that of inactive FNR. However, the change in inactive FNR resulting from changes in the amount of Isc protein complex is the largest of the anaerobic logarithmic gains. Thus, in the anaerobic state, inactive FNR is more responsive than active FNR to changes in the Isc proteins, which is contrary to the pattern for all other logarithmic gains.
Parameters that define the structure of biological systems are not fixed; rather, they vary with temperature, pH, genetic variation, and a multitude of other factors. Any reasonable model must be able to handle small parameter variations without differing qualitatively from the expected wild-type behavior. The parameter sensitivities characterize the extent to which variation in parameters is amplified or attenuated as their influence is transmitted throughout the system to generate variations in output signals (represented by the changes in the steady state of the dependent variables). For example, a 1% increase in β31,off results in a 0.091%±0.0081% decrease in the aerobic steady state of X3 (Table 4). Thus, parameter insensitivity provides a quantitative measure of system robustness to small variations in its structural determinants. As observed for the logarithmic gains, the errors in the parameter estimates do not significantly influence the sensitivities.
Table 4.
Percentage change in the aerobic and anaerobic steady states of dependent variables X1 (mRNA), X2 (inactive FNR), and X3 (active FNR) in response to variation in the parameters that define the system
| Sensitivities |
||||||
|---|---|---|---|---|---|---|
| Aerobic |
Anaerobic |
|||||
| Parameter | X1 | X2 | X3 | X1 | X2 | X3 |
| α1,max/α1 | 1 | 0.95±0.004 | 1.9±0.0081 | 0.68±0.011 | 0.35±0.0055 | 0.69±0.011 |
| α21 | 0 | 0.95±0.004 | 1.9±0.0081 | −0.32±0.011 | 0.35±0.0055 | 0.69±0.011 |
| α22 | 0 | 0.045±0.004 | −0.91±0.0081 | 0a | 0a | 0a |
| β1,off/β1,on | −1 | −0.95±0.004 | −1.9±0.0081 | −0.68±0.011 | −0.35±0.0055 | −0.69±0.011 |
| β21,off/β21,on | 0 | −0.91±0.0081 | −1.8±0.016 | 0.011±0.0011 | −0.012±0.0011 | −0.024±0.0021 |
| β22 | 0 | −0.045±0.004 | 0.91±0.0081 | −0.0055±0.0005 | −0.49±0.0005 | 0.012±0.0011 |
| β31,off/β31,on | 0 | −0.045±0.004 | −0.091±0.0081 | 0.31±0.011 | 0.16±0.0055 | −0.68±0.011 |
| g13 | —b | —b | —b | −0.18±0.015 | −0.091±0.0074 | −0.18±0.015 |
The parameters are as follows: α1,max/α1 (transcription rate), α21 (translation rate), α22 (rate of disassociation of active FNR dimer), β1,off/β1,on (rate of mRNA degradation), β21,off/β21,on (rate of degradation of inactive FNR monomer), β22 (rate of dimerization), β31,off/β31,on (rate of degradation of active FNR dimer), and g13 (kinetic order of repression of mRNA synthesis). The mean and standard deviation for the sensitivities are computed with respect to the parameter sets that define the confidence intervals.
The relevant flux for α22 is not present in the fully anaerobic state.
g13 is not defined for the aerobic state.
As illustrated in Table 4, under aerobic conditions, the effects of changing parameter values are attenuated in all cases for X2 (inactive FNR), whereas in four cases, X3 (active FNR) shows amplification of the parameter changes. If the aerobic role of inactive FNR is to provide a buffered supply of transcription factor prepped for activation the instant environmental changes demand it, then it is desirable to be insensitive to all parameter variations. While total insensitivity to all parameter variations is unrealistic, across all parameters, X2 is 2 to 21 times less sensitive than X3.
Anaerobic parameter sensitivities are reduced compared with their nontrivial aerobic counterparts for all cases except β22 (Table 4). This is analogous to the analysis of the logarithmic gains, reinforcing the idea that under anaerobic conditions, the system produces a strong signal promoting anaerobic growth and is less responsive to small parameter variations.
The model predicts a critical level of oxygen at which active FNR is significantly induced, and as oxygen drops beneath this threshold, the system becomes increasingly anaerobic. Concentrations of oxygen slightly above the critical level are expected to put the system into a partially aerobic state, and for oxygen levels well above the critical level, the system is fully aerobic. In the model, the critical level of oxygen is determined by equating the two segments of the piecewise approximation (i.e., when ) and solving for the corresponding concentration of oxygen (X6). The nominal parameter set predicts the critical level of oxygen to be 10.4 µM, and computing the critical oxygen level with respect to the parameter sets that define the confidence intervals in Table 2 gives a value of 10.4±0.46 µM. Further discussion regarding this predicted value in the context of the experimental literature is found in Discussion.
Steady-state induction characteristic for active FNR
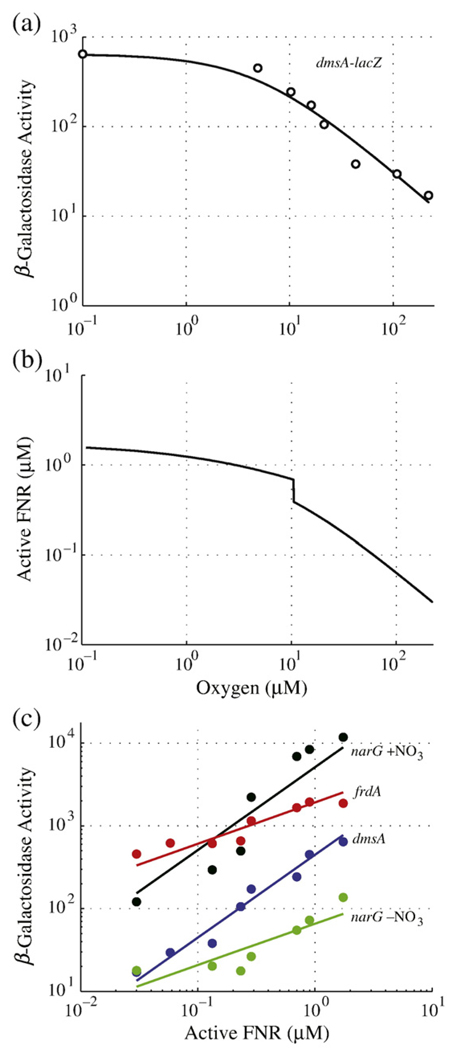
We compared model-generated expression profiles of active FNR at varying oxygen concentrations against the behavior of reporter-gene assays for anaerobic operons regulated by FNR. The frdABCD, dmsABC, and narGHJI operons encode proteins central to anaerobic respiration. Experimental work by Tseng et al.16 characterized the relationship between these three operons and oxygen saturation (Fig. 5a). These experiments provide an indirect measure of 4Fe-FNR activity, which has never been measured directly for technical reasons.
Fig 5.
Estimation of active FNR concentrations in vivo. (a) An example of experimental expression data (open circle) (replotted from Tseng et al.16 for the dmsA operon) fit with a Michaelis–Menten equation (continuous line). Half-maximal expression occurs at an O2 concentration of 4.9 µM. The leftmost data point occurs at [O2] = 0 µM and has been shifted along the x-axis to illustrate maximal dmsA expression on the logarithmic scale. (b) Standard curve estimating active FNR concentration as a function of oxygen saturation, calculated by setting the derivatives [Eqs. (1)–(3)] to zero and solving for active FNR (X3) over a range of oxygen (X6) concentrations. The equilibrium disassociation constant for active FNR binding to DNA is predicted to be 0.87 µM (i.e., the level corresponding to [O2] = 4.9 µM). (c) Correlation of active FNR levels with experimentally determined expression for anaerobic pathway genes (dmsABC, narGHJI, and frdABCD) at varying oxygen saturation levels. Experimental data (points) are replotted from Tseng et al.16 dmsA–lacZ (blue circle) with a fit of y=x+2.65 (blue line), narG–lacZ in the presence of nitrate (black circle) with a fit of y=x+3.71 (black line), narG–lacZ in the absence of nitrate (green circle) with a fit of y=0.5x+1.82 (green line), and frdA–lacZ (red circle) with a fit of y=0.5x+3.28 (red line).
Our model provides the first estimates of 4Fe-FNR concentration as a function of oxygen saturation (Fig. 5b), and we compared this prediction with the expression profiles of frdA, dmsA, and narG (±NO3). The standard induction curve of active FNR is calculated by setting the derivatives [Eqs. (1)–(3)] to zero and solving for X3 (active FNR) over a range of oxygen (X6) concentrations. The results indicate that active FNR levels as predicted by the model strongly correlate with the induction of these three anaerobic operons (Fig. 5c). Induction of dmsA and narG (+NO3) is directly proportional to that of active FNR (slope of ~1, with r-values of 0.96 and 0.87), which suggests simple binding of FNR dimer to a single DNA site without the involvement of any other mechanism. This is in agreement with the results in the literature, which indicate that dmsA activity is nearly abolished in Δfnr strains.16 The expression profiles of narG (−NO3) and frdA are clearly influenced by active FNR but are not directly proportional (slope of ~0.5, with r-values of 0.77 and 0.82). This suggests an alternative mechanism of regulation for these operons.
As suggested above, the activities of dmsA and narG (+NO3) are directly proportional to the level of active FNR. Under this assumption of single-site binding kinetics, the equilibrium dissociation constant is the concentration of active FNR that results in half-maximal expression of its target operon. As an example, this value can be determined from the curves in Fig. 5a and b. The value can also be determined from the correlation plots in Fig. 5c, and they yield a common estimate of 0.87 µM for the equilibrium dissociation constants of narGHJI (+NO3) and dmsABC operons.
Dynamic response
The dynamics of the aerobic-to-anaerobic transition are of particular interest as the FNR system regulates the process of switching between these environments. We have adopted the nominal set of values (Table 2), as well as the critical value of oxygen that is defined by our model, for use in performing our dynamic simulations. Although the mean value of the critical oxygen level (as determined by the parameter sets that define the confidence intervals) differs from its nominal value, the difference is within one standard deviation from the mean.
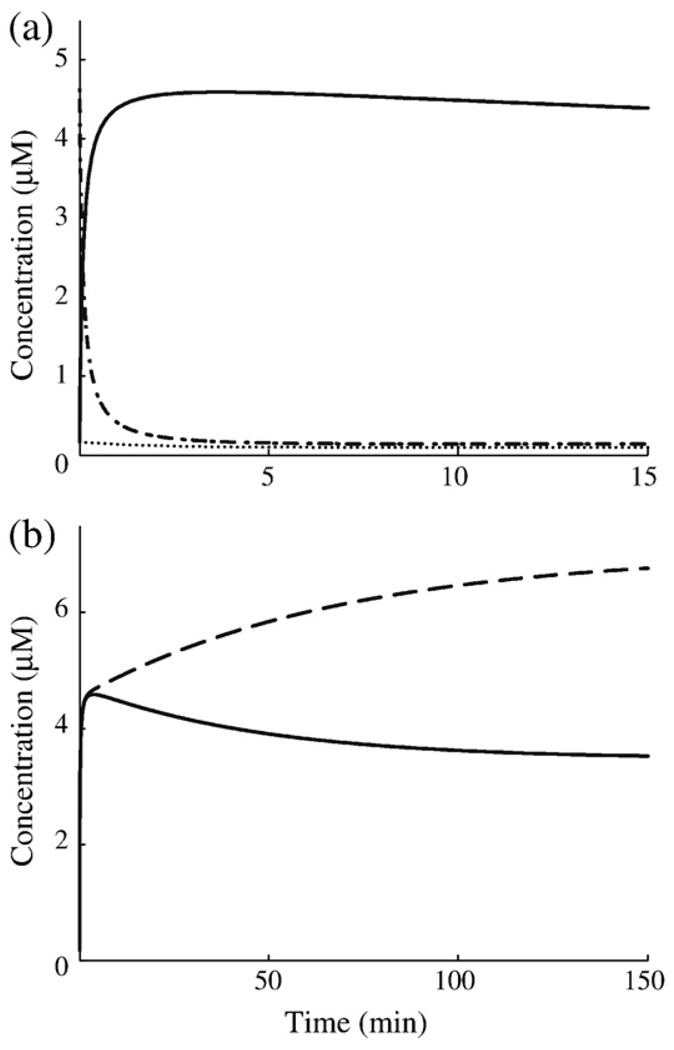
A typical dynamic response for the FNR model during an aerobic-to-anaerobic transition is shown in Fig. 6a. Inactive FNR undergoes an almost instant depletion, while active FNR experiences a rapid increase that overshoots the final steady state and settles back down (see longer timescale in Fig. 6b). The solution curves of the wild-type system reveal two key characteristic times: The settling time is defined as the time at which the solution reaches and remains within 5% of its final steady state, whereas the peak time is defined as the time at which the concentration of active FNR reaches its maximum. Corroborating the idea that rapid activation of FNR is the physiological constraint under which the FNR cycle operates, active FNR reaches its peak value approximately 3.7 min after the removal of oxygen and settles down to its anaerobic steady state after about 92 min. The futile cycling of FNR creates a fast switching mechanism allowing the initial transient accumulation of active FNR to be faster than the steady-state rate of synthesis of FNR under anaerobic conditions.
Fig 6.
Predicted dynamics of the FNR system during a shift to anaerobic growth. Initial steady states of the fnr mRNA, inactive FNR, and active FNR are 0.16, 4.63 and 0.08 µM, respectively. (a) Initial dynamics of fnr mRNA (dotted line), inactive FNR (dashed/dotted line), and active FNR (continuous line). (b) Comparison of the settling dynamics of active FNR with repression (continuous line) and that of active FNR without repression (broken line).
The overshoot in concentration of active FNR is an interesting prediction in itself, and this dynamic trait is observed across the parameter sets that define the confidence intervals of the nominal values. It is tempting to think that the purpose of a transient spike in active FNR would be to rapidly saturate available FNR target sites in the DNA and expedite the transition to anaerobic growth, but such a conclusion requires experimental backing. Alternatively, the overshoot might only be a side effect of quickly establishing a new steady state that satisfies the cell’s physiological requirements. To address the possibility that the overshoot arises from a unique arrangement of the parameters, we varied each parameter and asked what fold change is required to abolish the overshoot (Table 5). In many cases, the parameters do not influence the overshoot at all or require large fold changes in the range of 1080 to 1014. Only 5 of the 20 possible parameter shifts can reasonably influence the overshoot behavior (α21, β1, β21, β31, and X4), and of these, only 3 abolish the overshoot when doubled/halved.
Table 5.
Fold change in each parameter required to abolish the overshoot in active FNR during the aerobic-to-anaerobic transition
| Parameter |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| α1,max/α1 | α21 | α22 | β1,off/β1,on | β21,off/β21,on | β22 | β31,off/β31,on | g13 | X4 | X5 | |
| Tolerated increase | ∞ | ∞ | ∞ | 2.47 | 1.37 | 2150 | 6930 | ∞ | 1.37 | 2150 |
| Tolerated decrease | ∞ | 2.49 | 1080 | 3 × 108 | ∞ | 12,000 | 1.6 | 4.6 × 107 | ∞ | 12,000 |
The parameters are as follows: α1,max/α1 (transcription rate), α21 (translation rate), α22 (rate of disassociation of active FNR dimer), β1,off/β1,on (rate of mRNA degradation), β21,off/β21,on (rate of degradation of inactive FNR monomer), β22 (rate of dimerization), β31,off/β31,on (rate of degradation of active FNR dimer), and g13 (kinetic order of repression of mRNA synthesis).
The most sensitive parameters are β21 and X4, which affect the same flux, with a fold change of 1.37 required to remove the overshoot. As these two values determine the rate at which material is drawn out of the X2 (inactive FNR) pool before entering the X3 (active FNR) pool, it is easy to see that the overshoot in X3 would be sensitive to these values.
During the anaerobic buildup of active FNR, its rate of loss (β31) is by dilution due to growth. If this rate of growth-dependent dilution decreases by 1.6-fold, then the overshoot is not observed. However, this corresponds to a cellular doubling time of 96 min aerobically and 150 min anaerobically. While such lowered growth rates do not represent the data upon which the model was fit, experimentally altering the growth rates does provide one method to test the predictions regarding overshoot.
The mechanism responsible for the overshoot of active FNR involves the cyclic interconversion of FNR forms, the decay rates of the different forms of the protein, and the repression of fnr transcription by active FNR. The initial buildup of 4Fe-FNR results from the rapid conversion of a large pool of inactive FNR to the active form, coupled with the inhibition of its recycling back into the 2Fe-FNR pool. The transient increase in active FNR is augmented by a lower degradation rate, as compared with apoFNR or 2Fe-FNR, because 4Fe-FNR is not subject to degradation by ClpXP and is only diluted due to growth. The slow resolution of excess 4Fe-FNR results from active FNR repressing transcription of the fnr mRNA. In the absence of autorepression, the overshoot is not observed in the model and the effects that give rise to the rapid increase in FNR result in a sustained steady-state level of 4Fe-FNR that is 2-fold greater than wild type (Fig. 6b), as required by the experimental data for mutants lacking repression.13
The dynamics shown in Fig. 6a and b assume an instantaneous switch from fully oxygenated to anoxic conditions at time zero. This is of course a simplification, and it is more realistic to assume that oxygen depletion in the laboratory follows an exponential-like decay. We have repeated these simulations assuming an exponential rate of oxygen depletion and the qualitative behavior is unchanged; the dynamic responses in Fig. 6a and b are merely delayed. For example, if the half-time of oxygen depletion is 2 min or less, then there is no appreciable difference between instantaneous depletion and exponential depletion of oxygen (data not shown).
Discussion
Integrating quantitative data obtained from different laboratories under different conditions into a model often uncovers inconsistencies; in some cases, the model is nonetheless able to guide the identification of the inconsistent data.17 In other cases, the data are found to be internally self-consistent, and the numerous physical–chemical constraints in the model lead to a variety of experimentally testable predictions and the estimation of important parameter values. This is the case with our model of the FNR system.
Although the FNR system has been well studied, there are many open questions, and until now the experimental data have not been assembled into a coherent integrated model. We formulated such a model of the cyclic FNR regulatory network of E. coli based on data for the wild-type system that is available in the literature. This model was subsequently validated by correctly predicting the behavior of FNR mutants, the data from which were not used in the formulation of the model or the estimation of its parameter values.
The numerous physical–chemical constraints embedded in the model, together with the experimental landmarks from the wild-type system, have allowed us to estimate the nominal values for several kinetic parameters that have not been measured directly to date. These include the rate constant for transcription of fnr (α1=0.0871), the rate constant for translation of FNR (α21=0.484), the rate constant for dimerization of active FNR (β22=2.6), the aerobic rate constant for decay of the mRNA (β1,off=0.838), the anaerobic rate constant for decay of the mRNA (β1,on=0.613), and the maximal rate of transcription of fnr (α1,max=0.135).
The changes in steady-state behavior described by logarithmic gains and parameter sensitivities are presented in Steady-state response. In Table 3 and Table 4, we predicted the impact on the steady state when there are small variations in the parameters and independent variables. The results show that under aerobic conditions, active FNR is more responsive than inactive FNR to variations in the levels of the Isc complex, whereas this relationship is reversed anaerobically. This steady-state behavior is consistent with expectations for the FNR system to fulfill its physiological role as an environmental sensor and regulatory actuator.
Our most significant results follow from the deconvolution of the pulse-chase experiments that yield the first in vivo estimates of active FNR concentration. FNR levels are typically resolved from cell lysates using an immunoprecipitation step that does not differentiate the monomer from the dimer; consequently, the separate concentrations of active and inactive forms of FNR are not known. The model readily predicts the separate steady-state levels of the inactive FNR monomer and the active FNR dimer. The ability to track separately the different species of FNR allows us to generate the steady-state induction curve for active FNR shown in Fig. 5b. This has several important implications as discussed below.
The reporter assays of Tseng et al.16 for expression of anaerobic genes provide an indirect estimate of active FNR expression as a function of oxygen saturation. We have compared these data with our steady-state induction curve for active FNR. The results show an excellent correlation that allowed us to estimate the concentration of active FNR for half-maximal expression of the dmsABC and narGHJI (+NO3) operons, which is equivalent to the equilibrium dissociation constant for active FNR and its DNA binding site if one assumes simple binding of the dimer to a single site.
A key feature of the FNR network in need of elucidation is identifying the oxygen levels that correspond to transitions between fully aerobic, microaerobic, and anaerobic growth. The results of Tseng et al.16 showed that initial induction of three major operons encoding anaerobic respiratory proteins (frdABCD, dmsABC, and narGHJI) occurs when oxygen levels are lowered to 20 µM. In the case of dmsABC, maximal expression was observed in the absence of oxygen and half-maximal expression was reached around 10 µM O2. In the case of narGHJI, maximal expression was also reached in the absence of oxygen, whereas half-maximal induction was observed at 5 µM O2 in the presence of nitrate and at 10 µM O2 without nitrate. Expression of frdABCD differs in that expression peaked around 5 µM O2, and induction decreases either slightly in the absence of O2 or to its half-maximal value when the concentration of O2 rises to 15 µM. Thus, the experimental results assessing the oxygen levels that lead to induction of anaerobic operons are consistent with a framework in which active FNR is induced to a low level at ~20 µM O2, to an intermediate level at ~10 µM O2, and to its maximal level at or below ~0.1 µM O2. The steady-state induction curve (Fig. 5b) allows us to translate these levels of oxygen saturation into levels of active FNR. Thus, 20, 10, 5, and 0.1 µM O2 correspond to 0.25, 0.7, 0.87, and 1.6 µM concentrations of active FNR, respectively.
The dynamic behavior of the FNR system is critical because its physiological role requires rapid and reliable switching back and forth between aerobic and anaerobic growth. Our model exhibits dynamic behavior that is consistent with the regulatory role of the FNR system. The model also allows us to distinguish the contributions of post-translational and transcriptional mechanisms in this regulation. When active FNR is being induced (aerobic-to-anaerobic transition), the active FNR reaches its peak value approximately 3.7 min after the removal of oxygen and achieves its anaerobic steady state with a settling time of 92 min (Fig. 6b); when active FNR undergoes repression (anaerobic-to-aerobic transition), the active FNR reaches its basal value with a half-time of less than 1 min following full oxygenation and achieves its aerobic steady state with a settling time of 137 min (data not shown).
Rapid regulation at the post-translational level results in rapid buildup of active FNR during the transition to anaerobic growth, which results in an overshoot. The rapid post-translational regulation is balanced by a slow resolution of excess FNR by regulation at the transcript level. The predicted overshoot of active FNR during the dynamics of the aerobic-to-anaerobic transition supports the hypothesis that the post-transcriptional cyclic regulation of the FNR network is designed for fast and responsive oxygen sensing.
Although another computational study might be taken as support for the existence of an overshoot in active FNR,18 the method used indirectly measures 4Fe-FNR activity. While the rapid increase in activity predicted in their study may well be due to active FNR, it seems unlikely that the overshoot they observed is an accurate reflection of the concentration of 4Fe-FNR. The magnitude and rapid decrease of the overshoot [shown in Fig. 1b of Partridge et al.18] do not agree with the known physiology of the FNR protein. Since after the shift to anaerobic conditions the FNR protein is stabilized and can only be diluted by growth, the excess active FNR should require several generations to resolve.
In conclusion, the deconvolution of pulse-chase data for total FNR provides a direct estimate of the concentration for the active form of FNR, separated from the inactive forms. These results allow one to follow the dynamics of the aerobic-to-anaerobic transition and show that the rapid initial formation of active FNR results from the post-translational control of the FNR cycle and that the long-term resolution of the excess active FNR results from the transcriptional repression of the fnr gene. The steady-state induction characteristic relating concentration of active FNR to concentration of oxygen is well correlated with the expression of reporter constructs for several FNR target operons. Thus, the steady-state induction characteristic provides a “standard curve” that can be used to estimate the equilibrium dissociation constant for the binding of active FNR to its recognition sites in the DNA.
Modeling Procedures
Estimating parameters
Despite reasonable simplifications, we found ourselves with a model that has 4 inputs (independent variables) and 13 parameters. We must set values for all 17 of these unknowns in order to obtain experimentally testable predictions of the model’s behavior. To accomplish this task, we first turned to the literature in which some of the parameters of the FNR system have been measured or have established bounds. We used the experimental values when available and fixed the remaining unknowns with an optimization process. Experimentally determined values or bounds3,8,13 are available for α22, β31,off, β31,on, g13, X6,off, and X6,on, and we compared the expected results with those produced by the fitting process. To aid in fixing the remaining parameters, the literature provides guidelines for devising the criteria listed in Table 1. Finally, we optimized the model to satisfy these criteria, which include a set of pulse-chase data taken from wild-type cells (Fig. 3).
The model was fit to the pulse-chase data and other criteria in Table 1 using a genetic algorithm. The fitting process begins with an initial population of parameter sets randomly distributed in parameter space and converges on values occupying a distinct region in parameter space. The maximum root-mean-square deviation between pairs of parameter sets in the optimal region is 0.49, and the average root-mean-square deviation is 0.23. The parameter values and the goodness of fit are similar across the optimal region. The nominal parameter set (Table 2) was selected based on its score, which was marginally better than other parameter sets of the optimal region. The nominal values of Table 2 fit the criteria in Table 1, including accurately reproducing the pulse-chase data (Fig. 3).
At each iteration of the genetic algorithm, the parameters undergo a mutation step in which random variations are introduced, a recombination step in which parameters are chosen and exchanged between parameter sets, a scoring step in which each parameter set is scored against the criteria in Table 1, and, finally, a selection step in which 10% of the population is selected to seed the next iteration. The initial population is randomly distributed in parameter space and in order to achieve optimal starting conditions consists of 300,000 members as opposed to the 2000-member populations used in subsequent iterations. The genetic algorithm runs for a fixed number of iterations; 40,000 iterations were used throughout this study. To ensure that a quality minimum was reached and that the parameters were not significantly changing after 40,000 iterations, we checked that the root-mean-square deviation across iterations drops below 0.05. This occurs after 27,800 iterations or fewer in every run of the genetic algorithm.
The model is also fit against copies of the experimental data containing an additional ±10% error. Error is randomly introduced from a normal distribution for each of the quantitative criteria. Criteria describing qualitative inequalities are left unaffected by the additional error. The fitting with error is performed 50 times to provide confidence intervals for the final parameter values (Table 2). The intervals are narrowly defined in most cases, with width less than ±25% for all but six values. Specifically, the rate of ClpXP-dependent degradation (β21, X4), the level of iron–sulfur cluster assembly proteins (X5), the aerobic rate of mRNA degradation (β1,off), and the rate of mRNA transcription (α1, α1,max) have the broadest confidence intervals.
Compartmental analysis
This section details the process of augmenting the kinetic FNR model to represent the labeled pools observed in a pulse-chase experiment. Training the model to reproduce the two pulse-chase curves proves a great asset for parameter estimation. However, understanding what a pulse-chase experiment represents in the context of our model requires an augmented analysis. In order to mimic the pulse-chase experiment, we turned to compartmental analysis (for a review, see Carson & Cobelli19 and Jacquez20). Compartmental analysis describes a detailed method for using our model of FNR regulation to formulate a system of equations representing the labeled portion of material in each pool.
First, we needed to understand the nature of the pulse-chase experiments that we intended to reproduce. The experiments performed by Metter and Kiley8 used [35S]methionine to label the FNR protein. A pulse of labeled methionine is followed by a subsequent addition to the medium of a 200,000-fold molar excess of unlabeled methionine 1 min later. The data presented in the literature were a measure of total labeled FNR and were not normalized per cell mass; therefore, dilution of FNR due to growth is not observed in Fig. 3. In the same report, the doubling time is given. This allowed us to calculate the exponential growth rate and express the data in a normalized form that reflects dilution by growth. It is this form of the data that we used in the fitting process.
Under current methods, the antibody used in the immunoprecipitation step of the pulse-chase assay cannot distinguish between the different forms of FNR. As a result, the experimental pulse-chase curves represent decay of total labeled FNR in all three forms. The techniques of compartmental analysis allow us to decompose a single pulse-chase curve, representing total FNR, into the two subspecies of active FNR (4Fe-FNR) and inactive FNR (apoFNR and 2Fe-FNR). Consequently, we gain access to estimates of kinetic parameters for each subspecies. In particular, this decomposition of the pulse-chase curves affects the choice of β21,off, β21,on, β31,off, β31,on, β22, and α22. Without the ability to distinguish between the active and inactive forms of labeled FNR, it is difficult to pin down the exchange rates between the two forms, β22 and α22, and the rates of ClpXP-driven degradation of inactive FNR, β21,off and β21,on.
To make use of compartmental analysis, we began with the set of generalized mass-action equations that describe the kinetics of the FNR system [Eqs. (1)–(3)]. With the parameter values used in the text, these equations are in units of micromolar per minute and must be converted to units of mass per minute. We converted these equations to a form involving units of moles per minute by assuming a cellular volume of v and defining Yi = vXi. We then converted the equations from moles to mass by letting mj denote the atomic mass of compound Yi and defining Zi=miYi. Note that variable Z3 represents dimeric 4Fe-FNR and Z2 represents monomeric apoFNR–2Fe-FNR. Thus, the mass of Z3 is double that of Z2 (ignoring the extra sulfur and iron atoms), which implies m3=2m2. This gives us the following equations expressed in mass per minute:
| (4) |
| (5) |
| (6) |
We can apply compartmental analysis to Eqs. (4)–(6) and formulate a system of equations describing the labeled pool. Let εi denote the labeled material in pool Zi, and note that ε1 = 0, as pool Z1 for fnr mRNA contains no labeled protein. Radioactivity is typically expressed as the fraction of labeled material relative to total material (i.e., specific activity). The specific activity is given by Qi = εi/(εi + Z20 + Z30) ≈ εi/(Z20 + Z30) when εi ≪ Z20 + Z30. The resulting system of linear differential equations describing specific activity is as follows:
| (7) |
| (8) |
Qi is the labeled fraction of material in pool Xi. These equations describe the fraction of labeled material flowing through pools X2 and X3. Because methionine was labeled in the pulse-chase experiment of Fig. 3, Q1=0, as it would represent labeled fnr mRNA.
Recall that the immunoprecipitation step of the pulse-chase assay cannot distinguish between the different forms of FNR; thus, the data plotted in Fig. 3 represent total labeled FNR in all three forms. To account for this, we simply sum Q2 and Q3. This becomes important as it affects our choice of what to normalize against. We normalized against Q2,init + Q3,init representing total radioactivity at time zero, as observed in the experiment. We defined q2 = Q2/(Q2,init + Q3,init) and q3 = Q3/(Q2,init + Q3,init), where Q2,init and Q3,init are the initial values of Q2 and Q3, respectively. This ensures that q2,init + q3,init = 1. The normalized equations, written in terms of the original variables (recall that Zi = mivXi), are given by the following:
| (9) |
| (10) |
These normalized variables represent the fraction of labeled material in each pool at time t, normalized with respect to the fraction of labeled material in both pools at t = 0. This accounts for the normalization of radioactivity observed in the pulse-chase experiments. With the right choice of parameters and initial conditions, the sum of q2 + q3 should reproduce each of the pulse-chase curves in Fig. 3.
The initial values q2,init and q3,init can be calculated as follows: The nonnormalized initial values are defined as Q2,init = ε2,init/vm2(X20 + 2X30) and Q3,init = ε3,init/vm2(X20 + 2X30). Thus, q2,init = ε2,init/(ε2,init + ε3,init) and q3,init = ε3,init/(ε2,init + ε3,init). Moreover, we may assume thatε2,init = kZ20 and ε3,init = kZ30, where k is some proportionality constant. In other words, the amount of labeled material in each pool at time zero is proportional to the steady-state pool size. This implies that q2,init = kZ20/(kZ20 + kZ30) = X20/(X20 + 2X30) and q3,init = kZ30/(kZ20 + kZ30) = 2X30/(X20 + 2X30). Using Eqs. (9) and (10) with these initial values, we can now properly examine the ability of our model to reproduce the pulse-chase data of Fig. 3 for a given parameter set.
Simulating pulse-chase mutants
The simulations shown in Fig. 4 make use of the normalized pulse-chase equations [Eqs. (9) and (10)]. The normalized pulse-chase equations are augmented as follows: for the constitutive dimer mutations (Fig. 4a), the rate of disassociation of the active FNR dimer is set to zero (α22 = 0); for the constitutive monomer mutations (Fig. 4b), the rate of dimerization is set to zero (β22 = 0); and for the ClpXP-deficient mutations (Fig. 4c), the rate of proteolytic cleavage is set to zero (β21X2X4 becomes β′21X2; i.e., dilution by growth remains). Although dilution by growth is present in the model, it is necessary to remove growth-dependent dilution when relating the pulse-chase predictions back to the experimental work. This is because the original pulse-chase data do not account for dilution by growth. Therefore, β31 is set to zero, as it corresponds directly to the growth rate, and β21, which represents the aggregate decay rate of inactive FNR, must be augmented so that only the active decay process is properly accounted for. When adjusting the flux expression β21X2X4, the resulting flux expression is β″21X2X4, and the value of β″21 is derived from the differences between β21,on and β21,off.
Acknowledgements
This work was supported in part by the U.S. Public Health Service through grant R01-GM30054 and a Stanislaw Ulam Distinguished Scholar Award from the Center for Non-Linear Studies of the Los Alamos National Laboratory (M.A.S.) and by the U.S. Public Health Service through training grant T32-EB003827 and an Earl C. Anthony fellowship (D.A.T.). We thank Rick Fasani and Pedro Coelho for fruitful discussions on the FNR system. The authors are grateful to Dr. Patricia Kiley for her expert advice regarding FNR regulation.
Abbreviations used
- FNR
fumarate nitrate reduction
- apoFNR
apoprotein FNR
- 2Fe-FNR
[2Fe-2S]2+ FNR
- 4Fe-FNR
[4Fe-4S]2+ FNR
References
- 1.Kang Y, Weber KD, Qiu Y, Kiley PJ, Blattner FR. Genome-wide expression analysis indicates that FNR of Escherichia coli K-12 regulates a large number of genes of unknown function. J. Bacteriol. 2005;187:1135–1160. doi: 10.1128/JB.187.3.1135-1160.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Salmon K, Hung SP, Mekjian K, Baldi P, Hatfield GW, Gunsalus RP. Global gene expression profiling in Escherichia coli K12. The effects of oxygen availability and FNR. J. Biol. Chem. 2003;278:29837–29855. doi: 10.1074/jbc.M213060200. [DOI] [PubMed] [Google Scholar]
- 3.Sutton VR, Mettert EL, Beinert H, Kiley PJ. Kinetic analysis of the oxidative conversion of the [4Fe–4S]2+ cluster of FNR to a [2Fe–2S]2+ cluster. J. Bacteriol. 2004;186:8018–8025. doi: 10.1128/JB.186.23.8018-8025.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sutton VR, Stubna A, Patschkowski T, Munck E, Beinert H, Kiley PJ. Superoxide destroys the [2Fe–2S]2+ cluster of FNR from Escherichia coli. Biochemistry. 2004;43:791–798. doi: 10.1021/bi0357053. [DOI] [PubMed] [Google Scholar]
- 5.Lazazzera BA, Beinert H, Khoroshilova N, Kennedy MC, Kiley PJ. DNA binding and dimerization of the Fe-S-containing FNR protein from Escherichia coli are regulated by oxygen. J. Biol. Chem. 1996;271:2762–2768. doi: 10.1074/jbc.271.5.2762. [DOI] [PubMed] [Google Scholar]
- 6.Moore LJ, Kiley PJ. Characterization of the dimerization domain in the FNR transcription factor. J. Biol. Chem. 2001;276:45744–45750. doi: 10.1074/jbc.M106569200. [DOI] [PubMed] [Google Scholar]
- 7.Khoroshilova N, Popescu C, Munck E, Beinert H, Kiley PJ. Iron-sulfur cluster disassembly in the FNR protein of Escherichia coli by O2: [4Fe–4S] to [2Fe–2S] conversion with loss of biological activity. Proc. Natl Acad. Sci. USA. 1997;94:6087–6092. doi: 10.1073/pnas.94.12.6087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Mettert EL, Kiley PJ. ClpXP-dependent proteolysis of FNR upon loss of its O2-sensing [4Fe–4S] cluster. J. Mol. Biol. 2005;354:220–232. doi: 10.1016/j.jmb.2005.09.066. [DOI] [PubMed] [Google Scholar]
- 9.Flynn JM, Neher SB, Kim YI, Sauer RT, Baker TA. Proteomic discovery of cellular substrates of the ClpXP protease reveals five classes of ClpX-recognition signals. Mol. Cell. 2003;11:671–683. doi: 10.1016/s1097-2765(03)00060-1. [DOI] [PubMed] [Google Scholar]
- 10.Savageau MA. Design principles for elementary gene circuits: elements, methods, and examples. Chaos. 2001;11:142–159. doi: 10.1063/1.1349892. [DOI] [PubMed] [Google Scholar]
- 11.Savageau MA. Biochemical Systems Analysis. Reading, MA: Addison-Wesley; 1976. [Google Scholar]
- 12.Lazazzera BA, Bates DM, Kiley PJ. The activity of the Escherichia coli transcription factor FNR is regulated by a change in oligomeric state. Genes Dev. 1993;7:1993–2005. doi: 10.1101/gad.7.10.1993. [DOI] [PubMed] [Google Scholar]
- 13.Mettert EL, Kiley PJ. Contributions of [4Fe–4S]-FNR and integration host factor to fnr transcriptional regulation. J. Bacteriol. 2007;189:3036–3043. doi: 10.1128/JB.00052-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Savageau MA. Concepts relating the behavior of biochemical systems to their underlying molecular properties. Arch. Biochem. Biophys. 1971;145:612–621. doi: 10.1016/s0003-9861(71)80021-8. [DOI] [PubMed] [Google Scholar]
- 15.Savageau MA. Parameter sensitivity as a criterion for evaluating and comparing the performance of biochemical systems. Nature. 1971;229:542–544. doi: 10.1038/229542a0. [DOI] [PubMed] [Google Scholar]
- 16.Tseng CP, Albrecht J, Gunsalus RP. Effect of microaerophilic cell growth conditions on expression of the aerobic (cyoABCDE and cydAB) and anaerobic (narGHJI, frdABCD, and dmsABC) respiratory pathway genes in Escherichia coli. J. Bacteriol. 1996;178:1094–1098. doi: 10.1128/jb.178.4.1094-1098.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Okamoto M, Savageau MA. Integrated function of a kinetic proofreading mechanism: steady-state analysis testing internal consistency of data obtained in vivo and in vitro and predicting parameter values. Biochemistry. 1984;23:1701–1709. doi: 10.1021/bi00303a019. [DOI] [PubMed] [Google Scholar]
- 18.Partridge JD, Sanguinetti G, Dibden DP, Roberts RE, Poole RK, Green J. Transition of Escherichia coli from aerobic to micro-aerobic conditions involves fast and slow reacting regulatory components. J. Biol. Chem. 2007;282:11230–11237. doi: 10.1074/jbc.M700728200. [DOI] [PubMed] [Google Scholar]
- 19.Carson ER, Cobelli C. Modeling Methodology for Physiology and Medicine. San Diego, CA: Academic Press; 2001. [Google Scholar]
- 20.Jacquez JA. Compartmental Analysis in Biology and Medicine. 3rd edit. Ann Arbor, MI: BioMedware; 1996. [Google Scholar]