Shear Stress Regulation of Nitric Oxide Production in Uterine and Placental Artery Endothelial Cells: Experimental studies and Hemodynamic Models of Shear Stress Forces on Endothelial Cells

Abstract

Hemodynamic shear stress is the most powerful physiological regulator of endothelial Nitric Oxide Synthase (eNOS), leading to rapid rises in nitric oxide (NO). The substantial increases in uterine and placental blood flows throughout gestation rely heavily on the action of NO. We and others have investigated endothelial function in response to shear stress with cell culture models of shear stress. In order to apply the results of these studies most effectively, we need a more complete understanding of the origin and coupling of the hemodynamic forces and vascular tissue behavior. For example, equations commonly used to calculate in vivo shear stress incorporate assumptions of steady (non-pulsatile) blood flow and constant viscosity of blood (Newtonian fluid). Using computational models, we can estimate a waveform of shear stress over a cardiac cycle and the change in blood viscosity with shear rate and hematocrit levels, two variables that often change with size of vessel and location within a vascular tree. This review discusses hemodynamics as they apply to blood flow in vessels in hopes that an integration of these fields can lead to improved in vitro shear stress experiments and understanding of NO production in uterine and placental vascular physiology during gestation.

Introduction – Reason for Review

Substantial increases in uterine and placental blood flow are the major hallmark of the cardiovascular adaptations seen during gestation (1–3). These alterations in perfusion develop in order to meet the dramatically increasing nutrient and metabolic needs of the growing fetus. The magnitude of this response makes it by far the most striking physiologic cardiovascular adaptation observed during pregnancy (1–3). In order to allow parallel pathways for blood to flow, vasodilation, along with substantial remodeling and angiogenic growth of these vascular beds, are responsible for the dramatic decrease in vascular resistance that permit the increase in blood perfusion without a dramatic rise in blood pressure. In contrast, a mild fall or no change in blood pressure is observed when systemic vascular resistance falls dramatically in pregnancy.

Because there is no innervation of fetal placental vessels, vasodilation has been thought to occur primarily by the efforts of locally produced vasodilators (4–7). The most important fetal placental vasodilator may be nitric oxide (NO) because it is not only is constitutively produced, but also is dramatically stimulated by increases in shear stress, that occurs with increased blood flow (8–13). The growth and recruitment of parallel pathways for elevating blood flow and other changes in the maternal and developing fetal vasculature are also determined in part by shear stress since it substantially affects alterations in gene expression in endothelial cells (14) associated with altered proliferation, migration, orientation, stress fiber development and inflammatory responses (15–17).

We and others are investigating the role of endothelial-derived NO in adapting vascular function to pregnancy using cell culture and in vitro experimental models, by evaluating the endothelial cell transduction and signaling responses to shear stress (9–11, 18–20). What has become quite evident, however, is that a clearer understanding is needed of the pattern and magnitude of in vivo shear stress within the uterine and placental vasculature. Furthermore, a better understanding of uterine and placental hemodynamics is critical to improved design of in vitro experiments and ultimately interpreting the clinical significance of the observed in vitro data. To this end, we are also evaluating the vascular growth and remodeling of these dramatically altered vessels in pregnancy, and how these changes are affected by increased shear stress secondary to increased blood flow and other hemodynamic changes (e.g. impedance, vascular remodeling, etc.).

Preeclampsia is characterized by reduced uterine vascular growth and less vascular remodeling than that in normal pregnancy in conjunction with higher blood pressure and restricted fetal growth especially during the third trimester. Therefore, we hypothesize that this pathophysiological condition serves as a significant case of disruption of the normal positive feedback mechanism of greater blood flow causing greater shear stress, having a remodeling effect to normalize shear stress, and thereby allowing greater blood flow. Our hypothesis is supported by studies showing that the NO-mediated pathway of artery dilation has been found to be impaired with preeclampsia (19, 20), but not necessarily solely as a result of decreased NO production (18). Therefore, measuring and understanding values of shear stress within the preeclamptic uterine arterial bed might also hint where the artery response to shear stress is most lacking and therefore most disrupted from the normal healthy vessel remodeling.

Herein we review, the importance of NO production in pregnancy, experimental systems used to study the role of NO in pregnancy, the hemodynamic forces that act on vascular cells in vivo during pregnancy and the important and novel utility of mathematical and computer models for predicting forces and flows in vivo during pregnancy. It is our hope that future studies will take advantage of these mathematical and computer models to study the uterine and placental vasculature, paving the way for more sophisticated and relevant studies on the impact of blood flow changes (and thus shear stress) on the uterine and fetal placental vasculatures during healthy and pathologic pregnancies, where fetal growth is not optimal.

Nitric Oxide Production

NO synthesis is catalyzed by nitric oxide synthase (NOS), which converts L-arginine to L-citruline, with NO as a free radical by-product (21, 22). There are three isoforms of nitric oxide synthase (NOS) that produce NO. The predominant constitutive NOS isoform within the endothelium is eNOS and its activation leads to reduced vascular tone. Shear stress and eNOS signaling activity are regulated by Ca²⁺/calmodulin-dependent (23) and CA²⁺-independent mechanisms. De novo NO produced by the endothelium is thought to be highly labile (t1/2 3–5 sec) and is secreted adluminally to adjacent vascular smooth muscle cells where it binds to the heme binding region and activates soluble guanylate cyclase, which in turn converts GTP to cGMP (1, 22, 24). Inhibition of NOS using Nw-Nitro-L-arginine methyl ester hydrochloride (L-NAME) or NG-Monomethyl-L-arginine acetate salt (L-NMMA) increases arterial pressure, vascular resistance, and systemic pressor indicators i.e. vasoconstrictive responses to infused angiotensin II, norepinephrine, and arginine vasopressin (25–28). The increased pressor responsiveness is reversed only by pretreatment with L-Arginine, but not D-Arginine, phentolamine, saralasin, or captopril (29).

Importance of Nitric Oxide

Several vasodilators such as NO, natriuretic peptides (ANP/BNP and CNP), endothelium-derived hyperpolarizing factor (EDHF) and prostacyclin (PGI₂) are redundant mechanisms that collectively contribute to the low vascular resistance of the uterine and placental vascular in normal pregnancy. NO is considered by numerous investigators to play an important, if not an essential, role in pregnancy-related vascular adaptation (1, 22). This premise is supported to a great extent by evidence that NO is released in greater amounts by fetoplacental and uteroplacental endothelium (22, 30, 31) during pregnancy. The level of NO and its second messenger cyclic guanosine monophosphate (cGMP) are substantially elevated during pregnancy (22, 26, 30, 32, 33), especially in the uteroplacental and fetoplacental units (32–37). Moreover, chronic inhibition of NO production induces small for gestational age (SGA) weights and intrauterine fetal growth restriction (IUGR) (28, 38) associated with decreases in fetoplacental blood flow (39). Furthermore, NO production by ovine placenta and endothelial NO synthase (eNOS) protein expression in fetoplacental artery endothelium elevate gradually throughout the third trimester from 70–90% of gestation (110–130 days; term = 147 days), the time of the most dramatic growth rate of the ovine fetus (7, 35). Studies utilizing animal models have demonstrated that prolonged inhibition of NO production during pregnancy causes fetal growth restriction probably by decreasing fetal placenta and/or uterine blood flow (22, 28, 38). These data collectively establish a cause-and-effect relationship between locally produced endothelial derived NO and rises in blood flow to both the placenta and uterus to optimize fetal growth.

Stripping the endothelium or pretreatment with the NOS inhibitor L-NAME has been shown to substantially reduce or abolish the acute flow-induced dilation of isolated vessels. Moreover, NO inhibition of flow-mediated vasodilation can be reversed by the NOS substrate L-arginine, demonstrating substrate specificity of this inhibitor for the eNOS enzyme (13, 40). Considering first on the placental circulation, a major focal point of this review, elevations in fetoplacental blood flow/shear stress also increase NO production, eNOS expression, and phosphorylation of eNOS via posttranslational modifications in ovine fetoplacental arterial endothelial (OFPAE) cells. In our recent papers on this particular topic (9–11), we have focused primarily on eNOS because it is the only NOS family isoform identified in the endothelium of ovine fetoplacental vascular bed (7, 35). Additional projects contrasting the unique developmental responses of the uterine vascular bed in pregnancy are in progress.

Experimental models to induce shear stress on endothelial cells in vitro

In vivo studies of shear stress can well demonstrate the dilatory effects of varying magnitudes of shear stress using noninvasive imaging techniques. However, to draw more definitive conclusions about shear stress responses from these results that can go beyond the individual observations, shear stress must be accurately quantified. In vivo measurements of shear stress during each cardiac cycle in a pulsatile fashion however, are very technically difficult, therefore measurements of average or mean physiological flow rates and diameters are obtained. From these values, shear stress values are typically calculated based on assumed Newtonian properties of the blood but ignoring blood flow pulsatility. Although calculating shear stress in this way introduces some error, which may obscure important findings, it must be recognized that this is indeed the first step needed to define what is “physiologically relevant”.

To address the need to study cells in well-controlled shear stress environments, in vitro systems have been created for endothelia cell culture and have been invaluable for showing the impact of shear stress on endothelial cell signaling events, such as those related to NO. The most prevalent systems for exposing cells to defined shear stress are parallel plate and cone-and-plate apparati (41, 42). In both systems, endothelial cells that are cultured in static or shear conditions are treated with constant controlled levels of shear stress in constrained flow environments. Chronic endothelial cell adaptation to shear stress can also be studied with these systems. In this review we also describe the use of a CELLMAX artificial capillary module system for shear stress experiments, utilized for long-term endothelial cell culture and chronic shear stress adaptation studies (9–11, 43). This system maintains a flow environment in which endothelial cells are exposed to physiologically pulsatile shear stresses, and in which one can study the cellular responses to changing levels of shear stress in the absence and presence of placental-derived hormones and growth factors.

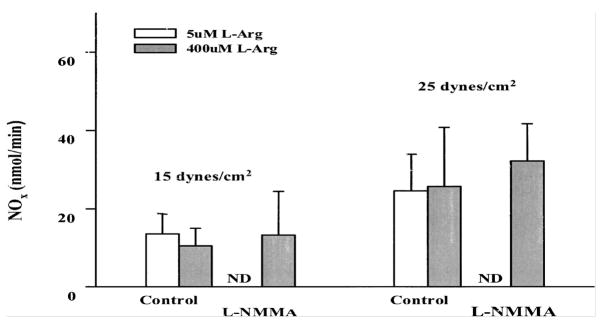
In in vitro experimental models using cell culture methods to expose endothelial cells to shear stress, steady shear stress has been shown to upregulate eNOS mRNA levels in bovine aortic endothelial cells (BAECs) and human umbilical vein endothelial cells (HUVECs) (44, 45) and ovine placental artery endothelial cells (9–11). Steady laminar shear stress applied to cells grown in static culture conditions induces a biphasic production of NO in cultured HUVECs (8). Although pulsatile laminar flow also was found to stimulate eNOS activity (46, 47), both eNOS mRNA and protein expression have been shown to be increased in an endothelial cell and smooth muscle cell cocultured pulsatile system (46). We recently were the first to show in ovine placental artery endothelial cells that were adapted to chronic flow conditions (1–2 weeks), the dynamic time course of NO production related to the time-dependent changes in eNOS expression during various levels of pulsatile shear stress. (9–11). We then determined that this NO production was both de novo and had a sterio-specific requirement for the eNOS substrate L-Arginine (Figure 1).

Figure 1.

Inhibition of acute NOx response of ovine fetal placental artery endothelial cells to shear stress by L-NMMA. Endothelial cells were grown and reached confluence at 3 dynes/cm². Before shear stresses were elevated to either 15 or 25 dynes/cm², the endothelial cells were pretreated with 50 uM of the NOS inhibitor L-NMMA for 30 min in the presence of either 5 uM or 400 uM L-arginine. Acute NOx production (at 20 min) were measured. ND=nondetectable levels. Data are means ± SE, n=4/group. (From Li et al 2003, 2005 with permission).

Although these in vitro systems can well mimic the shear stress caused by blood flow, understanding the true complexity of the complete picture of forces endothelial cells experience in vivo within the tunica intima is important for designing experiments and further interpreting the true significance of results. This latter somewhat ambitious goal may be achieved through sophisticated and novel mathematical and computer models for predicting shear forces in these important vascular beds. Creating these models requires a more comprehensive understanding of the coupled interaction between blood flow hemodynamics and vascular tissue mechanics as well as the vascular tissue response to hemodynamic forces.

Hemodynamic forces acting on the vascular wall

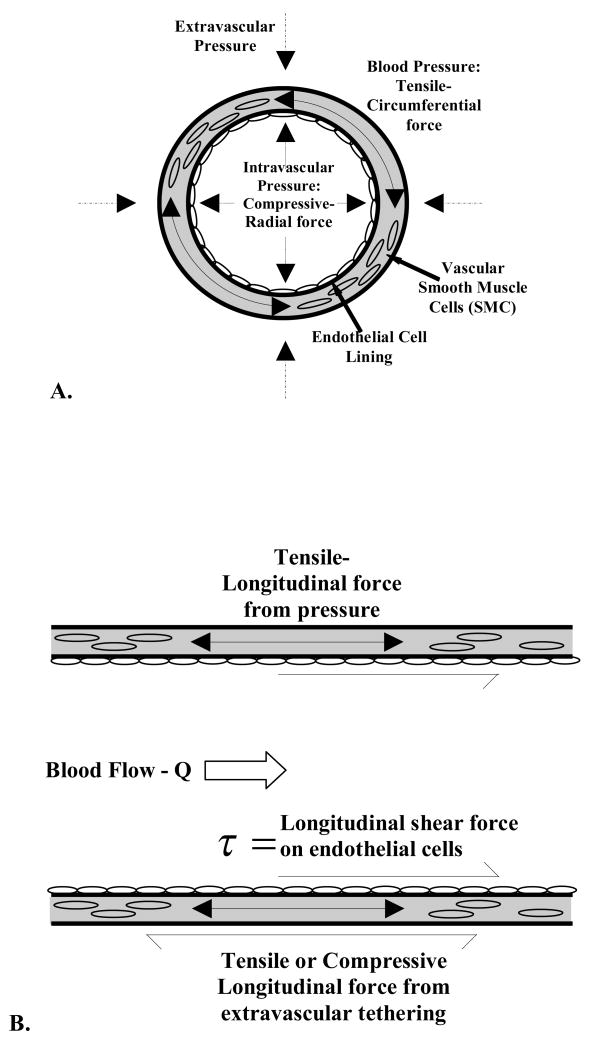
Blood pressure exerts compressive-radial and tensile-circumferential forces on all cell types in the vasculature wall as well as extracellular matrix proteins (Figure 2-A). Blood flow exerts longitudinal shearing forces on the cells of the blood vessel tunica intima and thus, the endothelial cells. Smooth muscle cells within the tunica media of the vessel are subjected to tensile forces in the longitudinal direction due to blood pressure and transference of shear forces on the endothelial cells (Figure 2-B). Therefore the smooth muscle cells are not physiologically exposed to shear stresses though they do not respond to shear stress in culture environment (48).

Figure 2.

Hemodynamic and extra-vascular forces on blood vessels, shown in the A) radial cross-section orientation and B) longitudinal orientation.

Since vessel circumference is typically larger than wall thickness, the effects of circumferential, tensile stresses (extensional forces per unit area) on cell types, especially smooth muscle cells, are the subject of more substantial research than radial, compressive stresses. The result of net pressure forces (i.e., intravascular minus extravascular pressure, or transmural pressure) is that blood vessels expand circumferentially, and in some cases we have seen longitudinally also, with the pulse pressure of a cardiac cycle. However, each of these types of forces and the strain they induce on a blood vessel can be partly counterbalanced by tethering of vascular tissue to surrounding structures. This tethering is best described as connective tissue surrounding and attached to the tunica adventitia of the vessel, clearly providing a support framework that reduces the amount of vessel strain.

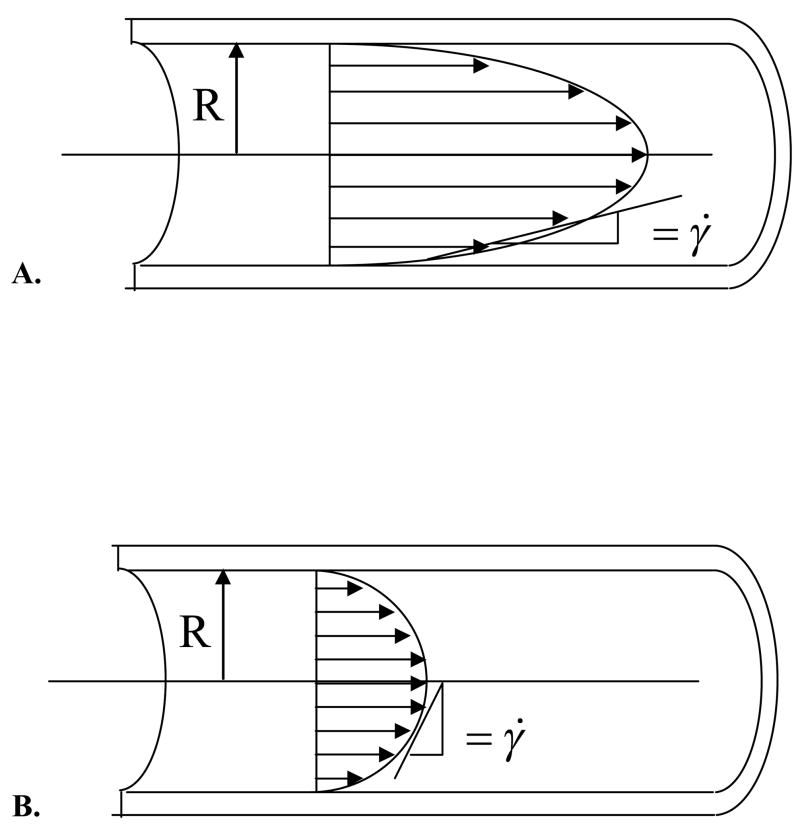
The longitudinal shearing force caused by the flow of blood – a viscous liquid – on the vessel wall results in a shear stress (force per unit area) on the cells lining the vessel lumen that is designated by τ (Fig 2B). The magnitude of this shear stress depends on the inner diameter of the vessel, blood flow rate, viscosity of the blood and pulsatility of blood flow. Under certain idealized conditions, blood flow can be considered to move in concentric layers, or lamina, such that all molecules (and cells) in one lamina are all moving at the same velocity and do not cross over into other lamina (Fig. 3). The velocity is at maximum in the central core and, in each lamina that is successively closer to the wall, the velocity is lower. Because the wall is not moving, the lamina of molecules at the wall may also be considered to not be moving. This is called the “no-slip” condition. The slope of the change in velocity from the wall to the center of the vessel is called the shear rate, signified by the symbol σ̇, and in part determines the frictional forces between the wall and the moving fluid. (49). The distribution and spatial dependence of fluid velocities can be well represented by a velocity profile, diagrammed in Figure 3.

Figure 3.

Velocity profiles of parabolic flow in cases of A) higher and B) lower shear rates. Because shear rate is essentially the rate of fluid deformation, it has units of 1/second.

Current calculations of in vivo shear stress

Most in vitro and ex vivo experiment models have studied shear stress by measuring mean flow rates and arterial inner diameters, and making several important assumptions. By assuming blood exhibits Newtonian fluid behavior and laminar flow, wall shear stress (τ) can be quantified by multiplying shear rate (σ̇) by the fluid viscosity (μ) in which shear rate and shear stress are linearly proportional (i.e., a Newtonian fluid) using:

$$\tau =\stackrel{.}{\gamma }·\mu$$ (Equation 1)

Combining this with the assumption that blood vessels are long, straight, rigid tubes, and other important criteria are met such that the velocity profile in the lumen is parabolic (as seen in Fig. 2), then the fluid shear rate (Equation 2) and vessel wall shear stress (Equation 3) can be written as:

$$\stackrel{.}{\gamma }=\frac{4·Q}{\pi ·R^3}$$ (Equation 2)

$$\tau =\frac{4·Q·\mu }{\pi ·R^3}$$ (Equation 3)

where Q is the flow rate, μ is the viscosity of the blood and R is the internal radius of the vessel. When standard calculations are made using these assumptions, it is called Poiseiulle flow analysis and is the most commonly used estimate of in vivo shear stress.

Observing the breakdown of Poiseiulle flow assumptions – the use of computer modeling

Shear stress varies over time

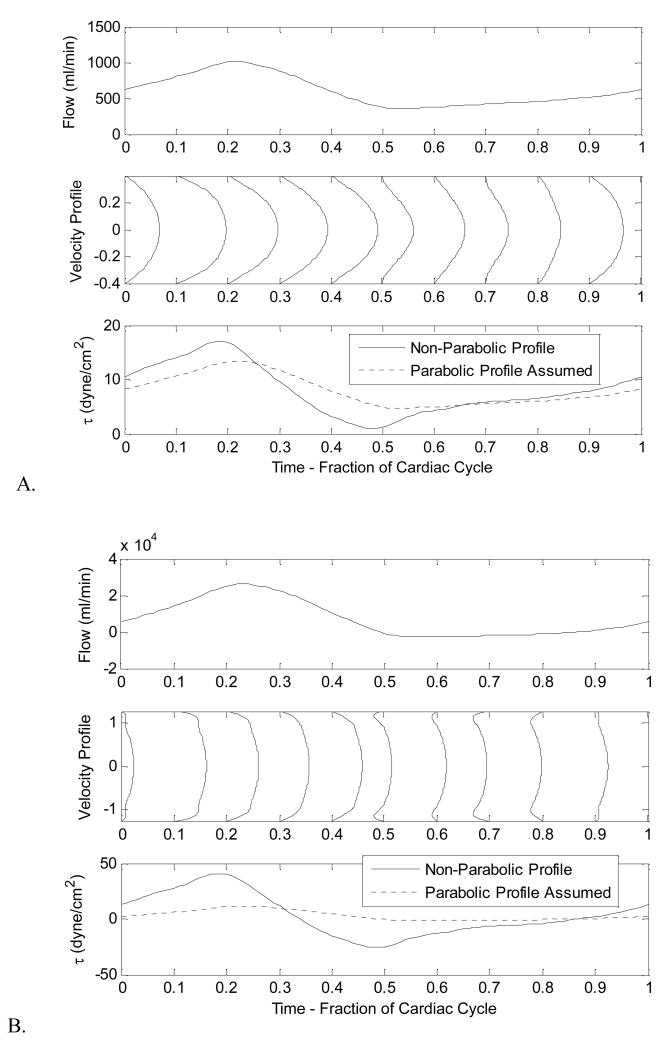
Under physiological conditions, however, especially in large distributing arteries and elastic arteries, blood flow is pulsatile in nature. The dynamic driving pressure from the heart causes blood flow to vary over each individual cardiac cycle. Under these pulsatile conditions, velocity profiles even in long, straight, rigid tubes with a Newtonian fluid are not consistently parabolic. Nevertheless, the equations that govern blood flow under these conditions can be solved for such that the variability in blood flow rate, velocity profile, and wall shear stress that occur over a cardiac cycle can be computed, modeling flow in both small and larger arteries of a cardiovascular network (Fig 4). The graph of wall shear stress contrasts the calculations made allowing for non-parabolic flow (solid line) with calculations of wall shear stress using Equation 3 that assumes parabolic flow and the calculated flow rate (dashed line). Assumptions of parabolic flow attenuate the absolute maximum of shear stress over the entire cardiac cycle. In larger vessels (Fig. 4B), this effect is especially pronounced due to the pulsatility of blood. In smaller diameter arteries (Fig. 4A), where blood pulsation is lessened due to the pulse damping effect of healthy arteries, Poiseiulle assumptions are indeed quite reasonable.

Figure 4.

Variation of flow rate, velocity, profile and, shear stress throughout the cardiac cycle (Systole + Diastole) for A) Smaller (radius = 0.4 cm) and B) Larger diameter arteries, like the aorta (radius = 1.2 cm). Within smaller arteries, the instantaneous velocity profile stays closer to a parabolic shape throughout the cardiac cycle than the larger artery.

Among the various flow types that have been studied in vitro, steady laminar flow-layered, unidirectional flow with no time dependence - has been the most investigated.

Shear stress also varies due to blood behavior

It is clear that inducing shear stress in a pulsatile fashion is an important improvement from steady shear stress to better model in vivo conditions, however many in vitro experimental models use Newtonian fluids to induce shear stress on cultured endothelial cells. However, blood is a non-Newtonian fluid, meaning the shear stress-to-shear rate of strain relationship is not linear and blood viscosity in vivo is not constant throughout the vasculature. Blood is a shear-thinning fluid, behaving with a lower apparent viscosity at high shear rates. In addition, it has a yield stress, meaning that at low enough shear stresses blood flow lamina travel at the same velocity in a fashion analogous a solid mass. Several mathematical formulations have been applied to experimental blood shear strain-shear strain rate data for better approximations of blood viscosity, many of which are reviewed by Neofytou in 2004 (50). The Casson model is an example of a non-linear model of blood viscosity.

$$\tau ={(\sqrt{{\tau }_y}+\sqrt{{\mu }_{\infty }·\stackrel{.}{\gamma }})}^2$$ (Equation 4)

Where, τ_y is the yield stress of the blood, and μ_∞ is the asymptotic viscosity the blood approaches with very high shear rates. Perhaps not surprisingly, an increase in red blood cell concentration, measured by hematocrit levels, also increases blood viscosity. In fact both τ_y and μ_∞ directly depend on the blood hematocrit; the dependence has been approximated with the following empirical equations based on experimental data:

$${\tau }_{\gamma }=80·{(\mathit{Hct}-0.05)}^3$$ (Equation 5)

$${\mu }_{\infty }=1.185e^{(2.463·\mathit{Hct})}$$ (Equation 6)

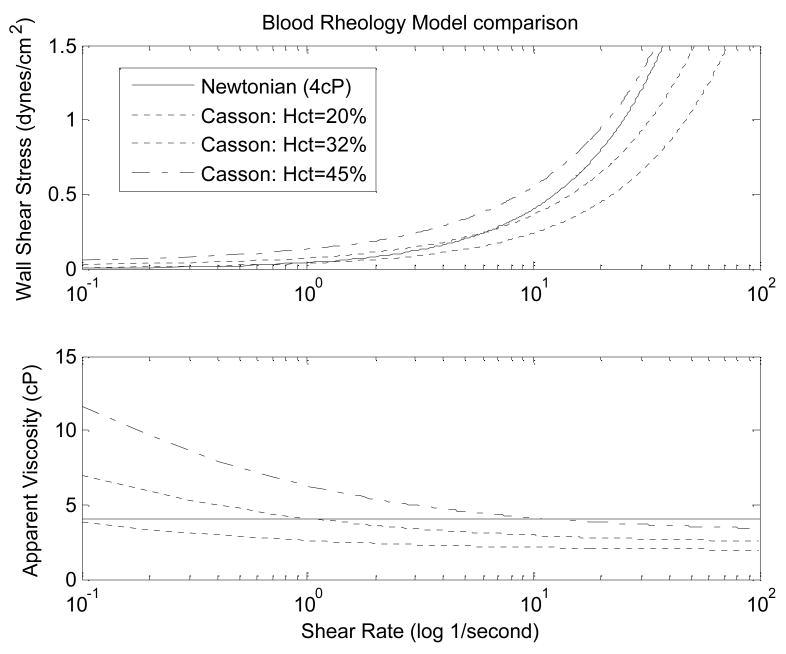
where the hematocrit (Hct) is entered in decimal form, and the units for yield stress and asymptotic viscosity are dynes/cm² and cP, respectively. The relationships between shear stress at the luminal surface (wall shear stress) and shear rate, and apparent viscosity and shear rate for this Hct-dependent Casson model are shown in Figure 5. For comparison, the results for a Newtonian fluid model are also shown.

Figure 5.

Comparison of the Newtonian fluid model of a single constant viscosity (solid) and Casson fluid models of blood hematocrit of 20%, 32%,, and 45%. At normal hematocrit levels of 32–43%, blood viscosity significantly varies from the Newtonian-assumed constant viscosity at shear rates less than 1/second.

The merits and drawbacks of several blood rheology models including this one are well descried in Neofytou’s 2004 review of blood rheology models and will not be reiterated. However, in order to apply this model for accurately determining physiological fluid shear stress, the shear rate and hematocrit of the blood for a given size artery must be known. Flow profiles, like those illustrated in Figure 3, along with accurate in vivo internal diameter measurements are easily obtained for larger arteries using non-invasive ultrasound, and from these shear rate and apparent blood viscosity can be approximated within an individual experimental subject. However, these measurements become increasing difficult for smaller arteries, especially resistance-sized arteries that would be expected to have the greatest difference in shear rate and the greatest difficulty in measuring both velocity and internal diameter.

In addition, this model of blood viscosity is only applicable for blood flow in vessels larger than 1 mm. Below this threshold, which is much larger than a capillary, the arrangement and orientation of individual red blood cells begin to play an influential role in the blood behavior as reviewed Christini and Kassab in 2005(51). Specifically, blood viscosity and hematocrit significantly decrease in vessels smaller than 1 mm diameter due to the Fahraeus-Lindqvist effect. In addition, in even smaller vessels, the mechanical interactions that occur between single red blood cells and the endothelial cell lining significantly impact the forces that blood flow exerts on endothelial cells. For this reason, the understanding gathered about endothelial cell response to shear stress from in vitro experimental models currently being done may mainly be applied to arteries larger than 1 mm. Different in vitro experimental models may need to be developed to mimic shear stress in smaller arteries to learn more about the response of resistance vessels to shear stress and the effects of individual red blood cells on endothelial cell surfaces.

Indeed, as suggested by Figure 5, it is within the capillaries that the Newtonian model of blood is least applicable. The slowed blood flow velocity (and therefore lower shear rate) necessary to allow for nutrient and oxygen exchange causes a significant increase in blood viscosity which is offset by the fall in hematocrit. Using a shear-thinning fluid within the in vitro experimental models to impose shear stress on endothelial cells would be a better model of in vivo conditions, but will add additional variables not addressed by this review (e.g. cell –cell interaction and adhesion markers).

Shear stress varies by location in body

As our equation for wall shear stress suggests (Equation 4), the shear stress in a given vessel will vary with the change of vessel diameter and blood flow rate that occurs at each bifurcation in an arterial tree. Several studies including our own (52, 53) have combined matched experimental data to governing equations that can be used to model and deduce shear stress distribution within these tree networks. However, the fluid flow assumptions of these studies have varied, as have their conclusions regarding shear stress distribution in the body. Although the increase in NO production with greater amounts of flow and shear stress is well known, to our knowledge, no studies have accurately predicted the distribution of shear stress within the vascular tree of the uterine or fetal placental arteries.

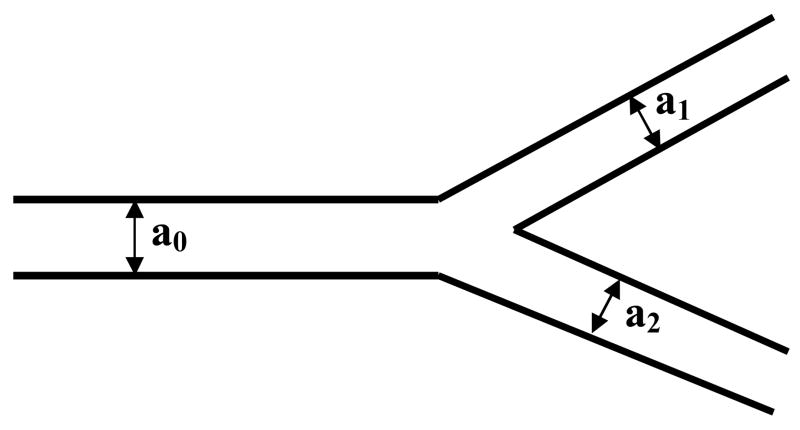
Conflicting predictions of the variance of wall shear stress within the systemic vascular system have been made based on a variety of modeling and data collection techniques. Historically, this dates back to Murray’s Law, originally developed in 1926, which hypothesizes that shear stress is normalized throughout a vascular branching network in order to optimize the metabolic cost of pumping blood within the body against the cost of maintaining that blood volume. This theory, along with blood volume conservation, predicts a bifurcation of vascular networks in which the parent vessel radius raised to the third power is equal to the sum of the daughter vessels radii also cubed, as shown in Equation 7 and Figure 6,

Figure 6.

Vessel branching configurations.

$$a_0^3=a_1^3+a_2^3$$ (Equation 7)

where a₀ is the radius of the parent vessel and a₁ and a₂ are the radii of the subsequent daughter vessels in the bifurcation (and a₁ is defined to be the larger of the two). More complex extensions of this theory incorporate the angle at which the daughter vessels branch from the parent vessel and, the changing of the viscosity of the blood (due to the shear thinning effect described above) to more accurately describe the metabolic cost of pumping blood (50).

Experimental and modeling studies comparing steady and pulsatile wall shear stress values between anatomical locations in a vascular network of an animal or human have shown shear stress to vary quite dramatically (54–56). But modeling of shear stress distribution within a single vascular network based on pulsatile flow wave forms (57) predicts a consistent amount of shear stress in medium and smaller size vessels, only deviating from the Murray’s Law prediction when comparing large arteries, such as the aorta, to smaller arteries, responsible for the resistance of vascular bed. Imaging of the rat renal vascular network has only somewhat shown adherence to Murray’s Law, (58); but structural measurements of the pig coronary tree found the power law relationship between parent and daughter radii to have an exponent closer to two, instead of three predicted by Murray’s Law. These data indicate an increase in average wall shear stress from larger to smaller arteries with each arterial bifurcation (59) and is consistent with our relative predictions of in vivo shear stress in the ovine uterine vascular network within the mesometrium (49, 50).

This difference in conclusions can possibly be explained by recent further theory development and modeling of Murray’s Law by Kassab’s group (60, 61). The maintenance of the vascular tissue of a branching network requires a certain metabolic expenditure. The cost of this maintenance varies with the morphology of the smaller arteries of the network, for example dependent on the ratio of artery wall thickness to outer diameter. Because this morphology, and therefore the metabolic cost and energy dissipation, can vary between different branching structures, the energy expenditure of the pumping heart can still be optimized while the amount of artery wall shear stress increases with each bifurcation. To our knowledge, no studies have gathered the necessary and complex information needed to do this form of accurate analysis on the placental or uterine vascular networks. One of our goals is to accurately and definitively collect matched viscosities, artery diameter, blood flow, and pressure measurements throughout the uterine vascular tree in order to calculate the shear stress distribution. By observing this distribution in healthy pregnancies and those with cardiovascular complications (e.g. preeclampsia and intrauterine growth retardation), we can better identify abnormalities in uterine hemodynamics and possibly verify and localize the deficiency in the NO-mediated dilation response to shear stress.

Conclusion

The use of mathematical modeling to understand mechanical, chemical and physiological phenomenon in the body has allowed us to anticipate the complexities of the cardiovascular system with more precision than any measurement tool could give us. In vitro experimental models of cultured endothelial cells have shown us that shear stress plays a critical role in regulating the production of nitric oxide, and expression of eNOS and thus eventually vascular smooth muscle cell tone. This thereby allows sufficient blood flow and nourishment to the fetus during gestation. But to learn more from these in vitro models, mathematical modeling of hemodynamics and rheology can be used to improve their congruency with in vivo conditions. Understanding the pulsatile nature of blood flow and the resulting transient nature of shear stress imposed on endothelial cells is the first step in this process.

In particular, blood viscosity directly affects the level and nature of shear stress exerted on endothelial cells. From past experimental data and computer modeling to match, we can quantify the non-linear relationship between shear rate and viscosity, and extrapolate to the effects of blood flow on endothelial cells including imaging techniques that capture vessel diameter. To mimic these forces on endothelial cells cultured in vitro, we propose the use of non-Newtonian fluids in addition to pulsatile flow to more accurately induce in vivo shear stresses on cultured endothelial cells.

Estimating the distribution of shear stress in uterine and placental arterial networks would allow in vitro models of cultured endothelial cells to accurately match in vivo conditions and provide a better understanding of the role of NO in the regulation of vascular tone and adaptation. If, as we anticipate, the level of wall shear stress is found to vary between locations in an arterial tree and changes with pregnancy, inferences could be made about the level of shear stress transduction and NO production/eNOS expression by endothelial cells at these locations. With this knowledge in hand, locations of defective mechanisms of vessel dilation could possibly be determined in states of insufficient blood flow to the fetus during gestation.