Adaptive landscapes and protein evolution

Abstract

The principles governing protein evolution under strong selection are important because of the recent history of evolved resistance to insecticides, antibiotics, and vaccines. One experimental approach focuses on studies of mutant proteins and all combinations of mutant sites that could possibly be intermediates in the evolutionary pathway to resistance. In organisms carrying each of the engineered proteins, a measure of protein function or a proxy for fitness is estimated. The correspondence between protein sequence and fitness is widely known as a fitness landscape or adaptive landscape. Here, we examine some empirical fitness landscapes and compare them with simulated landscapes in which the fitnesses are randomly assigned. We find that mutant sites in real proteins show significantly more additivity than those obtained from random simulations. The high degree of additivity is reflected in a summary statistic for adaptive landscapes known as the “roughness,” which for the actual proteins so far examined lies in the smallest 0.5% tail of random landscapes.

Attempts to control agents of infectious disease or their vectors have been frustrated time and again by the evolution of resistance in the targeted proteins. How proteins evolve under strong selection is therefore an important line of inquiry, particularly in regard to whether evolutionary pathways can be reproduced or predicted.

The modern concept of protein evolution as a kind of walk in sequence space seems to have originated with John Maynard Smith (1). Responding to a criticism of the theory of natural selection that the number of possible polypeptide sequences is so large that no functional protein could conceivably have arisen by random mutation, Maynard Smith emphasized that favorable mutations are incorporated into a protein sequentially, not simultaneously. He argued by analogy with a word game called change-one-letter, in which the object at each turn is to change one letter in a word to yield a meaningful different word. His example was sequential changes from WORD to GENE as follows: WORD → WORE → GORE → GONE → GENE. His rationale was that, in Darwinian evolution, each change in a protein sequence should be better (or at least no worse) than the present sequence. The basis of these assumptions, he argued, was “that no sensible alternatives have been suggested and that no evidence exists at the moment to invalidate them.” And so it is today, despite intelligent design and other creationist critiques.

One limitation of the analogy to the change-one-letter game is that it is usually unknown whether altering a particular amino acid in a protein results in a change in fitness that is beneficial, neutral, or deleterious, hence it is unclear which amino acid replacements are allowed. By means of studying a protein whose sequence can be changed experimentally, and choosing a proxy measure of fitness (such as catalytic activity, protein stability, or drug resistance), the change-one-letter analogy can be converted into an experimental program for studying the pathways of protein evolution (2–7). In most such studies, the number of amino sites allowed to change is deliberately chosen to be relatively small to keep the number of possible combinations of changed sites within the realm of what current technology allows.

Here, we summarize results from several studies that have followed this experimental program (2, 5, 7) and compare the results with expectations based on computer simulations in which the fitness of each combination of mutant sites is assigned at random. We find that, in each case, mutant combinations in actual proteins show significantly more additive effects than would be expected by chance. These results are discussed in the wider context of fitness landscapes in protein space.

The Roads Not Taken

For every realized evolutionary path in sequence space there are other roads not taken. General discussions of evolutionary pathways began ≈80 years ago in the work of Haldane (8) and Wright (9). Wright’s article is far better known than Haldane’s, probably because Wright’s had been written in response to a specific request for a short piece describing his mathematical evolutionary theories for an audience of nonspecialists (10). The general idea is that points in a multidimensional space consisting of gene combinations (appropriate for individuals) or allele frequencies (appropriate for populations) is projected onto two dimensions, and a third dimension representing the fitness of each genotype (or the average fitness of each population) is added. Because the simplest models of natural selection result in increasing fitness (11), evolution can be thought of as a sort of walk on a fitness landscape, which may be smooth with one highest fitness peak or rough with multiple submaximal fitness peaks separated by valleys of lower fitness.

Wright’s diagram (9) showed a surface with two local fitness maxima. It illustrated how he envisioned evolution to take place under increased mutation or relaxed selection, decreased mutation or intensified selection, weak or strong inbreeding, a change of environment, or in a subdivided population. The diagram was a great success and was picked up and republished in numerous other papers and books (10). The diagram prominently highlighted Wright’s shifting balance theory of evolution (12), in which random genetic drift plays a key role in enabling a population to explore its adaptive landscape notwithstanding peaks and valleys.

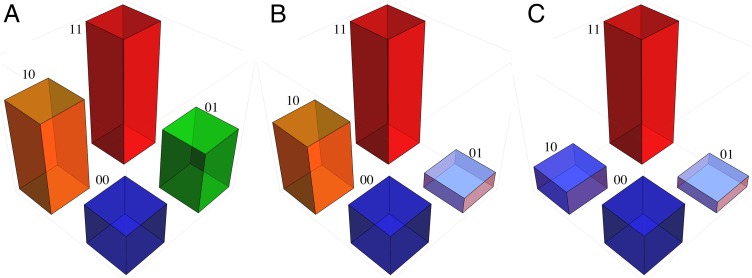
The problem that the shifting balance theory was supposed to solve is depicted in the context of protein evolution in Fig. 1. The height of each cube in Fig. 1 is proportional to the fitness of a haploid organism (or that of a homogeneous population of haploid individuals) whose genome encodes a protein with any of four possible combinations of amino acids at two distinct sites. For simplicity, only two possible amino acids at each site are considered, hence the choices are binary and the combinations can be designated as 00, 10, 01, and 11. The model of protein evolution is essentially that of Maynard Smith (1), which has become known as the strong-selection, weak-mutation model (13). Evolution on the landscape occurs through random mutation, one site at a time, with the probability of fixation of any beneficial amino acid replacement proportional to its selective advantage (14). The genetically heterogeneous populations that exist during the transitions between states are not depicted, on the grounds that, under strong selection and weak mutation, the time to fixation is short relative to the waiting time between favorable mutations.

Fig. 1.

Examples of gene interaction (epistasis) in fitness landscapes. Each cube’s height is proportional to the fitness of organisms having mutant proteins with combinations of two variant amino acids, arbitrarily designated 00, 10, 01, and 11. (A) Magnitude epistasis: One highest fitness peak, two allowed paths to 11. (B) Sign epistasis: One highest fitness peak, one allowed path to 11. (C) Reciprocal sign epistasis: One highest peak (combination 11) and one submaximal peak (00); no paths from 00 to 11.

Suppose the initial population in Fig. 1A is fixed for the all-0 amino acid sequence 00. Mutations to either 10 or 01 are likely to become fixed, and either of these states can mutate to the still more favorable state 11. In Fig. 1B, the evolutionary pathway to 11 through 10 is still accessible, but that through 01 is not, owing to the decrease in fitness between 01 and 00. In Fig. 1C, all pathways to 11 are blocked by the reduced fitness of the intermediates, and the population becomes stranded on the submaximal fitness peak 00. Random genetic drift can alleviate this situation because, with a small fitness differentials and a small enough population size, a population at 00 could, by chance, evolve into one fixed for either 10 or 01, and from either of these states go to 11, thereby achieving the highest fitness state in the landscape. In principle, the shifting balance theory would work in this manner, but there are many difficulties in practice (15). There is a convenient terminology for the types of fitness landscapes shown in Fig. 1: The pattern depicted in A exemplifies magnitude epistasis, that in B exemplifies sign epistasis, and that in C exemplifies reciprocal sign epistasis (16). Except when interpreted as a Wright-type metaphor (9), fitness landscapes with a greater dimensionality than that shown in Fig. 1 cannot be depicted in two dimensions.

Random Fitness Landscapes of Low Dimensionality

A rich literature deals with fitness landscapes in which the fitnesses of genotypes are assigned at random, either with statistical independence or specified patterns and strengths of correlation (17–21). Much but not all of this literature focuses on landscapes of high dimensionality, and it deals with issues such as the fitness ultimately achieved (22), the role of mutation bias (23), noisy fitness mappings (24), genetic robustness (25), and whether the likelihood of becoming stranded at a submaximal fitness peak is reduced at high dimensionality (26). Our present focus is on fitness landscapes of low dimensionality, because these are the types of landscapes presently amenable to experimental investigation.

Fig. 2 shows some results of simulated fitness landscapes whose dimensionality is in the range amenable to experimental study using current techniques. At each site the choices are binary (either 0 or 1). The combination of all zeroes is assigned a fitness of 0. We use malthusian parameters for fitness, which means that the growth rate of a homogeneous population consisting of organisms with a fitness of 0 is Exp[0] = 1 (11). The combination of all ones is assigned a fitness of 1. Every other mutant combination is assigned a fitness at random and independently with a uniform distribution on [0, 1]. This model is similar to the so-called NK model with K = N − 1 (17); however, it differs in that the fitnesses of the all-0 and all-1 states are not random variables. For each of 10,000 randomly assigned fitness landscapes, we assumed an initial population consisting of individuals of the all-0 genotype and let mutations occur to the alternative sites at random, one at a time. If a mutation decreases fitness it is discarded, but if the mutation increases fitness, it is regarded as defining an allowed step in an evolutionary pathway, and a transition to the mutant state takes place. The mutation-selection process was repeated until we had mapped all paths from the all-0 state to any state in which no single-step mutation could increase fitness further. Each allowed path was also assigned a probability of occurrence according to the rule that the probability of fixation of a favorable mutation is proportional to its selective advantage (14).

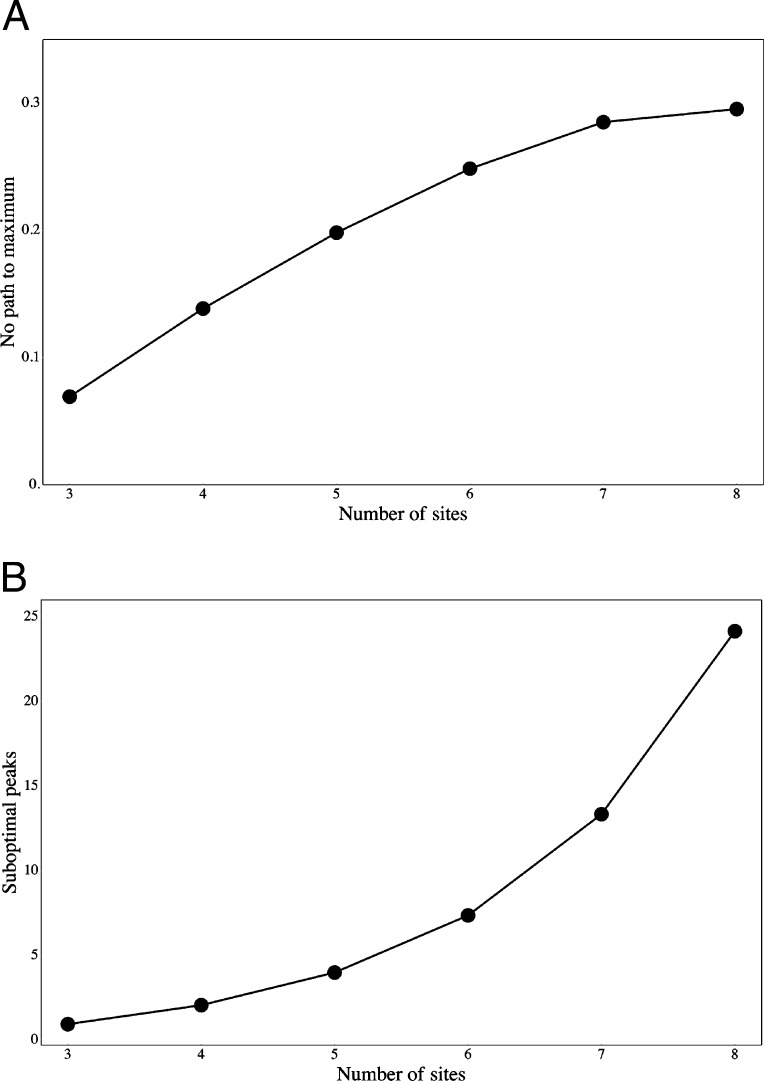
Fig. 2.

Some features of random fitness landscapes. (A) Average proportion of random fitness landscapes with no allowable paths to the maximum. (B) Average number of accessible submaximal fitness peaks among random fitness landscapes. Results of 10,000 simulations of random fitness landscapes are shown. Fitness of the all-0 combination was assigned a value of 0 (malthusian fitness), that of all-1 combination was assigned a value of 1.0, and those of all other combinations were taken from a random uniform distribution on [0, 1].

Fig. 2A shows the average proportion of random landscapes that have no allowable evolutionary path (an allowable path increases fitness at each step) from the all-0 state to the all-1 state, as a function of the number of amino acid sites. The minimum is at three sites, and the number increases almost linearly at first, but then seems to level off at ≈30%. The values for 9–13 sites are similar to those for 8 sites. At the same time, as the number of sites increases (Fig. 2B), the number of submaximal fitness peaks increases, from near 1 at n = 3 sites to ≈25 at n = 8, and the exponential increase continues for 9–13 sites. These are, we must emphasize, submaximal fitness peaks that are accessible through a sequence of single steps of mutation and selection, each step of which increases fitness. In our modification of the NK model, it can be shown from results in ref. 17 that the number of submaximal fitness peaks with n sites is given by 2ⁿ/(n + 1), but some of these submaximal fitness peaks may not be accessible. To revert to the landscape analogy, these submaximal fitness peaks are inaccessible because they are surrounded by a fitness “moat.”

Although the majority of random fitness landscapes of low dimensionality include one or more paths to the maximum (Fig. 2A), the chance of any population reaching the maximum is actually quite bleak. Weighing the probability of each successive fixation by the fitness advantage of the new mutant, the overall probability of reaching the maximum on a fitness landscape with three sites is 0.53 ± 0.38. This average is somewhat misleading because the distribution of probabilities is strongly bimodal: starting from the all-0 state, ≈1/3 of the landscapes have a probability of reaching the maximum of 1.0, and the remaining have an average probability of reaching the maximum of ≈0.30. For four binary sites, the probability of reaching the maximum averages 0.18 ± 0.25, and for five binary sites it is 0.04 ± 0.10. Each of the latter distributions is strongly skewed toward 0. If it was Wright’s intuition that complex interactions between genes result in fitness landscapes that make it difficult for any evolving population to attain the maximum fitness, then his intuition is validated, at least for random landscapes of low dimensionality.

Roughness

As might be expected, random fitness landscapes show considerable variation, and hence it is unclear how one might compare one landscape to the next or any set of landscapes with data from actual proteins. One feature of fitness landscapes that does admit of comparison is the “roughness,” defined as the root mean sum of squares of the residual variation after removing the main additive effects of each amino acid site (3). The main additive effects are obtained by least squares. For two amino acid sites, to take a concrete example, the main additive effects of sites 1 and 2 (ε₁ and ε₂) are obtained by minimizing

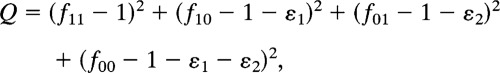where f_ij is the fitness of an organism whose genome encodes a protein with the amino acids i and j (i, j = 0, 1) at the two sites, and f₁₁ = 1. Hence ε₁ = (1/3)(f₀₀ + 2f₁₀ − f₀₁ − 2) and ε₂ = (1/3)(f₀₀ − f₁₀ − 2f₀₁ − 2). The roughness of a landscape is defined as roughness = 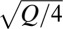. For a generalization to any number of alternative amino acids at any number of sites, see ref. 3. For a fitness landscape in which the main effects of the amino acid replacements are completely additive, the roughness equals 0. For example, if the fitnesses corresponding to the cubes in Fig. 1 are assigned values of 0.25, 0.50, 0.75, and 1.0 according to their height, then the roughness of the landscape in Fig. 1A is 0, that of Fig. 1B is 0.1443, and that of Fig. 1C is 0.2886.

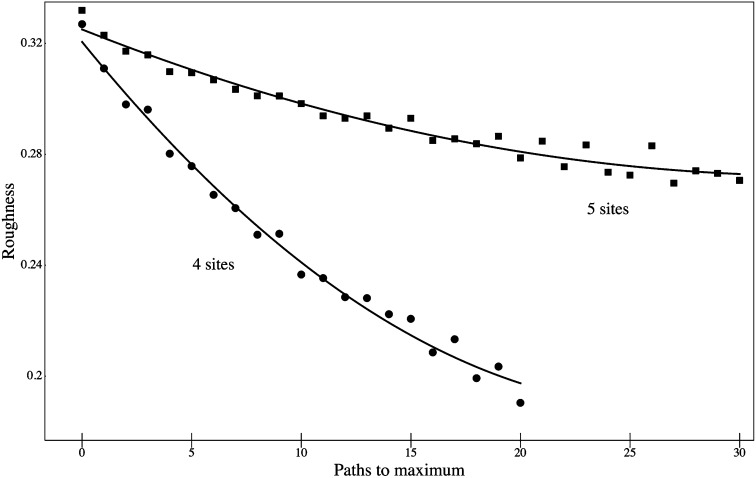
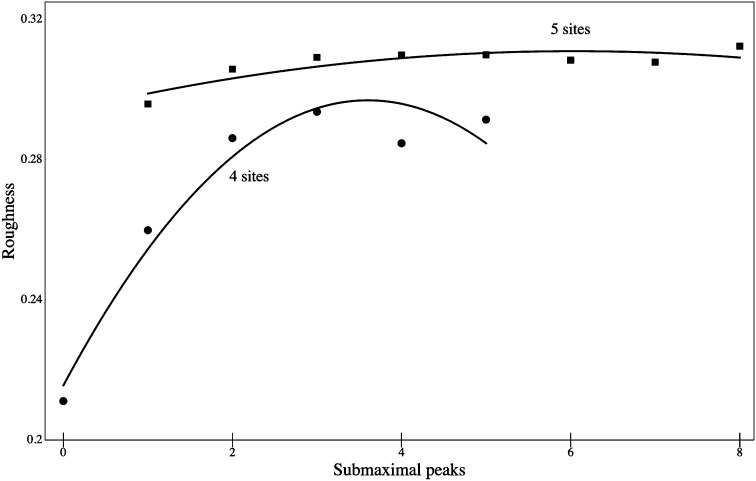
Roughness serves as one convenient metric by which fitness landscapes can be compared. Fig. 3 shows the relation between roughness and number of accessible paths to the maximum for landscapes with four or five binary sites. As might have been expected on intuitive grounds, the average roughness decreases as the number of paths to the maximum increase. Less intuitive are the patterns in Fig. 4, which show the relation between number of accessible submaximal fitness peaks and roughness. For landscapes with more than two such submaximal peaks, there is little or no relation to roughness. Virtually the same patterns emerge from an analysis of 100,000 random landscapes as those shown here for 10,000 landscapes.

Fig. 3.

Roughness of random fitness landscapes with four variant sites (●) or five variant sites (▪), as a function of number of paths to the maximum, among the random landscapes described in the Fig. 2 legend. Curves are quadratic fit by least squares.

Fig. 4.

Roughness of random fitness landscapes with four variant sites (●) or five variant sites (▪), as a function of number of accessible submaximal fitness peaks, among the random landscapes described in the Fig. 2 legend. Curves are quadratic fit by least squares.

Actual Fitness Landscapes

How do real fitness landscapes compare with those in which fitnesses are randomly assigned? Table 1 shows three examples with a small number of binary mutant sites in which all possible mutant combinations have been created and assayed for some measure of protein function or some proxy for fitness. In the case of lysozyme, the assay of protein function is thermal stability (2), for dihydrofolate reductase the fitness proxy is the concentration of pyrimethamine that decreases growth rate by 50% (7), and for TEM β-lactamase (TEM stands for Temoniera, the name of the patient from whom the enzyme was first isolated) the fitness proxy is minimal inhibitory concentration of cefotaxime (5). Lysozyme illustrates a case with three binary sites, dihydrofolate reductase with four binary sites, and TEM β-lactamase with five binary sites (g4205a is a regulatory site, not an amino acid-coding site).

Table 1.

Roughness of empirical fitness landscapes

Protein (Ref.)	Sites	Roughness	Mean	SD	P value
Lysozyme (2)	T40S, I55V, T91S	0.00388	0.0242	0.00653	<0.001
Dihydrofolate reductase (7)	N51I, C59R, S108N, I164L	0.22449	0.34520	0.04767	≈0.005
TEM β-lactamase (5)	g4205a, A42G, E104K, M182T, G238S	0.27667	0.36567	0.02491	≈0.0002

Mean roughness of simulated landscapes is based on random permutations. SD of simulated landscapes is based on random permutations. Approximate P value is for the difference between the observed and simulated mean roughness.

In each case, we estimated the roughness of the actual fitness landscape and compared it with the distribution of the roughness values of 10,000 simulated landscapes obtained by random permutations of all of the fitness values excluding those of the all-0 and all-1 states (3). Approximate P values were estimated based on the deviation between the observed roughness and the simulated mean in units of SD. In all cases the observed roughness is highly significantly less rough than that expected with random permutations. These results are consistent with other studies of empirical fitness landscapes that include more sites (3, 4, 6).

Biologically, the reduced roughness of actual fitness landscapes means that the effects of mutant sites show highly significantly more additivity than those obtained from random simulations. This inference does not diminish the potential importance of interactions among sites (epistasis). Perfect additivity would yield a roughness of 0, whereas the observed value for dihydrofolate reductase is 4.7 SD > 0, and that for TEM β-lactamase is 5.6 SD > 0. The result does, however, suggest that reciprocal sign epitasis, in which individually deleterious mutations become beneficial when combined (6, 16), is not pervasive in the handful of examples that have thus far been examined in detail.

A Tail of Random Landscapes

The significant additivity of actual fitness landscapes prompts another look at the seemingly bleak prospect of an evolving population attaining the highest fitness peak in a random landscape. It suggests that comparison with random landscapes is untenable, and that one should instead examine only the tail end of the roughness distribution of random landscapes in which the sites in the simulated landscapes are more additive than those in the distribution as a whole. Because the largest P value in Table 1 is ≈0.5%, we examined only those 500 landscapes comprising the least rough 0.5% of the roughness distribution among 100,000 random and uncorrelated fitness landscapes. The results were quite different from those described earlier. For three, four, and five binary sites, the probability of attaining the maximum was 0.993 ± 0.074, 0.708 ± 0.320, and 0.219 ± 0.225, respectively, and the number of allowable paths to the maximum was 5.96 ± 0.32, 18.6 ± 6.4, and 29.6 ± 21.1, respectively. It therefore appears that the subset of random landscapes showing approximately the levels of additivity as actual molecules would offer a good chance of fixation of the allele with maximum fitness, without the need to invoke random genetic drift, noisy fitnesses, changing environments, or other ad hoc processes. Each of these is an important process in its own right, but may not be essential in exploring fitness landscapes with the levels of additivity actually observed.

Evolutionary Pathways to Higher Fitness

Fitness landscapes with low but nonzero roughness result from sites that show more additivity than expected by chance. They nevertheless show magnitude epistasis, in which the fitness effects of a mutant site in different genetic backgrounds differ in magnitude but not in sign. Many also show sign epistasis, in which a mutant site has opposite effects depending on the genetic background. Although reciprocal sign epistasis, in which individually harmful mutations are favorable in combination, cannot be neglected because it is observed in a few combinations (5, 16), nevertheless it seems not to be pervasive. The major practical implication of landscapes featuring mainly magnitude and sign epistasis is that they constrain the pathways of protein evolution without shutting off pathways to the maximum. In the case of TEM β-lactamase (5), for example, only 18 of 120 theoretically possible evolutionary pathways to highest resistance are allowable (i.e., show increased resistance at each step), and a mere five pathways account for ≈80% of the probability. Likewise for transgenic bacteria carrying the dihydrofolate reductase gene from the malaria parasite (7), in which only 10 of 24 theoretically possible pathways are allowable, and just three pathways account for ≈90% of the probability.

The relatively high probabilities of a small number of pathways means that evolution on low-roughness pathways has a degree of predictability and reproducibility that would not necessarily be expected (27). Experimental studies of fitness landscapes may therefore be informative for processes that have happened, or are happening, in nature. For example, the high-probability evolutionary pathways identified for the evolution of pyrimethamine resistance of the malaria dihydrofolate reductase studied in Escherichia coli coincide exactly with the inferred stepwise acquisition of pyrimethamine resistance in the malaria parasite itself, as inferred from amino acid polymorphisms in extant populations and in vitro studies of the mutant enzymes (7). Such good agreement between studies in transgenic organisms (in this case, organisms in different kingdoms) may not be expected in general, but this particular example offers hope that much of importance can be learned from judicious choice of protein, model organism, and experimental protocol.

Should the Fitness Landscape Be Buried?

The landscape metaphor is continuously alluring, “a powerful quantitative concept in biology” (28). However, its acclaim has been mixed. Wright’s conflation of the landscape for individual fitness with that for population average fitness has led to confusion and controversy. Among the most severe critics is Wright’s biographer (ref. 10, p. 316), who called adaptive landscapes “unintelligible, … meaningless in any precise sense.” Another thoughtful observer has recommended that it “is time to give up the pictorial metaphor of the landscape entirely” (29). Wright himself seemed momentarily to have misgivings. In a 1986 letter to Provine, he says “The object [in 1932] was to give pictorial representations of elementary evolutionary processes, … but sources of confusion in the multidimensional nature of the field as a whole, and the contributions of each locus to the combinations, may have made this attempt a mistake.” But by 1988, in his last published article, appearing 2 months before his death, Wright seems to have changed his mind. He wrote “I think that [Provine] was looking for something more mathematical than was intended … It is assumed that the genotypes are packed, side by side, in a two-dimensional space in such a way that each is surrounded by genotypes that differ by only one gene replacement. Correspondence with geographical continuity is a secondary consideration … It is obvious that this two-dimensional surface of selective values cannot accurately represent relations that are multidimensional both among and within loci. It is useless for mathematical purposes” (30).

Poor Adaptive Landscape

If one may be permitted a metaphor for a metaphor, one could think of the adaptive landscape as a small pack burro that has been loaded with excessive baggage. The mistreated beast has been asked to carry central optimizing principles in population genetics, developmental biology, systems biology, gene regulation, neural dynamics, computer algorithms, protein folding, manufacturing strategy, technology policy, and who knows what else (e.g., refs. 19, 21, and 28). Should the overloaded landscape metaphor, therefore, be abandoned? We think yes and no. The adaptive landscape is a metaphor, nothing more, and like all metaphors and analogies is misleading when pushed too far. Even the change-one-letter game becomes absurd if you start the game with a word such as “syzygy.” It is asking too much of the adaptive landscape metaphor to accommodate limit cycles or changing environments. Wright invented it as nothing more than a visual aid for nonmathematical biologists who were attending the 1932 International Congress of Genetics in Ithaca, New York (10). It should be taken in the spirit in which he intended. Fitness landscapes should not be abandoned, but rather studied in less picturesque but more quantitative ways. An approach using summary statistics such as roughness seems promising, but there may be other characterizations of fitness landscapes that are equally or more informative.