Abstract
Objective
In studies of associations between genetic factors and outcomes where change in phenotype is of interest, proper modeling of the data, particularly the treatment of baseline trait values, is required to draw valid conclusions.
Methods
The authors compared models of blood pressure response to a cold pressor test with and without inclusion of baseline blood pressure as a regressor and evaluate the resultant biases.
Results
Adjustment for baseline presents a potential source of bias for assessment of genotype-phenotype associations. This bias was observed to occur both under the absence of a true effect, as well when a relation between genotype and change in phenotype was simulated. In simulations that incorporated measurement error, estimates were as great as two fold the true parameter values when unmeasured confounding was a factor.
Conclusions
Adjusting for baseline introduces bias in genetic association studies when change in phenotype is the outcome of interest. Model misspecification bias may impact inference and provide one possible source of non-replication of findings in the literature.
Key Words: Cold pressor test, DAG, Vasoconstriction, Bias, Regression
Introduction
Genetic association studies and genome-wide association studies are currently used to assess the genetic contribution to disease initiation and disease progression, response to a pharmacological intervention, and to assess gene by environment interaction [1,2,3]. In these study designs when the trait of interest is dynamic, it is common for the phenotype of interest to be measured at two distinct time points and the outcome to be the change in phenotype over time. A common concern among researchers is the proper modeling of baseline phenotype level in such analyses in order to avoid spurious findings.
Differing statistical analysis approaches for these kind of data have been proposed, and their relative merits vigorously debated, in the statistical and general epidemiologic literature [4,5,6]. While some have suggested that statistical adjustment for baseline trait values is necessary for valid estimation, Glymour and colleagues, using data from a longitudinal study of education and cognitive change among an old age cohort for illustration [7], have shown that adjustment for baseline trait levels may yield biased estimates when the exposure of interest is known to have effects prior to the baseline measurement. In the context of studies of genetic exposures, such effects are expected. The question of how to model such data has not been considered in the context of genetic association studies when change in phenotype is the outcome. Inconsistent analytic approaches are a potential source of discrepant findings in the literature.
In this report, we consider the causal assumptions implicit in a genetic association study of change in some phenotype, and describe the roles of measurement error and baseline trait values. Using the effect of genotype on blood pressure change during stress as a motivating example, we describe situations when adjusting for baseline risk factor levels is inappropriate and demonstrate the applicability of this situation to the problem of assessing genetic effects on changes in phenotype levels over time. Results of a simulation study conducted to assess bias on estimates of the effect are presented, using a range of true gene-phenotype relations and amounts of measurement error. Data from an on-going study of blood pressure response to a cold pressor stress test are used to assess assumptions made during simulations and demonstrate possible bias that can be induced by analytic strategies.
Methods
Causal Model
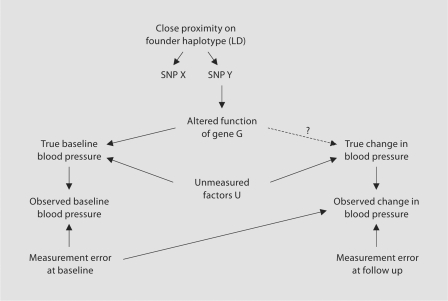
Figure 1 is a causal diagram that outlines the assumptions under study. For the sake of example, blood pressure response to a cold pressor stress test is described. The relationship of interest is that between the function of a gene G and the true change in blood pressure during the test; however, this association can not be addressed directly as true blood pressure is measured with some error and genotype, rather than gene function is the measured exposure. Current large scale genotyping platforms make it efficient to use genotypes at loci across the genome to act as proxies to identify altered functions or expression of genes. Therefore to investigate the relationship between the gene of interest and true change in blood pressure, we assess the association between the genotype at some locus X and the observed change in blood pressure.
Fig. 1.
Causal diagram describing the primary hypotheses of a short term intervention study of gene by environment interaction. Graph assumes the presence of unmeasured factors that affect baseline blood pressure that also effect change in blood pressure during a cold pressor test. Observed blood pressure is measured with error. Function of gene G is altered by SNP Y which is in linkage disequilibrium with SNP X and causes a change in true baseline blood pressure.
The assumption of any linkage disequilibrium mapping or genome-wide association study is that the marker genotyped (shown at locus X in fig. 1) is in sufficiently strong linkage disequilibrium with the true causal variant at the unobserved locus Y to act as a reasonable proxy. This relationship is shown in figure 1 by the close proximity of the two loci on a founder haplotype ‘causing’ the association of the alleles at the two loci in the population. The case of perfect linkage disequilibrium between loci X and Y is identical to that of observing the true causal locus Y directly. Thus for the rest of this paper we assume that locus X and locus Y are in perfect linkage disequilibrium or that locus Y was genotyped directly.
Factors that affect blood pressure through pathways related to vasoconstriction will be associated with both baseline blood pressure and change in blood pressure during the cold pressor test. In the current context, these vasoconstriction-related causes are unmeasured and are indicated as ‘U’ in figure 1 with pathways to the variables corresponding to true baseline blood pressure and true change in blood pressure. The hypothesis to be tested is that the gene of interest, G, is one of these vasoconstriction-related factors. Estimating the effect of G on true change in blood pressure during the cold pressor test is the goal of the study.
While unmeasured factors U have effects on both true baseline blood pressure and true change in blood pressure, there is no direct pathway between these two variables. That is to say, we have assumed that true baseline blood pressure does not have a direct casual effect on the change in blood pressure during the test. This assumption, which is similar to the assumption that the measuring instrument is not affected by a detection limit, may or may not hold true and its effect on estimates will be discussed later.
Blood pressure measurement error may occur due to sources including circadian variation, stress levels and other factors; these were considered so that any observed blood pressure measurement is the summation of the true underlying blood pressure and some measurement error. This is true for measurements made at baseline and during the stress test.
While this model describes the genetic contribution to a cold pressor test, it can be used as a more general model whenever a genetic effect on response to a stimulus, either investigator initiated, environmental or pharmaceutical, is thought to have some relevance to the underlying basal trait. For simulation purposes, the example of the cold pressor test benefits from the availability of data to accurately estimate effect sizes and measurement error.
Using the Model to Detect Bias
Under the condition that there is an association between the observed locus X and true baseline blood pressure, adjusting for observed baseline blood pressure in the analysis will induce bias through measurement error at baseline. Conditioning on observed blood pressure opens the path between the observed locus and observed change in blood pressure, resulting in collider-stratification bias (for a detailed explanation of collider stratification bias, please see [8, 9]). This is true with or without the presence of unmeasured factors U. Conditioning analysis on a common effect of both G and measurement error induces an association between the at-risk allele at the observed locus and measurement error. The measurement error at baseline is inversely associated with the observed change in blood pressure and thus a bias away from the null results.
Even if the trait can be measured without any error, conditioning on observed baseline induces correlation between any unmeasured factors U that are associated with both true baseline blood pressure and true change in blood pressure. This bias can operate either towards or away from the null. If the factors associated with a greater change in blood pressure are also associated with higher baseline levels (i.e. positively associated with both) then the bias will operate towards the null.
While causal diagrams are effective in detecting bias, they have limited power to quantify that bias. In the context of general change models, comparison between estimates from models that include adjustment for baseline with those not doing so has been demonstrated analytically, and depends upon measurement error and the relation between baseline values and the exposure of interest [10]. For this study, we explore the bias empirically through a simulation study; this simulation study demonstrates the amount of bias induced by adjusting for baseline in various circumstances using parameters from an on-going genetic association study.
Simulation
Simulations were performed to estimate the bias resulting from model misspecification. The simulations considered a range of values for the amount of measurement error in blood pressure assessment, the effect of unmeasured factors (U) on other variables in the system, the true effect of gene G on baseline blood pressure, as well as the true effect of the gene on change in blood pressure in mm Hg during the test. Simulation parameters were taken from observed measurements from the HAPI Heart Study to ensure simulation parameters were biologically relevant and are given in table 1. The mean blood pressure in the unexposed was simulated to be normally distributed with a mean of 116 mm Hg and a standard deviation of 11.5 mm Hg. The at-risk allele at the observed locus was assumed to be common (minor allele frequency = 30%) and two effect sizes relating genotype with baseline blood pressure under the additive genetic model were considered: small (1 mm Hg per copy of at-risk allele) and large (5 mm Hg per copy of at-risk allele). The standard deviation of the pre-test blood pressure measurements from the HAPI Heart Study were used to generate small, modest and large measurement error parameters. The median of the standard deviation of the blood pressure measurements was considered as modest error (4.5 mm Hg) and the 10th percentile (1.5 mm Hg) and 90th percentile (7.5 mm Hg) were used as the small and large measurement error parameters. Unmeasured factors were assumed to have small effects (5 mm Hg on baseline and 1 mm Hg on change in blood pressure) and large effects (10 mm Hg on baseline and 2 mm Hg on change in blood pressure). Simulations were run under a true null hypothesis where the effect of gene G on change in blood pressure was set as zero, as well as under the alternative hypothesis, simulated so that gene G had a 1 mm Hg effect on change in blood pressure.
Table 1.
Parameters used in simulation
| Parameter | Distribution | Mean (SD) |
|---|---|---|
| Allele frequency | binomial | 30% |
| Prevalence of U | binomial | 40% |
| Baseline in unexposed | normal | 116 (11.5) |
| Change due to stress in unexposed | normal | 10.5 (6.5) |
| Measurement error | normal | 0 (1.5), 0 (4.5), 0 (7.5) |
| SNP effect on baseline | normal | 1 (0.9), 5 (0.9) |
| Unmeasured Effect on baseline | normal | 5 (0.9), 10 (0.9) |
| Unmeasured Effect on change | normal | 1 (0.9), 2 (0.9) |
| SNP effect on change (alternative hypothesis) | normal | 1 (0.03) |
Simulated data for each scenario were created for 1000 datasets, each with a sample size of 1000 observations. Each observation comprised data for blood pressure at baseline and at the end of follow-up, both measured with error. Change was calculated for each individual as the difference in blood pressure between these two measures. Simple linear regression models of the effect of the genotype on observed change were run on each set of simulated data under the additive genetic model both controlling for and not controlling for observed baseline blood pressure. Simulations were performed using SAS version 9 (SAS Institute Inc., Cary, N.C., USA).
HAPI Heart Study
The HAPI Heart Study was begun in 2002 to study the genetic causes of cardiovascular disease. The study enrolled 868 individuals from the Old Order Amish community in Lancaster County, Pennsylvania and performed short term interventions to study gene by environment interactions [3]. In this paper we consider the cold pressor stress test. By artificially inducing sympathetic activation [11, 12], this intervention helps to identify genes that interact with vasoconstriction to modify blood pressure [13, 14]. The degree and maintenance of the blood pressure response to the cold pressor test is associated with cardiovascular disease [15] and hypertension [16, 17].
As part of the cold pressor test the individual was seated and asked to place his or her right hand and wrist up to the ulnar styloid into an ice water bath for 2.5 min. Blood pressure was measured repeatedly during the test (at 0, 1, 2, 3, 4, 5, 7.5, 10, 15, and 20 min) with use of a fitted automated blood pressure cuff. Baseline blood pressure measurements were taken prior to the test with the subject semi-reclined in a temperature controlled room (22°C) the morning following a 10-hour fast. Pre-test measurements were taken at 1-min intervals for up to 10-min until the individual's blood pressure stabilized. This approach, i.e. waiting for stabilization of blood pressure, acts to minimize measurement error. Multiple pre-test measurements also allowed for excellent estimation of the variance in blood pressure measurements in a clinical setting and thus provided high quality parameters of measurement error for our simulations.
Each participant in the HAPI Heart Study was genotyped with the use of the Affymetrix GeneChip® Human Mapping 500K Array Set (Affymetrix, Santa Clara, Calif., USA). To evaluate the effect of simulation results in an applied setting, genotype data for loci in an area of chromosome 2q previously shown to exhibit evidence for linkage [18] were identified. The 4,111 loci under the linkage peak with a minor allele frequency >5% were assessed for association with baseline blood pressure and their relationship with reactivity to the cold pressor test was estimated both accounting for and ignoring baseline blood pressure levels.
Results
Bias Is Induced by Adjusting for Baseline
Table 2 shows the simulation results illustrating the bias induced through measurement error when adjusting for observed baseline under the null hypothesis, i.e. the true effect on change in blood pressure = 0. One can see that not adjusting for baseline returns an unbiased estimate of the effect in all situations. Adjusting for baseline induces a bias and this bias increases with the strength of association between the observed locus and baseline blood pressure and with increasing measurement error.
Table 2.
Mean (standard error) of estimates of the effect of the observed locus on observed change in blood pressure (in mm Hg) under the null hypothesis (i.e. true effect = 0.0), no unmeasured confounding, as a function of relation with baseline blood pressure1 and amount of measurement error in blood pressure measurement2
| Not adjusted for baseline | Adjusted for baseline | |
|---|---|---|
| Small SNP association with baseline | ||
| No measurement error | 0.01 (0.01) | 0.01 (0.01) |
| Small measurement error | 0.00 (0.01) | 0.02 (0.01) |
| Medium measurement error | 0.01 (0.01) | 0.14 (0.01) |
| Large measurement error | 0.00 (0.02) | 0.29 (0.02) |
| Large SNP association with baseline | ||
| No measurement error | 0.02 (0.01) | 0.01 (0.01) |
| Small measurement error | 0.01 (0.01) | 0.10 (0.01) |
| Medium measurement error | 0.00 (0.01) | 0.67 (0.01) |
| Large measurement error | −0.01 (0.02) | 1.48 (0.02) |
Small association with baseline reflects 1 mm Hg higher blood pressure with each copy of the at-risk allele. Large reflects 5 mm Hg higher per copy. Standard deviation of measurement error simulated as follows: small = 1.5 mm Hg; medium = 4.5 mm Hg; large = 7.5 mm Hg.
Table 3 summarizes the results from simulations modeling the alternative hypothesis (true effect of observed locus on change in blood pressure = 1.0) allowing for unmeasured factors and when no measurement error is present. Again, not adjusting for observed baseline results in unbiased estimates of the true effect. Adjusting for baseline blood pressure biases the estimates towards the null and this bias is greater as the strength of the association between the observed locus and baseline blood pressure increases and when the effect of unmeasured mechanisms is large.
Table 3.
Mean (standard error) of estimates of the effect of the observed locus on observed change in blood pressure under the alternative hypothesis (i.e. true effect = 1.0)
| Not adjusted for Baseline | Adjusted for baseline | |
|---|---|---|
| Small SNP association with baseline | ||
| No unmeasured mechanisms | 1.00 (0.01) | 1.00 (0.01) |
| Small unmeasured mechanism | 0.99 (0.01) | 0.98 (0.01) |
| Large unmeasured mechanism | 1.02 (0.01) | 0.99 (0.01) |
| Large SNP association with baseline | ||
| No unmeasured mechanisms | 0.98 (0.01) | 0.99 (0.01) |
| Small unmeasured mechanism | 1.00 (0.01) | 0.96 (0.01) |
| Large unmeasured mechanism | 0.99 (0.01) | 0.84 (0.01) |
Adjusting for observed baseline bias estimates towards the null through unmeasured factors in the absence of measurement error.
Small association with baseline reflects 1 mm Hg higher blood pressure with each copy of the at-risk allele. Large reflects 5 mm Hg higher per copy. Unmeasured factors affect baseline blood pressure by 1 mm Hg for small mechanism, 10 mm Hg for large mechanism.
Table 4 gives the results when both large amounts of measurement error and large unmeasured mechanisms are acting simultaneously. As expected, not adjusting for observed baseline will return unbiased estimates. The bias induced by improperly adjusting for baseline is dependent upon the relative effects of measurement error and unmeasured mechanisms.
Table 4.
Mean (standard error) of estimates of the effect of the observed locus on observed change in blood pressure under the null and alternative hypothesis with large amounts of both measurement error and unmeasured mechanisms
| True effect | Not adjusted for baseline | Adjusted for baseline | |
|---|---|---|---|
| Null hypothesis | 0 | −0.01 (0.02) | 1.20 (0.02) |
| Alternative hypothesis | 1 | 0.98 (0.02) | 2.18 (0.02) |
Not adjusting for baseline returns unbiased estimates.
Assessment of Assumptions
The simulations illustrate the bias that is induced by adjusting for observed baseline blood pressure in the analysis under the assumptions reflected in figure 1. In some situations these assumptions may not accurately reflect true causal relations. The three most common violations, particularly in the GWAS scenario, are (1) Locus Y does not alter function of gene G; (2) Locus X is not in linkage disequilibrium with Locus Y, and (3) Gene G is not associated with baseline blood pressure.
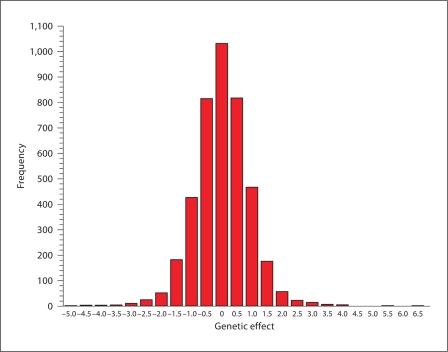
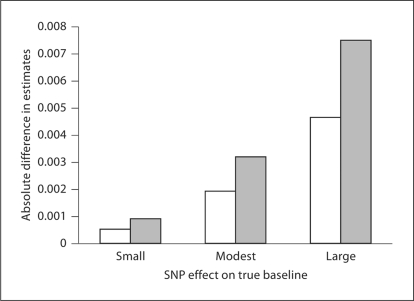
When any of these three violations are applicable, there will be no true association between the genotyped locus and baseline blood pressure. This is common when limited a priori knowledge is used to select the loci genotyped for a study, as is the case with many commercially available large-scale genotyping platforms. Figure 2 shows the distribution of estimates of the association between 4,111 loci in a linkage region on chromosome 2q with baseline blood pressure in participants of the HAPI Heart Study. The distribution appears approximately Gaussian, with the vast majority of SNPs in this chromosomal region displaying little or no association with baseline blood pressure. For such SNPs, the bias induced by adjusting for observed baseline is small, since the relationship between the locus and baseline blood pressure does not exist. If the assumptions in figure 1 are correct, the bias induced by adjusting for observed baseline would be expected to increase as the association with baseline increases, as shown by the simulation results. This is demonstrated in figure 3. The difference between the two estimates, one adjusting for baseline and one not adjusting for baseline, increases as the association with baseline increases as predicted by our simulations. Thus the ‘real world’ data from the HAPI Heart Study is consistent with the conclusions of the simulations based on the causal mechanisms described in figure 1.
Fig. 2.
Distribution of effects of 4,111 loci on baseline blood pressure in the HAPI Heart Study. Loci are from the Affymetrix 500K mapping chip on chromosome 2 in an area previously identified via linkage and have a minor allele frequency greater than 5% in the Amish.
Fig. 3.
Difference between estimates of effect of 4,111 loci on change in blood pressure during a cold pressor test by strength of association with baseline blood pressure. Solid bars are results from diastolic blood pressure and hatched bars are systolic blood pressure.
Discussion
We have explored the causal assumptions implicit in genetic studies of change in phenotype over time and used the cold pressor stress test as an example. We have demonstrated that under the primary null and alternative hypotheses of such studies that adjusting for baseline induces bias via measurement error and unmeasured causal factors. The resulting bias will depend upon the relationships that exist between variables. Conversely, not adjusting for observed baseline measurements returns unbiased estimates of effects under a plausible set of assumptions. Even in the presence of large measurement error and large unmeasured effects, models unadjusted for baseline blood pressure will yield unbiased estimates of the association of interest.
We have considered one set of causal scenarios represented by a single causal diagram. However, these conclusions apply beyond the circumstance examined here. For example, consider a causal relationship between true baseline and true change in phenotype. This may manifest when an upper limit applies to the measurement and that an increase in phenotype would be less for those with already high true baseline (this is analogous to using an instrument with a detection limit or ceiling [7] in measuring the trait of interest). First, it is easy to see in this case that baseline level is on the causal path between gene G and true change and thus controlling for baseline would lead to a biased estimate of the effect [8, 19, 20]. If the relationship between the gene and change in phenotype independent of the effect on baseline was instead the relationship of interest (e.g., the direct effect on blood pressure response to stimuli), controlling for baseline will still induce bias. In that case, both adjustment and non-adjustment for baseline are inadequate and estimates will be unstable by traditional modeling approaches. For separation of direct and indirect effects, a causal hypothesis not directly addressed by this paper, alternative analytic approaches are required, such as marginal structural models or bias correction [10, 21].
In summary, we have demonstrated that adjusting for baseline phenotype levels in genetic association tests will bias the results. It is our hope that this work will encourage other genetic epidemiologists to closely consider causal mechanisms when determining analytic strategy so that unbiased replication across genetic association studies can proceed in the future.
Disclosures
None.
Acknowledgements
This work was supported by research grant U01 HL72515. We thank Dr. Alan R. Shuldiner and the Amish Research Clinic Staff for their excellent work conducting the HAPI Heart Study. This study would not have been possible without the outstanding cooperation and support of the Amish community.
This research was supported in part by the Intramural Research Program of the Eunice Kennedy Shriver National Institute of Child Health and Human Development.
References
- 1.Evans WE, Johnson JA. Pharmacogenomics: the inherited basis for interindividual differences in drug response. Annu Rev Genomics Hum Genet. 2001;2:9–39. doi: 10.1146/annurev.genom.2.1.9. [DOI] [PubMed] [Google Scholar]
- 2.Jaquish CE. The Framingham Heart Study, on its way to becoming the gold standard for Cardiovascular Genetic Epidemiology? BMC Med Genet. 2007;8:63. doi: 10.1186/1471-2350-8-63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Mitchell BD, McArdle PF, Shen H, Rampersaud E, Pollin TI, Bielak LF, Jaquish C, Douglas JA, Roy-Gagnon MH, Sack P, Naglieri R, Hines S, Horenstein RB, Chang YP, Post W, Ryan KA, Brereton NH, Pakyz RE, Sorkin J, Damcott CM, O'Connell JR, Mangano C, Corretti M, Vogel R, Herzog W, Weir MR, Peyser PA, Shuldiner AR. The genetic response to short-term interventions affecting cardiovascular function: rationale and design of the Heredity and Phenotype Intervention (HAPI) Heart Study. Am Heart J. 2008;155:823–828. doi: 10.1016/j.ahj.2008.01.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Senn S. Change from baseline and analysis of covariance revisited. Stat Med. 2006;25:4334–4344. doi: 10.1002/sim.2682. [DOI] [PubMed] [Google Scholar]
- 5.Wainer H. Adjusting for differential base rates: Lord's paradox again. Psychol Bull. 1991;109:147–151. doi: 10.1037/0033-2909.109.1.147. [DOI] [PubMed] [Google Scholar]
- 6.Wright DB. Comparing groups in a before-after design: when t test and ANCOVA produce different results. Br J Educ Psychol. 2006;76:663–675. doi: 10.1348/000709905X52210. [DOI] [PubMed] [Google Scholar]
- 7.Glymour MM, Weuve J, Berkman LF, Kawachi I, Robins JM. When is baseline adjustment useful in analyses of change? An example with education and cognitive change. Am J Epidemiol. 2005;162:267–278. doi: 10.1093/aje/kwi187. [DOI] [PubMed] [Google Scholar]
- 8.Greenland S. Quantifying biases in causal models: classical confounding vs collider-stratification bias. Epidemiology. 2003;14:300–306. [PubMed] [Google Scholar]
- 9.Hernan MA, Hernandez-Diaz S, Robins JM. A structural approach to selection bias. Epidemiology. 2004;15:615–625. doi: 10.1097/01.ede.0000135174.63482.43. [DOI] [PubMed] [Google Scholar]
- 10.Yanez ND, III, Kronmal RA, Shemanski LR. The effects of measurement error in response variables and tests of association of explanatory variables in change models. Stat Med. 1998;17:2597–2606. doi: 10.1002/(sici)1097-0258(19981130)17:22<2597::aid-sim940>3.0.co;2-g. [DOI] [PubMed] [Google Scholar]
- 11.Hines J, Brown GE. A standard stimulant for measuring vasomotor reactions: its application in the study of hypertension. Proc Staff Meet Mayo Clin. 1932;7:332–335. [Google Scholar]
- 12.Hines J, Brown GE. The cold pressor test for measuring the reactibility of the blood pressure: Data concerning 571 normal and hypertensive subjects. Am Heart J. 1936;11:1–9. [Google Scholar]
- 13.Busjahn A, Faulhaber HD, Viken RJ, Rose RJ, Luft FC. Genetic influences on blood pressure with the cold-pressor test: a twin study. J Hypertens. 1996;14:1195–1199. doi: 10.1097/00004872-199610000-00007. [DOI] [PubMed] [Google Scholar]
- 14.Choh AC, Czerwinski SA, Lee M, Demerath EW, Wilson AF, Towne B, Siervogel RM. Quantitative genetic analysis of blood pressure response during the cold pressor test. Am J Hypertens. 2005;18:1211–1217. doi: 10.1016/j.amjhyper.2004.11.041. [DOI] [PubMed] [Google Scholar]
- 15.Keys A, Taylor HL, Blackburn H, Brozek J, Anderson JT, Simonson E. Mortality and coronary heart disease among men studied for 23 years. Arch Intern Med. 1971;128:201–214. doi: 10.1001/archinte.1971.00310200037002. [DOI] [PubMed] [Google Scholar]
- 16.Matthews KA, Katholi CR, McCreath H, Whooley MA, Williams DR, Zhu S, Markovitz JH. Blood pressure reactivity to psychological stress predicts hypertension in the CARDIA study. Circulation. 2004;110:74–78. doi: 10.1161/01.CIR.0000133415.37578.E4. [DOI] [PubMed] [Google Scholar]
- 17.Menkes MS, Matthews KA, Krantz DS, Lundberg U, Mead LA, Qaqish B, Liang KY, Thomas CB, Pearson TA. Cardiovascular reactivity to the cold pressor test as a predictor of hypertension. Hypertension. 1989;14:524–530. doi: 10.1161/01.hyp.14.5.524. [DOI] [PubMed] [Google Scholar]
- 18.Hsueh WC, Mitchell BD, Schneider JL, Wagner MJ, Bell CJ, Nanthakumar E, Shuldiner AR. QTL influencing blood pressure maps to the region of PPH1 on chromosome 2q31–34 in Old Order Amish. Circulation. 2000;101:2810–2816. doi: 10.1161/01.cir.101.24.2810. [DOI] [PubMed] [Google Scholar]
- 19.Greenland S. Basic methods for sensitivity analysis of biases. Int J Epidemiol. 1996;25:1107–1116. [PubMed] [Google Scholar]
- 20.Greenland S, Morgenstern H. Confounding in health research. Annu Rev Public Health. 2001;22:189–212. doi: 10.1146/annurev.publhealth.22.1.189. [DOI] [PubMed] [Google Scholar]
- 21.Robins JM, Hernan MA, Brumback B. Marginal structural models and causal inference in epidemiology. Epidemiology. 2000;11:550–560. doi: 10.1097/00001648-200009000-00011. [DOI] [PubMed] [Google Scholar]